可重复使用运载器(RLV)是指能够自由往返于地球表面与空间轨道之间且可重复使用的多用途飞行器.其再入过程往往伴有参数不确定和外界干扰[1-2]等问题.为了保证飞行器安全稳定地再入飞行,对于再入段轨迹的优化与制导律的设计尤为关键. RLV再入轨迹优化的目标是生成满足各种路径约束(动压、热流密度和过载约束)、状态和控制量约束以及边值约束条件并实现某个最优目标的飞行轨迹,引导飞行器从再入起始点安全到达要求的终端区域内.近年来求解轨迹优化问题运用较为广泛的是伪谱法[3],如Gauss伪谱法、Radua伪谱法等.该方法将最优控制问题离散化为非线性规划(nonlinear programming,NLP)问题,并通过数值方法求解NLP问题来获得最优轨迹.然而伪谱法由于计算量较大、求解时间不确定,实时性难以保证[4],难以应用到RLV的轨迹在线求解中.
与求解NLP问题相比,利用凸优化求解RLV再入轨迹优化问题在求解速度上具有较大的优势,且具备全局收敛性,使得其在RLV轨迹在线求解上的应用成为可能.文献[5]将凸优化方法中的二阶锥规划方法应用于多约束再入轨迹优化问题,并对其全局收敛性进行了证明.然而文章中对飞行速度采用近似化的能量函数进行逼近,轨迹求解的精确性可能因此受到影响.在文献[5]的基础上,文献[6]提出将序列凸规划(sequential convex programming,SCP)方法用于求解带有约束的行星再入轨迹优化问题,该方法具备良好的收敛速度,具有用于实时轨迹规划的潜力.序列凸规划化的主要思想是通过求解序列近似凸子问题,实现子问题的解向原问题的收敛.文献[6]提出的算法使用固定的信赖域约束,然而固定的信赖域可能导致算法失去提升收敛性能的机会,算法收敛速度因此受到约束.得益于其全局收敛性及优秀的收敛性能,序列凸规划方法不似伪谱法那般依赖于初始状态.但序列凸规划求解过程中仍存在初值猜测问题,若初始猜测轨迹与最优轨迹之间偏差较大,则需要较多的迭代次数,算法求解速度也相应下降.此外文中讨论的是终端时间固定的情况,对不确定的终端时间未做分析.文献[7]提出了一种信赖域更新策略的序列凸规划方法,设计了高精度返回快速轨迹优化算法并应用于火箭返回着陆问题中,进一步提高了算法的快速性,然而文章未给出具体的信赖域更新策略.本文提出了一种基于变信赖域策略的序列凸规划算法,在传统的序列凸规划算法的基础上,利用性能指标函数作为每次迭代后的判定条件,设计了信赖域更新策略,提高了算法的收敛性能.此外在序列凸规划求解过程中,利用预测校正算法解决序列凸规划的初值猜测问题,加快算法的收敛速度,与此同时获得了再入终端时间,解决了终端时间不确定问题.本文将所提出算法与SNOPT优化包下的Gauss伪谱法和传统的序列凸规划进行轨迹优化仿真对比,表明所提出算法在收敛性能和计算速度方面有着显著的提升.
考虑实际再入过程中,由于外界干扰导致飞行轨迹大幅度偏离参考轨迹以及在某些紧急情况下要求RLV临时更换着陆场时,飞行器可能无法继续按照原轨迹飞行,此时需要通过轨迹重构提供可行轨迹.文献[8]指出,突发情况下的轨迹重构需要解决两大问题:一是要有快速轨迹优化算法保证可以在线计算重构轨迹;二是需要量化扰动对模型和飞行器约束的影响.文献[9]提出实时轨迹重构策略以解决着陆点变更问题,并采用滚动时域策略以抑制由轨迹求解消耗时间引起的状态量跳变.然而文章由于采用实时轨迹重构替代了制导律的作用,因此轨迹重构是无条件的、不间断的,对于机载计算机负载过大.本文针对RLV再入过程中遭遇的突发事件,在线对轨迹进行重构,并考虑轨迹重构耗时,预测实际轨迹重构初始点,以抑制可能产生的状态量跳变.在重构轨迹求解完成后,为了保证实时性的要求,本文采用基于LQR的制导律对重构轨迹进行跟踪.文中通过仿真将所提出方法与近年来发展迅速的预测校正制导进行对比,表明本文提出的轨迹重构策略在保证安全性、鲁棒性的同时,具备良好的实时性.本文首先对RLV再入轨迹优化问题进行描述,并提出变信赖域序列凸规划轨迹快速求解方法,然后针对RLV再入返回中遭遇的突发事件进行轨迹重构并进行跟踪制导,最后给出仿真结果以及结论.
1 再入轨迹优化问题描述 1.1 动力学模型在RLV再入段,假设飞行器为无动力飞行的质点,考虑地球为旋转椭球时,忽略再入过程中侧力以及地球自转的影响,并取侧滑角为零. RLV再入三自由度运动方程[9]为
| $ \left\{ \begin{array}{l} \dot r = v\sin \gamma ,\\ \dot \theta = \frac{{v\cos \gamma \sin \chi }}{{r\cos \varphi }},\\ \dot \varphi = \frac{{v\cos \gamma \cos \chi }}{r},\\ \dot v = - \frac{D}{m} - g\sin \gamma ,\\ \dot \gamma = \frac{1}{v}\left[ {\frac{{L\cos \sigma }}{m} - \left( {g - \frac{{{v^2}}}{r}} \right)\cos \gamma } \right],\\ \dot \chi = \frac{{L\sin \sigma }}{{mv\cos \gamma }} + \frac{v}{r}\cos \gamma \sin \chi \tan \varphi . \end{array} \right. $ | (1) |
式中:r,θ,φ,v,γ,χ分别为地心距、经度、纬度、飞行速度、航迹角和航向角;σ为倾侧角;m为飞行器质量;g为重力加速度,g=μg/r2,其中μg为引力参数;L为升力,L=qdSCL;D为阻力,D=qdSCD,其中S为RLV气动参考面积,qd为动压,qd=0.5ρv2;ρ为大气密度,
在RLV再入过程中,为了保证安全稳定飞行,飞行器需要严格满足一些约束条件,主要包括边值约束、路径约束和状态量约束.边值约束规定了飞行器状态量
| $ \mathit{\boldsymbol{x}}\left( {{t_0}} \right) = {\mathit{\boldsymbol{x}}_0}, $ | (2) |
| $ \mathit{\boldsymbol{x}}\left( {{t_{\rm{f}}}} \right) = {\mathit{\boldsymbol{x}}_{\rm{f}}}. $ | (3) |
再入过程常见的路径约束包括热流密度约束、动压约束和过载约束, 计算公式分别为
| $ \dot Q = {c_1}\left( \mathit{\boldsymbol{x}} \right) = {k_{\rm{Q}}}{\rho ^{0.5}}{V^{3.15}} \le {{\dot Q}_{\max }}, $ | (4) |
| $ q = {c_2}\left( \mathit{\boldsymbol{x}} \right) = \frac{1}{2}\rho {v^2} \le {q_{\max }}, $ | (5) |
| $ n = {c_3}\left( \mathit{\boldsymbol{x}} \right) = \sqrt {{L^2} + {D^2}} \le {n_{\max }}. $ | (6) |
式中:kQ为与飞行器相关的常数;
此外,受飞行器性能影响,在再入过程中,控制量u=[α, σ]T和状态量x满足的约束为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{u}}_{\min }} \le \mathit{\boldsymbol{u}} \le {\mathit{\boldsymbol{u}}_{\max }},\\ {\mathit{\boldsymbol{x}}_{\min }} \le \mathit{\boldsymbol{x}} \le {\mathit{\boldsymbol{x}}_{\max }}. \end{array} \right. $ | (7) |
综合上述动力学模型和约束条件,考虑以终端状态量和再入过程热流、动压、过载积分函数为指标的目标函数为
| $ {J_1} = \phi \left[ {\mathit{\boldsymbol{x}}\left( {{t_{\rm{f}}}} \right)} \right] + \int_0^{{t_{\rm{f}}}} {G\left( \mathit{\boldsymbol{x}} \right){\rm{d}}t} . $ | (8) |
式中:tf为再入飞行总时间,ϕ[x(tf)]为与终端状态量相关的函数,G(x)为与再入过程热流、动压、过载相关的函数. RLV再入轨迹优化问题P0可描述为:满足条件式(1)~(7),求解目标函数J1最小.
2 变信赖域序列凸规划轨迹求解 2.1 问题的凸化经过上一节的描述,针对问题P0求解可以得到再入最优轨迹.但是问题P0是一个高度非线性的优化问题,其中动力学模型(1)、路径约束式(4)~(6)、以及目标函数式(8)都是非线性、非凸的[5],为了使用凸优化方法对问题进行求解,需要对问题P0中的非凸约束进行凸化处理.
2.1.1 控制量的重新选取在凸化处理过程中,若仅针对现有控制量进行处理,会引入高频抖振并对问题的收敛性产生影响[5],因此需要引入新的控制变量.动力学模型(1)中的控制量为攻角α和倾侧角σ, 其中攻角α由攻角-马赫数剖面确定,剩下需要设计的唯一控制量为倾侧角σ.引入新的辅助控制变量,从而实现控制量从状态量中解耦,令新的控制量为
| $ u' = \dot \sigma , $ | (9) |
则运动方程式(1)可改写为
| $ \mathit{\boldsymbol{\dot x'}} = \mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{x'}}} \right) + \mathit{\boldsymbol{B}}u'. $ | (10) |
式中:
| $ \mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{x'}}} \right) = \left[ {\begin{array}{*{20}{c}} {v\sin \gamma }\\ {\frac{{v\cos \gamma \sin \chi }}{{r\cos \varphi }}}\\ {\frac{{v\cos \gamma \cos \chi }}{r}}\\ { - \frac{D}{m} - g\sin \gamma }\\ {\frac{1}{v}\left[ {\frac{{L\cos \sigma }}{m} - \left( {g - \frac{{{v^2}}}{r}} \right)\cos \gamma } \right]}\\ {\frac{{L\sin \sigma }}{{mv\cos \gamma }} + \frac{v}{r}\cos \gamma \sin \chi \tan \varphi }\\ 0 \end{array}} \right], $ | (11) |
| $ \mathit{\boldsymbol{B}} = {\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0&1 \end{array}} \right]^{\rm{T}}}. $ | (12) |
从式(12)中可以看到控制矩阵B是与状态量x′无关的一个常数矩阵,如此便将u′从x′中完成了解耦.此外,对于新的控制量σ·的约束,有助于加强倾侧角σ的平滑性.经过上述变换,轨迹优化问题P0转变为新控制量下的优化问题P1:满足条件式(2)~(7)、式(10),求解目标函数J1最小.
值得注意的是,对于问题P1若存在最优解,那么该解是问题P0的一个可行解.这是由于问题P1是在问题P0上引入了一个新的辅助控制变量,而问题P0中对于倾侧角σ的控制量约束转化为问题P1中的状态量约束,问题P0的其他状态量约束也包含在问题P1中,由此得到问题P1中的最优解满足问题P0的所有约束,进而得出该解是问题P0的一个可行解.
2.1.2 线性化处理为了使问题能够利用凸优化求解,对问题P1进行凸化处理,对P1中的非凸约束进行线性化处理以将其转换为线性的凸约束.对轨迹优化问题P1中的非线性约束,包括运动方程式(10)、路径约束式(4)~(6)以及目标函数式(8),基于小扰动线性化理论进行线性化处理,在给定状态点x′*(t)处利用一阶泰勒展开式对方程进行逼近,有:
| $ \mathit{\boldsymbol{\dot x'}} \approx \mathit{\boldsymbol{f}}\left( {{{\mathit{\boldsymbol{x'}}}^ * }} \right) + \mathit{\boldsymbol{A}}\left( {{{\mathit{\boldsymbol{x'}}}^ * }} \right)\left( {\mathit{\boldsymbol{x'}} - {{\mathit{\boldsymbol{x'}}}^ * }} \right) + \mathit{\boldsymbol{B}}u', $ | (13) |
| $ c\left( {\mathit{\boldsymbol{x'}}} \right) \approx c\left( {{{\mathit{\boldsymbol{x'}}}^ * }} \right) + \frac{{\partial c\left( {\mathit{\boldsymbol{x'}}} \right)}}{{\partial \mathit{\boldsymbol{x'}}}}\left| {_{\mathit{\boldsymbol{x'}} = {{\mathit{\boldsymbol{x'}}}^ * }}} \right.\left[ {\mathit{\boldsymbol{x'}} - {{\mathit{\boldsymbol{x'}}}^ * }} \right], $ | (14) |
| $ \begin{array}{l} {J_2} \approx \phi \left[ {\mathit{\boldsymbol{x'}}\left( {{t_{\rm{f}}}} \right)} \right] + \int_0^{{t_{\rm{f}}}} {\left[ {G\left( {{{\mathit{\boldsymbol{x'}}}^ * }} \right) + } \right.} \\ \;\;\;\;\;\;\;\left. {\frac{{\partial G\left( {\mathit{\boldsymbol{x'}}} \right)}}{{\partial \mathit{\boldsymbol{x'}}}}\left| {_{\mathit{\boldsymbol{x'}} = {{\mathit{\boldsymbol{x'}}}^ * }}} \right.\left( {\mathit{\boldsymbol{x'}} - {{\mathit{\boldsymbol{x'}}}^ * }} \right)} \right]{\rm{d}}t. \end{array} $ | (15) |
式中A(x′*)为f(x′)在x′*(t)处的雅克比矩阵,
基于泰勒展开式的特点,只有优化变量在参考点附近取值时,线性化的运动方程式和约束式才是对原非线性问题的良好近似.因此为了尽可能地减小逼近误差,保证线性化约束合理逼近原约束,引入信赖域约束:
| $ \left| {\mathit{\boldsymbol{x'}} - {{\mathit{\boldsymbol{x'}}}^ * }} \right| \le \mathit{\boldsymbol{\varepsilon }}, $ | (16) |
式中ε为信赖域的半径.
经过上述线性化处理,新控制量下的轨迹优化问题P1可转化为凸优化问题P2:满足条件式(2)、(3)、(7)、(13)、(14)、(16),求解目标函数J2最小.
2.2 离散化处理由于凸优化问题P2描述的仍是一个连续的最优控制问题,为了求得问题P2的数值解,需要首先对问题进行离散化处理.本文中采用梯形离散化方法[10],将时域均匀划分为N段,产生N+1个节点,每一段的步长为Δt=(tf-t0)/N,终端时间tf在后续序列凸规划初值猜测时由预测校正算法给出.离散点表示为{t0, t1, t2, …, tN},其中ti=ti-1+Δt, i=1, 2, …, N.对应的状态量和控制量表示为{x′0, x′1, x′2, …, x′N},{u′0, u′1, u′2, …, u′N}.则离散化之后的运动方程式(13),路径约束式(14),目标函数式(15)可分别表示为
| $ \begin{array}{l} {\mathit{\boldsymbol{h}}_i} = \mathit{\boldsymbol{x}}_i^\prime - \mathit{\boldsymbol{x}}_{i - 1}^\prime - \frac{{\Delta t}}{2}\left[ {\left( {\mathit{\boldsymbol{A}}_{i - 1}^{k - 1}\mathit{\boldsymbol{x}}_{i - 1}^\prime + \mathit{\boldsymbol{B}}u_{i - 1}^\prime + \mathit{\boldsymbol{f}}_{i - 1}^{k - 1} - } \right.} \right.\\ \;\;\;\;\;\;\left. {\mathit{\boldsymbol{A}}_{i - 1}^{k - 1}\mathit{\boldsymbol{x}}_{i - 1}^{\prime k - 1}} \right) + \left( {\mathit{\boldsymbol{A}}_i^{k - 1}\mathit{\boldsymbol{x}}_i^\prime + \mathit{\boldsymbol{B}}u_i^\prime + \mathit{\boldsymbol{f}}_i^{k - 1} - } \right.\\ \;\;\;\;\;\;\left. {\left. {\mathit{\boldsymbol{A}}_i^{k - 1}\mathit{\boldsymbol{x}}_i^{\prime k - 1}} \right)} \right] = 0, \end{array} $ | (17) |
| $ \begin{array}{l} {\mathit{\boldsymbol{C}}_i} = \mathit{\boldsymbol{c}}\left( {\mathit{\boldsymbol{x}}_i^{\prime k - 1}} \right) + {\mathit{\boldsymbol{c}}^\prime }\left( {\mathit{\boldsymbol{x}}_i^{\prime k - 1}} \right)\left( {\mathit{\boldsymbol{x}}_i^\prime - \mathit{\boldsymbol{x}}_i^{\prime k - 1}} \right) - \left[ {{{\dot Q}_{\max }},} \right.\\ \;\;\;\;\;\;\;{\left. {{q_{\max }},{n_{\max }}} \right]^{\rm{T}}} \le 0, \end{array} $ | (18) |
| $ \begin{array}{l} {J_3} = \phi \left[ {{\mathit{\boldsymbol{x}}^\prime }\left( {{t_{\rm{f}}}} \right)} \right] + \sum\limits_{i = 1}^N {\left[ {G\left( {\mathit{\boldsymbol{x'}}_i^{k - 1}} \right) + } \right.} \\ \;\;\;\;\;\;\;\left. {G\left( {\mathit{\boldsymbol{x}}_i^{\prime k - 1}} \right)\left( {\mathit{\boldsymbol{x}}_i^\prime - \mathit{\boldsymbol{x}}_i^{\prime k - 1}} \right)} \right]\Delta t. \end{array} $ | (19) |
经过离散化处理,凸优化问题P2的最优解可通过求解离散序列凸规划问题P3得到,问题P3可表示为:满足条件式(2)、(3)、(7)、(16)~(18),求解目标函数J3最小. P3的收敛性证明在文献[6]中可以找到,本文不赘述.
2.3 变信赖域序列凸规划 2.3.1 初始轨迹求解针对离散化后的凸优化问题P3,采用序列凸规划算法对其进行求解.为了得到满足线性化近似需求的泰勒展开点,对凸优化问题进行迭代求解,迭代过程中参考点选取为上一次迭代求得的最优解,直到满足收敛约束.在传统的序列凸规划算法中,初始轨迹是基于给定的控制量常值积分得到的[6],如此便存在初值猜测问题.因此本文采用预测校正算法[11]对初始控制量进行求解,引入能量变量
| $ \dot e = \frac{{DV}}{m}. $ | (20) |
考虑终端能量
| $ \left| {z\left( {{\sigma _0}} \right)} \right| = \left| {s\left( {{e_{\rm{f}}}} \right) - {s_{\rm{f}}}} \right| = 0. $ | (21) |
式中待飞航程s(e)=arccos[sin φsin φf+cos φcos φfcos(θf-θ)].由式(1)、(20)可得到以能量为自变量,关于航程、高度和航迹角的运动方程为
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}s}}{{{\rm{d}}e}} = \frac{{ - m\cos \gamma }}{{rD}},\\ \frac{{{\rm{d}}r}}{{{\rm{d}}e}} = \frac{{m\sin \gamma }}{D},\\ \frac{{{\rm{d}}\gamma }}{{{\rm{d}}e}} = \frac{{m\left[ {L\cos \sigma - \left( {g - \frac{{{V^2}}}{r}} \right)\cos \gamma } \right]}}{{D{V^2}}}. \end{array} \right. $ | (22) |
在给定的攻角剖面下,由上一次迭代的倾侧角对式(22)积分得到预测航程差,基于预测航程差利用Gauss-Newton法式(23)对倾侧角进行迭代处理,直到预测航程差满足终端约束,从而得到最终可行的倾侧角幅值.并在侧向上则采用侧向反转逻辑以缩小航向角误差,从而确定倾侧角的符号.最终得到满足再入要求的倾侧角指令:
| $ \sigma _0^{\left( {k + 1} \right)} = \sigma _0^{\left( k \right)} - \frac{{z\left( {\sigma _0^{\left( k \right)}} \right)\left( {\sigma _0^{\left( k \right)} - \sigma _0^{\left( {k - 1} \right)}} \right)}}{{z\left( {\sigma _0^{\left( k \right)}} \right) - z\left( {\sigma _0^{\left( {k - 1} \right)}} \right)}}. $ | (23) |
得到初始猜测轨迹后,在序列凸规划后续迭代过程中,考虑式(16)中的信赖域,信赖域半径ε的大小决定了序列凸规划的收敛性能:若ε过大,则问题P3可能大幅度偏离原问题从而难以收敛;若ε过小,则迭代步长受到限制从而导致算法收敛速度不够快.因此,为了提高序列凸规划的收敛性能,在传统的序列凸规划的基础上提出了变信赖域策略:在每次迭代求解后,对比相邻迭代的实际性能指标函数ψ′与预测性能指标函数ψ,并基于对比结果设计信赖域更新策略.实际性能与预测性能指标函数分别表示为
| $ {\psi ^\prime } = {J^\prime } + {\mu _1}\sum\limits_{i = 1}^{N - 1} {\left\| {\mathit{\boldsymbol{h}}_i^\prime } \right\|} + {\mu _2}\sum\limits_{i = 1}^N {\left\| {\mathit{\boldsymbol{C}}_i^\prime } \right\|} , $ | (24) |
| $ \psi = J + {\mu _1}\sum\limits_{i = 1}^{N - 1} {\left\| {{\mathit{\boldsymbol{h}}_i}} \right\|} + {\mu _2}\sum\limits_{i = 1}^N {\left\| {{\mathit{\boldsymbol{C}}_i}} \right\|} . $ | (25) |
式中μ1、μ2分别为违反运动方程约束和违反路径约束的惩罚因子. J′、hi′、Ci′分别表示为
| $ {J^\prime } = \varphi \left[ {{\mathit{\boldsymbol{x}}^\prime }\left( {{t_{\rm{f}}}} \right)} \right] + \sum\limits_{i = 1}^N G \left( {\mathit{\boldsymbol{x}}_i^{\prime k - 1}} \right)\Delta t, $ | (26) |
| $ \mathit{\boldsymbol{h}}_i^\prime = \mathit{\boldsymbol{x}}_i^{' k} - \mathit{\boldsymbol{x}}{_{i - 1}' ^k} - \frac{{\Delta t}}{2}\left[ {\left( {\mathit{\boldsymbol{B}}u_{i - 1}^\prime + \mathit{\boldsymbol{f}}_{i - 1}^k} \right) + \left( {\mathit{\boldsymbol{Bu}}_i^{' k} + \mathit{\boldsymbol{f}}_i^k} \right)} \right], $ | (27) |
| $ \mathit{\boldsymbol{C}}_i^\prime = \mathit{\boldsymbol{c}}\left( {\mathit{\boldsymbol{x}}_i^{\prime k}} \right) - {\left[ {{{\dot Q}_{\max }},{q_{\max }},{n_{\max }}} \right]^{\rm{T}}}. $ | (28) |
实际性能指标函数给出了实际的离散点处的性能指标,相邻迭代的差值
综合上述初始轨迹求解与信赖域更新策略,得到基于变信赖域序列凸规划的最优轨迹求解步骤如下,整体轨迹优化流程如图 1所示.
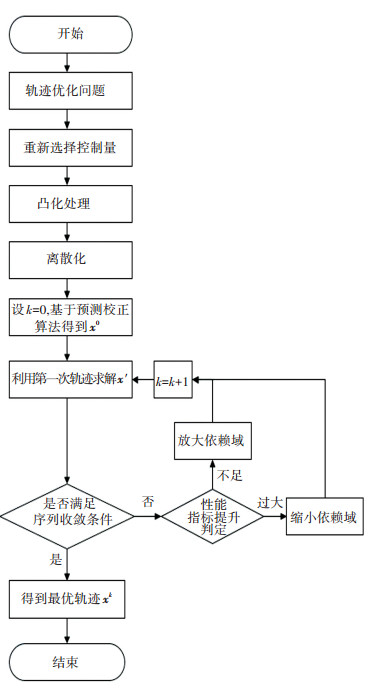
|
图 1 整体轨迹优化流程图 Fig. 1 Overall trajectory optimization flow chart |
步骤1 令k=0,k代表序列凸规划迭代次数,设置初始状态x′(t0)=x′0,基于预测校正算法得到初始轨迹x0.
步骤2 对于k≥1,在第k次迭代中对离散序列凸规划问题P3利用前一次的轨迹xk-1求解得到[x′k, u′k].
步骤3 检查序列收敛条件sup|x′k-x′k-1|≤δ是否满足,其中k≥2, δ为迭代收敛阈值.若条件满足,则转至步骤5,否则转至步骤4.
步骤4 计算预测性能指标函数ψ,和实际性能指标函数ψ′,并对
步骤5 得到最优轨迹xk,迭代停止.
3 突发事件下的轨迹在线重构与跟踪制导在实际再入飞行过程中,在正常飞行状态下,通过制导实现对参考轨迹的跟踪以消除不确定带来的影响;当遭遇突发事件时,则需要在线重构轨迹作为飞行器新的跟踪目标.本节研究了突发事件下再入轨迹快速重构方法,分析突发事件对约束条件及飞行目标的影响,结合上一节的内容实现轨迹在线快速重构,并结合LQR方法实现对重构轨迹的跟踪制导.
3.1 轨迹快速重构针对飞行过程中遇到的突发事件,首先考虑RLV偏离参考轨迹的情况,当外界突发干扰导致飞行器大幅度偏离参考轨迹,产生控制系统无法有效修正的大跟踪偏差,此时针对原定目标点进行轨迹重构.为了减少机载计算机的负荷,引入重构阈值走廊的概念.重构阈值走廊基于飞行走廊HC进行设计.飞行走廊HC下边界HCL为飞行器满足热流、动压以及过载约束的最低飞行高度;HC上边界HCU由拟平衡滑翔约束式(29)得到,对于确定的倾侧角σQEG,拟平衡滑翔约束即为H-V走廊上边界.
| $ \left( {g - \frac{{{V^2}}}{r}} \right)\cos \gamma - \frac{{L\cos {\sigma _{{\rm{QEC}}}}}}{m} \le 0. $ | (29) |
根据飞行走廊确定RLV的轨迹重构条件,设置阈值参数ζ1, ζ2∈[0, 1],飞行器再入重构阈值可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{H_{\max }}\left( v \right) = {H^*}\left( v \right) + {\zeta _1}\left( {{H_{{\rm{CU}}}}\left( v \right) - {H^*}\left( v \right)} \right),}\\ {{H_{\min }}\left( v \right) = {H^*}\left( v \right) - {\zeta _2}\left( {{H^*}\left( v \right) - {H_{{\rm{CL}}}}\left( v \right)} \right).} \end{array}} \right. $ | (30) |
式中H*(v)为离线最优轨迹高度,Hmax(v)为轨迹重构上边界阈值,Hmin(v)为轨迹重构下边界阈值.
当飞行器大幅度偏离参考轨迹,超出重构阈值走廊时,此时基于传统的制导方法已无法消除偏差,需要进行轨迹在线重构求得新的参考,轨迹优化算法在上一节中已经给出.这种情况下,飞行器本身模型以及终端约束都没有发生改变,相较于上一节给出的轨迹优化算法,改变的仅仅是问题的初始条件x0.假设轨迹重构的开始时间为tc,相应的状态量以及控制量为xc和uc,若以xc作为轨迹重构的初始状态,由于轨迹重构需要消耗一定的时间,轨迹重构完成时,实际的状态量与xc将产生偏差.因此,在tc时刻,对Tave后的状态进行预测,Tave为离线轨迹库中轨迹求解的平均时间.
考虑飞行目标终点变更的情况,此时的首要目标是求得飞行器当前可达到的终点区域,以选择可行的飞行目标终点.计算飞行器的可达域实际上是计算可达域的边界[12].求解完整的可达域边界可分为两步:1)求解初始状态下的最大经度θmax、最小经度θmin、最大纬度φmax和最小纬度φmin. 2)将目标函数式(8)中的关于终端状态量的部分选取为经度与纬度的加权组合,即
综合考虑对轨迹的跟踪性能与实时性的需求,本文采用LQR这一较为成熟的制导方法实现轨迹跟踪. LQR需要在制导采样点处进行小扰动线性化处理,得到如式(13)所示的用于求解反馈增益的线性时变系统,而线性化的泰勒展开点则可以从前文中得到的收敛性能较好的离散点中选择.
线性化后的轨迹跟踪制导问题可表示为:求最优控制律
为了验证设计算法的性能,本文以文献[14]中的RLV模型为例,基于MATLAB 2016a环境实现算法的仿真实验. PC机配置为core i5-8500,主频3 GHz,8 GB内存.
仿真基础参数设置:飞行器质量m=104.305 kg;引力参数μg=3.986×1014m3/s2;飞行器面积S=391.22 m2;海平面大气密度ρ0=0.002 38 kg/m3;常值系数β=1.387 5×10-4,kQ=9.44×10-5.再入约束参数设置:
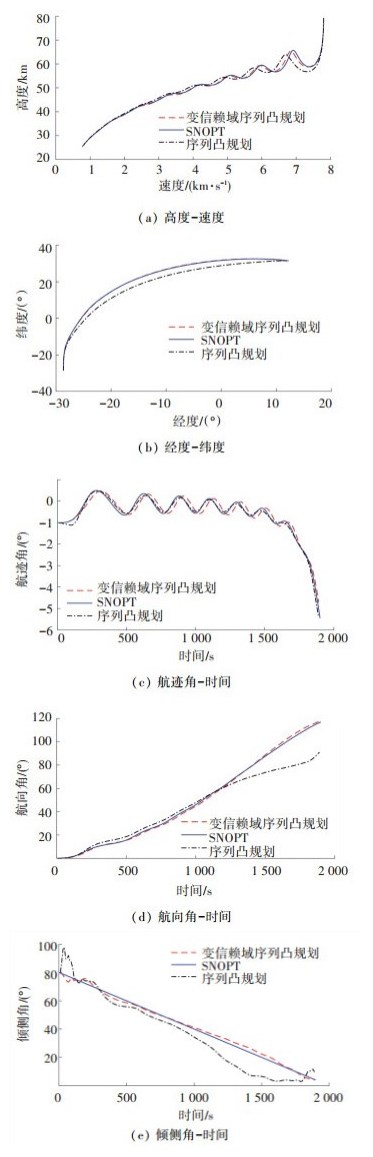
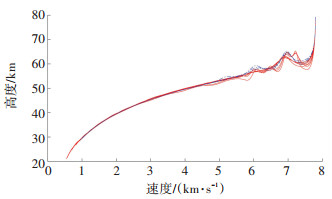
为了验证本文提出的变信赖域序列凸规划算法,进行仿真实验并将结果与传统的序列凸规划算法以及基于非线性规划求解器SNOPT[17]的Gauss伪谱法进行对比.仿真给定初始条件以及终端约束见表 1,考虑终端纬度最大的问题,性能指标函数设定为J=-φ(tf).再入轨迹对比仿真结果如图 2所示. 图 3给出了变信赖域序列凸规划算法与传统序列凸规划收敛情况的对比,图中红线和绿线分别表示传统序列凸规划算法和变信赖域序列凸规划算法的迭代收敛过程.
| 表 1 初始条件和终端约束 Tab. 1 Initial conditions and terminal constraints |
|
图 2 变信赖域序列凸规划与SNOPT和传统序列凸规划仿真结果对比 Fig. 2 Comparison of simulation results of variable trust region SCP with SNOPT and traditional SCP |
|
图 3 变信赖域序列凸规划与传统序列凸规划收敛情况对比 Fig. 3 Comparison of convergence between variable trust region SCP and traditional SCP |
从图 2中可以看出变信赖域序列凸规划、传统的序列凸规划和SNOPT得到的轨迹大体趋势是吻合的.变信赖域序列凸规划由于引入了预测校正初始轨迹以及变信赖域策略,收敛性能优于传统的序列凸规划.从倾侧角曲线可以看出,序列凸规划得到的控制曲线存在着抖动.总体来说,基于SNOPT的伪谱法得到的轨迹依然是三者中优化性能较好的.但是考虑求解时间方面,序列凸规划相较于SNOPT则具有显著的优势.仿真得出采用SNOPT方法的轨迹求解CPU时间为55.067 s,采用SCP方法的轨迹求解CPU时间为11.124 s,采用变信赖域SCP方法的轨迹求解CPU时间为5.892 s.此外,图 3给出了变信赖域SCP与SCP在收敛效率上的对比,图中红色实线代表SCP收敛迭代过程,蓝色点划线代表变信赖域SCP迭代过程,SCP求解迭代7次,变信赖域SCP求解迭代3次.通过上述仿真对比,验证了变信赖域序列凸规划算法在收敛性能和求解速度上的改进.
良好的求解速度以及较好的求解性能使得变信赖域序列凸规划算法具备应用于轨迹在线重构的潜力.分别针对大幅度偏离参考轨迹、飞行目标终点变更的情况进行轨迹重构仿真.
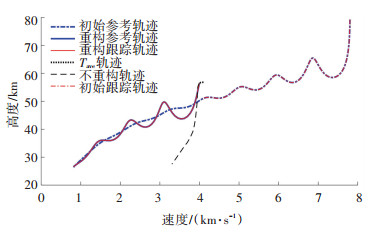
首先针对大幅度偏离参考轨迹情况,考虑沿离线最优轨迹飞行至某一状态点处x=[51 800 m, -7, 26°, 4 017 m/s,-0.17°, 60°]T,给定外界扰动带来的偏差Δh=5 000 m,Δv=100 m/s,采用ζ1=ζ2=0.2的阈值走廊,轨迹重构结果如图 4所示,从图 4可看出在扰动作用下,轨迹超出阈值重构走廊,需要进行轨迹在线重构,基于本文提出的轨迹重构方法,可以在短时间内生成一条满足约束的最优轨迹,求解CPU时间为5.73 s. 图 5给出了基于LQR制导律对初始参考轨迹以及重构轨迹跟踪的结果以及扰动下若对原参考轨迹进行跟踪或者采用预测校正制导律的制导结果.从图 5中可以看出,过大的偏差导致LQR制导律不具备跟踪原参考轨迹的能力,若依然对原参考轨迹进行跟踪,产生的轨迹将逐渐偏离最优轨迹,如图中黑色虚线所示,而重构后的轨迹能很好地满足LQR制导律的跟踪条件,引导飞行器安全再入返回,如图中红色实线所示.此外,由于重构轨迹求解时间预测策略的存在,轨迹重构时初始状态量偏差处于很小的范围内,重构求解平均时间取Tave=6 s.与预测校正制导进行对比,采用预测校正方法得到的轨迹仅仅是一条可行轨迹,而非本文中得到的最优轨迹.在求解制导指令速度方面,预测校正制导每次求解需要经过45次迭代,总用时0.265 s;而LQR制导律每次求解仅需0.04 s.综上所述,基于轨迹重构的LQR制导律在实时性和轨迹性能上都优于预测校正制导.
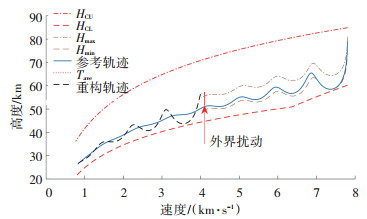
|
图 4 大幅度偏离轨迹下的轨迹重构 Fig. 4 Trajectory reconstruction under large deviation |
|
图 5 大幅度偏离轨迹下的跟踪制导 Fig. 5 Guidance under large deviation |
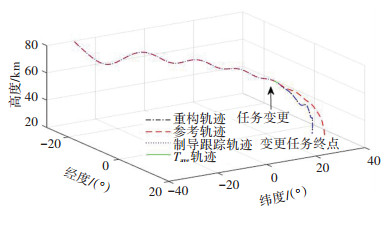
考虑与大幅度偏离参考轨迹情况下相同的状态点处变更目标终点,基于可达域选择新的目标终点[θf, φf]=[10°,30°],三维轨迹重构与LQR跟踪制导结果如图 6所示,重构后的轨迹引导飞行器飞向新的目标终点.
|
图 6 目标终点变更下三维轨迹重构与跟踪制导 Fig. 6 Three-dimensional trajectory reconstruction and guidance after target change |
1) 针对RLV的轨迹再入轨迹重构问题,提出变信赖域序列凸规划算法对再入轨迹在线快速求解.
2) 在传统序列凸规划算法的基础上,采用预测校正算法求解序列凸规划的初始迭代轨迹,以此提升算法的收敛效率,此外为了加快算法收敛速度,设计了信赖域更新策略.
3) 基于提出的轨迹快速求解算法,针对RLV再入过程中可能发生的如大幅度偏离参考轨迹及目标点变更等突发事件,在线重构轨迹并考虑轨迹重构耗时,对实际轨迹重构初始点进行了预测以抑制可能出现的状态量跳变,同时基于LQR制导方法实现对参考轨迹的快速跟踪.
4) 仿真结果表明所提出的轨迹求解算法具备良好的收敛性能以及求解速度,重构轨迹能够有效地引导RLV再入返回.
| [1] |
HALL C E, SHTESSEL Y B. Sliding mode disturbance observer-based control for a reusable launch vehicle[J]. Journal of Guidance Control & Dynamics, 2006, 29(6): 1315. DOI:10.2514/1.20151 |
| [2] |
GAO Z, JIANG B, SHI P, et al. Active fault tolerant control design for reusable launch vehicle using adaptive sliding mode technique[J]. Journal of the Franklin Institute, 2012, 349(4): 1543. DOI:10.1016/j.jfranklin.2011.11.003 |
| [3] |
黄长强, 国海峰, 丁达理. 高超声速滑翔飞行器轨迹优化与制导综述[J]. 宇航学报, 2014, 35(4): 369. HUANG Changqiang, GUO Haifeng, DING Dali. A survey of trajectory optimization and guidance for hypersonic gliding vehicle[J]. Journal of Astronautics, 2014, 35(4): 369. DOI:10.3873/j.issn.10001328.2014.04.001 |
| [4] |
WANG Z, MICHAEL J G. Improved sequential convex programming algorithms for entry trajectory optimization[C]//AIAA Scitech 2019 Forum. San Diego, California: AIAA Press, 2019: 0667
|
| [5] |
LIU X, SHEN Z, PING L. Entry trajectory optimization by second-order cone programming[J]. Journal of Guidance Control and Dynamics, 2015, 39(2): 1. DOI:10.2514/1.G001210 |
| [6] |
WANG Z, GRANT M J. Constrained trajectory optimization for planetary entry via sequential convex programming[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(10): 2603. DOI:10.2514/1.G002150 |
| [7] |
王劲博, 崔乃刚, 郭继峰. 火箭返回着陆问题高精度快速轨迹优化算法[J]. 控制理论与应用, 2018, 35(3): 389. WANG Jinbo, CUI Naigang, GUO Jifeng. High precision rapid trajectory optimization algorithm for launch vehicle landing[J]. Control Theory & Applications, 2018, 35(3): 389. DOI:10.7641/CTA.2017.70730 |
| [8] |
OPPENHEIMER M, DOMAN D, BOLENDER M. A method for estimating control failure effects for aerodynamic vehicle trajectory retargeting[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Providence, Rhode Island: AIAA Press, 2004: 5169. DOI: 10.2514/6.2004-5169
|
| [9] |
TIAN B, FAN W, SU R, et al. Real-time trajectory and attitude coordination control for reusable launch vehicle in reentry phase[J]. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1639. DOI:10.1109/TIE.2014.2341553 |
| [10] |
PING L, LIU X. Autonomous trajectory planning for rendezvous and proximity operations by conic optimization[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(2): 375. DOI:10.2514/1.58436 |
| [11] |
PING L. Entry guidance: a unified method[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 713. DOI:10.2514/1.62605 |
| [12] |
杜昕, 刘会龙. 探月飞船跳跃式再入轨迹可达域分析[J]. 载人航天, 2017, 23(2): 163. DU Xin, LIU Huilong. Analysis of reachable sets of lunar module skip entry trajectory[J]. Manned Spaceflight, 2017, 23(2): 163. DOI:10.16329/j.cnki.zrht.2017.02.004 |
| [13] |
DEAM E B, WEISSHAAR T, SNYDER R, et al. Aeroelastic optimization of a two-dimensional flapping mechanism[C]//18th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Orlando, Florida: AIAA Press, 2010: 2961
|
| [14] |
PING L. Entry guidance and trajectory control for reusable launch vehicle[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(1): 143. DOI:10.2514/2.4008 |
| [15] |
LÖFBERG J. A toolbox for modeling and optimization in MATLAB[C]//2004 IEEE International Conference on Robotics and Automation. New Orleans, LA: IEEE Press, 2004: 8304275
|
| [16] |
STURM J F. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones[J]. Optimization Methods and Software, 1999, 11(1): 625. DOI:10.1080/10556789908805766 |
| [17] |
GILL P E, MURRAY W, SAUNDERS M A, et al. User's guide for SNOPT 7:software for large-scale nonlinear programming[J]. SIAM Rev, 2015, 47: 99. |
 2020, Vol. 52
2020, Vol. 52


