全球卫星导航系统(global navigation satellite system, GNSS)的应用已经渗入到了军用和民用领域[1-2].用户使用GNSS接收机来接收、处理导航卫星发射的电磁信号来确定接收机的位置、速度、时间信息[3-4].信号捕获是接收机使用GNSS导航服务的前提条件,而捕获装置的设计需要考虑捕获性能和资源消耗的平衡.其中捕获性能主要指的是灵敏度、捕获时间,而资源消耗则包括消耗硬件数量和功耗.在不使用任何先验信息的前提下,传统的GNSS接收机信号捕获算法主要有串行捕获算法、基于快速傅立叶变换(fast Fourier transform, FFT)的并行频率捕获算法、基于FFT的并行码相位捕获算法、匹配滤波器(matched filter, MF)捕获算法、PMF-FFT捕获算法[5-7].串行捕获算法在载波频率和码相位两个维度进行搜索,硬件消耗较小,但是需要的搜索时间较长;其他的算法属于并行搜索方法,可以减小搜索时间,但是硬件资源消耗及功耗都会上升.
如果在信号捕获过程中使用卫星星历、接收机位置等先验信息进行辅助,可以提高捕获性能同时降低资源消耗.先验信息可以来自于外部通信网络,如辅助GNSS(assisted-GNSS)技术;同时也可以来自其他导航系统,如惯性导航系统(inertial navigation system, INS). A-GNSS技术通过外部通信网络向接收机提供星历、粗略时间、粗略位置信息来降低搜索区间数量[8-11].而接收机位置误差、动态运动、钟差、钟漂增加了搜索的不确定度.一些研究者研究了INS辅助卫星导航信号捕获的技术,但是都集中在对卫星多普勒频率的估计上,在码相位维度仍然采用串行搜索方式[12-14].如果能够对码相位估计进行辅助则可以进一步降低搜索区间数量.由导航滤波器辅助码相位估计算法可以借鉴矢量跟踪中对码环控制量的计算方法,但是矢量跟踪需要标量跟踪迁入后才能对码相位进行计算,无法应用于捕获阶段[15-17].目前文献中并没有对码相位直接计算算法的原理、算法的近似处理带来的影响、误差源及传播特性进行深入的分析.先验信息同时也可以来自于接收机导航滤波器本身,除了星历、定位结果、测速结果之外,导航滤波器还可以提供准确的接收机钟差和接收机钟漂估计,这些信息都可以提高辅助量的精度,从而减小搜索区间以及捕获引擎功耗,而导航滤波器辅助捕获技术缺少相应的理论研究.因此对GNSS接收机导航滤波器辅助捕获的研究具有较高的理论价值和实际意义.
本文以北斗B1I信号为研究对象,研究了导航滤波器对信号捕获的辅助算法、辅助量误差分析、对捕获性能的提升.本文介绍了研究的背景和目前研究存在的不足之处;推导了通过导航滤波器计算伪码相位、多普勒频率、NH码相位的计算方法;分析了导航滤波器辅助码相位和载波频率计算的误差源及传播特性;简要介绍了信号捕获的性能指标;通过理论分析证明了导航滤波器辅助捕获的优势.
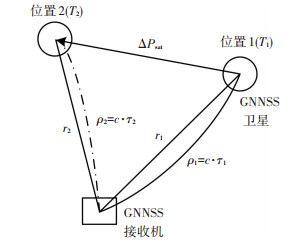
1 导航滤波器辅助捕获 1.1 伪码相位计算如图 1所示,导航卫星在北斗时(Beidou time, BDT)T1时刻发送的信号在北斗时T2时刻被接收机收到,此时卫星已经由位置1运动到了位置2,其运动矢量定义ΔPsat, 而接收机在T2时刻测量的伪距实际上是以T1时刻卫星的位置为基准的. 图 1中其他符号的含义解释如下:r为卫星与接收机之间的几何距离,m;τ为信号传播时间,s;c为光速,m/s;ρ1为T1时刻发送的信号到达接收机所走过的实际路径长度,m;虚线代表“虚拟路径”的概念,即假设卫星在位置2发射的信号走过该路径并在T2时刻到达接收机,虚拟路径的长度为ρ2.引入“虚拟路径”的概念便于对T2时刻导航信号中的伪码相位进行计算,相当于一条辅助线,而实际上来说信号并不存在这个传播路径.下面将通过“虚拟路径”的概念来计算T2时刻码相位的值,计算过程可分为以下4个步骤.
|
图 1 信号发射时间计算示意图 Fig. 1 Diagram of signal transmit time calculation |
步骤1 计算虚拟路径长度.由于信号传播时间τ1很短(小于0.2 s),因此为位置1和位置2之间的距离也很小.相对于卫星与接收机的距离来说,虚拟路径和实际路径几乎是重合的.因此对用户来说,信号在实际路径和虚拟路径上的电离层延迟、对流程延迟,以及两时刻卫星钟差具有高度的相关性.由差分定位理论可知,实际路径和虚拟路径中电离层延迟、对流层延迟以及两个时刻的卫星钟差可以认为是相等的.虚拟路径长度可表示为
| $ {\rho _2} = {r_2} + I + T, $ | (1) |
| $ {r_2} = \left| {{\mathit{\boldsymbol{P}}_{{\rm{sat}}}}\left( {{T_2}} \right) - {\mathit{\boldsymbol{P}}_{{\rm{rec}}}}} \right|. $ | (2) |
式中:ρ2为虚拟路径长度,m;I为电离层延迟,m;T为对流层延迟,m;Psat(T2)为T2时刻卫星在CGCS-2000坐标系内的位置坐标;Prec为T2时刻接收机的位置.
信号在虚拟路径上的传播时间可表示为
| $ {\tau _2} = \frac{{{\rho _2}}}{c}, $ | (3) |
式中τ2的值与真实路径上信号传播时间τ1近似相等,因此τ2可作为τ1的粗略估计值.第2节将讨论此近似过程所带来的码相位计算误差.
步骤2 计算实际传播路径长度. T2时刻的测量伪距实际上是以卫星在T1时刻的位置作为基准来定义的.信号走过的实际路径长度可定义为
| $ {\rho _1} = {r_1} + I + T. $ | (4) |
式中ρ1为实际路径长度,m.卫星在传播时间τ1(τ1≈ τ2)内,由位置1移动到了位置2.定义Δr为
| $ \Delta r = {r_2} - {r_1}. $ | (5) |
式中Δr实际上是卫星运动矢量ΔPsat在单位视距矢量上的投影,即
| $ \Delta r = \Delta {\mathit{\boldsymbol{P}}_{{\rm{sat}}}} \cdot \mathit{\boldsymbol{l}}. $ | (6) |
式中l为由接收机指向卫星的单位视距矢量,卫星的运动矢量可以通过两个时刻卫星位置的差分,得到其计算方法为
| $ \begin{array}{l} \Delta {\mathit{\boldsymbol{P}}_{{\rm{sat}}}} = {\mathit{\boldsymbol{P}}_{{\rm{sat}}}}\left( {{T_2}} \right) - \mathit{\boldsymbol{C}}\left( {{\tau _1}} \right){\mathit{\boldsymbol{P}}_{{\rm{sat}}}}\left( {{T_1}} \right) \approx \\ \;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{P}}_{{\rm{sat}}}}\left( {{T_2}} \right) - \mathit{\boldsymbol{C}}\left( {{\tau _2}} \right){\mathit{\boldsymbol{P}}_{{\rm{sat}}}}\left( {{T_1}} \right), \end{array} $ | (7) |
| $ \mathit{\boldsymbol{C}}\left( {\Delta t} \right) = \left[ {\begin{array}{*{20}{c}} {\cos \left( {{\mathit{\Omega }_{{\rm{ie}}}} \cdot \Delta t} \right)}&{\sin \left( {{\mathit{\Omega }_{{\rm{ie}}}} \cdot \Delta t} \right)}&0\\ { - \sin \left( {{\mathit{\Omega }_{{\rm{ie}}}} \cdot \Delta t} \right)}&{\cos \left( {{\mathit{\Omega }_{{\rm{ie}}}} \cdot \Delta t} \right)}&0\\ 0&0&1 \end{array}} \right]. $ | (8) |
式中Ωie为地球自转角速度,rad/s.对于CGCS-2000坐标系有Ωie=7.292 115 0×10-5 rad/s,由于CGCS-2000坐标系属于旋转坐标系,方程(7)中C(Δt)矩阵的意义在于将T1时刻卫星位置坐标变换到T2时刻的坐标系中.此外由于τ1的值不能预知,因此用τ2进行代替.在通过计算得到Δr后,并且结合式(1)、(4)、(5)可知,实际路径长度的计算方法为
| $ {\rho _1} = {\rho _2} - \Delta r. $ | (9) |
信号在实际路径上的传播时间τ1可由下式进行计算:
| $ {\tau _1} = \frac{{{\rho _1}}}{c}. $ | (10) |
步骤3 计算信号发射时间.由于接收机在定位之后掌握时间信息,而信号传播时间已经在步骤2中计算得到,因此在测量时刻处信号发射时间即为接收机时间修正接收机钟差和卫星钟差后再减去信号传播时延,即
| $ {t_{{\rm{trans}}}} = {t_{{\rm{rec}}}} - \delta {t_{{\rm{rec}}}} + \delta {t_{{\rm{sat}}}} - {\tau _1}. $ | (11) |
式中:ttrans为信号发射时间,s;trec为从接收机时钟上读出的T2时刻对应的接收机时间,s;δtrec为接收机钟差,s;δtsat为卫星钟差,s.需要注意的是,trec-δtrec实际上是将接收机时钟转换为此时刻的北斗时.由于信号的发射时间是以卫星钟作为基准的,因此计算发射时间时还需要将其转换为卫星钟上的时间.继续补偿δtsat这一项将此时刻的北斗时转换为该时刻卫星钟时间.
步骤4 把信号发射时间转换为码相位. 1 ms的发射时间对应一整周的B1I码(码相位取值为0~2 046),而B1I码的起点与卫星钟的整数毫秒时间严格对齐.根据BDS B1I信号发射时间与码相位的关系,可以得到码相位的计算公式为
| $ {\varphi _{{\rm{code}}}}\left( {{T_2}} \right) = \left( {{t_{{\rm{trans}}}} \cdot 1000 - \left[ {{t_{{\rm{trans}}}} \cdot 1000} \right]} \right) \cdot {l_{{\rm{code}}}}. $ | (12) |
式中:φcode(T2)为T2观测时刻码相位的值,chip;lcode为码长,chip,对B1I信号来说是2 046;[·]为取整函数; ttrans·1 000实质上将信号发射时间的单位由s转换为ms.
1.2 载波多普勒计算由导航滤波器计算多普勒频率的方法为
| $ {f_{\rm{d}}} = \frac{{\left[ {{\mathit{\boldsymbol{V}}_{{\rm{rec}}}} - {\mathit{\boldsymbol{V}}_{{\rm{sat}}}}\left( {{T_2}} \right)} \right] \cdot l}}{\lambda } - {\rm{ \mathsf{ δ} }}{f_{{\rm{rec}}}} + {\rm{ \mathsf{ δ} }}{f_{{\rm{sat}}}}, $ | (13) |
式中:Vsat为T2时刻卫星的速度,m/s;Vrec为T2时刻接收机的速度,m/s;δfrec为接收机时钟漂移,Hz;δfsat为卫星时钟漂移,Hz;λ为B1I信号载波的波长,m.由于卫星上采用了高稳定度的原子钟,卫星时钟漂移的量级很小(10-12Hz量级),因此多普勒频率计算公式可以简化为
| $ {f_{\rm{d}}} = \frac{{\left[ {{\mathit{\boldsymbol{V}}_{{\rm{rec}}}} - {\mathit{\boldsymbol{V}}_{{\rm{sat}}}}\left( {{T_2}} \right)} \right] \cdot \mathit{\boldsymbol{l}}}}{\lambda } - {\rm{ \mathsf{ δ} }}{f_{{\rm{rec}}}}. $ | (14) |
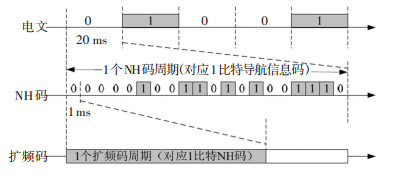
如图 2所示,北斗MEO/IGSO卫星信号中调制有D1电文,其数据位位宽为20 ms.信号中还调制有NH码,其周期为20 ms,每个NH码码宽为1 ms. NH码的周期与导航电文数据位持续时间一致.因此一个导航电文数据比特中包含1组NH码,也就是20个NH码符号位[18].其造成的影响类似于把20 ms电文宽度变成了1 ms.频繁的符号位跳变限制了捕获过程的相干积分时间,降低了信号捕获的灵敏度.在通过导航滤波器估算信号发射时间之后,可以进一步对NH码相位进行计算.在获得NH码相位后,可以将积分的起始位置选择为NH码相位为1的数据块,这样便可消除NH码跳变的影响,从而进行20 ms的相干积分.
|
图 2 NH码调制示意图 Fig. 2 Diagram of NH code modulation |
NH码相位与信号发射时间具有严格的对应关系.信号发射时间通常表示为周内秒,取值为[0 s, 604 800 s).信号发射过程中,卫星将发射时间刻在信号上,同时也同步地将NH码刻在信号上,并且以20 ms为周期不断循环.举例来说,在BDT为0~1 ms间隔中,此时刻入导航信号的NH码的码相位为1;而在BDT为19~20 ms间隔中,此时刻入导航信号的NH码的码相位为20;在BDT为21~ 22 ms间隔中,由于NH码的周期性,此时刻入导航信号的NH码对应相位重新回到1.因此,对于任意信号发射时刻ttrans,T2时刻信号中的NH码的码相位计算方法为
| $ {\varphi _{{\rm{NH}}}} =\text{ ceil}\left[ {\text{ rem}\left( {{t_{{\rm{trans}}}} \cdot 1000,20} \right)} \right]. $ | (15) |
式中:φNH为T2时刻接收信号中NH码相位,chip;rem(·)为取余函数;ceil(·)为向上取整函数.
2 辅助算法及辅助量误差分析 2.1 伪码相位计算算法误差分析在上一小节采用式(7)计算卫星运动矢量ΔPsat时,用传播时间τ2代替了传播时间τ1,由此可能会引起ΔPsat的计算误差,下面对这一项由于近似带来误差进行分析.将式(7)中“≈”两边的项进行作差,可得ΔPsat的计算误差为
| $ \delta \left( {\Delta {\mathit{\boldsymbol{P}}_{{\rm{sat}}}}} \right) = \left[ {\mathit{\boldsymbol{C}}\left( {{\tau _2}} \right) - \mathit{\boldsymbol{C}}\left( {{\tau _1}} \right)} \right] \cdot {\mathit{\boldsymbol{P}}_{{\rm{sat}}}}\left( {{T_1}} \right), $ | (16) |
τ2与τ1的时间差为
| $ \Delta \tau = {\tau _2} - {\tau _1} = \frac{{{\rho _2} - {\rho _1}}}{c} = \frac{{{r_2} - {r_1}}}{c}. $ | (17) |
式中r1和r2之差主要是由于卫星运动在视距矢量投影所导致的.北斗GEO/IGSO卫星轨道高度大概为35 786 km,MEO卫星轨道高度为21 528 km.两种高度卫星信号传播到地面上的传播时间大概为120、72 ms.另外,GEO卫星速度近似为0,IGSO卫星速度在1~3 km/s之间,MEO速度在2~4 km/s之间.考虑最差的情况,假定传播时间τ1=150 ms,卫星与载体相向而行,且相对速度为4 000 m/s,此时r1和r2之差为0.15 s×4 km/s = 600 m.实际的r1和r2之差应当小于此时的r1和r2之差,有
| $ \Delta \tau = \frac{{{r_2} - {r_1}}}{c} < \frac{{600\;{\rm{m}}}}{c} \approx 2 \times {10^{ - 6}}{\rm{s}}, $ | (18) |
将τ1=150 ms,Δτ=2×10-6s代入方程(16)中进行运算,可得
| $ \delta \left( {\Delta {\mathit{\boldsymbol{P}}_{{\rm{sat}}}}} \right) \approx {\mathit{\boldsymbol{O}}_{3 \times 3}} \cdot {\mathit{\boldsymbol{P}}_{{\rm{sat}}}}\left( {{T_1}} \right) = {\mathit{\boldsymbol{O}}_{3 \times 3}}. $ | (19) |
因此,即使在最差的情况下,用τ2代替τ1所带来的ΔPsat计算误差可以忽略不计.
2.2 伪码相位计算误差源及传播特性本小节将对导航滤波器计算得到的码相位及多普勒频率两个辅助信息的精度进行分析,寻找辅助量误差的误差源和及其传播特性.由式(12)可知,码相位的估计误差主要取决于信号发射时间的估计误差.将式(1)、(7)、(9)代入式(10),再将式(10)代入式(11),可以进一步展开T2时刻信号发射时间的计算公式:
| $ \begin{array}{l} {t_{{\rm{trans}}}} = {t_{{\rm{rec}}}} - \delta {t_{{\rm{rec}}}} + \delta {t_{{\rm{sat}}}} - \\ \;\;\;\;\;\;\;\;\;\frac{{\left| {{\mathit{\boldsymbol{P}}_{{\rm{sat}}}}\left( {{T_2}} \right) - {\mathit{\boldsymbol{P}}_{{\rm{rec}}}}} \right| + I + T - \Delta {\mathit{\boldsymbol{P}}_{{\rm{sat}}}} \cdot \mathit{\boldsymbol{l}}}}{c}, \end{array} $ | (20) |
将公式中的真值用导航滤波器给出的估计值进行替代,可得
| $ \begin{array}{l} {{\hat t}_{{\rm{trans}}}} = {t_{{\rm{rec}}}} - \delta {{\hat t}_{{\rm{rec}}}} + \delta {{\hat t}_{{\rm{sat}}}} - \\ \;\;\;\;\;\;\;\;\;\frac{{\left| {{{\mathit{\boldsymbol{\hat P}}}_{{\rm{sat}}}}\left( {{T_2}} \right) - {{\mathit{\boldsymbol{\hat P}}}_{{\rm{rec}}}}} \right| + \hat I + \hat T - \Delta {\mathit{\boldsymbol{P}}_{{\rm{sat}}}} \cdot \mathit{\boldsymbol{l}}}}{c}. \end{array} $ | (21) |
式中:δtrec为导航滤波器估计的接收机钟差,m;δtsat为通过卫星星历计算得到的卫星钟差,m;
信号发射时间估计误差可以由估计值减去真值得到,将式(20)和式(21)作差,信号发射时间计算误差为
| $ \begin{array}{l} \delta {t_{{\rm{trans}}}} = {{\hat t}_{{\rm{trans}}}} - {t_{{\rm{trans}}}} = \frac{1}{c}\delta {r_1} - \frac{1}{c}\delta I - \frac{1}{c}\delta T - \\ \;\;\;\;\;\;\;\;\;\;\delta \left( {\delta {t_{{\rm{rec}}}}} \right) + \delta \left( {\delta {t_{{\rm{sat}}}}} \right). \end{array} $ | (22) |
式中:
| $ \delta \left( {\delta {t_{{\rm{rec}}}}} \right) = \delta {{\hat t}_{{\rm{rec}}}} - \delta {t_{{\rm{rec}}}}, $ | (23) |
| $ \delta \left( {\delta {t_{{\rm{sat}}}}} \right) = \delta {{\hat t}_{{\rm{sat}}}} - \delta {t_{{\rm{sat}}}}, $ | (24) |
| $ \delta {r_1} = \left| {{{\mathit{\boldsymbol{\hat P}}}_{{\rm{sat}}}}\left( {{T_2}} \right) - {{\mathit{\boldsymbol{\hat P}}}_{{\rm{rec}}}}} \right| - \left| {{\mathit{\boldsymbol{P}}_{{\rm{sat}}}}\left( {{T_2}} \right) - {\mathit{\boldsymbol{P}}_{{\rm{rec}}}}} \right|, $ | (25) |
| $ \delta I = \hat I - I, $ | (26) |
| $ \delta T = \hat T - T. $ | (27) |
其中:δttrans为发射时间计算误差,s;δr1为T2时刻由于对接收机位置和卫星位置掌握不准确导致的接收机与卫星之间相对距离估计误差,m;δI为电离延迟估计误差,m;δT为对流层延迟估计误差,m;δ(δtrec)为接收机对钟差估计的误差,s,实质上表征了接收机对时间精度的掌握程度;δ(δtsat)为卫星钟差误差,s,代表用时钟模型改正卫星钟之后残余的卫星时间误差,实际表征接收机对卫星时间掌握的精确程度.
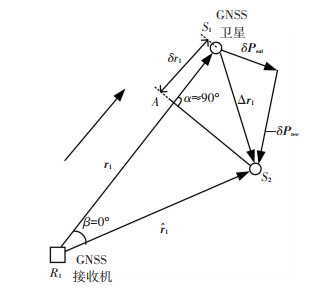
下面就式(22)体现的误差源分别进行讨论.首先对δr1这一项进行分析, 如图 3所示,R1为接收机实际位置点,S1为卫星实际位置点,r1为由接收机指向卫星的真实的视距矢量,即
| $ {\mathit{\boldsymbol{r}}_1} = {\mathit{\boldsymbol{P}}_{{\rm{sat}}}} - {\mathit{\boldsymbol{P}}_{{\rm{rec}}}}. $ | (28) |
|
图 3 相对距离误差与卫星、接收机位置误差关系 Fig. 3 Relation between relative distanceerror and satellite/receiver position error |
导航滤波器对接收机和卫星的位置估计存在偏差,其计算得到的视距矢量为
| $ {{\mathit{\boldsymbol{\hat r}}}_1} = {{\mathit{\boldsymbol{\hat P}}}_{{\rm{sat}}}} - {{\mathit{\boldsymbol{\hat P}}}_{{\rm{rec}}}} = \left( {{\mathit{\boldsymbol{P}}_{{\rm{sat}}}} + \delta {\mathit{\boldsymbol{P}}_{{\rm{sat}}}}} \right) - \left( {{\mathit{\boldsymbol{P}}_{{\rm{rec}}}} + \delta {\mathit{\boldsymbol{P}}_{{\rm{rec}}}}} \right). $ | (29) |
式中δPsat、δPrec分别为对卫星和接收机位置估计的误差矢量.将r1和
| $ \Delta {\mathit{\boldsymbol{r}}_1} = {{\mathit{\boldsymbol{\hat r}}}_1} - {\mathit{\boldsymbol{r}}_1} = \delta {\mathit{\boldsymbol{P}}_{{\rm{sat}}}} - \delta {\mathit{\boldsymbol{P}}_{{\rm{rec}}}}. $ | (30) |
在直线R1S1上确定A点,使得R1A = R1S2.则直线AS1的长度即为δr1.在△R1S2A中,根据余弦定理,有
| $ \cos \beta =\frac{\overline{AR}_{1}^{2}+\overline{{{S}_{2}}R}_{1}^{2}-\overline{AS}_{2}^{2}}{2{{\overline{AR}}_{1}}\cdot {{\overline{{{S}_{2}}R}}_{1}}}. $ | (31) |
又因为
| $ \delta {r_1} = \Delta {\mathit{\boldsymbol{r}}_1} \cdot \mathit{\boldsymbol{l}} = \left( {\delta {\mathit{\boldsymbol{P}}_{{\rm{sat}}}} - \delta {\mathit{\boldsymbol{P}}_{{\rm{rec}}}}} \right) \cdot \mathit{\boldsymbol{l}}. $ | (32) |
将式(32)代入式(22)中,可得
| $ \begin{array}{l} \delta {t_{{\rm{trans}}}} = \frac{1}{c}\delta {\mathit{\boldsymbol{P}}_{{\rm{rec}}}} \cdot \mathit{\boldsymbol{l}} - \frac{1}{c}\delta {\mathit{\boldsymbol{P}}_{{\rm{sat}}}} \cdot \mathit{\boldsymbol{l}} - \frac{1}{c}\delta I - \frac{1}{c}\delta T - \\ \;\;\;\;\;\;\;\;\;\;\;\delta \left( {\delta {t_{{\rm{rec}}}}} \right) + \delta \left( {\delta {t_{{\rm{sat}}}}} \right). \end{array} $ | (33) |
根据式(33),可对导航滤波器预测码的预测误差的主要误差源、传播特性、误差量级可归纳如下:误差源主要由卫星轨道误差δPsat、接收机位置误差δPrec、电离层延迟估计误差δI、对流层延迟估计误差δT,接收机钟差的估计误差δ(δtrec)、卫星钟差的估计误差δ(δtsat)所构成.由式(29)可知,δPsat和δPrec经过视距投影后,将会线性地传播到发射时间计算误差中去,而其他项则直接以线性的方式传播到发射时间计算误差中去. δPrec量级可以参照标准的卫星导航服务的定位精度,其三维均方根大概为7 m,投影到视距上要小于此值,但考虑最差的情况,由此引起的码相位计算误差均方根仍可假定为7 m;δ(δtrec)的均方根大概为7 m[19-20].卫星位置计算误差在视距上的均方根大概为2 m;经过模型矫正后δ(δtsat)均方根大概为2 m;经过模型估算后,电离层残余误差δI大概在1~5 m之间;经过模型估算后,对流层残余误差δT大概在0.1~1 m之间[4].综上所述,码相位计算误差的3σ值上限为
| $ \begin{array}{l} 3 \cdot \rm \sqrt {{{(7m)}^2} + {{(7m)}^2} + {{(2m)}^2} + {{(2m)}^2}} + \\ 5{\rm{m}} + 1{\rm{m}} \approx 36{\rm{m}}. \end{array} $ | (34) |
将式(14)中的真值用导航滤波器的估计值进行替代,可得
| $ {{\hat f}_{\rm{d}}} = \frac{{\left( {{{\mathit{\boldsymbol{\hat V}}}_{{\rm{rec}}}} - {{\mathit{\boldsymbol{\hat V}}}_{{\rm{sat}}}}} \right) \cdot \boldsymbol{l}}}{\lambda } - \delta {{\hat f}_{{\rm{rec}}}}. $ | (35) |
式中:
将式(14)与式(35)进行作差,可得到多普勒频率的估计误差:
| $ \delta {f_{\rm{d}}} = {{\hat f}_{\rm{d}}} - {f_{\rm{d}}} = \frac{1}{\lambda } \cdot \left( {\delta {\mathit{\boldsymbol{V}}_{{\rm{rec}}}} - \delta {\mathit{\boldsymbol{V}}_{{\rm{sat}}}}} \right) \cdot \mathit{\boldsymbol{l}} - \delta \left( {\delta {f_{{\rm{rec}}}}} \right). $ | (36) |
式中:δVsat为卫星速度估计误差,m/s;δVrec为用户速度估计误差,m/s;δ(δfrec)为接收机钟漂估计误差,Hz.
由式(36)可知,δVsat和δVrec经过视距投影后,将线性地传播到多普勒估计误差中,而δ(δfrec)将直接线性地传播到多普勒估计误差中.对于BDS B1I提供的导航服务来说,δVrec的三维均方根为0.1 m/s;δVsat的三维均方根应小于0.1 m/s[21];二者投影到视距矢量后转化成多普勒估计误差应小于投影前,但是考虑最差的情况计算多普勒频率估计误差3σ值的时候仍然可以不考虑视距投影的影响;接收机时钟频率由于受到卫导的校准,其稳定性较高,因此δ(δfrec)量级可假定为(应小于)2 Hz;载波波长λ可以取为B1I信号的波长,大概为0.19 m.则多普勒频率估计误差的3σ值上限为
| $ 3 \cdot \sqrt {{{\left( {\frac{{0.1}}{{0.19}}{\rm{Hz}}} \right)}^2} + {{\left( {\frac{{0.1}}{{0.19}}{\rm{Hz}}} \right)}^2} + {{\left( {2{\rm{Hz}}} \right)}^2}} \approx 6{\rm{Hz}}{\rm{.}} $ | (37) |
由上述分析可知,由导航滤波器计算的码相位误差的3σ值大概为36 m(0.24个B1I码宽),小于半个B1I伪码码宽;而多普勒频率估算误差的3σ值大概为6 Hz,小于采用500 Hz为步长时的捕获频率精度(250 Hz).由此可知,采用导航计算辅助捕获算法,只需要一次相关即可检测到导航信号是否存在.需要注意的是,对弱信号采用导航滤波器辅助捕获需要采用NH码相位估计和剥离,将相干积分时间扩展为20 ms.
3 捕获性能指标 3.1 捕获灵敏度信号捕获灵敏度代表满足一定虚警率和检测概率的条件下,卫星信号载噪比的最小值.实际上表征了满足一定捕获成功率条件下能够检测到的最弱的信号强度. GNSS中频信号与本地载波和伪码信号进行混频、相关运算,得到同相(I)、正交(Q)两路相关值,其数学模型为
| $ \left\{ {\begin{array}{*{20}{l}} {{I_k} = A \cdot R\left( {\delta {\tau _k}} \right) \cdot \text{sinc} \left( {{\rm{ \mathsf{ δ} }}{f_k}{T_{{\rm{coh}}}}} \right) \cdot \cos \left( {\delta {\varphi _k}} \right) + {n_I},}\\ {{Q_k} = A \cdot R\left( {\delta {\tau _k}} \right) \cdot \text{sinc} \left( {{\rm{ \mathsf{ δ} }}{f_k}{T_{{\rm{coh}}}}} \right) \cdot \sin \left( {\delta {\varphi _k}} \right) + {n_Q}.} \end{array}} \right. $ | (38) |
| $ A = \sqrt {2 \cdot \frac{c}{{{n_0}}} \cdot {T_{{\rm{coh}}}}} \cdot {\sigma _n}, $ | (39) |
| $ \frac{c}{{{n_0}}} = {10^{\frac{1}{{10}} \cdot \frac{C}{{{N_0}}}}}, $ | (40) |
式中:Ik为同相支路相关值;Qk为正交支路相关值;k为第k次搜索的结果;A为相关值信号幅度,由信号强度(载噪比)所决定;R(·)为伪码自相关函数;δφ为本地载波与接收载波的相位差,rad;δf为本地载波与接收载波的频率差,Hz;δτ为本地伪码与接收伪码的相位差,chip;Tcoh为相干积分时间,s;nI和nQ为相关值中噪声的量,二者服从零均值的高斯分布,均值为0,方差为σn2;C/N0为dB-Hz为单位的载噪比,c/n0为以Hz为单位的载噪比.信号捕获过程的检测统计量为
| $ V = \sqrt {I_k^2 + Q_k^2} . $ | (41) |
当信号不存在时,统计量V服从瑞利分布,如下式所示:
| $ {f_n}\left( v \right) = \frac{v}{{\sigma _n^2}}{{\rm{e}}^{ - \frac{{{v^2}}}{{2\sigma _n^2}}}}, $ | (42) |
式中fn(v)为瑞利分布的率密度函数.
当信号存在时,统计量V服从莱斯分布,如下式所示:
| $ {f_s}\left( v \right) = \frac{v}{{\sigma _n^2}}{{\rm{e}}^{ - \frac{{{v^2} + {a^2}}}{{2\sigma _n^2}}}}{I_0}\left( {\frac{{va}}{{\sigma _n^2}}} \right), $ | (43) |
式中fs(v)为信号存在时V的概率分布,I0(·)为第一类零阶修正贝塞尔函数,式中a定义为
| $ a = A \cdot R\left( {\delta {\tau _k}} \right) \cdot \text{sinc}\left( {\delta {f_k}{T_{{\rm{coh}}}}} \right). $ | (44) |
若检测门限选定为Vt,则虚警率Pfa可由下式计算:
| $ {P_{{\rm{fa}}}} = \int_{{V_{\rm{t}}}}^\infty {{f_n}} (v) \cdot {\rm{d}}v, $ | (45) |
一般情况下,都是先选择虚警概率(如0.1),再确定检测门限.若首先确定虚警率Pfa,则检测门限的计算公式为
| $ {V_{\rm{t}}} = {\sigma _n}\sqrt { - 2\ln {P_{{\rm{fa}}}}} . $ | (46) |
在确定检测门限Vt后,信号的捕获检测概率Pd的计算公式为
| $ {P_{\rm{d}}} = \int_{{V_{\rm{t}}}}^\infty {{f_s}} (v) \cdot {\rm{d}}v. $ | (47) |
在相干积分时间确定的情况下,捕获概率随着信号载噪比的上升而上升.信号捕获灵敏度定义为:当捕获概率大于某一数值(如0.95)的条件下,信号载噪比的最小值.
3.2 平均捕获时间捕获时间Tacq为接收机从开始搜索到搜索到信号所需要的时间.由于Tacq是一个随机变量,通常采用平均捕获时间Tacq来衡量接收机捕获速度,其数学计算方法为
| $ {{\bar T}_{{\rm{acq}}}} = \frac{{2 + \left( {2 - {P_{\rm{d}}}} \right)(q - 1)\left( {1 + {L_c} \cdot {P_{{\rm{fa}}}}} \right)}}{{2 \cdot M \cdot {P_{\rm{d}}}}}K \cdot {T_{{\rm{coh}}}}, $ | (48) |
其中:Tacq为平均捕获时间,Pd为检测概率,q为搜索区间数量,Lc为在无信号单元中由虚警率带来的时间损耗系数,M为并行搜索通道的个数,K为非相干累积的次数,Tcoh为相干积分时间.
4 辅助算法捕获性能分析 4.1 捕获灵敏度分析按照文献[12]给出的参数设定虚警率、检测概率、搜索区间和搜索步长:Pfa=0.1,Pd=0.95.对于无辅助的情况下,其多普勒频率搜索范围为[-10 kHz, 10 kHz],频率搜索步长为500 Hz,意味着最大的频率捕获误差为250 Hz;码相位搜索步长为0.5码片,意味着最大的码相位捕获误差为0.25码片.对于有导航滤波器辅助的情况,最大的频率搜索误差和码相位搜索误差可取为各自估计误差的3σ值上限:即6 Hz和0.24码片.
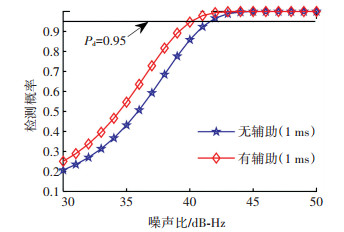
图 4展示了无辅助捕获情况下和有辅助捕获情况下对信号检测概率的分析.其中辅助算法只采用了导航滤波器辅助码相位和载波多普勒估计,相干积分时间由于存在NH码跳变的影响都选择为1 ms.从图中可以看出,当检测概率Pd=0.95时,无辅助条件下捕获灵敏度为41.2 dB-Hz,有辅助条件下捕获灵敏度为40.1 dB-Hz,导航滤波器对捕获的辅助将捕获灵敏度提高了1.1 dB.
|
图 4 有辅助和无辅助条件下的捕获概率分析 Fig. 4 Acquisition probability analysisof aided and unaided acquisition |
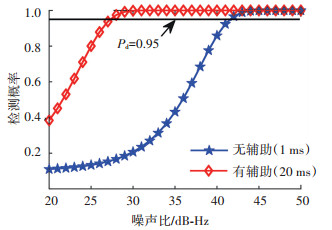
图 5展示了辅助算法加入对NH码相位估计的情况下,无辅助和有辅助条件下的捕获概率分析.导航滤波器对位同步进行辅助,从而消除了NH码跳变对相干积分的影响,将捕获算法的相干积分时间扩展为20 ms;而无辅助的情况下由于NH码跳变的影响,其相干积分时间仍然被限制为1 ms.从图中可以看出,当检测概率Pd=0.95时,无辅助条件下捕获灵敏度为41.6 dB-Hz,有辅助条件下捕获灵敏度为27.3 dB-Hz,导航计算对捕获的辅助将捕获灵敏度提高了14.3 dB,相对单纯的导航滤波器对多普勒频率和伪码相位辅助,NH码相位辅助可以额外提供12.8 dB的捕获灵敏度提升.
|
图 5 增加NH码相估计条件下捕获概率分析 Fig. 5 Acquisition probability analysis when providing NH code phase estimation |
对于无辅助的二维串行捕获来说,多普勒搜索区间为±10 kHz,搜索步长为500 Hz,因此频域搜索区间个数为20 kHz/500 Hz + 1 = 41.码相位搜索范围为[0, 2 046),搜索步长为0.5码片,因此码搜索区间数量为2 046/0.5 = 4 092.因此,二维搜索总共的搜索区间数量为4 092×41 = 167 772.文中无辅助串行捕获算法相关参数为:Pd=0.95,Pfa=0.1,K=1,Tcoh=1 ms,M=1,Lc=1.将这些参数代入式(48),得二维搜索的平均搜索时间为93.64 s.
对于导航计算辅助捕获算法,总共需要搜索的区间数量为1,其他参数与无辅助的二维捕获相同,通过式(48)计算可得需要的平均搜索时间,当Tcoh=1 ms时候平均捕获时间为1.1 ms;当Tcoh=20 ms时,平均捕获时间为21.1 ms.可见在导航滤波器的辅助下,捕获所需的时间大大降低了,扩展相关积分时间并没有明显的提高捕获时间.
5 结论1) 在接收机已经完成导航计算,并且掌握导航星历的前提下,可以采用导航滤波器对信号捕获进行辅助,从而提高捕获灵敏度,降低捕获时间,同时可以降低无辅助条件下捕获引擎频繁运行带来的功耗,更好地平衡捕获装置性能与资源消耗的关系.
2) 仿真表明,采用导航计算辅助载波多普勒和伪码相位搜索,可以提高1.1 dB的捕获灵敏度,平均捕获时间降低为1 ms;在辅助量包含位NH码相位的前提下,通过扩展相干积分时间可以进一步扩展相干积分时间为20 ms, 从而提供额外的12.8 dB的捕获灵敏度,平均捕获时间为20 ms左右.
3) 矢量跟踪环路通过导航计算与基带跟踪的融合来实现星间辅助与跟踪灵敏度提升,所提出的导航滤波器辅助捕获算法进一步扩展了矢量跟踪的概念:将导航滤波器先验信息用来辅助基带捕获和位同步,在更广泛的意义上实现接收机导航计算与基带处理的融合与相互增强,因此导航滤波器辅助捕获算法具有一定理论价值和实际价值.
| [1] |
李向阳, 慈元卓, 程绍驰. 国外卫星导航军事应用[M]. 北京: 国防工业出版社, 2015. LI Xiangyang, CI Yuanzhuo, CHENG Shaochi. The foreign military application of GNSS[M]. Beijing: National Defense Industry Press, 2015. |
| [2] |
HEGARTY C J, CHATRE E. Evolution of the global navigation satellite system (GNSS)[J]. Proceedings of the IEEE, 2009, 96(12): 1902. DOI:10.1109/jproc.2008.2006090 |
| [3] |
ENGE P. Global positioning system: signals, measurements, and performance[M]. Massachusetts: Ganga-Jamuna Press, 2011.
|
| [4] |
谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009. XIE Gang. The principle of GPS and receiver design[M]. Beijing: Electronic Industry Press, 2009. |
| [5] |
BORRE K, AKOS D M, BERTELSEN N, et al. A software-defined GPS and Galileo receiver: a single-frequency approach[M]. Boston: Birkhäuser Basel, 2007: 75.
|
| [6] |
李灯熬, 李帅, 赵菊敏, 等. 北斗系统信号捕获方法研究综述[J]. 计算机工程与科学, 2016, 38(5): 905. LI Dengao, LI Shuai, ZHAO Jumin, et al. Review on the signal acquisition of Beidou navigation satellite system[J]. Computer Engineering and Science, 2016, 38(5): 905. DOI:10.3969/j.issn.1007-130X.2016.05.010 |
| [7] |
LIU Ningqing, SUN Bin, GUAN Chunmeng. Research on an improved PMF-FFT fast PN code acquisition algorithm[J]. Communications and Network, 2013, 5(3): 266. DOI:10.4236/cn.2013.53B2049 |
| [8] |
汶晓勇, 肖越. GPS和A-GPS技术研讨[J]. 通信技术, 2011, 44(8): 76. WEN Xiaoyong, XIAO Yue. Discussion on GPS and A-GPS techno-logies[J]. Communications Technology, 2011, 44(8): 76. DOI:10.3969/j.issn.1002-0802.2011.08.027 |
| [9] |
谢棋军, 陈新, 刘佩林. 辅助北斗技术的捕获空间计算和误差分析[J]. 中兴通讯技术, 2016(1): 59. XIE Qijun, CHEN Xin, LIU Peilin. Search space compute and error analysis of assisted-Beidou acquisition technology[J]. ZTE Techno-logy Journal, 2016(1): 59. DOI:10.3969/j.issn.1009-6868.2016.01.015 |
| [10] |
严昆仑, 章红平, 张提升. AGPS系统原型设计与性能评估[C]//第四届中国卫星导航学术年会论文集.北京: 中国卫星导航系统管理办公室, 2013 YAN Kunlun, ZHANG Hongping, ZHANG Tisheng. AGPS system prototype design and evaluate[C]//Proceedings of the Fourth China Satellite Navigation Conference. Beijing: China Satellite Navigation System Management Office, 2013 |
| [11] |
DIGGELEN F, ABRAHAM C. Coarse-time AGPS; computing TOW from pseudorange measurements, and the effect on HDOP[C]//Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2007). Fort Worth: TX, 2007: 357
|
| [12] |
何晓峰, 聂祖国, 于慧颖, 等. 高动态条件下SINS辅助GNSS信号捕获的性能分析[J]. 中国惯性技术学报, 2011, 19(4): 447. HE Xiaofeng, NIE Zuguo, YU Huiying, et al. Performance analysis on high dynamic signal acquisition aided by SINS for GNSS satellites[J]. Journal of Chinese Inertial Technology, 2011, 19(4): 447. DOI:10.1080/0144929X.2011.553739 |
| [13] |
汤霞清, 程旭维, 武萌. INS辅助的PMF-FFT快速捕获算法[J]. 火力与指挥控制, 2017, 42(8): 128. TANG Xiaqing, CHENG Xuwei, WU Meng. Research on fast acquisition algorithm based on PMF-FFT with INS-aided[J]. Fire Control & Command Control, 2017, 42(8): 128. DOI:10.3969/j.issn.1002-0640.2017.08.029 |
| [14] |
张敏虎, 任章, 华春红. 惯性信息辅助的高动态弱GPS信号快速捕获[J]. 系统工程与电子技术, 2011, 33(2): 366. ZHANG Minhu, REN Zhang, HUA Chunhong. Fast acquisition of high-dynamic and weak GPS signals aided by inertial information[J]. Systems Engineering and Electronics, 2011, 33(2): 366. DOI:10.3969/j.issn.1001-506X.2011.02.27 |
| [15] |
ZHAO Sihao, AKOS D. An open source GPS/GNSS vector tracking loop-implementation, filter tuning, and results[C]// Proceedings of the 2011 International Technical Meeting of the Institute of Navigation. San Diego, CA: Institute of Navigation, 2011: 1293
|
| [16] |
ZHAO Sihao, LU Mingquan, FENG Zhenming. Implementation and performance assessment of a vector tracking method based on a software GPS receiver[J]. The Journal of Navigation, 2011, 64(S1): S151. DOI:10.1017/S0373463311000440 |
| [17] |
NG Y, GAO G X. Advanced multi-receiver vector tracking for positioning a land vehicle[C]// Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+2014). Tampa, Florida: ION, 2015: 3148
|
| [18] |
中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件[EB/OL]. (2016-11-07)[2018-10-17]. http://www.beidou.gov.cn/xt/gfxz/201710/P020171202693088949056.pdf China Satellite Navigation Office. Beidounavigation satellite system signal in space interface control document[EB/OL]. (2016-11-07)[2018-10-17]. http://www.beidou.gov.cn/xt/gfxz/201710/P020171202693088949056.pdf |
| [19] |
中国卫星导航系统管理办公室.北斗卫星导航系统公开服务性能规范[EB/OL]. (2013-10-20)[2018-10-17]. http://www.beidou.gov.cn/xt/gfxz/201710/P020171202693228603215.pdf China Satellite Navigation Office. Beidou navigation satellite system open service performance standard[EB/OL]. (2013-10-20)[2018-10-17]. http://www.beidou.gov.cn/xt/gfxz/201710/P020171202693088949056.pdf |
| [20] |
刘基余. GPS卫星导航定位原理与方法[M]. 北京: 科学出版社, 2003: 334. LIU Jiyu. Principle and method of GPS positioning[M]. Beijing: Science Press, 2003: 334. |
| [21] |
常志巧, 胡小工, 时鑫, 等. 基于位置观测的北斗广播星历速度精度分析[J]. 空间科学学报, 2018, 38(4): 553. CHANG Zhiqiao, HU Xiaogong, SHI Xin, et al. Accuracy analysis of satellite velocity with BDS broadcast ephemeris based on position observation[J]. China Journal of Space and Science, 2018, 38(4): 553. DOI:10.11728/cjss2018.04.55 |
 2020, Vol. 52
2020, Vol. 52


