现实世界中许多的复杂系统都可以抽象为网络模型,例如在社交网络[1]中,每个人都是节点,人与人之间的关系是网络中的边;在交通网络[2]中,每个交通枢纽是节点,交通路线是边;在传感器网络[3]中,传感器是节点,它们之间的通讯关系是边;在电力网络[4]中,电力器件是节点,器件的作用关系是边等.
传统数理方法很难分析这种研究对象众多、作用关系复杂的问题,于是复杂网络理论逐渐兴起,并成为人们分析与研究复杂系统的工具.复杂网络中有一类中观结构,如社团结构[5-6]、核心外围结构[7]等,研究这些中观结构有助于理解复杂系统本身的性质和特点.其中,社团结构的识别是复杂网络理论研究中的一项重要内容.社团是指在网络中具有相似特征一类节点;或是在内部连接比较紧密,与其他节点连接稀疏的一组节点[8].
网络在社团结构这一中观尺度上所表现出来的动力学特性、结构特性等和其在整体上所表现出来的特性相比差异很大,识别社团结构可以帮助挖掘那些网络中无法先验得知的功能模块,更好地分析复杂系统.例如寻找信息网络属于同一话题的信息、预测新陈代谢网络中未知蛋白质的功能、投放社交网站中的广告、挖掘Web社区中的数据、调度并行计算中的子程序[9-10]等都可以归为社团识别问题;社团结构揭示了网络的拓扑特点,能够帮助解析复杂系统内在的功能,分析复杂网络的动力学特性.故此,社团识别的研究具有重要的意义.
典型的社团识别算法整体上可作如下分类:基于网络拓扑的识别算法,这类算法又可以分为分裂式算法和聚类式算法两种,前者有谱划分算法等,后者有CNM算法[10]、利用相似性测度的层次聚类算法等;基于信息论的社团识别算法,将社团识别转化为信息论中的拓扑压缩问题[11],如基于随机游走的识别算法;基于网络动力学特性的识别算法,如基于一致性动力学的算法[12-15];基于统计学的识别算法,如随机块模型[16];基于优化方法的直接寻优识别算法,如基于遗传算法[17]、贪婪算法、粒子群算法的识别算法[6]等.
生物地理学优化(biogeography-based optimization, BBO)作为一种新颖的群体智能优化方法,尽管相关研究尚处于起步阶段,但由于其较好的全局搜索能力,使得其在高维问题上的表现超过了传统优化方法[18].另一方面,生物地理学优化方法仍受限于进化优化方法框架,普遍效率较低.
小世界效应是现实网络普遍具有的一种网络结构特征,典型的小世界网络模型由于少数长程连边的存在,使得网络整体平均连通路径长度显著降低,从而具有超快的信息传播能力[19-21].文献[19]通过矩阵特征值方法发现在小世界网络能够实现超快一致性动力学过程(ultrafast consensus dynamics).而另一方面,群体智能进化算法普遍基于不同个体(例如遗传算法中的染色体,蚁群算法中的蚂蚁)之间的信息交换与信息共享,从而完成对解空间的搜索与寻优过程[17].上述过程与网络中的信息传播过程[19-21]类似.由于提出的群体智能算法需要在多个栖息地之间传递与搜索网络社团结构信息,受此两者之间重要内在关联的启发,提出了利用小世界效应加速生物地理学优化过程的网络社团识别算法(biogeography-based optimization with small-world effects, BBOSW).建立了网络社团结构识别问题的BBOSW方法与框架.特别地,在栖息地之间的迁移操作建模中,利用具有小世界效应的典型网络模型来进行快速信息交换,从而建立了新颖的生物地理学优化栖息地迁移过程的更新策略,大幅度提升了算法的社团结构识别效率.
1 BBOSW 1.1 算法初始化生物地理学方法的核心思想是通过模拟物种的产生、灭绝与迁移来实现数学问题的优化[18]. BBO方法的生物模型为一组孤立的岛屿(栖息地),物种在栖息地之间迁移寻找更好的生存环境.用适宜度指数向量来描述栖息地的特征,向量中的每个值为栖息地的一个适宜度指数特征值(suitability index variable, SIV),可以是降雨量、气候、光照、地理环境等和生存相关的环境参数.栖息地适宜度指数向量SIVs组合在一起就构成了区域矩阵X,其中矩阵每个栖息地的SIVs作为矩阵的行向量.为了衡量栖息地适合物种生存的程度,引入与栖息地的物种多样性程度相关联的栖息地适应度指数(habitat suitability index, HSI).一般地,物种丰富的栖息地HSI值较大,但与此同时物种的生存压力也较大,物种更倾向于迁入HSI值较低的栖息地去,使迁入后的栖息地物种多样性增加,HSI值提高;如果迁入物种无法增加栖息地HSI值,则迁入的物种会趋于灭绝或是迁移到别的栖息地.
给定一个网络G=(V, E),V为网络G节点集,E为网络G边集,节点数n=|V|,边数m=|E|.使用矩阵XH×n表示一组栖息地(解空间),即
| $ \boldsymbol{X}_{H \times n}=\left[\begin{array}{ccccc} x_{11} & x_{12} & x_{13} & \cdots & x_{1 n} \\ x_{21} & x_{22} & x_{23} & \cdots & x_{2 n} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ x_{H 1} & x_{H 2} & x_{H 3} & \cdots & x_{H n} \end{array}\right]. $ | (1) |
式中栖息地的数目为H.矩阵X的行向量Xi表示一个栖息地,每个节点所属的社团编号xij为栖息地SIV值,xij的值满足1≤xij≤ k (k为社团数,满足1≤ k
图 1为一个简单的初始化示例,网络共有7个节点,在栖息地i最初的分配中,节点[1, 3, 7]被分配到社团1,剩下的节点被分配到社团2中.栖息地i的初始化向量见图 1.
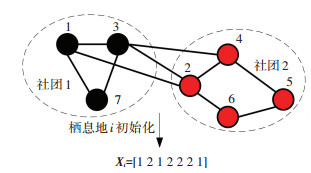
|
图 1 栖息地向量初始化 Fig. 1 Habitat vector initialization |
适应度函数的选择关系到潜在解的进化方向,不同的适应度函数对应不同的优化问题.模块度是最常用的衡量社团划分结果好坏的标准,因此选择的适应度函数为模块度函数.一般地,模块度的值越高,表明社团划分的结果越好.模块度Q的计算公式[22]为
| $ Q=\sum_{s=1}^{c}\left[\frac{l_{s}}{M}-\left(\frac{d_{s}}{2 M}\right)^{2}\right]. $ | (2) |
式中:c为社团个数,M为网络中总边数,ls为社团s内部总边数,ds为社团s内部所有节点的节点度之和.
1.3 应用小世界效应的迁移策略BBO方法利用迁移规则来更新潜在解,保持解的多样性,栖息地物种线性迁移模型见图 2.
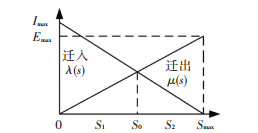
|
图 2 栖息地物种线性迁移模型 Fig. 2 Habitat species linear migration model |
从图 2中可以看到物种迁移行为分为迁入和迁出,Imax和Emax分别为最大迁入概率和最大迁出概率,在一个栖息地内,随着物种数的增加,迁出率逐渐升高,随着栖息地物种数目达到最高Smax,迁出率也达到最高迁出率Emax.迁入率变化与之相反,迁入率λ和迁出率μ的计算公式分别为
| $ \lambda=I_{\max }\left(1-\frac{s}{S_{\max }}\right), $ | (3) |
| $ \mu=\frac{s}{S_{\max }} E_{\max }. $ | (4) |
式中S为物种数.通常情况下,物种数量会在图 2中动态平衡点S0附近波动,物种数目一般处于[S1, S2].
迁移操作模型见图 3,图中栖息地i发生迁移,迁移对象为栖息地j.物种迁移后,栖息地的物种数目发生变化,栖息地i适宜度指数向量SIVs发生变化,其中适宜度指数特征SIV3的值(图中为1)变化为迁移对象栖息地j中SIV3的值(图中为2).初始化时,给予每个栖息地一个初始物种数目,依据式(3)、(4)计算迁移发生的概率.
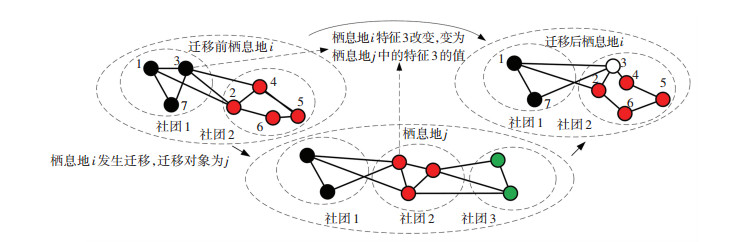
|
图 3 迁移操作 Fig. 3 Migration operation |
优化类社团识别算法一般采用随机更新规则,来确保解的多样性,避免陷入局部最优解,但随之而来的问题是潜在解更新效率的低下.在BBO方法中,发生迁移的栖息地由迁移率决定,信息交换效率同样不高.
栖息地之间的迁移过程类似网络中的信息交换,因此建立一个网络模型来刻画区域内的栖息地的信息交换过程,每个栖息地看作网络中的一个点,若是栖息地之间可以进行信息交换, 则其对应点之间存在一条边.选择合适的网络生成模型,既可以保证信息交换的充分性,同时也可以有效减少信息遍布整个区域的传播时间.
小世界效应是复杂网络中普遍存在的一种现象.具有该效应的网络模型具有较低的平均路径,即使网络规模较大,任两个节点之间也可以通过少数几个中间节点连接.与其他网络模型相比,在具有小世界效应的网络中信息的传播速度很快[19].将这一效应与迁移策略结合得到的新策略可以直接定向到达目的栖息地,在不影响解的多样性的情况下,大幅度提高栖息地之间迁移操作的效率,降低算法最后收敛所需要的时间.
小世界拓扑网络是利用小世界效应产生的网络模型,针对现存的小世界拓扑网络生成模型,经过实验和对比,选择小世界模型为NMW小世界拓扑网络模型[23],在社团识别算法初始化时,产生一个小世界网络G0 =(H, kn, p),其中H为栖息地数目,kn为最近邻网络节点度,p为小世界连接概率.为每个栖息地分配一个小世界网络中的节点,迁移操作仅在两个栖息地对应的节点有连接时发生. 图 4中小世界网络模型包含20个节点,其最近邻网络节点度为2,小世界连接概率为0.2.该网络对应的栖息地数目为20.将网络中的节点按顺时针方向编号,在每次迭代时,栖息地1对应小世界网络中的节点1.若栖息地1和3,1和6之间都满足迁移发生的条件,按照原迁移策略,迁移操作在两组栖息地之间会都发生;而依据改进后的迁移策略,在小世界拓扑网络中,节点1和3无连接,而节点1和6有连接,迁移操作只会在栖息地1和6之间发生.
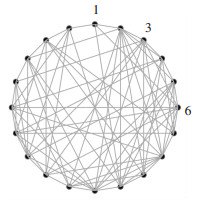
|
图 4 栖息地信息交换模型 Fig. 4 Habitat information exchange model |
除迁移操作外,变异操作也是BBO算法保持解的多样性的重要一步,变异率和栖息地的HSI值密切相关,栖息地的HSI值较低,表明该栖息地不适应物种生存,变异就越容易发生,以此来保证物种适应该栖息地的环境[18].变异率的计算和Ps(一个栖息地含有物种数量恰好为s的概率)有关.令Ps(t)表示栖息地在时刻t具有物种数量s的概率,λs与μs分别表示当栖息地具有物种数量s时对应的迁入率与迁出率.当Δt充分小时,物种数量变化超过1的概率可以忽略.在此条件下,要使栖息地在时刻t+Δt含有物种数量s,要么栖息地在时刻t含有物种数量s且Δt时间内无迁移发生;要么栖息地在时刻t含有物种数量s-1且Δt时间内发生1次迁入;要么栖息地在时刻t含有物种数量s+1且Δt时间内发生1次迁出.记o(Δt)为Δt的高阶无穷小项,则概率Ps(t+Δt)的计算公式可写为
| $\begin{aligned} P_{s}(t+\Delta T)=& P_{s}(t)\left(1-\lambda_{s} \Delta t-\mu_{s} \Delta t\right)+\\ & P_{s-1}(t) \lambda_{s-1} \Delta t+P_{s+1}(t) \mu_{x+1} \Delta t+\\ & o(\Delta t). \end{aligned} $ | (5) |
变异率的计算公式为
| $ M\left(X_{i}\right)=M_{\max }\left(1-\frac{P_{s}}{P_{\max }}\right). $ | (6) |
其中:M(Xi)为栖息地i的变异率;Mmax为最大变异率;Pmax为物种最大存在率,可以通过式(5)计算并排序得到.当发生物种变异时,栖息地适宜度指数向量发生变化,使用该栖息地的变异率选择SIV.当满足变异率条件时,改变该SIV值.
1.5 精英个体保留策略因为变异操作和迁移操作的随机性,在某一代进化中,栖息地也许会产生不可逆的变化,对应现实环境中栖息地如果发生了恶劣的自然灾害,比如山洪爆发、地震、火山喷发等,环境原有的特性可能发生巨变,影响物种的迁移.为此,算法同时提出了精英个体保留策略.精英个体为具有高HSI的栖息地,在不影响解的多样性的情况下,替换掉迁移和变异后较差的个体.使用α表示解空间中精英个体的比例,则精英个体数目可表示为
| $ E=\alpha H. $ | (7) |
在该算法过程中,计算各栖息地适应度函数值最为耗时.因此该算法的时间复杂度为O(GeHm),其中m为网络连边数,Ge为算法迭代次数参数,H为算法栖息地数目参数.
BBOSW算法的空间复杂度与传统BBO方法相比,增加了栖息地信息交换模型的临时存储空间.该部分存储空间与栖息地数目H和小世界网络模型平均节点度ks有关.当采用较为紧密的数据结构存储时(如边列表),空间复杂度为O(Hks),而BBO方法空间复杂度为O(Hn).因此在ks和H均远小于n的情况下,BBOSW算法的空间复杂度增加不显著.
2 实验及分析实验主要是将提出的算法同以下几类算法进行比较:1)基于模块度的社区划分算法,即FN算法[24]和确定性Louvain算法[25];2)基于进化算法的社区划分算法,即遗传算法的社团识别算法(GA-net)[17, 26];3)基于图的拓扑的社区划分算法,即基于最小生成树的社团识别算法(MST)[22].
同时使用模块度Q和标准化互信息(normalized mutual information, NMI)[6, 27-28]来衡量社团划分结果. Q值越高意味着该划分结果社团结构越显著,在拓扑连接上社团内部更加紧密,模块度的计算公式见式(2). NMI从信息论角度表征算法划分结果与标准划分之间的差异程度.现实世界网络标准划分来源于对网络中个体与连接性质的观察与统计,而合成网络上的标准划分源于网络模型生成的内部较为紧密的模块. NMI值越高意味着两组社团划分间差异越小. NMI计算公式为
| ${\mathop{\rm NMI}\nolimits} (A, B) = \frac{{ - 2\sum\limits_{i = 1}^{{C_A}} {\sum\limits_{j = 1}^{{C_B}} {\frac{{{N_{ij}}}}{N}} } \log \left( {\frac{{{N_{ij}}/N}}{{\left( {{N_{i.}}/N} \right)\left( {{N_{.j}}/N} \right)}}} \right)}}{{\sum\limits_{i = 1}^{{C_A}} {\frac{{{N_{i.}}}}{N}} \log \left( {\frac{{{N_{i.}}}}{N}} \right) + \sum\limits_{j = 1}^{{C_B}} {\frac{{{N_{.j}}}}{N}} \log \left( {\frac{{{N_{.j}}}}{N}} \right)}}. $ | (8) |
式中:A为标准社团划分,B为算法识别到的社团划分,CA、CB分别为两个社团划分中的社团个数,Ni.为标准划分中第i个社团的节点数,N.j为算法识别到的第j个社团的节点数,Nij为社团i和j中相同节点数,log(·)为对数函数.
2.1 参数选择一般而言,栖息地的数目H越高,解的多样性越高,最终收敛的代数较低,但每次迭代需要的运行时间较长.最大迁出率、最大迁入率以及变异率控制潜在社团划分的更新频率和程度,当三者较高时,潜在解更新频繁,且更新程度高,在搜索过程中不易陷入局部最优值,但收敛所需要的迭代代数增加,运行时间增长.
小世界参数的设置决定迁移过程中信息交换的充分性,节点度和连接概率越高,信息交换越充分,但随之而来的问题是迁移效率低下.精英个体的保留比例不宜过高,过高的精英个体比例会影响解的多样性,使迭代过程陷于局部最优.
根据前期实验结果选取的典型参数如下:栖息地数目H=50,最大迁入率Imax=1,最大迁出率Emax=1,最大变异率Mmax=0.05,精英个体比例α=4%,迭代次数Ge=500,最近邻网络节点度kn=4,小世界连接概率p=0.2.
2.2 现实网络实验用于实验的数据集有空手道俱乐部Karate网络[29],海豚社区Dolphins网络[30]和美国政治书Books网络[31].实验结果见表 1~4,其中BBO为没有采用新策略的社团识别算法,BBOSW为采用结合了小世界效应迁移策略的社团识别算法.在表 1~3中,针对进化算法,同时记录评价指标的平均值与最优值;针对其他算法,记录评价指标的最优值. avg Q、avg NMI分别为模块度和标准化互信息的均值;best Q、best NMI分别为模块度和标准化互信息的最优值.实验环境为MATLAB R2010a,CPU运行主频为2.99 GHz,运行内存为4.0 GB.
| 表 1 Karate网络上的模块度和标准化互信息比较 Tab. 1 Comparison between values of Q and NMI in the Karate club network |
| 表 2 Dolphins网络上的模块度和标准化互信息比较 Tab. 2 Comparison between values of Q and NMI in the Dolphins network |
| 表 3 Books网络上的模块度和标准化互信息比较 Tab. 3 Comparison between values of Q and NMI in the Books network |
| 表 4 算法平均收敛时间比较 Tab. 4 Average convergence time of algorithms |
从表 1~3(算法在每个网络上运行100次)中可以看到,所提出算法的识别效果与经典算法相近.在Karate网络上,BBOSW的平均NMI和最佳NMI高于其他算法;在Dolphins网络和Books网络上的平均模块度Q、平均NMI以及最佳模块度Q都要优于其他算法.从表 4(算法在每个现实网络上运行30次)中可以看到,采用改进策略的BBOSW算法的平均所需收敛时间得到减少.
进化算法普遍采用矩阵编码的方式进行算法的初始化,依据算法的特点不同,采用的矩阵编码方式不同,最终算法的收敛时间不同.一般而言,在高维问题上,BBO方法的表现要好于其他优化算法[18],即未采用改进策略的BBO社团识别算法与其他进化算法性能相近或优于其他进化算法,如遗传算法等.实验结果表明,基于小世界效应加速生物地理学优化的网络社团识别算法可以有效提高社团识别效率.
2.3 人工合成网络实验使用计算机合成网络(GN网络)来验证算法效果[32],实验结果见图 5.同其他算法相比(对于每个节点社团外度Zout生成20个随机网络,算法在每个网络上均运行30次),当Zout较小时,网络社团结构明显,模块度较高,此时各算法识别效果相差不大.随着Zout增加,模块度较低,网络社团结构逐渐不明显,各算法识别效果都下降.当Zout较大时, 新算法的识别能力要优于其他算法. 优化类算法采用直接寻优的方式寻找社团划分,对网络拓扑变化不敏感.在社团结构不明显的情况下,BBOSW算法识别效果优于或近似于测试的其他算法.
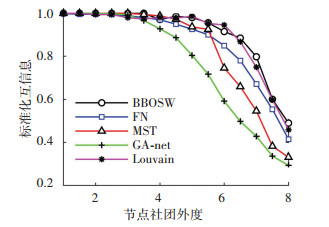
|
图 5 GN网络识别效果 Fig. 5 Detection results of GN networks |
为了验证BBOSW在实际网络中的效果,将算法应用到一个具有1 589个节点,2 742条边的科学家合作网络(netscience network)上.该网络描述了复杂网络科学家之间的合作关系[8].其中,每位学者都被抽象为一个节点,若是两位学者之间有过合作关系,则这两个节点之间存在一条连边.
科学家合作网络是一个具有较大规模的非连通网络,其包含多个连通片及大量孤立节点,这些复杂网络结构特性为社团结构的探测与识别提出了严峻的挑战.将不同算法应用于该网络. MST算法需要利用连通网络的最小生成树结构分析网络社团特征,而非连通网络无法生成该算法所需的最小生成树.因此该算法应用范围仅局限于连通网络,其无法应用于科学家合作网络. GA-net算法使用Locus-based初始化方法,然而该方法无法完成孤立节点的初始化.因为上述局限性,GA-net算法亦无法解决科学家合作网络的社团结构识别问题. FN算法采用局部贪婪优化策略.该算法在迭代过程中需要遍历所有使模块度上升的可能.科学家合作网络包含的多连通片及大量孤立节点使得算法探测到的社团个数长期维持在较高水平,因此需要合并的社团数目无法快速下降,从而导致算法运行效率很低,在超过24 h后依然无法完成运算(CPU运行主频2.99 GHz,运行内存4.0 GB),因此FN算法无法有效识别复杂的包含多连通片及大量孤立节点的较大规模非连通网络的社团结构.对于社团结构未知的较大规模现实网络(比如科学家合作网络),Louvain算法应选择初始聚合的网络社团结构作为算法的运行结果[33].将确定性Louvain算法应用于科学家合作网络得到的网络社团结构对应的模块度为0.875. BBOSW算法是随机算法,受随机波动影响.经过10次重复实验,BBOSW算法得到的平均模块度为0.867,标准差为0.005,最佳模块度为0.879.综上所述,尽管现实世界中的科学家合作网络所具有的多连通片及大量孤立节点特性使得社团结构探测非常困难,BBOSW算法和Louvain算法仍然能够对其进行有效且高质量的社团结构识别,两种算法得到的模块度相似.
根据随机选取的BBOSW单次实验结果绘制出科学家合作网络拓扑及其社团划分见图 6, 其对应的模块度为0.865. BBOSW算法将网络划分成44个社团.选择22和23号社团分析拓扑结构(分别包含21个节点和7个节点),在查阅相关节点对应的学者具体情况(22号社团对应节点标号646、1 430~ 1 449,MANSFIELD T等所在课题组;23号社团对应节点标号1515、1505~1510,SALAFF J等所在的研究小组)后,发现社团内部的研究人员分别处于同一研究小组. 22号社团学者的研究方向主要是生物和复杂网络的结合(发表多项关于蛋白质网络特性的研究成果),23号社团学者主要研究方向为社会网络,其社团内部的学者互相之间合作紧密.新算法识别到的社团为现实世界中存在的研究小组,表明新算法可以有效进行社团探测与识别.
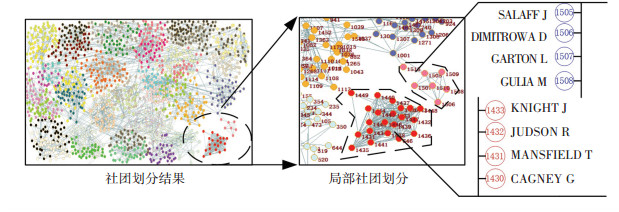
|
图 6 由网络科学家构成的合作网络的划分实验结果 Fig. 6 Experimental result for the netscience network |
1) 利用小世界效应加速优化算法,提出了一种新的社团识别算法.该算法利用BBO方法具有较强全局搜索能力的特点,初始化一个随机解空间,利用迁移和变异操作来更新个体,保证解的多样性,直接在潜在解中寻找最大化模块度的社团划分.
2) 结合小世界效应,利用具有小世界效应的拓扑网络具有较快信息传播速度的特点,建模栖息地之间迁移的过程,在保证解的多样性的情况下,来加快算法收敛的过程.
3) 使用现实网络以及人工合成网络测试算法效果,并与主流算法进行比较.实验结果表明所提出的算法精度较高,尤其对于社团结构较为模糊的网络,识别效果较好.
4) 将来的工作是利用小世界效应的性质来加速其他群体智能算法,将这种新策略扩展至其他算法中.
| [1] |
SUWEIS S, SIMINI F, BANAVAR J R, et al. Emergence of structural and dynamical properties of ecological mutualistic networks[J]. Nature, 2013, 500(7463): 449. DOI:10.1038/nature12438 |
| [2] |
GUIMERÀ R, MOSSA S, TURTSCHI A, et al. The worldwide air transportation network: anomalous centrality, community structure, and cities' global roles[J]. Proceedings of the National Academy of Sciences, 2005, 102(22): 7794. DOI:10.1073/pnas.0407994102 |
| [3] |
SAHAI T, SPERANZON A, BANASZUK A. Hearing the clusters of a graph: a distributed algorithm[J]. Automatica, 2012, 48(1): 15. DOI:10.1016/j.automatica.2011.09.019 |
| [4] |
WANG Jianwei, RONG Lili. Cascade-based attack vulnerability on the US power grid[J]. Safety Science, 2009, 47(10): 1332. DOI:10.1016/j.ssci.2009.02.002 |
| [5] |
LANCICHINETTI A, FORTUNATO S. Benchmarks for testing community detection algorithms on directed and weighted graphs with overlapping communities[J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2009, 80(1): 016118. DOI:10.1103/PhysRevE.80.016118 |
| [6] |
FORTUNATO S, HRIC D. Community detection in networks: a user guide[J]. Physics Reports, 2016, 59: 1. DOI:10.1016/j.physrep.2016.09.002 |
| [7] |
KOJAKU S, MASUDA N. Finding multiple core-periphery pairs in networks[J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2017, 96(5): 052313. DOI:10.1103/PhysRevE.96.052313 |
| [8] |
NEWMAN M E J. Finding community structure in networks using the eigenvectors of matrices[J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2006, 74(3): 036104. DOI:10.1103/PhysRevE.74.036104 |
| [9] |
NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2004, 69(2): 026113. DOI:10.1103/PhysRevE.69.026113 |
| [10] |
CLAUSET A, NEWMAN M E J, MOORE C. Finding community structure in very large networks[J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2004, 70(6): 06611. DOI:10.1103/PhysRevE.70.066111 |
| [11] |
FORTUNATO S, LATORA V, MARCHIORI M. Method to find community structures based on information centrality[J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2004, 70(5): 056104. DOI:10.1103/PhysRevE.70.056104 |
| [12] |
YANG Bo, FANG Huajing. Forced consensus in networks of double integrator systems with delayed input[J]. Automatica, 2010, 46(3): 629. DOI:10.1016/j.automatica.2010.01.013 |
| [13] |
YANG Bo, LI Xu, LIU Xiangwei, et al. Alternating between consensus and leader selection reveals community structure in networks[J]. Physica A: Statistical Mechanics and its Applications, 2019, 515: 693. DOI:10.1016/j.physa.2018.10.003 |
| [14] |
YANG Bo, HE He, HU Xiaoming. Detecting community structure in networks via consensus dynamics and spatial transformation[J]. Physica A: Statistical Mechanics and its Applications, 2017, 483: 156. DOI:10.1016/j.physa.2017.04.098 |
| [15] |
HE He, YANG Bo, HU Xiaoming. Exploring community structure in networks by consensus dynamics[J]. Physica A: Statistical Mechanics and its Applications, 2016, 450: 342. DOI:10.1016/j.physa.2015.12.140 |
| [16] |
KARRER B, NEWMAN M E J. Stochastic blockmodels and community structure in networks[J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2011, 83(1): 016107. DOI:10.1103/PhysRevE.83.016107 |
| [17] |
PIZZUTI C. Evolutionary computation for community detection in networks: a review[J]. IEEE Transactions on Evolutionary Computation, 2018, 22(3): 464. DOI:10.1109/TEVC.2017.2737600 |
| [18] |
DAN S. Biogeography-based optimization[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(6): 702. DOI:10.1109/TEVC.2008.919004 |
| [19] |
OLFATI-SABER R, FAX J A, MURRAY R M. Consensus and cooperation in networked multi-agent systems[J]. Proceedings of the IEEE, 2007, 95(1): 215. DOI:10.1109/JPROC.2006.887293 |
| [20] |
PENG Guansheng, TAN Suoyi, WU Jun, et al. Trade-offs between robustness and small-world effect in complex networks[J]. Scientific Reports, 2016, 6: 37317. DOI:10.1038/srep37317 |
| [21] |
QIU Tie, LUO Diansong, XIA Feng, et al. A greedy model with small world for improving the robustness of heterogeneous Internet of Things[J]. Computer Networks, 2016, 101: 127. DOI:10.1016/j.comnet.2015.12.019 |
| [22] |
SAOUD B, MOUSSAOUI A. Community detection in networks based on minimum spanning tree and modularity[J]. Physica A: Statistical Mechanicsand its Applications, 2016, 460: 230. DOI:10.1016/j.physa.2016.05.014 |
| [23] |
NEWMAN M E J, MOORE C, WATTS D J. Mean-field solution of the small-world network model[J]. Physical Review Letters, 2000, 84(14): 3201. DOI:10.1103/PhysRevLett.84.3201 |
| [24] |
NEWMAN M E J. Fast algorithm for detecting community structure in networks[J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2004, 69(6): 066133. DOI:10.1103/PhysRevE.69.066133 |
| [25] |
BLONDEL V D, GUILLAUME J L, LAMBIOTTE R, et al. Fast unfolding of communities in large networks[J]. Journal of Statistical Mechanics, 2008, 2008(10): 155. DOI:10.1088/1742-5468/2008/10/P10008 |
| [26] |
PIZZUTI C. Mesoscopic analysis of networks with genetic algorithms[J]. World Wide Web, 2013, 16(5): 545. DOI:10.1007/s11280-012-0174-4 |
| [27] |
FRED A L N, JAIN A K. Robust data clustering[C]//Proceedings of 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Madison, WI: IEEE Press, 2003: 128. DOI: 10.1109/CVPR.2003.1211462
|
| [28] |
FORTUNATO S. Community detection in graphs[J]. Physics Reports, 2009, 486(3): 75. DOI:10.1016/j.physrep.2009.11.002 |
| [29] |
ZACHARY W W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research, 1977, 33(4): 452. DOI:10.1086/jar.33.4.3629752 |
| [30] |
LUSSEAU D, SCHNEIDER K, BOISSEAU O J, et al. The bottlenose dolphin community of Doubtful Sound features a large proportion of long-lasting associations[J]. Behavioral Ecology and Sociobiology, 2003, 54(4): 396. DOI:10.1007/s00265-003-0651-y |
| [31] |
SOUAM F, AÏTELHADJ A, BABA-ALI R. Dual modularity optimization for detecting overlapping communities in bipartite networks[J]. Knowledge and Information Systems, 2014, 40(2): 455. DOI:10.1007/s10115-013-0644-8 |
| [32] |
GIRVAN M, NEWMAN M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences, 2002, 99(12): 7821. DOI:10.1073/pnas.122653799 |
| [33] |
LANCICHINETTI A, FORTUNATO S. Community detection algorithms:a comparative analysis[J]. Physical Review E, 2009, 80(5): 056117. DOI:10.1103/PhysRevE.80.056117 |
 2020, Vol. 52
2020, Vol. 52


