2. 佐治亚理工学院 乔治-伍德拉夫机械工程学院,佐治亚州 亚特兰大 30332-0405
2. George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta 30332-0405 GA, USA
在微观机械制造领域如纳米切削、微磨削、激光光整加工等,电子背散射衍射(electron backscatter diffraction,EBSD)作为一种新的微观图像采集与分析技术,其集成了显微组织分析与晶体学图像分析等模块,在晶体材料(如单晶铝、单晶铜)的亚微米级尺度对晶粒织构与微观特性分析中(如晶粒尺寸、取向、滑移位错、不同相分布、失效机理研究和应变评估)发挥了重要作用[1-3].然而,电子图像在采集、传输以及储存的过程中不可避免的受到外界噪声(如入射电子束加速电压、不稳定电流、取向成像步长过大等)的干扰,导致图像保真度差,影响了材料微观特性分析.在工程应用中,由于实时在线采集的需要,且为了防止材料晶粒发生驰豫现象,一般实验条件不允许图像重新采集,因此,对已污染微结构图像进行复原是微观机械制造领域中一个亟待解决的难题.
一般地,电子微结构图像复原表现在两个方面:有效去除干扰噪声以及保留或增强微结构图像的边缘与纹理等固有结构特征.传统的图像去噪方法可分为空间域去噪和变换域去噪.1)空间域去噪方法.如偏微分方程方法、维纳滤波方法、空间自适应滤波器等[4-6],其本质是考虑待估像素点与其邻域相邻像素点的加权平均来代替待估像素点的真实值,但该方法易造成边缘信息模糊以及纹理、边界丢失现象.2)变换域去噪方法.如正交基变换方法(如小波基等)、紧框架变换方法(如Ridgelet变换、Contourlet变换)等[7-8],正交基变换与多尺度紧框架变换去噪方法虽具有良好的时频域局部分析能力,但在图像边缘与细节处易产生平滑现象,且这两种方法均没有考虑图像结构纹理特征与冗余信息,无法对含有线、面等奇异特性的图像进行表征.因此,电子微结构图像去噪的难点在于:如何在抑制噪声的同时避免图像边缘被平滑且保留图像固有的结构与纹理特征.
稀疏表示方法利用过完备冗余字典取代传统的正交基与多尺度紧框架在稀疏域表示图像,过完备冗余字典充分考虑了微结构图像的冗余信息,可以更好地描述图像的线及边界等奇异特性,特别适合处理含有边界与纹理区域的电子图像.然而,冗余字典的设计是图像稀疏表示的关键环节,字典的选择直接影响稀疏向量的迭代计算与算法收敛性.因此,如何选择合适的冗余字典是本文研究的问题之一.
文献[9-10]提出了小波收缩去噪算法,其利用收缩函数对图像小波域系数进行取舍,该方法的核心表现为:1)收缩曲线的选取; 2)最优阈值的选择.目前,对于阈值的选取有Minimaxi阈值方法、Neighshrink阈值方法[11]以及SURE阈值方法[12].然而Neighshrink阈值与Minimaxi阈值多趋向于过扼杀小波变换系数,造成高频信息流失;SURE阈值多趋向于过保留小波变换系数,造成去噪效果不明显.
考虑到电子图像结构纹理信息与噪声信息的频率成分具有不确定性,且噪声干扰成分很可能掩盖图像特征信息,导致在去噪时,图像结构信息成分与噪声信息成分无法分离或相混叠,影响了图像特征信息的提取与分析.
对于冗余字典的设计问题,Haar小波是具有对称性和紧支撑特性的正交小波,且具有最优的时空域分辨率,故选择Harr小波冗余字典辅助图像稀疏表示.对于最优化的阈值计算问题,提出了一种基于Stein无偏风险估计准则的自适应阈值选择方法,该方法可计算得到最优化的阈值,有效平衡阈值选择的过大与过小问题,提高了图像信噪比.变分模态分解方法作为一种新的自适应信号与图像分解技术,该方法实质为多个自适应维纳滤波器,利用迭代搜寻求解约束变分模型,实现图像结构纹理部分与噪声成分的有效分离,最终得到若干个带通分量.因此,在图像去噪前,将二维变分模态分解方法引入到微结构图像分解中,实现图像固有特征信息与噪声的初步分离.
基于上述分析,提出了一种基于变分模态分解与Stein无偏风险估计方法相结合的电子图像噪声抑制方法,以铝合金、双相钢与钛合金Ti6Al4V 3种材料的晶粒取向EBSD图像为研究对象,利用提出方法对模拟含噪图像进行去噪,同时与一些主流的去噪方法如小波阈值方法、Neigh-Shrink方法、稀疏SURE方法以及KSVD方法进行比较分析,实验结果证实了本文提出算法的优越性.
1 变分模态分解不同于传统经验模态分解、局部均值分解与局部特征尺度分解等方法所使用的循环筛选与剥离的方式获取内禀模态分量或乘积模态分量,变分模态分解方法利用交替方向乘子算法(alternate direction method of multipliers, ADMM)不断搜寻约束变分模型的最优解,实现图像的自适应分解,其整体框架是一求解变分问题,每个模态的估计带宽与频率中心在迭代求解变分模型的过程中不断更新,最终将原始图像自适应剖分为若干个模态函数之和[13].一维信号变分模态分解方法的约束变分问题可表达为
| $ \left\{ \begin{array}{l} \min \left\{ {\sum\limits_k {{{\left\| {{\partial _t}\left[ {\delta (t) + \frac{j}{{\pi t}}} \right] * {u_k}(t){{\rm{e}}^{ - {\rm{j}}{\omega _k}t}}} \right\|}^2}} } \right\},\\ {\rm{S}}.\;{\rm{t}}.\;\;\sum\limits_k {{\omega _k}} = f. \end{array} \right. $ |
式中:f为原始信号;{uk}、{ωk}分别为分解得到的第k个模态的时域信号和中心频率;δ(t)为Dirac函数;k为模态总数;符号*为卷积.
推广至二维图像分解领域,对应的约束变分问题可变换为
| $ \begin{array}{l} L\left( {\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\},\lambda } \right) = \alpha \sum\limits_k {{{\left\| {\nabla \left[ {{u_{AS,k}}(x){{\rm{e}}^{ - {\rm{j}}\left( {{\omega _k},x} \right)}}} \right.} \right\|}^2}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\| {f\left( t \right) - \sum\limits_k {{u_k}} \left( t \right)} \right\|_2^2 + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\langle {\lambda \left( t \right),f\left( t \right) - \sum\limits_k {{u_k}} \left( t \right)} \right\rangle . \end{array} $ | (1) |
式中:f则变为原始图像;uAS, k(x)为uAS, k(x)= uk(x)*[δ(< x, ωk>)+
为求解上述变分约束模型的最优解,引入二次罚函数项参数α和Lagrange乘子λ(t), 变分约束模型(1)可简化为
| $\begin{aligned} L\left(\left\{u_{k}\right\},\left\{\omega_{k}\right\}, \lambda\right)=& \alpha \sum_{k}\left\|\nabla\left[u_{A S, k}(x) \mathrm{e}^{-j\left(\omega_{k}, x\right)} \|^{2}+\right.\right.\\ &\left\|f(t)-\sum_{k} u_{k}(t)\right\|_{2}^{2}+\\ &\left\langle\lambda(t), f(t)-\sum_{k} u_{k}(t)\right\rangle \end{aligned} $ |
利用ADMM算法求解上述变分约束问题的最优解[15-16],可将图像自适应分解为k个窄带IMF分量.具体算法步骤如下[13-14].
步骤1 初始化.
步骤2 执行循环, n=n+1.
步骤3 对于所有ω≥0,更新
| $ \begin{array}{l} \hat u_k^{n + 1}\left( \omega \right) = \\ \mathop {argmin}\limits_{{{\hat u}_k}} \left\{ {\alpha \left\| {j\left( {\omega - {\omega _k}} \right)\left[ {\left( {1 + sgn\left( {\omega \cdot {\omega _k}} \right)} \right){u_k}\left( \omega \right)} \right]} \right\|_2^2 + } \right.\\ \left. {\left\| {f\left( \omega \right) - \sum\limits_k {{{\hat u}_i}} \left( \omega \right) + \frac{{\lambda \left( \omega \right)}}{2}} \right\|_2^2} \right\}, \end{array} $ |
其中,(1+sgn(ω·ωk))uk(ω)=
| $ {{\hat u}_{AS,k}}\left( \omega \right) = \left\{ {\begin{array}{*{20}{l}} {2{u_k}\left( \omega \right),}&{{\rm{if }}\omega \cdot {\omega _k} > 0;}\\ {{{\hat u}_k}\left( \omega \right),}&{{\rm{if }}\omega \cdot {\omega _k} = 0;}\\ {0,}&{{\rm{if }}\omega \cdot {\omega _k} < 0.} \end{array}} \right. $ |
步骤4 更新
| $ \begin{array}{l} \omega _k^{n + 1}\left( \omega \right) = \\ \mathop {argmin}\limits_{{{\hat \omega }_k}} \left\{ {\alpha \left\| {j\left( {\omega - {\omega _k}} \right)\left[ {\left( {1 + sgn\left( {\omega \cdot {\omega _k}} \right)} \right){{\hat u}_k}\left( \omega \right)} \right]} \right\|_2^2} \right.. \end{array} $ |
步骤5 更新λ(ω), 即
| $ {\lambda ^{\hat n + 1}}\left( \omega \right) = {{\hat \lambda }^n}\left( \omega \right) + \tau \left( {\hat f\left( \omega \right) - \sum\limits_k {u_k^{\hat n + 1}} \left( \omega \right)} \right). $ |
步骤6 重复步骤2~步骤5,直至满足迭代停止条件,即
| $ \sum\limits_k {\left\| {u_k^{\hat n + 1} - \hat u_k^n} \right\|_2^2} /\left\| {\hat u_k^n} \right\|_2^2 < \varepsilon , $ |
结束循环.
最后,k个IMF分量可通过
为了有效地分离各个几何图案,且避免算法运算时间较长,将惩罚函数项参数α设为5 000,分量个数k设为5,利用二维变分模态分解算法(Bi-variational mode decomposition,BVMD)对合成重叠图像进行分解.图 2(a)~图 2(e)为分解得到的5个二维内禀模态分量,图 2(f)为重构图像,从图中可以看出BVMD方法分解得到的模态分量可显示清晰的椭圆图案与矩形图案.为了比较分解效果,利用二维经验模态分解方法(Bi-empirical mode decomposition, BEMD)对原始合成重叠图像进行分解[17-18].图 3为利用BEMD方法分解得到的BIMF分量,可发现BEMD方法仅得到1个BIMF分量,即各个分量分解失败.比较图 2、3可知,BEMD分解算法对于该重叠图像完全没有分解,即分解产生了严重的模态混叠现象;而BVMD方法不仅能有效去除伪分量,且每个IMF分量均为某一尺度范围内的的模态,彼此之间没有模态混叠,实现了对图像的多尺度表征.因此,二维变分模态分解方法分解效果优于二维经验模态分解方法.

|
图 3 二维经验模态分解方法分解得到的BIMF图像 Fig. 3 BIMF model images generated by BEMD method |
设y为含噪污染图像,x为理想无污染图像,A为冗余字典,图像稀疏表示可通过求解x的欧几里得范数表达为
| $ \mathop {\min }\limits_x \left\| x \right\|_2^2,{\rm{s}}{\rm{.t}}{\rm{. }}\left\| {y - \mathit{\boldsymbol{A}}x} \right\| \le \varepsilon , $ | (2) |
式中,ε为误差系数,通常ε=cNσ2,0.5≤c≤1.5,其中σ为噪声保准差,N为像素点.为求解式(2),引入拉格朗日乘子λ,有L(x)=‖x‖22+λ(Ax-y),公式两边分别对x求偏导,可得:
| $ \frac{{\partial L\left( x \right)}}{{\partial x}} = 2x + {\mathit{\boldsymbol{A}}^{\rm{T}}}\lambda , $ |
即
| $ {{\hat x}_{{\rm{opt}}}} = - \frac{1}{2}{\mathit{\boldsymbol{A}}^{\rm{T}}}\lambda , $ |
将该解带入到约束条件Ax=y中,可得:
| $ \mathit{\boldsymbol{A}}{{\hat x}_{{\rm{opt}}}} = - \frac{1}{2}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\lambda = y \Rightarrow \lambda = - 2{\left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right)^{ - 1}}y. $ | (3) |
将式(3)结果带入到
| $ {{\hat x}_{{\rm{opt}}}} = - \frac{1}{2}{\mathit{\boldsymbol{A}}^{\rm{T}}}\lambda = {\mathit{\boldsymbol{A}}^{\rm{T}}}{\left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right)^{ - 1}}y = {\mathit{\boldsymbol{A}}^ + }y. $ |
采用自适应阈值滤波算法,利用Haar小波构造字典A,去噪过程可由下式表示:
| $ \hat y = {\mathit{\boldsymbol{S}}_\lambda }\mathit{\boldsymbol{A}}{{\hat x}_{{\rm{opt}}}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{S}}_\lambda }\left( {{\mathit{\boldsymbol{A}}^ + }y} \right). $ |
式中: A+为字典A的Moore-Penrose逆; Sλ(z)为阈值标量算子; λ为阈值,即:当|z| < λ,Sλ(z)=0,否则,Sλ(z)=z. Haar小波冗余字典的构造过程如下:首先,对Haar小波进行2层分解,即利用核函数[+1, +1]/2与[+1, -1]/2的二维滤波器进行水平滤波,然后,利用同样核函数对2个输出进行垂直滤波,这样得到4副同样大小的图像,之后再对低通-低通(LL)图像进行相同的处理,最终得到7副同样大小的图像,字典冗余度即为7: 1[19].
由于Haar小波冗余字典A没有进行L2范数归一化,本文利用列范数来调整阈值[19],即向量A+y的第i元素ai+y可用‖ai‖2·λ为阈值进行处理,得到:
| $ \hat y = \mathit{\boldsymbol{AW}}{S_\lambda }\left( {{\mathit{\boldsymbol{W}}^{ - 1}}{\mathit{\boldsymbol{A}}^ + }y} \right), $ | (4) |
式中W为对角矩阵,对角线原子的范数为‖ai‖2.
不难发现,式(4)阈值参数λ是未知的,一般阈值参数λ可通过计算
| $ {\rm{MSE}} = E\left[ {\eta \left( {\hat y,y} \right)} \right] = E\left[ {\left\| {\hat y - {y_0}} \right\|_2^2} \right], $ |
展开上述表达式,得到:
| $ \begin{array}{l} E\left[ {\left\| {\hat y - {y_0}} \right\|_2^2} \right] = E\left[ {\left\| {h\left( {y,\theta } \right) - {y_0}} \right\|_2^2} \right] = \\ E\left[ {\left\| {h\left( {y,\theta } \right)} \right\|_2^2} \right] - 2E\left[ {h{{\left( {y,\theta } \right)}^{\rm{T}}} \cdot {y_0}} \right] + \left\| {{y_0}} \right\|_2^2 = \\ E\left[ {\left\| {h\left( {y,\theta } \right)} \right\|_2^2} \right] - 2E\left[ {h{{\left( {y,\theta } \right)}^{\rm{T}}} \cdot {y_0}} \right] + {\rm{Const}}. \end{array} $ | (5) |
可知式(5)第2项为未知量y0的函数,将y0=y-v带入式(5)第2项,可得:
| $ \begin{array}{l} E\left[ {h{{\left( {y,\theta } \right)}^{\rm{T}}} \cdot {y_0}} \right] = \\ E\left[ {h{{\left( {y,\theta } \right)}^{\rm{T}}} \cdot y} \right] - E\left[ {h{{\left( {y,\theta } \right)}^{\rm{T}}} \cdot v} \right]. \end{array} $ |
设h(y, θ)的第i元素为hi(y, θ),噪声v的第i元素为vi,计算:
| $ \begin{array}{l} E\left[ {h{{\left( {y,\theta } \right)}^{\rm{T}}} \cdot {y_0}} \right] = \\ E\left[ {h{{\left( {y,\theta } \right)}^{\rm{T}}} \cdot y} \right] - \sum\limits_{i = 1}^N {E\left[ {{h_i}{{\left( {y,\theta } \right)}^{\rm{T}}} \cdot {v_i}} \right]} = \\ E\left[ {h{{\left( {y,\theta } \right)}^{\rm{T}}} \cdot y} \right] - \sum\limits_{i = 1}^N {\int_{ - \infty }^\infty {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} \sigma }}{h_i}\left( {y,\theta } \right)} } \cdot \\ {v_i}\exp \left( { - \frac{{v_i^2}}{{2{\sigma ^2}}}} \right){\rm{d}}{v_i}. \end{array} $ | (6) |
假设hi(y, θ)关于y可微,对式(6)的积分项进行分部积分法求解,即∫u(x)v′(x)dx=u(x)v(x)- ∫u′(x)v(x)dx,有
| $ \begin{array}{l} E\left[ {{h_i}\left( {y,\theta } \right) \cdot {v_i}} \right] = \\ \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} \sigma }}\int_{ - \infty }^\infty {{h_i}} \left( {y,\theta } \right){v_i} \cdot \exp \left( { - \frac{{v_i^2}}{{2{\sigma ^2}}}} \right){\rm{d}}{v_i} = \\ - \frac{{{\sigma ^2}}}{{\sqrt {2{\rm{ \mathsf{ π} }}} \sigma }}\int_{ - \infty }^\infty {{h_i}} \left( {y,\theta } \right)\left[ {\frac{d}{{{\rm{d}}{v_i}}}\exp \left( { - \frac{{v_i^2}}{{2{\sigma ^2}}}} \right)} \right]{\rm{d}}{v_i} = \\ - \frac{\sigma }{{\sqrt {2{\rm{ \mathsf{ π} }}} }}\left\{ {\left[ {{h_i}\left( {y,\theta } \right)\exp \left( { - \frac{{v_i^2}}{{2{\sigma ^2}}}} \right)} \right]_{ - \infty }^\infty - \int_{ - \infty }^\infty {\frac{d}{{{\rm{d}}{v_i}}}} {h_i}\left( {y,\theta } \right) \cdot } \right.\\ \left. {\exp \left( { - \frac{{v_i^2}}{{2{\sigma ^2}}}} \right){\rm{d}}{v_i}} \right\}. \end{array} $ | (7) |
假设abs[hi(y, θ)]有界,式(7)第1项为0可消去,由
| $ \begin{array}{l} E\left[ {{h_i}\left( {y,\theta } \right) \cdot {v_i}} \right] = \\ \frac{\sigma }{{\sqrt {2{\rm{ \mathsf{ π} }}} }}\int_{ - \infty }^\infty {\frac{{{\rm{d}}{h_i}(y,\theta )}}{{{\rm{d}}{y_i}}}} \cdot \exp \left( { - \frac{{v_i^2}}{{2{\sigma ^2}}}} \right){\rm{d}}{v_i} = \\ {\sigma ^2}E\left[ {\frac{{{\rm{d}}{h_i}(y,\theta )}}{{{\rm{d}}{y_i}}}} \right]. \end{array} $ |
综上所述,最终最小均方误差为
| $ \begin{array}{l} {\rm{MSE}} = E\left[ {\left\| {h(y,\theta ) - {y_0}} \right\|_2^2} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;E\left[ {\left\| {h(y,\theta )} \right\|_2^2} \right] - 2E\left( {h{{(y,\theta )}^{\rm{T}}} \cdot y} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;2{\sigma ^2}\sum\limits_{i = 1}^N E \left[ {\frac{{{\rm{d}}{h_i}\left( {y,\theta } \right)}}{{{\rm{d}}{y_i}}}} \right] + {\rm{Const}} = \\ \;\;\;\;\;\;\;\;\;\;\;E\left[ {\left\| {h\left( {y,\theta } \right)} \right\|_2^2} \right] - 2h{\left( {y,\theta } \right)^{\rm{T}}} \cdot y + \\ \;\;\;\;\;\;\;\;\;\;\;\left. {2{\sigma ^2}\nabla \cdot h\left( {y,\theta } \right)} \right] + {\rm{Const}}. \end{array} $ | (8) |
因此,公式η(
| $ \begin{array}{*{20}{c}} {\eta (h(y,\theta ),y) = \left[ {\left\| {h(y,\theta )} \right\|_2^2} \right] - 2h{{{(^y},\theta )}^{\rm{T}}} \cdot y + }\\ {2{\sigma ^2}\nabla \cdot h(y,\theta ).} \end{array} $ | (9) |
根据式(4)可知,
| $ \frac{{{\rm{d}}h(y,\theta )}}{{{\rm{d}}y}} = {\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{S}}_\lambda ^\prime \left( {\mathit{\boldsymbol{A}}_1^ + y} \right)\mathit{\boldsymbol{A}}_1^ + , $ | (10) |
式中, S′λ(A1+y)为对角阵,其对角线的元素是收缩曲线的微分在向量A1+y上的投影.假设收缩曲线可导,此处用一偶数K对硬阈值曲线进行平滑处理,即
| $ {\mathit{\boldsymbol{S}}_\lambda }\left( z \right) = \frac{{{z^{K + 1}}}}{{{z^K} + {\lambda ^K}}} = z \cdot \frac{{{{(z/\lambda )}^K}}}{{{z^K}/\lambda + 1}}, $ | (11) |
求导可得:
| $ \begin{array}{l} \mathit{\boldsymbol{S}}_\lambda ^\prime (z) = \frac{{{z^{2K}} + (K + 1){{(z\lambda )}^K}}}{{{{\left( {{z^K} + {\lambda ^K}} \right)}^2}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{{{(z/\lambda )}^{2K}} + (K + 1){{(z/\lambda )}^K}}}{{{{\left( {{{(z/\lambda )}^K} + 1} \right)}^2}}}. \end{array} $ | (12) |
由于硬阈值收缩曲线不具有连续可导性质,为了保证收缩曲线连续且具有无穷阶导数,利用偶数K对硬阈值收缩曲线进行平滑逼近.本文选取K=20所对应的阈值曲线,该收缩曲线连续且具有无穷阶导数,便于数值计算[19].
将式(10)~式(12)带入式(9)中,可得:
| $ \begin{array}{l} \eta (h(y,\lambda ),y) = \left[ {\left\| {{\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{S}}_\lambda }\left( {\mathit{\boldsymbol{A}}_1^ + y} \right)} \right\|_2^2} \right] - \\ 2{\mathit{\boldsymbol{S}}_\lambda }\left( {\mathit{\boldsymbol{A}}_1^ + y} \right)\mathit{\boldsymbol{A}}_2^ + y + 2{\sigma ^2}tr\left( {{\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{S}}_\lambda ^\prime \left( {\mathit{\boldsymbol{A}}_1^ + y} \right)\mathit{\boldsymbol{A}}_1^ + } \right). \end{array} $ | (13) |
利用A1=AW-1, A2= AW, 式(13)第3项可简化为
| $ \begin{array}{l} tr\left( {{\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{S}}_\lambda ^\prime \left( {\mathit{\boldsymbol{A}}_1^ + y} \right)\mathit{\boldsymbol{A}}_1^ + } \right) = tr\left( {\mathit{\boldsymbol{S}}_\lambda ^\prime \left( {\mathit{\boldsymbol{A}}_1^ + y} \right)\mathit{\boldsymbol{A}}_I^ + {\mathit{\boldsymbol{A}}_2}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;tr\left( {\mathit{\boldsymbol{S}}_\lambda ^\prime \left( {\mathit{\boldsymbol{A}}_1^ + y} \right){\mathit{\boldsymbol{W}}^{ - 1}}{\mathit{\boldsymbol{A}}^ + }\mathit{\boldsymbol{AW}}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;tr\left( {\mathit{\boldsymbol{WS}}_\lambda ^\prime \left( {\mathit{\boldsymbol{A}}_1^ + y} \right){\mathit{\boldsymbol{W}}^{ - 1}}{\mathit{\boldsymbol{A}}^ + }\mathit{\boldsymbol{A}}} \right). \end{array} $ | (14) |
由于Sλ(A1+y)是一对角阵,左乘W与右乘W-1可以抵消,式(13)第3项可简化为:tr(A2S′λ(A1+y)A1+)=tr(S′λ(A1+y)W2).
最后,利用黄金分割搜索法[19-21]对式(13)进行全局最小值搜索,得到峰值信噪比(peak signal to noise ratio, PSNR)参数随阈值λ的变化曲线的峰值,即为最佳自适应阈值,最终得到无污染图像的逼近图像
实验采用牛津仪器公司(http://www.ebsd.cn)公开提供的铝合金、双相钢与钛合金Ti6Al4V 3种金属材料的电子微结构图像进行去噪分析.首先对材料进行去油污、打磨,然后利用丙酮溶液浸泡、机械-化学抛光等技术对表面进行预处理,最后利用电子背散射衍射仪(AZtecHKL系统)采集得到铝合金,双相钢与钛合金Ti6Al4V 3种样品晶粒取向成像图.由于电子背散射衍射仪在图像采集系统内部可能由电子束电压或电流不稳定等原因会引起噪声,而这种噪声可能是高斯噪声或斑纹噪声等多个噪声叠加而成,故本实验在理想晶粒取向图像中加入高斯噪声和Speckle斑纹噪声,模拟含噪晶粒取向成像图.图 4(a)为理想铝合金晶粒取向图像,图 4(b)为叠加了噪声标准差为30的高斯噪声与Speckle斑纹噪声的灰度图像,图像大小为391×391,可知被污染的图像质量严重下降、边缘特征较模糊.

|
图 4 铝合金原始晶粒取向图像与加噪图像 Fig. 4 Original crystal orientation image of aluminium alloy and its noisy image |
利用BVMD方法对含噪图像进行分解,模态个数k设为5,惩罚函数项参数α设为5 000.图 5为分解得到的5个BIMF模态分量结果,由图 5分解效果可看出BVMD方法能很好地克服模态混叠,实现了对加噪图像的多尺度表征,其中,前4个模态分量为高频分量或者噪声信息,而BIMF5模态分量包含了原始图像的固有特征信息,即BVMD方法实现了图像固有特征信息与干扰噪声的初步分离.由于BIMF1~BIMF4模态分量干扰斑纹过多,特征频率成分与原始固有特征无关,因此选取BIMF5模态分量,利用稀疏SURE方法进行去噪分析.

|
图 5 二维变分模态分解得到的BIMF分量(算法执行时间639.200 995 s) Fig. 5 BIMF model components generated by BVMD method (execution time: 639.200 995 s) |
为验证本文提出算法的有效性,分别利用小波阈值去噪方法、Neigh邻域阈值收缩法(Neigh shrink)[22], 单一稀疏SURE方法以及文献[23-24]提出的KSVD方法进行对比分析.字典A由冗余Haar小波字典构成,字典冗余度为7,收缩函数为图 5所示,偶数K取20,采用归一化均方误差(normalized mean squared error, NMSE)、峰值信噪比(PSNR)与结构相似度(structural similarity, SSIM)参数作为判定标准,衡量以上方法的去噪复原效果.各参数定义如下:
| $ {\rm{NMSE}} = \frac{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{\left[ {x\left( {i,j} \right) - \hat y\left( {i,j} \right)} \right]}^2}} } }}{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{\left[ {x\left( {i,j} \right) - x\left( {\bar i,j} \right)} \right]}^2}} } }}, $ |
| $ {\rm{PSNR}} = 10{\log _{10}}\left( {\frac{{{{255}^2}}}{{{\rm{MSE}}}}} \right), $ |
| $ {\rm{SSIM}} = \frac{{\left( {2{\mu _x}{\mu _{\hat y}} + {c_1}} \right)\left( {2{\sigma _{x,\hat y}} + {c_2}} \right)}}{{\left( {\mu _x^2 + \mu _{\hat y}^2 + {c_1}} \right)\left( {\sigma _x^2 + \sigma _{\hat y}^2 + {c_2}} \right)}}. $ |
式中:x为原始无污染图像;
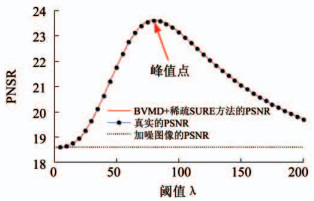
选择BIMF5模态分量作为稀疏SURE输入图像,图 6为PSNR参数随阈值λ变化而变化的趋势,图中虚线为含噪图像对无污染图像求得的PSNR值,可看出本文提出的方法(即BVMD+稀疏SURE)得到的PSNR曲线与真实PSNR曲线十分吻合.因此,可知BVMD+稀疏SURE曲线的峰值点(80, 23.593 5)所对应的去噪效果最佳,最佳阈值为80.
|
图 6 稀疏收缩PSNR与阈值λ的变化关系(峰值点:80, 23.593 5) Fig. 6 Relationship between sparse contraction PSNR and threshold λ (maximum point: 80, 23.593 5) |
图 7(a)~图 7(d)分别为利用小波阈值去噪方法、Neigh邻域阈值收缩法、单一稀疏SURE方法、KSVD方法与本文方法得到的去噪效果图,对于小波阈值去噪算法:本文利用小波软阈值去噪算法进行去噪,软阈值函数为

|
图 7 各类方法得到的铝合金晶粒取向图像去噪效果 Fig. 7 Denoising results of crystal orientation image of aluminium alloy via different methods |
| $ \hat \omega (j,l) = \left\{ {\begin{array}{*{20}{l}} {sign[\omega (j,l)](|\omega (j,l) - \beta |),\omega (j,l) \ge \beta ;}\\ {0,\omega (j,l) < \beta .} \end{array}} \right. $ |
式中:sign(x)为符号函数;β为预先设置的阈值,且
| 表 1 各类方法的去噪性能指标对比 Tab. 1 Comparison of denoising performance of different methods |
观察5种方法降噪图像的视觉质量,小波阈值去噪算法生成的图像比较模糊,依然残存大量的噪声斑点,去噪效果差;Neigh-Shrink方法提高了图像的去噪效果,但在图像边缘和细节处产生一定程度的平滑现象,使得轮廓不够清晰,原因在于该方法进行阈值处理是考虑其周围系数的分布特点;单一稀疏SURE方法与本文方法生成图像较好的保存了纹理细节,没有伪像,各类评价指标很接近,但单一稀疏SURE方法得到的图像整体比较平滑,晶界部分较模糊,而本文方法较好的克服了这一点,晶界线条更为清晰,视觉效果有明显改善,这验证了BVMD方法在微结构图像预分解起到了重要作用.在客观衡量指标上,由表 1可看出,本文提出的方法得到的峰值信噪比最高,达到23.593 5 dB,也突破了稀疏SURE收缩曲线得到最大值(23.445 1 dB),比Neigh-Shrink方法高0.39 dB,比KSVD方法高2.895 dB,比小波阈值去噪算法高3.07 dB.
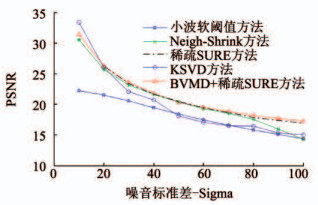
为了考察本文方法相对于其他几种方法对噪声的鲁棒性,选取标准差分别为10, 20, 30, …, 90, 100高斯噪声与Speckle斑纹噪声的10副微结构晶粒取向成像图作为去噪对象,采用峰值信噪比PSNR作为判定标准.图 8显示了各类方法的去噪效果PSNR随噪声标准差变化的趋势,可以看出,本文方法的PSNR相对于其他3种算法具有明显的优势,尤其是当噪声强度增大时优越性更加明显;小波阈值方法的去噪效果最差,这是由于阈值选择缺乏自适应性,获取的小波系数与真实小波系数有偏差,造成重构图像精度降低,产生振铃与伪Gibbs效应,导致图像模糊;当噪声标准差大于70时,Neigh-Shrink方法的去噪效果迅速降低,这是由于Neigh-Shrink方法是依赖小波变换所得细节子带系数与其邻域图像结构信息之间相关分布关系,噪声级数变大,邻域图像结构信息附带的噪声信息增多,导致去噪效果降低;另外,从整体来看,KSVD算法随噪声标准差变化幅度下降较快,在噪声方差较低时,KSVD冗余字典可有效刻画微结构图像的细节信息,重构精度高,但随着噪声方差进一步增大,KSVD字典过于冗余,字典含有较多无用信息,图像边缘细节信息无法表达,去噪效果大大降低.相比单纯稀疏SURE方法,本文提出的方法由于预先对含噪图像利用BVMD分解,去除了高频无用噪声,图像噪声抑制效果优于单纯稀疏SURE方法.
|
图 8 各类方法对晶粒取向图像去噪PSNR值随标准差-Sigma变化曲线 Fig. 8 Variation of crystal orientation image denoising PSNR value with noise standard variance-Sigma under different methods |
为了进一步验证提出方法的普适性,分别引入牛津仪器(http:www.ebsd.cn)公开的双相钢样品的EBSD相分布微结构图像(奥氏体和铁素体)与钛合金Ti6Al4V材料微结构EBSD图像再次进行去噪分析,在理想微结构图像中分别加入噪声标准差为30的高斯噪声和Speckle斑纹噪声,图 9(a)、图 9(b)分别为双相钢样品的EBSD相分布微结构图像与噪声污染图像,图 10(a)、图 10(b)分别为钛合金Ti6Al4V材料微结构图像与噪声污染图像.同样利用BVMD分解方法、构造Harr小波冗余字典以及Stein无偏风险估计方法进行去噪,最终两种材料的去噪图像分别如图 9(c)、图 10(c)所示,由于篇幅所限,此处省略BVMD分解结果.对比去噪前与去噪后的图像可知,双相钢材料图像的峰值信噪比由加噪前的18.598 1 dB提升至25.784 8 dB,钛合金Ti6Al4V材料图像的峰值信噪比由加噪前的18.569 9 dB提升至24.587 5 dB,噪声图像边缘特征模糊现象得到改善,去噪后的图像边界纹理信息更加清晰,视觉效果大大提升.图 11、图 12分别为利用小波软阈值方法、Neigh-Shrink方法、稀疏SURE方法与KSVD方法对双相钢材料与钛合金材料进行去噪得到的去噪图像对比图,结果进一步验证了本文所提出算法的优越性.

|
图 9 双相钢材料的EBSD微结构图像、噪声污染图像与本文方法去噪图像 Fig. 9 EBSD image, noisy image, and denoised image (generated by proposed method) of dual-phase steel |

|
图 10 钛合金Ti6Al4V材料微结构EBSD图像、噪声污染图像与本文方法去噪图像 Fig. 10 EBSD image, noisy image, and denoised image (generated by proposed method) of Ti6Al4V |

|
图 11 各类对比方法得到的双相钢材料晶粒取向图像去噪结果 Fig. 11 Denoising results of crystal orientation image of dual-phase steel via different methods |

|
图 12 各类对比方法得到的钛合金Ti6Al4V材料晶粒取向图像去噪结果 Fig. 12 Denoising results of crystal orientation image of Ti6Al4V via different methods |
1) 针对电子微结构图像的噪声干扰问题,提出了一种基于变分模态分解与稀疏Stein无偏风险估计方法相结合的去噪方法,具体以铝合金,含奥氏体和铁素体的双相钢与钛合金Ti6Al4V的背散射衍射含噪模拟图像为例进行降噪分析.
2) 利用二维变分模态分解方法可有效地将含噪电子微结构图像按照不同尺度、不同频率分离为固有特征信息成分与高频噪声信息成分.
3) 推导了基于稀疏Stein无偏风险估计的目标优化收缩曲线,并用黄金分割法搜索得到全局最佳自适应阈值,该阈值的选取接近真实峰值信噪比曲线的最大点.图像稀疏表示过程中利用了Haar小波冗余字典,其能充分考虑微结构图像的结构冗余模式,可以更好地刻画图像的边界、纹理等固有特性.
4) 结果表明, 无论在客观去噪指标还是视觉效果方面,相比其他去噪方法,本文提出的方法均显示较优越的去噪性能.以铝合金为例,证明了当噪声标准差为30时,该方法去噪结果的峰值信噪比PSNR值高于Neigh-Shrink去噪方法0.39 dB,比KSVD方法高2.895 dB,高于小波阈值去噪算法3.07 dB,较单纯稀疏SURE方法更大程度提高了图像视觉清晰度;并随着噪声标准差级别的增大,图像去噪鲁棒性较高,为海量的微结构图像去噪提供了新的思路.
5) 在BVMD预分解图像的过程中,模态个数k与二次罚函数项α的选择具有一定的经验性,且交替方向乘子算法求解变分约束问题最优解的循环计算,Haar小波冗余字典的构造,导致整体抑噪运行速率较慢,仍具有较大的改进空间.
| [1] |
LIN Y C, HE Daoguang, CHEN Mingsong, et al. EBSD analysis of evolution of dynamic recrystallization grains and δ phase in a nickel-based superalloy during hot compressive deformation[J]. Materials & Design, 2016, 97(5): 13. DOI:10.1016/j.matdes.2016.02.052 |
| [2] |
LANGLOIS C, DOUILLARD T, YUAN H, et al. Crystal orientation mapping via ion channeling: An alternative to EBSD[J]. Ultramicroscopy, 2015, 157: 65. DOI:10.1016/j.ultramic.2015.05.023 |
| [3] |
WU Mingwei, CAI Wenzhang. Phase identification in boron-containing powder metallurgy steel using EBSD in combination with EPMA[J]. Materials Characterization, 2016, 113: 90. DOI:10.1016/j.matchar.2016.01.016 |
| [4] |
NADERNEJAD E, NIPOUR M. Image denoising using new pixon representation based on fuzzy filtering and partial differential equations[J]. Digital Signal Processing, 2012, 22(6): 913. DOI:10.1016/j.dsp.2012.04.016 |
| [5] |
TU Zhigang, POPPE R, VELTKAMP R C. Adaptive guided image filter for warping in variational optical flow computation[J]. Signal Processing, 2016, 127: 253. DOI:10.1016/j.sigpro.2016.02.018 |
| [6] |
AKAR S A. Determination of optimal parameters for bilateral filter in brain MR image denoising[J]. Applied Soft Computing, 2016, 43: 87. DOI:10.1016/j.asoc.2016.02.043 |
| [7] |
HUANG Qiangui, HAO Boya, CHANG Sheng. Adaptive digital ridgelet transform and its application in image denoising[J]. Digital Signal Processing, 2016, 52: 45. DOI:10.1016/j.dsp.2016.02.004 |
| [8] |
LI Dongming, ZHANG Lijuan, YANG Jinhua, et al. Research on wavelet-based contourlet transform algorithm for adaptive optics image denoising[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(12): 5029. DOI:10.1016/j.ijleo.2016.02.042 |
| [9] |
DONOHO D L. De-noising by soft-thresholding[J]. IEEE Transactions Information Theory, 1995, 41(3): 613. DOI:10.1109/18.382009 |
| [10] |
DONOHO D L, JOHNSTONE I M. Ideal spatial adaptation by wavelet shrinkage[J]. Biometrika, 1994, 81(3): 425. DOI:10.1093/biomet/81.3.425 |
| [11] |
STEIN C M. Estimation of the mean of a multivariate normal distribution[J]. Annals of Statistics, 1981, 9(6): 1135. DOI:10.1214/aos/1176345632 |
| [12] |
DONOHO D L, JOHNSTONE I M. Adapting to unknown smoothness via wavelet shrinkage[J]. Journal of the American Statistical Association, 1995, 90(432): 1200. DOI:10.1080/01621459.1995.10476626 |
| [13] |
DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531. DOI:10.1109/TSP.2013.2288675 |
| [14] |
DRAGOMIRETSKIY K, ZOSSO D. Two-dimensional variational mode decomposition[C]//Proceedings of the 10th International Conference on Energy Minimization Methods in Computer Vision and Pattern Recognition (EMMCVPR). Cham: Springer, 2015: 197. DOI: 10.1007/978-3-319-14612-6_15
|
| [15] |
ROCKAFELLAR R T. A dual approach to solving nonlinear programming problems by unconstrained optimization[J]. Mathematical Programming, 1973, 5(1): 354. DOI:10.1007/bf01580138 |
| [16] |
HESTENES M R. Multiplier and gradient methods[J]. Journal of Optimization Theory and Applications, 1969, 4(5): 303. DOI:10.1007/bf00927673 |
| [17] |
XU Guanlei, WANG Xiaotong, XU Xiaogang. On analysis of bi-dimensional component decomposition via BEMD[J]. Pattern Recognition, 2012, 45(4): 1617. DOI:10.1016/j.patcog.2011.11.004 |
| [18] |
葛光涛, 虞露. 二维经验模态可分离度及其量化计算[J]. 电子学报, 2013, 41(7): 1313. GE Guangtao, YU Lu. The bidimensional empirical mode detachable degree and its quantum calculation[J]. ACTA Electronica Sinica, 2013, 41(7): 1313. DOI:10.3969/j.issn.0372-2112.2013.07.011 |
| [19] |
ELAD M. Sparse and redunclant representations: from theory to applications in signal and image processing[M]. New York: Springer, 2010.
|
| [20] |
单昊, 杨慧珠. 基于Curvelet的Stein无偏风险估计图像去噪[J]. 清华大学学报(自然科学版), 2010, 50(8): 1307. SHAN Hao, YANG Huizhu. Curvelet based Stein's unbiased risk estimate for image denoising[J]. Journal Tsinghua University (Science & Technology), 2010, 50(8): 1307. DOI:10.16511/j.cnki.qhdxxb.2010.08.031 |
| [21] |
武晓玥, 郭宝龙, 唐璐, 等. 一种新的基于非下采样Contourlet变换的自适应图像去噪算法[J]. 光学学报, 2009, 29(8): 2147. WU Xiaoyue, GUO Baolong, TANG Lu, et al. A new adaptive image denoising method based on the nonsubsampled Contourlet transform algorithm[J]. Acta Optica Sinica, 2009, 29(8): 2147. DOI:10.3788/AOS20092908.2147 |
| [22] |
ZHOU Dengwen, CHENG Wengang. Image denoising with an optimal threshold and neighbouring window[J]. Pattern Recognition Letters, 2008, 29(11): 1694. DOI:10.1016/j.patrec.2008.04.014 |
| [23] |
AHARON M, ELAD M, BRUCKSTEIN A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311. DOI:10.1109/TSP.2006.881199 |
| [24] |
LI Qing, LIANG S Y. Microstructure images restoration of metallic aterials based upon KSVD and smoothing penalty sparse representation approach[J]. Materials, 2018, 11(4): 637. DOI:10.3390/ma11040637 |
 2020, Vol. 52
2020, Vol. 52




