2. 上海科技大学 物理科学与技术学院, 上海 201210;
3. 中国科学院大学, 北京 100049
2. School of Physical Science and Technology, ShanghaiTech University, Shanghai 201210, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
带隙基准电压是模拟集成电路中的关键模块,低温度系数的带隙基准电压有利于提升电池管理芯片对电池剩余电量估算的准确性.为了改善基准电压的温度系数,文献[1]采用高阶曲率补偿方法,产生与温度成正比和与温度成反比的电流补偿基准电压,基准电压温度系数小,但电源抑制比也较小.文献[2]采用指数补偿方法,利用三极管电流增益的温度特性产生与温度成非线性电流补偿基准电压,结构相对简单,但温度系数较大,电源抑制比小.文献[3]采用电阻温度补偿的方法,将两个具有负温度系数的电流流过具有正温度系数的电阻产生基准电压,基准电路功耗低,但是温度系数大,电源抑制比小.为了得到高精度低温度系数、高电源抑制比的基准电压,本文提出一种分段曲率补偿带隙基准电压.同时使用修调电路来减小非理想性因素对基准电压造成的影响.
带隙基准电压的精度对半导体制造过程中引入的非理想因素的影响十分敏感,通过仿真软件可以有效的模拟和预测系统性误差,如厄利电压、沟道长度调制效应等,而器件失配、绝对值偏差和封装应力等非理想因素是随机的[4],且随着带隙基准电路复杂程度的提高,精度受误差影响更加严重.基准源电路的初始误差约为±2%~±3.5%[4].为获得高精度基准电压,可以采用电阻修调技术.本文提出一种新的芯片级修调方法来快速获得最低的温度系数.若使用逐次逼近最优温度曲线的方法时,测试10块芯片的平均修调次数为8.7次.若采用本文提出的基于计算斜率的修调方法,测试10块芯片的平均修调次数为3.5次,效率提升59.8%.通过设计分段曲率补偿结构和修调方法,得到温度系数低,电压幅值可调的基准电压,同时提高了工作效率.
1 分段曲率补偿带隙基准工作原理根据半导体器件基本原理,三极管的基极-发射极电压VBE具有负的温度系数,两个具有不同电流密度的三极管的基极-发射极电压差值△VBE具有正温度系数.带隙基准电压是将上述两个具有相反温度系数的电压以合适的权重相加,获得一阶补偿的接近零温度系数的基准电压[5].对于基极-发射极正向偏置工作的三极管,VBE和温度相关公式为[6-9]
| $V_{\mathrm{BE}}(T)=V_{\mathrm{G0}}-\left[V_{\mathrm{G0}}-V_{\mathrm{BE}}\left(T_{\mathrm{r}}\right)\right]\left(\frac{T}{T_{\mathrm{r}}}\right)-\\ (\eta-\alpha) V_{\mathrm{T}} \ln \left(\frac{T}{T_{\mathrm{r}}}\right). $ |
式中:VG0为硅在绝对零度下的带隙电压; T为绝对温度; Tr为参考温度; η为与工艺相关常数; α为集电极电流的温度指数; VT为热电压.
分段曲率补偿工作原理如图 1所示,VBE随温度变化存在高阶项,VPTAT是与绝对温度成正比的线性电压[10],VNL是高阶补偿电压,在一阶补偿带隙基准电压VBE+VPTAT基础上,分别在低温和高温对基准电压与温度相关的高阶项进行补偿,从而提高带隙基准电压的精度.Vref1是经过分段曲率补偿后产生的高精度的基准电压[11].

|
图 1 分段曲率补偿方法原理 Fig. 1 Principle of the piecewise curvature compensated method |
分段曲率补偿带隙基准电压电路如图 2所示,包含Brokaw核心电路、分段曲率补偿电路、启动电路、温度系数修调电路RTEMP和电压幅值修调电路ROUT.Brokaw核心电路产生的线性电流IPTAT与绝对温度T成正比,补偿电流IS由Q3和R5产生:

|
图 2 分段曲率补偿基准电路原理图 Fig. 2 Schematic of the piecewise curvature compensated bandgap reference circuit |
| $I_{\mathrm{PTAT}}=\frac{\Delta V_{\mathrm{BE}}}{R_{3}}=\frac{k T}{q R_{3}} \ln M, \\ I_{\mathrm{S}}=\frac{V_{\mathrm{ref1}}-V_{\mathrm{BE} 3}}{R_{5}}, \\ V_{\mathrm{ref1}}=V_{\mathrm{BE2}}+2 I_{\mathrm{PTAT}}\left(R_{\mathrm{TEMP}}+R_{4}\right)+I_{\mathrm{NL}} R_{4}=\\ V_{\mathrm{BE} 2}+\frac{2 k T \ln M}{q R_{3}}\left(R_{\mathrm{TEMP}}+R_{4}\right)+\left(I_{1}+I_{2}\right) R_{4}, $ |
式中M为三极管Q1和Q2的发射极面积之比,高阶补偿电流IS远小于线性电流IPTAT.
由于三极管电压VBE3与温度成负相关,所以补偿电流IS与温度成正相关.通过镜像电路(MP5、MP6和MP7),流过MP5和MP6的电流为IS.当MP1、MP2、MP3、MP4工作在亚阈值区时,分段曲率补偿电流I1和I2可由下面公式推导[12-13]得到:
| $\begin{aligned} V_{A}=& 2 I_{\mathrm{PTAT}}\left(R_{\mathrm{TEMP}}+R_{4}\right)+I_{\mathrm{NL}} R_{4} \approx \\ & 2 I_{\mathrm{PTAP}}\left(R_{\mathrm{TEMP}}+R_{4}\right), \end{aligned} $ | (1) |
| $\left\{\begin{array}{l}I_{1}+I_{3}=I_{2}+I_{4}=I_{\mathrm{S}} , \\ I_{1}=I_{0} \exp \left(\frac{V_{\mathrm{E}}-V_{\mathrm{L}}}{\zeta V_{\mathrm{T}}}\right), I_{2}=I_{0} \exp \left(\frac{V_{\mathrm{A}}-V_{\mathrm{R}}}{\zeta V_{\mathrm{T}}}\right) , \\ I_{3}=I_{0} \exp \left(\frac{V_{\mathrm{A}}-V_{\mathrm{L}}}{\zeta V_{\mathrm{T}}}\right), I_{4}=I_{0} \exp \left(\frac{V_{\mathrm{C}}-V_{\mathrm{R}}}{\zeta V_{\mathrm{T}}}\right)\end{array}\right., $ | (2) |
| $V_{\mathrm{E}}=\frac{R_{2}+R_{7}}{R_{1}+R_{2}+R_{7}} V_{\mathrm{ref1}}, $ | (3) |
| $\left\{\begin{array}{l}I_{1}+I_{3}=I_{2}+I_{4}=I_{\mathrm{S}}, \\ I_{1}=I_{0} \exp \left(\frac{V_{\mathrm{E}}-V_{\mathrm{L}}}{\zeta V_{\mathrm{T}}}\right), I_{2}=I_{0} \exp \left(\frac{V_{\mathrm{A}}-V_{\mathrm{R}}}{\zeta V_{\mathrm{T}}}\right), \\ I_{3}=I_{0} \exp \left(\frac{V_{\mathrm{A}}-V_{\mathrm{L}}}{\zeta V_{\mathrm{T}}}\right), I_{4}=I_{0} \exp \left(\frac{V_{\mathrm{C}}-V_{\mathrm{R}}}{\zeta V_{\mathrm{T}}}\right), \end{array}\right. $ |
| $\left\{\begin{aligned} I_{1}=\frac{I_{1}}{I_{1}+I_{3}} I_{\mathrm{S}}=& \frac{\exp \left(\frac{V_{\mathrm{E}}-V_{\mathrm{A}}}{\zeta V_{\mathrm{T}}}\right)}{\exp \left(\frac{V_{\mathrm{E}}-V_{A}}{\zeta V_{\mathrm{T}}}\right)+1} I_{\mathrm{S}}, \\ I_{2}=\frac{I_{2}}{I_{2}+I_{4}} I_{\mathrm{S}}=& \frac{\exp \left(\frac{V_{\mathrm{A}}-V_{\mathrm{C}}}{\zeta V_{\mathrm{T}}}\right)}{\exp \left(\frac{V_{\mathrm{A}}-V_{\mathrm{C}}}{\zeta V_{\mathrm{T}}}\right)+1} I_{\mathrm{S}}. \end{aligned}\right. $ | (4) |
式中:INL远小于IPTAP,INLR4可忽略;ζ为亚阈值非理想因子.
运算放大器反馈环路使Vref1与B点电压相等,通过电阻串R1、R2、R7分压得到C点和E点电压,从式(1)~式(3)中可以得知,电压VA、VC、VE的计算公式,Vref1为确定值,可以通过调节电阻RTEMP、R4、R1、R2、R7的阻值和电流IPTAT来控制电压VA、VC、VE的大小,使VC < VA < VE,仿真结果如图 3(a)所示.由式(4)和图 3(b)仿真结果可知,I1具有正温度系数,I2具有负温度系数.

|
图 3 电压和电流仿真温度特性曲线 Fig. 3 Simulated temperature dependence of voltage and current |
基于0.35 μm BCD工艺,基准电压的最优温度曲线和在不同工艺角下的温度曲线如图 4所示,在-40℃~125℃内,分段曲率补偿电压最优工艺角(TT)的温度系数为0.84×10-6/℃,最差工艺角(FF)的温度系数为5.72×10-6/℃.

|
图 4 基准电压仿真温度特性曲线 Fig. 4 Simulated temperature dependence of reference voltage |
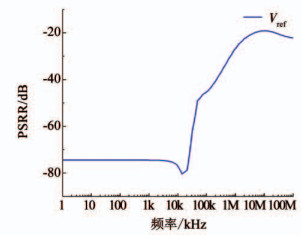
对基准电路进行电源抑制比(PSRR)仿真,如图 5所示,仿真基准电压Vref的电源抑制比为-74.43 dB@10 Hz,-74.43 dB@100 Hz,-74.43 B@1 kHz,-77.47 dB@10 kHz,-45.2 dB@ 100 kHz,-26.55 dB@1 MHz.
|
图 5 仿真基准电压Vref的电源抑制比 Fig. 5 Simulated PSRR of reference voltage Vref |
为了使电路脱离零状态开始工作,基准电路加入启动电路,如图 2所示,Dis为电路的使能端,P1、P2连接运放A1的偏置电路,当Dis为高电平时,MN1、MN2开启,MP10关闭,F点电压被拉至零电位,Vref1也被拉至零电位,整个电路关闭.当Dis为低电平使能时,MN1、MN2关闭,MP9、MP10开启,F点电位被抬升,因为三极管Q6的集电极和基极连在一起,F点电位约为三极管阈值的两倍,Q7、Q8导通迫使Vref1离开零电压工作状态,基准电路启动,当Vref1输出正常时,Q7,Q8关闭,启动电路工作完成.
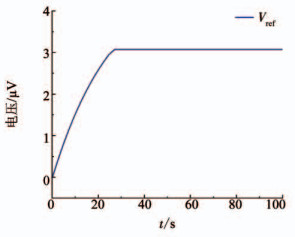
对分段曲率补偿基准电压的建立时间进行仿真,仿真结果如图 6所示,基准电压Vref在10 nF负载电容时的建立时间为27.5 us.
|
图 6 建立时间仿真 Fig. 6 Simulation of setting time |
为了减小非系统性误差产生的影响,通过温度系数修调电路RTEMP改善基准电压的温度系数[13].高阶补偿基准电压的非线性校正分量引入的随机误差与线性随机误差相比,通常情况下都比较小,这是由于非线性校正分量的幅度一般比一阶分量要小,所以对一阶线性校正电流2IPTAT流过的电阻RPTAP进行修调.
图 7为温度系数修调网络,每个修调电阻并联一个修调熔丝,根据二进制权重规则,从低位到高位,修调电阻阻值依次增大两倍,因此,该修调网络接入电路的电阻阻值可以通过7位二进制码N来控制.根据基准电压Vref1公式,将Vref1对绝对温度T进行求导[14-15]:

|
图 7 温度系数修调电路图 Fig. 7 Schematic of the temperature coefficient trimming circuit |
| $\begin{aligned} \frac{\partial V_{\mathrm{ref1}}}{\partial T}=& \frac{\partial V_{\mathrm{BE} 2}}{\partial T}+\frac{\partial\left[2 I_{\mathrm{PTAT}}\left(R_{\mathrm{TEMP}}+R_{4}\right)+I_{\mathrm{NL}} R_{4}\right]}{\partial T} \approx \\ & \frac{\partial V_{\mathrm{BE} 2}}{\partial T}+\frac{{2k\ln M}}{q}\frac{{\left( {{R_{{\rm{TEMP}}}} + {R_4}} \right)}}{{{R_3}}}, \end{aligned} $ |
| ${R_{{\rm{TEMP\_LSB}}}}=R_{\mathrm{TEMP}}(N+1)-R_{\mathrm{TEMP}}(N), $ |
| $\begin{aligned} \Delta S=& \frac{\partial V_{\mathrm{ref1}}}{\partial T}\left(R_{\mathrm{TEMP}}(N+1)\right)-\frac{\partial V_{\mathrm{ref1}}}{\partial T}\left(R_{\mathrm{TEMP}}(N)\right)=\\ & \frac{{2k\ln M}}{q}\frac{{{R_{{\rm{TEMP\_LSB}}}}}}{{{R_3}}}. \end{aligned}. $ |
式中:INL远小于IPTAP; ΔS为不同码值之间电压温度曲线斜率的差值;RTEMP_LSB为最低有效电阻.
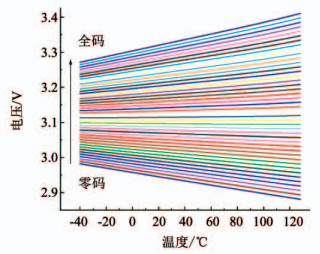
从上式可知ΔS是固定值.从零码(N=0000000)到全码(N=1111111)的基准电压与温度变化曲线如图 8所示.
|
图 8 零码到全码的基准电压与温度变化曲线 Fig. 8 Simulated temperature dependence of reference voltage from zero code to full code |
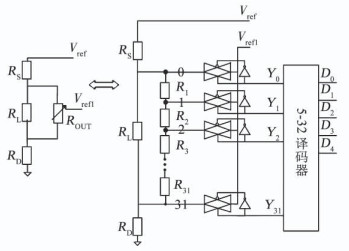
在上述温度系数修调的基础上,本文采用电压幅值修调电路ROUT来修调基准电压的输出电压幅值.图 9为电压幅值修调电路,Vref1为Brokaw电路产生的基准电压,Vref为幅值修调后的输出电压,串联电阻R1~R31,共有32个节点,传输门输出与节点相连,可以通过控制译码器的输入来决定Vref1的接入节点,带隙基准电压在满量程1/2处根据修条码上下波动,Vref与Vref1的关系为:
|
图 9 电压幅值修调电路 Fig. 9 Schematic of the voltage amplitude trimming circuit |
| $V_{\mathrm{ref}}=\frac{R_{\mathrm{OUT}}\left(R_{\mathrm{S}}+R_{\mathrm{L}} \| R_{\mathrm{OUT}}+R_{\mathrm{D}}\right) V_{\mathrm{ref1}}}{\left(R_{\mathrm{N}+1}+\cdots+R_{31}\right)\left(R_{\mathrm{L}} \| R_{\mathrm{OUT}}\right)+R_{\mathrm{D}} R_{\mathrm{OUT}}}\\ R_{\mathrm{OUT}}=R_{1}+R_{2}+\cdots+R_{31}, \\ R_{1}=R_{2}=\cdots=R_{31}, \\ N=0, 1, \cdots, 31, $ |
为了降低工艺中的非理想性因素的影响,提出一种新的芯片级快速优化基准电压温度系数的修调方法,快速获得最低温度系数对应码值并提升工作效率.
步骤1 测量零码和全码时温度特性曲线,线性拟合后分别得到其温度特性曲线的斜率值.
步骤2 将零码和全码值温度特性曲线斜率值作差,得到斜率变化范围,再除以位数,得到每修调一位得到的步长.
| $\Delta S = \frac{{S\left( {{\rm{全码}}} \right)\;\; - S\left( {{\rm{零吗}}} \right)}}{{\;\;\;\;\;127\;\;\;\;\;}}. $ | (5) |
步骤3 根据零码和全码的斜率值与每修调一位得到的步长,计算出斜率为零时的码值.
| ${T_1}\left( {{\rm{理论码值}}} \right) = \left| {\frac{{0 - S\left( {{\rm{零码}}} \right)}}{{\;\;\;\;\Delta S\;\;\;\;}}} \right|. $ | (6) |
步骤4 当得到最优的温度曲线时,修调电压幅值电路,获得目标电压值.
3 测试结果基于0.35 μm BCD工艺,采用分段曲率补偿技术,通过修调温度系数和电压幅值,获得高精度低温度系数的基准电压.图 10为芯片裸片显微图像和基准源版图.本文在-40℃~125℃内对带隙基准进行测试,提出一种新的芯片级修调方法以快速获得最低的温度系数.

|
图 10 芯片裸片显微图像和基准电路版图 Fig. 10 Microscopic image of bare chip and the layout of the proposed reference circuit |
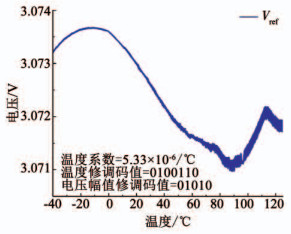
为了验证这种芯片级的修调方法,随机抽取了10颗芯片进行测试.图 11为实测芯片的零码和全码时温度特性曲线.表 1为测试数据,T1(温度系数理论码值)为理论温度系数修调码值,T2(温度系数实测码值)为实测温度系数修调码值,M(电压幅值码值)为输出目标基准电压时的电压幅值修调码值.步长ΔS和理论码值T1(温度系数理论码值)可根据式(5)、(6)计算得到.理论温度系数修调码值与实测温度系数修调码值接近,产生偏差的原因主要是测试误差和线性拟合误差.如图 12所示,当温度系数修调码值为0100110,电压幅值修调码值为01010时,温度在-40℃~125℃内,基准电压的实测最优温度系数为5.33×10-6/℃,且经过修调后,10块芯片的平均温度系数能达到7.47×10-6/℃.使用本文提出的基于计算斜率的修调方法,测试的10颗芯片的平均修调次数为3.5次.与使用逐次逼近最优温度曲线的方法测得10颗芯片的平均修调次数8.7次相比,效率提升59.8%.因此该修调方法给基准电压的温度系数提供良好的稳定性与灵活性,为寻找基准电压最低温度系数节约大量时间,提升工作效率.

|
图 11 实测10块芯片零码和全码的温度特性曲线 Fig. 11 Measured temperature dependence of full code and zero code for ten chips |
| 表 1 随机抽取10块芯片测试结果 Tab. 1 Measured results of ten chipsby random sampling |
|
图 12 实测最优码时基准电压温度特性曲线 Fig. 12 Measured temperature dependence of reference voltage with the optimal code |
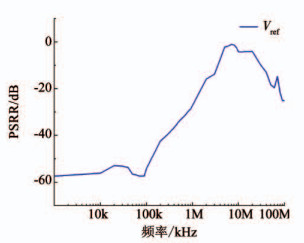
通过搭建测试环境,实测基准电压Vref的电源抑制比如图 13所示,-57.44 dB@1 kHz,-56.16 dB@10 kHz,-54.22 dB@100 kHz,-27.3 dB@1 MHz.电源抑制比的实测结果和仿真结果相近,电源抑制比测量对噪声非常敏感,实测结果与仿真结果产生差异的原因是环路区域的噪声和印刷电路板布局产生的噪声产生的影响.
|
图 13 实测基准电压Vref电源抑制比 Fig. 13 Measured PSRR of reference voltage Vref |
表 2总结了基准电压的性能并与文献[6, 15-17]中其他基准电压进行比较.实测输出基准电压为3.072 V,应用于电池检测芯片内高精度模数转换器(ADC)中.与文献[6, 15-17]比较,本文设计的基准有更低的仿真温度系数,实测温度系数与已有文献的结果相近,仿真结果与实测结果的差异来源于电阻绝对值偏差,工艺的漂移和封装应力的影响.与文献[6]中分段曲率补偿方法比较,产生补偿电流的结构不同,本文通过利用电阻分压和工作在亚阈值区域的MOSFET的电学特性,产生正温度系数和负温度系数的电流,实测温度系数在同一数量级,且输出基准电压精确可调.通过新的芯片级修调方法,在较大的温度范围内得到温度系数低,电压幅值精确可调的基准电压.
| 表 2 基准电压性能比较 Tab. 2 Comparison of the performance of the bandgap reference voltage |
1) 基于0.35 μm BCD工艺,本文设计了一种带有修调的分段曲率补偿基准电压电路,在低温段和高温段分别对基准电压进行补偿,在-40℃~125℃内,基准电压的最低温度系数为5.33×10-6/℃,随机抽取的10颗芯片的最低温度系数的平均值为7.47×10-6/℃.
2) 提出一种新的芯片级温度修调方法,可以快速找到基准电压的最优温度曲线,若采用本文提出的基于计算斜率的修调方法,测试10块芯片的平均修调次数为3.5次,若使用逐次逼近最优温度曲线的方法时,测试10块芯片的平均修调次数为8.7次.效率提升59.8%.实现了灵活的温度补偿.该低温度系数的带隙基准电压电路已成功应用于电池管理芯片内高精度模数转换器中,提升了电池管理芯片对电池剩余电量估算的准确性.
| [1] |
ZHOU Qianneng, CHENG Feihong, LI Hongjuan, et al. High-order curvature-compensated CMOS bandgap voltage reference[C]//Proceedings of the 12th International Conference on ASIC. Guiyang: IEEE, 2017: 525. DOI: 10.1109/asicon.2017.8252528
|
| [2] |
YIN Yongsheng, LI Dewu, DENG Honghui. A high precision CMOS bandgap reference with exponential curvature-compensation[C]//Proceedings of International Conference on Anti-Counterfeiting, Security and Identification. Shanghai: IEEE, 2013: 1. DOI: 10.1109/icasid.2013.6825293
|
| [3] |
LUO LI, CAI Xiaowei, LI Zheying. The design of sub-threshold reference circuit using resistor temperature[C]//Proceedings of the 52nd IEEE International Midwest Symposium on Circuits and Systems. Cancun, Mexico: IEEE, 2009: 78. DOI: 10.1109/mwscas.2009.5236149
|
| [4] |
RINCON-MORA G A. Voltage references from diodes to precision high-order bandgap circuits[M]. New York: Wiley-IEEE Press, 2002: 120.
|
| [5] |
李娅妮, 孙亚东, 王旭. 一种低失调高PSRR的带隙基准电路[J]. 西安电子科技大学学报(自然科学版), 2017, 44(5): 92. LI Yani, SUN Yadong, WANG Xu. Low-offset high-PSRR bandgap voltage reference[J]. Journal of Xidian University, 2017, 44(5): 92. DOI:10.3969/j.issn.1001-2400.2017.05.016 |
| [6] |
刘晓轩, 张玉明, 季轻舟, 等. 一种高精度低温漂带隙基准电路的设计与实现[J]. 西安电子科技大学学报(自然科学版), 2019, 46(2): 41. LIU Xiaoxuan, ZHANG Yuming, JI Qingzhou, et al. Design and realization of a high-precision and low temperature drift reference circuit[J]. Journal of Xidian University (Natural Science), 2019, 46(2): 41. DOI:10.19665/j.issn1001-2400.2019.02.008 |
| [7] |
WANG Ruocheng, LU Wengao, NIU Yuze, et al. A 2.1-ppm/℃ current-mode CMOS bandgap reference with piecewise curvature compensation[C]//Proceedings of International Symposium on Circuit and Systems. Baltimore, MD: IEEE, 2017: 254. DOI: 10.1109/iscas.2017.8050288
|
| [8] |
HU Jinlong, XU Huachao, ZHANG Yuanzhi, et al. A 1.2V supply 0.58 ppm/℃ CMOS bandgap voltage reference[J]. IEICE Electronic Express, 2018, 15(16): 1-6. DOI: 10.1587/elex.15.20180521
|
| [9] |
AKSHAYA R, SIVA YELLAMPALLI SIVA. Design of an improved bandgap reference in 180nm CMOS process technology[C]//Proceedings of the 2nd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT). Bangalore, India: IEEE, 2017: 521. DOI: 10.1109/rteict.2017.8256651
|
| [10] |
RINCON-MORA G, ALLEN P E. A 1.1 V current-mode and piecewise-linear curvature-corrected bandgap reference[J]. IEEE Journal of Solid-State Circuits, 1998, 33(10): 1551. DOI:10.1109/4.720402 |
| [11] |
LI Jinghu, WANG Yongsheng, YU Mingyan, et al. A novel piecewise curvature-corrected CMOS bandgap reference[C]//Proceedings of the 7th International Caribbean Conference on Devices Circuits and Systems. Cancun, Mexico: IEEE, 2008: 1. DOI: 10.1109/iccdcs.2008.4542606
|
| [12] |
ZHOU Qianneng, WANG Liangcai, XU Lan, et al. A high-order temperature-compensated CMOS bandgap voltage reference[C]//Proceedings of the 3rd Information Technology and Mechatronics Engineering Conference (ITOEC). Chongqing, IEEE, 2017: 200. DOI: 10.1109/ITOEC.2017.8122411
|
| [13] |
LI Hongjie, LI Li. A low temperature-drift and high precision bandgap[C]//Proceedings of the 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC). Xi'an: IEEE, 2018: 512. DOI: 10.1109/imcec.2018.8469493
|
| [14] |
CHO G R, HWANG K W, KIM T G. A high supply voltage bandgap reference circuit using drain-extended MOS devices[J]. IEICE Electronic Express, 2013, 10(8): 1. DOI:10.1587/elex.10.20130142 |
| [15] |
GUO Xiaoxin, CAI Min, HE Xiaoyong. A low power op-ampless bandgap reference with second-order compensation[C]//Proceedings of International Conference on Electron Devices and Solid-State Circuits (EDSSC). Hsinchu, Taiwan: IEEE, 2017: 1. DOI: 10.1109/edssc.2017.8126434
|
| [16] |
李树镇, 冯全源. 一种CMOS高阶曲率补偿的带隙基准源电路的设计[J]. 哈尔滨工业大学学报, 2017, 49(10): 95. LI Shuzhen, FENG Quanyuan. Design of a CMOS bandgap reference circuit with high order curvature compensation[J]. Journal of Harbin Institute of Technology, 2017, 49(10): 95. DOI:10.11918/j.issn.0367-6234.201604085 |
| [17] |
THUSHARA K C, DANIL S K. Design of 5.9ppm/℃ piecewise curve rectified start-up free bandgap voltage reference in 180 nm CMOS process[C]//Proceedings of International Conference on Emerging Trends and Innovations in Engineering and Technological Research (ICETIETR). Ernakulam, India: IEEE, 2018: 1. DOI: 10.1109/icetietr.2018.8529142
|
 2020, Vol. 52
2020, Vol. 52


