2. 北京科技大学 土木与资源工程学院,北京 100083
2. School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China
磁铁矿储量在中国铁矿总储量中占比近55.4%,对国民经济发展具有重要的支柱作用.磁铁矿石要经过采场爆破、选厂粗碎细碎等一系列的碎矿加工及富集过程才能被冶炼所利用.在将大块度矿岩通过爆破、机械破碎等手段逐步加工成细小颗粒的过程中,存在着能耗巨大且能量耗散率较低的问题,一定程度上制约了矿山生产效率的提高[1].因而磁铁矿石破碎过程中的能耗问题,已成为采选行业关注的热点之一.
在磁铁矿石破碎能耗研究中,国内外专家、学者及工程技术人员做了诸多探讨,主要从提高现有破碎设备性能、改进矿石破碎工艺流程、改变各破碎环节产品粒度以及对矿石进行预处理等方面进行了深入研究[2-4].然而,在磁铁矿石破碎过程中,关于矿石本身的耗能情况与破碎块度关系的研究仍有限.
磁铁矿石的破碎主要是通过动载冲击方式实现的.在冲击破坏下的耗能研究中,岩石类材料涉及较多,其中分离式霍普金森压杆装置(split Hopkinson pressure bar, SHPB)应用广泛.Zhang等[5]深入研究了不同加载速率下,岩石碎屑动能在岩石耗散能中的占比情况,指出弹射的碎屑所具有的动能在耗散能中的占比基本小于10%;张文清等[6]基于实测数据,指出岩石的耗散能随应变率提高而增大;平琦等[7]通过对砂岩的冲击载荷试验,得出了能耗密度可以反映砂岩在高应变率下强度本质的结论;许金余等[8]则进一步将该试验技术应用到了高温作用后的大理岩,发现同一高温处理的岩石能耗密度随着入射能的提高而增大,而在不同高温下的岩石能耗密度与入射能无明显的规律性变化;杨仁树等[9]通过含充填物节理岩石的冲击试验,指出充填物强度的变化,影响着能量的耗散行为.除了岩石材料的无轴压、无围压冲击外,Li等[10]系统研究分析了循环冲击载荷下,岩石破碎块度与单位体积吸收能的关系;殷志强等[11]指出当轴压较低时,破碎块度的分形维数与能耗密度近似呈线性分布,而当轴压较高时,两者则呈二次曲线分布;宫凤强等[12]发现当入射能保持不变时,岩石在低围压下的能耗密度值明显大于高围压状态.此外,Ju等[13]则从数值模拟的角度,研究了岩石能量耗散与孔隙率的变化规律,用冲击下的耗能变化来说明岩石内部损伤状况.由此可见,岩石的冲击破坏与能量耗散密切相关.
动载冲击下的岩石宏观破坏行为,是在不可逆的能量耗散驱动下,发生的一种破裂失稳现象,其破坏过程本身就是一个能量转化、耗散过程.然而在目前已有的成果中[6-9, 13-16],关于岩石动载下几种主要能量(耗散能、反射能、透射能)的分布转化,大多文献是对破坏实验现象的描述和破裂机理的解释,缺少对岩石破坏过程中能量运移分布、耗散规律的分析;同时,缺乏对能量耗散率与破碎效果之间关系的研究.
基于此,为探究磁铁矿石冲击破坏过程中的能量耗散以及能量耗散率与破碎效果的关系.本文利用SHPB技术对磁铁矿石进行冲击压缩试验,运用波动理论、岩石破碎学理论与断裂损伤理论,探究了冲击破坏下磁铁矿石的几种能量分布转化和耗散规律,揭示了不同耗散能对矿石破碎程度的影响,建立了能量耗散率与平均块度的分布关系,为磁铁矿石破碎工序中的能耗控制提供了参考价值.
1 冲击试验设备及实验结果 1.1 实验设备与原理本次试验在中南大学冲击实验室的Φ50 mm分离式霍普金森杆(SHPB)上进行.图 1为实验装置示意图,其包括SHPB压杆、超动态应变仪、示波器及数据采集系统.压杆直径50 mm,弹头长度为540 mm、入射杆与透射杆的长度为2 000 mm.弹头、入射杆、透射杆与吸收杆的材质均为40 Cr合金钢,密度为7 795 kg/m3,实测波速为5 198 m/s.
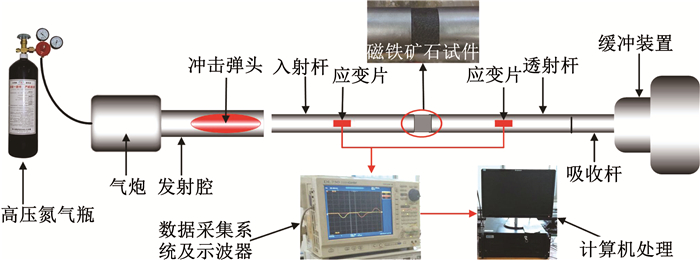
|
图 1 SHPB试验装置示意 Fig. 1 Schematic diagram of SHPB test apparatus |
粘贴在入射杆与透射杆上的应变片,将应力波信号传输给采集装置以及示波器,然后传输给计算机.实验前,需要进行设备的空冲测试,若入射波基本透射形成透射波(如图 2所示),则可进行下一步实验.
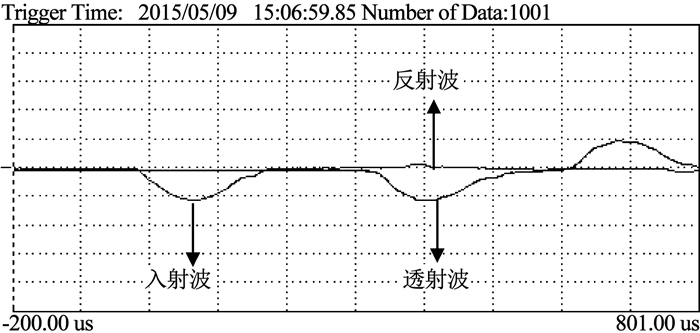
|
图 2 典型波形 Fig. 2 Typical waveform |
根据入射杆与透射杆上应变片传给分析系统的数据,可以计算出试件中的应力、应变以及应变率为[17]:
| $ \sigma \left( t \right) = \left[ {{\sigma _1}\left( t \right) - {\sigma _{\rm{R}}}\left( t \right) + {\sigma _{\rm{T}}}\left( t \right)} \right]{A_{\rm{e}}}/\left( {2{A_{\rm{s}}}} \right), $ |
| $ \varepsilon \left( t \right) = \frac{1}{{{\rho _{\rm{e}}}{C_{\rm{e}}}{L_{\rm{s}}}}}\int_0^t {\left[ {{\sigma _1}\left( t \right) + {\sigma _{\rm{R}}}\left( t \right) - {\sigma _{\rm{T}}}\left( t \right)} \right]} {\rm{d}}t, $ |
| $ \dot \varepsilon \left( t \right) = \frac{{{\sigma _1}\left( t \right) + {\sigma _{\rm{R}}}\left( t \right) - {\sigma _{\rm{T}}}\left( t \right)}}{{{\rho _{\rm{e}}}{C_{\rm{e}}}{L_{\rm{s}}}}} $ |
式中:σI(t)、σR(t)、σT(t)分别为t时刻的入射应力、反射应力和透射应力;ρeCe为弹性杆的波阻抗;Ls为试样的长度;Ae、As分别为弹性杆和试样的横截面积.
1.2 试件制备本研究所用的磁铁矿石采自首钢水厂铁矿同一块完整矿岩,其由磁铁石英岩与少量赤铁石英岩组成.结合杜晶[18]的冲击实验研究,当径长L与直径D之比在0.5~0.6范围内时,所得到的力学曲线较完整,因此本研究中的试件尺寸为:直径D=50 mm,径长L=27.5 mm,图 3为部分磁铁矿石试件.

|
图 3 磁铁矿石试件 Fig. 3 Specimens of magnetite ore |
为满足SHPB冲击试验中的入射波平面假设,可将磁铁矿石试件表面进行研磨抛光,使磁铁矿石试件端面的不平行度与不垂直度均小于0.02 mm.其他加工要求均符合GB/T 50266-2013《工程岩体试验方法标准》的相关规定.
1.3 冲击实验中能量计算在SHPB冲击试验中,高压气体驱动弹头撞击入射杆,将弹头的动能以应力波形式传给入射杆.入射杆再将入射能(记为WI(t))传输到试件中,其中一部分应力波以透射能形式(记为WT(t))传输到透射杆,一部分以反射能(记为WR(t))形式从入射杆反射回.WI(t)、WT(t)、WR(t)的计算为[5]:
| $ {W_{\rm{I}}}\left( t \right) = {E_{\rm{e}}}{C_{\rm{e}}}{A_{\rm{e}}}\int_0^t {\varepsilon _{\rm{I}}^2\left( t \right){\rm{d}}t, } $ |
| $ {W_{\rm{R}}}\left( t \right) = {E_{\rm{e}}}{C_{\rm{e}}}{A_{\rm{e}}}\int_0^t {\varepsilon _{\rm{R}}^2\left( t \right){\rm{d}}t, } $ |
| $ {W_{\rm{T}}}\left( t \right) = {E_{\rm{e}}}{C_{\rm{e}}}{A_{\rm{e}}}\int_0^t {\varepsilon _{\rm{T}}^2\left( t \right){\rm{d}}t, } $ |
式中:εI(t)、εR(t)、εT(t)分别为压杆上对应于入射波、反射波和透射波的应变;Ee为压杆弹性模量.
入射能WI除一部分转化为反射能WR、透射能WT、剩余部分能量可记为WL.WL包括矿石断裂破坏耗能WS、碎块动能WK以及摩擦能等.
据此,Zhang等[5]基于大量的实验数据,指出WK在WL中的占比小于8%,WS在WL中的占比高于85%.同时,在实验前,将磁铁矿石试件与压杆均匀涂抹润滑剂,可以忽略压杆与矿石试件间的摩擦耗能[6].因此,可近似认为用于矿石断裂破坏的耗能WS=WL,即磁铁矿石试件的耗散能等于入射能减去反射能与透射能之和,即
| $ {W_{\rm{S}}}\left( t \right) = {W_{\rm{I}}}\left( t \right) - \left[ {{W_{\rm{R}}}\left( t \right) + {W_{\rm{T}}}\left( t \right)} \right]. $ |
冲击试验中的磁铁矿石试件,需满足应力平衡条件,本文经电信号处理,得到了矿石试件的典型动态应力平衡图,如图 4所示.
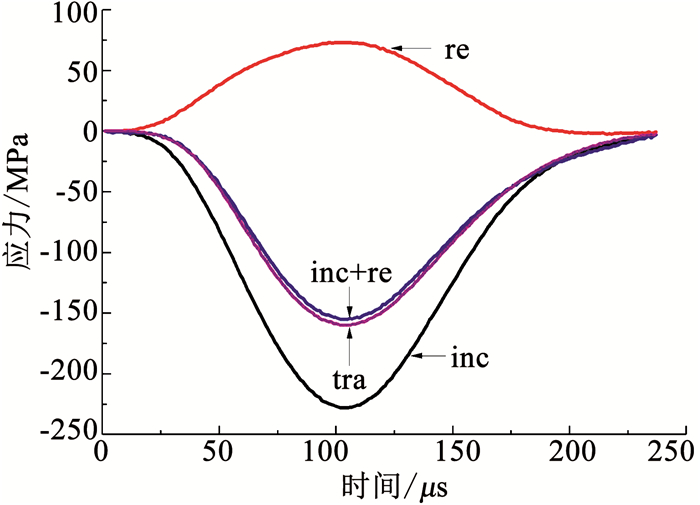
|
图 4 典型动态应力平衡图 Fig. 4 Typical dynamic stress equilibrium curves |
可知,入射波(标记为inc)与反射波(标记为re)的叠加波(标记为inc+re)与透射波(标记为tra)基本重叠,表明冲击载荷下的矿石试件处于动态应力平衡状态.
1.5 实验结果经预实验确定选用0.6~1.6 MPa的11种冲击气压,每组选用3块试件.选取每组中典型的磁铁矿石试件的平均应变率(简称应变率)及相关能量统计值,见表 1.
| 表 1 冲击载荷下的能量分布数据统计 Tab. 1 Statistics of energy distribution data under impactload |
分析表 1数据可以发现,随着入射能提高,耗散能、透射能及反射能不断增大,其大小为:透射能>耗散能>反射能,入射能主要以透射能和耗散能为主.
为进一步分析磁铁矿石原始入射能的运移转化情况.本文将3种能量与入射能的比率分别称为能量耗散率、能量反射率、能量透射率.图 5为三者与入射能的关系.可知,当应变率由31.02 s-1提高到89.09 s-1时,能量耗散率、反射率呈增加趋势,分别升高124%、150%;而能量透射率却降低35%.即随入射能提高,3种能量比率呈现明显差异.
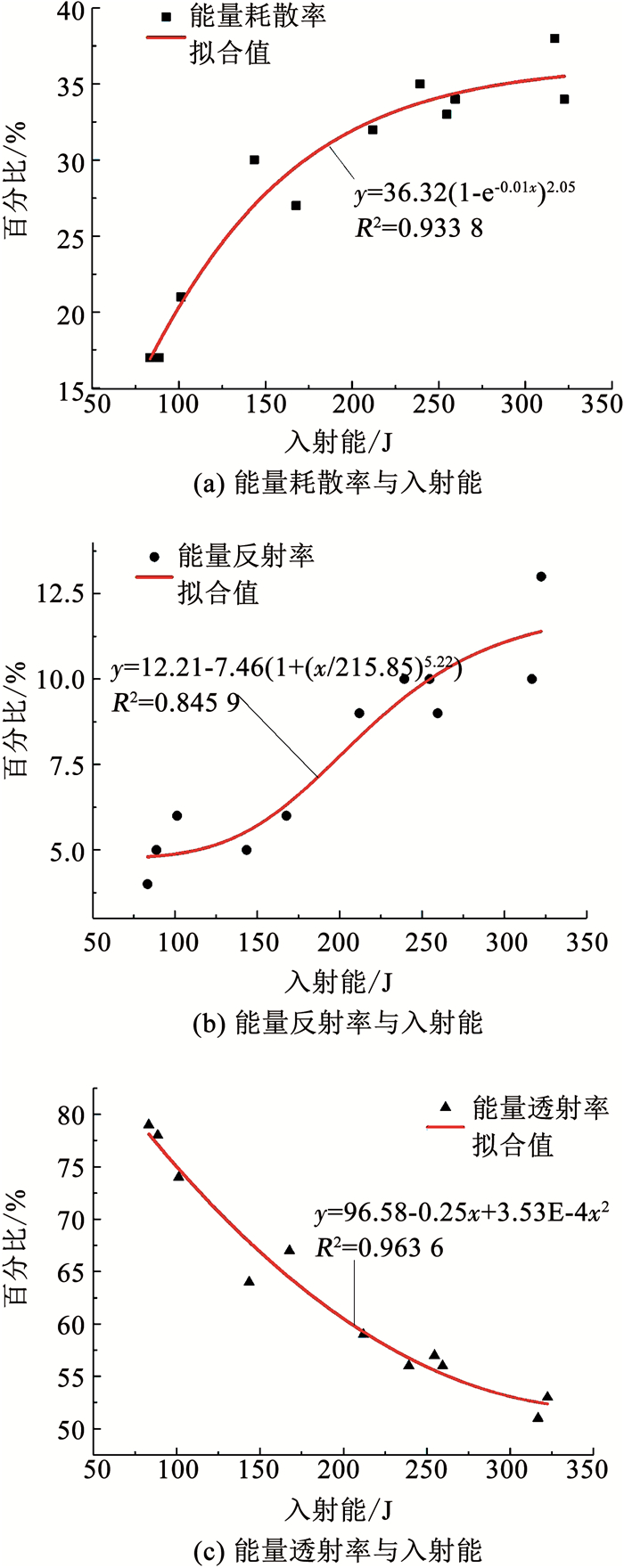
|
图 5 能量分布规律 Fig. 5 Distribution pattern of energy |
研究表明,介质波阻抗的改变影响着应力波在材料中的透射、反射情况[19].故引起图 5中能量透射率变化的原因,可根据波阻抗变化来解释.
如图 6所示,设入射杆与透射杆的波阻抗为ρ1c1、磁铁矿石波阻抗为ρ2c2,入射波σI在不同波阻抗的界面处,形成反射波σR与透射波σT.对于“入射杆—矿石”界面而言:
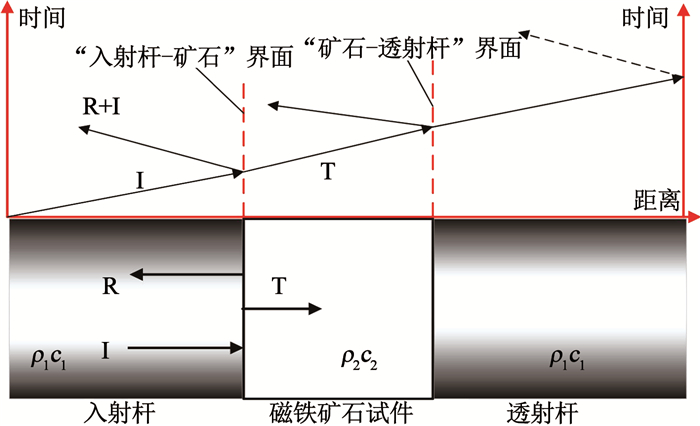
|
图 6 试件中应力波的传播过程 Fig. 6 Propagation process of stress wave in specimen |
由波阵面上动量守恒方程可知[17]:
| $ \begin{array}{l} {u_{\rm{I}}} = - \frac{{{\sigma _{\rm{I}}}}}{{{\rho _1}{c_1}}}, \\ {u_{\rm{R}}} = - \frac{{{\sigma _{\rm{R}}}}}{{{\rho _1}{c_1}}}, \\ {u_{\rm{T}}} = - \frac{{{\sigma _{\rm{T}}}}}{{{\rho _2}{c_2}}}, \end{array} $ | (1) |
由叠加原理和界面上质点状态一致原理,可知:
| $ \begin{array}{l} {\sigma _{\rm{I}}} + {\sigma _{\rm{R}}} = {\sigma _{\rm{T}}}, \\ {u_{\rm{I}}} + {u_{\rm{R}}} = {u_{\rm{T}}}, \end{array} $ | (2) |
将两式联立,有:
| $ \begin{array}{l} {\sigma _{\rm{R}}} = F{\sigma _{\rm{I}}}, \\ {\sigma _{\rm{T}}} = T{\sigma _{\rm{I}}}, \\ {u_{\rm{R}}} = - F{u_{\rm{I}}}, \\ {u_{\rm{T}}} = \left( {\frac{{{\rho _1}{c_1}}}{{{\rho _2}{c_2}}}} \right)T{u_{\rm{I}}}, \end{array} $ | (3) |
进一步合并,可得:
| $ \begin{array}{l} F = \frac{{{\rho _2}{c_2} - {\rho _1}{c_1}}}{{{\rho _2}{c_2} + {\rho _1}{c_1}}}, \\ T = \frac{{2{\rho _2}{c_2}}}{{{\rho _2}{c_2} + {\rho _1}{c_1}}}, \\ T = 1 + F. \end{array} $ | (4) |
式中:F为反射系数;T为透射系数.
随入射能提高,矿石内部发育扩展生成更多新生裂纹,波速逐渐降低,即波阻抗ρ2c2逐渐减小[20],由于ρ1c1>ρ2c2,由式(4)可知,F与T均减小;由式(3)可知,在“入射杆—矿石”界面处,应力逐渐减小,随应变率提高,应力的“反射卸载”现象越明显.同理,在“矿石—透射杆”界面处,应力逐渐增大,随应变率提高,应力的“反射加载”现象越明显.
综上分析可知,入射杆端的矿石所受应力,低于透射杆端矿石所受应力.故冲击破坏过程中,透射杆端的矿石优先于入射杆端矿石破坏,且其破坏程度高于入射杆端矿石.为佐证这一点,图 7(图中左侧为入射端,右侧为透射端)为高速摄影获得的3种应变率下矿石失稳前的状态,可知透射杆端的矿石最先发生破坏,入射杆端矿石其次破裂.

|
图 7 3种应变率下的矿石破坏前状态 Fig. 7 Pre-failure state of ore under three strain rates |
该现象在较大尺寸(长径比高于1)的SHPB实验中最明显,例如:文献[21]中,为更好地分辨入射端与透射端岩石破坏程度的差异,特对岩石两端面进行标记,得到了岩石破坏形态图,如图 8所示,可知透射杆端岩石的破坏程度明显高于入射杆端岩石.
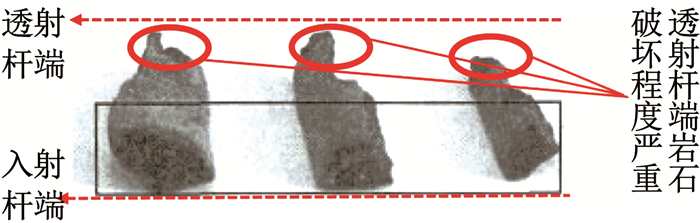
|
图 8 透射杆端矿石破碎程度高于入射杆端矿石[21] Fig. 8 Higher crushing degree of ore at the transmission bar end than at the incident bar end[21] |
上述分析可知,因入射杆端矿石所受应力高于透射杆端矿石,冲击过程中,透射杆端矿石先发生剥离,使透射杆与矿石间的接触面积减小.在矿石中传播的应力波,一部分只经剥离后的新生断面便反射到试件中(未传播到透射杆),且随入射能逐渐提高,透射杆端矿石“层裂”破坏愈加严重,加重了透射杆端矿石的破坏程度,降低了矿石中的应力波对透射杆的透射作用,即随入射能的提高,透射能增长量减小,能量透射率降低.即随入射能提高,能量反射率与能量耗散率逐渐增大,能量透射率却降低.
冲击载荷下,因矿石内部损伤引起的波阻抗变化,使入射端矿石的反射系数及透射端矿石的透射系数发生改变,从而影响着矿石的能量耗散特性.
矿石能量透射率逐渐减小,与煤岩试验[6, 16]具有一致性,且磁铁矿石能量透射率为51%~79%,远高于煤岩的0.1%~0.2%、0.16%~5.04%.这是因为坚硬致密的磁铁矿石,比松软类岩石更有利于应力波传播.
2.3 耗散能对破碎效果的影响利用标准方孔砂石筛与GZS-1高频振筛机对矿石碎屑进行筛分实验,并依次称量10种等级矿石的质量,各等级孔径及碎屑质量见表 2.
| 表 2 磁铁矿石破碎块度筛分实验结果 Tab. 2 Screening test results of the fragment size of magnetite ore |
从表 2中选取6种有代表性的耗散能与碎屑质量数据,得到了耗散能与矿石块度分布的关系,如图 9所示.
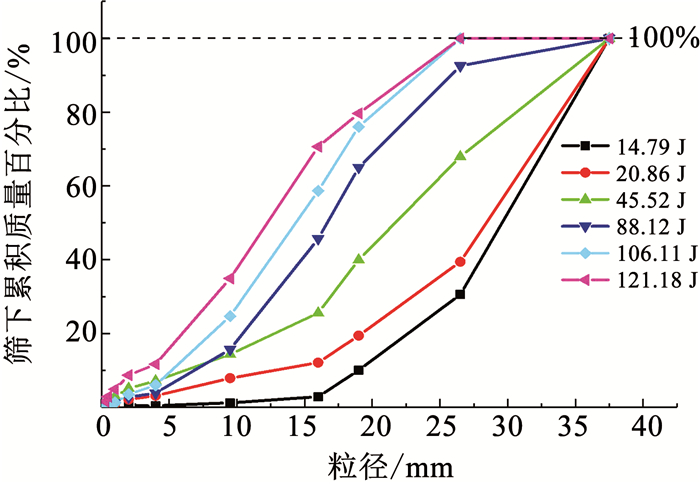
|
图 9 耗散能与矿石破碎块度分布 Fig. 9 Dissipated energy and ore fragmentation distribution |
由于曲线的斜率越大,代表在该粒度等级中质量越多.可知,当耗散能为14.79 J时,块度基本集中于26.5~37.5 mm区域,质量占总体的近70%;当耗散能为45.52 J时,粒径为16.0~37.5 mm的碎块质量占比近75%;随耗散能增大,小粒径碎块质量逐渐增多,当耗散能为88.12 J时,仅9.5~19.0 mm范围内的碎块占总体质量50%;当耗散能达到121.18 J时,仅4~16 mm范围内的碎块可占总体质量的60%.
分析可知,当耗散能由14.79 J提高到121.18 J时,矿石碎屑的主要分布区域逐渐由粗粒端(26.5 mm,37.5 mm)到细粒端(4 mm,16 mm)移动.随着耗散能的增大,碎屑的块度逐渐变小,破碎加剧.
2.3.2 不同耗散能下的矿石平均块度变化为进一步研究块度分布规律,结合文献[1]的实际采场、选矿厂的工程调研可知,平均块度是影响矿石破碎工序中能耗的一个关键指标.因此本文选取平均块度ds来表示矿石破碎程度,ds可由下式求得[22]:
| $ {d_{\rm{s}}} = \frac{{\sum {{r_i}{d_i}} }}{{\sum {{r_i}} }}. $ |
式中:di为不同孔径下的矿石块度尺寸; ri为当筛孔直径为di时,对应的碎块质量百分比.
图 10、11分别为不同耗散能下矿石平均块度、破坏形态的变化情况.由图 7可知,当耗散能从14.79 J提高到121.18 J时,矿石平均块度由28.41 mm降低到12.49 mm,减小近56.04%.拟合关系为:
| $ \begin{array}{l} {d_{\rm{s}}} = - 230.59\ln \left( {{W_{\rm{s}}} + 13.91} \right) + 876.29, \\ {R^2} = 0.974\;1. \end{array} $ |
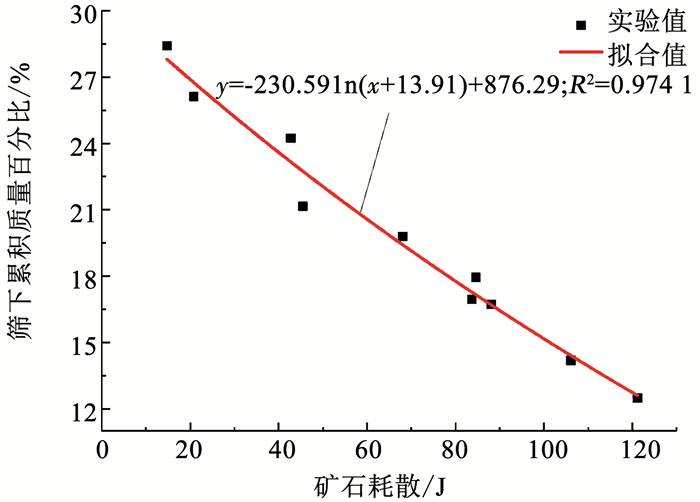
|
图 10 耗散能与平均块度 Fig. 10 Dissipated energy and average particle size |

|
图 11 不同耗散能下的磁铁矿石冲击破碎形态 Fig. 11 Failure modes of magnetite ore under different dissipated energy |
图 11中,随着耗散能的提高,磁铁矿石的宏观破坏模式是由沿轴向劈裂到整体体积破碎的转换过程.
矿石的冲击破坏过程,伴随着其内部弹性应变能的不断释放,当矿石内部质点所受应力超过其极限强度时,将发生断裂破坏,形成微观裂纹,并进一步扩展、贯通,直至破坏.分析认为,低耗散能下,矿石内部弹性应变能释放较少,新生裂纹较少,矿石宏观贯通裂纹与加载方向一致,即导致轴向劈裂破坏[23],此时张拉应力主导破坏.高耗散能下,矿石内部弹性应变能释放增多,产生的裂纹增加,各尺度的裂纹形成的交错复杂裂隙网,逐渐发育贯通切割矿石,矿石发生体积破碎,此时拉、剪应力共同主导破坏.
磁铁矿石在高耗散能下的体积破碎与文献[24]中的花岗岩破坏情况一致,但不同于文献[21]中山西黑花岗岩呈现的“体积破碎→赫兹破碎”,这是因为两者的应变率相差较大,高应变率下,山西黑花岗岩的体积破碎不能完全吸收冲击能量,便发生赫兹破碎.
图 12为应变率与耗散能的关系.可知,随着应变率提高,矿石内部新生裂纹的形成需要更多应变能的释放,对应了磁铁矿石的耗散能增大.综上所述,在磁铁矿石动载冲击破坏中,具有应变率效应的耗散能是影响矿石破碎效果的根本原因.
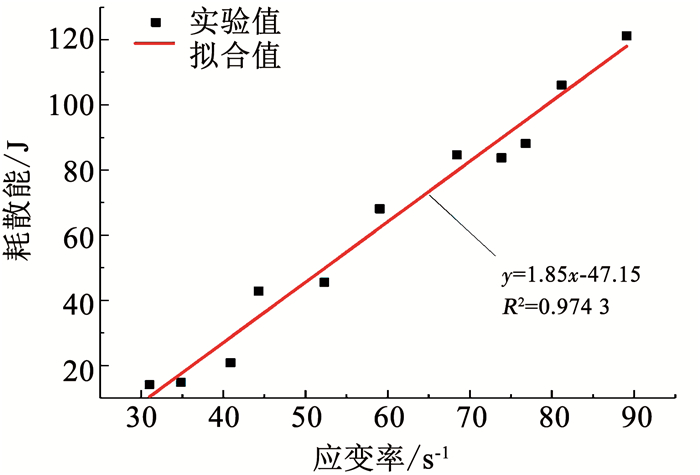
|
图 12 应变率与耗散能 Fig. 12 Strain rate and the dissipated energy |
冲击作用下,耗散能为磁铁矿石内部裂纹萌生、发育、汇合与贯通所消耗的能量.本文将能量耗散率记为η,由图 13可知,随入射能提高,矿石耗散能增大,η升高,矿石破碎程度加重.
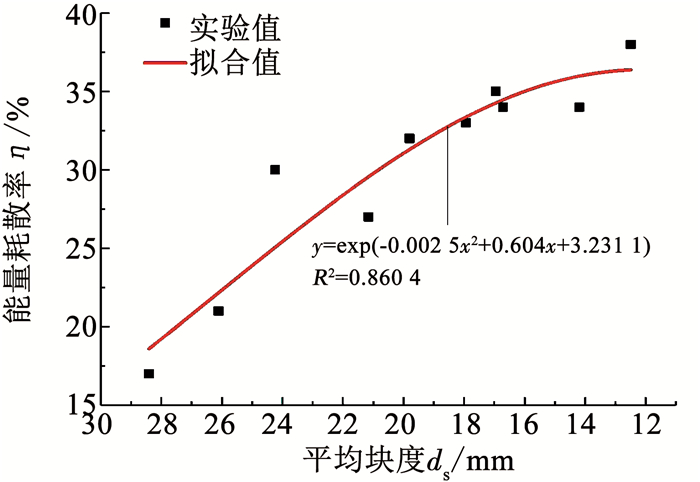
|
图 13 能量耗散率与平均块度的关系 Fig. 13 Relationship between energy dissipation rate and average particle size |
由图 13中ds与η关系可知,在起始阶段,随ds的减小,η逐渐升高,二者近乎呈线性关系,矿石的“破碎程度越高”与“η越高”呈正相关.然而,随着ds的进一步减小,η的增长量逐渐降低,两者的正相关性逐渐减弱.因此,η应存在最大值,对应着矿石“破碎程度越高”与“η越高”的正相关为零.此论点与文献[25]中的“岩石的破坏程度与应变率并不存在一一对应”,所反映的问题一致.该结论也可从冲击破坏下矿石的能耗分布角度得到进一步印证,即矿石的η增大与“应变率/耗散能”的提高,两者非正相关.
3.2 能量耗散率与平均块度关系上述分析表明,在矿石破碎程度较高时,以“η越高”来评价矿石“破碎程度越高”是不准确的.此时,ds应存在某一临界值,对应η达到最大值.
由于本文中的鞍山式磁铁矿石较致密,在常规动载冲击(单级、无轴围压)室内实验中,不易实现矿石的超高破碎(例如:ds < 10 mm),若完全基于实测数据,则难以反映两者的准确关系;且在目前冲击实验中,关于直接研究岩石dS与η分布的资料较少.因而,本文经整理文献[7-8, 14-15]中的数据,分别得到了“砂岩、大理岩、煤岩、齐大山磁铁石英岩” ds与η的关系,如图 14、15所示.可知,随着冲击入射能的提高,几种材料的ds逐渐减小,η却先增大后减小,即η与破碎程度呈现“先正相关,后负相关”的趋势,几种材料均存在某一临界值.
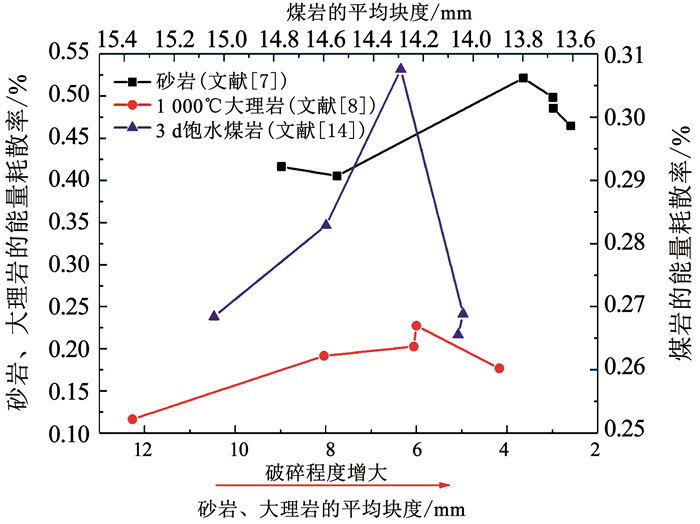
|
图 14 砂岩、大理岩与煤岩的能量耗散率与平均块度关系[7-8, 14] Fig. 14 Relationship between energy dissipation rate and average particle size of sandstone, marble, and coal rock[7-8, 14] |
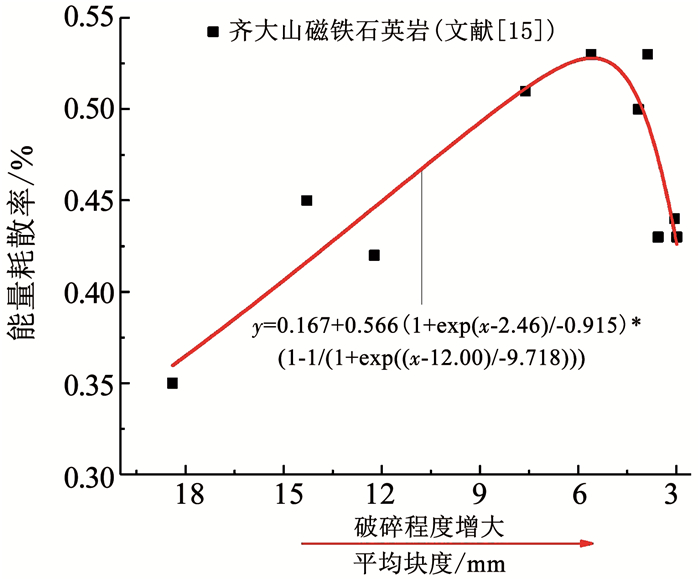
|
图 15 磁铁石英岩的能量耗散率与平均块度关系[15] Fig. 15 Relationship between energy dissipation rate and average particle size of magnetite quartzite[15] |
本文根据图 13中的拟合公式,绘制了η与ds的拟合图,如图 16所示.由图 16可知,在矿石破碎程度较高时,确实存在一个临界值(ds=12.08 mm,η=36.45 %),在超过该临界值后,尽管矿石破碎程度在加深,但η却降低,在该值下,可实现磁铁矿石的最优破碎.
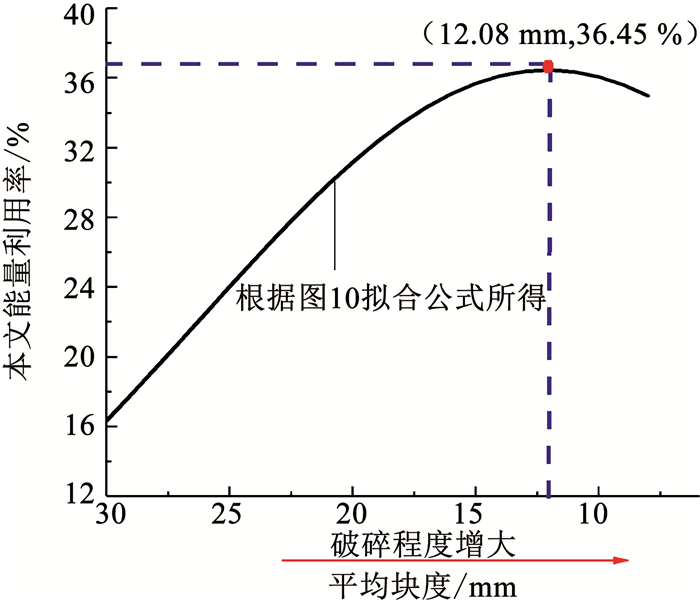
|
图 16 本文能量耗散率与平均块度拟合图 Fig. 16 Fitted diagram of the energy dissipation rate and the average particle size in this paper |
需要说明的是,由于单轴冲击破坏下,磁铁矿石不易实现超高破碎程度.然而,岩石类材料存在着一定的共性,即均属典型的非均质、各向异性材料,因此,本文结合已往文献,分析得出ds存在着一个临界值,对应η的逐渐降低,是合理的,这是因为在极高的入射能输入下,矿石破碎耗能有限,能量的耗散将以碎屑的弹射动能为主.
在矿石爆破及各级碎矿工序中,若仅提高矿石的破碎程度,η并非一直保持增大趋势,过高的破碎程度,势必将造成大量能量的损失.因此,应当在矿石破碎程度与η均呈正相关的范围内,根据下一级碎矿工序对破碎体粒度的要求,尽量提高η,即选择合理的破碎输入能,达到既满足产物粒度需要,又可降低破碎耗能的目的,实现最优破碎.
3.3 磁铁矿石的平均块度预测模型由上述可知,ds存在着一个临界值,其决定着η与矿石破碎程度是否呈正相关.因此,若能基于冲击破碎数据,根据影响块度分布的基本因素,结合理论推导,较为准确地获得磁铁矿石冲击破碎的平均块度ds预测表达式,便可直接得到η与破碎程度呈正相关的临界值.从而为碎矿作业中提高矿石破碎效率,实现矿石最优破碎提供更有力的参考依据.
同时,冲击作用下的矿石块度分布是在能量耗散下,各种尺度缺陷相互作用引起矿石内部损伤到宏观状态失稳的结果,而研究磁铁矿石的能耗问题,归根结底就是要定量地探究矿石破碎块度ds的分布情况.
在影响矿石块度分布的因素中,既有原生缺陷的影响,也有新生裂纹的影响.研究表明,岩石内部存在着大量的原生缺陷,而新生裂纹是在能量耗散下由激活状态的原生缺陷进一步扩展演化而来的.因此可知,原生缺陷影响着磁铁矿石的块度分布情况.
根据岩石断裂损伤理论[26],设Nσ为磁铁矿石单位体积内≤应力σ时活化的缺陷数,当因率效应所引起的内部应力达到矿石破坏时的极限应力σmax时,此时磁铁矿石破坏的平均块度为
| $ {d_{\rm{s}}} \sim n{\left( {{\sigma _{\rm{c}}}} \right)^{ - \frac{1}{3}}}. $ |
设Nσ满足Weibull分布,可知:
| $ {N_\sigma } = k{\left( {\frac{\sigma }{B}} \right)^m}, $ |
式中B、m均为Weibull分布参数,利用磁铁矿石动态冲击断裂时的应力可得到平均块度与应变率的幂函数表达式:
| $ {d_{\rm{s}}} = \frac{{f\left( m \right)}}{{{k^{1/3}}}}{\left[ {\frac{{\dot \varepsilon }}{{{C_b}{k^{1/3}}}}} \right]^{ - \frac{m}{{m + 3}}}}. $ | (5) |
式中:Cb、k分别与磁铁矿石固有性质有关,其中f(m)为
| $ f\left( m \right) = \frac{6}{{m + 2}}{\left[ {\frac{{8{\rm{ \mathsf{ π} }}}}{{\left( {m + 1} \right)\left( {m + 2} \right)\left( {m + 3} \right)}}} \right]^{ - \frac{1}{{m + 3}}}}. $ |
由于理论公式(5)中的两个未知参数Cb、k难以通过室内实验直接确定,因此本文利用表 1、2中应变率与平均块度的实测数据对式(5)进行两次测算,两次测算的拟合公式及得到的Cb、k值分别为:
| $ {d_{{\rm{s1}}}} = 449.952\dot \varepsilon _1^{ - 0.771\;5}, {R^2} = 0.972\;0; $ |
| $ {d_{{\rm{s2}}}} = 387.66\dot \varepsilon _2^{ - 0.732\;0}, {R^2} = 0.982\;5; $ |
| $ {C_b} = 4\;478.472\;9, k = 0.963\;9. $ |
最终确定了本文中磁铁矿石冲击破坏下的平均块度预测模型表达式为:
| $ {d_{\rm{s}}} = 0.692\;5{\left( {\frac{{\dot \varepsilon }}{{4\;423.98}}} \right)^{ - 0.771\;5}}, $ |
| $ \dot \varepsilon \in \left( {34.84\;{{\rm{s}}^{ - 1}}, 89.90\;{{\rm{s}}^{ - 1}}} \right). $ |
1) 在冲击作用下,随着应变率的提高,磁铁矿石耗散能增大,平均块度减小,破碎程度加剧.高耗散能下,可以有效使矿石发生体积破碎现象.
2) 磁铁矿石在冲击破坏过程中,随着应变率的提高,波阻抗逐渐降低,矿石与压杆间的透射系数、反射系数发生变化,从而使能量透射率逐渐降低,更多能量用于矿石破碎,波阻抗的变化影响着能量分布转化规律.
3) 冲击作用下,平均块度存在着一个临界值,超过该值后,能量耗散率将减小.因此,在实际碎矿作业中,为了实现既增强破碎效果,又提高能量耗散率的最优破碎目的.应当根据各级碎矿工序对破碎粒度的具体要求,结合临界值,选取合理的输入能冲击破碎磁铁矿石.
4) 建立了磁铁矿石的平均块度预测模型,该模型很好地反映了磁铁矿石平均块度随应变率提高而降低这一基本规律.同时,也为其他类岩石在冲击破坏下的块度研究提供了一个思路.
5) 在磁铁矿石平均块度预测模型中,存在着参数难以直接获取等缺陷.因此仍需对其进行深入推导分析,在不同加载条件下,考虑不同的影响因素,使该模型能够简洁有效地表达平均块度.
| [1] |
李占金, 乔国刚, 米雪玉, 等. 冀东磁铁矿石粉碎过程节能降耗研究[J]. 中国矿业大学学报, 2008, 37(5): 625. LI Zhanjin, QIAO Guogang, MI Xueyu, et al. Energy savings during magnetite ore preparation in eastern Hebei province[J]. Journal of China University of Mining & Technology, 2008, 37(5): 625. DOI:10.3321/j.issn:1000-1964.2008.05.009 |
| [2] |
叶贤东.超临速磨矿理论研究[D].昆明: 昆明理工大学, 2002: 126 YE Xiandong. The theoretical research on the ultracritical rotation speed grinding[D]. Kunming: Kunming University of Science and Technology, 2002: 126 |
| [3] |
任贺旭, 李占金, 李力. 铁矿石采选破碎系统节能途径研究[J]. 矿业研究与开发, 2015, 35(12): 97. REN Hexu, LI Zhanjin, LI Li. Study on the energy saving way in crushing system of iron ore mining and dressing[J]. Mining Research and Development, 2015, 35(12): 97. DOI:10.13827/j.cnki.kyyk.2015.12.022 |
| [4] |
彭操, 刘江林. 降低磨矿能耗技术在选矿厂中的应用剖析[J]. 云南化工, 2008, 35(2): 65. PENG Cao, LIU Jianglin. Application of grinding energy consumption reduction in concentrator[J]. Yunnan Chemical Technology, 2008, 35(2): 65. DOI:10.3969/j.issn.1004-275X.2008.02.020 |
| [5] |
ZHANG Z X, KOU S Q, JIANG L G, et al. Effects of loading rate on rock fracture: Fracture characteristics and energy partitioning[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(5): 745. DOI:10.1016/S1365-1609(00)00008-3 |
| [6] |
张文清, 石必明, 穆朝民. 冲击载荷作用下煤岩破碎与耗能规律实验研究[J]. 采矿与安全工程学报, 2016, 33(2): 375. ZHANG Wenqing, SHI Biming, MU Chaomin. Experimental research on failure and energy dissipation law of coal under impact load[J]. Journal of Mining & Safety Engineering, 2016, 33(2): 375. DOI:10.13545/j.cnki.jmse.2016.02.029 |
| [7] |
平琦, 骆轩, 马芹永, 等. 冲击载荷作用下砂岩试件破碎能耗特征[J]. 岩石力学与工程学报, 2015, 34(s2): 4197. PING Qi, LUO Xuan, MA Qinyong, et al. Broken energy dissipation characteristics of sandstone specimens under impact loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(s2): 4197. DOI:10.13722/j.cnki.jrme.2015.0585 |
| [8] |
许金余, 刘石. SHPB试验中高温下岩石变形破坏过程的能耗规律分析[J]. 岩石力学与工程学报, 2013, 32(s2): 3109. XU Jinyu, LIU Shi. Analysis of energy dissipation rule during deformation and fracture process of rock under high temperatures in SHPB test[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(s2): 3109. |
| [9] |
杨仁树, 王茂源, 杨阳, 等. 充填材料对节理岩石动力学性能影响的模拟试验[J]. 振动与冲击, 2016, 35(12): 125. YANG Renshu, WANG Maoyuan, YANG Yang, et al. Simulation material experiment on the dynamic mechanical properties of jointed rock affected by joint-filling material[J]. Journal of Vibration and Shock, 2016, 35(12): 125. DOI:10.13465/j.cnki.jvs.2016.12.019 |
| [10] |
LI X B, LOK T S, ZHAO J. Dynamic characteristics of granite subjected to intermediate loading rate[J]. Rock Mechanics and Rock Engineering, 2005, 38(1): 21. DOI:10.1007/s00603-004-0030-7 |
| [11] |
殷志强, 李夕兵, 马海峰, 等. 围压卸荷条件砂岩动静组合加载碎块分维特性[J]. 振动与冲击, 2014, 33(9): 83. YIN Zhiqiang, LI Xibing, MA Haifeng, et al. Fractal characteristics of sandstone fragmentation under coupled static and dynamic loading and confining pressure[J]. Journal of Vibration and Shock, 2014, 33(9): 83. DOI:10.13465/j.cnki.jvs.2014.09.015 |
| [12] |
宫凤强, 李夕兵, 刘希灵. 三轴SHPB加载下砂岩力学特性及破坏模式试验研究[J]. 振动与冲击, 2012, 31(8): 29. GONG Fengqiang, LI Xibing, LIU Xiling. Test for sandstone mechanical properties and failure model triaxial SHPB loading[J]. Journal of Vibration and Shock, 2012, 31(8): 29. DOI:10.13465/j.cnki.jvs.2012.08.006 |
| [13] |
JU Yang, WANG Huijie, YANG Yongming, et al. Numerical simulation of mechanisms of deformation, failure and energy dissipation in porous rock media subjected to wave stresses[J]. Science China Technological Sciences, 2010, 53(4): 1098. DOI:10.1007/s11431-010-0126-0 |
| [14] |
王文, 李化敏, 顾合龙, 等. 动静组合加载含水煤样能量耗散特征分析[J]. 岩石力学与工程学报, 2015, 34(S2): 3965. WANG Wen, LI Huamin, GU Helong, et al. Feature analysis of energy dissipation of water-saturated coal samples under coupled static-dynamic loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(s2): 3965. DOI:10.13722/j.cnki.jrme.2015.0546 |
| [15] |
王和平.不同冲击载荷作用下岩石的破碎与能量耗散的研究[D].鞍山: 辽宁科技大学, 2016: 27 WANG Heping. Study of fractured rock under different impact load and energy dissipation[D]. Anshan: University of Science and Technology Liaoning, 2016: 27 |
| [16] |
曹丽丽, 浦海, 李明, 等. 煤系砂岩动态拉伸破坏及能量耗散特征的试验研究[J]. 煤炭学报, 2017, 42(2): 492. CAO Lili, PU Hai, LI Ming, et al. Experimental research on the dynamic tensile fracture and the energy dissipation characteristics of coal-serial sandstone[J]. Journal of China Coal Society, 2017, 42(2): 492. DOI:10.13225/j.cnki.jccs.2016.6030 |
| [17] |
王礼立. 应力波基础[M]. 2版. 北京: 国防工业出版社, 2010: 39. WANG Lili. Foundation of stress waves[M]. 2nd ed. Beijing: National Defense Industry Press, 2010: 39. |
| [18] |
杜晶.不同长径比下岩石冲击动力学特性研究[D].长沙: 中南大学, 2011: 46 DU Jing. Size effect on the dynamic mechanical properties under impact loads of rock[D]. Changsha: Central South University, 2011: 46 |
| [19] |
汤文辉. 冲击波物理[M]. 北京: 科学出版社, 2011: 189. TANG Wenhui. Shock wave physics[M]. Beijing: Science Press, 2011: 189. |
| [20] |
金解放, 李夕兵, 殷志强, 等. 循环冲击下波阻抗定义岩石损伤变量的研究[J]. 岩土力学, 2011, 32(5): 1385. JIN Jiefang, LI Xibing, YIN Zhiqiang, et al. A method for defining rock damage variable by wave impedance under cyclic impact loadings[J]. Rock and Soil Mechanics, 2011, 32(5): 1385. DOI:10.16285/j.rsm.2011.05.012 |
| [21] |
姜峰, 李子沐, 王宁昌, 等. 高应变率条件下山西黑花岗岩的动态力学性能研究[J]. 振动与冲击, 2016, 35(8): 177. JIANG Feng, LI Zimu, WANG Ningchang, et al. Research on dynamic characteristics of Shanxi black granite under high strain rates[J]. Journal of Vibration and Shock, 2016, 35(8): 177. DOI:10.1346/j.cnki.jvs.2016.08.028 |
| [22] |
李夕兵, 古德生. 岩石冲击动力学[M]. 长沙: 中南工业大学出版社, 1994: 292. LI Xibing, GU Desheng. Rock dynamics fundamentals and applications[M]. Changsha: Central South University of Technology Press, 1994: 292. |
| [23] |
李晓峰, 李海波, 刘凯, 等. 冲击荷载作用下岩石动态力学特性及破裂特征研究[J]. 岩石力学与工程学报, 2017, 36(10): 2393. LI Xiaofeng, LI Haibo, LIU Kai, et al. Dynamic properties and fracture characteristics of rocks subject to impact loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(10): 2393. DOI:10.13722/j.cnki.jrme.2017.0539 |
| [24] |
李刚, 陈正汉, 谢云, 等. 高应变率条件下三峡工程花岗岩动力特性的试验研究[J]. 岩土力学, 2007, 28(9): 1833. LI Gang, CHEN Zhenghan, XIE Yun, et al. Test research on dynamic characteristics of three gorges granite under high strain rate[J]. Rock and Soil Mechanics, 2007, 28(9): 1833. DOI:10.16285/j.rsm.2007.09.023 |
| [25] |
于水生, 卢玉斌, 朱万成, 等. SHPB试验中花岗岩破坏程度与能量耗散关系分析[J]. 东北大学学报(自然科学版), 2015, 36(12): 1733. YU Shuisheng, LU Yubin, ZHU Wancheng, et al. Analysis on relationship between degree of damage and energy dissipation of granite in SHPB tests[J]. Journal of Northeastern University (Natural Science), 2015, 36(12): 1733. DOI:10.3969/j.issn.1005-3026.2015.12.014 |
| [26] |
阿特金森. 岩石断裂力学[M]. 北京: 地震出版社, 1992: 456. ATKINSON B K. Fracture mechanics of rock[M]. Beijing: Seismological Press, 1992: 456. |
 2020, Vol. 52
2020, Vol. 52


