2. 浙江大学 电气工程学院, 杭州 310027
2. College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China
永磁电机具有结构简单、比功率高、调速范围宽等优点,在精密数控机床、高速机车牵引和人工智能等领域得到了广泛应用[1-2].永磁电机速度控制算法通常采用以电流环为内环、以速度环为外环的级联控制结构,该种控制结构要求内环控制带宽远大于外环,以满足系统稳定性要求,但限制了电机转速的动态响应速度[3-5].有限集预测控制因具备动态性能优良、可实现多变量在线寻优、无需调制等显著优点,是构建永磁电机无级联直接速度控制结构的合适方案[6-7].
近年来,关于永磁电机直接预测速度控制(direct predictive speed control,DPSC)的研究备受关注[8-9].文献[10]较早提出了DPSC的完整实现方案,并成功用于永磁同步电机驱动系统.然而,考虑到速度预测模型维度高、运算复杂,该方法并没有讨论多步预测的实现问题,从而无法保证输出矢量为所设计优化问题的最优解.为降低算法的在线计算量,文献[11]通过将预测控制对应优化问题转化为多参数优化问题,可离线确定出不同凸分区下的输出矢量,但因凸分区数目过多,降低了算法的实用性.为此,文献[12]通过在电流参考值中引入数字PI控制器的形式,来保证短预测时域下算法的稳定性.然而,PI控制器的引入势必会降低DPSC的转速响应速度.近年来,随着研究的不断深入,无需PI控制器辅助,直接将转速误差项纳入DPSC价值函数,以取代多步预测,成为改进DPSC的可行途径之一,但仍缺乏有力的稳定性证明与价值函数权重整定方法[13-15].同时,为改善稳态速度控制精度,需要扩充DPSC控制集中的备选电压矢量数目,增加控制自由度[16].但是,由于经典速度预测模型过于繁杂,尚缺乏成熟的方法来实现基于扩张控制集的预测速度控制策略.此外,由于PI控制器和积分效应的缺失,DPSC的抗参数扰动能力较差[17].为此,有必要在其中增加相应的补偿环节,如扰动观测器[18]、比例-谐振控制器[19]、滑模结构[20]等来增强算法的参数鲁棒性.
为解决经典DPSC在线计算量大、控制自由度受限的难题,本文提出一种具有参数鲁棒性的增量式直接预测速度控制(incremental direct predictive speed control, IDPSC)策略.该策略中,借助增量式建模手段,以及通过合理近似来消去计算冗余部分,获得可离线确定所有参数的多步速度预测模型,以期在降低算法在线计算量,实现多步速度预测的同时,嵌入积分内模,改善算法参数鲁棒性.同时,扩充DPSC控制集中的备选电压矢量数目,并设计出与之相适应的边界矢量合成方法和两阶段穷举寻优方法,以期增加算法控制自由度,改善转速稳态控制精度.
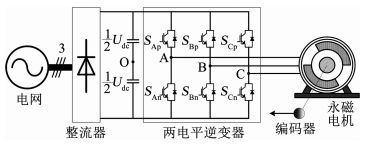
1 永磁电机系统增量式预测模型 1.1 系统组成由两电平逆变器驱动的永磁电机系统如图 1所示.
|
图 1 两电平电压型逆变器馈电永磁电机驱动系统 Fig. 1 Two-level inverter-fed PMSM drive system |
图中,SAp、SBp、SCp、SAn、SBn和SCn分别为2L-VSI三相(A、B和C)上、下桥臂IGBT的开关状态.因为2L-VSI上、下桥臂IGBT的开关状态互补,所以共存在8个开关组合,将这8种开关组合对应的输出线电压转换为空间矢量形式,可以得到2个零矢量V0和V7,以及6个幅值和空间位置固定的电压空间矢量:
| $ {\mathit{\boldsymbol{V}}_i} = \frac{2}{3}{U_{{\rm{dc}}}}{{\rm{e}}^{{\rm{j}}(\frac{{i\pi }}{3} - \frac{\pi }{3})}}. $ |
式中:Udc为直流母线电压; i=1, 2, …, 6为基本矢量序号.本文以“1”表示IGBT处于开通状态,“0”表示IGBT处于关断状态,例如SAp=1表示A相上桥臂的IGBT处于开通状态.定义列向量为
| $ {\mathit{\boldsymbol{S}}_i} \buildrel \Delta \over = {\left[ {\begin{array}{*{20}{l}} {{S_{{\rm{Ap}}}}}&{{S_{{\rm{Bp}}}}}&{{S_{{\rm{Cp}}}}} \end{array}} \right]^{\rm{T}}}, $ |
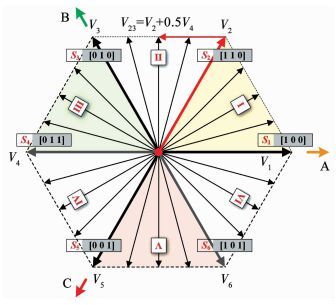
式中Si为电压矢量Vi对应的开关组合,各电压矢量对应的开关组合如图 2所示.
|
图 2 两电平电压型逆变器空间矢量分布 Fig. 2 Vector map of 2L-VSI |
表贴式永磁电机在d-q同步旋转坐标系下的数学模型可以表示为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\rm{d}}}{{{\rm{d}}t}}{i_d} = - \frac{{{R_{\rm{s}}}}}{{{L_{\rm{s}}}}}{i_d} + {\omega _{\rm{e}}}{i_q} + \frac{{{u_d}}}{{{L_{\rm{s}}}}},}\\ {\frac{{\rm{d}}}{{{\rm{d}}t}}{i_q} = - \frac{{{R_{\rm{s}}}}}{{{L_{\rm{s}}}}}{i_q} - {\omega _{\rm{e}}}{i_d} + \frac{{{u_q}}}{{{L_{\rm{s}}}}} - \frac{{{\psi _{\rm{f}}}}}{{{L_{\rm{s}}}}}{\omega _{\rm{e}}},}\\ {{T_{\rm{e}}} = 1.5p{\psi _{\rm{f}}}{i_q}}\\ {\frac{{\rm{d}}}{{{\rm{d}}t}}{\omega _{\rm{e}}} = \frac{{p{T_{\rm{e}}}}}{{{J_{\rm{m}}}}} - \frac{{p{T_{\rm{L}}}}}{{{J_{\rm{m}}}}} - \frac{{p{B_{\rm{m}}}}}{{{J_{\rm{m}}}}}{\omega _{\rm{e}}}.} \end{array}} \right. $ | (1) |
式中:ud、uq、id、iq分别为电机d、q轴定子电压和电流; Rs、Ls、ψf、p、Jm、Bm分别为电机定子电阻、电感、转子永磁磁链、极对数、转动惯量和摩擦系数; ωe为电机的电角速度; TL为负载转矩.
为了实施预测速度控制算法,需将连续时域内的数学模型进行离散化.采用泰勒级数法将式(1)离散化,可得:
| $ \begin{array}{l} \underbrace {\left[ {\begin{array}{*{20}{c}} {{i_d}(k + 1)}\\ {{i_q}(k + 1)}\\ {{\omega _{\rm{e}}}(k + 1)} \end{array}} \right]}_{\mathit{\boldsymbol{x}}(k + 1)} = {\mathit{\boldsymbol{A}}_{\rm{c}}}\underbrace {\left[ {\begin{array}{*{20}{c}} {{i_d}(k)}\\ {{i_q}(k)}\\ {{\omega _{\rm{e}}}(k)} \end{array}} \right]}_{\mathit{\boldsymbol{x}}(k)}\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{B}}_{\rm{c}}}\underbrace {\left[ {\begin{array}{*{20}{l}} {{u_d}(k)}\\ {{u_q}(k)} \end{array}} \right]}_{\mathit{\boldsymbol{u}}(k)} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \underbrace {\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {E{T_{\rm{L}}}(k)} \end{array}} \right]}_{{\mathit{\boldsymbol{D}}_{\rm{c}}}}, \end{array} $ | (2) |
其中:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{A}}_{\rm{c}}} = \left[ {\begin{array}{*{20}{c}} {1 - \frac{{{T_{\rm{s}}}{R_{\rm{s}}}}}{{{L_{\rm{s}}}}}}&{{\omega _{\rm{e}}}(k){T_{\rm{s}}}}&0\\ { - {\omega _{\rm{e}}}(k){T_{\rm{s}}}}&{1 - \frac{{{T_{\rm{s}}}{R_{\rm{s}}}}}{{{L_{\rm{s}}}}}}&0\\ {D{\omega _{\rm{e}}}(k)}&B&A \end{array}} \right],}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{B}}_{\rm{c}}} = \left[ {\begin{array}{*{20}{c}} {{T_{\rm{s}}}/{L_{\rm{s}}}}&0\\ 0&{{T_{\rm{s}}}/{L_{\rm{s}}}}\\ 0&C \end{array}} \right];} \end{array}\\ \begin{array}{*{20}{l}} {A = 1 - \frac{{{B_{\rm{m}}}{T_{\rm{s}}}}}{{{J_{\rm{m}}}}} + \frac{{B_{\rm{m}}^2T_{\rm{s}}^2}}{{2J_{\rm{m}}^2}} - \frac{{1.5{p^2}\psi _{\rm{f}}^2T_{\rm{s}}^2}}{{2{J_{\rm{m}}}{L_{\rm{s}}}}},}\\ {B = \frac{{1.5{p^2}{\psi _{\rm{f}}}{T_{\rm{s}}}}}{{{J_{\rm{m}}}}} - \frac{{1.5{p^2}{\psi _{\rm{f}}}{R_{\rm{s}}}T_{\rm{s}}^2}}{{2{J_{\rm{m}}}{L_{\rm{s}}}}} - \frac{{1.5{p^2}{\psi _{\rm{f}}}{B_{\rm{m}}}T_{\rm{s}}^2}}{{2J_{\rm{m}}^2}},}\\ {C = \frac{{1.5{p^2}{\psi _{\rm{f}}}T_{\rm{s}}^2}}{{2{J_{\rm{m}}}{L_{\rm{s}}}}},D = - \frac{{1.5{p^2}{\psi _{\rm{f}}}T_{\rm{s}}^2}}{{2{J_{\rm{m}}}}},E = \frac{{p{B_{\rm{m}}}T_{\rm{s}}^2}}{{2J_{\rm{m}}^2}} - \frac{{p{T_{\rm{s}}}}}{{{J_{\rm{m}}}}}.} \end{array} \end{array} $ |
式中:id(k+1)、iq(k+1)、ωe(k+1)、id(k)、iq(k)、ωe(k)分别为第(k+1)Ts时刻和第kTs时刻的d、q轴电流和电角速度; ud(k)、uq(k)分别为第kTs时刻作用于电机的d、q轴电压值; Ts为离散控制周期.
由于转速动态调节时间一般要长于离散控制周期,因而对于预测速度控制策略来讲,有必要实施多步预测以保证算法稳定性,且要求预测步长能够覆盖转速动态过程.若采用式(2)中的预测模型来实现速度多步预测,需要将该模型反复迭代,即
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{x}}(k + {N_{\rm{p}}}) = \mathit{\boldsymbol{A}}_{\rm{c}}^{{N_{\rm{p}}}}\mathit{\boldsymbol{x}}(k) + (\sum\limits_{n = 0}^{{N_{\rm{p}}} - 1} {\mathit{\boldsymbol{A}}_{\rm{c}}^n} {\mathit{\boldsymbol{B}}_{\rm{c}}})\mathit{\boldsymbol{u}}(k) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\sum\limits_{n = 0}^{{N_{\rm{p}}} - 1} {\mathit{\boldsymbol{A}}_{\rm{c}}^n} {\mathit{\boldsymbol{D}}_{\rm{c}}}),} \end{array} $ | (3) |
式中Np为预测步长.
式(3)为经典多步速度预测模型,该模型不仅需要采用高阶矩阵幂运算,且由于Ac,Dc中包含时变量ωe(k)和TL(k),导致其在线运算量较大,难以在现有微处理器水平下实现转速多步预测.
1.3 增量式速度预测模型为降低多步预测过程中的计算量,本文采用增量式建模方法,建立起增量式速度预测模型,以期在满足速度预测精度的同时,大幅降低多步预测计算量.
由式(2),系统状态x的增量可利用状态空间方程表示为
| $ \begin{array}{l} \underbrace {\left[ {\begin{array}{*{20}{c}} {\Delta {i_d}(k + 1)}\\ {\Delta {i_q}(k + 1)}\\ {\Delta {\omega _{\rm{e}}}(k + 1)} \end{array}} \right]}_{\Delta \mathit{\boldsymbol{x}}(k + 1)} = {\mathit{\boldsymbol{A}}_{\rm{I}}}\underbrace {\left[ {\begin{array}{*{20}{c}} {\Delta {i_d}(k)}\\ {\Delta {i_q}(k)}\\ {\Delta {\omega _{\rm{e}}}(k)} \end{array}} \right]}_{\Delta \mathit{\boldsymbol{x}}(k)}\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{B}}_{\rm{c}}}\underbrace {\left[ {\begin{array}{*{20}{l}} {\Delta {u_d}(k)}\\ {\Delta {u_q}(k)} \end{array}} \right]}_{\Delta \mathit{\boldsymbol{u}}(k)} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {E\Delta {T_{\rm{L}}}(k)} \end{array}} \right], \end{array} $ | (4) |
其中
| $ {\mathit{\boldsymbol{A}}_{\rm{I}}} = \left[ {\begin{array}{*{20}{c}} {1 - \frac{{{T_{\rm{s}}}{R_{\rm{s}}}}}{{{L_{\rm{s}}}}}}&{{\omega _{\rm{e}}}(k - 1){T_{\rm{s}}}}&0\\ { - {\omega _{\rm{e}}}(k - 1){T_{\rm{s}}}}&{1 - \frac{{{T_{\rm{s}}}{R_{\rm{s}}}}}{{{L_{\rm{s}}}}}}&0\\ {D{\omega _{\rm{e}}}(k - 1)}&B&{A + {i_{\rm{d}}}(k - 1)} \end{array}} \right], $ |
式中:Δid(k+1)=id(k+1)-id(k),Δid(k)=id(k)-id(k-1),Δiq(k+1)=iq(k+1)-iq(k),Δωe(k+1)=ωe(k+1)-ωe(k),Δωe(k)=ωe(k)-ωe(k-1).
考虑到在id=0控制中,id的数值近似为零.同时,ωeTs的数值较小,在实际计算中可令ωe(k-1)Ts≈ωeNTs,ωeN为额定电角速度.从而,AI可近似为
| $ {\mathit{\boldsymbol{A}}_{\rm{I}}} \approx \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {1 - \frac{{{T_{\rm{s}}}{R_{\rm{s}}}}}{{{L_{\rm{s}}}}}}&{{\omega _{{\rm{eN}}}}{T_{\rm{s}}}}&0\\ { - {\omega _{{\rm{eN}}}}{T_{\rm{s}}}}&{1 - \frac{{{T_{\rm{s}}}{R_{\rm{s}}}}}{{{L_{\rm{s}}}}}}&0\\ {D{\omega _{{\rm{eN}}}}}&B&A \end{array}} \right]. $ |
另外,忽略负载TL变化对速度预测的影响,即令ΔTL≈0,式(4)可整理为
| $ \Delta \mathit{\boldsymbol{x}}(k + 1) = \mathit{\boldsymbol{A}}\Delta \mathit{\boldsymbol{x}}(k) + {\mathit{\boldsymbol{B}}_{\rm{c}}}\Delta \mathit{\boldsymbol{u}}(k), $ | (5) |
将式(5)扩充为多步增量预测模型,可得:
| $ \Delta \mathit{\boldsymbol{x}}(k + {N_{\rm{p}}}) = {\mathit{\boldsymbol{A}}^{{N_{\rm{p}}}}}\Delta \mathit{\boldsymbol{x}}(k) + (\sum\limits_{n = 0}^{{N_{\rm{p}}} - 1} {{\mathit{\boldsymbol{A}}^n}} {\mathit{\boldsymbol{B}}_{\rm{c}}})\Delta \mathit{\boldsymbol{u}}(k). $ |
最终,增量式速度预测模型可建立为
| $ \mathit{\boldsymbol{x}}(k + {N_{\rm{p}}}) = \mathit{\boldsymbol{x}}(k) + \sum\limits_{n = 1}^{{N_{\rm{p}}}} \Delta \mathit{\boldsymbol{x}}(k + n). $ | (6) |
虽然利用式(6)来预测未来转速值仍需要实施高阶幂运算,但由于该式中的系数矩阵A和Bc已不包含时变参数,故式(6)可在离线确定系数矩阵的前提下,实现对未来转速值的预测,从而大幅降低了在线计算量.
2 增量式直接预测速度控制 2.1 控制集定义在经典有限集预测控制中,控制集仅包含基本有效电压矢量,电机控制自由度受限.为扩充经典算法的控制集,以实现更精确的速度、转矩控制,本文将电压矢量所在复平面以V1~V6为边界,划分为6个大扇区,扇区标号记为Ⅰ、Ⅱ、…、Ⅵ.同时,在各扇区内依照相同相角间隔虚拟出Nv个电压矢量,如图 2所示.将图中6个基本矢量和6Nv个虚拟矢量组成的矢量全部纳入控制集,作为备选控制矢量.
根据空间矢量调制理论,利用正弦定理,控制集中所有虚拟矢量可利用其所在扇区的相应矢量来合成.然而,采用此方法确定虚拟矢量的幅值和相角,势必会在预测过程中引入大量三角函数运算,导致多步预测算法在线计算量骤增.
为此,本文设计出一种“边界矢量合成方法”,在无需复杂三角函数运算,仅利用基本电压矢量的基础上,确定控制集内所有虚拟矢量的幅值与相角.定义虚拟矢量顺时针方向的边界基本矢量为“合成主矢量”Vm,由图 2可以看出,控制集中的任一虚拟矢量必可在其他基本矢量Vn的辅助下,沿边界合成该虚拟矢量,其合成关系为
| $ {\mathit{\boldsymbol{V}}_{\rm{s}}} = {\mathit{\boldsymbol{V}}_{\rm{m}}} + {\mathit{\boldsymbol{d}}_{\rm{n}}}{\mathit{\boldsymbol{V}}_{\rm{n}}}, $ |
式中Vm、Vn分别为合成虚拟矢量所需的主、辅矢量,见表 1.由表 1可知,同一扇区内的每个虚拟矢量的Vm和Vn相同,仅dn不同. dn∈[0, 1]为Vn的分配系数,本文称之为“合成占空比”.考虑到各扇区内虚拟矢量依照相同相角间隔分布,故在控制集中有dn=0, 1/(Nv+1), 2/(Nv+1), …, 1.例如,第Ⅱ扇区内Vm=V1;Vn=V4,在Nv=3时该扇区内沿逆时针方向的第2个虚拟矢量V23=V2+0.5V4,如图 2所示.
| 表 1 各扇区对应的合成主、辅矢量 Tab. 1 Master and slave vectors in different sectors |
借助上述矢量合成方法,从控制集中确定系统输出矢量需要两步完成:首先确定输出矢量所在扇区,查表 1得到Vm和Vn;其次,确定该矢量对应的dn.综上所述,利用扇区号和dn即可唯一标记控制集中的任一矢量.从而,扩充虚拟矢量后的控制集可表示为
| $ {\rm{CS}} = \left\{ {扇区号,{d_{\rm{n}}}\left| {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{V}}_{\rm{s}}} = {\mathit{\boldsymbol{V}}_{\rm{m}}} + {d_{\rm{n}}}{\mathit{\boldsymbol{V}}_{\rm{n}}};{\mathit{\boldsymbol{d}}_{\rm{s}}} = {S_{\rm{m}}} + {d_{\rm{n}}}{S_{\rm{n}}}}\\ {\,\,\,\,\,{d_{\rm{n}}} = 0,\frac{1}{{{N_{\rm{v}}} + 1}},\frac{2}{{{N_{\rm{v}}} + 1}}, \cdots ,1} \end{array}} \right.} \right\}. $ |
为从控制集中快速确定出最优输出矢量,本文提出与控制集对应的两阶段穷举寻优法,具体阐述如下.
预测速度控制的价值函数可定义为,
| $ \mathit{\boldsymbol{J}}(k) = \mathop \sum \limits_{n = 1}^{{N_{\rm{p}}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {[{\mathit{\boldsymbol{x}}^*} - \mathit{\boldsymbol{x}}(k + n)]^{\rm{T}}}\mathit{\boldsymbol{Q}}[{\mathit{\boldsymbol{x}}^*} - \mathit{\boldsymbol{x}}(k + n)] + \xi , $ | (7) |
其中
| $ \xi = \left\{ {\begin{array}{*{20}{l}} {0,}&{{I_{\rm{s}}} \le {I_{{\rm{ max }}}};}\\ {{\rm{inf}} ,}&{{I_{\rm{s}}} > {I_{{\rm{ max }}}}.} \end{array}} \right. $ |
式中:Is、Imax分别为定子电流有效值和最大值;x*为参考值向量.在id=0控制中,x*=[0 iqref ωeref]T,Q=diag[λd λq λω]T为权重系数矩阵,其中λd、λq、λω分别为d轴电流、q轴电流和转速的权重系数.
由式(7),结合增量式速度预测模型,预测速度控制策略对应的优化问题可表示为
| $ \begin{array}{*{20}{l}} {{\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{J}}(k)}\\ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{. }}\Delta \mathit{\boldsymbol{x}}(k + 1) = A\Delta \mathit{\boldsymbol{x}}(k) + {B_{\rm{c}}}\Delta u(k),}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{x}}(k + {N_{\rm{p}}}) = \mathit{\boldsymbol{x}}(k) + \sum\limits_{n = 1}^{{N_{\rm{p}}}} \Delta \mathit{\boldsymbol{x}}(k + n),}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \mathit{\boldsymbol{u}}(k){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{CS}}{\rm{.}}} \end{array} $ | (8) |
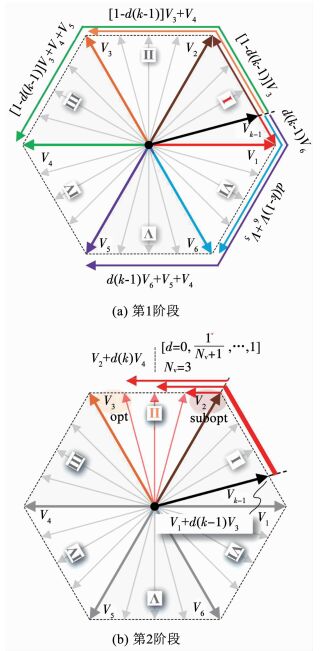
为确定最优矢量所在扇区,首先假定第(k-1)Ts时刻的最优电压矢量为Vk-1,位于第I扇区,如图 3(a)所示.按照空间电压矢量合成规则,此时Vk-1= V1+d(k-1)V3,其中d(k-1)为第(k-1)Ts时刻的最优占空比.
|
图 3 矢量寻优过程示意 Fig. 3 Process of vector exhaustion |
其次,沿“六边形边界”确定所有基本电压矢量V1~V6与Vk-1间的误差矢量Δu.以V3与Vk-1间的误差矢量Δu3为例,借助“六边形边界”来计算误差矢量Δu3,可得:
| $ \Delta {\mathit{\boldsymbol{u}}_3} = [1 - d(k - 1)]{\mathit{\boldsymbol{V}}_3} + {\mathit{\boldsymbol{V}}_4}. $ | (9) |
比较式(9)与传统空间矢量合成方法可以发现,沿六边形边界来计算Δu更加直观,且计算量更低.按照上述规律,V1~V6与Vk-1间的误差矢量Δu如图 3(a)所示.进而,将以上计算规律扩展至其他扇区,可得Vk-1处于Sector Ⅱ~Ⅵ时V1~V6与Vk-1间的误差矢量Δu,见表 2.
| 表 2 第1阶段各扇区对应的矢量增量 Tab. 2 Incremental vector calculation of each sector in Stage 1 |
最后,将表 2中的Δu代入式(8)中的优化问题,并采用穷举法求解该优化问题,得到6个有效矢量中令J最小的基本矢量Vopt和次小的Vsubopt.由图 3可知,扇区的分界线为6个基本电压矢量.那么,最优输出电压矢量所在扇区必为Vopt和Vsubopt所包围的扇区.
2.2.2 第2阶段:合成占空比穷举寻优在确定最优矢量所在扇区后,将该扇区内的各矢量依次代入价值函数进行二次寻优,以确定最优输出矢量及其合成占空比.
仍假定第(k-1)Ts时刻的最优电压矢量为Vk-1= V1+d(k-1)V3,位于第I扇区,如图 3(b)所示.同时,假定经过第1阶段的寻优,Vopt= V3,Vsubopt= V2,即最优扇区为第II扇区.那么,根据边界矢量合成方法,可得:
| $ {\mathit{\boldsymbol{V}}_k} = {\mathit{\boldsymbol{V}}_2} + d(k){\mathit{\boldsymbol{V}}_4}, $ | (10) |
式中:Vk为第kTs时刻的输出电压矢量;d(k)=0, 1/(Nv+1), 2/(Nv+1), …, 1表示其对应合成占空比.根据式(10),计算第kTs时刻的电压增量,可得:
| $ \Delta {\mathit{\boldsymbol{u}}_k} = {\mathit{\boldsymbol{V}}_k} - {\mathit{\boldsymbol{V}}_{k - 1}} = {\mathit{\boldsymbol{V}}_2} + d(k){\mathit{\boldsymbol{V}}_4} - {\mathit{\boldsymbol{V}}_1} - d(k - 1){\mathit{\boldsymbol{V}}_3}. $ |
考虑到d(k)共有Nv+2种备选方案,故第kTs时刻共有Nv+2个备选电压增量Δuk.将以上Δuk代入式(8)中的优化问题进行穷举寻优,确定出价值函数值最小的Δuk,即可得出最优输出电压矢量及其对应的合成占空比d(k).
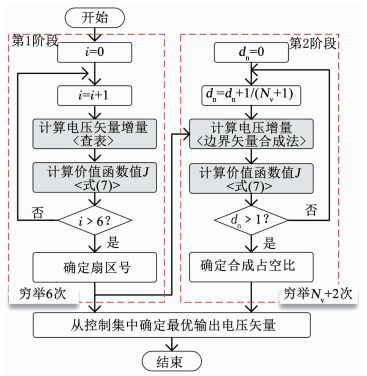
综上所述,第1阶段寻优需要开展6次穷举以确定最优矢量所在扇区,第2阶段寻优需要开展Nv+2次穷举以确定最优矢量对应合成占空比.因此,对于本文所提出的增量式预测速度控制算法,共需穷举Nv+8次穷举以确定最优输出矢量,具体算法流程图如图 4所示.
|
图 4 算法流程 Fig. 4 Flowchart of exhaustive optimization method |
本文所提出的增量式直接预测速度控制算法原理框图如图 5所示.
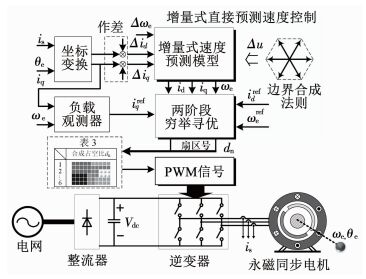
|
图 5 控制框图 Fig. 5 Control block diagram of proposed algorithm |
在所提出的算法中,通过构建龙贝格负载观测器,提供q轴电流参考值.负载观测器的数学表达式为
| $ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {{{\hat \omega }_{\rm{e}}}}\\ {{{\hat T}_{\rm{L}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{{p{B_{\rm{m}}}}}{{{J_{\rm{m}}}}}}&{ - \frac{p}{{{J_{\rm{m}}}}}}\\ 0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\hat \omega }_{\rm{e}}}}\\ {{{\hat T}_{\rm{L}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {1.5{p^2}{\psi _{\rm{f}}}}\\ {{J_{\rm{m}}}}\\ 0 \end{array}} \right]{i_q} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{L}}({\omega _{\rm{e}}} - {{\hat \omega }_{\rm{e}}}), \end{array} $ |
式中:标记“^”表示变量的观测值,L =diag(l1, l2)为观测器系数矩阵,其数值决定负载转矩的观测速度和精度.进而,考虑到
同时,根据矢量运算法则和幅秒平衡原理,可以发现合成占空比与三相输出占空比dA、dB和dC间存在之间直接对应关系,见表 3.
| 表 3 各扇区中合成占空比与输出占空比间的对应关系 Tab. 3 Relation between dn and dA, dB, and dC |
由表 3可知,在经过两阶段穷举寻优确定出最优矢量所在扇区和合成占空比后,可按照表 3中的对应关系,在无需SVPWM辅助的情况下直接确定三相输出占空比,实现对永磁电机的直接速度控制.
3 实验所提出的控制策略应用于一台2.3 kW永磁伺服电机中,电机参数见表 4.实验测试平台中,负载电机为一台同型号永磁伺服电机.实验中,控制算法由TI公司生产的浮点型双核数字处理器(MCU)TMS320F28377D和Intel公司生产的Cyclone V系列FPGA共同实现.其中,DSP主要负责算法执行,FPGA主要负责高精度ADC采样与DAC转换、分发脉冲等.
| 表 4 永磁电机参数 Tab. 4 PMSM parameters |
图 6给出了电机参考转速nref、实际转速N、A相电流iA,d/q轴电流id/iq和电角度θe的稳态实验波形.实验中,电机采用本文所提出的IDPSC算法控制,控制周期为50 μs,Np=Nv=10.图 6(a)中,电机参考转速nref=1 500 r/min,负载转矩9.5 Nm;图 6(b)中,电机参考转速nref=800 r/min,负载转矩由0 Nm阶跃至7 Nm.由图 6可以看出,本文所提出的IDPSC算法可实现对参考转速的无偏差跟踪,电机定子电流谐波含量较低,且在受到负载扰动时仍能够快速恢复对参考转速的跟踪,具有良好的转速稳态控制性能.
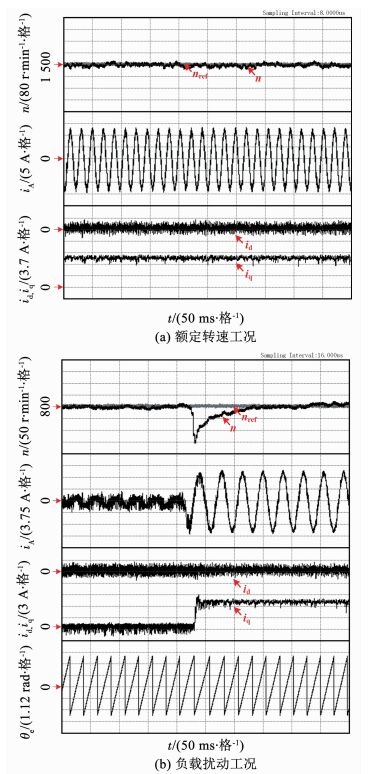
|
图 6 IDPSC算法稳态实验波形 Fig. 6 Waveforms of IDPSC in steady-state experiment |
图 7给出了不同控制参数(Nv)和电机参数失配(Jm和Ls)情况下的电机稳态实验波形.实验中,电机采用本文所提出的IDPSC算法控制,控制周期为50 μs.参考转速nref=1 000 r/min,Np=10.
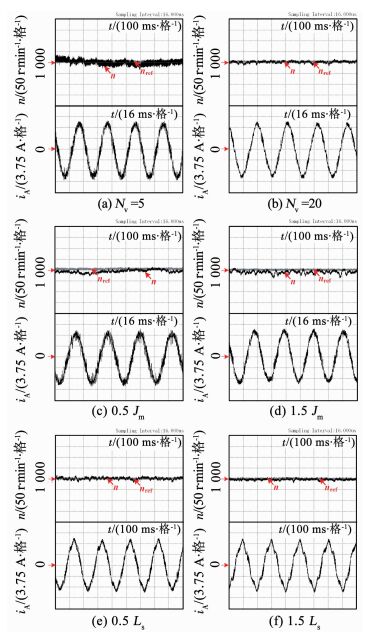
|
图 7 不同控制参数及电机参数失配情况下IDPSC算法的实验波形 Fig. 7 Experimental waveforms of IDPSC under different control parameters and parameter mismatches |
由图 7(a)和图 7(b)可以发现,随着控制集中虚拟矢量个数的增加,可提供更多的控制自由度,提升了算法对转速的控制精度,转速波动减小,电流的谐波畸变程度也会随着Nv的增大而逐渐下降.但是需要注意的是,由于IDPSC算法的穷举次数为Nv+8,因此随着Nv的增大,算法的在线计算量也会随之增大.综上,Nv的数值决定了控制集中虚拟矢量的个数,Nv的数值越大,备选矢量越多,系统稳态性能愈佳.然而,随着Nv的数值的增大,所产生的计算开销也更大,会增加处理器计算负担,导致算法实用性下降.为此,在实际应用中,建议在处理器水平允许的情况下,尽可能的增大Nv的数值,以保证较理想的稳态性能.
由图 7(c)~图 7(f)可以发现,在电机参数偏离标称值±50%时,由于增量式预测模型包含了积分内模,电机转速仅出现轻微跟踪偏差,稳态波动指标并未大幅改变,定子电流的谐波畸变程度也未显著上升,表明算法具备一定的参数鲁棒性.
3.3 动态跟踪性能图 8给出了电机参考转速nref、实际转速n、A相电流iA,d/q轴电流id/iq和电角度θe的动态实验波形.实验中,电机采用本文所提出的IDPSC算法控制,控制周期为50 μs,Np=Nv=10.图 8(a)中,参考转速nref由500 r/min阶跃至1 000 r/min.图 8(b)中,参考转速nref为0~1 200 r/min的三角波信号.由图 8可以看出,无论是阶跃信号,还是斜坡信号,IDPSC算法均能够快速、无差的跟踪转速参考信号,且不存在显著超调现象,表明其具有良好的转速动态控制性能.
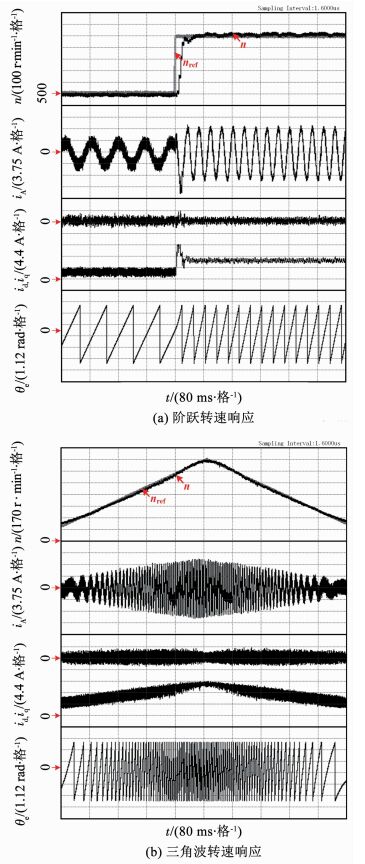
|
图 8 IDPSC算法动态实验波形 Fig. 8 Waveforms of IDPSC in dynamic experiment |
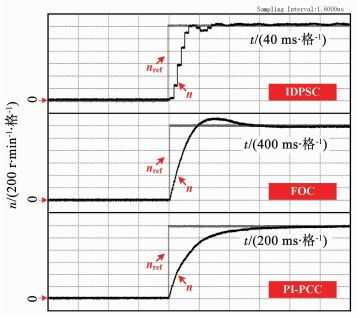
图 9给出了应用不同速度控制算法时电机参考转速nref和实际转速N的实验波形.实验中,电机空载起动,nref=1 200 r/min.图 9中,电机分别采用矢量控制(FOC,控制周期200 μs)、预测电流控制(PI-PCC,控制周期50 μs)和IDPSC(控制周期50 μs)进行控制.由图 9可以看出,IDPSC的起动时间最短,转速稳定时间约62 ms,PI-PCC的转速稳定时间约780 ms,FOC的起动时间最长,约1.2 s.这是因为IDPSC算法利用价值函数直接筛选出满足转速、电流和工况需求的电压矢量作用于电机,避免了级联控制结构,大幅缩短了电机的转速调节时间.
|
图 9 不同算法控制下的电机动态实验波形 Fig. 9 Waveforms of motor in dynamic experiment with different algorithms |
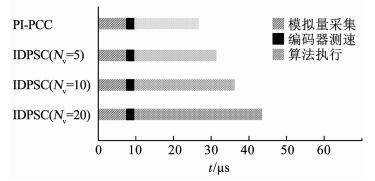
图 10给出了PI-PCC与IDPSC所需的执行时间.实验中,MCU工作频率为200 MHz,FPGA主时钟为50 MHz.由图 10可以看出,IDPSC的执行时间略长于PI-PCC,且随着Nv数值的增大,执行时间随之上升.这是由于在IDPSC中,共需穷举寻优8次来获得最优输出电压矢量,而在IDPSC中,共需穷举寻优Nv+2次来获得最优输出电压矢量.但是由图 10还可以看出,IDPSC并不会显著增加MCU的运算负担,现有数字处理器的运算水平完全能够胜任.这是由于本文所提出的增量式速度预测模型相比于经典电机数学模型,实现难度及计算复杂度更低,因此在一定程度上保证了IDPSC的执行效率.
|
图 10 算法执行时间对比分析 Fig. 10 Comparative analysis of execution efficiency |
1) 本文提出了一种适用于永磁电机系统的高性能无级联速度控制方案——增量式直接预测速度控制策略,有效改善了永磁电机的转速调控能力,且具有较好的可实施性.
2) 针对永磁电机系统,本文给出了一种增量式速度预测模型构建方法,可离线确定多步速度预测模型的所有参数,大幅降低了在线计算量,有效保证了预测速度控制算法的稳定性.同时,由于增量式预测模型中已内含积分内模,一定程度上提升了策略的参数鲁棒性.
3) 针对预测速度控制算法,本文设计了相应的扩张控制集及其特有的矢量合成和筛选方法,增加了控制自由度,使得电机具备了平稳的速度性能.
| [1] |
徐磊, 朱孝勇, 张超, 等. 直线旋转永磁电机及其控制技术综述与新发展[J]. 中国电机工程学报, 2020, 40(6): 1972. XU Lei, ZHU Xiaoyong, ZHANG Chao, et al. Overview and new development of linear and rotary permanent magnet machines and control technologies[J]. Proceedings of the CSEE, 2020, 40(6): 1972. DOI:10.13334/j.0258-8013.pcsee.191329 |
| [2] |
李晨, 谷鑫, 周湛清, 等.永磁同步电机低计算复杂度离散开关占空比预测转矩控制[J].中国电机工程学报, 2020-03-04[DOI:10.13334/j.0258-8013.pcsee.191656] LI Chen, GU Xin, ZHOU Zhanqing, et al. Low computational burden predictive torque control with discrete switching duty ratio for PMSM drives[J]. Proceedings of the CSEE, 2020-03-04.[DOI:10.13334/j.0258-8013.pcsee.191656] |
| [3] |
CHAOUI H, KHAYAMY M, OKOYE O, et al. Simplified speed control of permanent magnet synchronous motors using genetic algorithms[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3563. DOI:10.1109/TPEL.2018.2851923 |
| [4] |
JUNG J W, LEU V Q, DO T D, et al. Adaptive PID speed control design for permanent magnet synchronous motor drives[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 900. DOI:10.1109/TPEL.2014.2311462 |
| [5] |
SHI Tingna, YAN Yan, ZHOU Zhanqing, et al. Linear quadratic regulator control for PMSM drive systems using nonlinear disturbance observer[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 5093. DOI:10.1109/TPEL.2019.2947259 |
| [6] |
RODRIGUEZ J, CORTES P. Predictive control of power converters and electrical drives[M]. New Jersey: John Wiley & Sons, Ltd., 2012.
|
| [7] |
WANG Liuping. Model predictive control system design and implementation using MATLAB[M]. London: Springer, 2008.
|
| [8] |
TU Wencong, LUO Guangzhao, CHEN Zhe, et al. Predictive cascaded speed and current control for PMSM drives with multi-timescale optimization[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 11046. DOI:10.1109/TPEL.2019.2897746 |
| [9] |
BOLOGNANI S, BOLOGNANI S, PERETTI L, et al. Design and implementation of model predictive control for electrical motor drives[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1925. DOI:10.1109/TIE.2008.2007547 |
| [10] |
FUENTES E J, SILVA C A, YUZ J I. Predictive speed control of a two-mass system driven by a permanent magnet synchronous motor[J]. Transactions on Industrial Electronics, 2012, 59(7): 2840. DOI:10.1109/TIE.2011.2158767 |
| [11] |
FUENTES E, KALISE D, RODRíGUEZ J, et al. Cascade-free predictive speed control for electrical drives[J]. Transactions on Industrial Electronics, 2014, 61(5): 2176. DOI:10.1109/TIE.2013.2272280 |
| [12] |
KAKOSIMOS P, ABU-RUB H. Predictive speed control with short prediction horizon for permanent magnet synchronous motor drives[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2740. DOI:10.1109/TPEL.2017.2697971 |
| [13] |
GAO Xiaonan, ABDELRAHEM M, HACKL C, et al. Direct predictive speed control with a sliding manifold term for PMSM drives[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics (Early Access), 2020. DOI:10.1109/JESTPE.2019.2923285 |
| [14] |
SHADMAND M B, JAIN S, BALOG R S. Autotuning technique for the cost function weight factors in model predictive control for power electronic interfaces[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(2): 1408. DOI:10.1109/JESTPE.2018.2849738 |
| [15] |
ZHANG Xiaoguang, HE Yikang. Direct voltage-selection based model predictive direct speed control for PMSM drives without weighting factor[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 34(8): 7838. DOI:10.1109/TPEL.2018.2880906 |
| [16] |
ZHOU Zhanqing, XIA Changliang, YAN Yan, et al. Torque ripple minimization of predictive torque control for PMSM with extended control set[J]. Transactions on Industrial Electronics, 2017, 64(9): 6930. DOI:10.1109/TIE.2017.2686320 |
| [17] |
ZHANG Xiaoguang, CHENG Yu, ZHAO Zhihao, et al. Robust model predictive direct speed control for SPMSM drives based on full parameter disturbances and load observer[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8361. DOI:10.1109/TPEL.2019.2962857 |
| [18] |
XIA Changliang, LIU Ning, ZHOU Zhanqing, et al. Steady-state performance improvement for LQR-based PMSM drives[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10622. DOI:10.1109/TPEL.2018.2803760 |
| [19] |
ZHOU Zhanqing, XIA Changliang, YAN Yan, et al. Disturbances attenuation of permanent magnet synchronous motor drives using cascaded predictive-integral-resonant controllers[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1514. DOI:10.1109/TPEL.2017.2679126 |
| [20] |
赵峰, 罗雯, 高锋阳, 等.考虑滑模抖振和扰动补偿的永磁同步电机改进滑模控制[J/OL].西安交通大学学报, 2020-03-06http://kns.cnki.net/kcms/detail/61.1069.T.20200306.1344.004.html ZHAO Feng, LUO Wen, GAO Fengyang, et al. Improved sliding mode control for PMSM considering sliding mode chattering and disturbance compensation[J/OL]. Journal of Xi'an Jiaotong University, 2020-03-06.http://kns.cnki.net/kcms/detail/61.1069.T.20200306.1344.004.html |
 2020, Vol. 52
2020, Vol. 52


