2. 西南大学 工程技术学院, 重庆; 400715;
3. 浙江双环传动机械股份有限公司, 浙江 台州, 317600
2. College of Engineering and Technology, Southwest University, Chongqing 400715, China;
3. Shuanghuan Driveline co., LTD., Taizhou 317600, Zhejiang, China
齿轮是极其重要的核心基础件,影响齿轮传动性能的主要因素有啮合齿面、润滑状态、表面粗糙度、材料及热处理方式等,其中啮合齿面作为运动和动力变换的直接作用面,对齿轮的性能具有非常重要的影响,因此如何获得具有良好几何特性和接触特性的啮合齿面是提高齿轮性能的关键问题[1-3].国内外学者对啮合齿面进行了深入研究,主要方法有齿面修形和构建新的啮合齿面[4-7].
齿面修形主要有三维拓扑修形、齿形修形和齿向修形,国内外很多学者在该领域进行了大量的研究,如方宗德等对人字齿轮的主动轮进行三维修形[8],设计了对角修形斜齿轮齿面[9],建立了面齿轮修形简化模型[10-11],研究了鼓形修形对载荷分布的影响[12];彭先龙等[13]提出了齿面主动修形方法来预控斜齿面齿轮的啮合性能并消除边界接触;张西金等[14]提出了圆弧齿廓刀具修形及齿向鼓形修形的方案;Pedrero等[3]研究了修形对啮合刚度、载荷分布和传动误差的影响.目前,关于齿轮啮合理论的研究仍然以共轭曲面原理为基础,对常用齿轮传动齿形的优化、修正、构型仍然是研究的重点,这些研究对提高齿轮传动的性能起到了积极作用,但是仍然未从根本上解决问题.
在构建新的啮合齿面方面,陈扬枝等[15-16]建立了空间曲线沿接触点主法线方向的啮合方程及啮合曲线方程,获得了具有直径的钩杆曲齿传动;陈兵奎等[17]提出了曲线共轭啮合理论,将给定运动两构件上的光滑曲线始终保持相切接触定义为曲线啮合,给出了由共轭曲线形成啮合齿面的一般方法,并将该理论应用于平行轴和相交轴齿轮传动[18-21].由于共轭曲线的接触具有灵活性和多样性,既可以在节圆内啮合,又可以在节圆上啮合,还可以在节圆外啮合;齿轮在运动的过程中可以有多对共轭曲线同时参与啮合,共轭曲线对数目增加,同时接触的点的数目相应增加,接触区域扩大,可以减少跑合时间,增加齿轮的承载能力;多对曲线同时参与啮合时,共轭曲线对的分布对齿轮的传动性能有显著影响.前期的研究中,设计的共轭曲线凸齿齿轮在节圆外啮合,凹齿齿轮在节圆内啮合,在加工时需要设计两把刀具,如果齿轮能在节圆内和节圆外同时实现多对共轭曲线接触,且在加工时仅需一把刀具即可加工出相互啮合的一对齿轮,不仅可以显著降低制造成本,而且能大幅度提高齿轮传动的性能.
本文在共轭曲线啮合理论的基础上,提出分阶式多点接触齿轮,并以分阶式四点接触齿轮为例,开展齿轮的基本齿形设计,进而推导滚刀的齿面方程,求解齿面方程并建立滚刀的精确实体模型,根据实体模型,获得滚刀实体,完成分阶式四点接触齿轮副的滚切试制.
1 分阶式多点接触齿轮所谓分阶式多点接触齿轮,是指齿轮的啮合齿面分为上啮合齿面和下啮合齿面,呈阶梯分布,由过渡齿面连接.齿轮副运动时,小齿轮的上啮合面与大齿轮的下啮合面啮合,有两个或两个以上的接触点,小齿轮的下啮合面与大齿轮的上啮合面啮合,有两个或两个以上的接触点,上下啮合齿面同时在四个接触点接触.齿轮在啮合时,多对共轭曲线同时参与啮合,工作齿面在多个接触点同时接触.以分阶式四点接触齿轮为例,如图 1所示,齿轮啮合齿面上有4条共轭曲线,在啮合时,上啮合面有两个接触点,下啮合面有两个接触点.
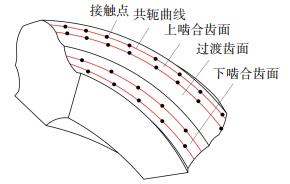
|
图 1 分阶式多点接触共轭曲线齿轮 Fig. 1 Multi-point contact gear with ladder shape of teeth |
分阶式四点接触齿轮副在运动时,如图 2所示,小齿轮上啮合齿面与大齿轮下啮合齿面啮合,小齿轮下啮合面和大齿轮上啮合面啮合,均为凹凸接触,加载之后,接触位置由于弹性变形从接触点扩展为接触面,承载能力提高,具有接触强度高、重合度高的特点.齿轮啮合时,接触点仅在齿宽方向移动,无齿高方向移动,相对于渐开线齿轮,传动比较平稳,滑动率很低,摩擦损失少,传动效率高.
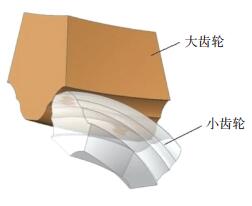
|
图 2 单齿啮合 Fig. 2 Single tooth meshing |
啮合齿面是由刀具基本齿形通过展成运动得到的,因此基本齿形对啮合齿面的传动性能具有重要影响.取刀具的法面齿廓为基本齿形,同侧齿面的基本齿形有两段工作齿廓,分别有两个接触点,在啮合时共有4个接触点,如图 3所示,图中α1、α2为接触点处的压力角.
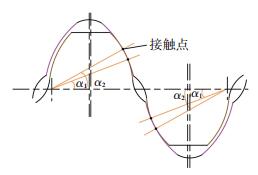
|
图 3 基本齿形啮合 Fig. 3 Basic tooth profile meshing |
刀具的法面齿廓如图 4所示.切削刃I是半径为ρ的圆弧,将切削出上啮合齿面; 切削刃II是半径为rf的圆弧,将切削出过渡齿面; 切削刃Ⅲ为抛物线,将切削出下啮合齿面; 切削刃IV是半径为rj的圆弧,将切削出齿根过渡曲面.ha和hf分别为齿顶高和齿根高; h为全齿高. Sa为凸齿齿廓部分齿厚; Sf为凹齿齿廓部分齿厚. δ1为工艺角.建立坐标系Sn(On; xn, yn, zn)与齿条固连,xnOnyn平面与齿条法面重合,坐标轴xn与齿廓的对称轴线重合,yn与齿条节线重合.
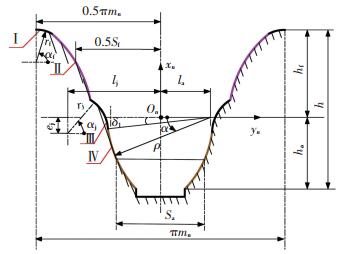
|
图 4 刀具法面齿廓 Fig. 4 Normal tooth profile of rack cutter |
根据齿条的几何形状,可得各切削刃在坐标系Sn中的方程为
| $ \begin{array}{l} \mathit{\boldsymbol{r}}_n^{({\rm{I}})}(\alpha ) = \left[ {\begin{array}{*{20}{c}} {x_n^{({\rm{I}})}(\alpha )}\\ {y_n^{({\rm{I}})}(\alpha )}\\ {z_n^{({\rm{I}})}(\alpha )}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \rho {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha }\\ { \mp (\rho {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha - {l_{\rm{a}}})}\\ 0\\ 1 \end{array}} \right], \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{{\rm{min}}}} \le \alpha \le {\alpha _{{\rm{max}}}}. \end{array} $ | (1) |
式中:α为自变量参数,ρ为圆弧的半径,(0, la)为圆弧圆心在坐标系xnOnyn中的坐标值.
切削刃Ⅱ用矢量rn(Ⅱ)(αj)表示,其在坐标系Sn中的表达式为
| $ \begin{array}{l} \mathit{\boldsymbol{r}}_n^{({\rm{ II }})}({\alpha _{\rm{j}}}) = \left[ {\begin{array}{*{20}{c}} {x_n^{({\rm{II}})}({\alpha _{\rm{j}}})}\\ {y_n^{({\rm{ II }})}({\alpha _{\rm{j}}})}\\ {z_n^{({\rm{ II }})}({\alpha _{\rm{j}}})}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - ({r_{\rm{j}}}{\kern 1pt} {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{j}}} + {e_{\rm{j}}})}\\ { \pm ({r_{\rm{j}}}{\kern 1pt} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{j}}} - {l_{\rm{j}}})}\\ 0\\ 1 \end{array}} \right], \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{{\rm{j}}{\kern 1pt} {\rm{min}}}} \le {\alpha _{\rm{j}}} \le {\alpha _{{\rm{j}}{\kern 1pt} {\rm{max}}}}. \end{array} $ | (2) |
式中:αj为自变量参数,rj为圆弧的半径,(ej, lj)为圆弧圆心在坐标系xnOnyn中的坐标值.
切削刃Ⅲ用矢量rn(Ⅲ)(τ)表示,其在坐标系Sn中的表达式为
| $ \begin{array}{l} \mathit{\boldsymbol{r}}_n^{({\rm{III}})}(\mathit{\boldsymbol{\tau }}) = \left[ {\begin{array}{*{20}{c}} {x_n^{({\rm{III}})}(\mathit{\boldsymbol{\tau }})}\\ {y_n^{({\rm{III}})}(\mathit{\boldsymbol{\tau }})}\\ {z_n^{({\rm{III}})}(\mathit{\boldsymbol{\tau }})}\\ 1 \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} { - \left( {\mathit{\boldsymbol{\tau }}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma + \frac{{{\mathit{\boldsymbol{\tau }}^2}}}{{2p}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma - {L_1}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma } \right)}\\ { \mp \left( { - \mathit{\boldsymbol{\tau }}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma + \frac{{{\mathit{\boldsymbol{\tau }}^2}}}{{2p}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma - {L_1}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma + {l_a} + 0.5\pi w{m_n}} \right)}\\ 0\\ 1 \end{array}} \right],\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{\tau }}_{{\rm{min}}}} \le \mathit{\boldsymbol{\tau }} \le {\mathit{\boldsymbol{\tau }}_{{\rm{max}}}}. \end{array} $ | (3) |
式中:τ为自变量参数; σ为设计参数, σ=0.5(α1+α2), α1和α2为法面压力角;p为抛物线参数, p=ρcos (σ/2); L1=0.5ρtanσsinσ+ρcos σ.
切削刃IV用矢量1n(IV)(αf)表示,其在坐标系Sn中的表达式为
| $ \begin{array}{l} \mathit{\boldsymbol{r}}_n^{({\rm{IV}})}({\alpha _f}) = \left[ {\begin{array}{*{20}{c}} {x_n^{({\rm{IV}})}({\alpha _{\rm{f}}})}\\ {y_n^{({\rm{IV}})}({\alpha _{\rm{f}}})}\\ {z_n^{({\rm{IV}})}({\alpha _{\rm{f}}})}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - ({r_{\rm{f}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{f}}} + {e_{\rm{f}}})}\\ { \pm ({r_{\rm{f}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{f}}} - {l_{\rm{f}}})}\\ 0\\ 1 \end{array}} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{{\rm{ fmin }}}} \le {\alpha _f} \le {\alpha _{{\rm{ fmax }}}}. \end{array} $ | (4) |
式中: αf为自变量参数;rf为圆弧半径,(ef, lf)为圆弧圆心在坐标系xnOnyn的坐标值.
在式(1)~(4)中,左侧法面齿廓的yn(i)(t)取上面的符号,右侧法面齿廓的yn(i)(t)取下面的符号(i=I时,t=α;当i=Ⅱ时,t=αj;当i=Ⅲ时,t=τ;当i=IV时,t=αf).
3 滚刀的齿面方程 3.1 坐标系与坐标变换如图 5,分别建立固定坐标系S0(O0-x0, y0, z0)和活动坐标系S1(O1-x1, y1, z1)与滚刀固连.坐标轴z0和z1重合,为滚刀的旋转轴线.活动坐标系Sp(Op-xp, yp, zp)与齿条固连.坐标轴zp与zn的夹角为β.u为坐标原点Op和On在zn轴上的距离.
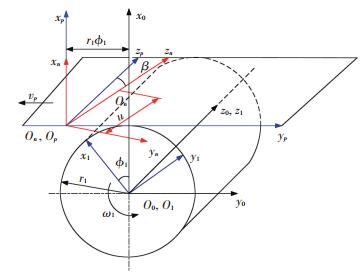
|
图 5 展成过程 Fig. 5 Gear generating |
在整个展成过程中,齿条刀具的节面和滚刀的节圆柱始终保持相切接触.滚刀绕回转轴线z1逆时针旋转,旋转角速度为ω1,同时齿条刀具将向左平移,速度为vp.当齿轮绕轴线旋转一个角度ϕ1,齿条刀具将向左平移r1ϕ1.
根据坐标变换理论,坐标系Sn与Sp之间的坐标变换矩阵为
| $ {\mathit{\boldsymbol{M}}_{pn}}(u) = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&{{\rm{cos}}{\kern 1pt} {\kern 1pt} \beta }&{{\rm{sin}}{\kern 1pt} {\kern 1pt} \beta }&{u{\rm{sin}}{\kern 1pt} {\kern 1pt} \beta }\\ 0&{ - {\rm{sin}}{\kern 1pt} {\kern 1pt} \beta }&{{\rm{cos}}{\kern 1pt} {\kern 1pt} \beta }&{u{\rm{cos}}{\kern 1pt} {\kern 1pt} \beta }\\ 0&0&0&1 \end{array}} \right] $ |
坐标系Sp与S0之间的坐标变换矩阵为
| $ {\mathit{\boldsymbol{M}}_{0p}}({\phi _1}) = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1}}&{ - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\phi _1}}&0&{{r_1}({\rm{cos}}{\kern 1pt} {\kern 1pt} {\phi _1} + {\phi _1}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\phi _1})}\\ {{\rm{sin}}{\kern 1pt} {\kern 1pt} {\phi _1}}&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\phi _1}}&0&{{r_1}({\rm{sin}}{\kern 1pt} {\kern 1pt} {\phi _1} - {\phi _1}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\phi _1})}\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]. $ | (6) |
式中: r1为齿轮的节圆半径;Mpn为坐标系Sn到Sp的变换矩阵,M0p为坐标系Sp到S的变换矩阵.
3.2 啮合方程设点M为啮合点,根据式(1)~(5)可以获得点M在坐标系Sp中的表达式为
| $ \begin{array}{l} {\mathit{\boldsymbol{r}}_p}(u, t) = \left[ {\begin{array}{*{20}{c}} {{x_p}(u, t)}\\ {{y_p}(u, t)}\\ {{z_p}(u, t)}\\ 1 \end{array}} \right] = {\mathit{\boldsymbol{M}}_{pn}}(u)\mathit{\boldsymbol{r}}_n^{(i)}(t)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = {\rm{I}}, {\rm{II}}, {\rm{III}}, {\rm{IV}}). \end{array} $ | (7) |
式中:当i=I时,t=α;当i=Ⅱ时,t=αj;当i=Ⅲ时,t=τ;当i=IV时,t=αf.
啮合点M的法线可以在坐标系Sp表示为
| $ \mathit{\boldsymbol{n}}_P^M = \frac{{\partial {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{r}}_p}(u, t)}}{{\partial t}} \times \frac{{\partial {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{r}}_p}(u, t)}}{{\partial u}} = \left[ {\begin{array}{*{20}{c}} {y_n^{(i)}{\rm{'}}(t)}\\ { - x_n^{(i)}{\rm{'}}(t){\rm{cos}}{\kern 1pt} {\kern 1pt} \beta }\\ {x_n^{(i)}{\rm{'}}(t){\rm{sin}}{\kern 1pt} {\kern 1pt} \beta } \end{array}} \right], $ | (8) |
啮合点M的相对速度在坐标系Sp中表示为
| $ \mathit{\boldsymbol{v}}_{0p}^M = {\mathit{\boldsymbol{v}}_p} - \mathit{\boldsymbol{v}} = {\mathit{\boldsymbol{v}}_p} - {\mathit{\boldsymbol{\omega }}_1} \times {\mathit{\boldsymbol{r}}_1} = {\omega _1}\left[ {\begin{array}{*{20}{c}} {{r_1}{\phi _1} - {y_p}(u, t)}\\ {{x_p}(u, t)}\\ 0 \end{array}} \right]. $ | (9) |
式中:vp为啮合点随刀具齿条的移动速度,vp=-r1ω1jp; v为啮合点随齿轮的运动速度,v=-ω1×r1; ω1=-ω1kp; r1=(r1+xp(u, t)ip+(-r1ϕ1+yp(u, t))jp+zp(u, t)kp.
根据齿轮啮合原理,任意啮合点处的公法线与相对速度方向垂直,其啮合方程可以在坐标系Sp中表示为
| $ \varPhi (t, u, {\phi _1}) = \mathit{\boldsymbol{n}}_p^M \cdot \mathit{\boldsymbol{v}}_{0p}^M = 0. $ | (10) |
将方程(8)和(9)代入方程(10),可得
| $ u = \frac{{{r_1}{\phi _1}}}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} \beta }} - y_n^{(i)}(t){\kern 1pt} {\rm{cot}}{\kern 1pt} {\kern 1pt} \beta - \frac{{x_n^{(i)}(t)x_n^{(i)}{\rm{'}}(t)}}{{y_n^{(i)}{\rm{'}}(t)}}{\rm{cot}}{\kern 1pt} {\kern 1pt} \beta . $ | (11) |
式(11)确定了齿条的移动距离参数u和滚刀的转角ϕ1以及切削刃参数t的关系.
3.3 齿面方程根据齿轮啮合原理,滚刀齿面可以用方程表示为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{r}}(t, u, {\phi _1}) = {\mathit{\boldsymbol{M}}_{0p}}({\phi _1}){\mathit{\boldsymbol{r}}_p}(t, u), }\\ {\varPhi (t, u, {\phi _1}) = \mathit{\boldsymbol{n}}_p^M \cdot \mathit{\boldsymbol{v}}_{0p}^M = 0.} \end{array}} \right. $ | (12) |
将式(6), (7)和(11)代入式(12), 滚刀齿面方程可以在坐标系S1中表示为
| $ \begin{array}{l} \mathit{\boldsymbol{r}}(t, {\phi _1}) = \\ \left[ {\begin{array}{*{20}{c}} {x_n^{(i)}(t){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} + \frac{{x_n^{(i)}(t)x_n^{(i)\prime }(t)}}{{y_n^{(i)\prime }(t)}}{\rm{cos}}{\kern 1pt} {\kern 1pt} \beta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} + {r_1}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1}}\\ {x_n^{(i)}(t){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} - \frac{{x_n^{(i)}(t)x_n^{(i)\prime }(t)}}{{y_n^{(i)\prime }(t)}}{\rm{cos}}{\kern 1pt} {\kern 1pt} \beta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} + {r_1}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1}}\\ {{r_1}{\phi _1}{\rm{cot}}{\kern 1pt} {\kern 1pt} \beta - \frac{{y_n^{(i)}(t)}}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} \beta }} - \frac{{x_n^{(i)}(t)x_n^{(i)}(t)}}{{y_n^{(i)}(t)}}{\rm{cos}}{\kern 1pt} {\kern 1pt} \beta {\rm{cot}}{\kern 1pt} {\kern 1pt} \beta }\\ 1 \end{array}} \right], \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = {\rm{I}}, {\rm{II}}, {\rm{III}}, {\rm{IV}}). \end{array} $ | (13) |
式中:当i=I时,t=α;当i=Ⅱ时,t=αj;当i=Ⅲ时,t=τ;当i=IV时,t=αf.
式(13)中齿面只有两个变量,切削刃参数和滚刀的旋转角度,当给出两个变量的变化范围,即可获得所需齿面.
将切削刃式(1)~(4)代入式(13),即可得到各切削刃展成得到的滚刀齿面方程
| $ {\mathit{\boldsymbol{r}}^{({\rm{I}})}}(\alpha , {\phi _1}) = \left[ {\begin{array}{*{20}{c}} { - \rho {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} \pm \rho {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha {\rm{co}}{{\rm{s}}^2}\beta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} + {r_1}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1}}\\ { - \rho {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} \mp \rho {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha {\rm{co}}{{\rm{s}}^2}\beta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} + {r_1}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1}}\\ {{r_1}{\phi _1}{\rm{cot}}{\kern 1pt} {\kern 1pt} \beta \mp \rho {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha {\rm{sin}}{\kern 1pt} {\kern 1pt} \beta \mp \frac{{{l_a}}}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} \beta }}}\\ 1 \end{array}} \right], $ | (14) |
| $ {\mathit{\boldsymbol{r}}^{({\rm{II}})}}({\alpha _{\rm{j}}}, {\phi _1}) = \left[ {\begin{array}{*{20}{c}} { - ({r_{\rm{j}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{j}}} + {e_{\rm{j}}}){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} \pm ({r_{\rm{j}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{j}}} + {e_{\rm{j}}})\cot {\alpha _{\rm{j}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} + {r_1}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1}}\\ { - ({r_{\rm{j}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{j}}} + {e_{\rm{j}}}){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} \mp ({r_{\rm{j}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{j}}} + {e_{\rm{j}}})\cot {\alpha _{\rm{j}}}{\rm{cos}}{{\kern 1pt} ^2}\beta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} + {r_1}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1}}\\ {{r_1}{\phi _1}{\rm{cot}}{\kern 1pt} {\kern 1pt} \beta \pm \frac{{({r_{\rm{j}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{j}}} - {l_{\rm{j}}})}}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \beta }} \mp \frac{{({r_{\rm{j}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{j}}} + {e_{\rm{j}}}){\rm{cot}}{\kern 1pt} {\kern 1pt} {\alpha _{\rm{j}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {{\kern 1pt} ^2}\beta }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \beta }}}\\ 1 \end{array}} \right], $ | (15) |
| $ \begin{array}{l} {\mathit{\boldsymbol{r}}^{({\rm{III}})}}(\tau , {\phi _1}) = \\ \left[ {\begin{array}{*{20}{c}} { - \left( {\tau {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma + \frac{{{\tau ^2}}}{{2p}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma - {L_1}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma } \right){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} \mp \frac{{\left( {\tau {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma + \frac{{{\tau ^2}}}{{2p}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma - {L_1}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma } \right)\left( {\frac{\tau }{p}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma + {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma } \right)}}{{\frac{\tau }{p}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma }}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \beta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} + {r_1}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1}}\\ {\left( {\tau {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma + \frac{{{\tau ^2}}}{{2p}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma - {L_1}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma } \right){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} \pm \frac{{\left( {\tau {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma + \frac{{{\tau ^2}}}{{2p}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma - {L_1}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma } \right)\left( {\frac{\tau }{p}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma + {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma } \right)}}{{\frac{\tau }{p}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma - \sin {\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma }}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \beta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} + {r_1}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1}}\\ {{r_1}{\phi _1}{\rm{cot}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \beta \pm \frac{{\left( {\tau {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma + \frac{{{\tau ^2}}}{{2p}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma - L{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma + {l_a} + 05\pi {m_n}} \right)}}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \beta }} \pm \frac{{\left( {\tau {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma - \frac{{{\tau ^2}}}{{2p}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma + L{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma } \right)\left( {\frac{\tau }{p}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma + {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma } \right)}}{{\frac{\tau }{p}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma - {\rm{sin}}\sigma }}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \beta {\rm{cot}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \beta }\\ 1 \end{array}} \right], \end{array} $ | (16) |
| $ {\mathit{\boldsymbol{r}}^{\left( {{\rm{IV}}} \right)}}({\alpha _{\rm{f}}}, {\phi _1}) = \left[ {\begin{array}{*{20}{c}} { - ({r_{\rm{f}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{f}}} + {e_{\rm{f}}}){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} \pm ({r_{\rm{f}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{f}}} + {e_{\rm{f}}}){\rm{cot}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{f}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} + {r_1}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1}}\\ { - ({r_{\rm{f}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{f}}} + {e_{\rm{f}}}){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} \mp ({r_{\rm{f}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{f}}} + {e_{\rm{f}}}){\rm{cot}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{f}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {{\kern 1pt} ^2}\beta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1} + {r_1}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _1}}\\ {{r_1}{\phi _1}{\rm{cot}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \beta \pm \frac{{({r_{\rm{f}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{f}}} - {l_{\rm{f}}})}}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \beta }} \mp \frac{{({r_{\rm{f}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{f}}} + {e_{\rm{f}}}){\rm{cot}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _{\rm{f}}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {{\kern 1pt} ^2}\beta }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \beta }}}\\ 1 \end{array}} \right]. $ | (17) |
在式(14)~(17)中,当取上面的符号时,方程为左侧齿面方程,当取下面的符号时,方程为右侧齿面方程.
4 滚刀精确实体建模与试制 4.1 滚刀精确实体建模通过给定的参数,逐一求解式(14)~(17),即可获得滚刀的各个齿面.通过编程运算,求解出轮齿齿面上点的坐标,绘制图形,并将坐标点导入三维建模软件,建立滚刀的实体模型,如图 6所示.

|
图 6 滚刀实体模型 Fig. 6 Model of hob |
滚刀的主要参数为:法面模数为6 mm,内孔直径为45 mm,外径为110 mm,前角为0°,长度为140 mm,容屑槽为12个,螺旋升角为3°16′25″,头数为1,旋向为右旋向.
根据滚刀模型,加工出的滚刀实体如图 7所示.

|
图 7 滚刀实体 Fig. 7 Image of hob |
用图 7中的滚刀进行滚削加工,如图 8所示,获得的分阶式四点接触齿轮副,如图 9所示.齿轮副的主要参数如下:法面模数mn=6 mm,中心距a=130 mm,小齿轮齿数z1=6,大齿轮齿数z2=30,传动比i=5,螺旋角β=33°49′19′′,齿宽B=80 mm.

|
图 8 滚齿加工 Fig. 8 Hobbing |

|
图 9 分阶式四点接触齿轮副 Fig. 9 Four-point contact gears with ladder shape of teeth |

|
图 10 齿轮装配 Fig. 10 Gear assembly |
齿轮副装配完成之后,将大小齿轮的轮齿表面清洗干净,把小齿轮的轮齿表面均匀地涂上红丹粉,旋转小齿轮轴,检查轮齿的接触情况,如图 11和图 12所示.对于8级精度的齿轮传动,在齿高方向上接触线的位置偏差不超过0.25mn,在整个齿长方向上不少于工作齿长的85%.从齿面的接触区域可以看出,装配后的齿轮副在齿长方向上的接触不少于工作齿长的90%;在齿高方向上,能保证在理论的接触线位置接触,由于加工误差和装配误差的存在,在齿高方向上有一定的位置偏差,约0.5 mm.

|
图 11 小齿轮接触印痕 Fig. 11 Contact pattern of pinion |

|
图 12 大齿轮接触印痕 Fig. 12 Contact pattern of gear |
1) 提出了分阶式多点接触齿轮传动,轮齿的啮合齿面分为上啮合面和下啮合齿面,在多个点同时接触,并且为凹凸接触,具有承载能力大、重合度高等特点;
2) 设计了分阶式四点接触齿轮的基本齿形,上、下啮合面的基本齿廓分别为圆弧和抛物线曲线,基本齿廓啮合时有4个接触点,采用圆弧曲线作为过渡曲线;
3) 建立了滚刀的数学模型,推导了滚刀的齿面方程,构建了滚刀的精确实体模型,加工获得了滚刀实体;
4) 开展了滚切试制,获得了分阶式四点接触的齿轮副,进行了接触印痕验证,满足设计要求,为后续的齿轮磨削加工及承载能力试验等进一步研究提供了基础;
5) 分阶式四点接触齿轮继承了多对曲线接触的特性,其齿面形成方法适用于其他分阶式多点接触齿轮,具有广阔的工程应用前景.
| [1] |
ZHOU Changjiang, HU Bo, QIAN Xuanlv, et al. A novel prediction method for gear friction coefficients based on a computational inverse technique[J]. Tribology International, 2018, 127: 200. DOI:10.1016/j.triboint.2018.06.005 |
| [2] |
NI Gaoxiang, ZHU Caichao, SONG Chaosheng, et al. Tooth contact analysis of crossed beveloid gear transmission with parabolic modification[J]. Mechanism and Machine Theory, 2017, 113: 40. DOI:10.1016/j.mechmachtheory.2017.03.004 |
| [3] |
SÁNCHEZ M B, PLEGUEZUELOS M, PEDRERO J I. Influence of profile modifications on meshing stiffness, load sharing, and trasnsmission error of involute spur gears[J]. Mach Mach Theory, 2019, 139: 506. DOI:10.1016/j.mechmachtheory.2019.05.014 |
| [4] |
SHEN Yunbo, LIU Xuan, LI Dayin, et al. A method for grinding face gear of double crowned tooth geometry on a multi-axis CNC machine[J]. Mechanism and Machine Theory, 2018, 121: 460. DOI:10.1016/j.mechmach-theory.2017.11.007 |
| [5] |
NI Gaoxiang, ZHU Caichao, SONG Chaosheng, et al. Effects of rack-cutter parabolic modification on loaded contact characteristics for crossed beveloid gears with misalignments[J]. International Journal of Mechanical Sciences, 2018, 141: 359. DOI:10.1016/j.ijmecsci.2018.04.003 |
| [6] |
LIU Siyuan, SONG Chaosheng, ZHU Caichao, et al. Effects of tooth modifications on mesh characteristics of crossed beveloid gear pair with small shaft angle[J]. Mechanism and Machine Theory, 2018, 119: 142. DOI:10.1016/j.mechmach-theory.2017.09.007 |
| [7] |
赵韩, 梁锦华, 刘红雨, 等. 微线段齿廓的形成原理及特性[J]. 机械工程学报, 1997, 33(5): 8. ZHAO Han, LIANG Jinhua, LIU Hongyu, et al. Constructing principle and features of tooth profiles with micro-segments[J]. Chinese Journal of Mechanical Engineering, 1997, 33(5): 8. |
| [8] |
贾超, 方宗德, 张永振. 高速内啮合人字齿轮多目标优化修形[J]. 哈尔滨工业大学学报, 2017, 49(1): 66. JIA Chao, FANG Zongde, ZHANG Yongzhen. Multi-objective optimal modification for internal double helical gears with high speed[J]. Journal of Harbin Institiute of Technology, 2017, 49(1): 66. DOI:10.11918/j.issn.0367-6234.2017.01.025 |
| [9] |
蒋进科, 方宗德, 彭先龙. 对角修形斜齿轮径向剃齿设计[J]. 哈尔滨工业大学学报, 2015, 47(5): 63. JIANG Jinke, FANG Zongde, PENG Xianlong. Grinding plunge shaving cutter for diagonal modified helical gears[J]. Journal of Harbin Institiute of Technology, 2015, 47(5): 63. DOI:10.11918/j.issn.0367-6234.2015.05.011 |
| [10] |
付学中, 方宗德, 贾超, 等. 面齿轮传动啮合刚度分析与修形减振优化[J]. 振动与冲击, 2019, 38(5): 265. FU Xuezhong, FANG Zongde, JIA Chao, et al. Meshing stiffness analysis and optimization of vibration reduction and modification for face-gear drives[J]. Journal of Vibration and Shock, 2019, 38(5): 265. DOI:10.13465/j.cnki.jvs.2019.05.038 |
| [11] |
ZHENG Fangyan, HAN Xinghui, LIN Hua, et al. Design and manufacture of new type of non-circular cylindrical gear generated by face-milling method[J]. Mechanism and Machine Theory, 2018, 122: 326. DOI:10.1016/j.mechmachtheory.2018.01.007 |
| [12] |
JIA Chao, FANG Zongde. Design and analysis of double-crowned high-contact-ratio cylindrical gears considering the load sharing of the multi-pair contact[J]. Mechanism and Machine Theory, 2019, 131: 92. DOI:10.1016/j.mechmachtheory.2018.09.021 |
| [13] |
彭先龙, 韩飞燕, 乔心州, 等.斜齿面齿轮传动齿面主动修形与边缘接触分析[J/OL].计算机集成制造系统, 2019.http://kns.cnki.net/kcms/detail/11.5946.tp.20190531.0935.002.html PENG Xianlong, HAN Feiyan, QIAO Xinzhou, et al. Tooth surface active modification and edge contact analysis for face gear drives with helical pinion [J/OL]. Computer Integrated Manufacturing Systems, 2019. http://kns.cnki.net/kcms/detail/11.5946.tp.20190531.0935.002.html |
| [14] |
张西金, 蒋进科, 贾超, 等. 圆弧齿廓刀具及齿向鼓形的斜齿轮拓扑修形[J]. 机械传动, 2018, 42(1): 7. ZHANG Xijin, JIANG Jinke, JIA Chao, et al. Topological modification of a helical gear with circular tooth profile in gear cutter and tooth drum-shaped[J]. Journal of Mechanical Transmission, 2018, 42(1): 7. DOI:10.16578/j.issn.1004.2539.2018.01.002 |
| [15] |
CHEN Yangzhi, DING Jiang, LV Yueling. Design of a polyhedral helix curve meshing reducer[J]. Journal of Mechanical Design, 2014, 136(4): 044503-1. DOI:10.1115/1.4026571 |
| [16] |
CHEN Yangzhi, LV Yueling, DING Jiang, et al. Fundamental design equations for space curve meshing skew gear mechanism[J]. Mechanism and Machine Theory, 2013, 70: 175. DOI:10.1016/j.mechmachtheory.2013.07.004 |
| [17] |
陈兵奎, 梁栋, 高艳娥. 齿轮传动共轭曲线原理[J]. 机械工程学报, 2014, 50(1): 130. CHEN Bingkui, LIANG Dong, GAO Yane. the principle of conjugate curves for gear transmission[J]. Journal of mechanical engineering, 2014, 50(1): 130. DOI:10.3901/JME.2014.01.130 |
| [18] |
陈兵奎, 高艳娥, 梁栋. 共轭曲线齿轮齿面的构建[J]. 机械工程学报, 2014, 50(3): 10. CHEN Bingkui, GAO Yane, LIANG Dong. Tooth profile generation of conjugate-curve gears[J]. Journal of mechanical engineering, 2014, 50(3): 10. DOI:10.3901/JME.2014.03.018 |
| [19] |
TAN Rulong, CHEN Bingkui, PENG Changyan, et al. Study on spatial curve meshing and its application for logarithmic spiral bevel gears[J]. Mechanism and Machine Theory, 2015, 86: 172. DOI:10.1016/j.mechmachtheory.2014.11.023 |
| [20] |
RAGHUWANSHI N K, PAREY A. Mesh stiffness measurement of cracked spur gear by photoelasticity technique[J]. Measurement, 2015, 73: 439. |
| [21] |
GAO Yane, CHEN Bingkui, LIANG Dong. Mathematical models of hobs for conjugate-curve gears having three contact points[J]. Journal of Mechanical Engineering Science, 2015, 229(13): 2402. DOI:10.1177/0954406214558674 |
 2020, Vol. 52
2020, Vol. 52


