2. 哈尔滨工业大学, 能源科学与工程学院, 哈尔滨 150001;
3. 北京航天动力研究所, 北京 100076
2. School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150001, China;
3. Beijing Aerospace Propulsion Institute, Beijing 100076, China
氢能被誉为21世纪的清洁高效能源,具有高热值、燃烧性能好、清洁无污染等优点,在世界各国加速能源转型的战略背景下,具有巨大的发展潜力[1].催化重整是使用最广泛的制氢方式之一,然而, 传统的固定床反应器因受热不均,颗粒表面易形成积碳,进而导致燃料转化率和氢气产量的下降.流化床反应器具有良好的传质、传热性能和连续运行潜力,在制氢工艺中逐渐受到了研究者们的关注[2].
为了进一步实现催化重整过程的强化,打破原有热力学平衡的限制,利用渗透膜将氢气从反应体系中分离,可大幅度提高氢气的产率,同时可以实现高纯度氢气的生产[3]. Rakib等[4]对流化床膜反应器内丙烷蒸汽重整制氢进行了实验研究,结果表明,与传统反应器相比,流化床膜反应器在较低的温度下可以获得相同的产氢率,有效地抑制了催化剂烧结和高温焦炭的形成. Mahecha-Botero等[5]利用实验室规模的流化床膜反应器对天然气蒸汽重整过程进行了研究,结果表明,减小渗透侧氢气分压力、增大膜面积和减小膜厚都有利于工艺整体效率的提升. Chen等[6]通过实验手段评价了反应侧压力对鼓泡流化床膜反应器内甲烷蒸汽重整和自热重整过程的反应性能的影响,认为较高的压力并不总能提高产氢率,因为较高的氢渗透率被较低的平衡转化率所抵消.二氧化碳吸附,作为另一种强化重整的有效手段,通过添加固体吸附剂捕获反应体系的二氧化碳,突破热力学限制,从而提高了重整过程中氢气产量和浓度,同时吸附反应是放热反应,为吸热的重整反应减小了外界能量输入[7]. Lindborg等[8]通过模拟手段,比较了有无二氧化碳吸附的鼓泡流化床反应器中甲烷重整反应性能,结果表明,二氧化碳吸附可以显著提高氢气浓度. Hildenbrand等[9]利用实验手段研究流化床反应器氧化钙吸附强化甲烷蒸汽重整过程.发现吸附剂多次循环再生后,氢氧化钙的形成会改变实际的水碳比,导致甲烷转化率和氢气产率降低.
上述研究表明,膜分离和二氧化碳吸附两种强化重整手段通过打破热力学平衡,可以进一步提高燃料转化率和氢气产率. Silva等[10]通过热力学分析,研究了氢气分离与二氧化碳吸附一体化对甘油蒸汽重整制氢过程的影响,发现二者结合不仅大大提高了氢气产率,而且吸附反应释放的热量可以使重整系统达到自热状态.然而,将两种强化技术同时应用于反应器重整制氢过程的研究较少,开展膜分离与二氧化碳吸附协同强化重整技术,探究两者之间的相互作用规律,对反应器的设计和过程的调控具有重要的意义.
本文基于双流体模型,结合化学反应动力学理论,对流化床反应器内膜分离与二氧化碳吸附协同强化甘油重整制氢过程开展了模拟研究,获得了流化床重整制氢系统中多相流动和反应行为,探究了二氧化碳吸附和氢气膜分离过程的相互作用规律,比较了不同条件下吸附速率与膜渗透率之间的相互影响.
1 数学模型 1.1 控制方程计算模拟采取欧拉-欧拉双流体模型,该模型基于连续性假设,物质被认定为在其所占据的空间连续分布.计算时采用如下的基本守恒方程.
质量守恒方程为
| $ \begin{array}{l} \frac{\partial }{{\partial t}}({\varepsilon _{\rm g}}{\rho _{\rm g}}) + \nabla {\rm{\cdot(}}{\varepsilon _{\rm g}}{\rho _{\rm g}}{u_{\rm g}}) = {S_{\rm gm}} + {S_{\rm{mass, {H_2}}}}, \\ \frac{\partial }{{\partial t}}({\varepsilon _{\rm m}}{\rho _{\rm m}}) + \nabla {\rm{\cdot(}}{\varepsilon _{\rm m}}{\rho _{\rm m}}{u_{\rm m}}) = {S_{\rm mg}}. \end{array} $ | (1) |
式中:Sgm和Smg为由反应引起的质量源项,Smass, H2为氢气分离引起的质量源项,u为速度,ρ和ε分别为密度和体积分数,下角标g表示气相,m表示固相的第m相.
动量守恒方程:
| $ \begin{array}{l} [\frac{\partial }{{\partial t}}({\varepsilon _{\rm g}}{\rho _{\rm g}}{u_{\rm g}}) + \nabla {\rm{\cdot(}}{\varepsilon _{\rm g}}{\rho _{\rm g}}{u_{\rm g}}{u_{\rm g}})] = - {\varepsilon _{\rm g}}\nabla {p_{\rm g}} + {\varepsilon _{\rm g}}\nabla {\rm{\cdot}}{\tau _{\rm g}} + {\varepsilon _{\rm g}}{\rho _{\rm g}}g - {\beta _{\rm gm}}({u_{\rm g}} - {u_{\rm m}}) + {S_{\rm gm}}{u_{\rm g}} + {S_{\rm{mom, {H_2}}}}, \\ [\frac{\partial }{{\partial t}}({\varepsilon _{\rm m}}{\rho _{\rm m}}{u_{\rm m}}) + \nabla {\rm{\cdot(}}{\varepsilon _{\rm m}}{\rho _{\rm m}}{u_{\rm m}}{u_{\rm m}})] = - {\varepsilon _{\rm m}}\nabla {p_{\rm g}} - \nabla {p_{\rm m}} + {\varepsilon _{\rm m}}\nabla {\rm{\cdot}}{\tau _{\rm m}} + {\varepsilon _{\rm m}}{\rho _{\rm m}}g + {\beta _{\rm gm}}({u_{\rm g}} - {u_{\rm m}}) + {\beta _{\rm mn}}({u_{\rm m}} - {u_n}) + {S_{\rm mg}}{u_{\rm m}}. \end{array} $ | (2) |
式中:p为压力,β为相间曳力系数,τ为剪切应力项,Smom, H2为氢气分离引起的动量源项.
能量守恒方程为
| $ \begin{array}{l} \frac{\partial }{{\partial t}}({\varepsilon _{\rm g}}{\rho _{\rm g}}{c_{\rm pg}}{T_{\rm g}}) + \nabla {\rm{\cdot(}}{\varepsilon _{\rm g}}{\rho _{\rm g}}{c_{\rm pg}}{T_{\rm g}}{u_{\rm g}}) = \nabla [{\varepsilon _{\rm g}}({\lambda _{\rm g}} + {c_{\rm pg}}\frac{{{\mu _{\rm gt}}}}{{{{\Pr }_t}}})\nabla {T_{\rm g}}] + \sum {{h_{\rm gm}}} ({T_{\rm m}} - {T_{\rm g}}) + \sum {{S_{\rm {g, i}}}{c_{pg, i}}} {T_{\rm g}} + {S_{en, {H_2}}}, \\ \frac{\partial }{{\partial t}}({\varepsilon _{\rm m}}{\rho _{\rm m}}{c_{\rm pm}}{T_{\rm m}}) + \nabla {\rm{\cdot}}({\varepsilon _{\rm m}}{\rho _{\rm m}}{c_{\rm pm}}{T_{\rm m}}{u_{\rm m}}) = \nabla [{\varepsilon _{\rm m}}({\lambda _{\rm m}} + {c_{\rm pm}}\frac{{{\mu _{\rm st}}}}{{{{\Pr }_t}}})\nabla {T_{\rm g}}] + {h_{\rm gm}}({T_{\rm g}} - {T_{\rm m}}) + \sum {{S_{\rm {m, i}}}{c_{pm, i}}{T_{\rm m}}.} \end{array} $ | (3) |
式中:cp为比定压热容,λ为导热系数,μ为黏度,hgm为气固相间换热系数,Sen, H2为氢气分离引起的能量源项.
组分输运方程为
| $ \begin{array}{l} \frac{\partial }{{\partial t}}({\varepsilon _{\rm g}}{\rho _{\rm g}}{Y_{\rm {g, i}}}) + \nabla {\rm{\cdot}}({\varepsilon _{\rm g}}{\rho _{\rm g}}{Y_{\rm {g, i}}}{u_{\rm g}}) = \nabla {\rm{\cdot}}[{\varepsilon _{\rm g}}({\rho _{\rm g}}{D_{\rm {g, i}}} + \frac{{{\mu _{\rm gt}}}}{{S{C_t}}})\nabla {\rm{\cdot}}{Y_{\rm {g, i}}}] + {S_{\rm {g, i}}} + {S_{mass, {H_2}}}, \\ \frac{\partial }{{\partial t}}({\varepsilon _{\rm m}}{\rho _{\rm m}}{Y_{\rm {m, i}}}) + \nabla {\rm{\cdot(}}{\varepsilon _{\rm m}}{\rho _{\rm m}}{Y_{\rm {m, i}}}{u_{\rm m}}{\rm{) = }}\nabla {\rm{\cdot}}[{\varepsilon _{\rm m}}({\rho _{\rm m}}{D_{\rm {m, i}}} + \frac{{{\mu _{\rm st}}}}{{S{C_t}}})\nabla {\rm{\cdot}}{Y_{\rm {m, i}}}] + {S_{\rm {m, i}}}. \end{array} $ | (4) |
式中:Y为质量分数,D为扩散系数.
氢气膜分离过程是通过在流化床边壁处的一层网格中加入源项来考虑的,对于气相的连续性方程和氢气组分守恒方程为
| $ \phi = - \frac{A}{V}\;\frac{{{P_{\rm e}}}}{l}\exp \left( { - \frac{{{E_a}}}{T}} \right)(P_{\rm{retentate, {H_2}}}^{0.5} - P_{\rm{permeate, {H_2}}}^{0.5}). $ | (5) |
式中:Pe、Ea和l分别为指前因子、活化能和膜厚, 其值分别为1.12×10-5 mol·s-1·-1·Pa-0.5、29.16 kJ·mol-1和30 μm, pretentate, H2和ppermeate, H2分别为反应器侧和渗透侧的氢气分压;A和V为单元网格的面积和体积.
1.2 反应动力学模型二氧化碳吸附强化甘油水蒸气重整制氢过程由一系列复杂的反应组成,其气相组分主要包括C3H8O3、H2O、H2、CO2、CO和CH4.本研究操作条件(蒸汽甘油比为6,且温度为873 K)下,可忽略积碳生成[11].主要反应如下:
| $ \begin{array}{l} {{\rm{C}}_{\rm{3}}}{{\rm{H}}_{\rm{8}}}{{\rm{O}}_{\rm{3}}}{\rm{(g) + }}{{\rm{H}}_{\rm{2}}}{\rm{O(g)}} \to {\rm{C}}{{\rm{H}}_{\rm{4}}}{\rm{(g) + 2C}}{{\rm{O}}_{\rm{2}}}{\rm{(g) + 3}}{{\rm{H}}_{\rm{2}}}{\rm{(g), }}\\ {\rm{C}}{{\rm{H}}_{\rm{4}}}{\rm{(g) + }}{{\rm{H}}_{\rm{2}}}{\rm{O(g)}} \leftrightarrow {\rm{CO(g) + 3}}{{\rm{H}}_{\rm{2}}}{\rm{(g) , }}\\ {\rm{CO(g) + }}{{\rm{H}}_{\rm{2}}}{\rm{O(g)}} \leftrightarrow {\rm{C}}{{\rm{O}}_{\rm{2}}}{\rm{(g) + }}{{\rm{H}}_{\rm{2}}}{\rm{(g), }}\\ {\rm{CaO(s) + C}}{{\rm{O}}_{\rm{2}}}{\rm{(g)}} \to {\rm{CaC}}{{\rm{O}}_{\rm{3}}}{\rm{(s)}}{\rm{.}} \end{array} $ | (6) |
采用Dou等[12]提出的层流有限元模型计算反应速率,并假设速率常数随温度的变化而变化.甘油重整和吸附反应的速率表达式如下:
| $ \begin{array}{l} {R_1} = 1.838 \times {10^5}\exp ( - 74\;210/T){C_{\rm {C_3}{H_8}{O_3}}}{C_{\rm {H_2}O}}{\rho _{\rm cat}},\\ {R_2} = 1.198 \times {10^{17}}\exp ( - 26\;830/T){C_{\rm C{H_4}}}{C_{\rm {H_2}O}}{\rho _{\rm cat}},\\ {R_3} = 0.017\;67\exp (4\;400/T){C_{\rm CO}}{C_{\rm {H_2}O}}{\rho _{\rm cat}},\\ {R_4} = {C_{\rm CaO}}{k_c}{({C_{\rm C{O_2}}} - {C_{\rm C{O_2},eq}})^{0.37}}{(1 - X/{X_u})^{2.61}}. \end{array} $ | (7) |
式中:C、X、CCO2, eq和kc分别为浓度、转化率、CO2平衡浓度和动力学系数,其具体表达式可见Iliuta等[13]的研究.对于双功能催化剂-吸附剂,反应速率可表示为[14]
| $ {R_i} = {v_{{R_1},i}}{R_1} + {v_{{R_2},i}}{R_2} + {v_{{R_3},i}}{R_3} + {v_{{R_{CO}}_{_2},i}}{R_4}. $ | (8) |
式中:vR1, i、vR2, i、vR3, i和vR4, i代表组分i的化学计量数(i =C3H8O3, H2O, H2, CO2, CO, CH4).
1.3 几何模型及计算参数模拟采用的流化床膜反应器,其高度为1.5 m,直径为0.3 m,结构示意图见图 1.
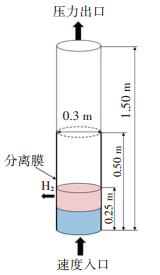
|
图 1 流化床膜反应器的结构示意 Fig. 1 Structure of a fluidized bed membrane reactor |
本文采用两种吸附剂设计(传统两颗粒和双功能颗粒设计),以探究吸附对重整性能的强化作用.双功能颗粒的催化组分和吸附组分与传统两颗粒设计一致.在无吸附重整过程中,选择惰性颗粒代替吸附剂颗粒,保证催化剂用量和总颗粒数保持不变.此模拟计算所采用的初始条件、边界条件以及相关的主要物性参数见表 1.
| 表 1 主要模拟参数 Tab. 1 Main simulation parameters |
为了验证甘油重整和氢气分离模型,进行了出口气体组分和氢气渗透速率的模拟,结果见图 2,并与Dou等[12]和Helmi等[15]的实验结果进行比较.由图 2可知,模型预测的出口组分摩尔分数和氢气渗透速率与实验值之间的最大相对误差不超过10%,在可接受的范围内.另外,经过网格无关性验证,采用了32 000个元素的网格.
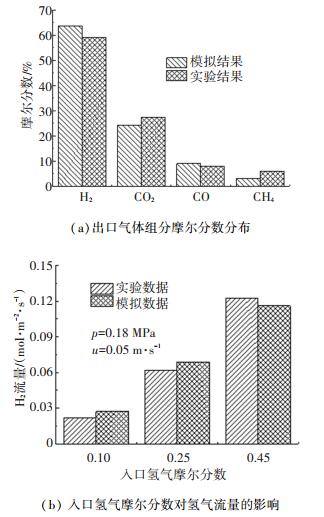
|
图 2 实验与模拟数据对比 Fig. 2 Comparison of simulation and measured data |
有、无吸附条件下,流化床内时均空隙率分布见图 3.由图 3可知,由于吸附剂、催化剂和惰性颗粒相似的物理性质,3种操作条件下床层空隙率分布和床层膨胀高度基本相同.同时可观察到,渗透膜附近存在局部的低空隙率区域,这是由于氢气分离和壁面摩擦抑制了颗粒流化,形成颗粒致密区域.同时发现使用双功能颗粒设计,颗粒致密区域范围扩大.
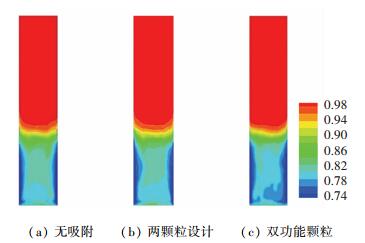
|
图 3 时均空隙率分布云图 Fig. 3 Contour plots of time-averaged voidage |
有、无吸附条件下,墙壁附近和中间区域两个监测点的空隙率随时间变化如图 4所示.

|
图 4 壁面和中心检测点空隙率随时间的变化 Fig. 4 Variation of voidage with time at wall and center of reactor |
由图 4可知,中心区域比墙壁附近的空隙率波动更加剧烈.这是由于致密区域的形成增加了墙壁附近气泡运动的阻力,使气泡运动主要集中在床层中间区域,从而导致了明显的空隙率振荡.与无二氧化碳吸附相比,二氧化碳吸附进一步增强了墙壁附近的空隙率波动程度.尤其是采用双功能吸附剂时,二氧化碳吸附的作用效果更加明显.这是由于二氧化碳吸附强化了催化重整反应,导致流化床气体量增大,同时扩大了致密区域的范围,导致更多的气泡沿着流化床中间区域上升.此外,二氧化碳的吸附也增大了墙壁附近的空隙率波动程度.这是由于重叠的催化剂和吸附剂局部高浓度区域形成导致了墙壁附近的气体产物也有所增加,从而加剧了墙壁附近的空隙率波动.
有、无二氧化碳吸附条件下,催化剂和吸附剂颗粒时均体积分数分布如图 5所示.氢气分离导致流化床膜周围形成催化剂和吸附剂(或惰性颗粒)的局部高浓度区.一方面由于墙壁处颗粒易受到摩擦;另一方面,此区氢气分离作用引起颗粒流化速度降低,两者共同导致墙壁处局部颗粒高浓度区.另外,二氧化碳吸附也明显导致该区域范围扩大,进一步验证了吸附对氢气分离的强化作用.虽然致密化区的形成不利于流化床床层和渗透膜间传质,且减小了气固相接触和气体停留时间,不利于流化床膜反应器性能.但此重叠高浓度区域内催化剂和吸附剂高度集中,促进催化剂和吸附剂间传质,一定程度上有利于吸附强化催化重整反应.
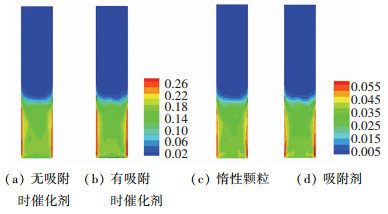
|
图 5 颗粒时均体积分数分布 Fig. 5 Contour plots of time-averaged solid volume fraction |
气相组分的时均质量分数分布如图 6所示.由于反应器底部的催化剂和吸附剂的浓度较高,重整反应剧烈,其组分变化较为明显.氢气分离通过直接提高反应物浓度和形成局部催化剂颗粒高浓度区域,促进了渗透膜周围甘油分解和产物生成,导致膜周围形成甘油局部低浓度区域、氢气和二氧化碳局部高浓度区.两种吸附设计条件下吸附作用是相似的,对重整过程生成的二氧化碳都实现了充分吸附,从而进一步强化了重整反应,扩大了局部氢气高浓度区域和局部甘油低浓度区域范围.尤其是采用双功能颗粒设计时,这一强化效果更加明显.

|
图 6 气相组分时均质量分数分布 Fig. 6 Contour plots of time-averaged mass fraction of gas composition |
二氧化碳吸附对氢气渗透的影响如图 7所示.由图 7可知,有无吸附条件下的氢气渗透速率的轴向分布趋势是相似的,都随着轴向高度升高而增大.这是由于随着重整反应进行,渗透膜表面氢气分压力沿轴向增大.图中同时比较了有无吸附条件下的总氢气渗透流量.由图 7可知,添加二氧化碳吸附剂大大提高了氢气渗透流量.这是因为二氧化碳的吸附强化了反应以及氢气的产量,进而提高了膜附近氢气的分压力,导致氢气的渗透量增加.使用双功能吸附剂时,二氧化碳吸附对氢渗透的增强作用更为明显.由于双功能颗粒时二氧化碳传质阻力较小,其二氧化碳吸附的作用效果更加明显.因此可以看到,吸附反应不仅强化了重整,而且在一定程度上促进了氢气的分离过程,当使用双功能颗粒时,相比于无吸附,氢气的渗透量提高了近20%.
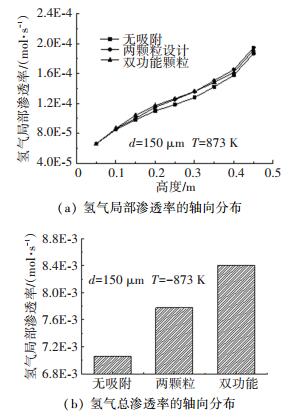
|
图 7 有无吸附条件下氢气渗透流率的分布 Fig. 7 Distribution of hydrogen permeation rate with or without sorption |
有、无二氧化碳吸附条件下,不同轴向高度处的气相温度径向分布如图 8所示.由图 8可知,无二氧化碳吸附条件下,催化重整反应吸收大量热量,不同轴向高度处的气相温度明显低于入口温度.渗透膜周围的温度存在明显降低趋势,这是由于氢气分离强化了重整反应, 导致此区域的温度降低程度更加明显.而加入二氧化碳吸附后,吸附反应释放热量,导致不同轴向高度处的气相温度都有所升高.并且气相温度随着轴向高度的升高而增大,这说明吸附反应可以提供重整反应所需要的热量,进而实现了系统的自热.
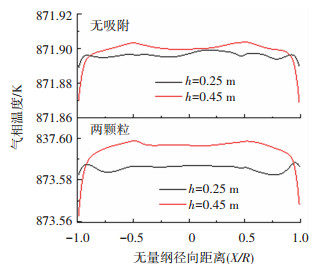
|
图 8 有无吸附条件下不同高度处气相温度径向分布 Fig. 8 Lateral distribution of gas temperature at different heights with or without sorption |
渗透膜厚度对燃料转化率和二氧化碳吸附速率的影响如图 9所示.由图 9可知,甘油转化率和吸附速率随着膜厚的减小而升高.这是由于随着膜厚的减小,氢气分离对重整制氢的强化作用增大,提高了燃料转化率.同时氢气分离导致其他气体的浓度升高的程度也有所增大.两者共同导致二氧化碳浓度升高,从而引起二氧化碳吸附速率的增大.当膜厚从300 μm减少到30 μm时,膜分离性能提高的同时,二氧化碳吸附速率可以提高1.4%,提升的程度不是很大,这是因为本文采用的是外置膜流化床反应器,而当膜管采用内置膜布置在床层中时,随着膜管数的增多,膜分离与二氧化碳吸附的相互作用会更强烈.
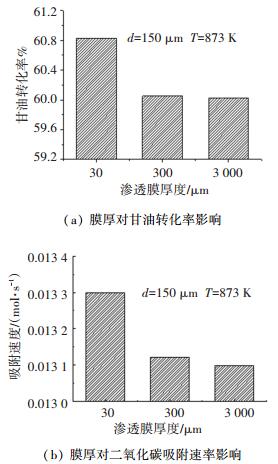
|
图 9 渗透膜厚度对燃料转化率和二氧化碳吸附速率的影响 Fig. 9 Effect of membrane thickness on fuel conversion and carbon dioxide sorption rate |
图 10(a)给出了吸附剂比例对氢气产量的影响.随着吸附剂比例的增大,氢气相对产量增大.这是由于随着吸附剂比例的增大,二氧化碳吸附对催化重整的强化作用也更加明显;同时吸附反应释放的热量随之增加,升高了床层温度,两者共同导致氢气相对产量升高.当吸附剂与催化剂比例为1:1时,氢气相对产量与没有吸附剂相比,提高了5%.对二氧化碳吸附强化甘油重整进行热力学分析[16]时发现,二氧化碳吸附大幅度提高了氢气产量,每摩尔甘油可以生成接近7 mol的氢气.而相较于热力学平衡,流化床反应器中由于颗粒与燃料的接触时间的限制,进而影响了甘油的转化与氢气的生成,因此有必要对过程实施调控,以更好地提高燃料转化率和氢气产率.
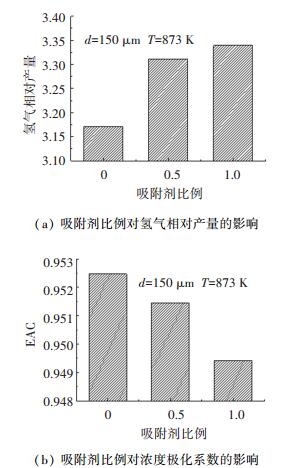
|
图 10 吸附剂比例对氢气产量及浓度极化系数的影响 Fig. 10 Effect of sorbent to catalyst ratio on hydrogen yield and EAC |
为了描述浓度极化的传质限制,本文引入了有效平均浓度极化系数(EAC)评价浓度极化水平[17]. 图 10(b)给出了吸附剂比例对浓度极化系数的影响.由图 10(b)可知,随着吸附剂比例的增大,渗透膜反应器的浓度极化水平减小.由于随着吸附剂比例的增大,膜周围的局部吸附剂颗粒高浓度区域范围也增大,导致二氧化碳吸附对催化重整反应强化程度增大,同时二氧化碳吸附程度的增大也导致包括氢气在内的其他气体浓度升高程度有所增加,两者都导致渗透膜表面氢气浓度梯度减小,从而引起反应器的浓度极化水平不断减小.
3 结论1) 基于双流体模型和反应动力学模型,探究了流化床反应器内二氧化碳吸附和氢气分离两种强化重整方式的相互作用规律,二氧化碳吸附可以抑制浓度极化阻力,提高氢气渗透速率,吸附剂与催化剂比例为1:1时,氢气相对产量与没有吸附剂相比,提高了5%.
2) 氢气分离通过直接提高二氧化碳浓度和强化甘油催化重整反应,提高了二氧化碳吸附速率,当膜厚从300 μm减少到30 μm时,膜分离性能提高的同时,二氧化碳吸附速率可以提高1.4%.
3) 与传统双颗粒设计相比,催化-吸附双功能颗粒的设计,使二氧化碳传质阻力较小,其二氧化碳吸附的作用效果更加明显,当使用双功能颗粒时,相比于无吸附,氢气的渗透量提高了近20%.
| [1] |
NIKOLAIDIS P, POULLIKKAS A. A comparative overview of hydrogen production processes[J]. Renewable and Sustainable Energy Reviews, 2017, 67: 597. DOI:10.1016/j.rser.2016.09.044 |
| [2] |
DURÁN P, SANZ-MARTÍNEZ A, SOLER J, et al. Pure hydrogen from biogas: intensified methane dry reforming in a two-zone fluidized bed reactor using permselective membranes[J]. Chemical Engineering Journal, 2019, 370: 772. DOI:10.1016/j.cej.2019.03.199 |
| [3] |
JOKAR S M, PARVASI P, BASILE A. The evaluation of methane mixed reforming reaction in an industrial membrane reformer for hydrogen production[J]. International Journal of Hydrogen Energy, 2018, 43(32): 15321. DOI:10.1016/j.ijhydene.2018.06.142 |
| [4] |
RAKIB M A, GRACE J R, LIM C J, et al. Steam reforming of propane in a fluidized bed membrane reactor for hydrogen production[J]. International Journal of Hydrogen Energy, 2010, 35(12): 6276. DOI:10.1016/j.ijhydene.2010.03.136 |
| [5] |
MAHECHA-BOTERO A, BOYD T, GULAMHUSEIN A, et al. Catalytic reforming of natural gas for hydrogen production in a pilot fluidized-bed membrane reactor: mapping of operating and feed conditions[J]. International Journal of Hydrogen Energy, 2011, 36(17): 10727. DOI:10.1016/j.ijhydene.2011.05.178 |
| [6] |
CHEN Zhongxiang, GRACE J R, LIM C J, et al. Experimental studies of pure hydrogen production in a commercialized fluidized-bed membrane reactor with SMR and ATR catalysts[J]. International Journal of Hydrogen Energy, 2007, 32(13): 2359. DOI:10.1016/j.ijhydene.2007.02.036 |
| [7] |
TAN L, ROGHAIR I, VAN SINT ANNALAND M. Simulation study on the effect of gas permeation on the hydrodynamic characteristics of membrane-assisted micro fluidized beds[J]. Applied Mathematical Modelling, 2014, 38(17/18): 4291. DOI:10.1016/j.apm.2014.04.044 |
| [8] |
LINDBORG H, JAKOBSEN H A. Sorption enhanced steam methane reforming process performance and bubbling fluidized bed reactor design analysis by use of a two-fluid model[J]. Industrial & Engineering Chemistry Research, 2009, 48(3): 1332. DOI:10.1021/ie800522p |
| [9] |
HILDENBRAND N, READMAN J, DAHL I M, et al. Sorbent enhanced steam reforming (SESR) of methane using dolomite as internal carbon dioxide absorbent: limitations due to Ca(OH)2 formation[J]. Applied Catalysis A: General, 2006, 303(1): 131. DOI:10.1016/j.apcata.2006.02.015 |
| [10] |
SILVA J M, SORIA M A, MADEIRA L M. Thermodynamic analysis of glycerol steam reforming for hydrogen production with in situ hydrogen and carbon dioxide separation[J]. Journal of Power Sources, 2015, 273: 423. DOI:10.1016/j.jpowsour.2014.09.093 |
| [11] |
AUTHAYANUN S, ARPORNWICHANOP A, PATCHARAVORACHOT Y, et al. Hydrogen production from glycerol steam reforming for low-and high-temperature PEMFCs[J]. International Journal of Hydrogen Energy, 2011, 36(1): 267. DOI:10.1016/j.ijhydene.2010.10.061 |
| [12] |
DOU Binlin, SONG Yongchen. A CFD approach on simulation of hydrogen production from steam reforming of glycerol in a fluidized bed reactor[J]. International Journal of Hydrogen Energy, 2010, 35(19): 10271. DOI:10.1016/j.ijhydene.2010.07.165 |
| [13] |
ILIUTA I, RADFARNIA H R, ILIUTA M C. Hydrogen production by sorption-enhanced steam glycerol reforming: sorption kinetics and reactor simulation[J]. AIChE Journal, 2013, 59(6): 2105. DOI:10.1002/aic.13979 |
| [14] |
ALOISI I, JAND N, STENDARDO S, et al. Hydrogen by sorption enhanced methane reforming: a grain model to study the behavior of bi-functional sorbent-catalyst particles[J]. Chemical Engineering Science, 2016, 149: 22. DOI:10.1016/j.ces.2016.03.042 |
| [15] |
HELMI A, VONCKEN R J W, RAIJMAKERS A J. On concentration polarization in fluidized bed membrane reactors[J]. Chemical Engineering Journal, 2018, 332: 464. DOI:10.1016/j.cej.2017.09.045 |
| [16] |
王帅, 王琦, 宋晓皎, 等. 生物甘油水蒸气重整制氢强化过程的参数评估[J]. 哈尔滨工业大学学报, 2018, 50(1): 102. WANG Shuai, WANG Qi, SONG Xiaojiao, et al. Parameter evaluation of enhancing glycerol steam reforming for hydrogen production[J]. Journal of Harbin institute of Technology, 2018, 50(1): 102. DOI:10.11918/j.issn.0367-6234.201607119 |
| [17] |
CARAVELLA A, SUN Yu. Correct evaluation of the effective concentration polarization influence in membrane-assisted devices[J]. International Journal of Hydrogen Energy, 2016, 41(27): 11653. DOI:10.1016/j.ijhydene.2015.12.068 |
 2020, Vol. 52
2020, Vol. 52


