2. 山东大学 机械工程学院, 济南 250061
2. School of Mechanical Engineering, Shandong University, Jinan 250061, China
自动驾驶显示出改善驾驶安全和交通系统效率的巨大潜力,是未来交通工具的发展方向[1].驾驶决策机制是保障自动驾驶车辆驾驶安全的关键技术[2].换道是驾驶过程中最常见同时也是危险程度较高的驾驶行为,在车道变换导致的事故中接近18%是由驾驶员不恰当的换道决策造成的[3].换道行为对通行能力、瓶颈形成以及交通安全等多方面存在重要影响[4].然而,在复杂的动态环境下使智能车辆做出符合社会规范的换道决策仍然是一个难点.因此,本文的研究重点是换道决策分析.
最早针对换道决策行为的建模方法是基于规则的数理模型,由Gipps[5]在1986年提出,主要从换道行为的必要性、倾向性和安全性三方面进行分析.在Gipps模型的基础上,Yang等[6]人考虑了车道变换概率,并且引入了随机误差;Hidas[7]将车道变换行为分为自由换道、协作换道和强制换道3种类型. Kesting等[8]利用车辆加速度值来表征车道变换收益,提出了一种基于加速度控制的MOBIL模型.随着人工智能的发展很多学者试图通过机器学习和深度学习的方法来提升车辆换道决策的准确率. Qiu等[9]提出利用人工智能方法贝叶斯网络(Bayesian networks)根据周围交通状况建立车辆换道模型. Motamedidehkordi等[10]引入了集成学习方法中的随机森林(random forest,RF)对换道决策行为进行建模. Díaz-Álvarez等[11]建立了基于神经网络的换道决策模型.张叠等[12]建立了基于支持向量机(SVM)的车辆换道决策模型,主要研究了决策数据处理与模型的参数优化,但是未对换道决策的影响因素进行分析. Zhang等[13]对路况及其对驾驶决策的耦合影响进行了深入分析,建立了基于优化支持向量机换道决策模型,但是只对道路状况对车道变换决策的影响进行了讨论.因此,基于支持向量机的车辆换道决模型还需要进一步研究.
目前,虽然很多关于车辆变道辅助或自动驾驶的研究,但是关于自由换道的研究却很少.自动驾驶车辆在什么情况下实施换道为最优决策这一重要问题仍未能很好地解决.因此,为解决上述问题,有必要研究安全而且可学习的自动驾驶车辆自由换道决策模型.本文的主要工作包括以下三个方面:
1) 分析了影响车辆换道的因素,并在传统模型的基础上建立了基于收益、安全性和必要性的自由变道决策模型,表明变道决策是一个多参数、非线性的问题,为支持向量机(SVM)模型的特征选择提供了依据;
2) 针对目前车辆换道决策模型存在特征选择不够全面的问题,提出从与车辆物理状态相关的特征、与交通交互相关的特征以及与道路结构相关的特征三个方面提取决策特征,使决策模型更加完善;
3) 针对自由换道决策的多参数、非线性问题,提出了基于BOA Gaussian-SVM的自由换道决策模型,保证了该决策模型能够更加符合驾驶员的驾驶习惯和决策特征.
本文提出的方法在NGSIM数据集上进行了验证,结果表明提出的BOA Gaussian-SVM换道决策算法具有较好的性能,同时利用Airsim平台对所提算法进行了仿真验证.最后,研究了驾驶环境对SVM模型的影响,并通过敏感分析量化了每个特征变量对驾驶决策的影响程度.实验结果进一步证明了BOA Gaussian-SVM换道决策模型的有效性.
1 车辆换道分析 1.1 车辆换道影响因素分析车辆换道主要受车辆状态、道路状况以及驾驶员特性等多方面因素的影响,因此,换道预测特征较多,预测特征在模式识别领域至关重要[14-15].一般而言,常用的换道预测特征可分为三类:1)与车辆物理状态相关的特征;2)与交通交互相关的特征;3)与道路结构相关的特征.
1.1.1 与车辆物理状态相关的因素基于物理的特征主要涉及周围车辆的状态(例如,位置、速度、加速度).由于车辆的运动满足运动学和动力学规律,因此可以利用具有运动学和动力学规律的车辆历史状态来推断车辆未来可能的状态.基于物理的特征会对自动驾驶车辆换道产生重要影响,这些特性主要包括以下5种:
1) 车辆分类(Vehicle Classification,VC)主要包括摩托车、卡车和小型汽车等.
2) 当前车道前车(Preceding Vehicle,PV)的转向指示灯(Turn Indicators, TI)和刹车指示灯(Brake Indicators,BI)的状态,其中包含开、关两种状态.
3) 横向速度方向(the Direction of Lateral Velocity,DLV),包含左右两种状态.
4) 道路切线的横摆率(Yaw Rate,YR).
5) 与相邻车道线的边界距离(Boundary Distance,BD).
1.1.2 与交通交互相关的因素交互感知特征在考虑车辆之间的依赖性的情况下预测周围车辆的轨迹.这些特征表示运动如何受到交通互动(例如,避撞、社会习惯)的影响,变道行为通常受周围车辆的间距和相对速度的影响.因此,我们利用的交互感知特性代表了这两个关键因素.假设执行换道的主体车辆SV的决策不受当前车道相邻后车状态的影响.此外,由于邻近车道的存在是相邻车辆存在的前提,后者的特征依赖于前者.因此,基于交互的特征可以分为如下3种:
1) 左车道的关注区域中SV之前和之后的相邻车辆的状态.状态包含前后车辆的存在状态以及与SV的相对速度.
2) 右车道的关注区域中PV之前和之后的相邻车辆的状态(RAFV/RBPV).
3) 同一车道的关注区域中SV前车的状态(CLPV).
1.1.3 道路结构的因素基于道路结构的特征主要是指道路拓扑结构、道路标志和交通规则.基于道路结构的特征主要包括以下2种:
1) 在SV的占用车道旁边存在左车道或右车道(LLE / RLE).
2) 行驶路段的车道曲率(Lane Curvature,LCU). LCU可以决定换道在概率上是否可以接受,例如,在曲率较大的道路上变道行为并不常见.
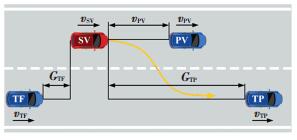
1.2 基于决策机理的车辆换道过程分析根据Yang等[16-17]人的研究,车辆换道执行过程是指主体车辆以目标车道相邻间隙为可接受间隙(Acceptable Gap, AG),并通过横向运动插入目标间隙的过程.变道决策受各种交通因素的影响,为了分析决策过程,建立了自由车道变换模型,其包括一个原始车道和一个目标车道,该模型可以简化为图 1.其中,SV表示执行换道的主体车辆,PV表示当前车道中的前车,TP和TF分别是目标车道中的前车和目标车道中的后车.
|
图 1 换道场景示意图 Fig. 1 Schematic diagram of lane changing environment |
由图 1可知主体车SV的换道决策受到TF、TP、PV的影响,但这些车辆如何影响自主车辆放弃原有车道选择新的车道,需要深入分析. Gipps换道模型认为影响换道决策的因素主要有三个,即,期望程度、执行换道的安全性以及换道的必要性[18].因此,本文将从换道收益、换道安全性和换道必要性三个方面对自由换道进行分析[19].
1.2.1 换道收益车道变换的目的是达到理想速度或获得更大的空间[20].对于自动驾驶车辆,未来的行驶速度可以转换为前导车辆的速度.因此,速度收益可以表示为
| $ {v_{{\rm{ benefit }}}} = f({v_{{\rm{ ideal }}}} - {v_{{\rm{PV}}}}, {v_{{\rm{TP}}}} - {v_{{\rm{PV}}}}). $ | (1) |
其中videal表示在该工况下自动驾驶车辆最理想的行驶速度.换道后前面的空间可以用相对距离来表示,所以距离收益可以表示为
| $ {G_{{\rm{ benefit }}}} = {G_{{\rm{TP}}}} - {G_{{\rm{PV}}}}, $ | (2) |
因此,换道收益模型可以建立为
| $ {f_{{\rm{ benefit }}}} = f({v_{{\rm{ benefit }}}}, {G_{{\rm{ benefit }}}}). $ | (3) |
安全性是指在执行换道过程中为了避免与目标车道后车TF之间的碰撞.显然,SV和TF之间的间隙和相对速度越大,车道变换过程就越安全.此外,车道变换需要最小的安全间隙.因此,可以建立如下安全模型:
| $ {f_{{\rm{ safety }}}} = \left\{ {\begin{array}{*{20}{l}} { - \infty , {G_{{\rm{TF}}}} < {G_{{\rm{TFmin}}}};}\\ {f({G_{{\rm{TF}}}}, \Delta {v_{{\rm{TF}}}}), {G_{{\rm{TF}}}} \ge {G_{{\rm{TFmin}}}}.} \end{array}} \right. $ | (4) |
式中GTFmin表示SV和TF之间的最小安全间隙,需要满足GTFmin>0;△vTF表示换道车辆SV与目标车道后车TF的速度差,△vTF=vSV-vTF.
1.2.3 换道必要性当车道变换过程的收益和安全性足够高时,自动驾驶车辆可能决定根据上述收益和安全函数执行换道,但是SV和PV之间的距离可能相当大,如果在这种情况下仍决定换道可能会导致自动驾驶车辆频繁换道,所以还需要建立必要性模型.当SV接近PV时,主体车辆将在ACC (Adaptive Cruise Control)模式下跟随PV,并且预期跟驰距离由速度和车头时距(Time Headway,THW)确定.因此,必要性模型可以建立为
| $ {f_{{\rm{ necessity }}}} = f({G_{{\rm{PV}}}} - {v_{{\rm{SV}}}} \cdot {t_{{\rm{THW}}}}). $ | (5) |
式中,tTHW表示车头时距.
1.3 基于规则的换道模型为了建立简单的车道变换模型,我们首先假设上述三个模型和影响因素是线性的.
| $ \left\{ {\begin{array}{*{20}{l}} {{f_{{\rm{ benefit }}}} = a \cdot {v_{{\rm{ benefit }}}} + b{G_{{\rm{ benefit }}}}, }\\ {{f_{{\rm{ safety }}}} = c({G_{{\rm{TF}}}} - {G_{{\rm{ TFmin }}}}) + d \cdot △ {v_{{\rm{TF}}}}, {G_{{\rm{TF}}}} \ge {G_{{\rm{ TFmin }}}}, }\\ {{f_{{\rm{ necessity }}}} = e({G_{{\rm{PV}}}} - {v_{{\rm{SV}}}} \cdot {t_{{\rm{THW}}}}).} \end{array}} \right. $ | (6) |
其中a、b、c、d、e是系数.
基于规则的决策模型可以建立如下:
| $ \begin{array}{*{20}{l}} {{\rm{ if }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {f_{{\rm{ safety }}}} > 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {f_{{\rm{ benefit }}}} - w{f_{{\rm{ neeessity }}}} > 0}\\ {\qquad {f_{{\rm{ decisison }}}} = {\rm{ yes }}}\\ {{\rm{ else }}}\\ \begin{array}{l} \qquad {f_{{\rm{ decision }}}} = {\rm{ no}}\\ {\rm{ end}} \end{array} \end{array} $ |
其中w是权重因子,fdecision是车道变换决策.然而,自由车道变换决策是一个多参数、非线性问题,很难建立一个特定的数学模型.因此,自由车辆的车道变换决策模型应表示为
| $ \begin{array}{l} {f_{{\rm{ decision }}}} = f({v_{{\rm{ income }}}}, {G_{{\rm{TP}}}} - {G_{{\rm{PV}}}}, {G_{{\rm{TF}}}}, {v_{{\rm{SV}}}} - {v_{{\rm{TF}}}}, {G_{{\rm{PV}}}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {v_{{\rm{SV}}}} \cdot {t_{{\rm{THW}}}}). \end{array} $ | (7) |
采用优化的Gaussian-SVM模型来解决自由换道决策过程中的多参数和非线性问题,确保模型更加符合驾驶员的驾驶习惯和决策特性,具有更强的合理性与适用性,本文提出的方法原理图如图 2所示.

|
图 2 本文提出的方法的示意图 Fig. 2 Schematic diagram of the proposed method |
本文使用的数据集是美国联邦公路局的车辆轨迹数据集中的NGSIM I-80和NGSIM US-101,如图 3所示.它们被广泛应用于智能交通系统和预测算法的验证[21-22]. 2个数据集包含6个15 min采集轨迹子集. NGSIM中的车辆状态数据是用10 Hz频率进行拍摄的多台高空相机对交通路况进行采集,然后再利用图像处理技术得到的,数据包括车辆ID、位置、速度、加速度、当前车道ID等数据[23].

|
图 3 NGSIM数据集研究区域 Fig. 3 Study area of NGSIM dataset |
由于NGSIM中的定位数据(如位置、速度和加速度)是通过视频分析获得的,因此它们含有大量的噪声.因此,我们首先使用对称指数移动平均(Symmetric Exponential Moving Average,SEMA)算法[24-25]来平滑原始数据.此外,如果驾驶员操纵车辆越过车道线到其相邻车道,则提取该车的所有地面实况车道变换数据.车辆换道轨迹指的是车辆越过车道线并且在车道线两侧具有固定行驶距离的运动轨迹.
2.3 特征提取车辆换道受到驾驶工况、周围车辆状态以及驾驶员特性等多种因素的影响,目前大多数微观交通仿真和自动驾驶中的换道研究多集中于研究周围车辆运动状态对换道行为的影响,考虑的因素较为单一.因此,本文从物理特性、交互感知特性和道路结构特性三个方面对换道决策进行分析.
2.3.1 基于车辆物理状态的特征与其他两种类型的特征不同,部分基于物理的特征(如:VC,SL / BL,LVD)可以通过原始感知数据直接获得,其余基于物理的特征YR和BD的提取过程如下.
计算道路切线(图 4中红色箭头线)与SV(图 4中绿色箭头线)的运动方向之间的偏航角φ后,对YR的状态进行离散.道路的切线可以用相邻车道线的切线来近似.离散化过程如下,其中阈值φYR是离散化的可调参数.
| $ {\rm{YR}} = \left\{ {\begin{array}{*{20}{l}} {0, {\rm{ if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi | < {\varphi _{{\rm{YR}}}};}\\ {1, {\rm{ if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi \ge {\varphi _{{\rm{YR}}}};}\\ {2, {\rm{ if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi \le - {\varphi _{{\rm{YR}}}}.} \end{array}} \right. $ | (8) |

|
图 4 基于物理特征的关键阈值参数描述:φYR和BD Fig. 4 Description of key threshold parameters of the physical-based features:φYRand BD |
BD的状态是根据它到每边相邻车道线的距离d离散的.离散化过程如下,其中阈值dBD是一个可调参数.
| $ {\rm{BD}} = \left\{ {\begin{array}{*{20}{l}} {0, {\rm{ if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {d_{left}} < {d_{{\rm{BD}}}};}\\ {1, {\rm{ if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {d_{right}} < {d_{{\rm{BD}}}};}\\ {2, {\rm{ otherwise}}{\rm{. }}} \end{array}} \right. $ | (9) |
其中dleft是到左车道线的距离,dright是到右车道线的距离.
2.3.2 基于交互感知的特征交互感知特征(LAFV、LBPV、RAFV、RBPV、CLPV)考虑的是SV关注区域内相邻的车辆,不能通过原始感知数据直接获得.如图 5所示,SV的关注区域被分成5个部分(图 5中的LA、LB、CB、RA、RB),由预定的距离阈值确定.同一车道的前车的距离阈值dthre2可能与其他车辆的距离阈值dthre1不同. SV关注区域的一部分为阈值dthre1生成一个圆与道路交集区域.通过相邻车辆的距离及其与SV的相对速度来判断该特征的状态.例如,LAFV的状态提取如下:
| $ {\rm{LAFV}} = \left\{ {\begin{array}{*{20}{l}} {0, {\rm{ if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {E_{{\rm{LA}}}} = 0;}\\ {1, {\rm{ if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {E_{{\rm{LA}}}} = 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {v_{{\rm{LA}}}} - {v_{{\rm{SV}}}} \ge 0;}\\ {2, {E_{{\rm{LA}}}} = 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {v_{{\rm{LA}}}} - {v_{{\rm{SV}}}} < 0.} \end{array}} \right. $ | (10) |

|
图 5 通过距离阈值将关注区域划分为5个部分 Fig. 5 The attention area is divided into five sections by the distance thresholds |
其中ELA表示LA区域是否存在车辆,0表示不存在,1表示存在. vLA是LA区域内最近车辆的速度,vSV是SV的速度.
2.3.3 基于道路结构的特征由于基于道路结构的特征(LCU,LLE和RLE)不能通过原始感知数据直接获得,所以提出的提取算法如下.
车道曲率的状态取决于车道边界的曲率.因此,应拟合可观测的车道边界.通常,车道边界可拟合为直线、高次多项式或样条曲线.在计算拟合线或曲线的曲率后,可以将其离散为不同的值.
LLE和RLE的状态可以用一种通用算法[25]来提取,只需要SV的中心点PSV和一组可观测的车道线.过程如算法1所示,分为四个步骤:1)对于每条车道线l,找出l中距离SV最近的点Pn;2)选取Pn点两侧相邻的两个点Pn-1和Pn+1,与PSV生成2个向量(
本文使用的换道决策数据为从NGSIM数据集中的US-101段和I-80段数据进行预处理和筛选后提取的,其中包括540条车道变换样本和845条车道保持样本,共计1385条样本数据.从样本数据中随机抽取80%(1108例)作为决策模型的训练样本,剩下的20%(277例)作为测试样本.
Algorithm 1: Extraction algorithm for road-[structure
features: LLE and RLE
Require:PSV(the center point of the SV), LS (the set of lane lines)
Ensure:states of LLE and RLE
1: for all l in Ls do
2: Pn← Find Nearest Point(l, PSV)
3: (
4: if (
5: NLLE← NLLE+1
6: else
7: NRLE← NRLE+1
8: end if
9: end for
10:NLLE>2: LLE=1?LLE=0
11:NRLE>2:RLE=1?RLE=0
3 支持向量机模型建立自动驾驶车辆换道决策场景是具有代表性的分类情况,SVM的目的就是试图获得一个超平面,这个超平面可以完美地分割不同的数据集.
| $ \left\{ {\begin{array}{*{20}{l}} {D = \{ ({x_1}, {y_1}), ({x_2}, {y_2}), \cdots , ({x_m}, {y_m})\} , }\\ {{x_i} = [{v_{{\rm{ income }}}}, {G_{{\rm{TP}}}} - {G_{{\rm{PV}}}}, {G_{{\rm{TF}}}}, {v_{{\rm{SV}}}} - {v_{{\rm{TF}}}}, {G_{{\rm{TP}}}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {v_{{\rm{SV}}}} \cdot {t_{{\rm{THW}}}}], }\\ {{y_i} = \{ - 1, + 1\} .} \end{array}} \right. $ | (11) |
假设给定训练样本{(xi, yi)},i=1, 2, …, m, x∈Rn, yi∈{-1, +1}, 其中xi是特征输入,即,第i个样本的多维特征向量(换道决策点处的特征参数),m为样本个数,Rn为n维实数空间,yi代表类别(自动驾驶车辆的决策结果).我们用下面的线性方程来表示这个超平面:
| $ {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{x}} + b = 0. $ | (12) |
其中ω=(ω1; ω2; …; ωd)是可调的权值向量,它决定了超平面的方向;b是偏置,它确定超平面和坐标原点之间的距离[26].对于车辆换道决策这样的非线性问题,线性可分支持向量机并不能有效解决,要使用非线性模型才能很好地分类.对于这样的问题,可以将训练样本从原始空间映射到一个更高维的空间,使得样本在这个空间中线性可分[27].对于线性不可分情况,最优分类超平面描述为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathop {{\rm{min}}}\limits_{\omega , b, {\xi _i}} \frac{1}{2}{{\left\| \mathit{\boldsymbol{\omega }} \right\|}^2} + C\sum\limits_{i = 1}^m {{\xi _i}} , }\\ {{\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {y_i}({\mathit{\boldsymbol{\omega }}^{\rm{T}}}\varphi ({x_i}) + b) \ge 1 - {\xi _i}, }\\ {{\xi _i} \ge 0, i = 1, 2, \cdots , m.} \end{array}} \right. $ | (13) |
其中C>0是一个常数,C越小,模型的复杂度越低,但与数据的拟合程度越低,容易出现欠拟合. C越大,模型的复杂度越大,对数据的拟合程度越高,越容易发生过拟合. ξi为引入的“松弛变量”,式(13)的对偶表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathop {{\rm{max}}}\limits_\alpha \sum\limits_{i = 1}^m {{\alpha _i}} - \frac{1}{2}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{\alpha _i}} } {\alpha _j}{y_i}{y_j}\kappa ({x_i}, {x_j}), }\\ {{\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} c \ge {\alpha _i} \ge 0, i = 1, 2, \cdots , m, }\\ {\sum\limits_{i = 1}^m {{\alpha _i}} {y_i} = 0.} \end{array}} \right. $ | (14) |
这里的函数κ(xi, xj)就是核函数,由于高斯核函数具有强大的映射能力,因此本文选用高斯核函数,其表达式如下:
| $ \kappa ({x_i}, {x_j}) = {\rm{exp}}( - \frac{{{{\left\| {{x_{i, }}, {x_j}} \right\|}^2}}}{{2{\sigma ^2}}}). $ | (15) |
σ是高斯核的带宽,σ越小高斯分布越集中,分的类别会越细,越容易过拟合;参数σ越大,分的类别会越粗,导致欠拟合,无法将数据区分开来.
最后利用如公式(16)所示的决策函数来确定最终分类结果.
| $ f(x) = {\rm{sgn}} ({\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^m {{\alpha _i}} {y_i}\kappa ({x_i}, {x_j}) + b{\kern 1pt} {\kern 1pt} ). $ | (16) |
从上文可以看出来,SVM的性能高度依赖于超参数C和σ的选择,因此,需要对这2个参数进行优化.贝叶斯优化算法[28](Bayesian optimization algorithm,BOA)试图最小化有界域中x的标量目标函数f(x)可以帮助找到最佳的C和σ.与其他参数优化方法相比,BOA可以获得更加稳定和高效的参数优化结果.将交叉验证的误差率f(C, σ)作为目标函数,假设f(C, σ)服从高斯过程
| $ f(x):GP(E(x), K(x, x{\rm{'}})), x = [C, \sigma ]. $ | (17) |
利用采集函数来计算最大预期改进量,以通过贝叶斯后验概率找到下一次要获取的x=[C, σ].
| $ {\rm{EI}}(x, Q) = {E_{\rm{Q}}}[{\rm{max}}(0, {\mu _Q}({x_{{\rm{best}}}}) - f(x))]. $ | (18) |
其中,xbest是当前最佳点,即交叉验证错误率最低的点,μQ(xbest)是当前最佳点的交叉验证错误率,EI(x, Q)是预期的改进,贝叶斯优化算法的运行步骤如算法2所示.
Algorithm2: Bayesian Optimization
1: for n=1, 2, …, do
2: select new xn+1 by optimizing acquisition function
a:
3: query objective function to obtain yn+1
4: augment the data Dn+1=Dn, (xn+1, yn+1)
5: update statistical model
6: end for
4.2 模型参数优化数据集中不同的维度的特征具有不同的量纲,需要消除不同量纲的影响.其次,有些维度参数具有较大变化范围,容易引起部分数据被淹没,进而影响模型的预测效果.此外,数据集变化范围太大会增加模型的训练时间和复杂程度, 因此需要进行数据归一化处理.对特征变量进行归一化处理后还能使最优解的寻优过程变得更加平缓,更容易快速正确地收敛到最优解.这里采用min-max方法对数据进行归一化处理,将特征变量的取值都转换到[0, 1],数据归一化的公式如下:
| $ {x{\rm{'}} } = (x - {x_{{\rm{min}}}})/({x_{{\rm{max}}}} - {x_{{\rm{min}}}}). $ | (19) |
式中:x为原始数据,x′为归一化后的数据,xmax和xmin分别为归一化前该维特征数据的最大值和最小值.
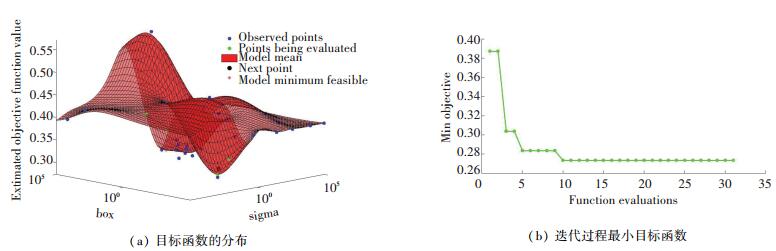
将归一化后的数据作为构建SVM模型的样本,选用高斯径向基函数(Radial Basis Function,RBF)作为核函数进行SVM建模,关于惩罚因子参数C和核函数参数σ的选择,采用贝叶斯优化算法进行优化,选取分类准确率最高的参数C和σ作为最优参数. 经过多次迭代后,得到Gaussian-SVM中C和σ的最佳值,其过程如图 6(a)所示.由图 6(b)可知,最小交叉验证误差与C和σ有很大关系,迭代时可达到27.45%.
|
图 6 贝叶斯优化过程 Fig. 6 Bayesian optimization process |
同时在python环境下利用贝叶斯优化工具包Bayesian-Optimization对RF、GBDT、KNN模型进行参数优化得到各自的最优参数.优化过程如图 7所示,其中i为迭代次数,AUC为接受者操作特性曲线(Receiver operating characteristic curve,ROC)的线下面积.

|
图 7 决策模型参数优化过程 Fig. 7 Parameter optimization process of decision model |
为了全面评估预测性能,我们采用了4个量化性能指标:精度(Precision,PRE)、召回率(Recall)、F1 Score和准确率(Accuracy,ACC).
1) 精度可以看作精确性的度量,是预测为正的所有事件中对应的正确分类比例,即
| $ {\rm{PRE}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FP}}}}. $ | (20) |
2) 召回率也称为真正类率(true positive rate, TPR),是在所有真实事件中,预测对的正例数占真正的正例数的比率,即
| $ {\rm{TPR}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FN}}}}. $ | (21) |
3) F1 Score是Precision和Recall两个指标的调和平均值,即
| $ {\rm{F1}} = \frac{{2 * {\rm{PRE}} * {\rm{TPR}}}}{{{\rm{PRE}} + {\rm{TPR}}}}. $ | (22) |
4) 正确率反映分类器对整个样本的判定能力,能将正的判定为正,负的判定为负的能力,即
| $ {\rm{ACC}} = \frac{{{\rm{TP}} + {\rm{TN}}}}{{{\rm{TP}} + {\rm{TN}} + {\rm{FP}} + {\rm{FN}}}}. $ | (23) |
式中:TP表示实际为正类,也被预测为正类的样本数;TN表示实际为负类,也被预测为负类的样本数;FP表示实际为负类,但被预测为正类的样本数;FN表示实际为正类,但被预测为负类的样本数.
确定好各个换道决策模型的参数后,将各模型参数寻优的结果在测试集上进行验证,结果如表 1所示.由表 1可知,基于规则的模型准确率较低,只有72.42%,这表明基于规则的模型对数据中隐含信息的挖掘能力较弱,无法准确反映真实情况下驾驶员车道变换决策的特性.贝叶斯优化高斯核函数支持向量机模型(BOA Gaussian-SVM)的准确率最高,达到了92.97%.此外,贝叶斯优化RF、GBDT、KNN模型也具有较好的效果,梯度提升树耗时最少,但准确率低于BOA Gaussian-SVM.在所有方法中BOA Gaussian-SVM模型的召回率最高,达到92.91%,平均综合得分F1得分最高,为93.05%.这表明该模型更符合实际情况中驾驶员的操作特性和决策习惯,具有较高的综合预测性能.
| 表 1 不同方法的性能比较 Tab. 1 Performance comparison of different approaches |
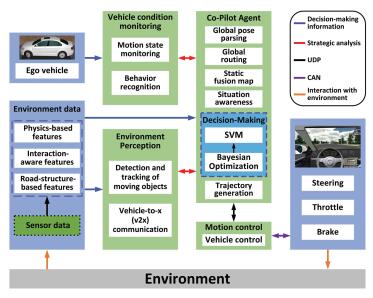
为了对Gaussian-SVM决策模型模型在交通场景中的有效性进行验证,我们对模型进行了仿真实验.使用Airsim作为仿真平台,基于python语言用tensorflow框架完成模型搭建,模拟平台遵循模块化设计,核心组件包括环境模型、车辆模型、物理引擎、传感器模型、公共API层和车辆固件接口层. Gaussian-SVM模型测试的环境系统架构如图 8所示.
|
图 8 描述核心组件及其交互的系统架构 Fig. 8 The architecture of the system that depicts the core components and their interactions |
在实验过程中,测试车辆可以通过Airsim平台实时获取当前车道和相邻车道内车辆的运动状态数据和位置数据.测试环境采用同向四车道高速工况,车道宽度为3.5 m,试验车型为小汽车.为了模拟动态交通流的变化,系统采用快车和慢车两种车型,快车的平均期望速度设置为28 m/s,每辆车的期望速度服从[23 m/s, 33 m/s]上的均匀分布;慢车的平均期望速度设置为20 m/s,每辆车的平均期望速度服从[15 m/s, 25 m/s]上的均匀分布.当车辆做出换道决策后,为满足车辆运动约束以及实时性要求,采用基于B样条曲线的方法来规划换道路径.
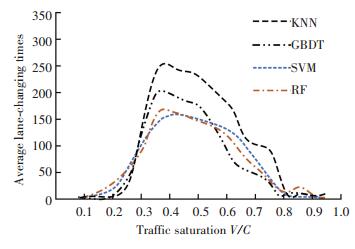
4.4.1 不同决策模型性能对比换道次数是换道成功的标志,也是评价决策模型的重要指标,可以通过对比决策模型在不同驾驶环境中换道次数来分析各个模型的性能和对驾驶环境变化的适应性.测试过程中按照饱和度值每递增0.1向系统内输入相应的车辆数来模拟驾驶环境的动态变化.理论上,交通流中车辆数增多则饱和度增大,间隔距离缩小,车辆所受约束条件变严格,这可能导致平均车速降低,具有换道动机的车辆增加.对RF、GBDT、KNN以及Gaussian-SVM4种决策模型在不同的饱和度下进行测试,不同决策模型在3 500 s时间内平均换道次数统计结果如图 9所示.
|
图 9 不同算法平均换道次数 Fig. 9 Average lane-changing times for different algorithms |
从图 9可以看出:当V/C < 0.2时,交通流中车辆较少,车辆间距较大,车流接近自由流状态,车速基本不受到前导车辆PV的影响,此时,车辆一般不会产生换道动机.随着V/C增大进入同步流状态后,车速受到限制,间距缩小,具有换道动机的车辆增多.在V/C=0.3时平均换道次数开始迅速增加,在V/C=0.4达到了极大值,随着V/C值进一步增加而呈现缓慢下降形态.在不同饱和度V/C情况下,KNN和GBDT模型换道次数变化率较大,而且变道较为频繁;RF模型换道次数最少,整个过程变化较平缓,Gaussian-SVM换道决策模型在不同饱和度时换道次数适中,且变化较为平滑.
4.4.2 车辆换道频率分析通过分析决策模型对每个决策变量变化的敏感性,定量评估BOA Gaussian-SVM换道决策模型的性能以及特征参数对驾驶决策的影响.以道路曲率ρ的变化为例,将ρ取值设为不同的值,其他决策参数仍然保持标准,每次ρ改变时都会获得一组新的驾驶决策样本并输入到决策模型中,根据模型的输出计算不同交通密度下的换道率.然后,分别在ρ取0、1、1.65和3的情况下得到换道率随交通密度变化的趋势.同样,在其他决策参数保持标准,改变慢车比例p的值也可以得出当系统中快、慢车比例采用不同值时换道率随交通密度变化的趋势,在此操作和数据统计之后的结果如图 10所示.

|
图 10 不同条件下车辆换道率 Fig. 10 The rate of lane changing under different conditions |
从图 10可以看出:
1) 车道曲率对换道率的影响:在中、低交通密度范围(5~15 veh/km)内,道路条件的变化对驾驶决策的影响较大,在高交通密度范围(ρ>25 veh/km)内影响较小(图 10(a)).所以我们可以得出结论:在低交通密度范围内,驾驶决策主要受道路条件的限制,因此,在不考虑道路条件的情况下,结果容易出错.另一方面,在高交通密度范围内,驾驶决策主要受到车辆状态的限制,因此即使不考虑道路条件,决策结果也不会受到太大影响.
2) 慢车比例对换道率的影响:慢车比例对换道率的影响因密度的不同而改变(图 10(b)).在中、低密度范围(5~15 veh/km),此时交通密度不高,能够提供刺激车辆产生换道动机的空间优势和速度优势,因此不同快、慢车比例时换道率都较高.当慢车比例在0.2~0.4之间时,车道变换率都超过了20%,因为此时交通流中具有换道动机的车辆多,而且快慢车相互干扰强,所以换道也最为频繁.在高密度范围(ρ>25 veh/km)内不同快、慢车比例时换道率都较低,均趋近于0.
3) 车流密度对换道率的影响:从图 10可知,换道率随密度的变化曲线趋于一致,均呈倒“V”形,且中密度范围(10~15 veh/km)内换道率都较高.情形1中,在不同道路曲率下,换道率随密度的增加先增加后下降,当密度大于25 veh/km时,换道率趋近于0.情形2中换道率随密度的变化趋势与情形1基本相同.在2种情形中,同一密度下慢车比例不同,导致车流速度不同,从而对速度优势和空间优势产生不同的影响.中密度范围内相邻车道中存在较大的行车空间,有利于速度优势或空间优势产生,所以换道最为频繁.随着交通密度继续增大,车辆“溢出”现象导致交通流中车速降低、间距缩小,难以产生激发车辆产生换道意图的速度优势或空间优势,因此换道率也逐渐降低.
4.4.3 车辆换道决策过程分析以下仅取交通流中任意单车换道过程进行研究,换道过程如图 11所示.实验开始时,测试车辆以videal=80 km/h的速度在虚拟环境中的高速工况下行驶.开始时测试车辆与前车速度接近,27.5 s之后测试车辆开始加速两车相对距离不断减小,30 s时测试车辆速度增加至58.91 km/h,两车相对距离减小到76.58 m,当前车道前车速度为54.92 km/h,此时Gaussian-SVM换道决策算法做出换道决策.然后,自动驾驶车辆通过调整横向速度(图 10(a))成功改变车道,车速逐渐提高到接近所设置理想车速(图 10(b)),达到了74.47 km /h.此时前导车辆变为TP,与前车的相对距离增加至107.12 m,如图 11(c)所示.改变车道后,测试车辆的速度提升了26.41%,与前车相对距离提升了39.88%.测试车辆换道决策过程与第1节换道决策机理分析相符,进一步证明了所提换道决策模型的合理性和有效性.

|
图 11 车辆换道过程 Fig. 11 Vehicle lane-changing process |
1) 传统的数理模型虽然能够在一定程度上体现驾驶员的决策机理,但是并不能充分体现实际驾驶决策过程中各方面的影响因素,其准确性和适用性明显不足.
2) 车辆换道主要受车辆状态和道路状况等多方面因素的影响,从基于道路结构特征、基于交互感知的特征与基于物理的特征三个方面提取决策特征,使决策模型考虑的因素更加全面,决策结果更符合驾驶员的操作特性和决策习惯.
3) BOA Gaussian-SVM决策模型在测试集上以92.97%的预测准确率超越了其他换道决策模型并远高于规则模型,能够较为准确地预测主体车辆的自由换道行为.实验结果进一步证明了所提模型的有效性,说明该模型在自动驾驶和辅助驾驶系统开发中具有应用价值和借鉴意义.
| [1] |
李克强. 汽车技术的发展动向及我国的对策[J]. 汽车工程, 2009, 31(11): 1005. |
| [2] |
倪捷, 刘志强. 基于驾驶人决策机制的换道意图识别模型[J]. 交通运输系统工程与信息, 2016, 16(1): 58. NI Jie, LIU Zhiqiang. Arecognition model of lane change intention based on driver's decision mechanism[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(1): 58. |
| [3] |
DOU Yangliu, YAN Fengjun, FENG Daiwei. Lane changing prediction at highway lane drops using support vector machine and artificial neural network classifiers [C] //2016 IEEE International Conference on Advanced Intelligent Mechatronics (AIM). Banff: IEEE, 2016: 901. DOI: 10.1109/AIM.2016.7576883
|
| [4] |
ANDERSEN G J, SAUER C W, SAUER C W. Optical information for car following: the driving by visual angle (DVA) model[J]. Human Factors: The Journal of the Human Factors and Ergonomics Society, 2007, 49(5): 878. DOI:10.1518/001872007X230235 |
| [5] |
GIPPS P G. A model for the structure of lane-changing decisions[J]. Transportation Research, Part B (Methodological), 1986, 20(5): 403. |
| [6] |
YANG Q, KOUTSOPOULOS H N. A microscopic traffic simulator for evaluation of dynamic traffic management systems[J]. Transportation Research Part C, 1996, 4(3): 113. |
| [7] |
HIDAS P. Modelling lane changing and merging in microscopic traffic simulation[J]. Transportation Research Part C, 2002, 10(5): 351. DOI:10.1016/s0968-090x(02)00026-8 |
| [8] |
KESTING A, TREIBER M, HELBING D. Generallane-changing model MOBIL for car-following models[J]. Transportation Research Record, 2007, 1999: 86. DOI:10.3141/1999-10 |
| [9] |
邱小平, 刘亚龙, 马丽娜, 等. 基于贝叶斯网络的车辆换道模型[J]. 交通运输系统工程与信息, 2015, 15(5): 67. QIU Xiaoping, LIU Yalong, MA Lina, et al. Alane change model based on Bayesian networks[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(5): 67. |
| [10] |
MOTAMEDIDEHKORDI N, AMINI S, HOFFMANN S, et al. Modeling tactical lane-change behavior for automated vehicles: a supervised machine learning approach [C] // 2017 IEEE International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS). Naples: IEEE, 2017: 268. DOI: 10.1109/MTITS.2017.8005678
|
| [11] |
DÍAZ-ÁLVAREZ A, CLAVIJO M, JIMÉNEZ F, et al. Modelling the human lane-change execution behaviour through multilayer perceptions and convolutional neural networks[J]. Transportation Research Part F: Traffic Psychology and Behaviour, 2018, 56: 134. DOI:10.1016/j.trf.2018.04.004 |
| [12] |
张叠, 杜荣华, 刘理. 基于支持向量机的车辆换道决策模型[J]. 武汉理工大学学报(交通科学与工程版), 2017, 41(5): 849. ZHANG Die, DU Ronghua, LIU Li. Decision model for vehicle lane changing based on support vector machine[J]. Journal of Wuhan University of Technology (Transportation Science and Engineering), 2017, 41(5): 849. |
| [13] |
ZHANG Junyou, LIAO Yaping, WANG Shufeng, et al. Study on driving decision-making mechanism of autonomous vehicle based on an optimized support vector machine regression[J]. Applied Sciences, 2018, 8(1). DOI:10.3390/app8010013 |
| [14] |
JALAL A, KIM S. Global security using human face understanding under vision ubiquitous architecture system[J]. World Acad. Sci. Eng. Technol, 2006, 13: 7. |
| [15] |
FAROOP A, JALAL A, KAMAL S. Dense RGB-D map-based human tracking and activity recognition using skin joints features and self-organizing map[J]. KSII Trans. Internet Information Systems, 2015, 9(5): 1856. DOI:10.3837/tiis.2015.05.017 |
| [16] |
YANG D, ZHU L, YANG F, et al. Modeling and analysis of lateral driver behavior in lane-changing execution[J]. Transportation Research Record: Journal of the Transportation Research Board, 2015(2490): 127. DOI:10.3141/2490-14 |
| [17] |
CHOUDHURY C F, RAMANUJAM V, BEN-AKIVA M E. Modeling acceleration decisions for freeway merges[J]. Transportation Research Record, 2009(2124): 45. DOI:10.3141/2124-05 |
| [18] |
韩珍.驾驶员-车辆Agent微观换道行为建模[D].合肥: 中国科学技术大学, 2011 HAN Zhen. A microscopic lane-changing model for driver-vehicle Agent[D]. Hefei: University of Science and Technology of China, 2011 |
| [19] |
LIU Yonggang, WANG Xiao, LI Liang, et al. A novel lane change decision-making model of autonomous vehicle based on support vector machine[J]. IEEE Access, 2019(7): 26543. DOI:10.1109/ACCESS.2019.2900416 |
| [20] |
PARK M, JANG K, LEE J, et al. Logistic regression model for discretionary lane changing under congested traffic[J]. Transportmetrica A: Transport Science, 2015, 11(4): 333. DOI:10.1080/23249935.2014.994686 |
| [21] |
SCHEEL O, SCHWARZ L, NAVAB N, et al. Situation assessment for planning lane changes: combining recurrent models and prediction[C]//Proceedings of the IEEE International Conference on Robotics and Automation (ICRA). Brisbane: IEEE, 2018: 7. DOI: 10.1109/ICRA.2018.8462838
|
| [22] |
LEE D, HANSEN A, KARL HEDRICK J. Probabilistic inference of traffic participants lane change intention for enhancing adaptive cruise control[C]//Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV). Los Angeles: IEEE, 2017: 11
|
| [23] |
LI Junxiang, DAI Bin, LI Xiaohui, et al. A dynamic Bayesian network for vehicle maneuver prediction in highway driving scenarios framework and verification[J]. Electronics, 2019, 8(1). DOI:10.3390/electronics8010040 |
| [24] |
THIEMANN C, TREIBER M, KESTING A. Estimating acceleration and lane-changing dynamics based on NGMIS trajectory data[J]. Transportation Research Record: Journal of the Transportation Research Board, 2008, 90. DOI:10.3141/2088-10 |
| [25] |
聂建强.高速公路车辆自主性换道行为[D].南京: 东南大学, 2017 NIE Jianqiang. Research on modeling discretionary lane-changing behavior of vehicles in freeway[D]. Nanjing: Southeast University 2017 |
| [26] |
祝俪菱, 刘澜, 赵新朋, 等. 基于支持向量机的车辆驾驶行为识别研究[J]. 交通运输系统工程与信息, 2017, 17(1): 91. ZHU Liling, LIU Lan, ZHAO Xinpeng, et al. Driver behavior recognition based on support vector machine[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(1): 91. |
| [27] |
陈永恒, 陶楚青, 白乔文, 等. 基于SVM的快速路合流区车辆间隙选择模型[J]. 东南大学学报(自然科学版), 2018, 48(4): 752. CHEN Yongheng, TAO Chuqing, BAI Qiaowen, et al. Gap choice model at urban expressway merging sections based on SVM[J]. Journal of Southeast University (Natural Science Edition), 2018, 48(4): 752. |
| [28] |
SHAHRIARI B, SWERSKY K, WANG Z Y, et al. Taking the Human out of the loop: a review of bayesian optimization[J]. Proceedings of the IEEE, 2016, 104(1): 148. DOI:10.1109/JPROC.2015.2494218 |
 2020, Vol. 52
2020, Vol. 52


