高压、高转速条件下, 柱塞泵的油液泄漏是造成柱塞泵容积效率降低的主要原因,而各运动副之间的间隙是造成油液泄露的重要因素之一[1-3].由于制造公差、流体的粘度系数和体积压缩系数、温度、外部载荷等工作条件影响,轴向柱塞泵各运动副间隙具有随机性,特别是轴向柱塞泵运行时所处的工况的不同,难以用确定性模型完成柱塞泵容积效率的相关分析,因此对柱塞泵容积效率的可靠性分析变得十分重要.
国内外对柱塞泵泄漏的研究多集中在泄漏量求解及实际流量脉动分析.文献[2, 4]通过对轴向柱塞泵三大运动副间隙的泄漏和摩擦损失进行分析,建立了新的物理尺寸模型.文献[1, 5]假设各运动副之间间隙是倾斜的,提出了一种新的轴向柱塞泵泄漏和实际流量波动模型.文献[6]讨论了现有柱塞泵流量损失模型与实测数据对比,分析不同模型的优缺点.文献[7]考虑了柱塞腔中油液的可压缩性及通过各个间隙的向外泄漏问题,应用数值积分法求解实际流量.上述方法在间隙泄漏分析中认为参数是确定的,而实际柱塞泵运行中大部分因素是随机和不确定的.
可靠性是指产品在规定的使用条件下、规定的时间内完成规定功能的能力[8-10].将可靠性技术与液压相结合,产生了液压可靠性这一方向.目前对液压柱塞泵可靠性研究较少,文献[11]提出了液压柱塞泵关键元件抗磨损和抗疲劳的可靠性设计和可靠性灵敏度分析方法.文献[12]对柱塞进行动力学分析,并结合应力—强度干涉模型对柱塞进行抗疲劳可靠性分析.针对柱塞泵可靠性的研究主要集中在磨损和疲劳等方向,对于柱塞泵间隙泄漏引起容积效率的可靠性分析很少涉及.本文对柱塞泵各运动副间隙瞬时泄漏流量进行了全面分析,推导出柱塞泵瞬时泄漏流量和容积效率计算方法,结合可靠性理论,四阶矩技术和随机摄动理论提出柱塞泵容积效率可靠性分析方法.采用Monte Carlo方法验证了文中所提方法的准确性和合理性,通过可靠性灵敏度分析得到各设计参数对柱塞泵可靠性的影响程度.本文所提方法为轴向柱塞泵研发设计、工艺、质量等人员在研发、制造、检验等环节提供理论参考.
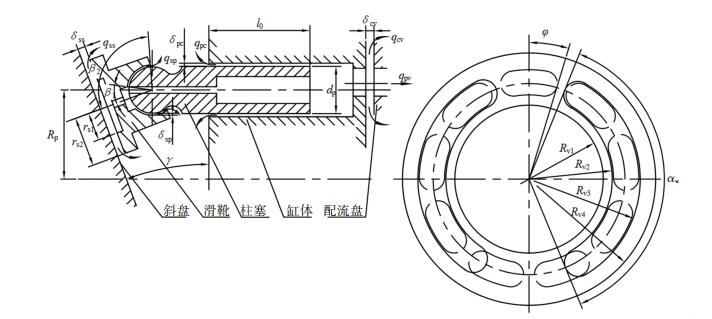
1 单柱塞瞬时流量及泄漏流量 1.1 单柱塞瞬时流量轴向柱塞泵主要由滑靴-斜盘副、柱塞-缸体副、缸体-配流盘副三对主要运动副组成(如图 1所示).柱塞组在缸体旋转作用下作回转运动,在斜盘作用下沿轴线方向作直线往复运动,通过配流盘的作用,将油液从吸油腔中吸入,从排油腔排出,其单个柱塞理论瞬时排油量qpv为
|
图 1 轴向柱塞泵间隙泄漏示意图 Fig. 1 Main clearance leakage flows of the axial piston pump |
| $ \begin{array}{*{20}{c}} {{q_{{\rm{pv}}}} = {A_{\rm{p}}}{v_{\rm{p}}} = {A_{\rm{p}}}\omega {R_{\rm{p}}}{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} \varphi = }\\ {\frac{{\pi d_{\rm{p}}^2\omega {R_{\rm{p}}}{\rm{tan}}{\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} \varphi }}{4}.} \end{array} $ | (1) |
式中:vp为柱塞相对柱塞腔的运动速度,dp为柱塞直径,ω为缸体转动角速度,Rp为柱塞分布圆半径,γ为斜盘倾斜角,φ为缸体转角.
1.2 单柱塞瞬时泄漏流量轴向柱塞泵各运动副之间要形成适当的油膜,以减少运动过程中摩擦副之间的摩擦磨损及其造成的功率损失,运动副之间形成的油膜间隙,势必造成一定的泄漏流量,从而降低容积效率[13].本文除上述三对运动副之外,还分析了滑靴与柱塞球铰接之间的间隙泄漏量.由于各运动副之间的间隙值是随缸体的转动周期变化的,间隙值一般在0.05~0.25 mm之间,在此假设它们是层流.
1.2.1 滑靴与斜盘之间间隙的瞬时泄漏量滑靴在旋转过程中,在离心力作用下产生倾覆与斜盘产生倾斜角,其间隙随着缸体转角的变化而发生周期性的波动,位于排油区时,其倾斜角和间隙相对较小,位于吸油区时,其倾斜角和间隙较大;当缸体转速增加时,间隙增大,当排油压力增大时,其间隙变小[14].当柱塞-滑靴组位于排油区时,高压油通过柱塞中心孔流入滑靴中心孔,滑靴中心孔高压pd和滑靴外回油压力p0产生压差,通过滑靴与斜盘之间的油膜间隙产生泄漏[15].其单个滑靴瞬时泄漏量qss为
| $ {q_{ss}} = \frac{{\pi \delta _{{\rm{ss}}}^3({p_{\rm{d}}} - {p_0})}}{{6\mu {\rm{ln}}({r_{{\rm{s2}}}}/{r_{{\rm{s1}}}})}}. $ | (2) |
式中:δss为滑靴与斜盘之间的间隙,μ为油液的动力粘度,rs2为滑靴底面外圆半径,rs1为滑靴底面内圆半径.
1.2.2 滑靴与柱塞球铰接之间间隙的瞬时泄漏量球铰接可以绕一个中心点完成两个方向转动,具有高负载能力、高抗冲击能力和自动调心能力而常被用于轴向柱塞泵[5].柱塞泵中滑靴与柱塞通过球铰运动副铰接在一起,其单个球铰副间隙泄漏量qsp为
| $ {q_{{\rm{sp}}}} = \frac{{\pi \delta _{{\rm{sp}}}^3({p_{\rm{d}}} - {p_0})}}{{3\mu [2{\rm{ln}}({\rm{tan}}{\beta _2}/{\rm{tan}}{\beta _1}) + {\rm{ta}}{{\rm{n}}^2}{\beta _2} - {\rm{ta}}{{\rm{n}}^2}{\beta _1}]}}. $ | (3) |
式中:δsp为滑靴与柱塞球铰接之间间隙,β1和β2分别为柱塞和滑靴球头有效作用角度.
1.2.3 柱塞与缸体柱塞腔之间间隙的瞬时泄漏量柱塞在缸体转动过程中会在柱塞孔内周期性地微运动,在离心力和斜盘倾斜力的作用下,其中心线与柱塞腔中心线发生偏心和倾斜;倾斜角和偏心量随缸体转角的变化而波动,随缸体转速的增加,偏心量减小,泄漏量也相应减小[16-17].柱塞与缸体柱塞腔之间的间隙泄漏量由柱塞两端压力差造成的压差泄漏和柱塞往复运动造成的剪切泄漏流量两部分组成.其泄流量qpc为
| $ \begin{array}{l} {q_{{\rm{pc}}}} = \frac{{\pi {d_{\rm{p}}}\delta _{{\rm{pc}}}^3({p_{\rm{d}}} - {p_0})}}{{12\mu ({l_0} + {R_{\rm{p}}}{\rm{tan}}\gamma (1 - {\rm{cos}}\varphi ))}}(1 + 1.5{\varepsilon ^2}) \pm \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\pi {d_{\rm{p}}}{\delta _{{\rm{pe}}}}{v_{\rm{p}}}}}{2}. \end{array} $ | (4) |
式中:δpc为柱塞与柱塞腔同心时的单边间隙,l0为柱塞在上止点时柱塞与缸体的接触长度,ε为相对偏心量.式中“±”号前半部分为缝隙压差形成的泄漏,后半部分为纯剪切流动的泄漏,压差方向与运动方向一致时取“+”号,反之取“-”号.
1.2.4 缸体与配流盘之间间隙泄漏量缸体与配流盘之间间隙随排油区压力的变化而波动,位于排油区间隙较小,吸油区间隙较大,在一个循环周期内其间隙为楔形并时刻发生着改变;伴随负载压力的升高,排油区间隙变小,吸油区间隙变大,即楔形角变大[18].在排油区时排油腰槽内高压与卸油口之间形成压差,通过缸体与配流盘之间的间隙,产生泄漏量qcv为[7]
| $ {q_{{\rm{cv}}}} = \frac{{{\alpha _{\rm{w}}}\delta _{{\rm{cv}}}^3({p_{\rm{d}}} - {p_0})}}{{12\mu }}\left[ {\frac{1}{{{\rm{ln}}({R_{{\rm{v4}}}}/{R_{{\rm{v3}}}})}} + \frac{1}{{{\rm{ln}}({R_{{\rm{v2}}}}/{R_{{\rm{v1}}}})}}} \right]. $ | (5) |
式中:αw为配流盘腰型槽包角,δcv为缸体与配流盘之间间隙,Rv1、Rv2为配流盘内封油带的内外半径,Rv3、Rv4为配流盘外封油带的内外半径.
2 轴向柱塞泵瞬时流量及泄漏量分析 2.1 轴向柱塞泵瞬时流量分析柱塞泵共有z个柱塞,这些柱塞在缸体中沿圆周方向均匀分布,任一相邻两柱塞夹角为2π/z,设同时处于排油区内柱塞的个数为m,若z为偶数,同时位于排油区和吸油区分布的柱塞数均为m=z/2;若z为奇数时,其同时位于排油区柱塞数m为
| $ m = \left\{ {\begin{array}{*{20}{l}} {\frac{{z + 1}}{2}, }&{0 \le {\varphi _1} \le \frac{\pi }{z};}\\ {\frac{{z - 1}}{2}, }&{\frac{\pi }{z} \le {\varphi _1} \le \frac{{2\pi }}{z}.} \end{array}} \right. $ | (6) |
其同时位于吸油区柱塞个数为z-m.柱塞泵的瞬时流量Qpv为
| $ \begin{array}{*{20}{l}} {{Q_{{\rm{pv}}}} = \sum\limits_{i = 1}^m {{q_{{\rm{pvi}}}}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^m {\frac{{\pi d_{\rm{p}}^2\omega {R_{\rm{p}}}{\rm{tan}}{\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} {\varphi _i}}}{4}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\pi d_{\rm{p}}^2\omega {R_{\rm{p}}}{\rm{tan}}{\kern 1pt} {\kern 1pt} \gamma }}{4}\sum\limits_{i = 1}^m {{\rm{sin}}} \left[ {{\varphi _1} + (i - 1)\frac{{2\pi }}{z}} \right].} \end{array} $ | (7) |
通过推导计算,柱塞泵的瞬时理论流量Qpv为
| $ {Q_{{\rm{pv}}}} = \left\{ \begin{array}{l} \frac{{\pi d_{\rm{p}}^2\omega {R_{\rm{p}}}{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{cos}}\left( {\frac{\pi }{z} - {\varphi _1}} \right)}}{{4{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\pi }{z}}}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} z{\rm{为偶数}};\\ \frac{{\pi d_{\rm{p}}^2\omega {R_{\rm{p}}}{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{cos}}\left( {\frac{\pi }{z} \pm \frac{\pi }{{2z}} - {\varphi _1}} \right)}}{{8{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\pi }{{2z}}}}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} z{\rm{为奇数}}{\rm{.}} \end{array} \right. $ | (8) |
假设柱塞泵中有n个柱塞与腔体之间存在间隙剪切泄漏,其n个柱塞的瞬时剪切流Qc为
| $ \begin{array}{*{20}{l}} {{Q_{\rm{c}}} = - \sum\limits_{i = 1}^m {\frac{{\pi {d_{\rm{p}}}{\delta _{{\rm{pe}}}}{v_{{\rm{pi}}}}}}{2}} = }\\ {\quad - \frac{{\pi {d_{\rm{p}}}{\delta _{pe}}\omega {R_{\rm{p}}}{\rm{tan}}\gamma }}{2}\sum\limits_{i = 1}^m {{\rm{sin}}} \left[ {{\varphi _1} + (i - 1)\frac{{2\pi }}{z}} \right] = }\\ {\quad - \frac{{\pi {d_{\rm{p}}}{\delta _{{\rm{pe}}}}\omega {R_{\rm{p}}}{\rm{tan}}\gamma }}{2}\frac{{{\rm{sin}}\left( {\frac{{m - 1}}{z}\pi } \right){\rm{sin}}\left( {\frac{{m\pi }}{z}} \right)}}{{\sin \frac{\pi }{z}}}.} \end{array} $ | (9) |
柱塞泵的柱塞与柱塞腔之间的间隙剪切泄漏不仅存在于排油区,当柱塞位于吸油区时依然存在,因此z个柱塞全部存在剪切泄漏,将m=z带入式(9)得Qc=0,即柱塞泵中柱塞与柱塞腔中产生的间隙瞬时剪切泄漏量为零,与柱塞个数为奇数或偶数无关.考虑单个柱塞泄漏分析时间隙剪切泄漏是有意义的,对于整个柱塞泵泄漏分析,其柱塞与缸体间隙瞬时剪切总泄漏流量为零,因此柱塞泵的瞬时泄漏只考虑压差泄漏.
2.2.2 柱塞泵泄漏量分析柱塞泵的瞬时泄漏量为任一时刻柱塞泵中滑靴-斜盘副、滑靴-柱塞副、柱塞-缸体副和缸体-配流盘副的间隙泄漏量之和,各运动副之间的间隙泄漏主要是由于压差引起,柱塞位于吸油区压力差值相对较小,本文仅考虑柱塞位于排油区时的泄漏问题.其瞬时总泄漏流量QL为
| $ \begin{array}{l} {Q_{\rm{L}}} = {Q_{{\rm{ss}}}} + {Q_{{\rm{sp}}}} + {Q_{{\rm{pc}}}} + {Q_{{\rm{cv}}}} = \sum\limits_{i = 1}^m ( {q_{{\rm{ss}}i}} + {q_{{\rm{sp}}i}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {q_{{\rm{pc}}i}}) + {q_{{\rm{cv}}}}. \end{array} $ | (10) |
当柱塞数z为偶数时
| $ \begin{array}{l} {Q_{\rm{L}}} = \frac{{({p_{\rm{d}}} - {p_0})}}{{6\mu }}\left\{ {\frac{{z\pi \delta _{{\rm{ss}}}^3}}{{2{\rm{ln}}({r_{{\rm{s2}}}}/{r_{{\rm{s1}}}})}} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{z\pi \delta _{{\rm{sp}}}^3}}{{2{\rm{ln}}({\rm{tan}}{\beta _2}/{\rm{tan}}{\beta _1}) + {\rm{ta}}{{\rm{n}}^2}{\beta _2} - {\rm{ta}}{{\rm{n}}^2}{\beta _1}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^{\frac{z}{2}} {\frac{{\pi {d_{\rm{p}}}\delta _{{\rm{pc}}}^3}}{{{l_0} + {R_{\rm{p}}}{\rm{tan}}\gamma \left\{ {1 - {\rm{cos}}\left[ {{\varphi _1} + (i - 1)\frac{{2\pi }}{z}} \right]} \right\}}}(1 + } \\ {\kern 1pt} \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1.5{\varepsilon ^2}) + \frac{{{\alpha _{\rm{w}}}\delta _{{\rm{cv}}}^3}}{2}\left[ {\frac{1}{{{\rm{ln}}({R_{{\rm{v4}}}}/{R_{{\rm{v3}}}})}} + \frac{1}{{{\rm{ln}}({R_{{\rm{v2}}}}/{R_{{\rm{v1}}}})}}} \right]} \right\}. \end{array} $ | (11) |
当柱塞数z为奇数时
| $ \begin{array}{l} {Q_{\rm{L}}} = \frac{{({p_{\rm{d}}} - {p_0})}}{{6\mu }}\left\{ {\frac{{\left( {z \pm 1} \right)\pi \delta _{{\rm{ss}}}^3}}{{2{\rm{ln}}({r_{{\rm{s2}}}}/{r_{{\rm{s1}}}})}} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\left( {z \pm 1} \right)\pi \delta _{{\rm{sp}}}^3}}{{2{\rm{ln}}({\rm{tan}}{\beta _2}/{\rm{tan}}{\beta _1}) + {\rm{ta}}{{\rm{n}}^2}{\beta _2} - {\rm{ta}}{{\rm{n}}^2}{\beta _1}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^{\frac{{z \pm 1}}{2}} {\frac{{\pi {d_{\rm{p}}}\delta _{{\rm{pc}}}^3}}{{{l_0} + {R_{\rm{p}}}{\rm{tan}}\gamma \left\{ {1 - {\rm{cos}}\left[ {{\varphi _1} + (i - 1)\frac{{2\pi }}{z}} \right]} \right\}}}(1 + } \\ {\kern 1pt} \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1.5{\varepsilon ^2}) + \frac{{{\alpha _{\rm{w}}}\delta _{{\rm{cv}}}^3}}{2}\left[ {\frac{1}{{{\rm{ln}}({R_{{\rm{v4}}}}/{R_{{\rm{v3}}}})}} + \frac{1}{{{\rm{ln}}({R_{{\rm{v2}}}}/{R_{{\rm{v1}}}})}}} \right]} \right\}. \end{array} $ | (12) |
式中“±”号的取值按照式(6)选取.
从式(11)~(12)可以看出液压柱塞泵的间隙泄漏量主要与各间隙值、柱塞泵几何尺寸、排油区压力和油液运动粘度有关.
3 容积效率可靠性及可靠性灵敏度设计 3.1 柱塞泵容积效率容积效率是衡量液压泵性能的一个重要指标,液压泵的油液泄漏是造成其容积效率降低的主要原因.通过运动副之间间隙泄漏模型分析,其容积效率ηv为实际输出流量与其理论流量之比,即
| $ {\eta _{\rm{v}}} = \frac{{{{\mathit{\boldsymbol{\bar Q}}}_{{\rm{pv}}}} - {{\mathit{\boldsymbol{\bar Q}}}_{\rm{L}}}}}{{{\mathit{\boldsymbol{Q}}_{{\rm{pv}}}}}} = 1 - \frac{{{{\mathit{\boldsymbol{\bar Q}}}_{\rm{L}}}}}{{{\mathit{\boldsymbol{Q}}_{{\rm{pv}}}}}}. $ | (13) |
根据应力-强度干涉模型,轴向柱塞泵容积效率极限状态方程和可靠度R分别表示为
| $ {g(\mathit{\boldsymbol{X}}) = {\eta _{\rm{v}}} - [{\eta _{\rm{v}}}] \ge 0, } $ | (14) |
| $ {R = P[g(\mathit{\boldsymbol{X}}) \ge 0].} $ | (15) |
式中[ηv]为容许容积效率,由JB/T7043- 2006《轴向柱塞泵》[19]可知在额定工况下,公称排量10≤V<25 mL/r时,轴向柱塞泵容许容积效率[ηv]≥91%.
二阶矩法是在已知基本随机参数的前两阶矩,可靠性指标定义为
| $ {\beta _{{\rm{SM}}}} = \frac{{{\mu _g}}}{{{\sigma _g}}} = \frac{{{\rm{E}}[g(\mathit{\boldsymbol{X}})]}}{{\sqrt { {\rm{Var}} [g(\mathit{\boldsymbol{X}})]} }}. $ | (16) |
在基本随机参数矩阵X服从正态分布时,可以获得可靠度的估计量:
| $ {R_{{\rm{SM}}}} = \Phi ({\beta _{{\rm{SM}}}}), $ | (17) |
式中Φ(·)为标准正态分布函数.
如果已知基本随机参数的前四阶矩,可靠性指标定义为
| $ {\beta _{{\rm{FM}}}} = \frac{{3({\alpha _{4g}} - 1){\beta _{{\rm{SM}}}} + {\alpha _{3g}}(\beta _{{\rm{SM}}}^2 - 1)}}{{\sqrt {(9{\alpha _{4g}} - 5\alpha _{3g}^2 - 9)({\alpha _{4g}} - 1)} }}. $ | (18) |
式中: α3g=θg/σg3为状态函数g(X)的偏态系数,α4g=ηg/σg4为状态函数g(X)的峰态系数.
四阶矩的可靠度为
| $ {R_{{\rm{FM}}}} = \varPhi ({\beta _{{\rm{FM}}}}). $ | (19) |
机械零部件基于四阶矩技术的可靠度对随机参数向量X均值和方差的灵敏度为
| $ \frac{{{\rm{D}}{R_{{\rm{FM}}}}({\beta _{{\rm{FM}}}})}}{{D{\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\bar X}}}^{\rm{T}}}}} = \frac{{\partial R({\beta _{{\rm{FM}}}})}}{{\partial {\beta _{{\rm{FM}}}}}}\frac{{\partial {\beta _{{\rm{FM}}}}}}{{\partial {\beta _{{\rm{SM}}}}}}\frac{{\partial {\beta _{{\rm{SM}}}}}}{{\partial {\mu _g}}}\frac{{\partial {\mu _g}}}{{\partial {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\bar X}}}^{\rm{T}}}}}, $ | (20) |
| $ \frac{{{\rm{D}}{R_{{\rm{FM}}}}}}{{ {\rm{DVar}} (\mathit{\boldsymbol{X}})}} = \left[ {\frac{{\partial {R_{{\rm{FM}}}}}}{{\partial {\beta _{{\rm{FM}}}}}}\left( {\frac{{\partial {\beta _{{\rm{FM}}}}}}{{\partial {\beta _{{\rm{SM}}}}}}\frac{{\partial {\beta _{{\rm{SM}}}}}}{{\partial {\sigma _g}}} + \frac{{\partial {\beta _{{\rm{FM}}}}}}{{\partial {\sigma _g}}}} \right)} \right]\frac{{\partial {\sigma _g}}}{{\partial {\rm{Var}} (\mathit{\boldsymbol{X}})}}. $ | (21) |
式中: D(·)/DXT为(·)对随机参数向量X均值的灵敏度,D(·)/DVar(X)为(·)对随机参数向量X方差的灵敏度.式(20)和式(21)右边的表达式分别为
| $ \frac{{\partial {R_{{\rm{FM}}}}}}{{\partial {\beta _{{\rm{FM}}}}}} = \varphi ({\beta _{{\rm{FM}}}}), $ | (22) |
| $ \frac{{\partial {\beta _{{\rm{FM}}}}}}{{\partial {\beta _{{\rm{SM}}}}}} = \frac{{3({\alpha _{4g}} - 1) + 2{\alpha _{3g}}{\beta _{{\rm{SM}}}}}}{{\sqrt {(9{\alpha _{4g}} - 5\alpha _{3g}^2 - 9)({\alpha _{4g}} - 1)} }}, $ | (23) |
| $ \frac{{\partial {\beta _{{\rm{SM}}}}}}{{\partial {\mu _g}}} = \frac{1}{{{\sigma _g}}}, $ | (24) |
| $ \frac{{\partial {\mu _g}}}{{\partial {{\mathit{\boldsymbol{\bar X}}}^{\rm{T}}}}} = \left[ {\frac{{\partial \bar g}}{{\partial {\mathit{\boldsymbol{X}}_1}}}\frac{{\partial \bar g}}{{\partial {X_2}}} \cdots \frac{{\partial \bar g}}{{\partial {X_n}}}} \right], $ | (25) |
| $ \frac{{\partial {\beta _{{\rm{SM}}}}}}{{\partial {\sigma _g}}} = - \frac{{{\mu _g}}}{{\sigma _g^2}}, $ | (26) |
| $ \frac{{\partial {\sigma _g}}}{{\partial {\rm{Var}} (\mathit{\boldsymbol{X}})}} = \frac{1}{{2{\sigma _g}}}\left[ {\frac{{\partial \bar g}}{{\partial \mathit{\boldsymbol{X}}}} \otimes \frac{{\partial \bar g}}{{\partial \mathit{\boldsymbol{X}}}}} \right], $ | (27) |
| $ \begin{array}{l} \frac{{\partial {\beta _{{\rm{FM}}}}}}{{\partial {\sigma _g}}} = \frac{{ - \left[ {\frac{{12{\alpha _{4g}}}}{{{\sigma _g}}}{\beta _{{\rm{SM}}}} + \frac{{3{\alpha _{3g}}}}{{{\sigma _g}}}(\beta _{{\rm{SM}}}^2 - 1)} \right]}}{{\sqrt {(9{\alpha _{{4_g}}} - 5\alpha _{{3_g}}^2 - 9)({\alpha _{4g}} - 1)} }} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}\frac{{\left[ {\left( { - \frac{{36{\alpha _{4g}}}}{{{\sigma _g}}} + \frac{{30\alpha _{3g}^2}}{{{\sigma _g}}}} \right)({\alpha _{4g}} - 1) - (9{\alpha _{4g}} - 5\alpha _{3g}^2 - 9)\frac{{4{\alpha _{4g}}}}{{{\sigma _g}}}} \right][3({\alpha _{4g}} - 1){\beta _{{\rm{SM}}}} + {\alpha _{3g}}(\beta _{{\rm{SM}}}^2 - 1)]}}{{\sqrt {{{(9{\alpha _{4g}} - 5\alpha _{3g}^2 - 9)}^3}{{({\alpha _{4g}} - 1)}^3}} }}. \end{array} $ | (28) |
为验证本文所提方法的准确性,以某柱塞泵为例进行仿真分析,其仿真参数为:dp= 0.016 7 m,Rp=0.030 65 m,P0=0 Pa,Pd=21×106Pa,γ=17.5°,μ=0.028 Pa·s,ω=157 rad/s,rs1=0.008 5 m,rs2=0.012 m,β1=0.261 7 rad,β2=2.006 rad,l0= 0.041 m,αw=2.686 4 rad,Rv1=0.024 4 m,Rv2= 0.029 6 m,Rv3=0.034 4 m,Rv4=0.036 7 m.
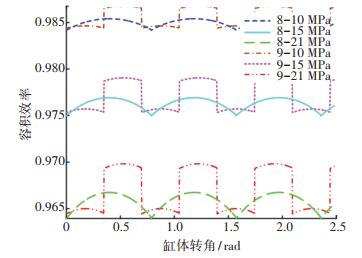
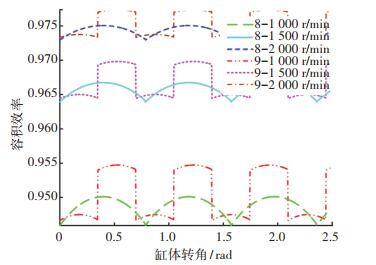
图 2和图 3分别为柱塞数为8和9时,在不同负载压力和不同转速下容积效率随瞬时转角变化的规律.从图中可以看出随着压力的增大,其泄漏量增加,容积效率下降;随着转速的升高,泵的流量增加,容积效率上升.
|
图 2 不同压力下容积效率变化曲线 Fig. 2 Volumetric efficiency variation curve under different pressures |
|
图 3 不同转速下容积效率变化曲线 Fig. 3 Volumetric efficiency variation curve under rotating speeds |
液压柱塞泵各运动副在运动过程中,其间隙的高度值随缸体旋转角度而瞬时变化的,且在不同工况下具有随机性;在设计过程中选取X=[δss δsp δpc δcv [ηv]]T为设计变量,其参数见表 1.
| 表 1 柱塞泵的相关参数 Tab. 1 Relative parameters of the piston pump |
Monte Carlo方法又称为计算机随机模拟法,是通过对随机变量反复的大量抽样,或产生随机数样本,对抽样结果进行统计分析,获得系统响应的统计规律. Monte Carlo方法在可靠性分析中具有通用性强、精度高等特点,但由于采用大量反复的抽样,工作量较大,在实际工程中很难应用,现阶段Monte Carlo方法通常作为标准验证其他方法准确性和有效性[20-22].
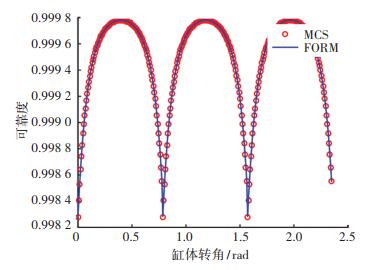
分别取柱塞数z为8和9时,利用Monte Carlo方法抽样108次和文中所提方法进行计算结果对比,得到的可靠度曲线如图 4和图 5所示.
|
图 4 柱塞个数为8时的可靠度变化曲线 Fig. 4 Reliability variation curve when the number of pistons is 8 |
|
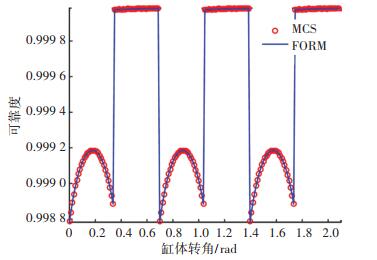
图 5 柱塞个数为9时的可靠度变化曲线 Fig. 5 Reliability variation curve when the number of pistons is 9 |
由图可知两种算法计算结果十分接近,验证了文中所提方法的准确性.基于容积效率的液压轴向柱塞泵可靠度随着缸体旋转角度呈周期性变化,当柱塞通过斜盘上止点时其可靠度最低.柱塞个数为8时其可靠度曲线波动相对较小,以缸体转角2π/8为周期变化;柱塞个数为9时其可靠度曲线波动相对较大,以缸体转角2π/9为周期变化,并当柱塞转角通过π/9时发生较大波动,但其整体可靠度水平高于柱塞个数为8时.
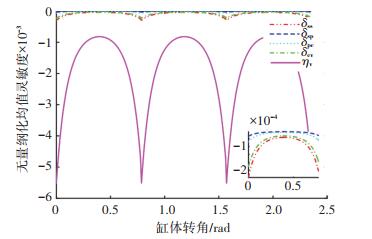
图 6和图 7为柱塞个数分别为8和9时的参数在均值点处无量纲化之后的灵敏度.从图中可以看出其整体变化趋势趋近于其可靠度变化趋势,各设计参数相对于可靠度负相关,即参数值越大,其可靠度越低.容许容积效率对可靠性影响最大,其次是滑靴与斜盘之间间隙δss和缸体与配流盘之间间隙δcv,柱塞与柱塞腔之间间隙δpc和滑靴与柱塞球铰接副之间间隙δsp对柱塞泵可靠度影响较小.
|
图 6 柱塞个数为8时的均值灵敏度变化曲线 Fig. 6 Mean sensitivity variation curve when the number of pistons is 8 |
|
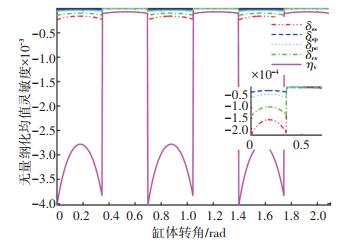
图 7 柱塞个数为9时的均值灵敏度变化曲线 Fig. 7 Mean sensitivity variation curve when the number of pistons is 9 |
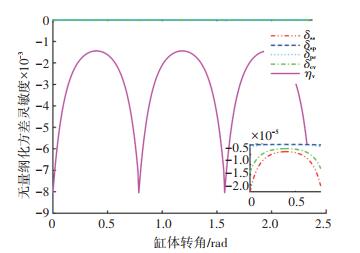
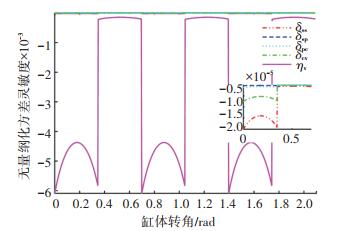
图 8和图 9为柱塞个数分别为8和9时的参数无量纲化方差灵敏度.从图中可以看出其整体变化趋势趋近于无量纲化均值灵敏度,各设计参数方差值相对于可靠度负相关,即方差值越大,其可靠度越低.容许容积效率方差值对可靠性影响最大,其次是滑靴与斜盘之间间隙δss和缸体与配流盘之间间隙δcv,柱塞与柱塞腔之间间隙δpc和滑靴与柱塞球铰接副之间间隙δsp影响较小.
|
图 8 柱塞个数为8时的方差灵敏度变化曲线 Fig. 8 Variance sensitivity variation curve when the number of pistons is 8 |
|
图 9 柱塞个数为9时的方差灵敏度变化曲线 Fig. 9 Variance sensitivity variation curve when the number of pistons is 9 |
1) 建立了基于容积效率的液压轴向柱塞泵四阶矩可靠性模型,并用Monte Carlo方法验证了该方法的准确性和合理性.
2) 对柱塞个数为8和9时进行分析,柱塞通过上止点位置时其可靠度最低,柱塞个数为9时其可靠度波动较大,但其整体可靠性水平优于8个柱塞.
3) 利用四阶矩理论建立了轴向柱塞泵可靠性灵敏度分析模型,通过各运动副间隙值和容许容积效率作为设计参数,对柱塞泵可靠度的影响程度进行分析.
4) 各运动副间隙值对可靠性影响程度中,滑靴与斜盘和缸体与配流盘之间间隙对可靠度影响较大,柱塞与柱塞腔和滑靴与柱塞球铰接副之间间隙对可靠度影响较小.
| [1] |
BERGADA J. M, KUMAR S, WATTON J. Axial piston pumps, new trends and development[M]. New York: Nova Science Publishers, 2017: 1.
|
| [2] |
HEON-SUL Jeong. A novel performance model given by the physical dimensions of hydraulic axial piston motors: model derivation[J]. Journal of Mechanical Science and Technology, 2007, 21(1): 83. DOI:10.1007/BF03161714 |
| [3] |
杨华勇, 张斌, 徐兵. 轴向柱塞泵/马达技术的发展演变[J]. 机械工程学报, 2008, 44(10): 1. YANG Huayong, ZHANG Bin, XU Bing. Development of axial piston pump/motor technology[J]. Chinese Journal of Mechanical Engineering, 2008, 44(10): 1. DOI:10.3321/j.issn:0577-6686.2008.10.001 |
| [4] |
HEON-SUL Jeong, HYOUNG-EUI Kim. A novel performance model given by the physical dimensions of hydraulic axial piston motors: experimental analysis[J]. Journal of Mechanical Science and Technology, 2007, 21(4): 630. DOI:10.1007/BF03026968 |
| [5] |
BERGADA J M, KUMAR S, DAVIES D L. A complete analysis of axial piston pump leakage and output flow ripples[J]. Applied Mathematical Modelling, 2011, 36(4): 1731. |
| [6] |
HALL, JASON S. Statistical analysis of multiple hydrostatic pump flow loss models[D]. Iowa: Iowa State University, 2014 https://www.zhangqiaokeyan.com/open-access_resources_thesis/0100022848361.html
|
| [7] |
郭卫东, 王占林. 斜盘式轴向柱塞泵实际流量的分析研究[J]. 北京航空航天大学学报, 1996, 22(2): 223. GUO Weidong, WANG Zhanlin. Analysis for the real flowrate of a swashplate axial piston pump[J]. Journal of Beijing University of Aeronautics and Astronautics, 1996, 22(2): 223. |
| [8] |
张义民. 机械可靠性设计的内涵与递进[J]. 机械工程学报, 2010, 46(14): 167. ZHANG Yimin. Connotation and development of mechanical reliability based design[J]. Chinese Journal of Mechanical Engineering, 2010, 46(14): 167. |
| [9] |
赵静一, 姚成玉. 我国液压可靠性技术概述[J]. 液压与气动, 2013(10): 1. ZHAO Jingyi, YAO Chengyu. Overview of China's hydraulic reliability technology[J]. Chinese Hydraulics & Pneumatics, 2013(10): 1. DOI:10.11832/j.issn.1000-4858.2013.10.001 |
| [10] |
ZHANG Yimin, LIU Qiaoling. Reliability-based design of automobile components[J]. Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering, 2002, 216(6): 455. DOI:10.1243/09544070260137390 |
| [11] |
张天霄.液压元件的可靠性设计和可靠性灵敏度分析[D].长春: 吉林大学, 2014 ZHANG Tianxiao. The reliability design and reliability sensitivity analysis of hydraulic components[D]. Changchun: Jilin University, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10183-1014267980.htm |
| [12] |
杨哲.基于柱塞泵振动特征的关键零件退化可靠性研究[D].秦皇岛: 燕山大学, 2018 YANG Zhe. Research on degradation reliability of key components based on vibration characteristics of the axial piston pump[D]. Qinhuangdao: Yanshan University, 2018 http://cdmd.cnki.com.cn/Article/CDMD-10216-1018877818.htm |
| [13] |
IVANTYSYNOVA M. A new approach to the design of sealing and bearing gaps of displacement machines[C]//Proceedings of the JFPS International Symposium on Fluid Power. Hamburg: JFPS, 1999: 45
|
| [14] |
刘俊.轴向柱塞泵滑靴副倾覆油膜特性研究[D].杭州: 浙江师范大学, 2019 LIU Jun. Study on the characteristics of oil film between slipper and swashplate in axial piston pump considering overturning[D]. Hangzhou: Zhejiang Normal University, 2019 http://d.wanfangdata.com.cn/thesis/Y1854677 |
| [15] |
WANG Xingjian, LIN Siru, WANG Shaoping, et al. Remaining useful life prediction based on the Wiener process for an aviation axial piston pump[J]. Chinese Journal of Aeronautics, 2016, 29(3): 779. DOI:10.1016/j.cja.2015.12.020 |
| [16] |
吕飞, 徐兵, 张军辉. 转速对EHA泵柱塞副柱塞位姿及泄漏量影响仿真分析[J]. 机械工程学报, 2018, 54(20): 123. LU Fei, XU Bing, ZHANG Junhui. Simulative analysis of piston posture and piston/cylinder interface leakage of EHA pumps by the influence of rotating speed[J]. Chinese Journal of Mechanical Engineering, 2018, 54(20): 123. |
| [17] |
XU Bing, ZHANG Junhui, YANG Huayong, et al. Investigation on the radial micro-motion about piston ofaxial piston pump[J]. Chinese Journal of MechanicalEngineering, 2013, 26(2): 325. |
| [18] |
KIM J K, JUNG J Y. Measurement of fluid film thickness on the valve plate in oil hydraulic axial piston pumps (I)-bearing pad effects-[J]. Journal of Mechanical Science and Technology, 2003, 17(2): 246. DOI:10.1007/BF02984396 |
| [19] |
液压轴向柱塞泵: JB/T 7043-2006[S].北京: 机械工业出版社, 2006 Hydraulic axial piston pumps: JB/T 7043-2006[S]. Beijing: Mechanical Industry Press, 2006 |
| [20] |
MELCHERS R E, BECK A T. Structural reliability analysis and prediction[M]. Third Edition. New York: Wiley, 2018.
|
| [21] |
ALESSANDRO Birolini. Reliability engineering: theory and practice[M]. 8th edition. Berlin: Springer, 2017.
|
| [22] |
WANG Wei, ZHANG Yimin, LI Changyou. Dynamic reliability analysis of linear guides in positioning precision[J]. Mechanism & Machine Theory, 2017, 116: 451. |
 2020, Vol. 52
2020, Vol. 52


