2. 浙江无限元组合结构桥梁设计有限公司,杭州 310000;
3. 浙江省交通规划设计研究院,杭州 310000
2. Zhejiang Infinite Element Composite Bridge Design Co., Ltd., Hangzhou 310000, China;
3. Zhejiang Provincial Institute of Communications Planning, Design & Research, Hangzhou 310000, China
悬索桥由于具有受力性能合理、抗震性能较好、大跨轻盈的特点,是特大跨径桥梁的首选桥型.当桥梁跨径超过1 200 m时,悬索桥被认为是最具有竞争力的桥型方案.随着跨径的增大,悬索桥的优势就越明显[1].主缆是悬索桥至关重要的受力构件.悬索桥施工质量的指标很大程度上要考虑桥梁施工完成后的实际主缆线形与设计主缆线形是否一致[2-3].对于特大跨径悬索桥,主缆的安全系数要求不小于2.5,这必然要对悬索桥进行精确的求解.目前的悬索桥计算分析方法已经比较成熟,但由于计算模型在假设时精度达不到要求,所以在处理一些局部受力问题时,悬索桥的计算内力和线形与实际受力与变形有一定偏差[4].悬索桥的索鞍起到了转向或分散主缆的作用,并限制了主缆的变形.对于悬索桥的成桥阶段,主缆在进出鞍座处与鞍座是处于相切状态的,两者在切点间是紧密接触的,主缆在鞍座内不能有任何的相对滑移.而在施工阶段,考虑到施工的实际情况,主缆与鞍座接触的切点是不断变化位置的,主缆与鞍座间存在着接触非线性[5].在进行悬索桥计算时,如果不能准确考虑主缆与鞍座间复杂的接触关系,主缆和吊索的下料长度将会减小,主缆架设控制标高的精度也会相应降低.
基于有限单元法的悬索桥的施工分析计算中,大多数方法是通过利用成桥理论点来建模分析.但这不能确保主缆与鞍座处于相切状态,从而造成了主缆与鞍座出现相交或分离[5].为了充分考虑鞍座对主缆的约束作用,文献[6]采用杆单元来模拟.桥塔顶部采用两个杆单元模拟,通过主从约束的方式与鞍座杆单元连接.通过修改杆单元的节点坐标,来模拟鞍座的顶推作用,改变鞍座杆单元的无应力长度,从而使得主缆在脱离点的斜率等于鞍槽曲线上此点处的斜率,进而得到切点的位置.文献[7]则采用4个梁单元来模拟鞍座及其顶推作用,用一个直杆代替散索鞍,该方法与文献[6]的方法实质是相同的.上述方法在修正悬空段主缆的无应力长度时,未考虑切点相对于鞍座位置的变化,使得悬索桥求解精度较低.另外,跨内主缆线形由假定的切点坐标迭代求出后,还必须验证主缆与鞍座是否相切,否则需重新迭代.因此,该方法计算效率也不高.
有形状的索鞍在其表面上包裹并支撑主缆,在施工过程中,主缆与索鞍间的切点位置在一直变化着.在悬索桥计算分析中,由理论顶点假设推导出的主缆线形而得到的考虑索鞍曲线修正后实际的主缆形状是比较繁琐的,其计算关键在于找到主缆与索鞍间的相切点.目前常用的解析算法是求解八元非线性方程组.即借助悬链线公式得到4个几何关系式、利用力平衡条件得到两个平衡方程、依据切点和索鞍圆心的距离关系得到两个公式,再加上一些工程经验性的约束条件后通过数值分析或Mathcad等软件进行计算.多位学者对此均有论述[8-10],但该方法计算效率并不高.另外,有学者采用通用有限元软件建立主缆与索鞍的接触关系进行数值仿真分析[11-15],也有部分学者考虑了主缆与鞍座之间的摩擦来提高计算精度[16-19].上述方法在精度方面虽然能满足工程需求,但计算比解析法更困难,效率更低.
目前的索鞍曲线修正计算分析理论推导繁琐、难以操作、效率较低.所以在实际工程中,索鞍曲线修正的影响基本只在悬索桥的成桥状态下考虑.但是为了满足人们建造更大跨径悬索桥的需求,仅在成桥状态进行索鞍修正无法满足施工对线形的控制要求[20].因此,推导一种便于计算、效率更高的索鞍曲线修正算法是十分有必要的.不仅可以实时进行索鞍曲线修正,还可为大跨径悬索桥的施工控制提供一定的参考.为此,本文从几何关系角度对索鞍曲线修正算法进行推导,并借助牛顿-拉斐森迭代法,提供了一种可行的数值求解方法.
1 主缆索段力学分析现代悬索桥主缆一般由钢丝集束形成,且其线形平顺,在转折处曲率半径很大,因此相比其轴向抗拉刚度,抗弯刚度很小,具有很强的柔性索结构特征.本文在推导悬索桥主缆的算法时,对主缆作3项前提假设:1)主缆是理想柔性的索,只承受轴向拉力,不承受轴向压力和弯矩;2)在设计悬索桥时通常会给主缆拉应力设置较大的安全系数,主缆在施工和使用过程中,材料均不会达到塑性阶段,因此其符合胡克定律,是线弹性的;3)主缆横截面积在外荷载作用下变化量微小,不予考虑.
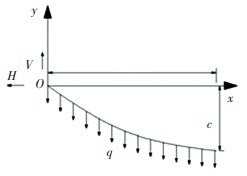
将一段只受自重的缆索分割出来,如图 1所示,H和V分别表示主缆的水平分力和竖向分力,q为缆索沿弧长均布的自重荷载,l为主缆在x轴的投影长度,c为主缆在y轴的投影长度.
|
图 1 悬链线缆索示意图 Fig. 1 Schematic diagram of the catenary cable |
显然,可以得到主缆在自重作用下的曲线形状为悬链线[8],具体表达式为
| $ y = \frac{H}{q} {\rm{ch }}\left( {\frac{{qx}}{H} - \alpha } \right) - {\alpha _1}. $ | (1) |
其中,各参数表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\alpha _1} = \frac{H}{q} {\rm{ch}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha ,}\\ {\alpha = {\rm{s}}{{\rm{h}}^{ - 1}}\frac{{\beta C/l}}{{ {\rm{sh}}\beta }} + \beta ,}\\ {\beta = \frac{{ql}}{{2H}}.} \end{array}} \right. $ | (2) |
对于原点处H、V已知,则有
| $ {y^\prime }(0) = {f^\prime }(0) = {\rm{sh}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha = \frac{V}{H} \Rightarrow \alpha = {\rm{sh}}{{\kern 1pt} ^{ - 1}}\frac{V}{H}. $ | (3) |
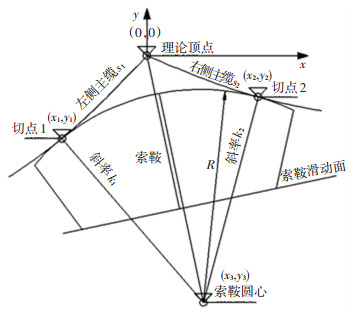
索鞍处的主缆线形如图 2所示,x为水平向,y为竖向.整体分析时为方便计算,会假设一个虚拟的主缆交点,即图中的理论顶点;本文将局部坐标系原点建立在理论顶点上,其坐标为(0, 0),左侧主缆与索鞍的切点标为切点1,其局部坐标为(x1, y1),右侧主缆与索鞍的切点标为切点2,其局部坐标为(x2, y2),索鞍与主缆接触面为圆弧,索鞍圆心局部坐标为(x3, y3),半径为R.另外,x1、x2与y1、y2的关系满足悬链线式(1),为推导过程简洁,用y=f(x)来表示.
|
图 2 索鞍与主缆关系示意图 Fig. 2 Schematic diagram of relationship between cable saddle and main cable |
根据左侧主缆与索鞍相切可以得到,切点1与索鞍圆心的连线斜率k1表达式为
| $ {k_1} = - \frac{1}{{{f^\prime }({x_1})}}. $ | (4) |
根据右侧主缆与索鞍相切可以得到,切点2与索鞍圆心的连线斜率k2表达式为
| $ {k_2} = - \frac{1}{{{f^\prime }({x_2})}}. $ | (5) |
其中k为理论切点位置索(索鞍)的切线斜率.
切点1与切点2同在以索鞍圆心为圆心,半径为R的圆上,根据几何关系, 可得
| $ \left\{ {\begin{array}{*{20}{l}} {{x_3} = {x_1} + \frac{{{f_1}^\prime ({x_1}) \cdot R}}{{\sqrt {1 + {f_1}^{\prime 2}({x_1})} }} = {x_2} + \frac{{{f_2}^\prime ({x_2}) \cdot R}}{{\sqrt {1 + {f_2}^{\prime 2}({x_1})} }},}\\ {{y_3} = {y_1} - \frac{R}{{\sqrt {1 + {f_1}^{\prime 2}({x_1})} }} = {y_2} - \frac{R}{{\sqrt {1 + {f_2}^{\prime 2}({x_1})} }}.} \end{array}} \right. $ | (6) |
左侧主缆方程为
| $ {f_1}(x) = \frac{{{H_1}}}{{{q_1}}} {\rm{ch}}\left( {\frac{{{q_1}x}}{{{H_1}}} + {\alpha _1}} \right) - {\alpha _{11}}. $ | (7) |
右侧主缆方程为
| $ {f_2}(x) = \frac{{{H_2}}}{{{q_2}}} {\rm{ch}} \left( {\frac{{{q_2}x}}{{{H_2}}} - {\alpha _2}} \right) - {\alpha _{21}}. $ | (8) |
其中,式(7)、(8)中的参数表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\alpha _1} = {\rm{sh}}{{\kern 1pt} ^{ - 1}}\frac{{{V_1}}}{{{H_1}}},}\\ {{\alpha _{11}} = \frac{{{H_1}}}{{{q_1}}} {\rm{ch}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _1},}\\ {{\alpha _2} = {\rm{sh}}{{\kern 1pt} ^{ - 1}}\frac{{{V_2}}}{{{H_2}}},}\\ {{\alpha _{21}} = \frac{{{H_2}}}{{{q_2}}} {\rm{ch}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _2}.} \end{array}} \right. $ | (9) |
另外,可以得到
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{f_1}^\prime ({x_1}) = {\rm{sh}} \left( {\frac{{{q_1}{x_1}}}{{{H_1}}} + {\alpha _1}} \right),}\\ {{f_2}^\prime ({x_2}) = {\rm{sh}} \left( {\frac{{{q_2}{x_2}}}{{{H_2}}} - {\alpha _2}} \right),} \end{array}\\ \begin{array}{*{20}{l}} {{y_1} = \frac{{{H_1}}}{{{q_1}}} {\rm{ch}} \left( {\frac{{{q_1}{x_1}}}{{{H_1}}} + {\alpha _1}} \right) - {\alpha _{11}},}\\ {{y_2} = \frac{{{H_2}}}{{{q_2}}} {\rm{ch}} \left( {\frac{{{q_2}{x_2}}}{{{H_2}}} - {\alpha _2}} \right) - {\alpha _{21}}.} \end{array} \end{array} \right. $ | (10) |
将f1′(x1)、f2′(x2)、y1、y2代入式(6)后得到求解主缆与索鞍切点的二元非线性方程组为
| $ \left\{ \begin{array}{l} {x_1} + \frac{{ {\rm{sh}} \left( {\frac{{{q_1}{x_1}}}{{{H_1}}} + {\alpha _1}} \right) \cdot R}}{{ {\rm{ch}} \left( {\frac{{{q_1}{x_1}}}{{{H_1}}} + {\alpha _1}} \right)}} = {x_2} + \frac{{ {\rm{sh}} \left( {\frac{{{q_2}{x_2}}}{{{H_2}}} - {\alpha _2}} \right) \cdot R}}{{ {\rm{ch}} \left( {\frac{{{q_2}{x_2}}}{{{H_2}}} - {\alpha _2}} \right)}},\\ \frac{{{H_1}}}{{{q_1}}} {\rm{ch}} \left( {\frac{{{q_1}{x_1}}}{{{H_1}}} + {\alpha _1}} \right) - {\alpha _{11}} - \frac{R}{{ {\rm{ch}} \left( {\frac{{{q_1}{x_1}}}{{{H_1}}} + {\alpha _1}} \right)}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{H_2}}}{{{q_2}}} {\rm{ch}}\left( { \frac{{{q_2}{x_2}}}{{{H_2}}} - {\alpha _2}} \right) - {\alpha _{21}} - \frac{R}{{ {\rm{ch}} \left( {\frac{{{q_2}{x_2}}}{{{H_2}}} - {\alpha _2}} \right)}}. \end{array} \right. $ | (11) |
通过牛顿-拉斐森迭代法[21]可对本文所述二元非线性方程组(11)进行数值求解,令
| $ \left\{ \begin{array}{l} {g_1}({x_1},{x_2}) = {x_1} + \frac{{ {\rm{sh}} \left( {\frac{{{q_1}{x_1}}}{{{H_1}}} + {\alpha _1}} \right) \cdot R}}{{ {\rm{ch}} \left( {\frac{{{q_1}{x_1}}}{{{H_1}}} + {\alpha _1}} \right)}} - {x_2} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{ {\rm{sh}} \left( {\frac{{{q_2}{x_2}}}{{{H_2}}} - {\alpha _2}} \right) \cdot R}}{{ {\rm{ch}} \left( {\frac{{{q_2}{x_2}}}{{{H_2}}} - {\alpha _2}} \right)}},\\ {g_2}({x_1},{x_2}) = \frac{{{H_1}}}{{{q_1}}} {\rm{ch}} \left( {\frac{{{q_1}{x_1}}}{{{H_1}}} + {\alpha _1}} \right) - {\alpha _{11}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{R}{{ ch (\frac{{{q_1}{x_1}}}{{{H_1}}} + {\alpha _1})}} - \\ \left[ {\frac{{{H_2}}}{{{q_2}}} {\rm{ch}} \left( {\frac{{{q_2}{x_2}}}{{{H_2}}} - {\alpha _2}} \right) - {\alpha _{21}} - \frac{R}{{ {\rm{ch}} \left( {\frac{{{q_2}{x_2}}}{{{H_2}}} - {\alpha _2}} \right)}}} \right]. \end{array} \right. $ | (12) |
再令
| $ {\mathit{\boldsymbol{X}}_i} = \left[ {\begin{array}{*{20}{c}} {{x_{1i}}}\\ {{x_{2i}}} \end{array}} \right],{\mathit{\boldsymbol{G}}_i} = \left[ {\begin{array}{*{20}{c}} {{g_1}({x_{1i}},{x_{2i}})}\\ {{g_2}({x_{1i}},{x_{2i}})} \end{array}} \right],{\mathit{\boldsymbol{A}}_i} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {g_1}}}{{\partial {x_{1i}}}}}&{\frac{{\partial {g_1}}}{{\partial {x_{2i}}}}}\\ {\frac{{\partial {g_2}}}{{\partial {x_{1i}}}}}&{\frac{{\partial {g_2}}}{{\partial {x_{2i}}}}} \end{array}} \right]. $ |
其中Ai为雅克比矩阵,矩阵各元素表达式为
| $ \left\{ \begin{array}{l} \frac{{\partial {g_1}}}{{\partial {x_1}}} = 1 + \frac{{R{q_1}}}{{{H_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{c}}{{\rm{h}}^2}\left( {\frac{{{q_1}{x_1}}}{{{H_1}}} + {\alpha _1}} \right)}},\\ \frac{{\partial {g_1}}}{{\partial {x_2}}} = - \left[ {\begin{array}{*{20}{c}} {1 + \frac{{R{q_2}}}{{{H_2}{\kern 1pt} {\kern 1pt} {\rm{ch}}{{\kern 1pt} ^2}\left( {\frac{{{q_2}{x_2}}}{{{H_2}}} - {\alpha _2}} \right)}} } \end{array}} \right],\\ \frac{{\partial {g_2}}}{{\partial {x_1}}} = {\rm{sh}} \left( {\frac{{{q_1}{x_1}}}{{{H_1}}} + {\alpha _1}} \right) \cdot \left[ {\begin{array}{*{20}{c}} {1 + \frac{{R{q_1}}}{{{H_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ch}}{{\kern 1pt} ^2}\left( {\frac{{{q_1}{x_1}}}{{{H_1}}} + {\alpha _1}} \right)}}} \end{array}} \right],\\ \frac{{\partial {g_2}}}{{\partial {x_2}}} = - {\rm{sh}} \left( {\frac{{{q_2}{x_2}}}{{{H_2}}} - {\alpha _2}} \right) \cdot \left[ {\begin{array}{*{20}{c}} {1 + \frac{{R{q_2}}}{{{H_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ch}}{{\kern 1pt} ^2}\left( {\frac{{{q_2}{x_2}}}{{{H_2}}} - {\alpha _2}} \right)}}} \end{array}} \right]. \end{array} \right. $ | (13) |
根据牛顿-拉斐森迭代,则有
| $ {\mathit{\boldsymbol{X}}_{i + 1}} = {\mathit{\boldsymbol{X}}_i} - {\mathit{\boldsymbol{A}}_i}^{ - 1}{\mathit{\boldsymbol{G}}_i}. $ | (14) |
取切点1、切点2的初始x坐标代入牛顿-拉斐森迭代,得到x1、x2的数值解,y1、y2代入前文提到的悬链线方程即可得到.值得注意的是,传统的八元非线性方程组的初始值选取原则较为繁琐,而本文算法对初始值的选取基本没有要求.
3 算例验证根据前述理论推导,索鞍曲线修正算法由传统的八元非线性方程组(传统方法)简化为二元非线性方程组(本文方法),可较为方便地将其嵌入有二次开发功能的有限元分析软件, 如:TDV、Ansys、Abaqus等,也可通过MATLAB等编程语言方便地进行求解.
本文分别选取主索鞍与散索鞍两个算例,对其正确性与计算效率进行验证.需要说明的是,表中左切点坐标(x1, y1)、右切点坐标(x2, y2)、索鞍圆心坐标(x3, y3)均为整体坐标系坐标.
3.1 主索鞍分析某悬索桥的其中一个主索鞍理论顶点坐标为(230.000 m, 131.425 m),主缆面积A1=A2=0.408 973 m2,主缆自重集度为q1=q2=33 kN/m,弹性模量E=198 GPa.索鞍半径R=6 m,索鞍左右两侧的主缆索力水平分量H1=H2=189 500 kN,V1=90 622.7 kN,V2=73 504.1 kN.
通过编程,对传统方法与本文方法(第2节的理论推导)进行对比,初始取值见表 1,计算过程见表 2,计算结果见表 3.
| 表 1 主索鞍曲线修正初始取值 Tab. 1 Initial values of curve correction of main cable saddle |
| 表 2 主索鞍曲线修正计算过程 Tab. 2 Calculation process of curve correction of main cable saddle |
| 表 3 主索鞍位置及主缆曲线计算结果 Tab. 3 Calculation results of main cable saddle position and main cable curve |
某悬索桥的其中一个散索鞍理论顶点坐标为(0 m, 54 m),主缆面积A1=A2=0.408 973 m2,主缆自重q1=q2=33 kN/m,弹性模量E=198 GPa.索鞍半径R=6 m,索鞍左右两侧的主缆索力水平分量H1=H2=189 500 kN,V1=137 557 kN,V2=-41 804.3 kN.
通过编程,对传统方法与本文方法(第2节的理论推导)进行对比,初始取值见表 4,计算过程见表 5,结果见表 6.
| 表 4 散索鞍曲线修正初始取值 Tab. 4 Initial values of curve correction of loose cable saddle m |
| 表 5 散索鞍曲线修正计算过程 Tab. 5 Calculation process of curve correction of loose cable saddle |
| 表 6 散索鞍位置及主缆曲线计算结果 Tab. 6 Calculation results of loose cable saddle position and main cable curve |
从上述两个算例的计算结果和计算效率对比可知,本文提出的二元非线性方程组求解方法与目前普遍采用的八元非线性方程组求解方法计算结果在0.01 mm的数量级上可以保持一致性,对于工程应用可以认为两种方法的计算结果是没有差别的.计算效率方面,本文提出的方法迭代次数减少了50%,计算耗时仅为目前普遍采用方法的10%.更重要的是,在设置初始参数时,本文提出的方法要简便很多,只需要设置x1和x2两个参数即可,且没有特殊要求.一般情况下,为便于编写程序可以直接设置初始x1=x3-R/2,x2=x3+R/2,即可很快迭代收敛.然而,参考文献[8]中的推导过程表明,目前普遍采用方法,需要设置8个初始参数,这8个参数中只有x1、x2较易设置,其余6个参数均需有一定的经验或者经过数次试算方可获得较好的计算结果,这给该算法实现程序自动进行索鞍曲线修正计算带来很大困难.由此说明,本文所提出方法更为方便,大大提高了计算效率,且精度可满足要求.
4 结论1) 根据主缆与索鞍的几何关系,推导了索鞍处主缆曲线的修正计算方法.相比于传统算法,减少了6个方程与6个初始输入参数,表达形式更明确,物理含义更清晰.
2) 利用牛顿-拉菲森迭代法,对所得二元非线性方程组进行求解.其中,关于输入参数的初始值设置没有严格要求,具有很强的可操作性.
3) 针对常见的主索鞍与散索鞍结构,相比于传统算法,迭代次数减少50%,计算时间不足10%,大大提高了计算效率,且精度可满足要求.
| [1] |
雷俊卿. 大跨度桥结构理论与应用[M]. 北京: 北京交通大学出版社, 2007. LEI Junqing. Long span bridge structure theory and application[M]. Beijing: Beijing Jiaotong University Press, 2007. |
| [2] |
肖海波, 俞亚南, 高庆丰. 自锚式悬索桥主缆成桥线形分析[J]. 浙江大学学报(工学版), 2004, 38(11): 1470. XIAO Haibo, YU Yanan, GAO Qingfeng. Analysis of finished main cable of self-anchored suspension bridge[J]. Journal of Zhejiang University (Engineering Science), 2004, 38(11): 1470. |
| [3] |
秦凤江, 周绪红, 梁博文, 等. 大跨度自锚式悬索桥主梁钢-混结合段模型试验[J]. 中国公路学报, 2018, 31(9): 56. QIN Fengjiang, ZHOU Xuhong, LIANG Bowen, et al. Experiment on steel-concrete joint of hybrid girder of a long-span self-anchored suspension bridge[J]. China Journal of Highway and Transport, 2018, 31(9): 56. |
| [4] |
齐东春.大跨径悬索桥主缆精细化计算研究[D].成都: 西南交通大学, 2012 QI Dongchun. A refined analysis method of main cable for long-span suspension bridge[D]. Chengdu: Southwest Jiaotong University, 2012 |
| [5] |
齐东春, 沈锐利, 陈卫国, 等. 悬索桥结构分析中鞍座单元的研究及应用[J]. 桥梁建设, 2011(1): 35. QI Dongchun, SHEN Ruili, CHEN Weiguo, et al. Research and application of saddle element in structural analysis of suspension bridge[J]. Bridge Construction, 2011(1): 35. |
| [6] |
潘永仁.悬索桥的几何非线性静力分析及工程控制[D].上海: 同济大学, 1996 PAN Yongren. Geometric nonlinear static analysis and engineering control of suspension bridges[D]. Shanghai: Tongji University, 1996 |
| [7] |
徐君兰. 大跨度桥梁施工控制[M]. 北京: 人民交通出版社, 2000. XU Junlan. Construction control of long-span bridges[M]. Beijing: China Communications Press, 2000. |
| [8] |
邵旭东, 程翔云, 李立峰. 桥梁设计与计算[M]. 北京: 人民交通出版社, 2007. SHAO Xudong, CHENG Xiangyun, LI Lifeng. Bridge design & computation[M]. Beijing: China Communications Press, 2007. |
| [9] |
唐茂林, 沈锐利, 强士中. 悬索桥索鞍位置设计[J]. 公路交通科技, 2001, 18(4): 55. TANG Maolin, SHEN Ruili, QIANG Shizhong. Design of suspension bridge saddle's position[J]. Journal of Highway and Transportation Research and Development, 2001, 18(4): 55. |
| [10] |
齐东春, 沈锐利, 郭永成. 悬索桥空间缆索线形的解析计算方法[J]. 武汉理工大学学报, 2013, 35(12): 109. QI Dongchun, SHEN Ruili, GUO Yongcheng. Analytical calculation method of main cable shape-finding of suspension bridge with spatial cables[J]. Journal of Wuhan University of Technology, 2013, 35(12): 109. |
| [11] |
柴生波, 肖汝诚, 王秀兰, 等. 多塔悬索桥主缆与鞍座抗滑解析计算方法[J]. 中国公路学报, 2016, 29(4): 59. CHAI Shengbo, XIAO Rucheng, WANG Xiulan, et al. Analytical method for calculating anti-slip safety factor between main cable and saddle in multi-tower suspension bridge[J]. China Journal of Highway and Transport, 2016, 29(4): 59. |
| [12] |
严琨, 沈锐利. 基于细长梁单元的悬索桥主缆线形分析[J]. 计算力学学报, 2016, 33(3): 381. YAN Kun, SHEN Ruili. Study on main cable shape of suspension bridge based on slender beam element[J]. Chinese Journal of Computational Mechanics, 2016, 33(3): 381. |
| [13] |
张永水, 吴章旭, 冯伟. 空间索面悬索桥空缆线形分析[J]. 重庆交通大学学报(自然科学版), 2017, 36(2): 7. ZHANG Yongshui, WU Zhangxu, FENG Wei. Hollow cable shape analysis of suspension bridge with spatial cable plane[J]. Journal of Chongqing Jiaotong University (Natural Science), 2017, 36(2): 7. |
| [14] |
韩旭辉, 袁阳光, 陈安洋, 等. 自锚式悬索桥主缆下料长度精细化计算[J]. 重庆交通大学学报(自然科学版), 2014, 33(5): 13. HAN Xuhui, YUAN Yangguang, CHEN Anyang, et al. A fine calculation method for the main cable fabrication length of self-anchored suspension bridge[J]. Journal of Chongqing Jiaotong University (Natural Science), 2014, 33(5): 13. |
| [15] |
端茂军, 李建慧, 索小灿, 等. 混凝土自锚式悬索桥鞍座的精细化模拟方法[J]. 南京工业大学学报(自然科学版), 2016, 38(6): 112. DUAN Maojun, LI Jianhui, SUO Xiaocan, et al. Refined analysis method of saddle for self-anchored concrete suspension bridge[J]. Journal of Nanjing Technology University (Natural Science), 2016, 38(6): 112. |
| [16] |
张清华, 李乔. 悬索桥主缆与鞍座间摩擦特性试验研究[J]. 土木工程学报, 2013, 46(4): 85. ZHANG Qinghua, LI Qiao. Study on cable-saddle frictional characteristics of long-span suspension bridges[J]. China Civil Engineering Journal, 2013, 46(4): 85. |
| [17] |
张清华, 李乔, 周凌远. 悬索桥主缆与鞍座摩擦特性理论分析方法[J]. 中国公路学报, 2013, 27(1): 44. ZHANG Qinghua, LI Qiao, ZHOU Lingyuan. Theoretical analysis of cable-saddle friction characteristics for suspension bridges[J]. China Journal of Highway and Transport, 2013, 27(1): 44. |
| [18] |
贺拴海, 陈英昊, 李源. 考虑摩阻力影响的悬索桥索鞍精确算法[J]. 长安大学学报(自然科学版), 2019, 39(2): 61. HE Shuanhai, CHEN Yinghao, LI Yuan. Exact algorithm for cable saddle of suspension bridge influences by frictional resistance[J]. Journal of Chang'an University (Natural Science Edition), 2019, 39(2): 61. |
| [19] |
王路, 沈锐利, 白伦华, 等. 悬索桥主缆与索鞍间滑移行为及力学特征试验[J]. 中国公路学报, 2018, 31(9): 79. WANG Lu, SHEN Ruili, BAI Lunhua, et al. Test for slip behavior and mechanical characteristics between main cable and saddle in suspension bridges[J]. China Journal of Highway and Transport, 2018, 31(9): 79. |
| [20] |
唐茂林.大跨度悬索桥空间几何非线性分析与软件开发[D].成都: 西南交通大学, 2003 TANG Maolin. 3D geometric nonlinear analysis of long-span suspension bridge and its software development[D]. Chengdu: Southwest Jiaotong University, 2003 |
| [21] |
王邵锐, 周志祥, 高燕梅, 等. 悬索桥索鞍预偏量的牛顿-拉斐森算法[J]. 中国公路学报, 2016, 29(1): 82. WANG Shaorui, ZHOU Zhixiang, GAO Yanmei, et al. Newton-Raphson algorithm for pre-offsetting of cable saddle on suspension bridge[J]. China Journal of Highway and Transport, 2016, 29(1): 82. |
 2020, Vol. 52
2020, Vol. 52


