2. 四川藏区高速公路有限责任公司,成都 610000;
3. 道路工程四川省重点实验室,成都 610031
2. Sichuan Tibet Expressway Co., Ltd., Chengdu 610000, China;
3. Key Laboratory of Highway Engineering of Sichuan Province, Chengdu 610031, China
目前,基于温度应力的计算方法已开始广泛用于沥青路面的服役性能研究,例如MEPDG设计方法[1].国内外学者也对沥青路面温度应力和临界开裂温度的计算展开了大量的研究.文献[2]证明了时温等效原理可充分表征低温条件下沥青混凝土的刚度与时间、温度相关的特性并初步提出了沥青混凝土的温度应力计算模型;文献[3]利用BBR试验和间接拉伸试验分别计算了沥青混合料的温度应力并进行了比较;文献[4]通过间接拉伸试验和线收缩系数试验提出了一种沥青混合料低温临界开裂温度的确定方法.但这些研究多集中于沥青混合料温度应力的计算,对于沥青胶结料温度应力的计算则鲜有报道.众所周知,沥青混合料主要由沥青和集料两部分组成.而根据美国SHRP计划的研究成果,在沥青路面的温度裂缝中,沥青的贡献率为87%[5].
《公路沥青路面设计规范》(JTG D50—2017)[6]增加了低温临界开裂温度作为沥青的低温性能评价指标,但并未具体说明临界开裂温度的计算方法.目前普遍采用弯曲梁流变试验和直接拉伸试验来获得沥青的低温临界开裂温度,通过BBR试验获得沥青的蠕变柔量D(t),利用数学转换得到松弛模量E(t),最后解卷积积分得到温度应力σ(t)和相应的低温临界开裂温度TCR.尽管这种方法被广泛使用,但其存在一定局限性:温度应力计算过程较为繁琐且将D(t)转化为E(t)这一步骤较为复杂.鉴于此,本文基于Laplace变换探索了一种更简洁的沥青胶结料温度应力及相应低温临界开裂温度的计算方法,并利用相关性分析和实测路表温度变化数据对计算方法予以验证.
1 材料与试验4种70#基质沥青分别为中海油70#,中石化金陵分公司70#,国产昆仑70#和广东茂名70#,PG分级均为64-22.为方便文章后面表述,用70#-1表示第1类70#基质沥青,其他以此类推.
为模拟实际路面经长期老化后的沥青,对4种70#基质沥青分别进行旋转薄膜老化(RTFO)和压力箱老化(PAV),并按照ASTM D6648-08[7]对老化后的沥青进行BBR试验. BBR试验的测试温度和低温养护温度为沥青低温等级最低温度以上10 ℃,本次试验所采用的4种70#基质沥青的PG低温等级均为-22,低温连续分级温度分别为-27.6、-23.9、-24.7、-25.5 ℃,因此本次试验共设置了两个试验温度,分别为-18 ℃(在沥青低温等级以上4 ℃)和-12 ℃(在沥青低温等级以上10 ℃),用于计算沥青胶结料的温度应力和低温临界开裂温度.对于每种沥青胶结料,浇筑3根(127±2)mm×(12.7±0.05)mm× (6.35±0.05)mm小梁作为平行试件,采用美国Cannon仪器公司生产的弯曲梁流变仪分别测量每个试样低温恒温养护1 h后在-18 ℃和-12 ℃两个试验温度下的劲度模量S和劲度模量变化率m.
2 计算方法 2.1 Hopkins & Hamming算法和CAM模型两步计算法Hills和Brien假设路面为一无限长的受约束条带,采用准弹性梁的力学模型提出了著名的路面温度应力近似计算公式[8]:
| $ \sigma (v) \approx \alpha \sum\limits_{{T_{\rm{s}}}}^{{T_{\rm{f}}}} S (t,T)\Delta T. $ | (1) |
式中:σ(v)为降温速率v下的温度应力,MPa;α为线收缩系数,℃-1;Ts、Tf分别为降温过程中的初始温度和终止温度,℃;ΔT=Ts-Tf为降温过程中的温度变化,℃;S(t, T)为随时间t和温度T变化的劲度模量,MPa.
然而,此温度应力计算公式中采用的劲度模量S(t, T)无法表征出沥青胶结料作为典型粘弹性材料的应力松弛特性.参考AASHTO R49-09[9],采用松弛模量代替公式中的劲度模量,得到温度应力计算公式为
| $ \sigma (\xi ) = E(\xi - {\xi ^\prime })\varepsilon . $ | (2) |
其中:σ(ξ)为时刻ξ下的温度应力,MPa;E(ξ-ξ′)为时刻ξ-ξ′下的松弛模量,MPa;ε为环境温度下降时的收缩应变;α为线收缩系数,取1.7×10-4 ℃-1[9];ΔT为降温过程中的温度变化,℃.
通过BBR试验可以获得沥青胶结料的蠕变柔量为
| $ S(t) = \frac{1}{{D(t)}} = \frac{\sigma }{{\varepsilon (t)}}. $ | (3) |
式中:S(t)为蠕变劲度,MPa;D(t)为蠕变柔量,MPa-1;σ为梁的弯曲应力,MPa;ε(t)为梁随时间t变化的应变.
Ferry等的研究结果表明,可将粘弹性材料的松弛模量和蠕变柔量通过卷积积分相关联[10],即
| $ t = \int\limits_0^t E (t - \tau )D(\tau ){\rm{d}}\tau = \int\limits_0^t E (\tau )D(t - \tau ){\rm{d}}\tau . $ | (4) |
其中:E为松弛模量,MPa;D为蠕变柔量,MPa-1.
一般采用Hopkins & Hamming算法[11]解上面的卷积积分.为计算温度应力,首先要获得沥青胶结料的松弛模量主曲线.通过CAM数学模型对松弛模量数据进行拟合[12],即
| $ E(t) = {E_{\rm{g}}}{\left( {1 + {{(\frac{t}{\lambda })}^\beta }} \right)^{ - \frac{k}{\beta }}}. $ | (5) |
其中:Eg为玻璃态模量,对于本文的沥青胶结料都取3 GPa[9]; λ、β、k皆为拟合参数;t为时间,s.
选取-18 ℃作为参考温度,将其他试验温度的松弛模量曲线向参考温度下的曲线水平平移,即可得到参考温度下的松弛模量主曲线.由Boltzmann叠加原理,总的应力等于各个时刻应力松弛的线性叠加,得到温度应力计算的积分式为
| $ \sigma (\xi ) = \int\limits_0^\xi {\frac{{{\rm{d}}\varepsilon ({\xi ^\prime })}}{{{\rm{d}}({\xi ^\prime })}}} E(\xi - {\xi ^\prime }){\rm{d}}({\xi ^\prime }). $ | (6) |
式(6)中的时间都为某一参考温度下的缩减时间,而不同参考温度下沥青胶结料的松弛特性不同,为计算降温过程中不同温度条件下沥青胶结料的温度应力,应把某一参考温度下的缩减时间转化为不同温度条件下的物理时间,即
| $ \xi (t) = \int\limits_0^t {\frac{{{\rm{d}}{t^\prime }}}{{{a_T}}}} . $ | (7) |
式中:aT为水平移位因子,根据Williams-Landel-Ferry(WLF)方程[13],
| $ \sigma (t) = \int\limits_0^t {\frac{{{\rm{d}}(\alpha \times \Delta T)}}{{{\rm{d}}({t^\prime })}}} E(\xi (t) - {\xi ^\prime }(t)){\rm{d}}({t^\prime }). $ | (8) |
基于Hopkins & Hamming算法和CAM模型计算沥青胶结料的温度应力需分为两步,首先将BBR试验得到的蠕变柔量D(t)转化为松弛模量E(t),再由松弛模量求沥青的温度应力.计算过程较为繁琐, 且将D(t)转化为E(t)这一步骤较为复杂.为了简化温度应力计算的过程,本文采用了拉普拉斯变化法,直接由蠕变柔量求温度应力,此方法已成功应用于沥青混合料温度应力的计算[14].
根据以下等式:
| $ D(\xi ) = a \times {\xi ^b} + c \times {\xi ^d}, $ | (9) |
在-12 ℃和-18 ℃的缩减时间域中构建BBR试验数据的蠕变柔量主曲线,其中a、b、c和d为拟合参数,ξ为参考温度下的缩减时间.
在理想一维条件下,热应变可表示为[14]
| $ {\varepsilon _t} = \int\limits_0^\xi D (\xi - {\xi ^\prime })\frac{{\partial \sigma }}{{\partial {\xi ^\prime }}}{\rm{d}}{\xi ^\prime } + \int\limits_0^\xi \alpha (\xi - {\xi ^\prime })\frac{{\partial (\Delta T)}}{{\partial {\xi ^\prime }}}{\rm{d}}{\xi ^\prime } = 0. $ | (10) |
对方程(10)进行拉普拉斯变换,可得
| $ \mathcal{L}({\varepsilon _t}) = s \times \bar D(s) \times \bar \sigma (s) + s \times \bar \alpha (s) \times \Delta \bar T(s) = 0. $ | (11) |
则温度应力可表示为
| $ \bar \sigma (s) = - \bar \alpha (s) \times \Delta \bar T(s)/\bar D(s). $ | (12) |
将式(9)代入式(12),并采用拉普拉斯逆变换和Stehfest算法[15],温度应力最终可表示为
| $ \sigma (\xi ) = a + b \times {\xi ^c}. $ | (13) |
将缩减时域下的σ(ξ)转化为实际时域下的σ(T, t),降温由10 ℃到-40 ℃,降温速率分别取0.2、1、5、20 ℃/h.
图 1为两种温度应力计算方法的对比,从图上可以直观看出,相比于Hopkins & Hamming算法和CAM模型两步计算法,拉普拉斯变换一步计算法要更为简便.

|
图 1 两种温度应力计算方法的对比 Fig. 1 Comparison of two methods for calculating thermal stress |
早期的研究工作主要通过直接拉伸(DT)试验得到沥青胶结料强度数据, 结合BBR试验获得的蠕变数据来确定胶结料的低温临界开裂温度[16],但是DT试验结果重复性较差,美国公路合作研究计划(NCHRP)建议沥青结合料的抗拉强度应在5种温度、4种应变速率、每组6个平行试样的组合下确定,试验量较大[17].而且直接拉伸试验设备成本高昂,目前越来越少的制造商对DT设备提供升级与维护.因此,出现了替代的实验或分析解决方案来估计沥青的临界开裂温度,如Kim[18]提出的沥青胶结料开裂装置(asphalt binder cracking device,ABCD)和Shenoy[19]提出的单渐近线程序(single asymptote procedure,SAP).考虑到ABCD装置制作的繁琐及成本问题[18],本文采用SAP理论来计算沥青胶结料的临界开裂温度. Shenoy提出的SAP理论仅通过BBR试验蠕变数据来计算沥青胶结料的低温临界开裂温度[19]. Shenoy发现,降温过程中的沥青胶结料温度应力曲线先是缓慢上升,最后变成急剧上升,曲线起始端和末尾端的渐近线分别代表温度应力积累的极限曲率.因而Shenoy把两条渐近线的交点作为沥青胶结料的临界开裂温度,如图 2所示,其中σ为温度应力,T为温度,图中切线与T轴的交点即为低温临界开裂温度. Shenoy的试验结果表明,基于SAP理论的计算结果与DTT试验结果具有极好的相关性.在绝大多数情况下两者差异小于1.5 ℃,最大差异约为2.0 ℃,相关系数达0.9以上[19].

|
图 2 SAP理论 Fig. 2 SAP method |
4种70#基质沥青的BBR试验结果如图 3所示.图中CoV表示变异系数(coefficient of variation). BBR试验的蠕变劲度S越小,蠕变劲度变化率m越大,沥青低温性能越好,由图中BBR试验的蠕变劲度S和蠕变劲度变化率m结果可以直观地判断出,4种70#沥青中70#-1和70#-4性能最优,70#-3性能较好,70#-2性能最劣.

|
图 3 S(60)和m (60)试验结果 Fig. 3 Test results of S(60) and m(60) |
根据ASTM D7643-10[20],计算得到4种70#基质沥青的低温PG分级,见表 1.其中,TC(S)为沥青胶结料蠕变劲度S=300 MPa时的临界温度,℃;TC(m)为沥青胶结料蠕变劲度变化率m=0.3时的临界温度,℃;TC为沥青胶结料的低温连续分级,℃.由沥青的低温PG结果可知,4种70#沥青的性能从优到劣排序为70#-1、70#-4、70#-3、70#-2.这与上面蠕变劲度S和蠕变劲度变化率m的分析结果基本一致.
| 表 1 4种基质沥青的低温PG Tab. 1 Low-temperature PG of four matrix asphalt |
为更好地比较两种温度应力计算方法结果的差异,本文采用显著性水平为5%(α=0.05)的t检验法来对计算结果进行分析,对本文计算结果设置了两个统计假设.假设1:温度应力σ(低温临界开裂温度TCR)近似服从正态分布;假设2:温度应力σ(低温临界开裂温度TCR)具有相同(或相似)的标准差.
假设检验为
| $ {{\mu _{\rm{A}}}(\sigma ,{T_{{\rm{CR}}}}) = {\mu _{\rm{B}}}(\sigma ,{T_{{\rm{CR}}}}),{\rm{ 原假设; }}} $ | (14) |
| $ {{\mu _{\rm{A}}}(\sigma ,{T_{{\rm{CR}}}}) \ne {\mu _{\rm{B}}}(\sigma ,{T_{{\rm{CR}}}}),{\rm{ 备择假设}}{\rm{. }}} $ | (15) |
其中μA(σ, TCR)、μB(σ, TCR)分别为不同组别70#基质沥青σ或TCR计算结果的平均值.
采用t统计量作为检验统计量[21],即
| $ t = \frac{{{\mu _{\rm{A}}}(\sigma ,{T_{{\rm{CR}}}}) - {\mu _{\rm{B}}}(\sigma ,{T_{{\rm{CR}}}})}}{{{S_P}(\sigma ,{T_{{\rm{CR}}}}) \times \sqrt {\frac{1}{{{n_{\rm{A}}}}} + \frac{1}{{{n_{\rm{B}}}}}} }}. $ | (16) |
式中nA、nB分别为A、B两组试验样本数量,即平行试件数,都为3;SP(σ, TCR)为合并样本标准差,计算公式[21]为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {S_P}(\sigma ,{T_{{\rm{CR}}}}) = \\ \sqrt {\frac{{({n_{\rm{A}}} - 1) \times S_{\rm{A}}^2(\sigma ,{T_{{\rm{CR}}}}) + ({n_{\rm{B}}} - 1) \times S_{\rm{B}}^2(\sigma ,{T_{{\rm{CR}}}})}}{{{n_{\rm{A}}} + {n_{\rm{B}}} - 2}}.} \end{array} $ | (17) |
其中:SA2(σ, TCR)、SB2(σ, TCR)分别为A、B两组基质沥青σ或TCR计算结果的方差;统计自由度DF=nA+nB-2=4.
最后,基于t检验法输出的结果p值来比较两种温度应力计算方法结果的差异.当p值< 0.05,统计学上则认为两组数据存在显著差异,即两种温度应力计算结果存在显著差异.
3.2.2 温度应力计算结果对比4种70#基质沥青在不同降温速率下的温度应力计算结果如图 4所示.其中H&H(0.2 ℃/h)、La(0.2 ℃/h)分别为0.2 ℃/h降温速率下基于Hopkins & Hamming算法和基于拉普拉斯变化法得到的沥青胶结料温度应力,其他以此类推.

|
图 4 沥青的温度应力 Fig. 4 Thermal stress of asphalt |
由图 4可知,不同降温速率下沥青胶结料温度应力积累趋势是一样的,应力曲线先是缓慢上升,而后逐渐变为急剧上升;随着降温速率的增加,温度应力曲线σ值变大,沥青胶结料的温度应力增大,沥青更容易开裂.由图 4还可以得到,两种温度应力计算方法得到的结果是非常接近的,从温度应力曲线上很难看出区别.因而,本文采用t检验法的p值计算结果来评价两种温度应力计算方法结果的差异.
4种不同降温速率下,4种70#基质沥青的温度应力σ基于t检验法的p值计算结果如图 5所示,其中红线代表p值等于0.05时的临界值.由p值计算结果可知,基于Hopkins & Hamming算法和基于拉普拉斯变化法得到的沥青胶结料温度应力不存在显著差异.除70#-1基质沥青在两种温度应力计算方法下的计算结果相关性极高,p值接近1外,另外3种70#基质沥青的p值在特定温度(-10~-30 ℃)时会减小,其他温度条件下的p值保持较大值,但减小后的p值仍远大于0.05.

|
图 5 沥青胶结料的p值 Fig. 5 p-value of asphalt binder |
两种温度应力计算方法下的低温临界开裂温度的计算结果见表 2,两种温度应力计算方法t检验法的p值计算结果见表 3.其中v为降温速率,v分别取0.2、1、5、20 ℃/h;TCR为低温临界开裂温度,℃. Hopkins & Hamming算法和Laplace算法分别指基于Hopkins & Hamming法和Laplace变换法的计算结果.由表 2可以得到以下结论:1)随着降温速率的增加,沥青胶结料的低温临界开裂温度升高,降温速率从0.2 ℃/h变为20 ℃/h时TCR上升了约6 ℃,降温速率越快沥青越容易开裂;2)由低温临界开裂温度的结果可知,4种70#基质沥青的性能由优到劣排序为70#-1、70#-4、70#-3、70#-2,这与前文得到的结论是一致的;3)基于Hopkins & Hamming法和基于Laplace变换法得到的TCR计算结果非常接近,Laplace变换法得到的TCR要略低于Hopkins & Hamming法,但二者之间的最大差异不超过0.04 ℃,且随着降温速率的增大,两种计算方法得到的TCR差异也会随之增大;4)从p值计算结果中可以得到,两种温度应力计算得到的TCR不存在显著差异,p值基本在0.9以上,相关性极高.
| 表 2 两种方法的TCR计算结果 Tab. 2 Calculation results of TCR of two methods |
| 表 3 两种方法的p值计算结果 Tab. 3 Calculation results of p-value of two methods |
本文通过Huet流变模型[22]对70#基质沥青的BBR试验数据进行拟合. Huet流变模型由一个弹簧元件和两个缓冲元件串联而成,如图 6所示.缓冲元件(parabolic element)是一种等同于弹簧元件和粘壶元件的模型元件,蠕变柔量形式类似于抛物线. Huet模型中蠕变柔量可表示为
| $ D(t) = \frac{1}{{S(t)}} = \frac{1}{{{E_{\rm{g}}}}}[1 + \frac{{\delta {{\left( {\frac{t}{\tau }} \right)}^k}}}{{\varGamma (k + 1)}} + \frac{{{{\left( {\frac{t}{\tau }} \right)}^h}}}{{\varGamma (h + 1)}}]. $ | (18) |

|
图 6 Huet模型 Fig. 6 Huet model |
其中:D(t)、E(t)分别为蠕变柔量和蠕变劲度;Eg为玻璃态模量,取3 GPa[9];δ为无量纲常数;k、h为缓冲元件的粘弹参数,0 < k < h < 1;τ为特征时间,与材料的松弛性能相关;Γ为伽马函数,Γ(n+1) =nΓ(n).
Huet流变模型的k、h值拟合结果见表 4. 表 5对不同70#基质沥青的k、h值拟合结果进行了t检验法p值计算,p值< 0.05时加粗表示.
| 表 4 Huet模型参数结果 Tab. 4 Results of Huet model parameters |
| 表 5 Huet模型参数的p值计算结果 Tab. 5 Calculation results of p-value of Huet model parameters |
Huet和Falchetto等的研究结果表明越硬的材料对应的Huet模型k、h值越低[17, 22],即低温抗裂性能越差.由表 4可以看出,4种70#基质沥青的低温性能由优到劣的排序为70#-1、70#-4、70#-3、70#-2,这验证了前文BBR试验、低温临界开裂温度得到的结论.由表 5中的p值计算结果可知,70#-1的低温性能要显著优于70#-3、70#-2,70#-4的低温性能要显著优于70#-2,其他沥青之间的性能无显著差异.
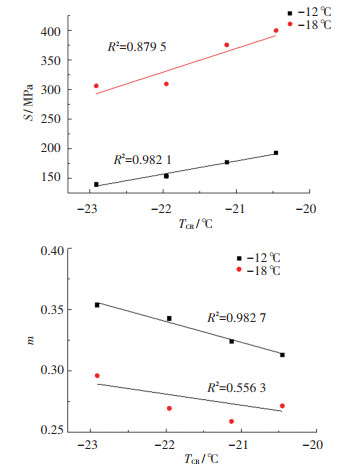
3.3.2 相关性分析与实测温度数据验证为验证本文计算方法的有效性,考虑到弯曲梁流变试验应用较为广泛,将按照本文计算方法得到的低温临界开裂温度TCR与BBR试验得到的蠕变劲度S、蠕变劲度变化率m、综合评价指标S/m,并结合Huet流变模型得到的k、h值进行相关性分析.分析结果见表 6和图 7,其中v为降温速率.由于两种温度应力得到的TCR基本一致,因此这里只选用了基于Laplace变换法的计算结果进行分析,由分析结果可得出以下结论:1)蠕变劲度S与临界开裂温度TCR的相关系数在-12 ℃试验温度时可达0.93以上,在-18 ℃时达0.78以上,相关性较好;蠕变劲度变化率m在-12 ℃试验温度时可达0.93以上,相关性极好,在-18 ℃时为0.55左右,相关性一般.研究[23]表明,单一的蠕变劲度S或蠕变劲度变化率m仅单独考虑了沥青的模量或松弛能力,存在片面性.因此,综合考虑沥青的变形能力和松弛能力,采用S/m来评价沥青性能更为准确. S/m与临界开裂温度TCR的相关系数在-12 ℃和-18 ℃时分别达到了0.93和0.84以上,相关性极强,这证明了本文计算方法的有效性.而Huet流变模型得到的k、h值与临界开裂温度TCR的相关性分析结果再次证明了这一点. 2)由表 6可以看出,随着降温速率的增大,各指标与临界开裂温度TCR的相关系数逐渐减小,相关性减弱.本文认为这是由于BBR试验是在固定试验温度下进行的试验,Huet模型也是基于BBR试验数据建立的模型,而临界开裂温度TCR是降温条件下得到的开裂温度.降温速率越大,两者差异越大,因此增大降温速率会减弱各指标与临界开裂温度TCR的相关性.但当降温速率为20 ℃/h时,S/m、k、h值与临界开裂温度TCR的相关系数仍达到0.836以上,这说明本文的计算方法在这种急剧降温条件下仍具有有效性.
| 表 6 相关系数计算结果 Tab. 6 Calculation results of correlation coefficients |
|
图 7 降温速率为1 ℃/h时S,m与TCR的相关性分析 Fig. 7 Correlation analysis between S, m, and TCR when cooling rate is 1 ℃/h |
将本文温度应力计算结果与国内外相关研究成果进行对比,发现温度应力曲线趋势基本一致[9-10].同时为了进一步验证本文研究方法的有效性与实际可行性,本文选取实测路面结构温度数据来模拟沥青胶结料的现场连续变速降温工况.由于缺乏国内实测路面结构温度数据,本文选用了加拿大多伦多2018年1月12日起连续60 h实测的路表温度变化数据,基于差分法计算降温速率,采用本文的温度应力计算方法,计算结果如图 8所示.其中T为环境温度,σ为温度应力,t为时间.由图 8可以看出,沥青胶结料的温度应力变化趋势与实际路表温度变化基本完全保持一致,这再一次验证了本文温度应力计算方法的有效性.同时说明了本文的温度应力计算方法不仅适用于匀速降温工况,还适用于任意降温速率下的现场连续变速降温工况.

|
图 8 实际温度场下沥青胶结料的温度应力 Fig. 8 Thermal stress of asphalt binder at field temperature |
1) 通过BBR试验获得沥青胶结料的蠕变柔量,分别采用Hopkins & Hamming算法和CAM模型两步计算法以及Laplace变换一步计算法来获得沥青的温度应力,基于SAP理论计算相应的低温临界开裂温度,计算结果表明,两种方法具有良好的一致性.
2) 临界开裂温度计算结果和Huet流变模型拟合结果表明,4种70#基质沥青的性能由优到劣排序为70#-1、70#-4、70#-3、70#-2.另外,由t检验法的p值计算结果可知,70#-1的低温性能要显著优于70#-3、70#-2,70#-4的低温性能要显著优于70#-2,其他沥青之间的性能无显著差异.
3) 随着降温速率的加大,沥青胶结料的温度应力的积累速度加快,温度应力增大,沥青胶结料的低温临界开裂温度升高,沥青更容易开裂.不同降温速率下沥青胶结料温度应力曲线趋势应是一致的,曲线先是缓慢上升,而后慢慢变为急剧上升.
4) 低温临界开裂温度TCR与蠕变劲度S、蠕变劲度变化率m、综合评价指标S/m、Huet流变模型的k、h值等指标的相关性分析结果证明了此计算方法的有效性,而实测路表温度变化数据的计算结果证明了此方法不仅适用于匀速降温工况,也适用于任意降温速率下的现场连续变速降温工况.
5) 在计算沥青胶结料的温度应力时,按照AASHTO标准将热膨胀系数取为定值,存在一定局限性.此外,此计算方法的有效性需要增加沥青混合料部分的试验进行进一步论证.
| [1] |
陈兴伟. 力学-经验路面设计指南(MEPDG)简介[J]. 上海公路, 2011(3): 1. CHEN Xingwei. Introduction to mechanistic-empirical pavement design guide[J]. Shanghai Highways, 2011(3): 1. DOI:10.3969/j.issn.1007-0109.2011.03.005 |
| [2] |
HILTUNEN D R, ROQUE R. A mechanics-based prediction model for thermal cracking of asphalt concrete pavement[J]. Proceedings of AAPT, 1994, 63(8): 81. |
| [3] |
MOON K H, MARASTEANU M O, TUROS M. Comparison of thermal stresses calculated from asphalt binder and asphalt mixture creep tests[J]. Journal of Materials in Civil Engineering, 2013, 25(8): 1059. DOI:10.1061/(ASCE)MT.1943-5533.0000651 |
| [4] |
付国志, 曹丹丹, 赵延庆, 等. 沥青混合料低温临界开裂温度的确定[J]. 复合材料学报, 2019, 36(4): 237. FU Guozhi, CAO Dandan, ZHAO Yanqing, et al. Determination of critical thermal cracking temperature of asphalt concrete[J]. Acta Materiae Compositae Sinica, 2019, 36(4): 237. |
| [5] |
薛忠军, 张肖宁, 詹小丽, 等. 基于蠕变试验计算沥青的低温松弛弹性模量[J]. 华南理工大学学报(自然科学版), 2007, 35(2): 64. XUE Zhongjun, ZHANG Xiaoning, ZHAN Xiaoli, et al. Calculation of low-temperature relaxed modulus of elasticity for bitumen via creep test[J]. Journal of South China University of Technology (Natural Science Edition), 2007, 35(2): 64. DOI:10.3321/j.issn:1000-565X.2007.02.014 |
| [6] |
公路沥青路面设计规范: JTG D50—2017[S].北京: 人民交通出版社, 2017 Specifications for design of highway asphalt pavement: JTG D50—2017[S]. Beijing: China Communication Press, 2017 |
| [7] |
Standard test method for determining the flexural creep stiffness of asphalt binder using the bending beam rheometer (BBR): ASTM D6648-08[S]. Wisconsin: ASTM Committee, 2016
|
| [8] |
HILLS J F, BRIEN D. The fracture of bitumens and asphalt mixes by temperature induced stresses[C]// Proceedings of the Association of Asphalt Paving Technologists. Ann Arbor: The Association of Asphalt Paving Technologists, 1966, 35: 292
|
| [9] |
Standard practice for determination of low-temperature performance grade (PG) of asphalt binders: AASHTO R49-09[S]. Washington DC: American Association of State Highway and Transportation Officials (AASHTO), 2013
|
| [10] |
FALCHETTO A C, MOON K H. Comparisons of analytical and approximate interconversion methods for thermal stress computation[J]. Canadian Journal of Civil Engineering, 2015, 42(10): 705. DOI:10.1139/cjce-2014-0558 |
| [11] |
HOPKINS I L, HAMMING R W. On creep and relaxation[J]. Journal of Applied Physics, 1957, 28(8): 906. DOI:10.1063/1.1722885 |
| [12] |
MARASTEANU M O. Role of bending beam rheometer parameters in thermal stress calculations[J]. Transportation Research Record Journal of the Transportation Research Board, 2004, 1875(1875): 9. |
| [13] |
王超.沥青结合料路用性能的流变学研究[D].北京: 北京工业大学, 2015 WANG Chao. Rheological characterization on paving performance of asphalt binder[D]. Beijing: Beijing University of Technology, 2015 |
| [14] |
FALCHETTO A C, MOON K H, WISTUBA M P. An alternative method for computing thermal stress in asphalt mixture: the Laplace transformation[J]. Road Materials and Pavement Design, 2017, 18(2): 226. |
| [15] |
STEHFEST H. Algorithm 368: numerical inversion of Laplace transform[J]. Communication of the ACM, 1970, 13(1): 47. DOI:10.1145/361953.361969 |
| [16] |
詹小丽, 张肖宁, 卢亮, 等. 沥青临界开裂温度的研究[J]. 公路, 2007(3): 125. ZHAN Xiaoli, ZHANG Xiaoning, LU Liang, et al. A study on critical cracking temperature of asphalt[J]. Highway, 2007(3): 125. |
| [17] |
BAHIA H U, HANSON D I, ZENG M, et al. Characterization of modified asphalt binders in superpave mix design[R]. Washington DC: National Academy Press, 2001
|
| [18] |
KIM S S. Development of an asphalt binder cracking device[R]. Washington DC: Transportation Research Board, 2007
|
| [19] |
SHENOY A. Single-event cracking temperature of asphalt pavements directly from bending beam rheometer data[J]. Journal of Transportation Engineering, 2002, 128(5): 465. DOI:10.1061/(ASCE)0733-947X(2002)128:5(465) |
| [20] |
Standard practice for determining the continuous grading temperatures and continuous grades for PG graded asphalt binders: ASTM D7643-10[S]. Wisconsin: ASTM Committee, 2010
|
| [21] |
盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 4版. 北京: 高等教育出版社, 2008: 184. SHENG Zhou, XIE Shiqian, PAN Chengyi. Probability theory and mathematical statistics[M]. 4th ed. Beijing: Higher Education Press, 2008: 184. |
| [22] |
HUET C. Coupled size and boundary-condition effects in viscoelastic heterogeneous and composite bodies[J]. Mechanics of Materials, 1999, 31(12): 787. DOI:10.1016/S0167-6636(99)00038-1 |
| [23] |
谭忆秋, 符永康, 纪伦, 等. 橡胶沥青低温性能评价指标[J]. 哈尔滨工业大学学报, 2016, 48(3): 66. TAN Yiqiu, FU Yongkang, JI Lun, et al. Low temperature performance evaluation index of rubber asphalt[J]. Journal of Harbin Institute of Technology, 2016, 48(3): 66. |
 2020, Vol. 52
2020, Vol. 52


