2. 空间智能控制技术重点实验室(北京控制工程研究所), 北京 100190
2. Science and Technology on Space Intelligent Control Laboratory (Beijing Institute of Control Engineering), Beijing 100190, China
随着世界经济的不断发展,作为当今科学技术中发展最快的尖端技术之一,航天科技得到了越来越多国家的高度重视,发挥着愈加重要的作用.由于航天任务复杂程度日益增加,对火箭、卫星等航天器的可靠性提出了更高的要求.为确保航天器的安全性、可靠性及航天任务的顺利进行,深入开展航天器故障诊断与容错控制技术具有重要的理论研究意义与实际应用价值.
近年来,国内外学者针对故障诊断与容错控制方面进行了广泛研究. 2007年英国埃克塞特大学的Edwards等[1]针对不确定非线性系统设计滑模观测器进行故障检测并采用等效输出注入的方法估计出故障信息. 2010年加拿大温莎大学Mehrdad Saif等[2]针对一系列不确定动态系统,提出一种二阶滑模观测器进行故障诊断. 2012年韩国蔚山大学Mien Van等[3]研究了机械臂的鲁棒故障检测算法,解决了传统的利用等价输入注入重构故障时需要引入滤波器的问题,设计三阶滑模观测器实现故障的重构,但未考虑不确定及干扰影响. 2012年意大利帕维亚大学Capisani等[4]针对机械臂执行器与传感器故障问题,采用高阶滑模观测器实现执行器故障估计. 2012年韩国学者Dong-Jae Lee等[5]提出了一种同时估计不确定系统状态和扰动的鲁棒H∞滑模广义观测器,并采用滑模策略对输入故障进行重构,但未能实现故障和干扰的完全解耦估计. 2014年哈尔滨工业大学刘建兴等[6]针对非线性不确定系统,提出一种基于观测器的故障重构策略.通过多次坐标变换,将不确定及故障分别解耦在不同的子系统,并利用自适应增益二阶滑模观测器来观测系统状态. 2015年南京航空航天大学姜斌等[7]针对存在干扰不确定以及驱动器故障下的四旋翼无人机系统提出了一种鲁棒滑模反步控制器. 2015年法国波尔多大学De Loza等[8]针对带有故障的线性系统,无需故障检测与隔离,设计连续容错控制分配,首次提出基于固定控制分配的连续积分滑模,利用高阶滑模观测器估计状态,避免了抖振,估计了故障. 2016年韩国蔚山大学Mien Van等[9]考虑了不确定影响,建立超螺旋观测器同时估计系统状态和故障信息. 2016年英国埃克塞特大学Edwards等[10]研究了如何在干扰存在条件下提高自适应观测器的性能,提出一种滑模自适应观测器. 2017年哈尔滨工业大学罗文生等[11]提出一种非线性观测器的故障诊断方法, 利用一种改进的超螺旋进行观测器设计, 这种观测器不仅可以估计状态,还可以估计故障信息. 2017年西北工业大学穆凌霞等[12]将H∞性能指标引入到观测器设计中, 从而抑制不确定性和输出扰动对状态估计的影响,但此方法未能完全消除不确定和扰动带来的影响. 2018年北京航空航天大学胡庆雷等[13]针对执行器故障、外部干扰和输入饱和同时存在情况下的航天器系统,提出了一种包含符号函数的迭代学习观测器,降低了计算复杂度, 在鲁棒控制分配策略中引入故障估计信息,提高了容错能力. 2019年伊朗阿米尔卡比尔大学Nemati等[14]考虑模型的不确定性、输入和环境干扰,针对卫星编队飞行的故障诊断问题,设计了一组非线性鲁棒未知输入观测器,可以对未知输入干扰进行解耦,减弱模型不确定和外部干扰的影响,但同样未能实现完全解耦.
综上所述,传统的故障诊断方法首先检测故障发生,并设计故障估计器对故障大小进行估计,进而利用故障估计值进行容错控制器设计,从而保证故障发生后系统的稳定性.但这种处理方法在完成故障估计后,干扰则需进一步通过自适应或观测器等手段解决,这会增加系统计算量,且带来一定的时间延迟.相关学者对此展开了一系列研究,但都未能完全消除干扰带来的影响.
因此,针对以上问题,本文对干扰及故障影响下的航天器姿态控制系统,首先通过设计未知输入观测器进行故障检测及估计一体化设计,实现干扰影响下对系统状态和故障的有效估计;在此基础上,考虑到此方法中故障必须可导需求,进一步考虑传感器测量误差,设计新型的自适应滑模未知输入观测器,减小干扰处理带来的时间延迟,同时实现对故障及干扰的解耦估计,并设计多变量终端滑模容错控制器,保证航天器控制性能的快速恢复.
1 航天器姿态控制模型建立为建立航天器姿态模型,首先给出地心惯性坐标系及机体坐标系的定义如下.
地心惯性坐标系:所有的运动都要参照地球惯性坐标系,记为OIXIYIZI.地球惯性坐标系的坐标原点OI为地球中心,以赤道面为基准面,OIXI轴沿地球赤道面与黄道面的交线,并指向春分点,OIZI轴指向北极方向,OIYI轴在赤道面内与OIXI轴和OIZI轴构成右手坐标系.
机体坐标系:记为OBXBYBZB,本体坐标系与航天器本身连接在一起,与航天器的主惯量轴一致,航天器质心为其坐标原点OB,滚动轴为OBXB轴,俯仰轴为OBYB轴,偏航轴为OBZB轴,满足右手系准则.
基于上述坐标系,建立航天器姿态动力学模型:
| $ \mathit{\boldsymbol{J\dot \omega }} = - {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }} + {\mathit{\boldsymbol{T}}_{\rm{u}}} + {\mathit{\boldsymbol{T}}_{\rm{d}}}. $ | (1) |
式中:ω=[ωx, ωy, ωz]T为航天器角速度;J为转动惯量, J=diag[Jx, Jy, Jz],其中Jx、Jy、Jz为航天器主惯量轴;Tu为系统控制力矩,Tu=[Tux, Tuy, Tuz]T;Td为系统干扰力矩, Td=[Tdx, Tdy, Tdz]T.
航天器运动学模型表达形式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\omega _x} = \dot \varphi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta + \dot \theta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi ,}\\ {{\omega _y} = - \dot \varphi {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta + \dot \theta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi ,}\\ {{\omega _z} = \dot \psi + {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta .} \end{array}} \right. $ | (2) |
式中φ、θ、ψ分别为滚转角、俯仰角及偏航角.
考虑较小的航天器姿态偏差,以及低轨运行航天器所受到的干扰力矩主要为重力梯度力矩,上述航天器模型、可转化为
| $ {\mathit{\boldsymbol{M}}_2}\mathit{\boldsymbol{\ddot p}} + {\mathit{\boldsymbol{M}}_1}\mathit{\boldsymbol{\dot p}} + {\mathit{\boldsymbol{M}}_0}\mathit{\boldsymbol{p}} = {\mathit{\boldsymbol{G}}_{\rm{u}}}{\kern 1pt} {\mathit{\boldsymbol{T}}_{\rm{u}}} + {\mathit{\boldsymbol{G}}_{\rm{d}}}{\kern 1pt} {\mathit{\boldsymbol{T}}_{\rm{d}}}. $ | (3) |
式中p=[φ, θ, ψ]T为姿态角,其余变量表达形式为
| $ {\mathit{\boldsymbol{M}}_0} = \left[ {\begin{array}{*{20}{c}} {4\omega _0^2({J_y} - {J_z})}&0&0\\ 0&{3\omega _0^2({J_x} - {J_z})}&0\\ 0&0&{\omega _0^2({J_y} - {J_x})} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{M}}_1} = \left[ {\begin{array}{*{20}{c}} 0&0&{ - {\omega _0}({J_x} - {J_y} + {J_z})}\\ 0&0&0\\ {{\omega _0}({J_x} - {J_y} + {J_z})}&0&0 \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{M}}_2} = \left[ {\begin{array}{*{20}{c}} {{J_x}}&0&0\\ 0&{{J_y}}&0\\ 0&0&{{J_z}} \end{array}} \right],{\mathit{\boldsymbol{G}}_{\rm{u}}} = {\mathit{\boldsymbol{G}}_{\rm{d}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right]. $ |
加性故障在航天器系统中是一种常见的故障形式,也称为偏移故障,通常可能由于航天器执行机构老化、电源电压下降或电阻增加等原因引起,当系统出现加性故障时,会影响系统状态,进而影响航天器系统的稳定.因此本文考虑航天器加性故障f= [f1 f2 f3]T,定义状态量
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{Bu}} + {\mathit{\boldsymbol{B}}_{\rm{d}}}\mathit{\boldsymbol{d}} + {\mathit{\boldsymbol{B}}_{\rm{f}}}\mathit{\boldsymbol{f}},}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Cx}}.} \end{array}} \right. $ | (4) |
式中:x∈R6为系统状态,u∈R3为控制输入,y∈R3为系统输出,d∈R3为外部干扰,f∈R3为航天器故障,
针对航天器线性化模型,考虑干扰d及故障f影响,通过将故障f扩展为系统状态量,获得扩展状态系统,并设计未知输入观测器,保证干扰影响下对扩展状态的有效估计,从而实现故障检测及估计一体化设计.
假设所考虑的故障形式满足
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot {\bar x}}} = \mathit{\boldsymbol{\bar A\bar x}} + \mathit{\boldsymbol{\bar Bu}} + {{\mathit{\boldsymbol{\bar B}}}_{\rm{d}}}d,}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{\bar Cx}}.} \end{array}} \right. $ | (5) |
式中:
假设1 rank(C, Bd)=rank(Bd),(C, A)是可观测的.
基于航天器扩展系统动态,设计未知输入观测器(unknown input observer, UIO):
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot {\bar z}}} = \mathit{\boldsymbol{R\bar z}} + \mathit{\boldsymbol{T\bar Bu}} + \mathit{\boldsymbol{Ky}},}\\ {\mathit{\boldsymbol{\hat {\bar x}}} = \mathit{\boldsymbol{\bar z}} + \mathit{\boldsymbol{My}}.} \end{array}} \right. $ | (6) |
式中:
| $ \mathit{\boldsymbol{M}} = \mathit{\boldsymbol{\bar B}}{(\mathit{\boldsymbol{\bar C{\bar B}}})^*}, $ | (7) |
其中(CB)*=[(CB)TCB]-1(CB)T.
定义状态估计误差为
| $ \mathit{\boldsymbol{\bar e}} = \mathit{\boldsymbol{\bar x}} - \mathit{\boldsymbol{\hat {\bar x}}}. $ | (8) |
由式(5)、(6)可得
| $ \mathit{\boldsymbol{\bar e}} = \mathit{\boldsymbol{\bar x}} - \mathit{\boldsymbol{\hat {\bar x}}} = \mathit{\boldsymbol{\bar x}} - \mathit{\boldsymbol{\bar z}} - \mathit{\boldsymbol{M\bar C\bar x}} = (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{M\bar C}})\mathit{\boldsymbol{\bar x}} - \mathit{\boldsymbol{\bar z}}. $ | (9) |
定理1 针对航天器系统(5),在假设1存在的条件下,设计如式(6)所示的未知输入观测器形式,如果存在正定矩阵P及Q,使得
| $ \mathit{\boldsymbol{\bar A}}_1^{\rm{T}}\mathit{\boldsymbol{P}} + \mathit{\boldsymbol{P}}{\kern 1pt} {\mathit{\boldsymbol{\bar A}}_1} - {\mathit{\boldsymbol{\bar C}}^{\rm{T}}}{\mathit{\boldsymbol{Q}}^{\rm{T}}} - \mathit{\boldsymbol{Q\bar C}} < 0. $ | (10) |
其中A1=(I-MC)A, Q=PK1.那么,观测器估计误差e能够渐近收敛到0,即能够实现对未知状态x及故障f的有效估计.
证明 定义Lyapunov函数:
| $ V(\mathit{\boldsymbol{\bar e}}) = {\mathit{\boldsymbol{\bar e}}^{\rm{T}}}\mathit{\boldsymbol{P\bar e}}. $ | (11) |
基于式(5)、(6)、(9),对状态估计误差e求导可得
| $ \begin{array}{l} \mathit{\boldsymbol{\dot {\bar e}}} = (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{M\bar C}})\mathit{\boldsymbol{\dot {\bar x}}} - \mathit{\boldsymbol{\dot {\bar z}}} = (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{M\bar C}})(\mathit{\boldsymbol{\bar A\bar x}} + \mathit{\boldsymbol{\bar Bu}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\bar B}}}_{\rm{d}}}\mathit{\boldsymbol{d}}) - \mathit{\boldsymbol{R\bar z}} - \mathit{\boldsymbol{T\bar Bu}} - \mathit{\boldsymbol{K\bar C\bar x}} = (\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{M\bar C\bar A}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{K}}_1}\mathit{\boldsymbol{\bar C}})\mathit{\boldsymbol{\bar e}} + [(\mathit{\boldsymbol{\bar A}} - \mathit{\boldsymbol{M\bar C\bar A}} - {\mathit{\boldsymbol{K}}_1}\mathit{\boldsymbol{\bar C}})\mathit{\boldsymbol{M}} - {\mathit{\boldsymbol{K}}_2}]\mathit{\boldsymbol{y}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({{\mathit{\boldsymbol{\bar B}}}_{\rm{d}}} - \mathit{\boldsymbol{M\bar C}}{{\mathit{\boldsymbol{\bar B}}}_{\rm{d}}})\mathit{\boldsymbol{d}} + (\mathit{\boldsymbol{\bar B}} - \mathit{\boldsymbol{M\bar C\bar B}} - \mathit{\boldsymbol{T\bar B}})\mathit{\boldsymbol{u}}. \end{array} $ | (12) |
其中R=A-MCA -K1C.为避免干扰等对故障诊断的耦合影响,参数设计如下:
| $ {\mathit{\boldsymbol{T}} = \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{M\bar C}},} $ | (13) |
| $ {(\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{H\bar C}}){{\mathit{\boldsymbol{\bar B}}}_{\rm{d}}} = {\bf{0}},} $ | (14) |
| $ {{\mathit{\boldsymbol{K}}_2} = \mathit{\boldsymbol{RM}}.} $ | (15) |
那么,系统(12)可转化为
| $ \mathit{\boldsymbol{\dot {\bar e}}} = \mathit{\boldsymbol{R\bar e}}. $ | (16) |
基于式(12)及式(16),对Lyapunov函数(11)进行求导,可得
| $ \begin{array}{l} \mathit{\boldsymbol{\dot V}}(\mathit{\boldsymbol{\bar e}}) = {{\mathit{\boldsymbol{\bar e}}}^{\rm{T}}}\mathit{\boldsymbol{P\dot {\bar e}}} + {{\mathit{\boldsymbol{\dot {\bar e}}}}^{\rm{T}}}\mathit{\boldsymbol{P\bar e}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\bar e}}}^{\rm{T}}}(\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\bar A}}}_1} + \mathit{\boldsymbol{\bar A}}_1^{\rm{T}}\mathit{\boldsymbol{P}} - {{\mathit{\boldsymbol{\bar C}}}^{\rm{T}}}{\mathit{\boldsymbol{Q}}^{\rm{T}}} - \mathit{\boldsymbol{Q\bar C}})\mathit{\boldsymbol{\bar e}}. \end{array} $ | (17) |
因此,通过选取合适的矩阵P和Q,保证式(10)成立,那么可得
注1 由于观测器设计过程中相关参数过多,下面对式(10)及式(13)~(15)的参数选择过程进行详细说明:1)按照式(7)形式确定矩阵M;2)通过求解式(10)所示的线性矩阵不等式,获得矩阵P及Q的取值,同时利用K1=P-1Q求得K1;3)基于式(13)~(15),计算增益矩阵R、T、K2的取值.
3 干扰及故障同时解耦估计策略上节观测器(6)能够实现对故障的有效估计,但无法对干扰进行同时处理,且此方法只能解决可导的故障类型.因此,为解决以上问题,并进一步考虑传感器测量误差,本节针对航天器系统,设计自适应滑模未知输入观测器,避免先估计故障后处理干扰的时间延迟,且无需故障可导,同时实现对故障及干扰的解耦估计.
考虑传感器测量误差,航天器模型(4)可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{Bu}} + {\mathit{\boldsymbol{B}}_{\rm{d}}}\mathit{\boldsymbol{d}} + {\mathit{\boldsymbol{B}}_{\rm{f}}}\mathit{\boldsymbol{f}},}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Cx}} + {\mathit{\boldsymbol{B}}_{\rm{s}}}\mathit{\boldsymbol{d}}.} \end{array}} \right. $ | (18) |
式中Bs∈R6×3为已知的系数矩阵.
假设2 (A, C)是可观测的,(A, B)是可控的.
假设3 存在未知正数f0,满足‖f‖≤f0.干扰d是范数有界的.
3.1 自适应滑模未知输入观测器设计通过将系统干扰扩展为系统状态,基于线性化模型(18),建立如下扩展系统模型:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{E\dot {\tilde x}}} = \mathit{\boldsymbol{\tilde A\tilde x}} + \mathit{\boldsymbol{Bu}} + {\mathit{\boldsymbol{B}}_{\rm{f}}}\mathit{\boldsymbol{f}},}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{\tilde C\tilde x}}.} \end{array}} \right. $ | (19) |
式中:
设计如式(20)所示的自适应滑模未知输入观测器:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot z}} = \mathit{\boldsymbol{Nz}} + \mathit{\boldsymbol{Ju}} + \mathit{\boldsymbol{Ly}} + \mathit{\boldsymbol{Wv}},}\\ {\mathit{\boldsymbol{\hat {\tilde x}}} = \mathit{\boldsymbol{z}} + \mathit{\boldsymbol{Hy}},}\\ {\mathit{\boldsymbol{\hat y}} = \mathit{\boldsymbol{\tilde C{\hat {\tilde x}}}}.} \end{array}} \right. $ | (20) |
式中:z为观测器状态,
| $ \mathit{\boldsymbol{v}} = (\mathit{\boldsymbol{\hat \rho }} + \delta )\frac{{{\mathit{\boldsymbol{e}}_y}}}{{\left\| {{\mathit{\boldsymbol{e}}_y}} \right\|}}. $ | (21) |
式中:ey=y-
| $ \mathit{\boldsymbol{\dot {\hat \rho} }} = {\sigma _0}\left\| {{\mathit{\boldsymbol{e}}_y}} \right\|. $ | (22) |
定义
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot \varepsilon }} = \mathit{\boldsymbol{N\varepsilon }} + (\mathit{\boldsymbol{T\tilde A}} - \mathit{\boldsymbol{NTE}} - \mathit{\boldsymbol{L\tilde C}})\mathit{\boldsymbol{\tilde x}} + }\\ {(\mathit{\boldsymbol{TB}} - \mathit{\boldsymbol{J}})\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{TBf}} - \mathit{\boldsymbol{Wv}}.} \end{array} $ | (23) |
定义
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot \varepsilon }} = \mathit{\boldsymbol{N\varepsilon }} + (\mathit{\boldsymbol{T\tilde A}} - \mathit{\boldsymbol{NTE}} - \mathit{\boldsymbol{L\tilde C}})\mathit{\boldsymbol{\tilde x}} + (\mathit{\boldsymbol{TB}} - \mathit{\boldsymbol{J}})\mathit{\boldsymbol{u}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{TBf}} - \mathit{\boldsymbol{Wv}},\\ \mathit{\boldsymbol{e}} = \mathit{\boldsymbol{\varepsilon }} + ({\mathit{\boldsymbol{I}}_9} - \mathit{\boldsymbol{H\tilde C}} - \mathit{\boldsymbol{TE}})\mathit{\boldsymbol{\tilde x}}. \end{array} \right. $ | (24) |
对估计误差e进行求导,并设计参数满足如下约束:
| $ {\mathit{\boldsymbol{T\tilde A}} - \mathit{\boldsymbol{NTE}} - \mathit{\boldsymbol{L\tilde C}} = {\bf{0}},} $ | (25) |
| $ {\mathit{\boldsymbol{TB}} - \mathit{\boldsymbol{J}} = {\bf{0}},} $ | (26) |
| $ {{\mathit{\boldsymbol{I}}_9} - \mathit{\boldsymbol{H\tilde C}} - \mathit{\boldsymbol{TE}} = {\bf{0}}.} $ | (27) |
可以得到
| $ \mathit{\boldsymbol{\dot e}} = \mathit{\boldsymbol{Ne}} + \mathit{\boldsymbol{TBf}} - \mathit{\boldsymbol{Wv}}. $ | (28) |
设计参数W=
| $ \mathit{\boldsymbol{\dot e}} = \mathit{\boldsymbol{Ne}} + {\mathit{\boldsymbol{\tilde P}}^{ - 1}}{\mathit{\boldsymbol{C}}^{\rm{T}}}(\mathit{\boldsymbol{\tilde Qf}} - \mathit{\boldsymbol{v}}). $ | (29) |
由式(29)可知,若估计误差e收敛至0,则故障f可由滑模项v求解获得.
定理2 针对航天器系统(18),如果存在正定矩阵
| $ {\mathit{\boldsymbol{\tilde PN}} + {\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{\tilde PK}} < - \xi {\mathit{\boldsymbol{I}}_9},} $ | (30) |
| $ {\mathit{\boldsymbol{\tilde PTF}} = {{\mathit{\boldsymbol{\tilde C}}}^{\rm{T}}}\mathit{\boldsymbol{\tilde Q}}\mathit{\boldsymbol{.}}} $ | (31) |
那么,所设计的自适应滑模UIO(20)可以保证对扩展状态
| $ \mathit{\boldsymbol{\hat f}} = {(\mathit{\boldsymbol{\tilde C}}{\kern 1pt} {\mathit{\boldsymbol{\tilde P}}^{ - 1}}{\mathit{\boldsymbol{\tilde C}}^{\rm{T}}}\mathit{\boldsymbol{\tilde Q}})^ + }\mathit{\boldsymbol{\tilde C}}{\kern 1pt} {\mathit{\boldsymbol{\tilde P}}^{ - 1}}{\mathit{\boldsymbol{\tilde C}}^{\rm{T}}}{\mathit{\boldsymbol{v}}_{{\rm{eq}}}}. $ | (32) |
式中(·)+为矩阵的广义逆,veq为等价输出注入项.
证明 下面将从两步进行定理2的证明.
第1步 扩展状态估计.
设计Lyapunov函数:
| $ {V_1} = {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{\tilde Pe}} + \frac{1}{{{\sigma _0}}}{(\rho - \hat \rho )^2}, $ | (33) |
其中
| $ \begin{array}{l} {{\dot V}_1} = {\mathit{\boldsymbol{e}}^{\rm{T}}}(\mathit{\boldsymbol{\tilde PN}} + {\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{\tilde P}})\mathit{\boldsymbol{e}} + 2{\mathit{\boldsymbol{e}}^{\rm{T}}}{{\mathit{\boldsymbol{\tilde C}}}^{\rm{T}}}(\mathit{\boldsymbol{\tilde Qf}} - \mathit{\boldsymbol{v}}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{2}{{{\sigma _0}}}\mathit{\boldsymbol{\tilde \rho }}( - {\sigma _0}\left\| {{\mathit{\boldsymbol{e}}_y}} \right\|). \end{array} $ | (34) |
定义ey=
| $ \begin{array}{l} {{\dot V}_1} = {\mathit{\boldsymbol{e}}^{\rm{T}}}(\mathit{\boldsymbol{\tilde PN}} + {\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{\tilde P}})\mathit{\boldsymbol{e}} + 2(\mathit{\boldsymbol{e}}_y^{\rm{T}}\mathit{\boldsymbol{\tilde Qf}} - \mathit{\boldsymbol{e}}_y^{\rm{T}}\mathit{\boldsymbol{v}}) + \\ \frac{2}{{{\sigma _0}}}\tilde \rho ( - {\sigma _0}\left\| {{\mathit{\boldsymbol{e}}_y}} \right\|) \le {\mathit{\boldsymbol{e}}^{\rm{T}}}(\mathit{\boldsymbol{\tilde PN}} + {\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{\tilde P}})\mathit{\boldsymbol{e}} + \\ \begin{array}{*{20}{l}} {2\left\| {{\mathit{\boldsymbol{e}}_y}} \right\|(\rho - \hat \rho - \delta ) - 2(\rho - \hat \rho )\left\| {{\mathit{\boldsymbol{e}}_y}} \right\| \le }\\ { - \xi {{\left\| \mathit{\boldsymbol{e}} \right\|}^2}.} \end{array} \end{array} $ | (35) |
式(35)两端同时求积分可得
第2步 故障估计.
基于ey=
| $ {\mathit{\boldsymbol{\dot e}}_y} = \mathit{\boldsymbol{\tilde CNe}} + \mathit{\boldsymbol{\tilde C}}{\kern 1pt} {\mathit{\boldsymbol{\tilde P}}^{ - 1}}{\mathit{\boldsymbol{\tilde C}}^{\rm{T}}}(\mathit{\boldsymbol{\tilde Qf}} - \mathit{\boldsymbol{v}}). $ | (36) |
与第1步同理可得ey= 0,
| $ {\bf{0}} = \mathit{\boldsymbol{\tilde CNe}} + \mathit{\boldsymbol{\tilde C}}{\kern 1pt} {\mathit{\boldsymbol{\tilde P}}^{ - 1}}{\mathit{\boldsymbol{\tilde C}}^{\rm{T}}}(\mathit{\boldsymbol{\tilde Qf}} - \mathit{\boldsymbol{v}}). $ | (37) |
因此,故障f的估计值
| $ \mathit{\boldsymbol{\hat f}} = {(\mathit{\boldsymbol{\tilde C}}{\kern 1pt} {\mathit{\boldsymbol{\tilde P}}^{ - 1}}{\mathit{\boldsymbol{\tilde C}}^{\rm{T}}}\mathit{\boldsymbol{\tilde Q}})^ + }\mathit{\boldsymbol{\tilde C}}{\kern 1pt} {\mathit{\boldsymbol{\tilde P}}^{ - 1}}{\mathit{\boldsymbol{\tilde C}}^{\rm{T}}}{\mathit{\boldsymbol{v}}_{{\rm{eq}}}}. $ | (38) |
定义故障估计误差ef=f-
| $ {\mathit{\boldsymbol{e}}_{\rm{f}}} = - {(\mathit{\boldsymbol{\tilde C}}{\kern 1pt} {\mathit{\boldsymbol{\tilde P}}^{ - 1}}{\mathit{\boldsymbol{\tilde C}}^{\rm{T}}}\mathit{\boldsymbol{\tilde Q}})^ + }\mathit{\boldsymbol{\tilde CNe}}. $ | (39) |
由于状态估计误差e会收敛到0,故ef也会收敛到0.因此,
考虑到观测器设计过程中涉及到待设计参数较多,包括
首先,式(27)可以转化为
| $ \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{T}}&\mathit{\boldsymbol{H}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{E}}\\ {\mathit{\boldsymbol{\tilde C}}} \end{array}} \right] = {\mathit{\boldsymbol{I}}_9}. $ | (40) |
为书写方便,定义
| $ \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{T}}&\mathit{\boldsymbol{H}} \end{array}} \right] = {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1}{\kern 1pt} \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1^ + - {\mathit{\boldsymbol{Y}}_1}({\mathit{\boldsymbol{I}}_9} - {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1}{\kern 1pt} \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1^ + ). $ | (41) |
式中Y1为任意正实数矩阵.故矩阵T、H可分别表示为
| $ {\mathit{\boldsymbol{T}} = {\mathit{\boldsymbol{T}}_1} - {\mathit{\boldsymbol{Y}}_1}{\kern 1pt} {\mathit{\boldsymbol{T}}_2},} $ | (42) |
| $ {\mathit{\boldsymbol{H}} = {\mathit{\boldsymbol{H}}_1} - \mathit{\boldsymbol{Y}}{{\kern 1pt} _1}{\mathit{\boldsymbol{H}}_2}.} $ | (43) |
式中:
因此,确定Y1即可确定T、H的取值. Y1的取值将在后面给出.
将式(27)代入式(25)可得
| $ \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{N}}&{\mathit{\boldsymbol{\bar L}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{I}}_9}}\\ {\mathit{\boldsymbol{\bar C}}} \end{array}} \right] = \mathit{\boldsymbol{T\bar A}}. $ | (44) |
式中L=L-NH.
同理可得
| $ {\mathit{\boldsymbol{N}} = {\mathit{\boldsymbol{N}}_1} - {\mathit{\boldsymbol{Y}}_2}{\kern 1pt} {\mathit{\boldsymbol{N}}_2},} $ | (45) |
| $ {\mathit{\boldsymbol{\bar L}} = {{\mathit{\boldsymbol{\bar L}}}_1} - {\mathit{\boldsymbol{Y}}_2}{\kern 1pt} {{\mathit{\boldsymbol{\bar L}}}_2}.} $ | (46) |
式中:
因此,只要确定Y2即可确定N、L的取值.
基于文献[15],可得Y1、Y2的取值过程:给定正常数ξ、β,存在正定对称矩阵
| $ g(\mathit{\boldsymbol{\tilde P}}{\kern 1pt} {\mathit{\boldsymbol{T}}_1}\mathit{\boldsymbol{\varphi }} - \mathit{\boldsymbol{\tilde S}}\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{T}}_2}\mathit{\boldsymbol{\varphi }}}\\ {{\mathit{\boldsymbol{N}}_2}} \end{array}} \right]) < - \mathit{\boldsymbol{\xi }}{\kern 1pt} {\mathit{\boldsymbol{I}}_9}, $ | (47) |
| $ \left[ {\begin{array}{*{20}{c}} {\beta \mathit{\boldsymbol{I}}}&{(\mathit{\boldsymbol{P}}{\kern 1pt} {\mathit{\boldsymbol{T}}_1} - \mathit{\boldsymbol{S}}{\kern 1pt} {{\mathit{\boldsymbol{\hat T}}}_2})\mathit{\boldsymbol{F}} - {{\mathit{\boldsymbol{\bar C}}}^{\rm{T}}}\mathit{\boldsymbol{Q}}}\\ *&{\beta \mathit{\boldsymbol{I}}} \end{array}} \right] > 0. $ | (48) |
式中:
| $ {{\mathit{\boldsymbol{Y}}_1} = {{\mathit{\boldsymbol{\tilde P}}}^{ - 1}}\mathit{\boldsymbol{S}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{12}}}\\ {\bf{0}} \end{array}} \right],} $ | (49) |
| $ {{\mathit{\boldsymbol{Y}}_2} = {{\mathit{\boldsymbol{\tilde P}}}^{ - 1}}\mathit{\boldsymbol{S}}\left[ {\begin{array}{*{20}{c}} {\bf{0}}\\ {{\mathit{\boldsymbol{I}}_{15}}} \end{array}} \right],} $ | (50) |
进一步基于式(42)、(43),可得T、H.进而基于式(45)、(46),求得N、L(L=L-NH),从而可以求得L.最后,基于式(26)、(27),求得J=TB,W=
基于2、3节可知,状态估计值
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot x}}}_1} = {\mathit{\boldsymbol{x}}_2},}\\ {{{\mathit{\boldsymbol{\dot x}}}_2} = \mathit{\boldsymbol{A}}{\kern 1pt} {\mathit{\boldsymbol{x}}_2} + \mathit{\boldsymbol{Bu}} + {\mathit{\boldsymbol{B}}_{\rm{d}}}\mathit{\boldsymbol{\hat d}} + {\mathit{\boldsymbol{B}}_{\rm{f}}}\mathit{\boldsymbol{\hat f}} + \mathit{\boldsymbol{D}}.} \end{array}} \right. $ | (51) |
其中D=Bded+Bfef为包含故障及干扰估计误差在内的系统综合不确定.
基于航天器姿态控制系统(51),设计滑模面:
| $ \mathit{\boldsymbol{s}} = {\mathit{\boldsymbol{x}}_1} + \lambda {\kern 1pt} {\mathit{\boldsymbol{x}}_2}, $ | (52) |
式中λ>0.
设计如下式所示的多变量终端滑模容错控制器:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{u}} = {{(\lambda \mathit{\boldsymbol{B}})}^{ - 1}}( - \lambda \mathit{\boldsymbol{A}}{\kern 1pt} {\mathit{\boldsymbol{x}}_2} - {\mathit{\boldsymbol{x}}_2} - \lambda {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{B}}_{\rm{f}}}\mathit{\boldsymbol{\hat f}} - \lambda \mathit{\boldsymbol{D}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_1}\mathit{\boldsymbol{s}} - {k_2}{{\left\| \mathit{\boldsymbol{s}} \right\|}^r}\frac{\mathit{\boldsymbol{s}}}{{\left\| \mathit{\boldsymbol{s}} \right\|}}).} \end{array} $ | (53) |
式中:k1>0,k2>0,r>0.
定理3[16] 考虑航天器模型(18),设计如式(53)所示的控制器,则存在正常数k1、k2、λ、r,使得状态量x,即姿态角q会收敛至平衡点.
注2 基于多时间尺度原理,容错控制器及观测器分别进行稳定性证明[17-18],见定理1、定理2及定理3.此外,在容错控制器设计过程中进一步将观测器估计误差考虑在内,以提高系统性能.
5 仿真与分析为了验证所提出的航天器故障诊断与容错控制设计的有效性,该部分将基于航天器模型进行仿真验证分析.其中,航天器的姿态角初值为
| $ \mathit{\boldsymbol{q}}(0) = {\left[ {\begin{array}{*{20}{c}} {0.349{\kern 1pt} {\kern 1pt} {\kern 1pt} 1}&{0.174{\kern 1pt} {\kern 1pt} 5}&{ - 0.261{\kern 1pt} {\kern 1pt} 8} \end{array}} \right]^{\rm{T}}}{\kern 1pt} {\kern 1pt} {\rm{rad}}, $ |
| $ \mathit{\boldsymbol{\dot q}}(0) = {\left[ {\begin{array}{*{20}{c}} {0.031{\kern 1pt} {\kern 1pt} {\kern 1pt} 6}&{0.042{\kern 1pt} {\kern 1pt} 4}&{0.05{\kern 1pt} {\kern 1pt} 6} \end{array}} \right]^{\rm{T}}}{\kern 1pt} {\kern 1pt} {\rm{rad}}/{\rm{s}}. $ |
系统参数为
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1\\ 0&0&0&0&0&{0.001{\kern 1pt} {\kern 1pt} {\kern 1pt} 1}\\ 0&0&0&0&0&0\\ 0&0&0&{ - 0.000{\kern 1pt} {\kern 1pt} 8}&0&0 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 0&0&0\\ 0&0&0\\ 0&0&0\\ {0.041{\kern 1pt} {\kern 1pt} 7}&0&0\\ 0&{0.031{\kern 1pt} {\kern 1pt} {\kern 1pt} 3}&0\\ 0&0&{0.032{\kern 1pt} {\kern 1pt} {\kern 1pt} 3} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{B}}_{\rm{d}}} = \left[ {\begin{array}{*{20}{c}} { - 0.2}&{0.01}&{ - 0.02}\\ { - 0.1}&{0.02}&{ - 0.04}\\ {0.1}&{ - 0.02}&{0.04}\\ {0.2}&{0.02}&{ - 0.04}\\ { - 0.2}&{0.01}&{ - 0.02}\\ { - 0.1}&{0.02}&{ - 0.04} \end{array}} \right],{\mathit{\boldsymbol{B}}_{\rm{s}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1\\ 1&0&0\\ 0&1&0\\ 0&0&0 \end{array}} \right]. $ |
给定的外界干扰为
| $ \mathit{\boldsymbol{d}} = 0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 1 \times {[{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} t,{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} t,{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} t]^{\rm{T}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}}. $ |
本节中故障设计为
| $ {f_1} = \left\{ {\begin{array}{*{20}{l}} {0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}},\;\:t < 20{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}};}\\ {0.1(t - 20){\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}},\;\:20{\rm{s}} \le t < 25{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}};}\\ {0.1(30 - t){\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}},\;\:25 \le t < 30{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}};}\\ {0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}},\;\:t \ge 30{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}.} \end{array}} \right. $ |
| $ {f_2} = \left\{ {\begin{array}{*{20}{l}} {0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}},\;\:t < 40{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s;}}}\\ {0.1(40 - t){\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}},\;\:40{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}} \le t < 45{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s;}}}\\ { - 0.5{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}},\;\:45{\rm{s}} \le t < 50{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s;}}}\\ \begin{array}{l} 0.1(t - 55){\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}},\;\:50{\rm{s}} \le t < 55{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s;}}\\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}},\;\:t \ge 55{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.}} \end{array} \end{array}} \right. $ |
| $ {f_3} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}}. $ |
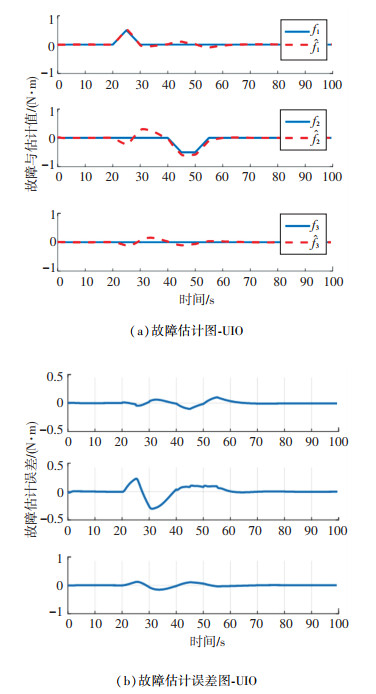
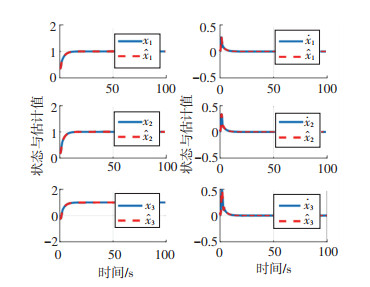
仿真结果如图 1~3所示. 图 1为故障估计及其对应的误差图,图中蓝色实线为故障真实值,红色虚线为故障估计值,可以看出红色虚线可以基本实现对故障真实值的估计,从而验证了所设计的未知输入观测器的有效性.故障估计误差在较小范围内波动,这种波动是由于故障之间的耦合相互影响造成的,属于故障估计中的正常范围. 图 2为状态估计图,图中显示航天器的状态可以在有限时间内到达平衡点,且状态估计值可以有效跟踪真实值,从而验证了所设计未知输入观测器的有效性.
|
图 1 故障估计及其误差图-UIO Fig. 1 Fault estimation and its errors-UIO |
|
图 2 基于未知输入观测器的状态估计图 Fig. 2 UIO-based state estimation |
|
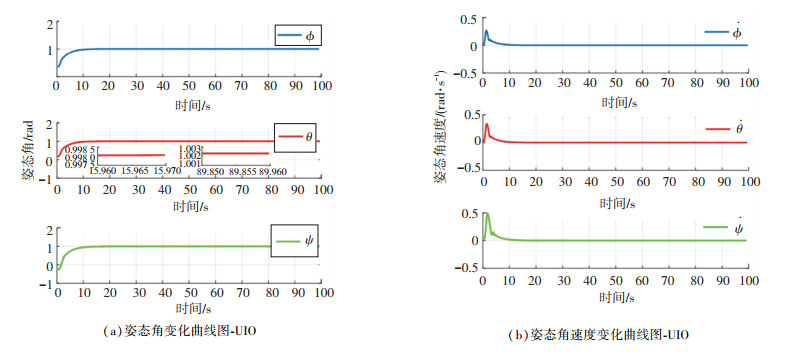
图 3 姿态角及姿态角速度变化曲线图-UIO Fig. 3 Variation of attitude angle and attitude angular velocity-UIO |
图 3为姿态角及姿态角速度的变化曲线图,从图中可以看出,在未知输入观测器-容错控制器综合作用下,航天器的姿态角及角速度可以在有限时间内到达平衡点.未发生故障时观测精度为1.9×10-3,而发生故障后在所设计的观测器-容错控制器综合作用下,控制精度为2.2×10-3,系统控制性能较无故障时降低15.7%.
5.2 干扰及故障解耦估计仿真结果本节中故障设计为
| $ {f_1} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}}; $ |
| $ {f_2} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}}; $ |
| $ {f_3} = \left\{ {\begin{array}{*{20}{l}} {0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}},t < 40{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}};}\\ {0.1(t - 40){\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}},40{\rm{s}} \le t < 45{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}};}\\ {0.1(50 - t){\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}},45{\rm{s}} \le t < 50{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}};}\\ {0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{N}} \cdot {\rm{m}},t \ge 50{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}.} \end{array}} \right. $ |
此外,自适应滑模未知输入观测器及容错控制器参数设置见表 1.
| 表 1 自适应滑模未知输入观测器及控制器参数 Tab. 1 Parameters of adaptive sliding mode unknown input observer (ASUIO) and controller |
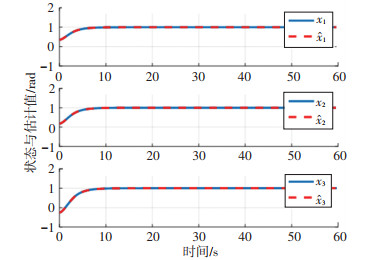
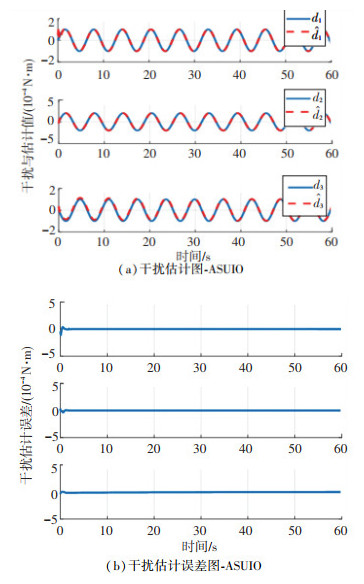
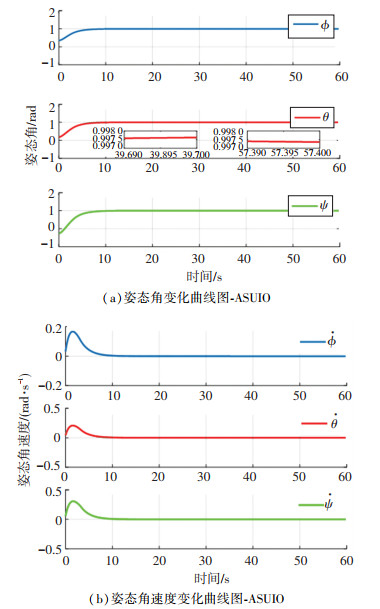
仿真结果如图 4~7所示. 图 4为所设计的等效输出注入项对故障估计及其误差图,图中故障估计误差在零值左右浮动,所设计的观测器可以基本实现对故障的估计;图 5为状态估计图,从图中可以看出,估计曲线与实际曲线基本重合,所设计的观测器可以实现对系统状态的有效估计;图 6为干扰估计及其误差图,在开始时刻,干扰估计误差会出现略微波动,但波动值很小并很快稳定,从而验证了自适应滑模未知输入观测器对干扰估计的有效性. 图 7为姿态角及姿态角速度变化曲线,从图中可以看出,基于所设计的自适应滑模未知输入观测器,实现对故障及干扰的有效估计后,设计的容错控制器可以保证航天器的姿态角及角速度在有限时间内到达平衡点.未发生故障时姿态控制精度为1.2×10-3,而发生故障后在所设计的观测器-容错控制器综合作用下,控制精度为1.3×10-3,控制性能较无故障时降低8.3%.

|
图 4 故障估计及其误差图-ASUIO Fig. 4 Fault estimation and its errors-ASUIO |
|
图 5 基于自适应滑模未知输入观测器的状态估计图 Fig. 5 ASUIO-based state estimation |
|
图 6 干扰估计及其误差图-ASUIO Fig. 6 Disturbance estimation and its errors-ASUIO |
|
图 7 姿态角及姿态角速度变化曲线图-ASUIO Fig. 7 Variation of attitude angle and attitude angular velocity-ASUIO |
针对故障和干扰影响下的航天器线性系统,首先,基于扩展状态系统设计基于未知输入观测器,进行故障检测及故障估计一体化设计,实现了干扰影响下对系统状态和故障的有效估计.其次,基于等价输出的概念,设计新型自适应滑模未知输入观测器,减小了干扰处理带来的时间延迟,同时实现了对故障及干扰的解耦估计,且可以处理更广泛的故障类型.最后设计多变量终端滑模容错控制器,提高了控制性能,保证了输出跟踪的鲁棒性.下一步考虑将所提出的方法进行扩展,以处理具有故障和扰动的非线性系统.
| [1] |
YAN X G, EDWARDS C. Nonlinear robust fault reconstruction and estimation using a sliding mode observer[J]. Automatica, 2007, 43(9): 1605. DOI:10.1016/j.automatica.2007.02.008 |
| [2] |
WU Qing, SAIF M. Robust fault diagnosis of a satellite system using a learning strategy and second order sliding mode observer[J]. IEEE Systems Journal, 2010, 4(1): 112. DOI:10.1109/JSYST.2010.2043786 |
| [3] |
VAN M, KANG H J, SUH Y S. Third order sliding mode observer based robust fault diagnosis for robot manipulators[J]. Journal of Institute of Control, Robotics and Systems, 2012, 18(7): 669. DOI:10.5302/J.ICROS.2012.18.7.669 |
| [4] |
CAPISANI L M, FERRARA A, De LOZA A F, et al. Manipulator fault diagnosis via higher order sliding-mode observers[J]. IEEE Transactions on Industrial Electronics, 2012, 59(10): 3979. DOI:10.1109/TIE.2012.2189534 |
| [5] |
LEE D J, PARK Y, PARK Y. Robust H∞ sliding mode descriptor observer for fault and output disturbance estimation of uncertain systems[J]. IEEE Transactions on Automatic Control, 2012, 57(11): 2928. DOI:10.1109/TAC.2012.2195930 |
| [6] |
LAGHROUCHE S, LIU Jianxing, AHMED F S, et al. Adaptive second-order sliding mode observer-based fault reconstruction for PEM fuel cell air-feed system[J]. IEEE Transactions on Control Systems Technology, 2014, 23(3): 1098. DOI:10.1109/TCST.2014.2361869 |
| [7] |
CHEN Fuyang, JIANG Rongqiang, ZHANG Kangkang, et al. Robust backstepping sliding-mode control and observer-based fault estimation for a quadrotor UAV[J]. IEEE Transactions on Industrial Electronics, 2016, 63(8): 1. DOI:10.1109/TIE.2016.2552151 |
| [8] |
De LOZA A F, CIESLAK J, HENRY D, et al. Output tracking of systems subjected to perturbations and a class of actuator faults based on HOSM observation and identification[J]. Automatica, 2015, 59: 200. DOI:10.1016/j.automatica.2015.06.020 |
| [9] |
VAN M, FRANCIOSA P, CEGLAREK D. Fault diagnosis and fault-tolerant control of uncertain robot manipulators using high-order sliding mode[J]. Mathematical Problems in Engineering, 2016, 2016: 1. DOI:10.1155/2016/7926280 |
| [10] |
EFIMOV D, EDWARDS C, ZOLGHADRI A. Enhancement of adaptive observer robustness applying sliding mode techniques[J]. Automatica, 2016, 72: 53. DOI:10.1016/j.automatica.2016.05.029 |
| [11] |
LIU Jianxing, LUO Wensheng, YANG Xiaozhan, et al. Robust model-based fault diagnosis for PEM fuel cell air-feed system[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3261. DOI:10.1109/TIE.2016.2535118 |
| [12] |
穆凌霞, 余翔, 李平, 等. 自适应广义滑模观测器之状态估计和故障重构[J]. 控制理论与应用, 2017, 34(4): 483. MU Lingxia, YU Xiang, LI Ping, et al. State estimation and fault reconstruction from an adaptive descriptor sliding mode observer[J]. Control Theory & Applications, 2017, 34(4): 483. |
| [13] |
HU Qinglei, NIU Guanglin, WANG Chenliang. Spacecraft attitude fault-tolerant control based on iterative learning observer and control allocation[J]. Aerospace Science and Technology, 2018, 75: 245. DOI:10.1016/j.ast.2017.12.031 |
| [14] |
NEMATI F, HAMAMI S M S, ZEMOUCHE A. A nonlinear observer-based approach to fault detection, isolation and estimation for satellite formation flight application[J]. Automatica, 2019, 107: 474. DOI:10.1016/j.automatica.2019.06.007 |
| [15] |
CORLESS M, TU J. State and input estimation for a class of uncertain systems[J]. Automatica, 1998, 34(6): 757. DOI:10.1016/S0005-1098(98)00013-2 |
| [16] |
ZHANG Xiuyun, ZONG Qun, TIAN Bailing, et al. Continuous robust fault-tolerant control and vibration suppression for flexible spacecraft without angular velocity[J]. International Journal of Robust and Nonlinear Control, 2019, 29(12): 3915. DOI:10.1002/rnc.4584 |
| [17] |
TIAN Bailing, FAN Wenru, SU Rui, et al. Real-time trajectory and attitude coordination control for reusable launch vehicle in reentry phase[J]. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1639. DOI:10.1109/TIE.2014.2341553 |
| [18] |
DONG Qi, ZONG Qun, TIAN Bailing, et al. Adaptive disturbance observer-based finite-time continuous fault-tolerant control for reentry RLV[J]. International Journal of Robust and Nonlinear Control, 2017, 27(18): 4275. DOI:10.1002/rnc.3796 |
 2020, Vol. 52
2020, Vol. 52


