2. 华北电力大学 控制与计算机工程学院, 河北 保定 071003
2. School of Control and Computer Engineering, North China Electric Power University, Baoding 071003, Hebei, China
电动机的可靠运行是游梁式采油机正常工作的基础.采油井所处背景环境复杂,加之三相电机驱动大型游梁式采油机工况的特殊三相电机驱动大型游梁式采油机工况的特殊性,对其进行准确故障诊断实际上更为困难.电动机机械故障常表现为轴承偏心、绕组短路、堵转或供电电源故障等[1].前人的研究大多集中在电机振动信号和定子电流信号[2-4],对于电流信号分析诊断故障而言,由于与故障存在相关性的频率分量较小,直接对电动机机械故障不够敏感;利用非侵入式振动信号诊断电机故障方法简单有效,实用性强,通常采用压电式加速度传感器采集信号,但传感器安装和耦合方式影响信号频率响应范围.鉴于声音信号可由非接触式传感器获取,测量频带宽,且往往伴随电机振动同源产生,可以有效弥补振动传感器非刚性连接问题和频带限制产生的失效现象.探索声振信号联合互补的处理方法,利用非侵入式多传感器监测优势,对大型异步电机进行故障诊断具有重要研究价值.
许多学者研究了声振联合方法诊断高压断路器运行状态,文献[5]对声振信号进行改进集合经验模式分解,对分解后固有模态函数(IMF)求其二维谱熵作为特征向量进行故障诊断.文献[6]利用互补总体经验模态分解算法对声振信号进行分解,求取IMF分量的能量系数、样本熵、功率谱熵作为特征向量进行故障诊断.文献[7]对声振信号进行局部均值分解,然后对PF分量求取近似熵作为特征向量进行故障诊断.上述方法对断路器故障诊断取得了一定效果,但仅限于将声振信号两者进行机械地联合,未考虑背景情况和声振信号差异性互补.在分布式油井所处的恶劣环境下,如何发挥声振信号联合优势进行设备故障诊断更有挑战性.
声振信号分析有Fourier变换、小波变换、EMD分解、LMD分解等,其特征提取方法常依靠人工选择和专家知识,故障模式识别算法主观性过强,容易造成故障信息的遗漏和丢失[8].遴选、提取特征后再选择合适的分类器进行故障分类,样本数据变动时需要有针对性地不断对特征阈值和方法进行调整,诊断模型及算法总体泛化能力差[9].随着深度学习理论的不断发展,卷积神经网络(convolutional neural network,CNN)在图像识别、语音识别等领域得到了广泛应用. CNN作为典型的深度学习算法,具备强大的特征学习能力,自适应性好、运行速度快,具备良好的自学习和并行处理能力,在机械设备的故障诊断中具有一定优势[10-11].文献[12]把电机的电流信号进行CNN的故障诊断,文献[13]对轴承振动信号进行了单层卷积,文献[14]对振动信号进行EEMD分解,然后构造特征数据集.上述研究对机械故障诊断取得了一定效果,但缺乏对信号提纯处理,其特征提取过程复杂,需要人工干预,且受到样本数据量限制造成故障识别准确率不高,没有把CNN的自学习和分类能力最大化.
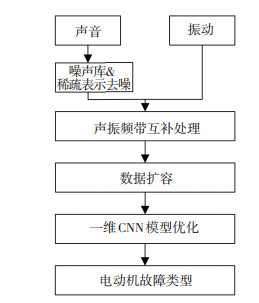
1 大型电动机的故障诊断流程针对游梁式采油机配套的大型三相电动机,本文提出联合运行中声音和振动信号特征各自频带优势,运用滤波处理后的数据扩容,构成足量数据样本输入CNN进行故障识别的新方法,其流程如图 1所示.
|
图 1 电机诊断流程 Fig. 1 Motor diagnosis flow |
采油井分布于野外或道路两旁,人文背景和抽油泵皮带连接噪声严重影响电机运行信号的质量,非平稳声音时间序列有明显形态特征,诊断故障的第一步要基于背景噪声库联合稀疏表示对此类噪进行处理.
电机旋转驱动抽油泵上下往复运动,限于振动传感器安装方式信号呈现可靠的窄带(量程一定,灵敏度与有效频率平方成反比)特点,仅靠低频振动信号显然不能覆盖电机发生故障的全部频率范围,因此需要同源声音信号对振动进行频带互补拓展.
将叠频后声振信号转化为一维形式,避免原始信号空间序列相关性遭到破坏,再利用数据扩容提供1D-CNN所需数据,最后采用一维卷积神经网络对声振信号进行故障诊断.实现本文提出方法的关键环节在于声振信号去噪、频带互补拓展、以及CNN输入数据扩容和诊断方法优化过程.
2 声振信号预处理过程考虑采油井现场声振信号的频带特点,首先建立背景噪声库去除模板噪声,利用稀疏表示去除声音信号的残余噪声,再将振动和声音有机联合控制表征故障信息的频率范围,提纯的原始样本数据为电机故障诊断准确率的提高奠定了基础.
2.1 背景噪声库联合稀疏表示去噪采油机工作现场夹杂风声、打雷声、汽笛声和人语声等环境噪声,也会出现抽油机皮带摩擦、减速箱异响和游梁机械运行噪声.在采集这些背景噪声样本形成特征库基础上,第1步通过拾音器获得声音信号进行双门限端点检测计算起始点,再使用Mel倒谱系数(MFCC)获取频域信息,提取背景信号特征,最后采用动态时间规整进行模板匹配(DTW)去除模板噪声.
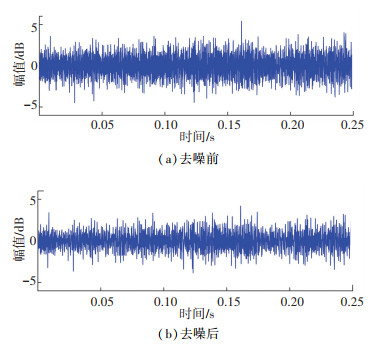
针对仍有残余噪声、信噪比不高的电机声音信号,根据其尖峰和突变形态特征差异明显特点,第2步采用一个或者几个形态结构去逼近,即稀疏表示,利用广义K-奇异值分解(K-SVD)算法求得基于稀疏和冗余的训练字典,得到降噪后的信号. K-SVD训练能够有效反应信号结构,选用冲击原子构建冗余字典,然后再用0范数贪婪算法中的正交匹配追踪(OMP)算法选择原子进行模型逼近,达到50次迭代后停止,原始信号(去除模板噪声)减去残余背景信号从而实现去噪[15].本文对某平原地区采油井Y2-280M-8型电动机的声音信号进行上述信号处理过程,如图 2所示.
|
图 2 去噪前后的声音信号对比 Fig. 2 Comparison of sound signal before and after denoising |
由上图和多种实际信号验证,去噪后声信号的背景噪声明显减少,原始信号细节信息被保留,均方误差和平均绝对误差降低,声信号的信噪比得到了提高.
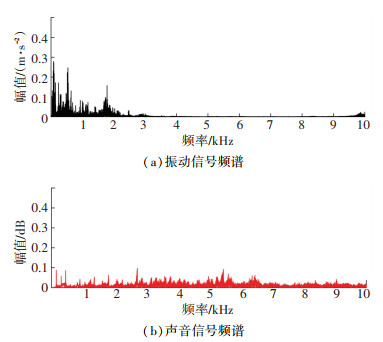
2.2 声振信号的频带互补处理选用频率为1~10 000 Hz压电式(CK 8605)传感器和频率为20~20 000 Hz的(WM-025N)拾音器,同时采集电机运行振动和声音信号.以电机载荷过重情况为例,声振信号虽为同源,频谱分布明显不同,如图 3所示.
|
图 3 载荷过重频谱图 Fig. 3 Load overweight spectrum |
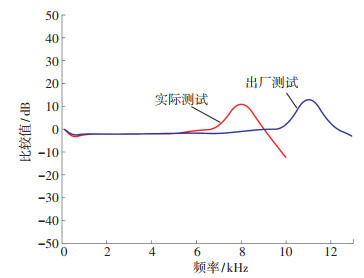
实测信号分析结果可以看出振动谱峰只出现在3 kHz以下,显然无法全面反应电机的多类型故障.实际上,传感器频率响应曲线是出厂时刚性连接下测得的,而在实际压电式加速度应用强磁吸附或胶粘很难达到刚性连接[16],其频响曲线差异如图 4所示.
|
图 4 CK 8605传感器频率响应曲线 Fig. 4 Frequency response curves of CK 8605 sensor |
图 4中,横坐标是实测频率值,纵坐标是幅值比较值,等于20log(A2/A1),A2为所测点频率振幅,A1为所测全部数据平均振幅.非刚性方式连接的传感器频响范围减小30%,最佳频率响应为0.1~7 kHz,测电机高频振动容易造成信号失真.
电机故障诊断中声振信号同源,振动传感器直接与电机本体吸附,信号在7 kHz以内有很强抗扰性;声音传感器置于电机附近,信号频率可达20 kHz.本文将去噪后的声音信号,先采用有限长单位冲激响应(finite impulse response,FIR)带通滤波器滤除低于7 kHz和高于20 kHz声音信号,再采用低通滤波器滤除7 kHz以上振动信号,将两者互补特性联合从而可以精准地掌握整个故障阶段的信息,为卷积神经网络准确诊断故障提供精准的样本数据.
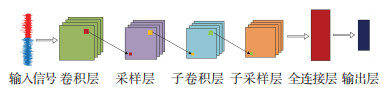
3 CNN诊断方法及优化 3.1 CNN诊断原理CNN作为深度学习的典型代表,是由输入层、卷积层、池化层、全连接层和输出层组成的神经网络结构,如图 5所示.每一层的权值矩阵与特征矩阵进行卷积,前一层的卷积结果经过激活函数运算会输出成为下一个神经元,以便构造下一层对应的特征.
|
图 5 卷积神经网络结构示意图 Fig. 5 Schematic diagram of CNN structure |
卷积层通过卷积核对输入数据进行卷积,利用非线性激活函数构造特征矢量.同一个卷积核在卷积过程中共享参数,故一个卷积核得到一类特征.计算公式为
| $ {x_j}^l = f(\sum\limits_{i \in {N_j}} {{x_i}^{l - 1} \times {k_{ij}}^l + {b_j}^l} ). $ | (1) |
式中:xjl-1为第l层输入,l为第l层网络,k为卷积核,b为卷积核的偏置.
通常选择修正线性单元(rectified linear unit,ReLU)作为非线性激活函数,可以使得一部分的神经元输出为0,减少参数的相互依赖,提高网络的稀疏性. ReLU的计算公式为
| $ {g_i}^{l + 1}\left( j \right) = f({y_i}^{l + 1}\left( j \right)) = {\rm{max}}\left\{ {0, {y_i}^{l + 1}\left( j \right)} \right\}. $ | (2) |
式中:gil+1(j)为yil+1(j)的激活值,yil+1(j)为卷积运算的输出值.
池化层通过池化核对输入数据进行缩放映射,对数据降维同时提取特征.池化包含平均池化和最大池化,其变换函数为
| $ \begin{array}{l} {P_i}^{l + 1}\left( j \right) = \mathop {{\rm{max}}}\limits_{\left( {j - 1} \right)W + 1 \le t \le jW} \left\{ {{q_i}^l\left( t \right)} \right\}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \in \left[ {\left( {j - 1} \right)W + 1, jW} \right]. \end{array} $ | (3) |
式中:W为卷积核宽度,qil(t)为第l层第i个特征中第t个神经元的值,Pil+1(j)为第l+1个神经元对应的值.
CNN的输出层对最后一个池化层的输出进行全连接,然后采用Soft-Max分类器解决多分类问题,模型为
| $ O = f({\mathit{\boldsymbol{b}}_o} + {\mathit{\boldsymbol{f}}_v}{\mathit{\boldsymbol{w}}_o}). $ | (4) |
式中:bo为偏差向量,fv为特征矢量,wo为权值矩阵.
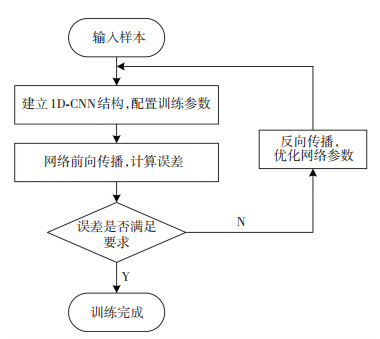
3.2 参数设置分别对Y2-280M-8型45 kW三相电动机进行正常运行、轴承偏心、载荷过重和定子绕组短路试验,在不同状态下采集声音和振动信号数据样本.每类样本采集600组数据,每组数据包含50 000个采样点,分割样本长度设定为1 024. 2/3组数据样本用作训练,1/3组数据样本作为测试. 1D-CNN的特征提取层由卷积层和池化层组成,在进行池化操作前,选择ReLU作为激活函数增加模型的非线性.选定两个特征提取层,其特征提取层设置卷积核数量分别为32和64,设定卷积核尺寸为1×15,池化层采用大小为1×2,步长为2的最大池化,两个全连接层的节点分别设置为256和64.采用RMSprop优化器,初始学习率设置为0.03,衰减率为0.99,迭代次数为500,模型的训练步骤如图 6所示.
|
图 6 模型训练示意图 Fig. 6 Schematic diagram of model training |
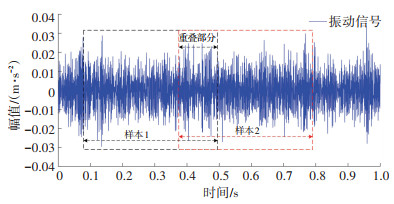
实现1D-CNN准确电机故障诊断必须有大量的一维训练样本作为支撑,针对1D-CNN需求数据量大、数据获取时间长的特点采取重叠式数据扩容,数据扩容后模型在相同的采样率下获得同等数量样本所需的时间更短,缩减了1D-CNN的故障诊断时间.扩容示意图如图 7所示.
|
图 7 数据扩容示意图 Fig. 7 Schematic diagram of data expansion |
采用有重叠样本分割可以完整保留相邻样本的相关性,同时避免样本截断导致的特征丢失. 对长度为N的信号x,设置样本长度为L,重叠率为λ,扩容分割方法如下:
1) 求得当前信号长度下最大可分割样本数量
2) 求取每个分割样本,其中第i个样本在原信号的位置表示为
| $ {x_i} = X\left[ {\left( {i - 1} \right) \times L \times \left( {1 - \lambda } \right) + \left( {0:1} \right) \times L} \right], $ | (5) |
式中: i∈[1, n],xi为分割后的样本数据.
样本分割长度太短可以提高模型收敛速度,节省训练时间,但是易造成非线性特征信息缺失;样本分割长度太长会影响模型收敛速度,影响诊断的实时性,经过试验分析,本文设定λ为0.5.
3.3.2 模型结构优化卷积神经网络由于特殊结构使得其具有很强的泛化能力,但是对于采油机而言,电动机通过皮带拖动减速箱使游梁做上下冲程运动导致数据变动很大,限制了1D-CNN泛化性能和准确率的提高.
1D-CNN的卷积核之间存在相关性,而相关性越小,卷积提取的特征越全面,泛化性和准确率越好[17].为了提高泛化性和准确率,本文对核函数进行小波分解得到多分辨率小波系数,选取相互正交方向的小波分解系数对卷积核误差修改量处理去除核函数的相关性.与此同时,对每个卷积-池化层之后增加一个局部响应归一化(local response normalization,LRN)降低模型所需参数较多的影响. LRN层可以模仿生物的“侧抑制”机制,使响应较大的值变得更大,响应归一化表示[18]为
| $ {s_{x, y}}^i = {q_{x, y}}^i/{\left( {k + \alpha \sum\limits_{j = {\rm{max}}\left( {0, i - n/2} \right)}^{{\rm{min}}\left( {N - 1, i + n/2} \right)} {{{\left( {{q_{x, y}}^i} \right)}^2}} } \right)^\beta }. $ | (6) |
式中:n为同一空间位置经过邻近映射核数,N为此层总核数,qx, yi为第i个核在(x, y)处ReLU非线性神经元输出,k、α、β均为验证集超参数,其值分别为2、0.000 2、0.5.
训练过程中为了避免发生过拟合现象,在模型全连接层中引入Early-Stopping机制,其系数分别为0.5、0.01.本文的模型结构见表 1.
| 表 1 1D-CNN结构表 Tab. 1 1D-CNN structure |
模型采用软件Python与Tensorflow,操作系统为MacOS,处理器为Intel(R) Core(TM) i5-4440 CPU@3.10 GHz,运行内存为8 GB.
对本模型进行500次训练,采用最小均方误差(mean square error,MSE)作为损失函数,公式为
| $ {\rm{MSE}} = \frac{{\sum\limits_{i = 1}^N {{{({x_p}^i - {x_t}^i)}^2}} }}{N}. $ | (7) |
式中:xpi为第i个样本的预测,xti为第i个样本的真实分类.
为了对学习到的效果进行验证,利用主成分分析(principal components analysis,PCA)对倒数第2层(全连接层)的学习特征进行可视化,如图 8所示.

|
图 8 学习特征可视化 Fig. 8 Learning feature visualization |
由图 8可知,模型各状态下的学习特征聚集在相应的区域内,说明模型的区分性很好.
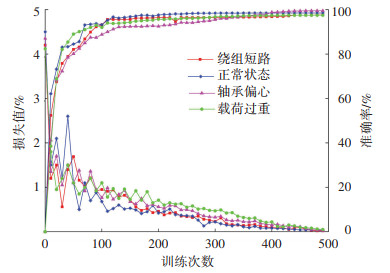
采用Soft-Max作为分类器进行分类,识别效果如图 9所示(其中图形的上半部分指准确率,下半部分指训练损失值).由图 9可知,随着训练次数的增加,模型的识别准确率逐渐上升,在训练350次后准确率趋于稳定并不再提高.与此同时,损失值逐渐下降,此时卷积神经网络的训练效果最佳.
|
图 9 模型的准确率和损失值 Fig. 9 Model accuracy and loss values |
虽然本文设定训练次数为500,但迭代400次后准确率不再提高且损失值相应降为最低.由于引入Early-Stopping机制,当模型的准确率和损失值不再显著变化时停止模型的训练,有效地避免了过拟合现象.
经过训练后,模型总的分类准确率达到了97.75%,证明了声振联合更能全面准确地反映电动机的运行状态,分类结果见表 2.
| 表 2 1D-CNN分类结果 Tab. 2 1D-CNN classification results |
为了验证本文提出声振联合方法的有效性,将之与文献[5-7]所用的传统联合方法进行对比,结果如图 10所示.

|
图 10 声振联合诊断结果对比 Fig. 10 Comparison of diagnostic results of sound-vibration joint methods |
由对比图表可知,本文联合方法进行故障诊断的正确分类组数远高于传统联合方法,传统联合方法的总体分类准确率为91.8%,说明本文提出的方法对信号预处理有效.原因是背景噪声库联合稀疏表示去噪有效抑制了背景噪声的干扰,再使用声信号弥补振动信号的频段失真,通过原始样本信号的提纯控制使得CNN的学习效果更好.
4.2.2 不同模型的准确率和泛化性对比对比所提方法与SVM、BP和RVM三种智能算法的优势,针对同样的训练样本,采用文献[14]提到的EEMD算法对原始信号(未经预处理)进行分解,然后利用SVM、BP和RVM进行诊断,结果见表 3.由表 3可知,CNN的分类准确率远远高于其他算法,其中平均准确率高于SVM平均准确率11.50%,高于BP平均准确率12.50%,高于RVM平均准确率10.75%.这主要得益于CNN权值共享、池化、全连接等独特结构,这些结构使得CNN具有尺度位移与不变性、区域感知的特点,能对特征进行全面学习,容错能力强,弥补了其他浅层分类算法特征学习不充分、泛化能力差的缺点.
| 表 3 不同诊断模型的结果对比 Tab. 3 Comparison of results of different diagnostic models |
由于在实际的油田作业中数据的来源和结构不同,故需对同种类型、不同表征的故障数据进行分类.因而,换用Y2-315S-8型号的电动机,采样频率由40 kHz变成30 kHz,换用PCB357B21型号的传感器,同时更改传感器安放位置,诊断结果见表 4.
| 表 4 变动后不同诊断模型的结果对比 Tab. 4 Comparison of results of different diagnostic models after changes |
由表 4可知,传统智能诊断方法在数据结构和来源发生变动的情况下诊断准确率明显降低,而1D-CNN模型由于其优良的泛化性能仍然保持了非常高的准确率.
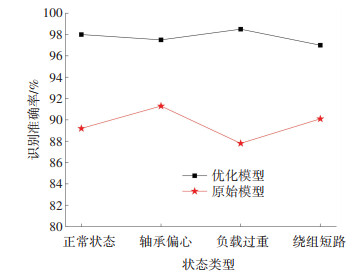
4.2.3 优化模型泛化能力验证为了验证优化模型的泛化能力,使用原模型进行对照,诊断结果如图 11所示.
|
图 11 不同模型诊断效果对比 Fig. 11 Comparison of diagnostic effects of different models |
由图 11可知,在数据的来源、采集参数设置、传感器位置发生了变化的情况下,优化后的1D-CNN模型总体诊断准确率依旧达到了97.75%,远高于未优化的模型,说明优化后的模型对新鲜样本的自适应能力更强,泛化能力更好.
4 结论1) 针对大型电机声振信号的同源互补性,提出了一种基于声振信号联合的1D-CNN故障诊断方法,大大提高了故障诊断的准确率.
2) 提出基于背景噪声库联合稀疏表示去噪后,进行声振互补联合处理的控制信号提纯新方法,对原始数据进行了有效剪辑,为1D-CNN准确诊断电机现场故障奠定了基础.
3) 数据扩容为模型提供了大量数据,采用LRN和核函数去相关性对模型进行了优化,验证了故障诊断算法效果及其广泛通用性,提高了1D-CNN的泛化能力.
| [1] |
杨国安. 电动机故障诊断实用技术[M]. 北京: 中国石化出版社, 2012. YANG Guoan. Practical technology for motor fault diagnosis[M]. Beijing: China Petrochemical Press, 2012. |
| [2] |
赵玉辉.基于小波分析的异步电动机的故障诊断[D].哈尔滨: 哈尔滨理工大学, 2016 ZHAO Yuhui. Fault detection of induction motor based on wavelet analysis[D]. Harbin: Harbin University of Science and Technology, 2016 |
| [3] |
刘智勇. 交流异步电动机故障综合诊断方法研究[J]. 自动化应用, 2018(7): 124. LIU Zhiyong. Research on fault diagnosis method of AC asynchronous motor[J]. Automation Application, 2018(7): 124. DOI:10.3969/j.issn.1674-778X.2018.07.052 |
| [4] |
左志文.基于HHT和RBF神经网络的异步电动机故障诊断的研究[D].太原: 太原理工大学, 2015 ZUO Zhiwen. The study on fault diagnosis of asynchronous motor based on HHT and RBF neural network[D]. Taiyuan: Taiyuan University of Technology, 2015 |
| [5] |
赵书涛, 张佩, 申路, 等. 高压断路器振声联合故障诊断方法[J]. 电工技术学报, 2014, 29(7): 216. ZHAO Shutao, ZHANG Pei, SHEN Lu, et al. Vibration and acoustic joint mechanical fault diagnosis method of high voltage circuit breakers[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 216. DOI:10.3969/j.issn.1000-6753.2014.07.028 |
| [6] |
孙曙光, 于晗, 杜太行, 等. 基于多特征融合与改进QPSO-RVM的万能式断路器故障振声诊断方法[J]. 电工技术学报, 2017, 32(19): 107. SUN Shuguang, YU Han, DU Taihang, et al. Vibration and acoustic joint fault diagnosis of conventional circuit breaker based on multi-feature fusion and improved QPSO-RVM[J]. Transactions of China Electrotechnical Society, 2017, 32(19): 107. DOI:10.19595/j.cnki.1000-6753.tces.160769 |
| [7] |
HE Mengyuan, DING Qiaolin, ZHAO Shutao, et al. Research of circuit breaker intelligent fault diagnosis method based on double clustering[J]. IEICE Electronics Express, 2017, 14(17): 20170463. DOI:10.1587/elex.14.20170463 |
| [8] |
李舜酩, 郭海东, 李殿荣. 振动信号处理方法综述[J]. 仪器仪表学报, 2013, 34(8): 1907. LI Shunming, GUO Haidong, LI Dianrong. Review of vibration signal processing methods[J]. Chinese Journal of Scientific Instrument, 2013, 34(8): 1907. DOI:10.3969/j.issn.0254-3087.2013.08.031 |
| [9] |
曲建岭, 余路, 袁涛, 等. 基于一维卷积神经网络的滚动轴承自适应故障诊断算法[J]. 仪器仪表学报, 2018, 39(7): 134. QU Jianling, YU Lu, YUAN Tao, et al. Adaptive fault diagnosis algorithm for rolling bearings based on one-dimensional convolutional neural network[J]. Chinese Journal of Scientific Instrument, 2018, 39(7): 134. |
| [10] |
任浩, 屈剑锋, 柴毅, 等. 深度学习在故障诊断领域中的研究现状与挑战[J]. 控制与决策, 2017, 32(8): 1345. REN Hao, QU Jianfeng, CHAI Yi, et al. Deep learning for fault diagnosis: the state of the art and challenge[J]. Control and Decision, 2017, 32(8): 1345. |
| [11] |
黄新波, 胡潇文, 朱永灿, 等. 基于卷积神经网络算法的高压断路器故障诊断[J]. 电力自动化设备, 2018, 38(5): 136. HUANG Xinbo, HU Xiaowen, ZHU Yongcan, et al. Fault diagnosis of high-voltage circuit breaker based on convolutional neural network[J]. Electric Power Automation Equipment, 2018, 38(5): 136. |
| [12] |
INCE T, KIRANYAZ S, EREN L, et al. Real-time motor fault detection by 1-D convolutional neural networks[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11): 7067. DOI:10.1109/TIE.2016.2582729 |
| [13] |
JANSSENS O, SLAVKOVIKJ V, VERVISCH B, et al. Convolutional neural network based fault detection for rotating machinery[J]. Journal of Sound & Vibration, 2016, 377. |
| [14] |
肖良君.基于卷积神经网络的胶印机滚动轴承故障诊断方法研究[D].西安: 西安理工大学, 2018 XIAO Liangjun. Research on fault diagnosis method of offset rolling bearing based on convolutional neural network[D]. Xi'an: Xi'an University of Technology, 2018 |
| [15] |
叶华, 谭冠政, 李广, 等. 基于稀疏表示与粒子群优化算法的非平稳信号去噪研究[J]. 红外与激光工程, 2018, 47(7): 328. YE Hua, TAN Guanzheng, LI Guang, et al. De-noising nonstationary signal based on sparse representation and particle swarm optimization[J]. Infrared and Laser Engineering, 2018, 47(7): 328. |
| [16] |
王锴, 刘志国, 刘刚, 等. 压电式加速度传感器的频响检测分析[J]. 测控技术, 2014, 33(9): 116. WANG Kai, LIU Zhiguo, LIU Gang, et al. Research on frequency response based on piezoelectric accelerometer[J]. Measurement & Control Technology, 2014, 33(9): 116. DOI:10.3969/j.issn.1000-8829.2014.09.031 |
| [17] |
孟格格.基于CNN的绝缘子状态识别研究[D].北京: 华北电力大学, 2018 MENG Gege. Research of insulator state identification based on CNN[D]. Beijing: North China Electric Power University, 2018 |
| [18] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc., 2012: 1097
|
 2020, Vol. 52
2020, Vol. 52


