地震作用下地下管线的破坏形式主要有三种[1]:管线接口破坏,管体破坏,在三通弯头、阀门以及管线与地下构筑物连接处破坏(图 1)。其中承插式管线的接口破坏是最主要的破坏形式[2]。地震对地下管线产生破坏的原因可分为两类[3]:一类是永久性地面变形,如由断层运动,砂土液化,滑坡等引起的场地破坏;另一类是地震波传播过程中导致的土体瞬态变形。永久性地面变形造成的管线平均破坏率较高,但通常发生在局部特殊场地区域;地震波传播造成的管线平均破坏率相对较低,但地震波动传播效应对地下管线影响范围较广[4]。因此,地震动对研究地下管线结构抗震可靠度具有重要的理论和工程意义。

|
图 1 地震造成的地下管线破坏 Fig. 1 Damage to buried pipelines caused by earthquakes |
地震波动作用下管线响应问题的分析方法可分为解析法和有限元法两大类。共同变位法[5]是最早提出的假定管体与周围土体同步变形的地下管线抗震解析法;Shinozuka等[6]考虑管-土之间的变形滑动,引入应变转换系数β来反映场地土体应变与管线应变之间的关系。解析法的优点是概念清晰、方便应用,缺点是地震动荷载以PGV或PGA的函数表征,不能考虑地震动频谱特性以及不同位置处管线结构、土体参数变化的影响。鉴于此,国内外学者基于有限元法进行地震作用下管线动力时程响应分析。一种是考虑土体存在的精细化有限元模型;另一种是弹性地基梁模型[7],将埋地管线理想化为弹性地基梁模型,管线与土体之间的相互作用简化为管-土连接弹簧,从弹簧支座处输入地震动,求解管线响应。相比于精细化模型,弹性地基梁模型物理意义明确,计算效率高,在地下管线地震分析中被广泛应用[8-10]。
地下管线一般埋设分布于较大的区域内,很难准确获取管线模型中每个位置处的外部荷载、管材和土体特性参数等建模参数。因此,进行地下管线的抗震能力分析时有必要考虑模型参数的不确定性。有限元模型进行地下管线抗震可靠度分析时,由于结构响应与模型输入之间的非线性关系难以使用显式表达,一般采用Monte Carlo模拟方法(MCS)[11]。当管线失效概率较小时,MCS需要大量的抽样计算,耗时较长。很多学者使用改进的MCS方法以期达到高效计算的目的。Tee等[12]以及Ebenuwa等[13]提出的改进抽样方法仍需要大量的样本点,即有限元模型计算次数很多,计算量减少不明显;Babu等[14]使用代理模型响应面函数结合一阶可靠度方法对地下管-土系统进行可靠性分析,与上述改进抽样的方法相比,代理模型方法虽然求解功能函数的次数减少,但模型结果的准确性取决于样本点的选取,容易导致代理模型的计算精度不高。近年来,基于主动学习Kriging代理模型法(active learning based Kriging, AK),广泛应用于多种工程可靠度分析[15-17],主动学习Kriging代理模型方法仅需少量的样本模型计算便可达到较准确的可靠度分析结果,对于由大量管线构成的实际城市地下管网系统的抗震可靠度计算具有重要的现实应用价值,但该方法在管线抗震可靠度问题的适用性尚待研究。本文采用AK-MCS方法研究地下管线抗震可靠度问题,分析Kriging模型方法的适用性和计算效率,以期为地下管网抗震可靠度计算提供依据。
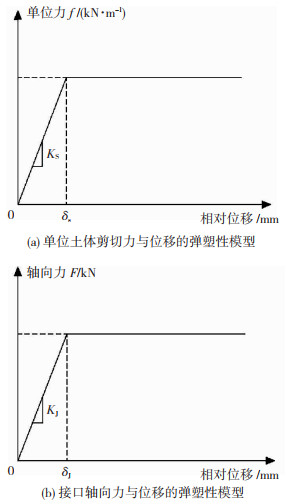
1 地下管线地震响应分析模型承插式接口地下管线地震反应分析模型如图 2所示。模型由管道、管道接口弹簧和模拟“管-土”相互作用的土弹簧组成,地震动位移时程从土弹簧底部输入。地震动行波作用下,由于承插式管道接口刚度较小,管道接口承担了大多数的变形和转角,而管道结构本身的变形较小。因此,在图 2的分析模型中,地下管道采用弹性梁单元模拟,边界条件采用与Shi[8]和Kuwate等[9]类似的处理方式,即管线两端无约束;每根管道单元通过两个土弹簧与土体连接;在土弹簧底部输入沿管道轴向的地震动位移时程;采用管道接口相对位移的允许值作为管线结构安全性的判别准则。图 2中的管道长度L通常为3~6 m,管道接口长度与管道单元长度相比可忽略不计,但为了确保有限元模型数值计算的稳定性,参照Shi[8]和Liu等[18]的方法,本文分析模型中设置管道接口长度为ΔL。沿管道轴向的土弹簧采用图 3(a)所示的双折线模型[19-20],图 3(a)显示了土体对单位长度管道的剪切力f和管道-土体相对位移之间的关系,在管-土相对位移≤δs(土弹簧的弹性极限位移)时线性上升到fy(管-土轴向弹性极限摩擦力),当管-土相对位移>δs后,土体传递给单位长度管道的剪切力为常数fy。fy的表达式为[19]:
| $ f_{\mathrm{y}}= \begin{cases}0.5\left(1+K_{0}\right) \gamma H \pi D \tan \varphi & \text { 砂土 } \\ \alpha S_{\mathrm{u}} \pi D & \text { 黏土 }\end{cases} $ | (1) |

|
图 2 地下管线有限元模型示意 Fig. 2 Schematic of finite element model of buried pipeline |
|
图 3 力与相对位移的弹塑性关系 Fig. 3 Elastoplastic relationship between force and relative displacement |
式中:K0为土的静止侧向土压力系数(回填沟管道一般为0.5≤K0≤1.0);γ为土体容重(N/m3); H为管道中心线的埋深(m); D为管道外径(m); φ为砂土内摩擦角(通常取值范围为25°~45°); Su为周围土体的不排水抗剪强度,对于浅埋且回填压实黏土中的管线, Su的取值范围为25~60 kN/m2; α是决定管道与土体黏结程度的黏附因子,可由Su的数值估算出来[19]。
图 3(b)为反映管道接口轴向拉拔力与相对位移关系的折线模型,当接口两侧管道端点相对位移≤δJ (接口弹性极限位移)时,接口受到的拉拔力呈线性上升;当接口相对位移>δJ后,接口拉拔力为弹性极限拉力常数(FJ)。
一般认为埋设在土体中的地下管线结构在地震波动作用下的结构响应主要受管线周围土体变形的控制,管线结构的惯性力可以忽略不计[5]。简化计算公式得到的地震波动作用下承插式管线接口的张开量可表示为[3]
| $ u_{0}=\varepsilon_{\mathrm{g}} \times L=\frac{V_{\mathrm{a}}}{C_{\mathrm{a}}} \times L $ | (2) |
式中:εg为土体应变; L为管道长度(m); Va为地震波传播方向上的最大水平土体质点速度(m/s); Ca为地震波的传播速度(m/s)[3, 10]。本文中地下管线的非一致地震动主要考虑地震动的行波效应,地震波在土体的运动传播过程中保持波形和振幅不变,沿地震波传播路径上距离为ΔX的两个土体质点振动的加速度、速度和位移时程均只存在一个时滞Δt[10, 21]:
| $ \Delta t=\frac{\Delta X}{C_{\mathrm{a}}} $ | (3) |
式中ΔX为土体中两个位置点间的直线距离(m)。
2 地下管线抗震可靠度分析方法 2.1 随机变量及其分布类型在地下管线的抗震分析模型中,地震动、接口弹簧、土体类型、管线结构等参数的随机性导致了管线抗震安全性分析结果的不确定性。Manolis等[22]在研究地下管线在土体中的动力响应时,将土体密度和摩擦角作为随机变量;Ebenuwa等[13]进行埋地钢管的抗震可靠度分析时,将土体黏聚力、容重,管道容重、埋深、杨氏模量、壁厚等参数作为随机变量;Wijaya等[23]进行不确定性条件下埋地分段式管线地震反应分析时,将黏性土的密度、黏聚力和内摩擦角视为相关的随机变量,同时认为管道渗漏极限接口容许位移为正态分布随机变量;Jahangiri等[24]对15组不同埋深与管径比、场地条件和钢材型号的埋地钢管进行了地震波动作用下的IDA分析;Shi[8]在研究地震波在埋地分段管道中的传播效应时,考虑了峰值地面应变、管道接口特性的变化规律,认为管道渗漏极限接口容许位移是接口插入深度的0.52倍,变异系数为10%。综上,管线结构性能在很大程度上取决于管土相互作用和接口容许位移。综合上述文献的参数选取,本文选择管道参数(接口允许位移、管道埋深),土体参数(容重、内摩擦角)作为管线模型可靠度分析的随机变量。
2.2 地下管线结构安全判别准则图 2所示的管线模型中,在地震动位移时程荷载作用下,不同管道接口的位移响应是随时间变化的随机过程g(x, t):
| $ g(\boldsymbol{x}, t)=R(\boldsymbol{x})-S(\boldsymbol{x}, t) $ | (4) |
式中:R(x)表示管道接口容许位移值;S(x, t)表示地震动荷载输入下,t时刻的管接口的相对位移响应值; x为管线结构地震反应分析模型中不确定性参数对应的随机变量。
若地震动位移时程的持时为Ts,根据动力可靠度的首次超越失效准则,式(4)中随机过程g(x, t)在时段[0, Ts]内进入失效域g(x, t)≤0的概率表示为
| $ P_{f}=\operatorname{prob}\left\{g(\boldsymbol{x}, t) \leqslant 0, \forall t \in\left[0, T_{\mathrm{s}}\right]\right\} $ | (5) |
若令
| $ \begin{gathered} P_{f}=\operatorname{prob}\{G(\boldsymbol{x}) \leqslant 0\}= \\ \int_{G(\boldsymbol{x}) \leqslant 0} q(\boldsymbol{x}) \mathrm{d} \boldsymbol{x}=E[\boldsymbol{G}(\boldsymbol{x}) \leqslant 0] \end{gathered} $ | (6) |
式中q(x)为随机变量集x的联合概率密度函数。
2.3 基于Monte Carlo模拟的可靠度计算在管线结构抗震可靠度计算式(6)中,假定随机变量集中的元素个数为n(即x=(x1, x2, …, xn)),由于G(x)和q(x)难以使用显式表达,则不可直接通过对式(6)积分求解得到管线结构的抗震可靠度。一般采用MCS法求解E[G(x)≤0]估计值,则进行N次随机模拟后得到的管线结构抗震可靠度的估计值
| $ \hat{p}_{f}=\frac{1}{N} \sum\limits_{k=1}^{N} I[G(\boldsymbol{x}(k)) \leqslant 0] $ | (7) |
式中:x(k) =[x1(k), x2(k), x3(k), …, xn(k)]为第k次模拟抽样得到的x样本值;I取值为{0, 1}的函数,当G(x(k))≤0时,I[G(x(k))]=1,否则=0。
3 主动学习Kriging代理模型计算管线可靠度 3.1 构建Kriging代理模型Kriging代理模型一般包含两部分:回归部分和随机误差[25]。对于k个样本点初始样本集(design of experiment, DoE),输入变量样本点X=[x1, x2, …, xk]T及其对应的响应值(输出变量)Y=[S(x1), S(x2), …, S(xk)]T,采用Kriging模型表示的输出变量S(x)与输入变量x之间的表达式为
| $ S(\boldsymbol{x})=\sum\limits_{i=1}^{m} \beta_{i} f(\boldsymbol{x})+z(\boldsymbol{x})=f(\boldsymbol{x})^{\mathrm{T}} \boldsymbol{\beta}+z(\boldsymbol{x}) $ | (8) |
式中:每个样本点中输入变量的个数为n,x=[x1, x2, …, xn]T,f(x)=[f1(x), f2(x), …, fm(x)]T为回归多项式基函数向量,m为回归多项式的数量;β=[β1, β2, …, βm]T为多项式参数向量;z(x)为服从正态分布N(0, σ2)的随机过程,其协方差方程为
| $ \begin{gathered} \operatorname{cov}\left(z\left(\boldsymbol{x}_{i}\right), z\left(\boldsymbol{x}_{j}\right)\right)=\sigma^{2} R\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right) \\ (i, j=1,2,3, \cdots, k) \end{gathered} $ | (9) |
式中R(xi, xj)为任意2个样本点xi和xj的空间相关方程,通常采用高斯相关方程,其表达式为
| $ R\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\exp \left[-\sum\limits_{l=1}^{n} \theta_{l}\left(x_{i}^{l}-x_{j}^{l}\right)^{2}\right] $ | (10) |
式中:xil为输入样本xi的第l个分量;θl为相关参数,可通过最大似然估计得到
| $ \max \limits_{\theta>0}\left\{-\left[\frac{1}{2} \ln (|\boldsymbol{R}|)+\frac{k}{2} \ln \left(\sigma^{2}\right)\right]\right\} $ | (11) |
式中R为相关矩阵,元素Rij=R(xi, xj) (i, j=1, 2, …, k)。
基于给定的样本点,多项式参数向量β与随机过程方差σ2的估计值计算式分别为
| $ \left\{\begin{array}{l} \hat{\boldsymbol{\beta}}=\left(\boldsymbol{F}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{F}\right)^{-1} \boldsymbol{F}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{Y} \\ \hat{\sigma}^{2}=\frac{1}{K}(\boldsymbol{Y}-\boldsymbol{F} \hat{\boldsymbol{\beta}})^{\mathrm{T}} \boldsymbol{R}^{-1}(\boldsymbol{Y}-\boldsymbol{F} \hat{\boldsymbol{\beta}}) \end{array}\right. $ | (12) |
式中F为由回归多项式函数值构成的矩阵,其中元素Fij=fj(xi),且有i=1, …, k;j=1, …, m。
对于任意输入变量x0,假定x0与输入变量样本点X之间的相关系数向量为r0=[R(x0, x1), …, R(x0, xk)]T,利用式(8)构建的Kriging模型表达式,可以得到与x0对应的系统响应(输出变量)值S(x0)的预测值
| $ \left\{\begin{array}{l} \hat{S}\left(\boldsymbol{x}_{0}\right)=\boldsymbol{f}^{\mathrm{T}}\left(\boldsymbol{x}_{0}\right) \hat{\boldsymbol{\beta}}+\boldsymbol{r}_{0}^{\mathrm{T}} \boldsymbol{R}^{-1}(\boldsymbol{Y}-\boldsymbol{F} \hat{\boldsymbol{\beta}}) \\ \hat{\sigma}_{\hat{S}}^{2}\left(\boldsymbol{x}_{0}\right)=\hat{\sigma}^{2}\left(1+\boldsymbol{u}^{\mathrm{T}}\left(\boldsymbol{F}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{F}\right)^{-1} \boldsymbol{u}-\boldsymbol{r}_{0}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{r}_{0}\right) \end{array}\right. $ | (13) |
式中u=FTR-1r0-f。本文进行管线结构抗震可靠度分析时,式(8)~(13)中应用Kriging模型构建和模型预测应用的过程,采用MATLAB软件支持开发的Kriging模型工具包DACE实现[26-27]。
3.2 主动学习更新Kriging代理模型在采用Monte Carlo方法计算结构可靠度时,采用式(8)~(13)的Kriging代理模型预测抽样样本的结构响应,可以减少抽样样本结构有限元模型计算次数,从而加速Monte Carlo方法的求解速度。为了保证可靠度计算的准确性,一般需要较多的初始样本点{X; Y}建立精度较高的Kriging模型;而初始样本点{X; Y}的建立,仍然需要较多的计算量。为了提高Kriging模型的精度和计算效率,近年来发展了采用主动学习方法逐步提高Kriging模型精度的方法,仅需少量的样本就可构造精度较高的Kriging模型,也即:根据学习函数选择最佳样本点,增补该样本点后更新拟合Kriging模型,迭代多次更新以提升Kriging代理模型的精度。
为使Kriging模型不断优化,Echard等[28]提出了类似可靠度指标的定义学习函数U评价样本点x对于现有Kriging模型的潜在影响:
| $ U(\boldsymbol{x})=\frac{|\hat{S}(\boldsymbol{x})|}{\hat{\sigma}_{\hat{S}}(\boldsymbol{x})} $ | (14) |
式中:
对于样本点x的学习函数U(x),较小的U值对应于较小的
| $ x^{*}=\arg \min \limits_{x} U(\boldsymbol{x}) $ | (15) |
本文采用Echard提出的min{U(x)}≥2作为Kriging模型停止学习准则,通过式(15)得到x*。
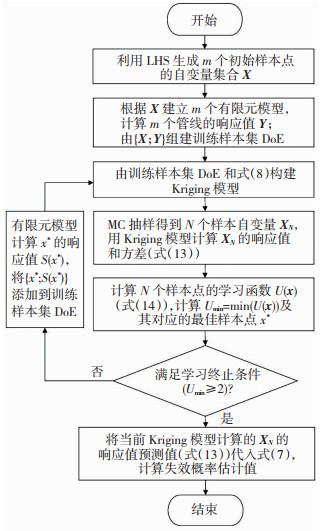
3.3 基于AK-MCS的管线抗震可靠度计算在管线结构系统的有限元模型中,管线接口响应与荷载、场地和管道属性参数之间的关系难以显式表达。基于2.3节和3.2节的描述,采用主动学习Kriging代理模型(active learning based Kriging, AK)结合Monte Carlo随机模拟的方法(AK-MCS)计算地下管线的抗震动力可靠度的流程如图 4所示。具体计算步骤如下:
|
图 4 AK-MCS方法求解管线抗震可靠度流程图 Fig. 4 Flow chart for seismic reliability evaluation of pipeline by AK-MCS method |
步骤1:在随机变量的x取值空间中使用拉丁超立方抽样方法(LHS)随机生成包含m个自变量样本的输入样本集X。根据初始样本的物理参数取值,利用ABAQUS软件构建管线有限元模型,并计算管线接口的最大位移响应值,作为初始样本X对应的功能函数响应值Y,此响应值为所有时间范围内接口位移最大值。其中,初始样本点的个数m≥(n+1)(n+2)/2[29],n为随机变量个数。初始样本X和响应值Y作为Kriging模型的训练样本集DoE。
步骤2:基于训练样本集DoE,采用MATLAB的DACE工具箱实现式(8)~(12)的计算过程,构建管线接口位移响应安全状态的Kriging模型。其中,Kriging模型的回归部分为一次多项式,相关函数为高斯函数。
步骤3:使用MC抽样产生N个自变量样本点XN,利用构建的Kriging模型求得自变量样本点XN对应的管线接口位移响应预测值和预测方差(式(13))。计算这些样本点的学习函数值U(式(14)),并从中挑选学习函数最小值(Umin)对应的样本点x*(式(15))作为最佳样本点。
步骤4:如果最佳样本点自变量x*的学习函数值满足学习停止条件Umin=U(x*)≥2,则构建Kriging模型的主动学习过程结束,转步骤5;否则,建立最佳样本点自变量x*对应的管线有限元模型,计算管线接口位移响应真实值S(x*),将{x*, S(x*)}加入Kriging模型训练样本集DoE中,转步骤2。
步骤5:主动学习过程结束,当前Kriging模型即为满足精确需求的模型。根据步骤3计算得到XN对应的结构响应值,利用式(7)求得管线地震失效概率Pf的估计值。
4 算例分析 4.1 算例参数根据图 2所示的管线模型,在ABAQUS有限元软件中建立了承插式接口球墨铸铁管线的地震反应分析模型,沿管线轴向输入地震动荷载。管线结构参数和周围覆土的参数见表 1,其中管线周围土体为无黏性回填土,根据式(1)可算得土弹簧的轴向弹性极限力fy =20.5 kN/m。管道外径61 cm和周向土体抗拉能力0.15 kN/mm,计算得接口的弹性极限拉力FJ =287 kN。土弹簧和接口轴向弹簧建模采用图 3所示的折线模型,土弹簧的弹性极限位移δs =0.3 cm,接口轴向弹簧的弹性极限位移δJ =0.25 cm[8]。根据2.1节的分析,本节进行管线抗震可靠度算例分析时,选择的模型不确定性参数及其分布特征见表 2。
| 表 1 管线有限元模型参数 Tab. 1 Finite element model parameters of pipeline |
| 表 2 管线模型中随机变量参数及其概率分布参数 Tab. 2 Random variables and corresponding distribution properties in pipeline model |
为分析地震动频谱特性对管线地震反应的影响,本节沿管线轴向输入正弦波、EL-Centro记录以及汶川安县地震动位移时程记录。其中,正弦波位移时程的参数为沿管道轴向最大速度Va=30 cm/s(中国地震烈度Ⅷ度),传播速度Ca =120 m/s,周期T=3.5 s,持时28 s,此参数与1985年Michoacan地震[30]中产生大量管线破坏的面波特征相似。EL-Centro地震动时程取自1940-05-19 Imperial Valley南北向地震动记录,持时40 s,将地震动速度时程调幅至Va=30 cm/s;汶川安县地震动时程取自2008-05-12安县地震动记录,将地震动速度时程调幅至Va=30 cm/s,积分得到位移时程。为体现非一致地震动输入的影响,图 2所示的管线不同位置处的土弹簧底部输入的地震动之间的时间延迟采用式(3)计算。
本节算例中不同工况的模型和荷载参数见表 3。为了验证本文分析模型的正确性,工况1采用与Shi[8]相同的模型参数,即:管线总长3 660 m,单根管道长度4.55 m,地震动位移荷载为沿管线轴向分布的静力荷载。参数研究表明接口长度对数值模拟结果的影响很小,为了数值模拟的稳定性,模型中接口长度设置为2.5 cm。管道服役年限增加、接口胶圈老化等原因均可能导致管道接口抗拉拔能力下降,Shi[8]和Zhong等[10]研究了管线模型中间存在一个薄弱接口对管线结构响应的影响。本节假定管线模型中间位置处的接口为薄弱接口,工况2~8计算了中间位置处接口的弹性极限拉力为FW={0.2, 0.4, 0.6, 0.8, 1.0}×FJ的不同结果。根据《连续铸铁管》[31],国内承插式接口球墨铸铁管道的有效长度一般为6 m,因此工况3~8中管道长度取为6 m。
| 表 3 地下管线地震反应分析工况 Tab. 3 Analysis for seismic responses of buried pipeline in different cases |
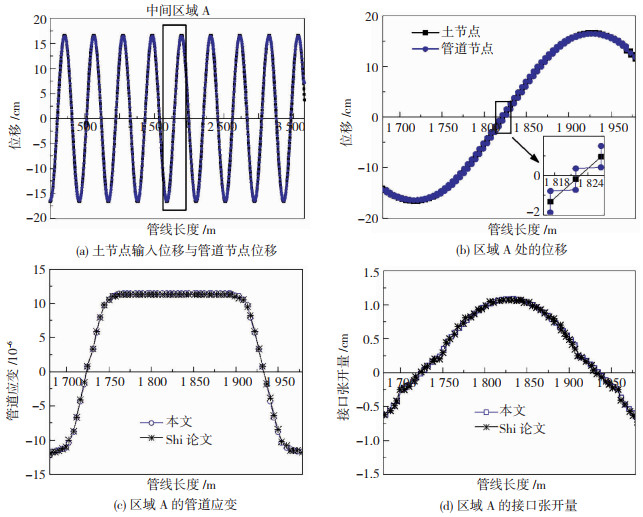
确定性模型参数工况1的计算结果见图 5。图 5(a)绘制了沿管线长度上各点处的输入位移和管线位移响应(土弹簧两个端点的轴向位移)。由图 5(b)可看出管线随着土体位移一起变形,管道中间位置土节点的位移等于管道节点位移。图 5(c)是沿管线长度方向的管道应变,管道应变从0开始线性增加,直到接口轴向力达到接口的抗拉能力时,管道应变趋于稳定。图 5(d)是沿管线长度方向的接口张开量,接口张开量从0到0.25 cm(接口弹性位移极限)呈线性增加,之后的变化呈正弦曲线趋势,最大接口位移约1.10 cm。工况1与Shi[8]的模型采用相同的参数,计算结果与Shi[8]相同,验证了本文管线分析模型的正确性。
|
图 5 工况1计算结果 Fig. 5 Pipeline response in case 1 |
本文采用的管线分析模型(图 2)的两侧端点处(0 m和3 660 m)并未设置端部约束,对于考虑位移时程荷载非一致输入的工况1和工况2,管道接口最大张开量分布如图 6所示。由图 6中工况1的结果可知,接口最大张开量从管道两端开始逐渐增大,经过一定距离(约20 m)后达到稳定值,管线中部接口最大张开量值基本相同(约为1.10 cm)(图 6),这与Liu等[18]的结论一致。根据图 6中的结果,可知两个工况的边界条件影响区域的接口位移变化规律相同、中间区域的管线接口最大位移响应相等,可认为本文承插式接口管线模型两侧约20 m范围为边界条件影响区域。若将管线建模长度选择在300 m左右,仍可得到不受边界条件影响的管线接口的位移响应,从而缩小管线模型的计算量。

|
图 6 工况1与工况2(FW=FJ)沿管线长度的接口张开量比较 Fig. 6 Comparison of axial joint opening between case 1 and case 2(FW=FJ) |
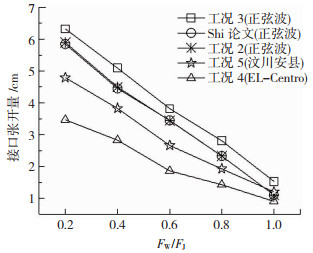
对于管线中部存在薄弱接口时,图 7给出了工况2~5中薄弱接口最大张开量随接口刚度变化的关系。由图可知,薄弱接口张开量随着FW减小而近似线性增加;与工况2计算结果相比,工况3管道长度6 m对薄弱接口张开量的影响更大;工况3(正弦波)、工况4(EL-Centro波)、工况5(汶川安县波)的弱接口张开量不相等,而根据式(2)可算得三种工况的解析结果相等,说明接口张开量不仅受地震波峰值影响,频谱特征不同也会引起接口张开量不同,体现出进行管线地震动力时程响应分析的重要性。
|
图 7 工况2~5中间薄弱接口张开量 Fig. 7 Opening of middle weak joint in cases 2-5 |
分别采用2.3节的标准Monte Carlo模拟(MCS)方法、3.3节的基于主动学习Kriging模型的Monte Carlo模拟方法(AK-MCS)计算工况6~8中管线模型的抗震可靠度。在工况6~8的可靠度算例模型中,随机变量参数个数为n=4。根据3.3节步骤1的描述,构建Kriging代理模型所需要的最小为初始样本点为m≥15。为了增加初始样本点的代表性,本节采用拉丁超立方抽样产生m=20个初始样本点建立初始Kriging模型。步骤3中MC抽样个数为N=1 000,生成自变量样本点,利用Kriging模型预测响应值(接口最大张开量)。
表 4给出了在工况7(FW=0.4FJ)中使用AK-MCS方法计算不同样本点的管线失效概率及直接采用MCS方法的失效概率结果,将MCS方法计算结果视为“精确解”。有限元计算次数是指需要调用ABAQUS有限元软件执行管线计算的次数。由表 4可知,当采用初始样本个数m=20,基于此样本点所建立的Kriging模型进行可靠度评估计算的失效概率为0.112,计算的相对误差为9.80%,误差较大,说明所建立的模型精度有待进一步提高。该模型通过主动学习,增加新的样本点至初始样本集,重新构建Kriging模型。当样本点达到23时,其失效概率相对误差降低至3.92%,此时Kriging模型符合精度要求。为验证所建立的模型精确性,图 8比较了Kriging模型预测值与真实响应值。图 8(a)是通过初始样本点构建的Kriging模型,图 8(b)是经过主动学习后的Kriging模型。可以看出,经过主动学习的Kriging模型预测得到的响应值基本接近真实值,两者响应值的相对差值也逐渐变小,说明构建的Kriging模型是准确的。
| 表 4 MCS与AK-MCS的可靠度结果(工况7(FW=0.4FJ)) Tab. 4 Reliability of MCS method and AK-MCS method(case 7(FW=0.4FJ)) |

|
图 8 工况7(FW=0.4FJ)MCS与AK-MCS结果比较 Fig. 8 Comparison of results between MCS method and AK-MCS method in case 7(FW=0.4FJ) |
表 5为MCS方法和AK-MCS方法的地下管线抗震可靠度计算结果对比。在FW=FJ时,从图 7可知此时管线接口最大张开量远小于接口允许位移(5.2 cm),三种地震波的失效概率均为0。在不同地震波作用下,随着弱接口抗拉能力的减小,管线的失效概率均逐渐增大。需要说明的是,尽管表 5中工况6~8采用相同的地震动参数(Va=30 cm/s和Ca=120 m/s),由于地震动荷载时程的周期成分不同,导致管线的地震反应和抗震可靠度计算结果差异较大。而按照式(2)的简化方法计算接口张开量,计算结果保持不变,不能体现管线薄弱接口刚度变化、地震动周期成份对管线地震反应的影响,因此建立地下管线结构的地震动力时程响应分析模型是进行管线抗震可靠度分析的必要支撑。
| 表 5 AK-MCS和MCS计算的管线失效概率 Tab. 5 Pipeline failure probability evaluated by AK-MCS method and MCS method |
由表 5可以看出,AK-MCS方法得到的管线失效概率Pf与MCS方法的Pf相对误差(|MCS-AK-MCS|/MCS)为0.00%~3.92%,而AK-MCS方法的计算时间仅为MCS方法的2%;同时,其计算有限元次数仅为MCS方法的2%左右。因此,对于地下管线抗震可靠度计算问题,AK-MCS方法是一种准确且高效的计算方法。
5 结论地下管线结构的抗震可靠度分析是管线抗震安全性评估的重要内容。本文主要考虑土体、管道结构等参数的不确定性,采用主动学习Kriging模型可靠度方法(AK-MCS)对地下承插式球墨铸铁管线进行抗震可靠度评价,得出的主要结论如下:
1) 本文算例结果表明,AK-MCS法所得的管线失效概率与标准Monte Carlo模拟方法的相对差值在5%以内;AK-MCS法中有限元模型计算次数和计算时间约为标准Monto Carlo模拟方法的2%左右。表明采用AK-MCS法计算地下管线抗震可靠度是可行且高效的。
2) 当地震烈度为Ⅷ度(VPG=30 cm/s)时,新建成的承插式球墨铸铁管线接口失效概率为0,管线处于安全状态;随着管道服役年限增加、接口胶圈老化等,管线接口的抗拉拔能力下降到原接口的60%时,管线失效概率显著上升。因此,进行现役管线的抗震可靠度分析时,需要注意管线接口模型刚度的合理性。
3) 由于地震动时程的频谱成份不同,不同地震动导致的地下管线地震反应结果差异显著。仅利用公式简化方法计算的接口张开量,不能体现管线薄弱接口刚度变化、地震动周期成分对管线地震反应的影响,因此建立地下管线的地震动力时程响应分析模型是进行管线抗震可靠度分析的必要支撑。
| [1] |
李杰. 生命线工程抗震: 基础理论与应用[M]. 北京: 科学出版社, 2005: 52. LI Jie. Earthquake resistance of lifeline engineering: basic theory and application[M]. Beijing: Science Press, 2005: 52. |
| [2] |
韩阳. 城市地下管网系统的地震可靠性研究[D]. 大连: 大连理工大学, 2002 HAN Yang. Study on seismic reliability of urban buried pipeline network systems[D]. Dalian: Dalian University of Technology, 2002 |
| [3] |
O'ROURKE M J, LIU X. Seismic design of buried and offshore pipelines[M]. New York: Multidisciplinary Center for Earthquake Engineering Research, 2012: 3.
|
| [4] |
ELHMADI K, O'ROURKE M J. Seismic damage to segmented buried pipelines[J]. Earthquake Engineering and Structural Dynamics, 1990, 19(4): 529. DOI:10.1002/eqe.4290190405 |
| [5] |
NEWMARK N M. Problems in wave propagation in soil and rock[C]//Proceedings of International Symposium on Wave Propagation and Dynamics Properties of Earth Materials. Albuguerque: University of New Mexico Press, 1967: 7
|
| [6] |
SHINOZUKA M, KOIKE T. Estimation of structural strains in underground lifeline pipes[J]. International Journal of Pressure Vessels and Piping, 1979, 31. |
| [7] |
WANG R L, CHENG K M. Seismic response behavior of buried pipelines[J]. Journal of Pressure Vessel Technology, 1979, 101: 21. DOI:10.1115/1.3454594 |
| [8] |
SHI Peixin. Seismic wave propagation effects on buried segmented pipelines[J]. Soil Dynamics and Earthquake Engineering, 2015, 72: 90. DOI:10.1016/j.soildyn.2015.02.006 |
| [9] |
KUWATE Y, TAKADA S, YAMASAKI S. Seismic performance of complicated pipeline network[C] //Proceedings of 14th World Conference of Earthquake Engineering. Beijing: [s. n. ], 2008: 4
|
| [10] |
ZHONG Zilan, WANG Shurui, ZHAO Mi, et al. Performance of ductile iron push-on joints rehabilitated with CIPP liner under repetitive and seismic loadings[J]. Soil Dynamics and Earthquake Engineering, 2018, 115: 783. DOI:10.1016/j.soildyn.2018.09.031 |
| [11] |
TEE K F, KHAN L R. Reliability analysis of underground pipelines with correlations between failure modes and random variables[J]. Journal of Risk & Reliability, 2014, 228(4): 362. DOI:10.1177/1748006X13520145 |
| [12] |
TEE K F, KHAN L R, LI H. Application of subset simulation in reliability estimation of underground pipelines[J]. Reliability Engineering & System Safety, 2014, 130: 125. DOI:10.1016/j.ress.2014.05.006 |
| [13] |
EBENUWA A U, TEE K F. Reliability estimation of buried steel pipes subjected to seismic effect[J]. Transportation Geotechnics, 2019, 20: 6. DOI:10.1016/j.trgeo.2019.100242 |
| [14] |
BABU G L S, SRIVASTAVA A. Reliability analysis of buried flexible pipe-soil systems[J]. Journal of Pipeline Systems Engineering and Practice, 2010, 1(1): 33. DOI:10.1061/(ASCE)PS.1949-1204.0000041 |
| [15] |
李牧晨. 基于AK-MCS法的框架结构抗震可靠度分析[D]. 兰州: 兰州理工大学, 2019 LI Muchen. The reliability research of structural reliability based on AK-MCS[D]. Lanzhou: Lanzhou University of Technology, 2019 |
| [16] |
韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197. HAN Zhonghua. Kriging surrogate model and its application to design optimization: A review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197. DOI:10.7527/S1000-6893.2016.0083 |
| [17] |
朱丽莎, 向磊, 王钰烁, 等. Kriging模型在齿面磨损预测中的应用[J]. 哈尔滨工业大学学报, 2018, 50(7): 164. ZHU Lisha, XIANG Lei, WANG Yushuo, et al. Wear prediction of gear surface with Kriging model[J]. Journal of Harbin Institute of Technology, 2018, 50(7): 164. DOI:10.11918/j.issn.0367-6234.201711001 |
| [18] |
LIU W, SONG Z, WANG Y. Seismic analysis of the connections of buried segmented pipes[J]. Computer Modeling in Engineering and Sciences, 2020, 123(1): 257. DOI:10.32604/cmes.2020.07220 |
| [19] |
Seismic guidelines for water pipelines: G & E Report 80.01.01, Revision 0[S]. Washington DC: FEMA, 2005
|
| [20] |
油气输送管道线路工程抗震技术规范: GB 50470—2017[S]. 北京: 中国计划出版社, 2017 Seismic technical code for oil and gas transmission pipeline engineering: GB 50470—2017[S]. Beijing: China Planning Press, 2017 |
| [21] |
韩俊艳, 杜修力, 侯本伟, 等. 纵向非一致地震激励下管-土结构响应的简化分析模型[J]. 岩土力学, 2018, 39(12): 4651. HAN Junyan, DU Xiuli, HOU Benwei, et al. A simplified analysis model for pipe-soil structural seismic responses under longitudinal non-uniform seismic excitations[J]. Rock and Soil Mechanics, 2018, 39(12): 4651. DOI:10.16285/j.rsm.2017.0735 |
| [22] |
MANOLIS G D, STEFANOUS G, MARKOU A A. Dynamic response of buried pipelines in randomly structured soil[J]. Soil Dynamics and Earthquake Engineering, 2020, 128: 5. DOI:10.1016/j.soildyn.2019.105873 |
| [23] |
WIJAYA H, RAJEEV P, GAD E. Effect of seismic and soil parameter uncertainties on seismic damage of buried segmented pipeline[J]. Transportation Geotechnics, 2019, 21: 4. DOI:10.1016/j.trgeo.2019.100274 |
| [24] |
JAHANGIRI V, SHAKIB H. Reliability-based seismic evaluation of buried pipelines subjected to earthquake-induced transient ground motions[J]. Bulletin of Earthquake Engineering, 2020, 18(8): 3603. DOI:10.1007/s10518-020-00852-w |
| [25] |
SACKS J, SCHILLER S B, WELCH W J. Designs for computer experiments[J]. Technometrics, 1989, 31(1): 41. |
| [26] |
黄晓旭, 陈建桥. 基于主动学习Kriging模型的可靠性分析[J]. 固体力学学报, 2016, 37(2): 174. HUANG Xiaoxu, CHEN Jianqiao. Reliability analysis based on active learning Kriging model[J]. Chinese Journal of Solid Mechanics, 2016, 37(2): 174. DOI:10.19636/j.cnki.cjsm42-1250/o3.2016.02.007 |
| [27] |
魏娟, 张建国, 邱涛. 基于改进的动态Kriging模型的结构可靠度算法[J]. 北京航空航天大学学报, 2019, 45(2): 374. WEI Juan, ZHANG Jianguo, QIU Tao. Structural reliability algorithm based on improved dynamic Kriging model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(2): 374. DOI:10.13700/j.bh.1001-5965.2018.0301 |
| [28] |
ECHARD B, GAYTON N, LEMAIRE M. AK-MCS: An active learning reliability method combining Kriging and Monte Carlo simulation[J]. Structural Safety, 2011, 33(2): 145. DOI:10.1016/j.strusafe.2011.01.002 |
| [29] |
JIANG Chen, QIU Haobo, YANG Zan, et al. A general failure-pursuing sampling framework for surrogate-based reliability analysis[J]. Reliability Engineering and System Safety, 2019, 183: 47. DOI:10.1016/j.ress.2018.11.002 |
| [30] |
AYALA A G, O'ROURKE M J, ESCOBAR J A. Evaluation of the effects of the 1985 Michoacan earthquake on the water systems in metropolitan Mexico City[J]. Earthquake Spectra, 1990, 6(3): 473. DOI:10.1193/1.1585583 |
| [31] |
连续铸铁管: GB/T 3422—2008[S]. 北京: 中国标准出版社, 2008 Cast-iron pressure pipe made by continuous casting process: GB/T 3422—2008[S]. Beijing: China Standard Press, 2008 |
 2021, Vol. 53
2021, Vol. 53


