2. 北京交通大学 土木建筑工程学院,北京 100044
2. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
盾构法修建水下隧道已经广泛应用于实际工程中,如武汉长江隧道、杭州钱江隧道、广深港高铁狮子洋隧道等。随着水下隧道修建数量的增多,所需穿越的地层也越加复杂,如南京长江隧道[1]穿越的地层有:黏土地层、砂土地层、卵石地层以及黏- 砂复合土地层等。开挖面稳定性问题是盾构隧道修建过程中最为关心的问题,由于模型试验法可以较直观地反映有关过程的物理力学规律而被广泛采用。然而大多数试验研究的对象为单一砂土、黏土或卵石地层,关于黏- 砂土地层水下盾构隧道开挖面稳定性问题的研究鲜有报道。
针对砂土地层,李君等[2-6]进行了重力模型试验,研究了干砂地层开挖面的失稳模式和支护力变化规律。吕玺琳等[7-8]通过离心模型试验,对饱和砂土地层开挖面的失稳机制进行了深入研究。Chen等[9-11]分别开展了离心模型试验和重力模型试验,通过开挖面排水在砂土地层中产生稳态渗流场,研究了开挖面的失稳模式以及有效支护压力随开挖面位移的变化规律,探究了开挖面极限有效支护压力与开挖面- 地层水头差的关系。
针对黏土地层,Mair[12]通过离心模型试验,研究了开挖面的主动破坏失稳模式。徐佳伟等[13-14]开展了离心模型试验,通过离心机对泥浆进行固结,研究了具有一定含水率的软黏土地层开挖面的主动破坏模式和被动破坏模式以及相应的极限支护压力。Ng等[15]开展了离心模型试验,研究了经过离心机超重力(100g)固结后的饱和黏土地层开挖面的被动破坏机理以及支护压力和孔隙水压力随开挖面位移的变化规律。
针对砂卵石地层,范祚文等[16]采用小型土压平衡盾构机模型,研究了邻近建筑物和埋深对地表沉降规律以及开挖面极限支护压力和失稳模式的影响。胡雄玉等[17]采用小型土压平衡盾构机模型,研究了砂卵石地层和砂土地层开挖面的破坏模式,详细对比了两种地层的破坏特性。吕玺琳等[18]通过重力模型试验,对饱和圆砾地层开挖面的失稳变化过程进行了深入研究。
上述研究主要是针对单一土地层,缺乏针对黏- 砂复合土地层开挖面稳定性问题的试验研究。本文针对饱和含黏粒砂土地层浅埋盾构隧道开挖渗流稳定性问题,通过模型试验,量测了开挖面的水土压力以及附近地层的沉降量和孔隙水压力,研究了不同黏土含量以及有无渗流对开挖面稳定性的影响。
1 试验 1.1 试验设计如图 1所示,基于米博等[11]的试验装置,饱和含黏粒砂土地层浅埋盾构隧道开挖渗流试验模型主要由模型箱、水循环系统、盾构隧道与开挖面模型、饱和地层模型和量测系统组成。

|
图 1 试验模型及测点布置(mm) Fig. 1 Test model and layout of measuring points (mm) |
模型箱底面和背面均采用5 mm厚的钢板,其他各面均采用20 mm厚的有机玻璃板。其中,x、y、z分别表示沿隧道模型纵向、横向、竖向的坐标; δ表示支护板后移距离; Δ表示开挖面- 地表水头差。
水循环系统由进水管、水泵和出水管组成,可将水由开挖面运送至地层表面。测压管接入隧道模型内部,实时监测开挖面水头,通过调节水泵阀门产生所需的开挖面- 地表水头差。
盾构隧道模型采用厚度为20 mm的半圆形截面铝筒制成,开挖面模型由前板和支护板组成。前板固定,采用厚度为20 mm、开孔率为31.36%的半圆形带孔有机玻璃板制成,模拟对开挖面前方土体起一定支撑作用的盾构刀盘; 支护板由两片钢丝网以及钢丝网之间的海绵和钢条骨架构成,可以通过丝杠和转轮控制其向后移动,模拟开挖面支护压力不足。
地层模型材料由黏土与粒径为0.425~0.850 mm的黑色机制石英砂分别按照黏- 砂比(mc/ms)为0、0.1、0.2混合并充分搅拌而成,试验测得的材料参数如表 1所示。
| 表 1 材料参数 Tab. 1 Material parameters |
量测系统由用于量测开挖面饱和土压力的微型土压力盒(量程100 kPa,精度0.1 kPa)、开挖面前方地层孔隙水压力的微型渗压计(量程15 kPa,精度0.075 kPa)、地层模型内部沉降的联测系统(量程200 mm,精度3 μm)、地层模型表面沉降的位移传感器(LVDT,量程100 mm,精度0.1 mm)以及相应的数据采集系统组成。
1.2 试验方案如图 1和表 2所示,隧道埋深为隧道直径D的2倍。针对不同的地层黏- 砂比,开展了开挖面- 地表相对水头差(Δ/D)分别为0、1和1.67以及黏- 砂比(mc/ms)分别为0、0.1和0.2的模型试验。
| 表 2 试验参数 Tab. 2 Model test parameters |
调节水泵阀门,维持测压管水位与地表水位的差值在整个试验过程中不变。逆时针转动转轮,使开挖面支护板逐步向后移动,每步1 mm(移动速率为0.1 mm/s)累计向后移动60 mm。
2 试验结果与分析 2.1 黏土含量和渗流对开挖面失稳模式的影响图 2为支护板位移对地表沉降的影响,其中,v表示地表沉降值。可以看出,地表沉降随开挖面支护板位移(或开挖面体积损失)的增大先缓慢增大后快速增大,对应于开挖面前方地层失稳范围先逐渐增大后基本达到了极限。

|
图 2 开挖面支护板位移对地表沉降的影响(A点) Fig. 2 Influence of support plate displacement at tunnel face on ground face settlement (point A) |
对比图 2中曲线可知,无渗流(Δ/D=0)时,黏土含量的增大会使地表最大沉降值略微增大,有渗流(Δ/D=1)时,黏土含量的增大会使地表最大沉降值明显增大; 这主要是由于渗流条件下,渗透水流会携带一部分黏粒进入开挖仓使得土体密度明显降低,土体在渗透力的作用下得到压缩使地表沉降明显增大,黏土含量越大这种携带作用越明显。
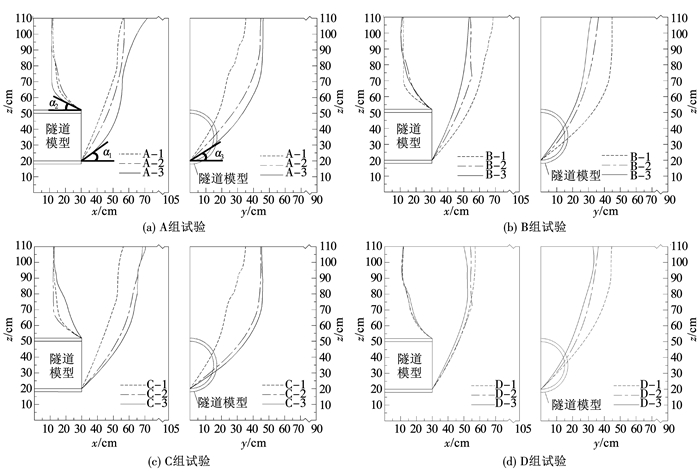
为分析地层失稳模式,对试验所测地层沉降数据进行拟合,认为失稳区域为1 mm(约为0.003D)等值线所围部分。图 3为不同渗流条件下地层黏- 砂比对纵截面和横截面(x=34 cm)(试验发现,在x=34 cm附近地表沉降最大,故选取该截面)地层极限失稳范围的影响。由图 3(c)和3(d)可知,渗流对地层极限失稳范围的影响具有明显的一致性,或增大或减小; 以D组试验为例,如图 3(d)所示,相对于无渗流条件(试验D-1,Δ/D=0),不同开挖面- 地表水头差(试验D-2,Δ/D= 1;试验D-3,Δ/D=1.67)均会使地层极限失稳范围减小; 鉴于这种一致性,主要针对Δ/D=0(A组无渗流试验)和Δ/D=1 (B组有渗流试验)这两种情况进行详细对比分析。
|
图 3 隧道模型中心纵截面(y=0)和开挖面前方横截面(x=34 cm)地层极限失稳范围 Fig. 3 Limit collapse range of soil in central longitudinal plane (y=0) and transverse plane (x=34 cm) of tunnel model |
定义隧道模型开挖面底部和顶部失稳土体边界面与水平方向的夹角为失稳破裂角。以试验A-3为例,如图 3(a)所示,开挖面前方破裂角α1、开挖面后方破裂角α2、横向破裂角α3对极限失稳范围起决定作用。为便于对比分析,将各试验的3个失稳破裂角列于表 3。
| 表 3 盾构隧道模型失稳土体破裂角 Tab. 3 Rupture angles of collapsed soil in shield tunnel model(°) |
由图 3和表 3可知,无渗流(Δ/D=0)时,开挖面前方破裂角α1和横向破裂角α3均会因地层黏- 砂比的增大而减小,而开挖面后方破裂角α2(α2=30°±4°)变化不大,整体地层极限失稳范围随黏- 砂比的增大而增大,这主要是由于黏- 砂比的增大会明显降低土体强度; 有渗流(Δ/D=1)时,开挖面前方破裂角α1和横向破裂角α3均会因黏- 砂比的增大而增大,而开挖面后方破裂角α2(α2=34°±4°)变化不大,整体地层极限失稳范围随黏- 砂比的增大而减小,这主要是由于黏- 砂比的增大会明显减小土体的渗透系数,使得渗流对地层的影响范围减小。
结合图 3、表 3和图 2可知,当黏- 砂比较小(mc/ms < 0.1)时,渗流的作用主要表现为增大地层极限失稳范围,地表最大沉降值只是略有增大。以试验A-1(mc/ms=0,Δ/D=0)和B-1(mc/ms=0,Δ/D=1)为例,相较试验A-1,试验B-1开挖面前方破裂角α1和横向破裂角α3分别减小了44%和45%,而地表最大沉降值仅增大了15%;当黏- 砂比较大(mc/ms>≥0.1)时,渗流主要增大地表最大沉降值,而极限失稳范围有所减小。以试验A-3(mc/ms= 0.2,Δ/D=0)和B-3(mc/ms=0.2,Δ/D=1)为例,相较试验A-3,试验B-3地表最大沉降值增大了79%,而开挖面前方破裂角α1和横向破裂角α3分别增大了33%和43%。
2.2 黏土含量和渗流对开挖面有效土压力的影响图 4为开挖面支护板位移对有效土压力的影响,其中,p′表示开挖面有效土压力(压力盒所测开挖面饱和土压力均值与渗压计所测开挖面孔隙水压力值的差值),p′0表示开挖面初始有效土压力(开挖面- 地表水头差稳定且开挖面支护板位移为零时的有效土压力)。

|
图 4 有效土压力与支护板位移的关系 Fig. 4 Relationship between effective earth pressure and displacement of support plate |
由图 4可以看出,随着开挖面支护板位移(或开挖面体积损失)的增大,开挖面附近地层逐渐失稳破坏且失稳范围逐渐扩大,开挖面有效土压力逐渐减小且在失稳范围扩大到极限失稳范围后达到最小值(极限有效土压力p′lim)并基本保持不变; 黏- 砂比对开挖面有效土压力的影响具有明显的规律性,除试验A-1外,无渗流和有渗流条件下,在达到极限有效土压力之前的曲线斜率均因黏- 砂比的增大而减小,极限有效土压力均因黏- 砂比的增大而增大,这主要是由于黏- 砂比的增大会减小土体强度; 渗流对开挖面有效土压力的影响同样具有明显的规律性,除试验A-1外,相较无渗流条件,渗流条件下,在达到极限有效土压力之前的曲线斜率较小且极限有效土压力较大,这主要是由于渗透力对开挖面有效土压力的贡献较大; 试验A-1有效土压力下降较为缓慢可能是由于开挖面附近土体填筑过于密实,土压力盒附近土体卸载较为缓慢。
图 5为渗流和地层黏- 砂比对开挖面极限有效土压力的影响,其中,γd表示土体干重度。可以看出,无渗流和有渗流条件下,开挖面极限有效土压力与黏- 砂比均基本呈线性增加关系; 相较无渗流条件,有渗流条件下,开挖面极限有效土压力明显增大,且随着黏- 砂比的增大,这种增大程度逐渐增大。

|
图 5 渗流和黏- 砂比对开挖面极限有效土压力的影响 Fig. 5 Influence of seepage and clay-sand ratio on limit effective earth pressure at tunnel face |
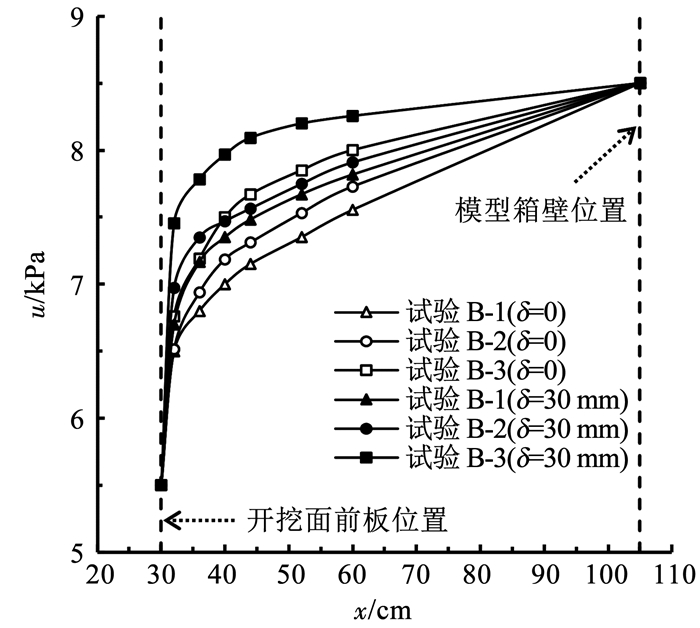
无渗流条件下,地层孔隙水压力基本维持静止水压力不变,故仅对渗流条件下地层孔隙水压力分布进行对比分析。图 6为渗流条件下不同黏- 砂比地层,开挖面中轴线上开挖面前方地层孔隙水压力的分布,其中,u表示孔隙水压力。可以看出,开挖面前方地层孔隙水压力会因地层黏- 砂比的增大而增大,这主要是由于地层黏- 砂比越大,渗透系数越小,渗流的影响范围越小; 开挖面前方地层孔隙水压力会因开挖面支护板位移(或开挖面体积损失)的增大而增大,这主要是由于随着支护板位移的增大,开挖面附近地层变得较为松散,土体孔隙率增大,在渗透水流的携带作用下,小颗粒土体(主要为黏土颗粒,对比图 7中E、F两个区域可得)逐渐集中于开挖面附近土体孔隙中,使得开挖面附近土体渗透系数变小。故在实际工程中,可以将开挖面前方地层孔隙水压力值的变化作为调整开挖面支护力大小的一个参考参数。
|
图 6 盾构隧道模型开挖面中轴线前方地层孔隙水压力分布 Fig. 6 Distribution of pore water pressure of soil in front of tunnel face central axis of shield tunnel model |

|
图 7 渗流对黏粒的携带作用(试验B-2) Fig. 7 Carrying effect of seepage on clay (Test B-2) |
1) 渗流条件下,地层黏- 砂比越大,渗透系数越小,渗流的影响范围越小,开挖面前方地层孔隙水压力越大; 随着开挖面体积损失的逐渐增大,集中于开挖面附近的小颗粒土体(主要为黏土颗粒)逐渐增多,开挖面附近土体的渗透系数逐渐减小,开挖面前方地层孔隙水压力逐渐增大。
2) 渗流会使开挖面极限有效土压力明显增大,且随黏- 砂比的增大,这种增大程度逐渐增大; 开挖面极限有效土压力与地层黏- 砂比基本呈线性增加关系。
3) 地层极限失稳范围主要取决于开挖面前方破裂角、开挖面后方破裂角以及横向破裂角,其中,开挖面后方破裂角受地层黏土含量和渗流的影响较小。
4) 无渗流时,由于地层黏- 砂比的增大会明显降低土体强度,地层极限失稳范围会因黏- 砂比的增大而增大; 有渗流时,由于黏- 砂比的增大会使渗流对地层的影响范围减小,地层极限失稳范围会因黏- 砂比的增大而减小。
5) 对于地层黏- 砂比较小(< 0.1)的情况,渗流主要增大极限失稳范围; 对于黏- 砂比较大(≥0.1)的情况,渗流主要增大地表最大沉降值。
上述研究改进了对含黏粒砂土地层浅埋盾构隧道开挖渗流稳定性的认识,可以为实际工程以及有关的稳定性极限分析提供参考。
值得说明的是,本文所研究地层的黏- 砂比较小,黏粒大部分处于砂粒孔隙之中,内摩擦角较大; 针对地层黏- 砂比进一步增大,增大到砂粒悬浮于黏土中的情况,有待进一步的研究。
| [1] |
肖明清. 我国水下盾构隧道代表性工程与发展趋势[J]. 隧道建设, 2018, 38(3): 360. XIAO Mingqing. Representative projects and development trend of underwater shield tunnels in China[J]. Tunnel Construction, 2018, 38(3): 360. DOI:10.3973/j.issn.2096-4498.2018.03.003 |
| [2] |
李君, 陈仁朋, 孔令刚. 干砂地层中盾构开挖面失稳模式及土拱效应试验研究[J]. 土木工程学报, 2011, 44(7): 142. LI Jun, CHEN Renpeng, KONG Linggang. Model test study of the failure mechanism of shallow tunnels in dry sands[J]. China Civil Engineering Journal, 2011, 44(7): 142. DOI:10.15951/j.tmgcxb.2011.07.003 |
| [3] |
陈仁朋, 李君, 陈云敏, 等. 干砂盾构开挖面稳定性模型试验研究[J]. 岩土工程学报, 2011, 33(1): 117. CHEN Renpeng, LI Jun, CHEN Yunmin, et al. Large-scale tests on face stability of shield tunnelling in dry cohesionless soil[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 117. |
| [4] |
李姣阳, 刘维, 邹金杰, 等. 浅埋盾构隧道开挖面失稳大比尺模型试验研究[J]. 岩土工程学报, 2018, 40(3): 562. LI Jiaoyang, LIU Wei, ZOU Jinjie, et al. Large-scale model tests on face instability of shallow shield tunnels in sand[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(3): 562. DOI:10.11779/CJGE201803022 |
| [5] |
KIRSCH A. Experimental investigation of the face stability of shallow tunnels in sand[J]. Acta Geotechnica, 2010, 5(1): 43. DOI:10.1007/s11440-010-0110-7 |
| [6] |
CHEN R P, LI J, KONG L G, et al. Experimental study on face instability of shield tunnel in sand[J]. Tunnelling and Underground Space Technology, 2013, 33: 12. DOI:10.1016/j.tust.2012.08.001 |
| [7] |
吕玺琳, 周运才, 李冯缔. 粉砂地层盾构隧道开挖面稳定性离心试验及数值模拟[J]. 岩土力学, 2016(11): 3324. LV Xilin, ZHOU Yuncai, LI Fengdi. Centrifuge model test and numerical simulation of stability of excavation face of shield tunnel in silty sand[J]. Rock and Soil Mechanics, 2016(11): 3324. DOI:10.16285/j.rsm.2016.11.035 |
| [8] |
金大龙, 袁大军, 郑浩田, 等. 高水压条件下泥水盾构开挖面稳定离心模型试验研究[J]. 岩土工程学报, 2019, 41(9): 1653. JIN Dalong, YUAN Dajun, ZHENG Haotian, et al. Centrifuge model test of slurry shield tunnel face stability under high water pressure[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1653. DOI:10.11779/CJGE201909009 |
| [9] |
CHEN R, YIN X, TANG L, et al. Centrifugal model tests on face failure of earth pressure balance shield induced by steady state seepage in saturated sandy silt ground[J]. Tunnelling and Underground Space Technology, 2018, 81: 315. DOI:10.1016/j.tust.2018.06.031 |
| [10] |
LV X, ZHOU Y, HUANG M, et al. Experimental study of the face stability of shield tunnel in sands under seepage condition[J]. Tunnelling and Underground Space Technology, 2018, 74: 195. DOI:10.1016/j.tust.2018.01.015 |
| [11] |
米博, 项彦勇. 砂土地层浅埋盾构隧道开挖渗流稳定性的模型试验和计算研究[J]. 岩土力学, 2020, 41(3): 837. MI Bo, XIANG Yanyong. Model test and calculation analysis of excavation-seepage stability for shallow shield tunneling in sandy ground[J]. Rock and Soil Mechanics, 2020, 41(3): 837. DOI:10.16285/j.rsm.2019.0792 |
| [12] |
MAIR R J. Centrifuge modeling of tunnel construction in soft clay[D]. Cambridge, UK: Cambridge University, 1979
|
| [13] |
徐佳伟. 黏土地层盾构隧道开挖面稳定性的离心模型试验研究[J]. 路基工程, 2017(5): 100. XU Jiawei. Experimental study on centrifuge model of the excavation face stability of shield tunneling in clay stratum[J]. Subgrade Engineering, 2017(5): 100. DOI:10.13379/j.issn.1003-8825.2017.05.22 |
| [14] |
付亚雄, 贺雷, 马险峰, 等. 软黏土地层盾构隧道开挖面稳定性离心试验研究[J]. 地下空间与工程学报, 2019, 15(2): 387. FU Yaxiong, HE Lei, MA Xianfeng, et al. Centrifuge model tests on face stability of shield tunneling in soft clay[J]. Chinese Journal of Underground Space and Engineering, 2019, 15(2): 387. |
| [15] |
NG C W W, WONG K S. Investigation of passive failure and deformation mechanisms due to tunnelling in clay[J]. Canadian Geotechnical Journal, 2013, 50(4): 359. DOI:10.1139/cgj-2012-0098 |
| [16] |
范祚文, 张子新. 砂卵石地层土压力平衡盾构施工开挖面稳定及邻近建筑物影响模型试验研究[J]. 岩石力学与工程学报, 2013, 32(12): 2506. FAN Zuowen, ZHANG Zixin. Model test of excavation face stability of EPB shield in sandy cobble ground and adjacent building effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(12): 2506. |
| [17] |
胡雄玉, 晏启祥, 何川, 等. 土压平衡盾构掘进对散粒体地层扰动和开挖面破坏特性研究[J]. 岩石力学与工程学报, 2016, 35(8): 1618. HU Xiongyu, YAN Qixiang, HE Chuan, et al. Study on the disturbance and excavation face failure feature of granular mixtures stratum due to EPB shield tunneling[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(8): 1618. DOI:10.13722/j.cnki.jrme.2016.0075 |
| [18] |
吕玺琳, 曾盛, 王远鹏, 等. 饱和圆砾地层盾构隧道开挖面稳定性物理模型试验[J]. 岩土工程学报, 2019, 41(增刊2): 129. LÜ Xilin, ZENG Sheng, WANG Yuanpeng, et al. Physical model tests on stability of shield tunnel face in saturated gravel stratum[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S2): 129. DOI:10.11779/CJGE2019S2033 |
 2021, Vol. 53
2021, Vol. 53


