2. 中国科学院大学, 北京 100190
2. University of Chinese Academy of Sciences, Beijing 100190, China
随着空间探测任务需求日益提升,航天器携带的载荷设备趋于精密多样,星地链路传输数据量大幅增加.而大部分对地观测卫星为近地轨道(low Earth orbit, LEO)卫星,其特点是单次过境时间短,为保证在有限时间内传输更多数据,星地链路需支持更高的数传速率[1].在传输带宽不变的情况下,通常将高阶调制技术与高效编译码算法相结合来提升数传速率,但同样误码率接收高阶调制信号相较于低阶调制信号需要更大的信噪比,意味着需要提高信号发射功率.另一方面,LEO卫星通常采用固定编码调制(constant coding modulation, CCM)数传体制,其按照确保地面天线5°仰角时的数据接收设计编码调制方式,而卫星过境过程中,由于天气、传输距离变化等原因,星上发射功率并未得到充分利用[2].为充分利用星上发射功率并最大化卫星过境时下传的载荷数据量,可采用可变编码调制(variable coding modulation, VCM)数传体制[3-4].
目前有两种支持VCM的通信标准:一种是蓝皮书中的串行级联卷积码(serially concatenated convolutional codes, SCCC)[5],另一种是基于欧洲电信标准化协会(European Telecommunication Standards Institute, ETSI)制定的第二代数字视频广播(the second generation digital video broadcast, DVB-S2)标准[6], 其中DVB-S2标准采用BCH(Bose-Chaudhuri-Hochquenghem)为外码,LDPC(low-density parity-check)码为内码的级联编码方式.LDPC码[7]由Gallager于1962年提出,是一种逼近Shannon极限的线性分组码[8],具有译码复杂度低、误码平层低等优势.文献[9-16]对DVB-S2标准LDPC编码进行了研究,其中文献[11]实现了基于DVB-S2标准的LDPC编码器,设计时将双口RAM配置成先读后写模式,同一时刻完成两个校验比特更新,可使编码速率达到328 Mb/s,但其采用的存储结构最多支持两路并行,不能满足更高传输速率的要求; 文献[12]提出了一种新型的校验比特存储方案,设计实现了串行和并行两种编码器,最高编码速率可达926 Mb/s,但其采用了45个RAM存储块,需要占用较多逻辑资源实现对RAM存储块的读写控制; 文献[13-16]基于DVB-S2标准非规则重复累积LDPC码(Irregular repeated accumulated, IRA-LDPC)的特点,充分利用编码算法中的并行性,实现了吞吐率高达Gb/s的编码器,但编码输出不是按顺序输出,需要与较复杂的比特交织模块相结合.本文基于实际卫星型号任务VCM数传应用,提出了一种基于DVB-S2标准的快速累加并向递归编码算法,并在XC7K325t-3fbg900 FPGA上设计实现了一种高效低功耗LDPC编码器.
1 编码算法 1.1 DVB-S2标准基本编码算法DVB-S2标准中采用的LDPC码是IRA-LDPC码,其校验矩阵为
| $ {\mathit{\boldsymbol{H}}_{(n - k) \cdot n}} = \left[ {{\mathit{\boldsymbol{A}}_{(n - k) \cdot k}}\mid {\mathit{\boldsymbol{B}}_{(n - k)}} \cdot (n - k)} \right] =\\ \left[ {\left. {\begin{array}{*{20}{c}} {{a_{00}}}&{{a_{01}}}& \cdots &{{a_{0,k - 1}}}\\ {{a_{10}}}&{{a_{11}}}& \cdots &{{a_{1,k - 1}}}\\ \vdots & \vdots &{}& \vdots \\ {{a_{n - k - 2,0}}}&{{a_{n - k - 2,1}}}& \cdots &{{a_{n - k - 2,k - 1}}}\\ {{a_{n - k - 1,0}}}&{{a_{n - k - 1,1}}}& \cdots &{{a_{n - k - 1,k - 1}}} \end{array}} \right| \begin{array}{*{20}{c}} 1&0&0& \cdots &0&0\\ 1&1&0& \cdots &0&0\\ \vdots &{}&{}& \ddots &{}& \vdots \\ 0&0& \cdots &1&1&0\\ 0&0& \cdots &0&1&1 \end{array}} \right]. $ | (1) |
式中:B为下三角阶梯矩阵; A为稀疏矩阵,且A的列向量按顺序每360列构成一个分组,每个分组第j(1≤j≤360)个列向量中1的位置可根据式(2)计算得到.
| $ \left\{ {{d_i} + (j - 1) \cdot q} \right\}\,\bmod \,(n - k),i \in \{ 1,2, \cdots ,v\} . $ | (2) |
式中:di为每个分组首列列向量中第i个1的初始校验地址,v为此列向量的列重,q为标准中给出的数值,n为码长,k为信息比特长度.
IRA-LDPC码是系统码,其码字为
| $ \mathit{\boldsymbol{C}} = [\mathit{\boldsymbol{I}}\mid \mathit{\boldsymbol{P}}]. $ | (3) |
式中I=[i0 i1 … ik-2 ik-1]为信息比特序列,P=[p0 p1 … pn-k-1]为校验比特序列.
LDPC编码的实质为在二元域上求解式(4)所示的线性方程组.
| $ \mathit{\boldsymbol{H}} \cdot {\mathit{\boldsymbol{C}}^{\rm{T}}} = \mathit{\boldsymbol{0}}\mathit{\boldsymbol{.}} $ | (4) |
由于B矩阵的双对角线结构,校验比特可由方程组(5)递归计算得到:
| $ \left\{ {\begin{array}{*{20}{l}} {{p_0} = {a_{00}}{i_0} \oplus {a_{01}}{i_1} \cdots \oplus {a_{0,k - 1}}{i_{k - 1}},}\\ {{p_1} = {a_{10}}{i_0} \oplus {a_{11}}{i_1} \cdots \oplus {a_{1,k - 1}}{i_{k - 1}} \oplus {p_0},}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots }\\ {{p_{n - k - 1}} = {a_{n - k - 1,0}}{i_0} \oplus {a_{n - k - 1,1}}{i_1} \cdots \oplus }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {a_{n - k - 1,k - 1}}{i_{k - 1}} \oplus {p_{n - k - 2}},} \end{array}} \right. $ | (5) |
式中
由上述分析知,DVB-S2标准LDPC编码的关键就是对方程组(5)的求解,令IN(r)表示与校验节点r相连的所有变量节点集合,CN(c)表示与变量节点c相连的所有校验节点集合,引入中间变量Sr=
| $ \left\{ \begin{array}{l} {p_0} = \mathop \oplus \limits_{z \in {\rm{IN}}(0)} {i_z} = {S_0},\\ {p_1} = \mathop \oplus \limits_{z \in {\rm{IN}}(1)} {i_z} \oplus {p_0} = {S_1} \oplus {S_0},\\ \vdots \\ {p_r} = {S_r} \oplus {p_{r - 1}} = \mathop \oplus \limits_{i = 0}^r {S_i}. \end{array} \right. $ | (6) |
由方程组(6)可知,校验比特的计算是一个对Sr在二元域累加的过程.设编码并行度为M,即同一时刻参与运算的信息比特为M位,实际应用时,M的取值可根据VCM模式设置.进一步,可根据式(7)并向递归计算Sr.
| $ \begin{array}{l} {\rm{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} c = 0:M:k - M\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{each}}{\kern 1pt} {\kern 1pt} {\kern 1pt} r \in {\rm{CN}}(c){\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{do}}\\ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {S_r} = {S_r} \oplus {i_c}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {S_{(r + q)\,\bmod \,(n - k)}} = {S_{(r + q)\,\bmod \,(n - k)}} \oplus {i_{c + 1}}} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {S_{r + (M - 1) \cdot q\,\bmod \,(n - k)}} = {S_{r + (M - 1) \cdot q\,\bmod \,(n - k)}} \oplus {i_{c + M - 1}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{end}}\\ {\rm{end}} \end{array} $ | (7) |
利用二进制计算的特点,式(7)中Sr计算可简化为
| $ {S_r} = \left\{ {\begin{array}{*{20}{l}} {{S_r},{i_c} = 0;}\\ {\overline {{S_r}} ,{i_c} = 1.} \end{array}} \right. $ | (8) |
式中
为快速并向递归计算Sr,根据编码并行度M,可按式(9)存储Sr,其中L=(n-k)/M.
| $ \mathit{\boldsymbol{S}} = {\left[ {\begin{array}{*{20}{c}} {{S_0}}&{{S_1}}& \cdots &{{S_{M - 1}}}\\ {{S_M}}&{{S_{M + 1}}}& \cdots &{{S_{2M - 1}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{S_{(L - 1)M}}}&{{S_{(L - 1)M + 1}}}& \cdots &{{S_{LM - 1}}} \end{array}} \right]_{L \times M}}. $ | (9) |
当所有信息比特参与完运算,按式(10)快速并向递归计算校验比特,且输出为顺序输出.
| $ \left\{ \begin{array}{l} \left[ {\begin{array}{*{20}{l}} {{S_0}}&{\mathop \oplus \limits_{r = 0}^1 {S_r}}& \cdots &{\mathop \oplus \limits_{r = 0}^{M - 1} {S_r}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{p_0}}&{{p_1}}& \cdots &{{p_{M - 1}}} \end{array}} \right],\\ \begin{array}{*{20}{c}} {{M^\prime }b\left\{ {{p_{M - 1}}} \right\} \oplus \left[ {{S_M}\mathop \oplus \limits_{r = M}^{M + 1} {S_r} \cdots \quad \mathop \oplus \limits_{r = M}^{2M - 1} {S_r}} \right] = }\\ {\left[ {\begin{array}{*{20}{l}} {{p_M}}&{{p_{M + 1}}}& \cdots &{{p_{2M - 1}}} \end{array}} \right],} \end{array}\\ \vdots \\ \begin{array}{*{20}{c}} {{M^\prime }b\left\{ {{p_{(L - 1)M - 1}}} \right\} \oplus \left[ {{S_{(L - 1)M}}\mathop \oplus \limits_{r = (L - 1)M}^{(L - 1)M + 1} {S_r} \cdots \mathop \oplus \limits_{r = (L - 1)M}^{LM - 1} {S_r}} \right] = }\\ {\left[ {\begin{array}{*{20}{l}} {{p_{(L - 1)M}}}&{{p_{(L - 1)M + 1}}}& \cdots &{{p_{LM - 1}}} \end{array}} \right].} \end{array} \end{array} \right. $ | (10) |
以运行高度为600 km的近地卫星为例,卫星在仰角>5°时建立数传链路,其链路参数见表 1.
| 表 1 某近地卫星数传链路设计参数 Tab. 1 Design parameters for data transmission link of a LEO satellite |
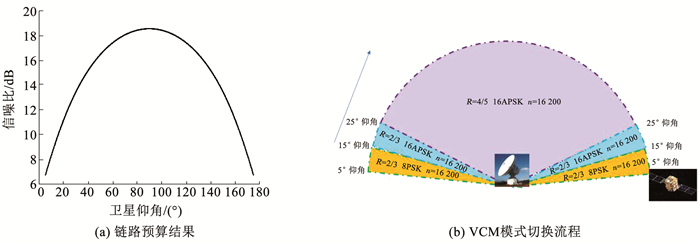
图 1(a)所示为链路预算结果.从图中可看出随着仰角变化,链路预算结果动态变化,在本例中,卫星过境期间存在着11.8 dB的链路信噪比波动.(注:图中90°~175°仰角对应实际90°~5°仰角)
|
图 1 链路预算结果和VCM模式切换流程 Fig. 1 Link budget and VCM mode change process |
根据链路预算结果和文献[3]中提出的VCM流程设计方法,确定了本文如图 1(b)所示VCM模式切换方案:当5°≤卫星仰角≤15°时,采用码长n=16 200,码率R=2/3,调制方式为8PSK的modcod1模式; 当15° < 卫星仰角≤25°时,采用码长n=16 200,码率R=2/3,调制方式为16APSK的modcod2模式; 当卫星仰角>25°时,采用码长n=16 200,码率R=4/5,调制方式为16APSK的modcod3模式.
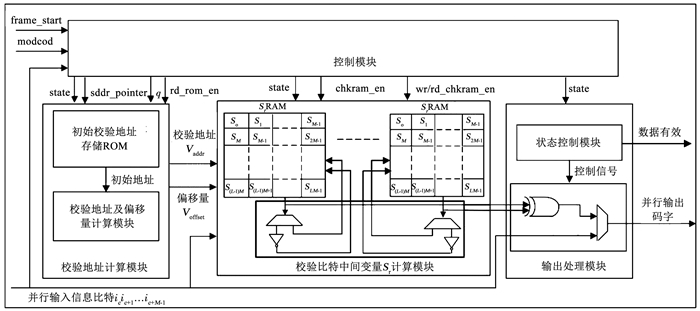
针对上述VCM数传系统需求,设计了基于快速累加并向递归编码算法的高效低功耗LDPC编码器,结构框图见图 2.主要包括控制模块、校验地址计算模块、校验比特中间变量Sr计算模块、输出处理模块.其中校验地址计算模块包括初始校验地址存储ROM、校验地址及偏移量计算模块; 校验比特中间变量Sr计算模块包括校验比特中间变量存储SrRAM和取反逻辑; 输出处理模块包括状态控制模块和异或逻辑.
|
图 2 高效低功耗LDPC编码器结构框图 Fig. 2 Hardware architecture of high efficient and low power LDPC encoder |
控制模块是编码器的核心模块,主要由状态机和控制信号组成,其作用是根据VCM模式的设置动态重构编码器,完成各模块间的有序切换并保证模块内部各功能的正确实现.编译时,针对VCM设置参数进行综合适配,改变模块内部结构和相互之间的连接关系,生成针对用户设定的可执行文件.控制模块端口信号及其说明见表 2.
| 表 2 控制模块端口信号及说明 Tab. 2 Signal ports descriptions of control module |
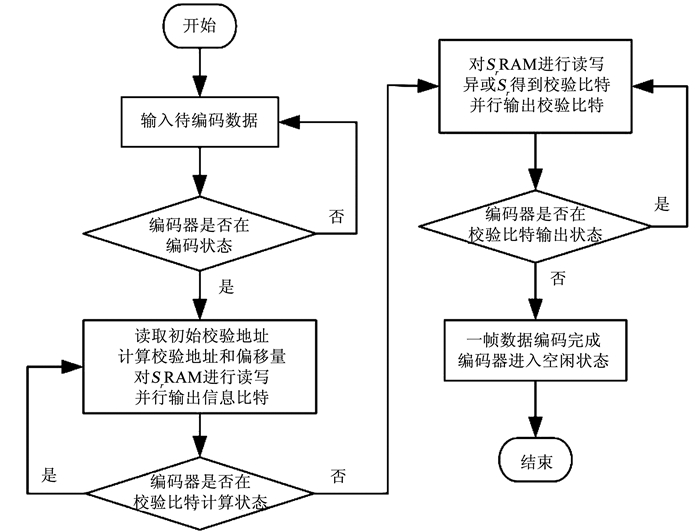
图 3为高效低功耗LDPC编码器的工作流程图.校验地址计算模块按照分级存储指针从ROM中对分级存储的初始校验地址进行读取,并根据初始校验地址计算出该信息比特对应的校验地址和偏移量; 校验比特中间变量Sr计算模块在SrRAM读写时序及读写使能控制下,读取该校验地址中的数值,并根据当前信息比特的取值在下一时钟周期将取反后的数值写入同一地址; 当一帧数据的所有信息比特输入完毕,Sr计算也随之结束,此时从零地址开始读取SrRAM中的值送入输出处理模块,并将SrRAM中内容清零,保证下一帧数据编码的正确性; 输出处理模块通过编码器状态参数的控制对分布式存储的Sr进行异或得到最终的校验比特,按顺序并行输出信息比特和校验比特.
|
图 3 编码器工作流程 Fig. 3 Encoding process of high efficient and low power encoder |
图 4为校验地址计算模块结构.校验地址计算模块由初始校验地址存储ROM、校验地址及偏移量计算模块组成,用于完成当前信息比特对应的校验地址和偏移量计算.

|
图 4 校验地址计算模块结构框图 Fig. 4 Hardware architecture of calculation of parity-check bits address module |
利用ROM存储初始校验地址,且对不同VCM模式的初始校验地址进行指针式分级存储.当输入为每个分组的第1个信息比特时,根据分级存储指针从ROM相应地址中读取初始校验地址,组内其余信息比特的校验地址由式(2)计算.为节省资源,式中乘法用累加方式代替,求模运算用减法和选择器实现.针对式(9)设计的Sr存储结构,利用除法器按照式(11)、(12)计算组内信息比特对应的SrRAM校验地址Vaddr和偏移量Voffset.
| $ {{V_{{\rm{addr }}}} = {\rm{ floor }}(x/M),} $ | (11) |
| $ {{V_{{\rm{offset }}}} = \,\bmod \,(x,M).} $ | (12) |
式中:floor为取整函数,mod为取模函数,x为由式(2)计算出的校验地址.
2.4 校验比特中间变量Sr计算模块校验比特中间变量Sr计算模块是高效低功耗LDPC编码器的重要模块,该模块利用双端口RAM按照式(7)、(8)、(10)完成对中间变量Sr的存储与更新计算.由式(7)内层循环可知,每个Sr更新需要v个时钟,为缩短编码周期,提高编码数据吞吐率,本文采用分布式存储技术,利用v·M个SrRAM并行处理一个信息比特对v个Sr的更新计算的同时并行计算Sr, S(r+q)mod(n-k), …, Sr+(M-1)·qmod(n-k).根据3种VCM模式需求,本文支持3、4两种编码并行度,分别对应8PSK和16APSK两种调制方式,为兼容各VCM模式,本文采用最大化存储编码策略,利用vmax·Mmax块深度为(n-k)/Mmin、宽度为Mmax的双端口RAM,完成Sr的存储与更新计算,其中vmax为校验矩阵列向量列重v的最大值,Mmin和Mmax分别为编码并行度M的最小值和最大值.编码时由控制模块根据VCM模式置v·M个SrRAM的使能信号有效,完成Sr的存储与更新计算.
并行输入的信息比特icic+1…ic+M-1分别送入M个存储器,当输入信息比特ic为1时,SrRAM读使能有效,根据Vaddr读取SrRAM中的数据,同时根据Voffset值对读出数据的相应比特位置取反,并延迟一个时钟周期再写回同一地址.当输入信息比特ic为0时,SrRAM读使能无效,不做任何操作,降低了编码器功耗.当k个信息比特全部输入参与完运算后,Sr更新计算完成,此时将v·M个SrRAM中的内容从零地址开始同时读出,并将零值写入该地址,以保证后续的数据帧能正确编码.
2.5 输出处理模块输出处理模块将编码后的码字包括信息比特和校验比特并行输出至数字调制器.当编码器处于校验比特计算状态时,输出处理模块将并行输入的信息比特直接输出,并置输出数据有效; 当编码器处于校验比特输出状态时,根据式(10)对分布式存储的Sr进行异或操作,每个时钟完成M个校验比特的计算且按顺序并行输出M个校验比特,同时置输出数据有效.
3 实现结果与分析 3.1 编码器硬件资源消耗分析对提出的高效低功耗LDPC编码器,在Xilinx XC7K325t-3fbg900型号FPGA上进行了实现,开发环境为ISE14.7,与其他文献编码器硬件资源消耗对比结果见表 3.
| 表 3 不同文献编码器资源消耗情况 Tab. 3 Hardware utilization of encoders of different references |
文献[13-15]均是对单一码长码率LDPC编码器的实现,文献[16]支持2种码长和11种码率,本文设计的编码器兼容3种VCM模式,控制模块有效保证了编码器在LEO卫星切换VCM模式时动态自适应调整,提高了编码器的灵活性.
为兼容3种VCM模式,需对各VCM模式下不同初始校验地址进行存储,且为实现快速累加并向递归编码算法,采用了分布式存储技术和最大化存储编码策略,因此本文的寄存器和存储资源消耗比文献[13-15]多.文献[16]中设计的编码器需要用RAM对中间变量结果以及输入信息比特进行缓存,占用了较多的RAM资源,而本文提出的编码器不需要对信息进行缓存,降低了RAM资源占用.本文设计的编码器实现了硬件资源和编码灵活性的动态平衡.
3.2 编码器功耗分析本文提出的编码器在输入信息比特为1时,SrRAM读使能有效,将SrRAM中的数据读出,并用取反操作代替异或操作; 而输入信息比特为0时,读使能无效,不对SrRAM进行操作,降低了编码器的功耗.使用XPower Analyzer工具对本文设计的编码器和未经低功耗设计的编码器进行功耗分析,对比结果见表 4.
| 表 4 功耗分析对比 Tab. 4 Power consumption comparison |
表中未经低功耗设计的编码器是指相同硬件平台,每个时钟均对SrRAM进行读写,用异或进行Sr更新与计算,其他模块与本文一致的编码器.由表 4可知,利用本文方案设计的编码器降低了21.7%的功耗,对功耗要求苛刻的LEO卫星星上系统具有重要意义.
3.3 编码器性能分析编码数据吞吐率是衡量编码器性能的重要指标之一,借助Timing Analyzer工具,对本文编码器进行评估,其计算公式为
| $ T = \frac{{n \cdot R \cdot {f_{{\rm{clk}}}}}}{{{t_{\rm{d}}} + 360/M \cdot w + L}}. $ | (13) |
式中:n为码长; R为码率; fclk为系统时钟,综合编译结果为347.5 MHz; M为编码并行度; w为标准中给出的初始校验地址行数; L=(n-k)/M; td为系统延时,定义为第1个信息比特进入编码器到第1个信息比特输出所需时钟周期数,实测值为26.本文提出的编码器的数据吞吐率见表 5.
| 表 5 本文编码器吞吐率 Tab. 5 Throughput of proposed encoder |
本文设计的编码器编码并行度可动态切换为3或4,分别对应8PSK和16APSK两种调制方式,提高了编码数据吞吐率,编码数据吞吐率最高可达1.104 Gb/s; 且编码数据按顺序输出,不需要与复杂的交织模块相结合,简单的行列交织之后,即可进行比特星座映射,降低了整个VCM系统的实现复杂度,具有高效性.
对于VCM数传系统,其数据吞吐量TVCM,即卫星在数传时间内向地面传输的总信息量为
| $ \begin{array}{c} T_{\mathrm{vCM}}=T_{\text {modcodl }} \cdot \Delta t_{\text {modcodl }}+T_{\text {modeod2 }} \cdot \Delta t_{\text {modeod2 }}+ \\ T_{\text {modcod3 }} \cdot \Delta t_{\text {modcod3 }}. \end{array} $ | (14) |
利用STK仿真软件得到每种模式持续时间Δtmodcod1= 380 s,Δtmodcod2= 280 s,Δtmodcod3= 420 s; 计算得到CCM数传系统(采用单一modcod1模式)数据吞吐量为746.28 Gb,而VCM数传系统数据吞吐量为984.14 Gb,较CCM数传系统提高了31.9%.
4 结论面对LEO卫星VCM数传系统对高通量、低功耗、高可靠性信道编码的应用需求,本文提出了一种基于快速累加并向递归编码算法的高效低功耗LDPC编码器.利用输入比特的随机性和二进制计算的特点,简化了Sr的计算,降低了21.7%编码器功耗; 通过控制模块动态重构编码结构,能够兼容3种VCM模式,提高了编码器的灵活性; 采用与调制方式相匹配的存储方案,能够顺序输出M个并行比特,提高了编码数据吞吐率,且不需要与复杂交织模块相结合,具有高效性.结果表明,编码数据吞吐率最高可达1.104 Gb/s,整个VCM数传系统数据吞吐量较CCM系统提高了31.9%,且该编码器具有低功耗、灵活性与高效性的特点,在LEO卫星VCM数传系统中具有较高应用价值.
| [1] |
李炯卉.基于可变编码多载波调制技术的星地高速数传系统研究[D].北京: 中国科学院大学, 2018 LI Jionghui. Satellite-ground high-rate data transmission system based on variable coding multi-carrier modulation[D]. Beijing: University of Chinese Academy of Sciences, 2018 |
| [2] |
王万玉, 毛伟, 何元春. 遥感卫星星地链路数据传输技术分析[J]. 物联网技术, 2017, 7(7): 34. WANG Wanyu, MAO Wei, HE Yuanchun. Analysis of satellite-to-ground data transmission technology for remote sensing satellites[J]. Internet of Things Technologies, 2017, 7(7): 34. DOI:10.16667/j.issn.2095-1302.2017.07.007 |
| [3] |
李炯卉, 熊蔚明, 梅凡. 优化卫星数传链路效率的VCM流程设计[J]. 哈尔滨工业大学学报, 2016, 48(10): 162. LI Jionghui, XIONG Weiming, MEI Fan. Design of a VCM-based satellite data transmission architecture for down-link efficiency enhancement[J]. Journal of Harbin Institute of Technology, 2016, 48(10): 162. DOI:10.11918/j.issn.0367-6234.2016.10.024 |
| [4] |
LI Jionghui, XIONG Weiming, SUN Geng, et al. Doppler-robust high-spectrum-efficiency VCM-OFDM scheme for low Earth orbit satellites broadband data transmission[J]. IET Communications, 2018, 12(1): 35. DOI:10.1049/iet-com.2017.0229 |
| [5] |
Consultative Committee for Space Data Systems (CCSDS). TM synchronization and channel coding: CCSDS 131.0-B-2[S]. Washington DC: CCSDS, 2011
|
| [6] |
European Telecommunications Standards Institute (ETSI). European Standard: Digital Video Broadcasting (DVB); Second generation framing structure, channel coding and modulation systems for broadcasting, interactive services, news gathering and other broadband satellite applications: ETSI EN 302 307 V1.2.1 (2009-08)[S]. Sophia Antipolis: ETSI, 2014
|
| [7] |
GALLAGER R G. Low-density parity-check codes[J]. IRE Transactions on Information Theory, 1962, 8(1): 21. DOI:10.1109/TIT.1962.1057683 |
| [8] |
RICHARDSON T J, SHOKROLLAHI M A, URBANKE R A. Design of capacity-approaching irregular low-density parity-check codes[J]. IEEE Transactions on Information Theory, 2001, 47(2): 619. DOI:10.1109/18.910578 |
| [9] |
DIGDARSINI D, MISHRA D, MEHTA S, et al. FPGA implementation of FEC encoder with BCH & LDPC codes for DVB S2 system[C]// 2019 6th International Conference on Signal Processing and Integrated Networks (SPIN). Noida: IEEE, 2018: 78. DOI: 10.1109/SPIN.2019.8711664
|
| [10] |
ZINCHENKO M Y, LEVADNIY A, GREBENKO Y. Development of the LDPC coder-decoder of the DVB-S2 standard on FPGA[C]// 2018 Systems of Signal Synchronization, Generating and Processing in Telecommunications (SYNCHROINFO). Minsk: IEEE, 2018: 1. DOI: 10.1109/SYNCHROINFO.2018.8456924
|
| [11] |
范光荣, 王华, 夏添琦, 等. 基于DVB-S2的高速多码率LDPC编码器的FPGA设计与实现[J]. 北京理工大学学报, 2008, 28(9): 813. FAN Guangrong, WANG Hua, XIA Tianqi, et al. FPGA design and implementation of high speed multi-rate LDPC encoder based on DVB-S2[J]. Transactions of Beijing Institute of Technology, 2008, 28(9): 813. |
| [12] |
武学彬, 薛永林. 用于DVB-S2的LDPC编码器设计[J]. 电视技术, 2007, 31. WU Xuebin, XUE Yonglin. Design of LDPC encoder in DVB-S2 based on FPGA[J]. Video Engineering, 2007, 31(S1): 114. DOI:10.3969/j.issn.1002-8692.2007.z1.039 |
| [13] |
GOMES M, FALCAO G, SENGO A, et al. High throughput encoder architecture for DVB-S2 LDPC-IRA codes[C]// 2007 IEEE International Conference on Microelectronics. Cairo: IEEE, 2007: 271. DOI: 10.1109/ICM.2007.4497709
|
| [14] |
LEE I, KIM M, OH D, et al. High-speed LDPC encoder architecture for digital video broadcasting systems[C]// 2013 IEEE International Conference on ICT Convergence (ICTC). Jeju: IEEE, 2013: 606. DOI: 10.1109/ICTC.2013.6675433
|
| [15] |
华力, 雍玲, 雷菁. 基于FPGA的DVB-S2通用LDPC编码器设计与实现[J]. 通信技术, 2008, 41(1): 12. HUA Li, YONG Ling, LEI Jing. Design and implementation of universal LDPC code encoder in the DVB-S2 based on FPGA[J]. Communications Technology, 2008, 41(1): 12. DOI:10.3969/j.issn.1002-0802.2008.01.005 |
| [16] |
兰亚柱, 杨海钢, 林郁. 面向DVB-S2标准LDPC码的高效编码结构[J]. 电子与信息学报, 2016, 38(7): 1781. LAN Yazhu, YANG Haigang, LIN Yu. Efficient encoding architecture for LDPC code based on DVB-S2 standard[J]. Journal of Electronics and Information Technology, 2016, 38(7): 1781. DOI:10.11999/JEIT151198 |
 2021, Vol. 53
2021, Vol. 53


