近年来,由于预制拼装结构具有现场施工工期短、施工质量可控[1-3]以及节省临时占地和人工等优点已被大力推广[4-5],而预制拼装桥梁连接钢筋与灌浆料之间的有效粘结和锚固是保证装配化桥梁结构服役性能的关键[6-8]. 目前对于预制拼装混凝土结构连接钢筋锚固长度的设计,通常按照现浇结构的相关规定考虑,但是由于预制拼装连接构造的特点,其连接钢筋的保护层厚度一般比现浇结构大50 mm以上,故在计算其锚固长度时可以忽略保护层厚度的影响. 而现有规范和学者提出的钢筋与混凝土界面粘结强度计算方法[9-13]将混凝土保护层厚度与混凝土强度、钢筋锚固长度和钢筋直径均作为主要影响因素来考虑,可能无法准确评估预制拼装结构连接钢筋的锚固性能. 已有研究表明,当混凝土保护层厚度较小时,外围混凝土易产生水平裂缝,混凝土握裹层易发生劈裂破坏,导致钢筋粘结强度降低,从而造成钢筋临界锚固长度增加[12],因此,对于混凝土保护层厚度足够的预制拼装构件,如果仍按传统现浇结构钢筋锚固长度要求设计预制拼装桥梁中的连接钢筋,可能会导致锚固长度设计过长,增加盖梁等预制构件高度,增加施工难度,提高了施工成本.
目前,现有装配式混凝土结构的相关规范对连接钢筋的锚固长度仍沿用现浇结构的相关规定进行设计,不适用于具有大保护层厚度的预制拼装桥梁连接钢筋的粘结锚固性能计算,此方面研究还有待深入. 文献[9]通过大量钢筋混凝土拉拔试验研究,探讨了界面粘结强度的变化规律,并以此导出了现浇结构中钢筋的临界锚固长度,给出了基于可靠度分析的设计锚固长度建议值. 文献[10]发现国内外文献对预制装配结构中灌浆料与钢筋的粘结滑移关系研究甚少,并考虑保护层厚度、钢筋直径和锚固长度3个参数,进行了27个带肋钢筋-灌浆料拉拔试验,基于试验数据提出了钢筋在灌浆料中的锚固长度经验值约为0.67lab. 文献[11]研究发现,以往对钢筋与混凝土粘结性能的研究通常基于宏观层次,将钢筋简化,忽略带肋钢筋横肋的作用,从而无法捕捉钢筋外形的差异对粘结性能的影响,并建立了钢筋混凝土构件的细观数值分析模型,模拟了带肋钢筋与混凝土之间的粘结破坏机理. 文献[12]针对钢筋在高强灌浆料中的锚固性能和高强灌浆料与预留孔孔壁间的粘结性能进行了探索性试验,考虑混凝土强度、钢筋直径和连接钢筋灌浆保护层厚度等因素,制作了27个预制混凝土墩头钢筋预留孔灌浆连接拉拔试件和24个预制混凝土直钢筋预留孔灌浆连接拉拔试件,建议墩头钢筋锚固长度取为0.6lab,试验所得直钢筋锚固长度与规范锚固长度之比约为0.5. 文献[13]总结归纳了国内外学者对于钢筋混凝土粘结锚固性能的试验研究、理论计算方法和数值分析模型,发现不同学者提出的粘结强度计算存在一定的差异性和局限性. 且已有试验研究未明确区分试件破坏模式对粘结强度计算的影响,若粘结强度计算仍按界面完全失效的方法进行,会导致得到的钢筋与混凝土界面粘结强度偏小,锚固长度偏大,不适用于预制拼装桥梁的设计施工. 因此,如何准确地分析保护层厚度充足情况下的钢筋混凝土粘结界面的力学特征,成为预制拼装桥梁设计及施工规范化的重要问题.
本文针对预制拼装桥梁连接钢筋的锚固特征,进行了钢筋混凝土粘结锚固试验研究和有限元分析,探究钢筋直径、混凝土强度和锚固长度等主要参数对粘结界面的影响. 分析大保护层厚度下的钢筋混凝土界面粘结的破坏规律和破坏特征. 最后,采用多元回归分析方法,确定影响粘结性能的主要因素,给出预制拼装桥梁设计中钢筋的粘结强度与锚固长度计算公式和建议值.
1 试验 1.1 试件设计与制作为研究装配式桥梁连接钢筋与混凝土之间的粘结锚固性能及其主要影响因素,以江西省昌九高速改扩建中的桥南村天桥装配式设计图纸为依据,在试件设计时参照预制拼装混凝土结构的构造特征,采用较大的保护层厚度,设计制作了22个钢筋混凝土拉拔试件. 试件的截面尺寸均为300 mm×300 mm,试验参数包括钢筋直径、混凝土强度和锚固长度. 混凝土强度等级分别为C30和C50,钢筋锚固长度分别为200、300、400 mm,变形钢筋直径分别为8、12、16、20、22 mm,光圆钢筋直径分别为8、20 mm. 同时,为探究试验结果是否具有重现性,制作两组参数相同的试件进行对比分析,各试件的参数见表 1. 表中试件按混凝土强度等级-钢筋直径-锚固长度方式编号,如C30-12-300, 表示混凝土强度等级为C30,钢筋直径为12 mm,锚固长度为300 mm的试件.
| 表 1 试件参数汇总 Tab. 1 Summary of test piece parameters |
制作两组标准混凝土试验块进行抗压试验,每组3个试件,同时对直径12 mm和16 mm的HRB400带肋钢筋进行抗拉试验,两组混凝土试验块的弹模均值分别为34 429、33 206 MPa,立方体抗压强度均值分别为53.8、50.3 MPa. 钢筋的材料性能试验结果见表 2.
| 表 2 普通钢筋材性参数 Tab. 2 Properties of ordinary steel bars |
如图 1所示,采用加载量程为0~500 kN,位移量程为0~50 mm,显示精度分别为0.01 kN和0.01 mm的HCYL-60锚杆综合参数测定仪进行加载. 加载初期荷载增量为2~5 kN,加载后期荷载增量为5~10 kN. 同时,分别在加载端和自由端设置电子位移计,钢筋应变片端部间距70 mm,中部间距100 mm. 采集每级荷载作用下试件加载端与自由端位移值和试件内部钢筋应变值.

|
图 1 钢筋拉拔试验加载及测试装置 Fig. 1 Schematic of loading and test devices |
由钢筋拉拔试验各试件的破坏模式和极限荷载可以看出(表 3),编号C50-10-300的两个试件的极限荷载分别为50.12、50.9 kN,破坏模式为钢筋拉断破坏,极限荷载差值为1.5%;编号C50-10-300的两个试件的极限荷载分别为68.9、71.1 kN,破坏模式为钢筋拉断破坏,极限荷载差值为3.1%,表明试验具有较好的重现性. 试件C50-16-300和C50-16-400的极限荷载与试件C50-12-300和C50-12-400相比,分别提高了85.7%和49.9%,与C30-16-300和C30-16-400试件相比,分别提高了19.8%和20.8%,说明对于保护层较大的预制混凝土构件,混凝土强度等级和钢筋直径对钢筋与混凝土粘结界面的极限荷载影响较大. 由于变形钢筋与混凝土的界面粘结力由两者的机械咬合力、化学粘结力和摩擦力组成,光圆钢筋与混凝土的界面粘结力由化学粘结力和摩擦力组成[14],带肋钢筋试件C50-20-300的极限荷载相比于光圆钢筋试件C50-Ø20-300提升了8.5倍,可以估算机械咬合力约占变形钢筋与混凝土粘结强度的88%. 另外,对比不同试件的破坏模式得出,随着混凝土强度的减小和钢筋直径的增大,试件的破坏模式逐渐由钢筋拉断破坏转为钢筋拔出破坏.
| 表 3 试验结果汇总 Tab. 3 Summary of test results |
预制拼装混凝土结构连接钢筋拉拔试件主要有两种破坏形式:钢筋拔出破坏和钢筋拉断破坏.
1) 钢筋拔出破坏. 当锚固不充分时,拉拔力大于钢筋混凝土粘结界面承载力,试件发生粘结界面失效的钢筋拔出破坏,如光圆钢筋试件和混凝土强度等级为C30的试件和均发生此类破坏. 由图 2(a)、2(b)可知,带肋钢筋拔出时加载端混凝土呈锥形破坏,钢筋未发生明显颈缩. 由图 2(c)、2(d)可知,拔出钢筋与混凝土粘结处的钢筋横肋完好,在拉拔荷载作用下钢筋连同部分肋间混凝土被一起拔出,残留肋间混凝土约占钢筋横肋间距的50%.

|
图 2 带肋钢筋拔出破坏 Fig. 2 Ribbed bar pullout failure |
2) 钢筋拉断破坏. 如图 3所示,当钢筋锚固充足时,试件发生钢筋拉断破坏,如混凝土强度等级为C50,钢筋直径为8、10、12 mm的试件均发生此种破坏. 钢筋混凝土粘结界面的承载力大于钢筋抗拉能力,试件的承载力由钢筋的抗拉能力决定. 试件发生钢筋拉断破坏时,加载端混凝土呈锥形破坏现象,自由端无明显滑动.

|
图 3 钢筋拉断破坏 Fig. 3 Steel bar break failure |
利用ABAQUS建立钢筋混凝土拉拔试件的轴对称有限元模型,模拟预制混凝土构件中连接钢筋与混凝土的粘结锚固特征,模型参数取值与试验试件相同,为保证模型的精确性,提高计算效率,钢筋与混凝土单元类型均选择四结点通用双线性轴对称四边形减缩积分单元CGAX4R. 粘结界面、钢筋轴线和混凝土边缘的网格划分密度分别为0.5、0.5、2.0 mm. 模型示意图和网格划分见如图 4所示.

|
图 4 有限元模型网格划分 Fig. 4 Meshing of finite element model |
考虑钢筋和混凝土粘结界面的细部特征,接触面的法向行为采用“硬接触”模拟,通过经典的拉格朗日乘子法实施,即接触面之间传递压应力大小不受限制,当接触面的压力变为负值或者零时表示两个接触面发生分离;切向行为采用“罚摩擦”模拟,即经典库伦摩擦模型,临界摩擦应力取决于接触压力,允许接触表面有弹性滑移,假定接触面间的各向摩擦系数μ相同,均取0.1[15].
3.2 材料本构模型为模拟钢筋混凝土粘结界面的破坏和裂缝开展过程,钢筋采用理想弹塑性模型,弹性模量Es取2.06×105 MPa,泊松比取0.3. 混凝土采用塑性损伤本构模型,通过分析有限元结果中的混凝土受拉损伤(DAMAGET)和受压损伤(DAMAGEC)云图来观察分析钢筋混凝土粘结界面的破坏过程. 混凝土受压损伤和受拉损伤的本构模型[16]如图 5所示.
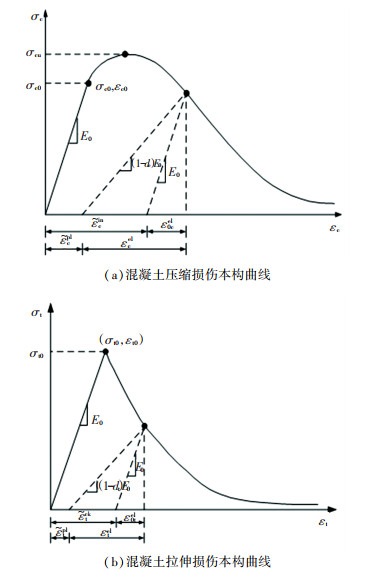
|
图 5 混凝土塑性损伤本构曲线 Fig. 5 Constitutive curves of plastic damage of concrete |
图中本构模型可以表示为
| $ \sigma_{\mathrm{t}, \mathrm{c}}=\left(1-d_{\mathrm{t}, \mathrm{c}}\right) E_{0}\left(\varepsilon_{\mathrm{t}, \mathrm{c}}-\widetilde{\varepsilon}_{\mathrm{t}, \mathrm{c}}^{\mathrm{pl}}\right). $ | (1) |
式中:dt, c为混凝土损伤因子,E0为混凝土弹性模量,εt, c为混凝土应变,
通过在混凝土模型中引入“拉伸硬化”来模拟钢筋与混凝土的界面效应(如粘结滑移和锁固行为)和荷载传递过程. 拉伸硬化根据开裂应变
| $ \widetilde{\varepsilon}_{\mathrm{t}}^{\mathrm{pl}}=\widetilde{\varepsilon}_{t}^{\mathrm{ck}}-\frac{d_{\mathrm{t}}}{\left(1-d_{\mathrm{t}}\right)} \frac{\sigma_{\mathrm{t}}}{E_{0}}. $ | (2) |
在定义受压硬化时,硬化数据根据非弹性应变
| $ \widetilde{\varepsilon}_{\mathrm{c}}^{\mathrm{pl}}=\widetilde{\varepsilon}_{\mathrm{c}}^{\mathrm{inl}}-\frac{d_{\mathrm{c}}}{\left(1-d_{\mathrm{c}}\right)} \frac{\sigma_{\mathrm{c}}}{E_{0}}. $ | (3) |
以重现性试件组C50-12-300为例建立其有限元模型,根据有限元分析结果,提取两个重现性试件的荷载位移曲线与试验曲线进行对比(图 6),可以看出有限元模型与相同参数的两个试验试件的上升阶段趋势一致,有限元模型的上升段略低于试验值1,略高于试验值2;有限元模型的极限荷载与试验值1和试验值2的误差分别为2.4%和0.8%,极限荷载非常接近.
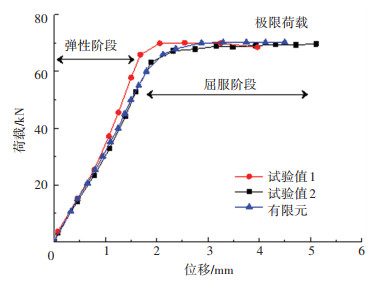
|
图 6 试验-有限元对比 Fig. 6 Experiment-finite element comparison |
钢筋与混凝土的粘结强度由两者接触面的属性决定,主要包括3个因素:1)混凝土基质与钢筋表面涂层的化学粘结力;2)钢筋与混凝土沿接触面产生相对滑移的摩擦阻力;3)钢筋混凝土接触面的不平整度引起的机械咬合力[14]. 试验表明,在拉拔荷载作用下,钢筋混凝土界面粘结试件的破坏形式主要分为:钢筋屈服断裂破坏和界面混凝土破坏.
带肋钢筋与混凝土的粘结强度由化学粘结力、摩擦力和机械咬合力组成. 加载初期,粘结界面的滑移阻力由化学粘结力承担,机械咬合力和摩擦力暂不发挥作用. 随着荷载的增大,化学粘结力失效,粘结界面发生相对滑移,机械咬合力和摩擦力开始发挥作用,界面滑移阻力由钢筋横肋与混凝土的斜向挤压力提供. 斜向挤压力的轴向分力使肋间混凝土像悬臂梁那样受弯剪作用,斜向挤压力的径向分力使钢筋周围的混凝土产生环向拉应力,此时钢筋周围混凝土处于三相受力状态. 如图 7(a)、7(d)所示,斜向挤压力使钢筋横肋后混凝土受拉,肋前混凝土受压,随着荷载的增大,首先在肋后产生径向裂缝,并沿与钢筋轴向成60°(钢筋横肋倾角)的方向发展,且裂缝的径向开裂深度近似等于钢筋横肋间距. 如图 7(b)、7(e)所示,由于钢筋约束了混凝土的径向变形,随着裂缝的发展,接触面达到界面粘结强度,肋间混凝土在径向压力和轴向剪力共同作用下逐渐破碎,接触面的机械咬合力开始失效并快速减小,界面粘结力由摩擦力和残余机械咬合力提供,直到机械咬合力完全失效,钢筋连同被压碎的混凝土被一起拔出,这一破坏过程称为带肋钢筋剪切粘结破坏,如图 7(c)、7(f)所示.
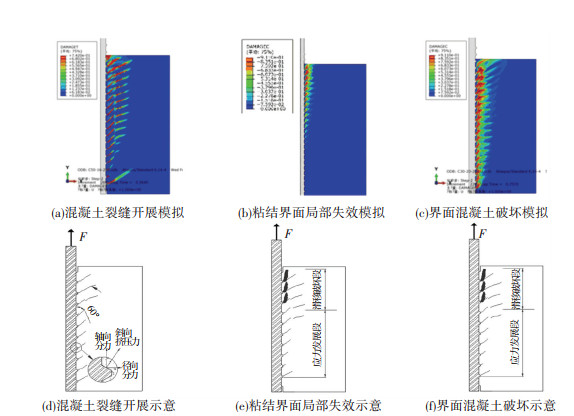
|
图 7 粘结界面破坏过程 Fig. 7 Bonding interface failure process |
以混凝土强度、钢筋直径和锚固长度为参数开展参数化分析,各试件的参数、破坏模式、极限荷载和粘结强度结果见表 4. 表 4中粘结应力计算公式[9]为
| $ \tau=\frac{F}{{\rm{ \mathsf{ π}}} d l}. $ | (4) |
| 表 4 计算结果 Tab. 4 Calculation results |
式中:τ为钢筋混凝土粘结强度,F为拉拔荷载,d为钢筋直径,l为有效粘结长度.
4.1 混凝土强度等级图 8为不同混凝土强度等级条件下钢筋拔出或拉断破坏的荷载位移曲线,以荷载位移曲线的割线斜率作为钢筋混凝土粘结界面的刚度,可将各试件的受力过程分为弹性阶段和刚度降低阶段,弹性阶段内钢筋混凝土界面粘结较好,割线斜率和界面刚度逐渐减小,但变化幅值较小. 随着拉拔荷载的进一步增加,粘结界面逐渐失效,界面刚度快速减小,直到拉拔荷载大于钢筋混凝土界面承载力,钢筋拔出.

|
图 8 不同混凝土强度试件的荷载位移曲线对比 Fig. 8 Comparison of load-displacement curves of test pieces with different concrete strengths |
图 9比较了不同混凝土强度的试件的粘结强度和极限荷载,图中d16-100系列代表钢筋直径为16 mm,锚固长度为100 mm,混凝土强度不同的5个试件,图中其他试件系列意义类似. 由图 9(a)得出,钢筋与混凝土的粘结强度随混凝土强度的增大而增大,混凝土强度等级为C80的试件与C30、C40、C50和C60试件相比,粘结强度分别提高了44.2%、34.7%、16.4%和5.8%. 同时,由图 9(a)可以看出,不同锚固长度试件系列的粘结强度与锚固长度关联度较小,即对于具有较大保护层厚度的预制拼装混凝土结构连接钢筋而言,在粘结强度计算时可以忽略锚固长度的影响. 从图 9(b)中的d16-150结果可以看出,随着混凝土强度的增加,试件破坏模式从钢筋拔出破坏变为钢筋拉断破坏,极限承载力明显提升. 结果表明,当发生钢筋拔出破坏,即在锚固长度不足时,混凝土强度对试件极限承载力影响显著. 但当试件发生钢筋拉断破坏,即锚固长度充足时,如d16-200系列和d16-300系列,凝土强度几乎没有影响.

|
图 9 混凝土强度等级影响 Fig. 9 Influence of concrete strength levels |
图 10对比了不同钢筋直径试件的荷载位移曲线,在锚固长度和混凝土强度等级相同时,随着钢筋直径的增加,试件的承载力逐渐变大,但试件的破坏模式却从钢筋拉断破坏(试件C30-12-200和C30-16-200)转为钢筋拔出破坏(试件C30-20-200和C30-25-200),表明试件不发生钢筋拔出破坏所需的锚固长度明显增加,即锚固长度与钢筋直径密切相关.
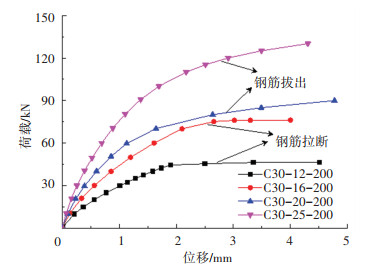
|
图 10 不同钢筋直径试件的荷载位移曲线对比 Fig. 10 Comparison of load-displacement curves of test pieces with different steel bar diameters |
由前文分析可知,连接钢筋与混凝土的界面粘结强度主要由钢筋横肋与肋间混凝土的机械咬合力组成,而决定机械咬合力大小的主要钢筋外形参数为横肋高度和横肋间距. 以相对肋面积(横肋在钢筋表面上的投影面积与钢筋表面积的比值)作为评价粘结性能的指标,相对肋面积越大,粘结性能越好[17]. 由《钢筋混凝土用钢第2部分:热轧带肋钢筋》[18]可知,钢筋的相对肋面积随钢筋直径的增大而减小,则连接钢筋与混凝土的粘结性能亦随之降低. 如图 11(a)所示, 钢筋直径为25 mm的粘结强度与8、12、16、20 mm的试件相比,粘结强度分别减少了33.9%、28.1%、15.6%、11.1%. 由图 11(b)可知,随着钢筋直径的增加,试件的破坏模式由钢筋拉断破坏转变为钢筋拔出破坏(如C30-200系列),当钢筋直径增加时,钢筋与混凝土的粘结面积增大,粘结面积增加引起的界面承载力增量大于同等条件下粘结强度降低所引起的减小值,故其极限荷载仍随钢筋直径的增加而增加.
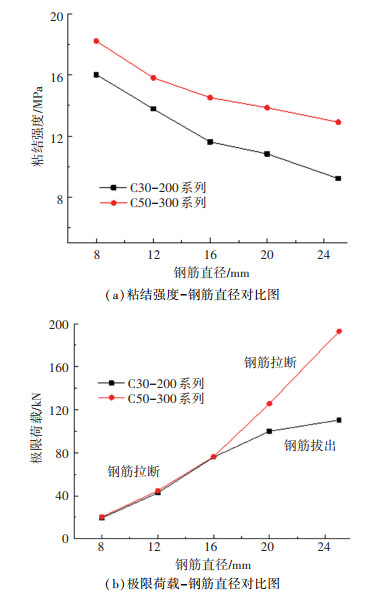
|
图 11 钢筋直径影响 Fig. 11 Influence of steel bar diameter |
从图 12(a)中的C50-16-100试件可以看出,当钢筋锚固不充分时,试件发生拔出破坏,钢筋拔出前,界面刚度随荷载的增加迅速降低,钢筋与混凝土的粘结界面失效. 钢筋锚固充分时,试件发生钢筋拉断破坏(图 12(a)中的C50-16-200和C50-16-300试件),钢筋屈服之前界面刚度随荷载增加而逐渐减小,但变化幅值较小. 由图 12(b)可知,锚固长度对连接钢筋与混凝土的粘结强度影响较小. 对比图 12(c)中不同试件的极限荷载发现,C30-16系列中锚固长度为200 mm的试件与锚固长度为150 mm和100 mm的试件相比,试件的极限荷载分别提高了21.5%、64.2%,即在锚固长度不足时,极限荷载随着锚固长度的增大而增大,试件的破坏形式会随锚固长度的增加由钢筋拔出破坏转为钢筋拉断破坏.

|
图 12 锚固长度影响 Fig. 12 Influence of anchorage length |
对于钢筋与混凝土粘结强度的计算,国内外学者和现行规范综合考虑不同因素给出了相应的半经验半理论计算公式[19-22],相关公式多从混凝土强度、保护层厚度、锚固长度和钢筋直径等方面考虑,典型的粘结强度计算公式见表 5. 国内混凝土结构设计规范仅以混凝土抗拉强度的角度计算钢筋与混凝土的粘结强度,未考虑钢筋类型、钢筋直径、锚固长度和保护层厚度等影响因素;澳大利亚规范与美国规范以混凝土强度、混凝土保护层厚度与钢筋直径之比等作为粘结强度计算的关键指标,而装配式结构中的混凝土保护层充分,不会出现因保护层厚度过小而对连接钢筋粘结强度产生影响. 因此,现有规范的钢筋粘结强度计算公式不适用于预制拼装桥梁连接钢筋计算,进而会导致预制构件的预留连接钢筋偏长,对施工难度和拼装精度控制具有不利影响. 由前文分析可知,预制拼装混凝土结构连接钢筋拔出试件粘结强度主要影响因素为钢筋直径和混凝土强度,以此可以对连接钢筋粘结强度的计算公式进行分析.
| 表 5 粘结强度计算公式 Tab. 5 Calculation formulas of bonding strength |
表 5中,τu为钢筋混凝土界面粘结强度,fcu为混凝土抗压强度标准值,ft, r为混凝土抗拉强度特征值,ft为混凝土劈裂强度,d为钢筋直径,c为保护层厚度,l为锚固长度,ρsv为配筋率.
利用多元线性回归分析的方法确定上述试件各因素的影响比重,结果如图 13所示. 可以看出,钢筋与混凝土界面的粘结强度与混凝土强度呈正相关,与钢筋直径呈负相关. 由此可以拟合出预制混凝土结构连接钢筋的粘结强度计算公式为
| $ {\tau _{\rm{u}}} = 0.108{f_{{\rm{cu}}}} - 0.344d + 14.84. $ | (5) |
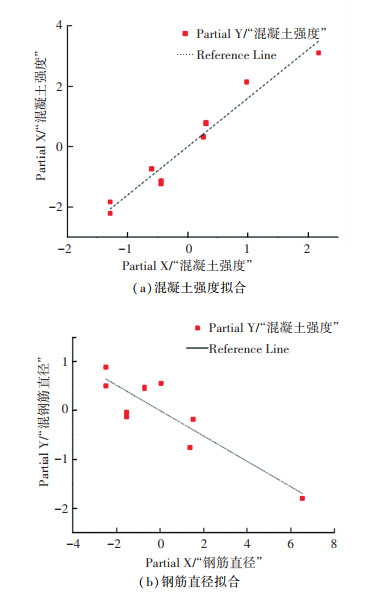
|
图 13 粘结强度拟合曲线 Fig. 13 Bonding strength fitting curves |
式中:τu为钢筋与混凝土界面粘结强度,fcu为混凝土抗压强度标准值,d为钢筋直径.
按照界面完全破坏的原则,将式(5)与本文试验结果和文献[10, 23]试验中钢筋拔出破坏的试件进行对比分析,对比结果见图 14. 分析发现,粘结强度拟合值与试验值的平均比值为1.04,比值的标准差和变异系数分别为0.06和5.77%,拟合值与实测值的拟合优度R2为0.87,表明拟合值与试验值较吻合,离散度较低.
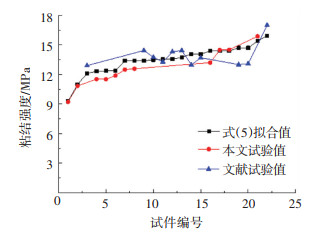
|
图 14 粘结强度拟合值与试验值对比曲线 Fig. 14 Comparison curves of fit values and test values of bonding strength |
以预制混凝土构件连接中常用的25 mm钢筋直径,85 mm保护层厚度为例,对比国内外规范与本文拟合公式关于粘结强度计算的差异如图 15所示. 可以看出,ACI318-11的粘结强度计算值比AS3600和GB 50010—2010分别大25%和15.9%,表明国内外规范对于粘结强度计算存在一定差异. 本文拟合公式(5)的计算结果与AS3600、GB 50010—2010、ACI318-11相比,粘结强度分别提高了62.7%、50.9%和30.25%,说明在不需要考虑保护层厚度影响的情况下,国内外规范公式计算结果明显偏小,不适用于预制混凝土构件连接钢筋与混凝土粘结强度的计算.

|
图 15 国内外规范粘结强度计算对比图 Fig. 15 Comparison of bonding strength formulas in domestic and foreign standards |
当钢筋与混凝土的粘结强度一定时,试件的破坏模式由锚固长度决定,存在一个钢筋拔出破坏与钢筋拉断破坏的临界长度,称为临界锚固长度Lcr. 当钢筋锚固长度小于临界锚固长度时试件发生界面粘结失效的钢筋拔出破坏,当锚固长度大于临界锚固长度时,粘结界面的承载力大于钢筋抗拉极限荷载,试件发生钢筋拉断破坏. 对于预制拼装混凝土结构连接钢筋,可以根据其粘结强度计算公式,给出临界锚固长度的计算公式为
| $ L_{\mathrm{cr}}=\frac{P_{\mathrm{u}}}{{\rm{ \mathsf{ π}}} d \tau_{\mathrm{u}}}=\frac{\sigma_{\mathrm{s}} d}{4 \tau_{\mathrm{u}}}=\frac{\sigma_{\mathrm{s}} d}{4\left(0.108 f_{\mathrm{cu}}-0.344 d+14.84\right)}. $ | (11) |
式中:Pu为钢筋抗拉极限荷载,σs为钢筋极限强度,d为钢筋直径,τu为粘结强度.
规范规定的钢筋基本锚固长度La一般以对应的粘结强度计算出的临界锚固长度为基础并乘以相应的安全系数来确定,国内外规范中钢筋基本锚固长度计算公式以及基本锚固长度与临界锚固长度的比值La/Lcr见表 6.
| 表 6 国内外规范规定的基本锚固长度计算公式 Tab. 6 Calculation formulas of anchorage length in domestic and foreign standards |
表中各参数:n为混凝土强度系数,fy为钢筋抗拉强度设计值,fcu为混凝土抗压强度标准值,ft为混凝土轴心抗拉强度设计值,d为锚固钢筋直径,α为锚固钢筋外形系数,c为钢筋保护层厚度,ψt、ψe和ψs分别为钢筋定位系数、涂层系数和品种系数,λ为混凝土品种系数,Ktr为配筋系数,k1和k2为AS3600规范的钢筋定位系数,A为锚固钢筋横截面积.
从国内外的钢筋临界锚固长度对比图(图 16)可以看出,本文拟合公式对应的临界锚固长度分别为GB 50010—2010、ACI318-11、AS3600和JTG 3362—2018中临界锚固长度的0.66倍、0.56倍、0.79倍和0.31倍,显然,预制拼装混凝土结构连接钢筋的锚固长度需求远小于现有规范规定值. 同时,由表 6可知,各规范规定的基本锚固长度La为其临界锚固长度Lcr的1.0~1.68倍,且JTG 3362—2018规定的基本锚固长度最长,分别是GB 50010—2010、ACI318-11和AS3600中的1.37倍、1.61倍和2.14倍(图 17),可知中国行业规范对钢筋锚固长度的规定取值最大. 综合上述规范的基本锚固长度取值规定,对于装配式混凝土桥梁连接钢筋,在本文临界锚固长度的基础上,考虑1.7倍安全系数,建议其基本锚固长度取值如下:当混凝土强度等级为C35及以下时,建议取为18 d;当混凝土强度等级为C40及以上时,建议取为15 d. 上述基本锚固长度建议取值约为澳大利亚规范AS3600取值的1.05倍,是美国规范ACI318-11取值的79%,是JTG 3362—2018建议基本锚固长度设计值的53%,是GB 50010—2010规范建议锚固长度的68%.
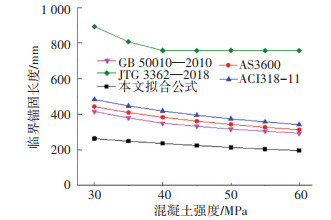
|
图 16 临界锚固长度计算对比 Fig. 16 Comparison of critical anchorage length |

|
图 17 基本锚固长度对比 Fig. 17 Comparison of basic anchorage length |
结合试验研究和数值分析方法,探究了预制拼装构件连接钢筋与混凝土的界面粘结强度的主要影响因素和粘结界面的受力特征,对比分析了国内外规范对于粘结强度与锚固长度计算的差异. 主要结论如下:
1) 预制混凝土构件连接钢筋与混凝土粘结界面的承载力与混凝土强度、钢筋直径、锚固长度呈正相关;界面粘结强度与混凝土强度呈正相关,与钢筋直径呈负相关,与锚固长度相关性较小.
2) 根据试验和有限元分析结果给出了预制拼装混凝土构件连接钢筋与混凝土界面的粘结强度和临界锚固长度计算公式.
3) 结合现有国内外规范的基本锚固长度取值规定,对于装配式混凝土桥梁连接钢筋的基本锚固长度建议取值如下:当混凝土强度等级为C35及以下时,建议取为18 d;当混凝土强度等级为C40及以上时,建议取为15 d.
| [1] |
王晟, 桂晓明, 宁平华, 等. 全装配式桥梁在国内的发展与建设经验[J]. 公路与汽运, 2019, 192(3): 155. WANG Sheng, GUI Xiaoming, NING Pinghua, et al. Development and construction experience of fully assembled spindle in China[J]. Highway and Automobile Transportation, 2019, 192(3): 155. DOI:10.3969/j.issn.1671-2668.2019.03.037 |
| [2] |
朱晓辉. 新型装配式钢筋混凝土桥梁施工工艺与质量控制分析[J]. 资源信息与工程, 2017(1): 158. ZHU Xiaohui. Analysisof construction technology and quality control of new fabricated reinforced concrete bridges[J]. Resource Information and Engineering, 2017(1): 158. |
| [3] |
蒋勤俭, 黄清杰, 常双九, 等. 装配式混凝土结构工程质量管理与验收[J]. 工程质量, 2016(4): 5. JIANG Qinjian, HUANG Qingjie, CHANG Shuangjiu, et al. Quality management and acceptance of prefabricated concrete structure engineering[J]. Engineering Quality, 2016(4): 5. DOI:10.3969/j.issn.1671-3702.2016.04.001 |
| [4] |
张利铨. 桥梁装配式预制技术研究综述[J]. 华东公路, 2015(5): 22. ZHANG Liquan. Review of prefabricated prefabrication technology of bridges[J]. East China Highway, 2015(5): 22. |
| [5] |
田春雨, 黄小坤, 李然, 等. 装配式混凝土结构的研究与应用[J]. 工程质量, 2015(4): 37. TIAN Chunyu, HUANG Xiaokun, LI Ran, et al. Research and application of prefabricated concrete structure[J]. Engineering Quality, 2015(4): 37. |
| [6] |
中国工程院土木水利与建筑学部. 混凝土结构耐久性设计与施工指南[M]. 北京: 中国建筑工业出版社, 2004. Department of Civil Engineering, Water Conservancy and Architecture, Chinese Academy of Engineering. Design and construction guidelines for durability of concrete structures[M]. Beijing: China Building Industry Press, 2004. |
| [7] |
GAO Xiangling, LI Naikun, REN Xiaodan. Analytic solution for the bond stress-slip relationship between rebar and concrete[J]. Construction and Building Materials, 2019, 197: 385. DOI:10.1016/j.conbuildmat.2018.11.206 |
| [8] |
YAZICI S, AREL H S. The effect of steel fiber on the bond between concrete and deformed steel bar in SFRCs[J]. Construction and Building Materials, 2013, 40: 299. DOI:10.1016/j.conbuildmat.2012.09.098 |
| [9] |
徐有邻, 沈文都, 汪洪. 钢筋砼粘结锚固性能的试验研究[J]. 建筑结构学报, 1994(3): 26. XU Youlin, SHEN Wendu, WANG Hong. Experimental study on bonding and anchoring performance of reinforced concrete[J]. Journal of Building Structures, 1994(3): 26. DOI:10.3321/j.issn:1000-6869.1994.03.001 |
| [10] |
余琼, 许雪静, 尤高帅. 带肋钢筋与灌浆料黏结性能试验[J]. 哈尔滨工业大学学报, 2017, 49(12): 91. YU Qiong, XU Xuejing, YOU Gaoshuai. Experimental study on bond behavior for ribbed steel bars and grout[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 91. DOI:10.11918/j.issn.0367-6234.201701088 |
| [11] |
王海龙, 李朝红, 徐光兴. 带肋钢筋与混凝土粘结性能的细观数值模拟[J]. 西南交通大学学报, 2011, 46(3): 365. WANG Hailong, LI Chaohong, XU Guangxing. Mesoscopic numerical simulation of ribbed bars and concrete[J]. Journal of Southwest Jiaotong University, 2011, 46(3): 365. DOI:10.3969/j.issn.0258-2724.2011.03.002 |
| [12] |
刘程炜, 曹万林, 秦成杰, 等. 预制剪力墙中墩头钢筋预留孔灌浆连接锚固性能[J]. 北京工业大学学报, 2017(4): 116. LIU Chengwei, CAO Wanlin, QIN Chengjie, et al. Anchorage performance of prefabricated shear wall pier head reinforcement with reserved holes[J]. Journal of Beijing University of Technology, 2017(4): 116. |
| [13] |
郑山锁, 裴培, 张艺欣, 等. 钢筋混凝土粘结滑移研究综述[J]. 材料导报, 2018, 32(23): 159. ZHENG Shansuo, PEI Pei, ZHANG Yixin, et al. Review of research on bond-slip of reinforced concrete[J]. Materials Reports, 2018, 32(23): 159. |
| [14] |
赵卫平, 肖建庄. 带肋钢筋与混凝土间粘结滑移本构模型[J]. 工程力学, 2011, 28(4): 164. ZHAO Weiping, XIAO Jianzhuang. On bond-slipconstitutive model between ribbed steel bars and concrete[J]. Engineering Mechanics, 2011, 28(4): 164. |
| [15] |
KHABAZ A. Analysis of sliding mechanism of straight steel fibers in concrete and determine the effect of friction[J]. Archives of Civil and Mechanical Engineering, 2017, 17(3): 599. DOI:10.1016/j.acme.2017.01.005 |
| [16] |
刘巍, 徐明, 陈忠范. ABAQUS混凝土损伤塑性模型参数标定及验证[J]. 工业建筑, 2014(增刊1): 167. LIU Wei, XU Ming, CHEN Zhongfan. Parameters calibration and verification of concrete damage plasticity model of ABAQUS[J]. Industrial Construction, 2014(S1): 167. |
| [17] |
山显彬. 变形钢筋与自密实混凝土之间粘结锚固性能试验研究[D]. 哈尔滨: 哈尔滨工业大学: 2008 SHAN Xianbin. Experimental study on bonding and anchorage properties between deformed steel bar and self-compacting concrete[D]. Harbin: Harbin Institute of Technology, 2008 |
| [18] |
中华人民共和国国家质量监督检验检疫总局. 钢筋混凝土用钢第2部分: 热轧带肋钢筋: GB 1499.2—2018[S]. 北京: 中国质检出版社, 2018 General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. Steel for reinforced concrete Part 2: hot rolled ribbed bars: GB 1499.2—2018[S]. Beijing: China Quality Inspection Press, 2018 |
| [19] |
中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Designcode for concrete structures: GB 50010—2010[S]. Beijing: China Construction Industry Press, 2010 |
| [20] |
Standards Australia International.Standard concrete structures: AS-3600[S]. Sydney: [s. n.], 2001
|
| [21] |
ACI Committee 318. Building code requirements for structural concrete: ACI318-11[S]. Michigan: American Concrete Institute, 2011
|
| [22] |
徐有邻, 邵卓民, 沈文都. 钢筋与混凝土的粘结锚固强度[J]. 建筑科学, 1988(4): 10. XU Youlin, SHAO Zhuomin, SHEN Wendu. Bonding and anchor strength of reinforcement and concrete[J]. Architecture Science, 1988(4): 10. |
| [23] |
王晨霞, 魏宏刚, 吴瑾, 等. 钢筋再生混凝土的粘结滑移试验研究与数值模拟[J]. 广西大学学报(自然科学版), 2013(4): 218. WANG Chenxia, WEI Honggang, WU Jin, et al. Experimental research and numerical simulation on bond behavior between recycled concrete and rebar[J]. Journal of Guangxi University (Natural Science Edition), 2013(4): 218. |
| [24] |
中交公路规划设计院. 公路钢筋混凝土及预应力混凝土桥涵设计规范: JTG 3362—2018[S]. 北京: 人民交通出版社, 2018 China Communications Highway Planning and Design Institute. Code for design of highway reinforced concrete and prestressed concrete bridges and culverts: JTG 3362—2018[S]. Beijing: China Communications Press, 2018 |
 2021, Vol. 53
2021, Vol. 53


