2. 交通运输部公路科学研究院,北京 100088;
3. 哈尔滨工业大学 交通科学与工程学院,哈尔滨 150090
2. Research Institute of Highway Ministry of Transport, Beijing 100088, China;
3. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China
沥青混合料是典型的温敏性材料,其力学性能具有显著的温度依赖性[1-2],沥青面层的疲劳开裂作为在役沥青路面使用性能最为常见的衰减形式之一[3],研究环境温度对其作用的重要性不言而喻.根据Miner线性累积原理,1 a中沥青路面结构受到的累计损伤等于恒定温度下相同交通量对路面造成的总损伤,该恒定温度即为沥青路面的疲劳等效温度[4]. 沥青路面结构设计是在一定的温度下进行的,因此疲劳等效温度的准确计算对沥青路面结构的安全性与使用寿命具有决定性作用.文献[5]在总结美国的MEPDG和Shell设计方法的基础上分析全国各地区不同结构形式的沥青面层疲劳等效温度的规律,但交通量分布均匀的假设并不符合实际路况.文献[6]认为路面温度越高,该时刻对应的交通量越大,因此交通量均匀分布的假设将使路面结构设计偏安全对后续的结构寿命带来巨大影响.文献[7]以路表温度为各地区的代表温度得到相应沥青混合料的疲劳方程来计算沥青路面的疲劳等效温度,此方法中的路面温度不能代表沥青层内部的温度场变化规律,产生的误差较大.文献[8]从日疲劳温度应力系数的角度出发,提出了水泥混凝土路面疲劳等效温度应力系数,但计算过程繁琐,不宜推广.本文在总结上述方法的优缺点的基础上,基于Miner线性累积原理提出一种考虑交通量非均匀分布的沥青路面疲劳等效温度的计算方法,该方法符合实际路况,更加科学可靠.
1 沥青层当量温度的计算温度场的复杂分布对沥青路面的使用性能具有显著影响[9].一般来说,用于评价沥青路面使用性能的环境温度指标有路面结构内部温度、路面路表温度和大气温度等.但是在实际工程中,同一时段的这3个温度数值并不相等,有时甚至相差很大,由于不同路面结构使用性能指标各自本身的特点,不同的路面使用性能指标有不同的最密切的温度指标,因此确定与疲劳性能最密切的代表温度是探讨沥青路面疲劳性能问题的关键.疲劳开裂自上而下或者自下而上整个过程贯穿沥青层结构[10],路表温度和沥青层层底温度既无法避免偶然误差更不能表征整个沥青层对路面疲劳性能的影响,沥青层平均温度则无法体现温度在路面结构内部的梯度分布、滞后性和累积性[11]等特点.路面结构存在一定厚度,为了获取结构层内部不同深度的温度,需要在路面结构不同深度位置埋设温度传感器,但各处的温度并不相等,因此需要找到一个具有代表性的温度,来反映路面结构整体温度状态,前期研究发现沥青层的当量温度可代表沥青层层内复杂的温度场,弥补上述温度指标存在的不足,充分反映沥青层温度场变化趋势,下面介绍沥青层当量温度的计算方法.
以位于北京的交通运输部公路科学研究院足尺环道试验路面(下称RIOHTrack)为例,选取强基薄面型半刚性基层结构STR1、中国常用沥青路面结构形式STR9和沥青混凝土与半刚性基层组合形式STR16 3种典型沥青路面结构[12],3种沥青路面具体的结构与材料组成设计见表 1,其中STR4、STR9、STR19沥青层的总厚度分别为12、18、36 cm.RIOHTrack所处的北京通州地区四季节气分明,温度浮动范围较大,利于开展沥青路面温度场的研究.
| 表 1 3种路面结构的沥青层材料与结构组成 Tab. 1 Asphalt layer materials and structure compositions of three pavement structures |
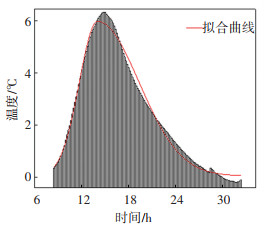
首先,计算各个沥青层底处传感器的代表温度,即日当量平均温度.以表 1中STR4为例,分别计算4、10、12 cm处传感器的代表温度,以每个月5 d为单元平均温度,以减小由传感器测量、温度骤变带来的误差.RIOHTrack温度传感器数据采样周期为1/6 h,以此为步长,采用Bigaussion函数[13]拟合得到24 h内沥青层某一深度处的时间温度曲线,由于该模型积分较困难,将此曲线与时间轴围成的图形分割为144个近似梯形见图 1.加权计算几何图形面积为
|
图 1 沥青层某一深度处的时间与温度曲线 Fig. 1 Time and temperature curve at a certain depth of asphalt layer |
| $ A=\sum\limits_{i=1}^{144} \frac{\left(T_{i}+T_{i-1}\right)\left(t_{i}-t_{i-1}\right)}{2}, $ | (1) |
除以24即得到某一传感器深度H处的日当量平均温度为
| $ \bar{T}=\frac{A}{24}. $ | (2) |
式中:A为时间曲线围成的面积,ti与ti-1为传感器相邻温度采集时刻,Ti与Ti-1分别为ti与ti-1时刻对应的温度沥青层某一深度处的温度.
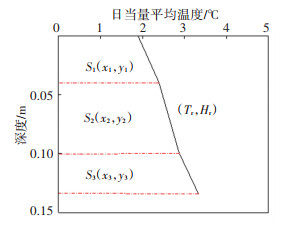
其次,计算整个沥青层的代表温度,即沥青层当量温度.把STR4沥青层4、10、12 cm深度处传感器的日当量平均温度,绘制深度温度曲线,如图 2所示,按照沥青层分层数将深度温度曲线分割成3个梯形,计算每个梯形的质心坐标(xi,yi),再以各个梯形的面积S1、S2、S3为加权值,计算整个沥青层温度与深度轴围成的几何图形的质心见图 2,得到STR4沥青层当量温度为
|
图 2 沥青层结构内部深度与温度曲线 Fig. 2 Internal depth and temperature curve of asphalt layer structure |
| $ T_{\mathrm{r}}=\frac{\sum\limits_{i=3}^{n} x_{i} S_{i}}{\sum\limits_{i=3}^{n} S_{i}}, $ | (3) |
STR4沥青层当量温度对应的当量深度为
| $ H_{\mathrm{r}}=\frac{\sum\limits_{i=3}^{n} y_{i} S_{i}}{\sum\limits_{i=3}^{n} S_{i}}. $ | (4) |
RIOHTrack设置有气象站,采用式(1)、(2)计算出大气日当量平均温度TS,引入沥青层厚度变量H,建立大气日当量平均温度与沥青层的当量温度关系模型为
| $ {T_{\rm{r}}} = - 1.965{\kern 1pt} {\kern 1pt} 3 + 1.100{\kern 1pt} 4{T_{\rm{s}}} + 8.343{\kern 1pt} {\kern 1pt} 3H,{R^2} = 0.948{\kern 1pt} {\kern 1pt} 0. $ | (5) |
这样可以计算任意厚度沥青层的当量温度,弥补实际工程中没有布设足够传感器的局限,提高了模型的实用性,也为后续建立沥青路面的温度场提供了理论支撑.
2 交通量非均匀分布的沥青路面疲劳等效温度在役沥青路面的沥青层结构内部温度和交通量随时间均呈现非正弦波的周期性变化规律,夜间温度低且交通量小,白天温度高且交通量大.沥青层结构内部温度的高温区间一般集中在在1 d之中的13:00—15:00,若交通量峰值与沥青层结构内部温度峰值之间的滞后性很小将对沥青路面造成更大的损伤与破坏,文献[14]统计了某高速公路5 a间的交通量,得出交通量最大时9月份大约是最小时2月份的1.5倍.文献[6]通过对济南、西安、上海和广州4个地区交通量与温度分布研究发现,沥青路面处于高温区间的交通量要高于均匀分布的交通量. 因此将在役沥青路面承受的交通量均匀分布的假设来计算疲劳等效温度的方法将导致沥青路面的结构设计偏安全,因而需寻求一种考虑交通量非均匀分布的沥青路面疲劳等效温度计算方法是有必要的.根据前节所述,本文得到了沥青层的日当量平均温度,以5 ℃为区间长度划分温度区间,计算每个温度区间的年温度分布频率,以时间轴为纽带统计每天对应的交通量,即得出每个温度区间对应的年交通量分布频率.
2.1 沥青路面疲劳等效温度的基本计算原理根据Miner线性累积原理和沥青路面疲劳等效温度的定义可得
| $ \sum\limits_{i} \frac{n\left(\theta_{i}\right)}{N\left(\theta_{i}\right)}=\frac{\sum\limits_{i} n\left(\theta_{i}\right)}{N\left(\theta_{\mathrm{eq}}\right)}, $ | (6) |
则沥青路面的基本损伤为
| $ \frac{1}{N\left(\theta_{\mathrm{eq}}\right)}=\frac{\sum\limits_{i} \frac{n\left(\theta_{i}\right)}{N\left(\theta_{i}\right)}}{\sum\limits_{i} n\left(\theta_{i}\right)}. $ | (7) |
式中:N(θi)为车辆荷载随机作用下沥青路面产生疲劳破坏承受的标准轴载作用次数,n(θi)为温度为θi条件下沥青路面产生疲劳破坏承受的交通量的轴载作用次数,N(θeq)为疲劳等效温度下沥青路面承受的标准轴载作用次数.
当式(6)的值等于1时,沥青路面即发生疲劳破坏,由式(7)计算等效温度θeq下的沥青路面基本损伤,即可得到等效温度值.
2.2 沥青混合料疲劳方程推导等效温度的步骤步骤1 绘制沥青混合料的基本损伤值与温度关系曲线.开展不同温度θi和频率fi(一般为25 Hz)的沥青混合料室内疲劳实验,得到沥青混合料疲劳方程为
| $ N({\theta _i}) = a\varepsilon {({\theta _i})^b}. $ | (8) |
式中:ε(θi)为初始弯拉应变,N(θi)为沥青混合料的疲劳寿命次数,a、b为依赖于沥青混合料特性的回归参数.
根据ε6(θi)推导可得到温度θi和频率fi下的沥青混合料基本损伤值为
| $ \frac{1}{N\left(\theta_{i}\right)}=\left[\frac{\varepsilon_{6}\left(\theta_{i}\right)}{\varepsilon\left(\theta_{i}\right)}\right]^{b} \times 10^{-6}. $ | (9) |
式中:ε6(θi)为温度θi、频率fi和疲劳次数为100万次时试件的弯拉应变值,由式(8)的疲劳方程求出;ε(θi)为温度θi下的沥青层层底最大拉应变;轴载作用方式为13 t的双圆荷载,荷载圆半径R= 10.65 cm,两荷载圆中心点距离为3倍半径.通过对应的沥青混合料的模量值求得ε(θi).
这样即可得到不同温度θi和频率fi下的沥青混合料的基本损伤值并绘制与温度的关系曲线.
步骤2 计算等效温度θeq下的沥青混合料基本损伤值.将温度划分为n个区间,假设等效温度下,温度分布频率为100%对应的交通量分布频率为bj,非等效温度下,温度的分布频率为ai对应的交通量分布频率为bi,则等效温度下的基本损伤值推导过程为
| $ {b_1}\frac{1}{{N\left( {{\theta _{{\rm{eq}}}}} \right)}} = {a_1}{b_1}\frac{1}{{N\left( {{\theta _1}} \right)}} + \cdots + {a_i}{b_i}\frac{1}{{N\left( {{\theta _i}} \right)}} \cdots + {a_n}{b_n}\frac{1}{{N\left( {{\theta _n}} \right)}}, $ | (10) |
| $ \begin{array}{c} \vdots \\ {b_i}\frac{1}{{N\left( {{\theta _{{\rm{eq}}}}} \right)}} = {a_1}{b_1}\frac{1}{{N\left( {{\theta _1}} \right)}} + \cdots + {a_i}{b_i}\frac{1}{{N\left( {{\theta _i}} \right)}} \cdots + {a_n}{b_n}\frac{1}{{N\left( {{\theta _n}} \right)}}, \end{array} $ | (11) |
| $ \begin{array}{c} \vdots \\ {b_n}\frac{1}{{N\left( {{\theta _{{\rm{eq}}}}} \right)}} = {a_1}{b_1}\frac{1}{{N\left( {{\theta _1}} \right)}} + \cdots + {a_i}{b_i}\frac{1}{{N\left( {{\theta _i}} \right)}} \cdots + {a_n}{b_n}\frac{1}{{N\left( {{\theta _n}} \right)}}. \end{array} $ | (12) |
将式(10)~(12)左右分别累加得到基本损伤值为
| $ \frac{1}{{N\left( {{\theta _{{\rm{eq}}}}} \right)}} = n\left[ {{a_1}{b_1}\frac{1}{{N\left( {{\theta _1}} \right)}} + \cdots + {a_i}{b_i}\frac{1}{{N\left( {{\theta _i}} \right)}} \cdots + {a_n}{b_n}\frac{1}{{N\left( {{\theta _n}} \right)}}} \right]. $ | (13) |
式中:a1、an为各个温度区间对应的温度分布频率,b1、bn为各个温度区间对应的交通量分布频率,两种分布频率无直接联系并具有一定随机性.
从式(13)可以看出,沥青层当量温度区间的划分,各个温度区间对应的温度分布频率、交通量分布频率和沥青路面基本损伤值都对等效温度的计算结果产生影响.
3 不同交通量分布方式计算结果的对比与验证基于式(13)计算交通量均匀和非均匀两种分布方式的沥青路面疲劳等效温度并进行验证对比,依托某高速公路,开展室内沥青混合料动态模量和疲劳实验并观测采集相应的温度场和交通量数据,某高速公路沥青路面沥青层材料与结构参数见图汇总于表 2.
| 表 2 某高速公路沥青层材料与结构组成 Tab. 2 Asphalt layer materials and structure compositions of a highway |
按照前节所述计算沥青路面疲劳等效温度所需参数,采用法国梯形梁设备M2F开展BBSG和GB4两种沥青混合料在10 Hz下-5、0、5、10、15、20、25、30 ℃的两点弯曲动态模量和GB4沥青混合料在25 Hz下-5、0、5、10、15、20、25、30 ℃的两点弯曲疲劳试验,得到BBSG和GB4两种沥青混合料在10 Hz下-5、0、5、10、15、20、25、30 ℃的复模量和GB4沥青混合料在25 Hz下-5、0、5、10、15、20、25、30 ℃的疲劳方程,汇总BBSG和GB4两种沥青混合料的复模量值和与基本损伤值有关的GB4沥青混合料疲劳方程参数见表 3,按照式(8)、(13)分别计算每个温度下的弯拉应变值和基本损伤值,统计某高速公路的沥青层当量深度处的当量温度与交通量,相关信息汇总于表 3,其中b为疲劳方程回归参数.
| 表 3 沥青路面疲劳等效温度计算所需参数 Tab. 3 Parameters required for calculating the fatigue equivalent temperature of asphalt pavement |
由表 3可知n=8,假设交通量均匀分布,则b1=bi=bn,按式(13)计算沥青路面基本损伤值为0.15,假设交通量按表 3中非均匀分布则为0.1. 表 3中沥青路面-5、0、5、10、15、20、25、30 ℃时的基本损伤值与对应的试验温度关系模型为
| $ \frac{1}{N\left(\theta_{i}\right)}=7.36 \times 10^{-4} \mathrm{e}^{0.276 T}, R^{2}=0.999\ 6 . $ | (14) |
其中T为试验温度.
由模型可知相关系数非常高,拟合结果良好,由该模型计算等效温度正确可靠.将上述两种基本损伤值代入式(14)得到交通量均匀分布的沥青路面疲劳等效温度为19.6 ℃,考虑交通量非均匀分布的沥青路面疲劳等效温度为18.0 ℃,两者相差1.6 ℃,可见交通量的非均匀分布对沥青路面疲劳等效温度的计算结果是有一定影响的,在今后的沥青路面疲劳等效温度计算中将交通量视为变量是有必要的.
需要说明的是:1)沥青层日当量平均温度与大气日当量平均温度的关系是基于RIOHTrack提出的,由于客观因素算例中某高速沥青路面沥青层的日当量平均温度是根据式(5)计算得到的,后续应埋设传感器验证式(5)的准确性并对利用式(5)计算得到的沥青层日当量平均温度进行修正;2)交通量非均匀分布的假设前提是某一温度区间内车辆轴载比列是不变的,后续应当加强观测,得出更细化的计算理论.
4 与其他方法的对比目前国际上主流的沥青路面疲劳等效温度的计算方法主要有AASHTO、Shell和SHRP 3种,但都有需要进一步完善之处.
美国各州公路和运输工作者协会AASHTO制定的沥青路面设计规范力学-经验路面设计指南MEPDG将分析周期内的实时路面温度场分布与轴载作用下的路面力学响应一一对应,然后采用Miner叠加原理进行疲劳寿命的预估[15],首先以标准正态分布来表示基本分析周期内路面内的某深度z处的温度Tz并求出z处的代表温度,其次按照一定规则将路面结构分层,以路表、路表以下0.5英寸以及沥青层层底为疲劳损坏计算点,分别计算上述各计算点在每个基本分析周期内的力学响应以及疲劳寿命,最后再根据Miner叠加原理,得到整个设计年限内的路面疲劳寿命并反算出等效温度.该方法更准确地考虑路面温度对疲劳寿命的影响,但需要大量、长期的气象数据库,至少提供相应或相近地区2 a每小时的相关气象数据[15-16],而中国高速公路发展起步较晚,缺乏全面的路面温度场观测数据.
Shell设计方法则是根据沥青层的有效粘度等效原则,建立了大气平均温度与沥青层等效温度之间的关系[17],该方法的关键在于给出了沥青面层有效粘度与沥青层温度的经验关系图,并以此为依据,提出了基于气温和沥青面层厚度的疲劳等效温度推算方法,国外发达国家高速公路发展起步较早,与路面温度场相关的气象数据库也相对较为完备,根据大量、长期的试验数据,建立路面等效温度与相关的气候参数、沥青路面结构参数等之间的关系,直接推算沥青路面的疲劳等效温度,因此采用经验法预估沥青路面等效温度较为简单、方便和可靠.然而经验法的不足之处在于其适用性受到限制,仅在交通条件、气候条件、路面结构、材料性能等相关因素处于相似的状态具有较好的可靠性和适用性.
美国公路战略研究计划SHRP采用了Witczak对沥青路面疲劳等效温度的研究成果,考虑了地理位置、路面有效深度、路面结构、材料类型及轮胎胎压5个主要因素[18-19],通过分析发现,疲劳等效温度与沥青面层1/3深度处的年均温度MAPT有很好的相关性,可直接计算疲劳等效温度,但采用面层某特定位置处的温度作用代表温度进行路面疲劳寿命计算是不合理的,某特定位置处的温度并不能反映路面内的实际分布状况,忽略了路面温度场分布梯度的影响,该处温度下的路面力学相应与真正温度场分布条件下路面力学响应往往会存在较大差别,最终导致疲劳寿命计算出现较大偏差.
由此可知,上述国际主流的3种沥青路面疲劳等效温度计算方法均有一定的缺点,本文以沥青层当量温度为沥青层代表温度,基于室内沥青混合料疲劳实验与室外为期1 a的温度和交通量观测数据,通过理论推导计算出疲劳等效温度,弥补了上述方法的不足,并推进了交通量不均匀分布问题的解决,后续需要加强观测以验证和完善计算方法.
5 结论1) 沥青层当量温度充分考虑温度在沥青层结构内部的梯度分度,更加密切地体现温度场在结构内部分复杂分布,可以作为沥青层的代表温度.构建的大气5 d日当量度、沥青层厚度和沥青层结构内部当量温度的关系模型,提高了模型的实用性,为后续建立沥青路面温度场和当量温度在实际工程的应用提供理论依据.
2) 利用Miner线性累积原理并在考虑交通量非均匀分布的基础上提出了沥青路面疲劳等效温度计算方法, 在理论上改进了现有方法的不足.基于沥青混合料动室内试验与室外温度和交通量实测数据验证了模型的有效性和实用性.同等条件下,考虑交通量非均匀分布计算的沥青路面疲劳等效温度同比减小了1.6 ℃,这对沥青路面的结构设计会产生一定的影响,利用该等效温度值将使沥青路面的结构设计更加合理、科学.沥青路面交通量的非均匀分布,沥青层日当量温度区间的划分,各个温度区间的温度频率分布、交通量频率分布和基本损伤值都会对沥青路面的疲劳等效温度的计算结果产生影响.
3) 与国际上主流的沥青路面疲劳等效温度计算方法对比,考虑交通量非均匀分布的沥青路面疲劳等效温度计算方法具有一定的创新性与优越性,但后续还应加强温度与交通量的观测与统计,以便得到更加精确的计算结果.
| [1] |
宋小金, 樊亮. 沥青路面结构温度随深度变化规律研究[J]. 土木工程学报, 2017, 50(9): 110. SONG Xiaojin, FAN Liang. Study on the variation rules of temperature with depth for asphalt pavement structure[J]. China Civil Engineering Journal, 2017, 50(9): 110. DOI:10.15951/j.tmgcxb.2017.09.011 |
| [2] |
张肖宁. 沥青与沥青混合料的粘弹力学原理及应用[M]. 北京: 人民交通出版社, 2006. ZHANG Xiaoning. Principle and application of viscoelastic mechanics of asphalt and asphalt mixture[M]. Beijing: China Communications Press, 2006. |
| [3] |
栾利强. 半刚性基层沥青路面疲劳裂缝扩展与寿命预估研究[J]. 土木工程学报, 2017, 50(9): 118. LUAN Liqiang. Research on fatigue crack propagation and fatigue life prediction of semi-rigid base asphalt pavement[J]. China Civil Engineering Journal, 2017, 50(9): 118. DOI:10.15951/j.tmgcxb.2017.09.012 |
| [4] |
孟岩, 潘峥嵘, 李艳春. 疲劳当量温度计算方法研究[J]. 公路交通科技, 2009, 26(5): 6. MENG Yan, PAN Zhengrong, LI Yanchun. Research on fatigue equivalent temperature calculation method[J]. Journal of Highway and Transportation Research and Development, 2009, 26(5): 6. |
| [5] |
谈至明, 吁新华. 沥青面层的疲劳等效温度[J]. 同济大学学报(自然科学版), 2013, 41(2): 197. TAN Zhiming, YU Xinhua. Fatigue equivalent temperature for asphalt pavements[J]. Journal of Tongji University (Natural Science), 2013, 41(2): 197. DOI:10.3969/j.issn.0253-374x.2013.02.007 |
| [6] |
王健. 基于影响因素非线性特性的沥青路面永久变形预估研究[D]. 西安: 长安大学, 2011 WANG Jian. Research on prediction of permanent deformation of asphalt pavement based on nonlinear characteristics of influencing factors [D]. Xi'an: Chang'an University, 2011 |
| [7] |
李静, 戴经梁. 沥青混合料有效温度的计算和应用[J]. 重庆交通学院学报, 2004, 23(3): 32. LI Jing, DAI Jingliang. Calculation and application of effective temperature of asphalt mixture[J]. Journal of Chongqing Jiaotong University, 2004, 23(3): 32. DOI:10.3969/j.issn.1674-0696.2004.03.009 |
| [8] |
牛开民, 田波. 水泥混凝土路面等效疲劳温度应力系数[J]. 中国公路学报, 2006, 19(5): 23. NIU Kaimin, TIAN Bo. Equivalent fatigue thermal stress coefficient of cement concrete pavement[J]. China Journal of Highway and Transport, 2006, 19(5): 23. DOI:10.19721/j.cnki.1001-7372.2006.05.006 |
| [9] |
秦健, 孙立军. 沥青路面温度场的分布规律[J]. 公路交通科技, 2006, 23(8): 18. QIN Jian, SUN Lijun. Study on asphalt pavement temperature field distribution pattern[J]. Journal of Highway and Transportation Research and Development, 2006, 23(8): 18. |
| [10] |
姚祖康. 沥青路面结构设计[M]. 北京: 人民交通出版社, 2011. YAO Zukang. Asphalt pavement structure design[M]. Beijing: China Communications Press, 2011. |
| [11] |
顾兴宇, 袁青泉, 倪富健. 基于实测荷载和温度梯度的沥青路面车辙发展影响因素分析[J]. 中国公路学报, 2012, 25(6): 30. GU Xingyu, YUAN Qingquan, NI Fujian. Analysis of factors on asphalt pavement rut development based on measured load and temperature gradient[J]. China Journal of Highway and Transport, 2012, 25(6): 30. DOI:10.19721/j.cnki.1001-7372.2012.06.005 |
| [12] |
王旭东. 足尺路面试验环道路面结构与材料设计[J]. 公路交通科技, 2017, 34(6): 30. WANG Xudong. Design of pavement structure and material for full-scale test track[J]. Journal of Highway and Transportation Research and Development, 2017, 34(6): 30. DOI:10.3969/j.issn.1002-0268.2017.06.005 |
| [13] |
肖倩, 许兵, 王旭东, 等. 足尺路面试验环道路面温度曲线特征及拟合研究[J]. 公路交通科技, 2019, 36(3): 1. XIAO Qian, XU Bing, WANG Xudong, et al. Study on feature and fitting of RIOHTrack pavement temperature curve[J]. Journal of Highway and Transportation Research and Development, 2019, 36(3): 1. DOI:10.3969/j.issn.1002-0268.2019.03.001 |
| [14] |
黄大喜, 赵延庆. 昼夜温度及交通量变化对沥青路面响应及性能的影响[J]. 内蒙古公路与运输, 2008, 10(3): 8. HUANG Daxi, ZHAO Yanqing. Influence of day and night temperature and traffic volume on the response and performance of asphalt pavement[J]. Highways and Transportation in Inner Mongolia, 2008, 10(3): 8. |
| [15] |
ARA Inc.. Guide for mechanistic-empirical design of new and rehabilitated pavement structures [R]. Washington DC: National Research Council, 2004.
|
| [16] |
东南大学交通学院. AASHTO2002设计方法中文解释[R]. 南京: 东南大学, 2005 School of Transportation, Southeast University. Chinese interpretation of AASHTO2002 design method [R]. Nanjing: Southeast University, 2005 |
| [17] |
Shell International Ltd.. Shell pavement design manual: asphalt pavements and overlays for road traffic [R]. London: Shell International Ltd., 1981
|
| [18] |
WITCZAK M W. Effective temperature analysis for permanent deformation of asphaltic mixtures [R]. Washington DC: National Research Council, 1992
|
| [19] |
SHRP. Superpave mix design manual for new construction and overlays [R]. Washington DC: National Research Council, 1994
|
 2021, Vol. 53
2021, Vol. 53


