2. 山地城镇建设与新技术教育部重点实验室(重庆大学),重庆 400045
2. Key Lab of New Technology for Construction of Cities in Mountain Area (Chongqing University), Ministry of Education, Chongqing 400045, China
在抗震设防地区,传统的建筑结构抗震设计理念是通过构件的塑性变形消耗地震能量,确保结构在罕遇地震下不至倒塌。然而,震后结构构件的破坏和较大的残余变形将导致建筑丧失使用功能,进而造成巨大的经济损失。近年来,地震工程领域提出了可恢复功能结构的概念,文献[1-2]对其进行了阐述,即结构在地震后能最快地恢复其正常使用功能,这样建筑不仅能够在地震中保护人们的生命财产安全,在地震后也能帮助人们尽快恢复正常生活。自复位结构作为可恢复功能结构的一种形式,其利用预应力钢绞线提供的张拉力进行梁柱连接或柱脚基础连接,并在节点连接部位设置阻尼器耗能,震后仅需更换阻尼器即可快速恢复结构使用功能。国内外学者通过设置不同形式的阻尼器,如文献[3-13]分别采用耗能角钢、摩擦阻尼器、沙漏阻尼器、记忆合金阻尼器等,对自复位结构的抗震性能进行了研究,证明了该结构具有良好的抗震性能和自复位能力。以上研究成果多针对梁柱节点连接,对柱脚基础连接研究较少。文献[14]提出一种自复位H型钢柱脚,以防屈曲钢板作为耗能构件,对柱脚的抗弯承载力公式进行了理论推导,通过低周往复荷载试验分析表明该柱脚节点具有良好的抗震性能和自复位能力。文献[15]针对H型钢柱平面内受力和复位模式的局限性,提出了自复位方钢管混凝土柱脚,该柱脚不仅在两个方向具有自复位能力,而且增大了柱脚节点的抗弯承载力。文献[16]提出以沙漏阻尼器作为耗能元件的自复位H型钢柱脚,建立了有限元模型对五层框架结构进行了动力弹塑性分析,结果表明,地震后设置该柱脚的结构具有良好的自复位能力,抗震性能良好,实现了预定的抗震性能目标。
本文提出一种带防屈曲消能杆的自复位钢柱脚,框架柱为矩形钢管,采用后张预应力钢绞线进行柱脚基础连接,将钢绞线设置在框架柱外侧,增大抵抗矩的同时亦便于钢绞线张拉。防屈曲消能杆较之防屈曲钢板和沙漏阻尼器,具有承载力高、便于更换的特点。对该自复位柱脚的力学性能进行分析后,设计制作了不同消能杆参数和不同轴压力组成的四组试件,通过低周往复荷载试验研究了试件的自复位能力和抗震性能。
1 自复位钢柱脚构造及力学特性 1.1 自复位钢柱脚构造自复位钢柱脚的构造见图 1。框架柱采用矩形钢管,底部设置钢板封闭,钢管内灌注混凝土。框架柱放置于基础梁顶部,通过后张拉体外预应力钢绞线和防屈曲消能杆与基础连接。基础梁为钢筋混凝土构件,底部设置U形槽,便于锚固钢绞线,基础梁顶部预埋钢板,可将剪力键等上部结构构件焊接于预埋钢板上。钢绞线上部锚固于框架柱伸出的锚固钢板,下部穿过基础梁锚固于梁底,为防止局部变形过大,在锚固钢板上设置了加劲肋。防屈曲消能杆上部与框架柱伸出的耳板连接,下部与基础梁顶部伸出的耳板连接,连接形式为销轴连接。

|
图 1 自复位钢柱脚构造图 Fig. 1 Configuration of self-centering steel column base |
当框架柱承受水平荷载时,将在柱底产生倾覆弯矩,弯矩达到一定程度后,柱底与基础间将产生开口缝隙。柱脚开口后,防屈曲消能杆产生轴向拉压变形,消耗能量。卸载后,预应力钢绞线拉力使得框架柱复位,为其提供复位能力。
1.2 力学特性根据自复位柱脚的力学特性,其理想状态下的荷载-位移加卸载曲线,见图 2,定义理想状态下力学特征点,见表 1。

|
图 2 理论荷载-位移加卸载曲线 Fig. 2 Theoretical load-displacement curve |
| 表 1 力学特征点 Tab. 1 Mechanical characteristics |
阶段1-2:柱脚未开口,钢绞线、消能杆未变形,结构刚度与固结柱脚相同,由框架柱提供;阶段2-3:外力产生的弯矩超过预应力钢绞线初始张拉力提供的抵抗弯矩时,柱脚开口,结构刚度由钢绞线和消能杆提供,钢绞线拉力增加,消能杆开始受力,产生轴向变形,但处于弹性状态;阶段3-4:开口侧消能杆受拉屈服,刚度降低,结构刚度由钢绞线和消能杆提供,钢绞线拉力持续增大;阶段4-5:中间侧消能杆受拉屈服,刚度进一步降低,结构刚度由钢绞线和消能杆提供,钢绞线拉力持续增大;阶段5-6:转动侧消能杆受压屈服,刚度进一步降低,结构刚度由钢绞线和消能杆提供,其中消能杆均为屈服后刚度,钢绞线拉力持续增大,加载至最大位移点;阶段6-7:结构从6点开始卸载,柱脚开口宽度减小,钢绞线拉力和消能杆轴力减小,卸载刚度由钢绞线和消能杆提供,其中消能杆卸载刚度同构件屈服前刚度;阶段7-8:钢绞线拉力持续减小,开口侧消能杆反向屈服,卸载刚度降低,卸载刚度由钢绞线和消能杆提供;阶段8-9:钢绞线拉力持续减小,中间侧消能杆反向屈服,卸载刚度进一步降低,卸载刚度由钢绞线和消能杆提供,加载至9点,柱脚开口闭合;阶段9-10:柱脚开口闭合后,钢绞线和消能杆内力不再变化,钢绞线拉力与初始张拉力相同,此时结构刚度同阶段A,由于钢绞线张拉力作用,卸载后结构无残余位移。整个加卸载过程,除消能杆产生塑性变形外,其余构件均为弹性状态。
2 试验概况 2.1 试件设计自复位柱脚在承受水平荷载时,受力简图见图 3。图中,FPTu和FPTd分别为开口侧和转动侧钢绞线的内力,FEDu、FEDm和FEDd分别为开口侧、中部和转动侧消能杆的内力。本文提出的自复位柱脚在各力学特征点位置的内力和刚度计算公式,参考了文献[16]的方法,并将阻尼器更换为防屈曲消能杆重新进行抵抗矩的计算,此处不再赘述。根据现行国家规范[17],结构抗震设计需满足“小震不坏、中震可修、大震不倒”的基本目标。假定结构在多遇地震下,自复位柱脚需满足不开口的条件,根据此时力的平衡关系可得预应力钢绞线截面积AsPT为

|
图 3 柱脚受力简图 Fig. 3 Free body diagram of column base |
| $A_{\mathrm{sPT}}=\frac{M-0.5 N d_{\mathrm{C}}}{2 \cdot 0.3 f_{\mathrm{ptk}}\left(d_{\mathrm{PTu}}-d_{\mathrm{PTd}}\right)} $ | (1) |
式中:M和N分别为作用于柱顶的弯矩和轴力;dC为框架柱宽度;fptk为钢绞线极限强度标准值,初始张拉应力为0.3fptk;dPTu为开口侧钢绞线与转动点的距离;dPTd为转动侧钢绞线与转动点的距离。
罕遇地震下,结构层间位移角不大于2%,以此确定预应力钢绞线长度为
| $l_{\mathrm{PT}}=\frac{\theta_{\mathrm{t}} d_{\mathrm{PTu}}}{f_{\mathrm{ptk}}} E_{\mathrm{PT}} $ | (2) |
式中:θt为柱底转角,取2%;EPT为钢绞线弹性模量。
假定柱脚达到最大层间位移角时,开口端消能杆达到极限应变,根据平截面假定可得消能杆长度lED为
| $l_{\mathrm{ED}}=\frac{\theta_{\mathrm{t}} d_{\mathrm{EDu}}}{\frac{f_{\mathrm{yED}}}{E_{\mathrm{eED}}}+\frac{f_{\mathrm{uED}}-f_{\mathrm{yED}}}{f_{\mathrm{pED}}}} $ | (3) |
式中:消能杆核心钢板屈服强度为fyED;极限强度为fuED;消能杆弹性阶段弹性模量为EeED;弹塑性阶段弹性模量为EpED,EpED取0.05EeED。
βsc参数为开口端钢绞线产生的抵抗矩与消能杆产生抵抗矩的比值,根据结构预先设定的抗震性能目标设置βsc数值,文献[18-19]对该参数的合理取值范围作了详细介绍,并以此确定消能杆截面积AsED为
| $A_{\mathrm{sED}}=\frac{2 \cdot 0.3 f_{\mathrm{ptk}} A_{\mathrm{sPT}} d_{\mathrm{PTu}}}{\beta_{\mathrm{sc}} f_{\mathrm{yED}} d_{\mathrm{EDu}}} $ | (4) |
上述根据力的平衡条件对柱脚绕转动点进行的计算亦确保了自复位柱脚的倾覆稳定性能够满足要求,同时,剪力键根据柱脚承担的剪力进行设计,亦确保了柱脚的滑移稳定性能够满足要求。框架柱设计与柱脚固结的常规框架相同,此处不再赘述。
按照上述设计流程,设计制作了四组试件,试件分组见表 2,自复位钢柱脚尺寸见图 4(a)。钢柱采用截面尺寸300 mm×300 mm×20 mm的矩形钢管,钢材型号为Q345。为避免加载过程中钢管局部变形(局部失稳)对试验结果的影响,在管内灌注C30微膨胀混凝土。预应力钢绞线型号为1×7公称直径15.2 mm,极限强度标准值fptk=1 860 MPa,长度2 800 mm,共4根。钢绞线设计初始应力为0.3fptk,即558 MPa。为避免试验中钢绞线预应力损失对后续试验造成影响,实际张拉控制应力为744 MPa,张拉完成后,对未组装消能杆的试件加载至最大目标位移,卸载后实测应力为571 MPa,每根钢绞线的初始张拉力FPTi为79.9 kN,与设计值误差仅为2.3%。
| 表 2 试验分组 Tab. 2 Test groups |

|
图 4 构件尺寸(mm) Fig. 4 Dimension of specimen and components (mm) |
耗能元件是自复位柱脚的重要组成构件,为结构提供抗弯承载力的同时,通过塑性变形耗散地震能量,因此需结合结构对承载力和变形的需求对耗能元件进行设计,且易于更换。为此,设计了一种类似于防屈曲支撑的防屈曲消能杆作为耗能元件,由工作段核心钢板、高强无收缩灌浆料和约束钢管组成,通过中部核心钢板塑性变形耗能,外围钢管填充高强无收缩灌浆料防止其受压时发生屈曲,核心钢板外裹聚乙烯薄膜确保其轴向变形不受灌浆料影响。BRB-1的工作段核心钢板截面为15 mm×10 mm(AED=150 mm2),BRB-2为22 mm×14 mm(AED=308 mm2), 钢材型号为Q345。文献[20]对防屈曲消能杆的力学性能进行了研究,结果表明,其滞回曲线稳定饱满,承载力、变形和耗能能力良好,且工作段截面积越大,力学性能越好。图 4(b)为BRB-1构件尺寸。
2.2 材料力学性能钢材的材料力学性能试验结果见表 3,由于钢材批次不同,出现了部分厚度越大的钢板强度亦越大的现象。混凝土立方体抗压强度为38.28 MPa,弹性模量为3.4×104 MPa。
| 表 3 钢材材料力学性能 Tab. 3 Mechanical properties of steel |
试验加载装置见图 5。水平荷载通过1 000 kN液压伺服作动器进行施加,作动器中心与框架柱顶部预留的连接件对齐。竖向荷载采用1 000 kN液压千斤顶施加,千斤顶上端通过滑车作用于反力梁,下端通过球铰作用于框架柱顶部,确保千斤顶随柱顶水平移动并减小摩擦力的影响。

|
图 5 试验加载装置 Fig. 5 Test setup |
加载时先对试件施加竖向力,并在试验过程中保持不变,然后通过水平作动器进行水平加载。水平加载采用位移控制,加载点最大水平位移为40 mm,对应结构层间位移角为2%,采用分级加载方式,共8级,逐级递增,每级循环两次,位移增量为5 mm,各位移幅值包含一组正值和一组等大负值,加载制度见图 6。

|
图 6 加载制度 Fig. 6 Loading protocol |
测量内容为:加载点水平位移和水平荷载、框架柱特征点水平位移、防屈曲消能杆变形、柱脚开口宽度、预应力钢绞线拉力、框架柱应变。测点布置见图 7。

|
图 7 测点布置 Fig. 7 Measuring points layout |
试验共布置10个位移计,DC1至DC4测量框架柱特征点水平位移,DE1至DE4测量消能杆变形,DO1、DO2测量柱脚开口宽度。预应力钢绞线拉力通过锚索计测量。在框架柱身共布置16片应变花,加载侧从上至下分别为S11至S14,沿顺时针旋转至侧面为S21至S24,以此类推。采用力传感器测量水平力和竖向力。
3 试验结果及分析 3.1 试验现象当加载点位移为5.5 mm时,SCCB1和SCCB3柱脚开口;当加载点位移为8.1 mm时,SCCB2和SCCB4柱脚开口。各组试件加载至最大位移40 mm时,柱脚最大开口宽度为7.5 mm,与理论计算值基本一致,见图 8(a),并且明显可见柱身倾斜,见图 8(b)。卸载时,缓慢松开油泵阀门,可见柱脚开口逐渐减小,最终闭合,自复位效果明显。卸载后,松开销轴并取出消能杆,可见消能杆端部有拉伸后伸长的痕迹。单组试验完成后,对消能杆进行更换并调整柱顶竖向力,即可进行下一组试验,消能杆更换过程操作方便,各组试件的试验现象基本相同,达到了预期效果。

|
图 8 试验现象 Fig. 8 Test phenomena |
各组试件的加载点水平荷载-位移滞回曲线见图 9。加载初期,曲线呈线性变化,柱脚未开口,消能杆未参与受力,结构处于弹性变形阶段。随着水平位移的增大,柱脚开口,消能杆参与受力,预应力钢绞线拉力增大,结构刚度有所下降。持续加载后,柱脚开口不断增大,消能杆屈服,结构刚度下降明显。加载至各目标位移后卸载,卸载过程中,由于预应力钢绞线拉力的作用,柱脚自行复位。整个加卸载过程中滞回曲线的变化规律与1.2节所述基本一致。滞回曲线表现出自复位结构特有的“双旗帜”形特征,中部有捏缩现象,自复位效果明显。

|
图 9 荷载-位移滞回曲线 Fig. 9 Load-displacement hysteretic curves |
试件的骨架曲线见图 10。各组试件骨架曲线的变化规律基本一致,柱脚开口前,刚度由框架柱提供,柱脚开口后,刚度由钢绞线和消能杆提供,刚度较开口前减小。柱脚开口时对应的加载点位移与柱顶轴向力有关,轴向力越大,加载点位移越大。另外,柱顶轴向力越大,结构承载力亦越大。βsc参数主要影响柱脚开口后刚度及承载力,βsc越大,结构刚度及承载力越小。加载至最大位移后,骨架曲线并未出现下降段,除消能杆产生塑性变形外,框架柱和钢绞线均为弹性状态,试件承载力储备充足。
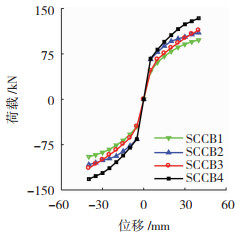
|
图 10 骨架曲线 Fig. 10 Skeleton curves |
预应力钢绞线拉力随加载点位移的变化曲线见图 11。图中同时给出了加载侧和转动侧钢绞线的数据。试验结果表明,预应力钢绞线在整个加载过程中均保持弹性状态,由于采取了提前超张拉的措施,试验过程中基本未发生预应力损失。钢绞线拉力与柱顶轴力和βsc参数均无关。

|
图 11 预应力钢绞线拉力 Fig. 11 Force of prestressed steel strand |
各位移加载步的消能杆变形见图 12,其中DE1和DE3位于加载(转动)侧,DE2和DE4位于中间侧。由于加载制度为位移控制加载,结合试验结果,各组试件的消能杆变形曲线基本一致,故图中仅给出竖向力最大且水平力最大的一组试件,即SCCB4的变形数据。DE1和DE3受拉变形最大为6.2 mm(伸长率1.03%),受压变形最大为2.1 mm(伸长率0.35%)。DE2与DE4受拉变形最大为2.6 mm(伸长率0.43%)。以上实测数据略小于理论计算值:DE1和DE3受拉变形为8 mm,受压变形为2 mm;DE2和DE4受拉变形为3 mm。其原因在于试验中消能杆端部发生了一定的弯曲变形,而理论计算时仅考虑了消能杆的轴向变形,另外,销轴与连接耳板间存在少量空隙亦会对试验结果造成影响。结合文献[20]的结果,消能杆屈服时伸长率约为0.33%,断裂时约为4.2%,试验中,消能杆已屈服,通过塑性变形耗散能量,其承载力仍存在一定富余。

|
图 12 消能杆变形 Fig. 12 Deformation of buckling-restrained bars |
框架柱主要测点应变随加载点位移的变化曲线见图 13。结合试验结果,各组试件相同测点的应变曲线变化规律基本一致,故图中仅给出竖向力最大且水平力最大的一组试件,即SCCB4的应变数据。另外,框架柱加载侧和转动侧的应变明显大于中间侧,故选取S31至S34的应变数据。结果表明,框架柱最大应变为4.95×10-4,远小于钢材屈服应变,框架柱在加载过程中处于弹性状态,综合钢绞线拉力以及消能杆变形数据,塑性变形集中于消能杆,实现了预期的设计意图。框架柱应变沿柱身由上至下递增,在钢绞线锚固板位置和消能杆连接耳板位置存在应力突变,与理论推导一致,设计时应特别注意,防止局部变形过大影响抗震性能。

|
图 13 框架柱主要测点应变 Fig. 13 Strain of column at main measuring points |
试件的自复位能力采用残余层间位移角进行评价。参考文献[21]的评价方法,即地震后结构的残余层间位移角小于0.002 rad时,可不对结构采取鉴定加固措施仍可继续使用。各位移加载步试件的残余层间位移角见图 14。结果表明,SCCB3残余层间位移角最大,正向、负向加载均为0.001 rad,小于0.002 rad,自复位能力良好。柱顶轴压力和βsc参数对试件的自复位能力影响较大,轴压力越大,残余层间位移角越小,自复位能力越好;βsc越大,残余层间位移角越小,自复位能力越好。柱脚开口前,各组试件的残余层间位移角基本相同。

|
图 14 残余层间位移角 Fig. 14 Residual story drifts |
试件的变形能力采用位移延性系数μΔ进行评价,其计算方法为
| $\mu=\frac{\mathit{\Delta }_{\mathrm{u}}}{\mathit{\Delta }_{\mathrm{y}}} $ | (5) |
式中:Δy为屈服位移,取柱脚开口时加载点位移;Δu为极限位移,取加载点最大位移。各组试件位移延性系数见表 4。结果表明,各组试件的位移延性系数均大于3,变形能力良好,变形能力主要与框架柱刚度相关,而βsc参数对其影响较小。柱顶轴压力对试件变形能力有较大影响,轴压力越小,试件变形能力越好。
| 表 4 位移延性系数 Tab. 4 Displacement ductility coefficients |
试件的耗能能力采用等效黏滞阻尼系数ξeq进行评价,结合文献[22-23],其计算方法为
| $\zeta_{\mathrm{eq}}=\frac{1}{2 \pi} \cdot \frac{S_{A B C}}{S_{O B E}} $ | (6) |
式中:SABC为某级加载循环下,滞回环所包围的面积;SOBE为对应滞回环卸荷段至横坐标之间三角形的面积。
由滞回曲线计算得到的试件等效黏滞阻尼系数见图 15。柱脚开口前,各组试件等效黏滞阻尼系数较小,约为0.02。柱脚开口后,由于阻尼器参与受力,屈服后通过其塑性变形耗能,等效黏滞阻尼系数迅速增大,最大加载位移时,该系数为0.15~0.18,对于自复位结构而言,具有良好的耗能能力。βsc参数对试件的耗能能力影响较大,βsc越小,耗能能力越好。柱顶轴向力基本不影响试件的耗能能力。

|
图 15 等效黏滞阻尼系数 Fig. 15 Equivalent viscous damping coefficients |
1) 设计制作了带防屈曲消能杆的自复位钢柱脚试件,通过低周往复荷载试验,其各阶段的受力状况与理论分析结果吻合良好,结构的塑性变形集中于防屈曲消能杆,框架柱和预应力筋均处于弹性状态,达到了预期的设计目标。
2) 试件的荷载-位移滞回曲线为典型的“双旗帜”形,加载至最大目标位移卸载后,试件残余层间位移角最大为0.001 rad,小于其限值0.002 rad的规定,具有良好的自复位能力。
3) 试件的位移延性系数最小值为4.9,等效黏滞阻尼系数为0.15~0.18,表明该自复位柱脚具有良好的变形能力和耗能能力。
4) 作用于框架柱顶的轴向力和βsc参数对柱脚的自复位能力和抗震性能影响较大。随着βsc参数增大,柱脚自复位能力提高,承载力和耗能能力降低,而对变形能力影响不大;随着框架柱轴力增大,自复位能力和承载力提高,变形能力降低,而对耗能能力影响不大。
5) 带防屈曲消能杆的自复位钢柱脚,具有可恢复功能结构的特点,但消能杆端产生的弯曲变形和销轴与连接板间的空隙会造成消能杆轴向变形偏小,对抗震性能有一定影响,设计时应注意。
| [1] |
GRIGORIAN M, MOGHADAM A S, MOHAMMADI H, et al. Methodology for developing earthquake-resilient structures[J]. The Structural Design of Tall and Special Building, 2019, 28(2): e1571. DOI:10.1002/tal.1571 |
| [2] |
吕西林, 全柳萌, 蒋欢军. 从16届世界地震工程大会看可恢复功能抗震结构研究趋势[J]. 地震工程与工程振动, 2017, 37(3): 1. LV Xilin, QUAN Liumeng, JIANG Huanjun. Research trend of earthquake resilient structures seen from 16WCEE[J]. Earthquake Engineering and Engineering Dynamics, 2017, 37(3): 1. DOI:10.13197/j.eeev.2017.03.1.lvxl.001 |
| [3] |
RICLES J M, SAUSE R, GARLOCK M M, et al. Posttensioned seismic-resistant connections for steel frames[J]. Journal of Structural Engineering, 2001, 127(2): 113. |
| [4] |
RICLES J M, SAUSE R, PENG S W, et al. Experimental evaluation of earthquake resistant posttensioned steel connections[J]. Journal of Structural Engineering, 2002, 128(7): 850. DOI:10.1061/(ASCE)0733-9445(2002)128:7(850) |
| [5] |
HERNING G, GARLOCK M E M, VANMARCKE E. Reliability-based evaluation of design and performance of steel self-centering moment frames[J]. Journal of Constructional Steel Research, 2011, 67(10): 1495. DOI:10.1016/j.jcsr.2011.03.023 |
| [6] |
MORADI S, ALAM M S. Multi-criteria optimization of lateral load-drift response of posttensioned steel beam-column connections[J]. Engineering Structures, 2017, 130: 180. DOI:10.1016/j.engstruct.2016.10.005 |
| [7] |
SARVESTANI H A. Structural evaluation of steel self-centering moment-resisting frames under far-field and near-field earthquakes[J]. Journal of Constructional Steel Research, 2018, 151: 83. DOI:10.1016/j.jcsr.2018.09.013 |
| [8] |
HUANG Xiaogang, ZHOU Zhen, XIE Qin, et al. Force distribution analysis of self-centering coupled-beams for moment-resisting-frames without floor elongation[J]. Engineering Structures, 2017, 147: 328. DOI:10.1016/j.engstruct.2017.05.055 |
| [9] |
ZHANG Yanxia, LI Quangang, ZHUGE Yan, et al. Experimental study on spatial prefabricated self-centering steel frame with beam-column connections containing bolted web friction devices[J]. Engineering Structures, 2019, 195: 1. DOI:10.1016/j.engstruct.2019.05.085 |
| [10] |
VASDRAVELLIS G, KARAVASILIS T L, UY B. Large-scale experimental validation of steel posttensioned connections with web hourglass pins[J]. Journal of Structural Engineering, 2013, 139(6): 1033. DOI:10.1061/(ASCE)ST.1943-541X.0000696 |
| [11] |
XU Xian, CHENG Guangming, ZHENG Junhua. Tests on pretrained superelastic NiTi shape memory alloy rods: towards application in self-centering link beams[J]. Advances in Civil Engineering, 2018, 2018: 2037376. DOI:10.1155/2018/2037376 |
| [12] |
XU Xian, TU Jiaqi, CHENG Guangming, et al. Experimental study on self-centering link beams using post-tensioned steel-SMA composite tendons[J]. Journal of Constructional Steel Research, 2019, 155: 121. DOI:10.1016/j.jcsr.2018.12.026 |
| [13] |
FENG Weikang, FANG Cheng, WANG Wei. Behavior and design of top flange-rotated self-centering steel connections equipped with SMA ring spring dampers[J]. Journal of Constructional Steel Research, 2019, 159: 315. DOI:10.1016/j.jcsr.2019.04.046 |
| [14] |
CHI H, LIU J. Seismic behavior of post-tensioned column base for steel self-centering moment resisting frame[J]. Journal of Constructional Steel Research, 2012, 78: 117. DOI:10.1016/j.jcsr.2012.07.005 |
| [15] |
WANG Xiantie, XIE Chuandong, LIN Linhui, et al. Seismic behavior of self-centering concrete-filled square steel tubular (CFST) column base[J]. Journal of Constructional Steel Research, 2019, 156: 75. DOI:10.1016/j.jcsr.2019.01.025 |
| [16] |
KAMPERIDIS V C, KARAVASILIS T L, VASDRAVELLIS G. Self-centering steel column base with metallic energy dissipation devices[J]. Journal of Constructional Steel Research, 2018, 149: 14. DOI:10.1016/j.jcsr.2018.06.027 |
| [17] |
建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2016: 47 Code for seismic design of buildings: GB 50011—2010[S]. Beijing: China Architecture and Building Press, 2016: 47 |
| [18] |
杨溥, 沈培文, 黄诚, 等. 新型自复位钢桁架梁的设计及参数分析[J]. 重庆大学学报, 2019, 42(1): 25. YANG Pu, SHEN Peiwen, HUANG Cheng, et al. Design and parameter analysis for new self-centering steel truss beam[J]. Journal of Chongqing University, 2019, 42(1): 25. DOI:10.11835/j.issn.1000-582X.2019.01.003 |
| [19] |
MAURYA A, EATHERTON M R. Experimental study of the restoring force mechanism in the self-centering beam (SCB)[J]. Frontiers of Structural and Civil Engineering, 2016, 1. DOI:10.1007/s11709-016-0346-x |
| [20] |
沈培文, 杨溥, 洪基豪, 等. 不同柱脚连接的自复位钢梁框架抗震性能试验[J]. 哈尔滨工业大学学报, 2020, 52(8): 30. SHEN Peiwen, YANG Pu, HONG Jihao, et al. Experiment on seismic behavior of self-centering steel beam frame with different column foot connection[J]. Journal of Harbin Institute of Technology, 2020, 52(8): 30. DOI:10.11918/201909103 |
| [21] |
FEMA. Seismic performance assessment of buildings: Volume 1—Methodology: FEMA P-58-1[R]. Washington, DC: Federal Emergency Management Agency, 2018
|
| [22] |
徐军, 李英民, 赖永余, 等. 设有接地梁的掉层钢筋混凝土框架抗震性能试验及有限元分析[J]. 建筑结构学报, 2019, 40(12): 60. XU Jun, LI Yingmin, LAI Yongyu, et al. Experiment and finite element analysis of seismic behavior of split-foundation RC frame with earthing beam[J]. Journal of Building Structures, 2019, 40(12): 60. DOI:10.14006/j.jzjgxb.2017.0873 |
| [23] |
潘鹏, 叶列平, 钱稼茹, 等. 建筑结构消能减震设计与案例[M]. 北京: 清华大学出版社, 2014: 10. PAN Peng, YE Lieping, QIAN Jiaru, et al. Seismic design of building structures equipped with energy dissipation devices[M]. Beijing: Tsinghua University Press, 2014: 10. |
 2021, Vol. 53
2021, Vol. 53


