2. 同济大学 土木工程学院, 上海 200092
2. College of Civil Engineering, Tongji University, Shanghai 200092, China
近20年来,中国排水管网系统发展迅速.随着管网规模的不断扩大和服役年限的增长,排水管道退化和缺陷问题也逐步凸显,有些管道缺陷直接导致路面塌陷、水体污染等严重事故,不仅影响城镇居民工作和生活,还对生命健康构成威胁.排水管道内部缺陷的识别、诊断是制定管网养护计划和修复计划的重要依据,也是城市安全运行监管的重要内容之一.
排水管道缺陷包括管道破裂、腐蚀、渗漏、变形等结构性缺陷,以及沉积、结垢、障碍物等功能性缺陷.管道闭路电视(closed circuit television, CCTV)检测是目前国内外用于管道状况检查最为成熟、有效、安全的技术手段.能直观反映和记录管道内部真实情况,通过管道影像的判读,识别内部缺陷类型、位置和等级,并做进一步评估分析[1].不过,CCTV检测要求对管道先进行一定清理,降低管内水位,前期工作量大;另外,主要依靠人工目测对管道内部状况和缺陷进行诊断评估,效率较低.国内外学者采用统计和机器学习方法研究建立了多种管道状况模型.例如,Micevski等[2]基于马尔科夫链构建雨水管道结构退化模型,并用贝叶斯方法进行校准;刘威等[3]结合全概率公式及线性腐蚀模型给出管线面积腐蚀率的概率密度随服役时间变化的解析表达式;Mashford等[4]建立了基于支持向量机的管道状况预测模型,并应用于澳大利亚阿德莱德市排水管网状况评价;Rober等[5]利用CCTV检测数据和随机森林算法,对加拿大圭尔夫市下水管道的结构性状态进行预测.此外,Tran等[6-7]利用神经网络模型预测排水管道的结构性状况和水力性状况.不过,已有研究更多的是对管道整体状况的建模,从结构性或功能性方面预测管道风险等级,具体缺陷类型的分类诊断和评价方面还有待更深入的研究.
鉴于管道退化和缺陷影响因素复杂,数据驱动的神经网络模型无需深入理解管道病害机理,通过数据样本监督学习即可建立管道缺陷状况同相关特征变量的关联模式,无疑具有良好的适用性和应用前景[8].极限学习机(extreme learning machine, ELM)是Huang等[9]基于Moore-Penrose矩阵理论提出的一种单隐含层前馈神经网络算法,相对传统的神经网络,具有结构简单、学习效率高、泛化能力强等优点.不过,ELM随机生成输入层权值以及隐含层节点偏置等网络参数的特点,可能造成部分隐含层节点的失效[10];其次,ELM分类预测精度与隐含层节点数密切相关,但过多隐含层节点数会导致模型泛化能力的下降,影响管道缺陷分类诊断的能力.
为此,采用遗传算法(genetic algorithm,GA)[11]优化ELM网络参数,充分利用管道基础数据和CCTV检测资料,建立一个新型的城市排水管道缺陷诊断模型,并以上海市洋山港保税区排水管道结构性缺陷的分类诊断为例开展实证研究,验证模型方法的适用性和有效性.
1 GA-ELM诊断模型 1.1 ELM原理设n,L,m分别为输入层、隐含层和输出层的节点数,给定N组任意的排水管道数据样本(xi, ti)∈Rn×Rm,ELM的输出可以表示为
| $ {f_L}\left( \mathit{\boldsymbol{x}} \right) = \mathop \sum \limits_{i = 1}^L {\mathit{\boldsymbol{\beta }}_i}g\left( {\mathit{\boldsymbol{w}}{_i} \cdot {\mathit{\boldsymbol{x}}_j} + {b_i}} \right) = {\mathit{\boldsymbol{o}}_j}, j = 1, \ldots , N. $ | (1) |
式中:g(x)为激励函数,wi=wi=[wi1, wi2, …, win]T为隐含层第i个神经元与输入层的连接权值,βi=[βi1, βi2, …, βim]T为隐含层第i个神经元与输出层的连接权值,bi为隐含层神经元的阈值.wi·xj为wi和xj的内积.
若L=N,则对于任意给定的βi和wi,ELM能零误差逼近学习样本[12],式(1)可以由矩阵形式表达为
| $ \mathit{\boldsymbol{H\beta }} = \mathit{\boldsymbol{T}}. $ | (2) |
其中
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{H}} = \left[ \begin{array}{l} h\left( {{X_1}} \right)\\ \;\;\;\; \vdots \\ h\left( {{X_N}} \right) \end{array} \right] = \\ {\left[ \begin{array}{l} g\left( {\mathit{\boldsymbol{w}}{_1} \cdot {\mathit{\boldsymbol{x}}_1} + {b_1}} \right){\rm{ }}\;\;\; \cdots \;\;\;{\rm{ }}g\left( {\mathit{\boldsymbol{w}}{_L} \cdot {\mathit{\boldsymbol{x}}_1} + {b_1}} \right)\\ \;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ g\left( {\mathit{\boldsymbol{w}}{_1} \cdot {\mathit{\boldsymbol{x}}_N} + {b_1}} \right){\rm{ }}\;\; \ldots {\rm{ }}\;g(\mathit{\boldsymbol{w}}{_L} \cdot {\rm{ }}\mathit{\boldsymbol{x}}{_N} + {b_L}) \end{array} \right]_{N \times L}}, \end{array} $ | (3) |
| $ \mathit{\boldsymbol{\beta }} = {\left[ \begin{array}{l} \mathit{\boldsymbol{\beta }}_1^{\rm{T}}\\ \; \vdots \\ \mathit{\boldsymbol{\beta }}_L^{\rm{T}} \end{array} \right]_{L \times m}}, $ | (4) |
| $ \mathit{\boldsymbol{T}} = {\left[ \begin{array}{l} \mathit{\boldsymbol{t}}_1^{\rm{T}}\\ \; \vdots \\ \mathit{\boldsymbol{t}}_L^{\rm{T}} \end{array} \right]_{N \times m}}. $ | (5) |
N较大时,为减少计算量通常取L<N,此时,对ELM的网络训练等价于如下优化问题:
| $ \left\| {\mathop {\mathit{\boldsymbol{H\beta }}}\limits^ \wedge - \mathit{\boldsymbol{T}}} \right\| = \mathop {\min }\limits_\beta \left\| {\mathit{\boldsymbol{H\beta }} - \mathit{\boldsymbol{T}}} \right\|. $ | (6) |
当g(x)无限可微时,随机给定网络参数wi和bi,ELM模型训练过程可看作求解线性系统Hβ=T关于
| $ {\mathit{\boldsymbol{\hat \beta }}^ = }\mathit{\boldsymbol{H}} + \mathit{\boldsymbol{T}}. $ | (7) |
H+为隐含层输出矩阵H的Moore-Penrose广义逆.
1.2 GA优化ELM与BP模型相比,ELM学习速度快、泛化性能强、不易陷入局部极值,但仍有一些问题,如该算法中输入权值和隐含层偏置的随机选取导致隐含层神经元几乎不存在调节能力,这就对网络参数的优化提出了较高的要求.同时,ELM可能存在网络结构复杂、稳定性差等问题,选择合适的隐含层神经元个数和激活函数十分重要.
GA是模拟自然界遗传机制和物种进化而形成的一种并行随机搜索优化方法,将需要优化的参数编码形成串联群体,然后按照适应度函数通过选择、交叉和变异对个体进行筛选,最终选择适应度最优的个体[11].采用GA优化ELM神经网络的输入权值wi和隐含层偏置bi,得到最优的网络参数建立GA-ELM神经网络,提高模型输出的准确度和稳定性.
GA-ELM算法集成了GA全局搜索最优能力和ELM的强学习能力.在该算法中,将ELM训练数据的输入权值和隐含层节点偏置映射为GA种群中每条染色体上的基因,GA的染色体适应度对应于ELM的训练误差,将求取最优输入权值、偏置问题转化为计算染色体适应度,选择最优染色体问题.图 1给出GA-ELM算法流程,主要包括ELM网络确定、遗传算法优化和ELM网络的训练、预测等.
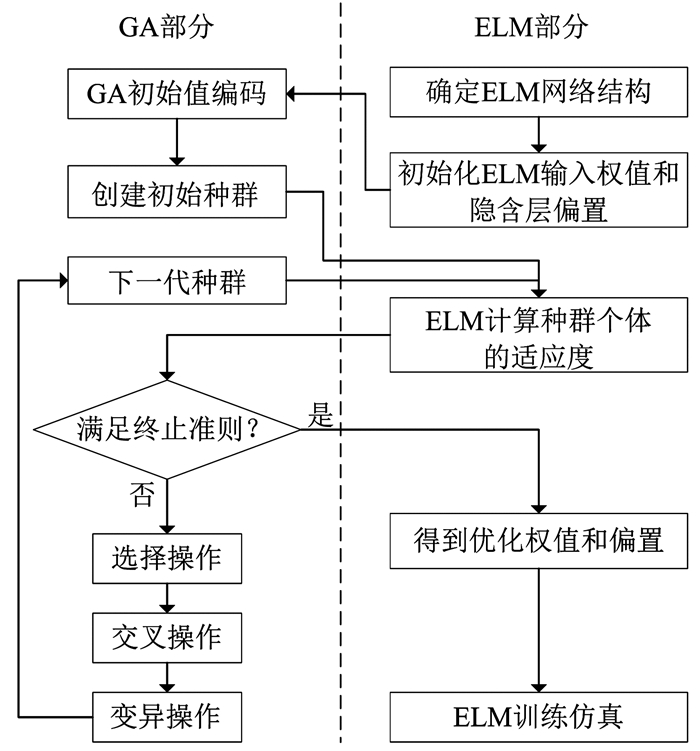
|
图 1 GA-ELM算法流程 Fig. 1 Calculation flow of GA-ELM algorithm |
算法相关思路及处理方法如下:
1) 种群初始化.确定ELM神经网络的拓扑结构,即输入层、隐含层和输出层的神经元个数;设置最大进化代数G;随机生成ELM神经网络的输入权值和隐含层偏置,并对其进行二进制编码,产生初始种群;个体的长度由隐含层输入权值矩阵和偏置向量构成,即D=(n+1)L,其中L为隐含层节点数,n为输入层神经元个数,即输入向量维度.
2) 个体适应度评价.对于每一代种群中的任意一个个体,采用ELM算法计算输出权值矩阵,并得到样本的期望输出与实际输出的均方根误差,作为GA目标函数
| $ {E_{{\rm{RMS}}}} = \sqrt {\frac{{\mathop \sum \limits_{i = 1}^n {{\left( {{y_i} - y} \right)}^2}}}{n}} . $ | (8) |
式中:i为样本个体,n为样本总数,yi为仿真输出值,y为样本期望输出值.目标函数数值越小,模型越精确.
3) 种群进化.根据个体的适应度,采用轮盘赌法对每一代种群中的染色体进行选择,利用基于概率的交叉、变异操作对选中的个体进行优化,产生新的种群,直至满足约束条件,如达到最大迭代次数或相邻种群的平均目标值、最小目标值变化很小时终止进化,得到最终的种群.
4) ELM网络训练和预测.对迭代优化后的最终种群解码,得到优化后的输入权值和偏置,赋予ELM,使用训练样本对ELM网络进行训练,采用最小二乘法计算输出层权值
排水管道退化机理复杂,影响因素较多,本文只针对管道结构性缺陷识别,利用GA-ELM算法建立分类诊断模型,通过样本数据训练学习确定影响因素与结构性缺陷之间的非线性关系.图 2给出模型的网络拓扑结构.其中,xj代表模型的输入变量,即管道结构性退化影响因素;ti代表模型输出变量,即结构性缺陷类型,如破裂、渗漏、脱节、变形、错位、腐蚀等.

|
图 2 模型网络拓扑 Fig. 2 Structure of neural network |
影响管道结构性退化的因素包括管道自身物理属性,如管材、管龄、管径、管长、埋深、坡度等;外部环境因素,如路面交通荷载、环境温度变化、临近施工、土壤类型、地下水位、树根侵入因素等.借鉴已有退化指标分析成果[8, 13-14],结合工程应用中数据获取条件,选取管材、管龄、管径、埋深、管长、坡度、管道类型、土壤类型和所在道路等级共9项特征参数作为神经网络模型的输入变量.其中,管道埋深取上下游节点埋深的平均值;管道所在道路等级分为主干道、次干道和其他道路3类,间接表征路面交通荷载.结构性缺陷类型,即样本标签由CCTV检测结果给定.
为了检验GA-ELM模型分类诊断效果,采用混淆矩阵方法对分类器性能进行分析评价.假定nij表示被分类为j类的i类样本数,K为样本种类,则分类精度A以正确分类的样本数与总样本数N的比值表示,即
| $ A = \frac{{\mathop \sum \limits_{i = 1}^K {n_{ii}}}}{N} \times 100\% . $ | (9) |
定义Ri为第i类样本的查全率(Recall),即
| $ {R_i} = \frac{{{n_{ii}}}}{{\mathop \sum \limits_{j = 1}^K {n_{ij}}}} \times 100\% . $ | (10) |
定义Gmean为样本所有类别查全率的几何平均值:
| $ {G_{{\rm{mean}}}} = {\left( {\mathop \prod \limits_{i = 1}^K {R_i}} \right)^{\frac{1}{K}}} \times 100\% . $ | (11) |
Gmean的基本思想是使每一分类正确率尽可能大的同时,保持各类之间的平衡,是评价不平衡数据集上分类器性能的重要指标.
2 实验分析 2.1 实验数据以上海市浦东新区洋山保税港区公共排水管道为对象,开展实证研究.主要数据来源包含两部分:一是测绘部门提供的管道GIS数据,包含管材、管龄、管径、埋深、管长、坡度、管道类型和所在道路等属性数据;二是由管道养护单位提供的实验区2018年10月份管道CCTV检测数据,检测管道里程约45.5 km.CCTV检测报告给出了具体管段的缺陷类型、等级,并计算了管段修复指数和养护指数.为简化网络模型,提高模型分类预测性能,研究仅选取实验区管道"破裂"、"脱节"、"渗漏"3类主要结构性缺陷类型和"正常"共4类样本数据.基于管段唯一性标识建立管网GIS和CCTV检测数据的对应关系,提取有效样本数据共1 251条.按4类样本的占比随机选取1/4样本作为测试样本集,3/4样本作为训练样本集,样本数据组成如表 1所示.
| 表 1 样本数据 Tab. 1 Sample data |
对于管材、道路等级、土壤类型、缺陷类型等离散的分类特征数据,采用独热编码进行数字化.另外,为避免各指标量纲和数量级不同造成的不平衡性,提高神经网络模型的收敛速度和学习预测能力,采用最大最小法对样本数据进行了归一化处理,使得处理后的数据分布范围在[0, 1],公式如下:
| $ {X^*} = \frac{{X - {X_{{\rm{min}}}}}}{{{X_{{\rm{max}}}} - {X_{{\rm{min}}}}}}. $ | (12) |
式中:X为实测值,Xmin为样本数据的最小值, Xmax为样本数据的最大值.
2.2 参数设置利用标准ELM构建管道缺陷分类诊断模型时,仅需要设定隐含层神经元节点数L和激励函数g(x)的构造形式就可以求算输出权值矩阵.实际工程应用中隐含层神经元节点数L一般远小于样本数N,L过小网络预测误差较大,L过大则会增加模型预测的时间空间成本,容易出现过拟合现象.图 3给出sigmoid、sin和hardlim 3种常见激励函数下隐含层神经元节点数L对分类器能力的影响.其中,sigmoid函数的分类器性能整体较好,L增至120时Gmean相对较高,为55.39%.对于标准ELM模型,选定sigmoid激励函数,隐含层神经元节点数L设定为120.

|
图 3 3种激励函数下隐含层节点数对ELM分类性能的影响 Fig. 3 Effect of number of hidden nodes on ELM performance under three activation functions |
为方便比较,选择同样的激励函数和隐含层节点数,对GA-ELM分类器性能进行仿真分析.设定GA参数如下:种群大小为40,最大遗传代数为100,交叉概率0.7,变异概率0.01,代沟0.95.将样本输入GA-ELM模型进行训练,如图 4误差进化曲线所示,当进化到44代时,误差最小,满足要求.因此,将44代优化后的权值和偏置代入极限学习模型中对测试样本进行预测.
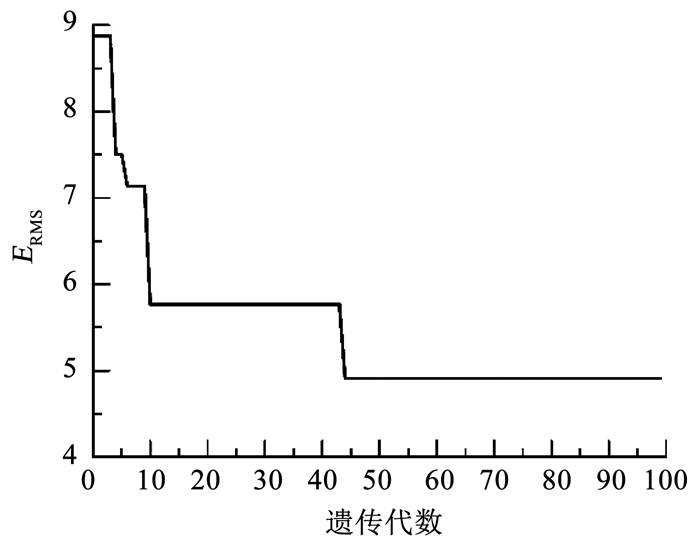
|
图 4 误差进化曲线 Fig. 4 Error evolution curve |
表 2给出标准ELM和GA优化后模型分类性能的比较.其中,ELM在训练集上的分类精度A=70.74%,Gmean=65.21%;测试集训练精度A=65.59%,Gmean=55.39%.GA优化ELM网络参数后,对于训练样本和测试样本的分类能力均有显著提升,达到80%以上,而且GA-ELM整体上具有更好的稳定性和泛化能力.
| 表 2 GA-ELM和ELM模型分类性能比较 Tab. 2 Performance comparison between GA-ELM and ELM |
为进一步分析模型对不同管道缺陷类型的诊断、识别能力,表 3以混淆矩阵形式给出GA-ELM和ELM在测试集上的分类诊断结果以及不同缺陷类型的查全率.其中,"破裂"的管道样本62条,GA-ELM诊断模型准确预测48条, 查全率77.42%;"脱节"的管道样本48条,准确预测36条,查全率为75.00%;"渗漏"的管道样本89条,准确预测68条,查全率为76.40%.ELM诊断模型对于上述3类缺陷管道的查全率则分别为59.68%、52.08%和65.17%.可见,相比ELM,GA-ELM诊断模型对于缺陷管段的识别能力更强,具有更优的分类预测性能.不过,由表 3结果也发现,两个模型对"正常"管段的识别能力均高于其他缺陷管段,这估计与实验区排水管道样本的非均衡分布有关.
| 表 3 GA-ELM和ELM诊断结果 Tab. 3 Diagnosis results of GA-ELM and ELM |
图 5给出测试集上逐个样本GA-ELM诊断结果与观测值的比照.结果也表明,GA-ELM能够较好地对排水管道结构性缺陷进行诊断识别,且分类精度可较好满足应用要求.
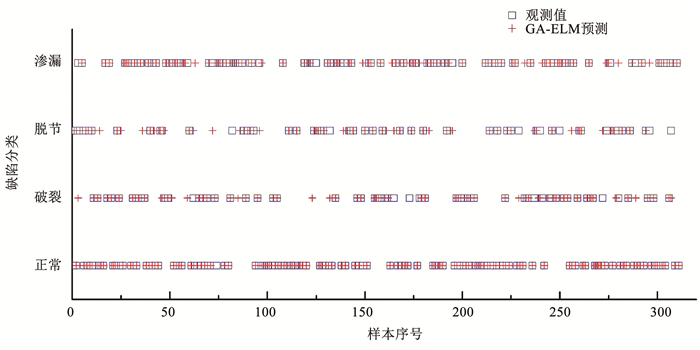
|
图 5 GA-ELM分类诊断结果 Fig. 5 Contrast between predicted results and observed results of GA-ELM |
1) 提出了基于GA-ELM的排水管道缺陷诊断模型,采用GA算法优化ELM神经网络输入连接权值和隐含层偏置,避免参数随机初始化造成的分类结果不稳定、准确率偏低的弊端.
2) 利用CCTV检测样本集对GA-ELM、ELM进行仿真测试,结果表明,在采用同样的激励函数和隐含层节点数的条件下,通过GA优化ELM网络参数能够获得更高的分类诊断性能,测试集分类精度由65.59%提高到82.96%;参数优化提高了ELM模型的拟合能力和稳定性.
3) 本文为城市排水管道缺陷识别和诊断提供了一个新型的数据驱动建模方法,具有较好的可行性和适用性.后续将收集更多的样本数据训练优化模型,并探讨非均衡样本对缺陷诊断性能的影响,进一步提高排水管道缺陷诊断模型的预测精度和泛化能力.
| [1] |
中华人民共和国住房和城乡建设部. 城镇排水管道检测与评估技术规程: CJJ 181—2012[S]. 北京: 中国建筑工业出版社, 2012 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Technical specification for inspection and evaluation of urban sewer: CJJ 181—2012[S]. Beijing: China Architecture & Building Press, 2012 |
| [2] |
MICEVSKI T, KUCZERA G, COOMBES P. Markov model for storm water pipe deterioration[J]. Journal of Infrastructure Systems, 2002, 8(2): 49. DOI:10.1061/(ASCE)1076-0342(2002)8:2(49) |
| [3] |
刘威, 李杰. 埋地管线面积腐蚀率概率密度的模拟分析[J]. 同济大学学报(自然科学版), 2007, 35(10): 1295. LIU Wei, LI Jie. Simulation analysis for probability density of buried pipeline's area corrosion ratio[J]. Journal of Tongji University (Natural Science), 2007, 35(10): 1295. DOI:10.3321/j.issn:0253-374X.2007.10.001 |
| [4] |
MASHFORD J, MARLOW D, TRAN D, et al. Prediction of sewer condition grade using support vector machines[J]. Journal of Computing in Civil Engineering, 2011, 25(4): 283. DOI:10.1061/(ASCE)CP.1943-5487.0000089 |
| [5] |
HARVEY R R, MCBEAN E A. Predicting the structural condition of individual sanitary sewer pipes with random forests[J]. Canadian Journal of Civil Engineering, 2014, 41(4): 294. DOI:10.1139/cjce-2013-0431 |
| [6] |
TRAN D H, NG A W M, PERERA B J C, et al. Application of probabilistic neural networks in modelling structural deterioration of stormwater pipes[J]. Urban Water Journal, 2006, 3(3): 175. DOI:10.1080/15730620600961684 |
| [7] |
TRAN D H, NG A W M, PERERA B J C. Neural networks deterioration models for serviceability condition of buried stormwater pipes[J]. Engineering Applications of Artificial Intelligence, 2007, 20(8): 1144. DOI:10.1016/j.engappai.2007.02.005 |
| [8] |
TRAN D H, PERERA B J C, NG A W M. Comparison of structural deterioration models for stormwater drainage pipes[J]. Computer-Aided Civil and Infrastructure Engineering, 2009, 24(2): 145. DOI:10.1111/j.1467-8667.2008.00577.x |
| [9] |
HUANG Guangbin, ZHU Qinyu, SIEW C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1/2/3): 489. DOI:10.1016/j.neucom.2005.12.126 |
| [10] |
WANG Yuguang, CAO Feilong, YUAN Yubo. A study on effectiveness of extreme learning machine[J]. Neurocomputing, 2011, 74(16): 2483. DOI:10.1016/j.neucom.2010.11.030 |
| [11] |
HOLLAND J H. Adaptation in natural and artificial systems[J]. Ann Arbor, 1975, 6(2): 126. |
| [12] |
HUANG Guangbin, ZHOU Hongming, DING Xiaojian, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics Part B: Cybernetics, 2012, 42(2): 513. DOI:10.1109/tsmcb.2011.2168604 |
| [13] |
ANA E, BAUWENS W, PESSEMIER M, et al. An investigation of the factors influencing sewer structural deterioration[J]. Urban Water Journal, 2009, 6(4): 303. DOI:10.1080/15730620902810902 |
| [14] |
HARVEY R R, MCBEAN E A. Comparing the utility of decision trees and support vector machines when planning inspections of linear sewer infrastructure[J]. Journal of Hydroinformatics, 2014, 16(6): 1265. DOI:10.2166/hydro.2014.007 |
 2021, Vol. 53
2021, Vol. 53


