2. 同济大学 地下建筑与工程系,上海 200092;
3. 路易斯安那州立大学 土木与环境工程学院,巴吞鲁日 70803
2. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China;
3. Department of Civil and Environmental Engineering, Louisiana State University, Baton Rouge 70803, USA
软黏土具有高孔隙比、高含水量、高压缩性、低渗透性的特点,其流变现象十分明显[1].流变的内在机制是黏土颗粒体积压缩及微观颗粒间的错动,即有效应力恒定不变的情况下,变形随时间不断增长.软黏土地层中的静压桩在沉桩结束后,桩周土中超孔隙水压力消散,其有效应力逐渐提高,使短期内基桩承载力呈现出明显的时效性[2].初始固结完成后,桩侧土体有效应力将趋于稳定,但桩周土体在流变作用下孔隙比降低、强度增长,伴随桩承载力随时间进一步增加.合理评估既有旧桩的长期承载力可以为上部建筑物移除后旧桩的再利用提供理论指导,有益于经济、环保的理念在基础工程中实现,有极强的理论和现实意义.
针对单桩承载力时间效应的问题,国内外学者开展了较为广泛的研究.Karsurd等[3-4]通过软黏土中单桩不同时间的测试数据,观测到了孔隙水压力消散完成后承载力持续增长的现象;Skov等[5]基于承载力随对数时间线性增长,提出了适用于黏性土和无黏性土的预测公式;Dohert等[6]建立旧桩测试的数据库并提出了以可靠度为基础的设计方法;胡琦等[7-8]通过统计黏土中基桩在不同休止期的静载荷试验数据,基于回归分析法提出了单桩长期承载力的预测公式;Karlsson等[9]通过应力路径法模拟沉桩过程,结合流变本构建立数值模型,模拟了软黏土中承载力随时间的发展.上述研究运用了经验公式、数值模拟等方法,具有较强的理论和工程意义.但由于沉桩扰动、桩周土初始固结,竖向荷载传递以及长期流变的影响,静压桩周土体应力状态的变化极为复杂,经验公式不能反映出各阶段土体力学特性的变化,数值模拟建模复杂,对计算量提出了较高的要求,不便于实际应用.而目前,针对软黏土中静压桩长期承载力理论计算方法的研究还较少.
为此,在考虑静压沉桩效应和孔压消散引起桩周土初始固结的基础上,采用荷载传递法得出了承载条件下桩周土的应力状态.进而根据桩周土体的受力状态和流变模型,分析了承载状态下桩周土体的流变特性及其强度的发展变化规律.在此基础上,对静压桩的长期承载力问题展开研究,提出了软黏土中静压桩长期承载力的理论计算方法,并通过静载荷试验对本文方法进行了实例验证.
1 桩周土力学特性的演变 1.1 静压沉桩效应由于软黏土的渗透性较小,静压沉桩过程可以近似看作初始孔径为0的不排水柱孔扩张问题[10].根据Li等[11]基于K0固结条件下修正剑桥模型推导的柱孔扩张理论弹塑性解答,沉桩完成后,桩侧土临界状态下的三向有效应力和超孔隙水压力可以分别表示为
| $ \left\{\begin{array}{l} \sigma_{\mathrm{zf}}^{\prime}=\frac{3 p_{\mathrm{f}}^{\prime}}{2 K_{0}+1}, \\ \sigma_{\mathrm{rf}}^{\prime}=\frac{3 K_{0} p_{\mathrm{f}}^{\prime}}{2 K_{0}+1}+\frac{\beta}{2} p_{\mathrm{f}}^{\prime}, \\ \sigma_{\theta \mathrm{f}}^{\prime}=\frac{3 K_{0} p_{\mathrm{f}}^{\prime}}{2 K_{0}+1}-\frac{\beta}{2} p_{\mathrm{f}}^{\prime}. \end{array}\right. $ | (1) |
| $ \begin{aligned} \Delta u=& \frac{\sqrt{3}}{3} q_{\mathrm{f}} \ln \frac{4 G_{0}^{2}}{\left(\sigma_{\mathrm{rp}}^{\prime}-\sigma_{\mathrm{r} 0}^{\prime}\right)\left(4 G_{0}-\sigma_{\mathrm{rp}}^{\prime}+\sigma_{\mathrm{r} 0}^{\prime}\right)}-\\ & p_{\mathrm{f}}^{\prime}-\frac{\sqrt{3}}{3} M p_{\mathrm{f}}^{\prime}+\sigma_{\mathrm{rp}}. \end{aligned} $ | (2) |
式中:G0为桩周土初始剪切模量;σ′r0=K0σ′z0,为桩周土初始径向有效应力,其中,K0为土体静止侧压力系数,σ′z0为桩周土初始垂直向有效应力;M为临界状态应力比;临界状态下的平均有效应力p′f和偏应力qf、桩周弹塑性边界上的径向应力σrp、弹塑性边界上的偏应力qp及参数β的表达式如下:
| $ \left\{ \begin{array}{l} p_{\rm{f}}^\prime = p_0^\prime {\left( {\frac{{{R_{\rm{OC}}}}}{2}} \right)^\mathit{\Lambda }},\\ {q_{\rm{f}}} = Mp_{\rm{f}}^\prime , \end{array} \right. $ | (3) |
| $ {\sigma _{{\rm{rp}}}} = \sigma _{{\rm{r}}0}^\prime + \sqrt {\frac{{q_{\rm{p}}^2 - \left( {\sigma _{{\rm{r}}0}^\prime - \sigma _{{\rm{z}}0}^\prime } \right)}}{3}} + {p_{\rm{w}}}, $ | (4) |
| $ q_{\mathrm{p}}=M p_{0}^{\prime} \sqrt{R_{\mathrm{OC}}\left(1+\frac{\eta_{0}^{2}}{M^{2}}\right)-1} , $ | (5) |
| $ \beta=\frac{2 \sqrt{3\left[M^{2}\left(2 K_{0}+1\right)^{2}-9\left(1-K_{0}\right)^{2}\right]}}{3\left(2 K_{0}+1\right)}. $ | (6) |
式中:p′0为初始平均有效应力;ROC为土体超固结比;Λ=1-κ/λ,为土体塑性体应变比,其中λ和κ分别为等向加载曲线和卸载曲线在v-ln p′平面上的斜率; pw为计算深度处的静水压力;η0=q0/p′0,为初始状态应力比.
鉴于本文着重研究桩的长期承载特性,孔隙水压力消散过程中短期的承载力时效性不作详细推导,但超孔隙水压力消散对桩侧土力学特性的影响应合理考虑.根据式(1)和式(2),结合有效应力原理和径向固结理论[12],当沉桩引起的超孔隙水压力Δu完全消散后,临界区域内桩周土的三向有效应力和平均有效应力可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {\sigma _{{\rm{zc}}}^\prime = \frac{{3p_{\rm{f}}^\prime }}{{2{K_0} + 1}} + \frac{{{v^\prime }}}{{1 - {v^\prime }}}\Delta u,}\\ {\sigma _{{\rm{rc}}}^\prime = \frac{{3{K_0}p_{\rm{f}}^\prime }}{{2{K_0} + 1}} + \frac{\beta }{2}p_{\rm{f}}^\prime + \Delta u,}\\ {\sigma _{\theta {\rm{c}}}^\prime = \frac{{3{K_0}p_{\rm{f}}^\prime }}{{2{K_0} + 1}} - \frac{\beta }{2}p_{\rm{f}}^\prime + \frac{{{v^\prime }}}{{1 - {v^\prime }}}\Delta u.} \end{array}} \right. $ | (7) |
| $ p_{\rm{c}}^\prime = \frac{{\sigma _{{\rm{zc}}}^\prime + \sigma _{{\rm{rc}}}^\prime + \sigma _{\theta {\rm{c}}}^\prime }}{3} = p_{\rm{f}}^\prime + \frac{{1 + {v^\prime }}}{{3\left( {1 - {v^\prime }} \right)}}\Delta u. $ | (8) |
由于沉桩过程中桩体剪切挤压作用,桩周临近土体处于临界状态,其原位潜在强度和结构性消失,故对于不同原位固结比的土体,可以认为沉桩后土体近似为正常固结状态[13].进而,由修正剑桥模型可将桩周土体初始固结后的三轴不排水强度表示为[14]
| $ S_{\mathrm{utc}, \mathrm{c}}=\frac{1}{2} M p_{\mathrm{c}}^{\prime}\left(\frac{1}{2}\right)^{\varLambda}. $ | (9) |
随着超孔隙水压力消散,桩周土体孔隙压缩,有效应力增长,其剪切模量也发生改变,基于临界状态土力学[14],可将桩周土主固结完成后的剪切模量表示为
| $ G_{\mathrm{c}}=\frac{3\left(1-2 v^{\prime}\right) v_{\mathrm{c}} p_{\mathrm{c}}^{\prime}}{2\left(1+v^{\prime}\right) \kappa}. $ | (10) |
式中vc为初始固结后土体的比体积.
1.2 承载条件下桩侧土应力状态解析实际工程中,桩间土长期流变沉降可能会与承台脱离,导致桩顶荷载发生变化.本文主要研究单桩在上部荷载作用下桩周土体的流变机理,进而根据土体流变过程中强度和模量的变化研究单桩荷载-沉降特性随时间的演变,因此,不考虑土体流变沉降后与承台脱开引起桩顶的荷载变化.为确定上部荷载作用下桩侧土体流变过程所处的有效应力状态,应用双曲线荷载传递函数模拟加载过程中桩侧和桩端的荷载传递,通过荷载传递法求解承载条件下桩侧土体的受力状态.双曲线荷载传递模型既能较好地模拟软土中桩体沿桩长方向承载能力发挥过程,又有参数简单、物理意义明确等特点[15-16],其表达式为
| $ \tau_{\mathrm{s}}(z) =\frac{s(z)}{A_{\mathrm{s}}+B_{\mathrm{s}} s(z)} , $ | (11) |
| $ \tau_{\mathrm{b}} =\frac{s_{\mathrm{b}}}{A_{\mathrm{b}}+B_{\mathrm{b}} s_{\mathrm{b}}}. $ | (12) |
式中:τs(z)和s(z)为z深度处桩-土界面的剪应力和桩土相对位移;τb和sb为桩端应力和沉降;As和Bs、Ab和Bb为模型参数,可由桩侧土和桩端土的强度和刚度参数确定.
如图 1所示,参数As和Ab为初始剪切刚度的倒数.Randolph等[17]将桩侧刚度表示为
| $ A_{\mathrm{s}}=\frac{r}{G_{\mathrm{s}, \mathrm{c}}} \ln \left(\frac{r_{\mathrm{m}}}{r}\right). $ | (13) |

|
图 1 双曲线型桩侧和桩端荷载传递曲线 Fig. 1 Hyperbolic load transfer curve for pile shaft and pile base |
式中:r为桩截面半径;rm为受侧阻力影响的桩侧土距桩中心的最大距离;Gs, c为初始固结后桩侧土的剪切模量,可由式(10)确定.
Randolph等[17]将桩端视作半无限弹性体上的刚性圆盘,得到桩端刚度的表达式,结合图 1可得
| $ {A_{\rm{b}}} = \frac{{{\rm{ \mathsf{ π} }}r\left( {1 - {v^\prime }} \right)}}{{4{G_{{\rm{b}},{\rm{c}}}}}}. $ | (14) |
式中Gb, c为初始固结后桩端以下8r内土体的平均剪切模量,可由式(10)确定.
参数Bs和Bb分别为极限摩阻力和极限端阻力的倒数.Li等[18]结合总应力法和SMP强度准则,推导了极限摩阻力与土体三轴不排水强度的关系:
| $ \tau_{\mathrm{su}}=\frac{3 \sqrt{3} \sin \varphi_{0} \cos \varphi^{\prime}}{2 M \cos \psi_{\mathrm{f}} \sqrt{2+\sin ^{2} \varphi_{0}}} S_{\mathrm{utc}}, $ | (15) |
| $ \sin \varphi_{0}=\frac{\sqrt{2} M}{\sqrt{9+3 M}}, $ | (16) |
| $ \psi_{\mathrm{f}}=\frac{1}{3} \cos ^{-1}\left[-\left(\frac{3}{2+\sin ^{2} \varphi_{0}}\right)^{\frac{3}{2}} \sin \varphi_{0} \cos 3 \theta\right] . $ | (17) |
式中:φ0和ψf为应力转换参数,θ为应力罗德角,平面应变条件下θ=π/6.结合式(9)可得
| $ B_{\mathrm{s}}=\frac{M^{2} \cos \psi_{\mathrm{f}} \sqrt{2+\sin ^{2} \varphi_{0}}}{3 \sqrt{3} \sin \varphi_{0} \cos \varphi^{\prime}} p_{\mathrm{c}}^{\prime}\left(\frac{1}{2}\right)^{\varLambda}. $ | (18) |
根据总应力法可以计算极限单位端阻力
| $ \tau_{\mathrm{bu}}=N_{\mathrm{c}} S_{\mathrm{utc}}. $ | (19) |
式中Nc为端阻力系数,黏土中一般取9.0[19].
通过式(9)可得
| $ B_{\mathrm{b}}=\frac{2^{\varLambda+1}}{N_{\mathrm{c}} M p_{\mathrm{c}}^{\prime}}. $ | (20) |
如图 2所示,根据双曲线型荷载传递函数和荷载传递法的迭代算法即可得到基桩在设计荷载作用下桩侧不同深度处土体单元的摩阻力τi, s和桩端阻力τb.如图 3所示,由于桩侧土单元的受力状态在剪切过程中近似于直剪试验,垂直向有效应力σ′i, z、径向有效应力σ′i, r、环向有效应力σ′i, θ在剪切过程中基本不发生改变[13].基于上述方法求得的τi, s和式(7)中三向有效应力的解答,可将桩侧土的应力状态表达为
| $ \boldsymbol{\sigma}_{\mathrm{s}}=\left(\begin{array}{ccc} \sigma_{i, \mathrm{z}}^{\prime} & {\tau}_{i, \mathrm{~s}} & 0 \\ \boldsymbol{\tau}_{i, \mathrm{~s}} & {\sigma}_{i, \mathrm{r}}^{\prime} & 0 \\ 0 & 0 & {\sigma}_{i, \theta}^{\prime} \end{array}\right). $ | (21) |

|
图 2 桩-土荷载传递解析模型 Fig. 2 Analytical model for pile-soil load transfer |

|
图 3 加载时桩周土单元的应力状态 Fig. 3 Stress state of soil elements adjacent to pile shaft and pile base during loading |
基于上述求解,荷载传递法得到的端阻力等于桩端以下土单元的竖向压力,即τb=σ′b, z.如图 3所示,由于竖向加载,桩端下方土体近似处于三轴压缩状态,土单元竖向压力σ′b, z大于侧向压力σ′b, r,桩端土的应力状态可表示为
| $ \left\{\begin{array}{l} p_{\mathrm{b}}^{\prime}=\frac{\sigma_{\mathrm{b}, \mathrm{z}}^{\prime}+2 \sigma_{\mathrm{b}, \mathrm{r}}^{\prime}}{3} ,\\ q_{\mathrm{b}}=\sigma_{\mathrm{b}, \mathrm{z}}^{\prime}-\sigma_{\mathrm{b}, \mathrm{r}}^{\prime}. \end{array}\right. $ | (22) |
正常承载条件下土体尚未达到破坏,桩端土单元介于静止状态和被动破坏状态.因此,考虑到软黏土中桩端阻力占比较小,桩端土的侧压力近似取两种状态的平均值,即
| $ \sigma_{\mathrm{b}, \mathrm{r}}^{\prime}=\frac{K_{0}+K_{\mathrm{p}}}{2} \sigma_{\mathrm{b}, 2}^{\prime}. $ | (23) |
式中Kp=tan2(π/4+φ′/2),为被动土压力系数,其中φ′为有效内摩擦角.
1.4 流变效应解析Kelln等[20]基于临界状态下修正剑桥模型的理论,建立了土体比体积在等向压缩条件下的数学描述,结合相关联流动法则推导了流变模型的本构方程,直观地反映了流变对于土体结构特征的影响,且具有模型参数不随流变而改变的优点.
试验表明,土体在当前有效应力状态(p′-q)与对应的各向同性应力状态(p′=p′m, q=0)下的塑性体应变增量可以等效[21],因此,可将承载条件下的应力状态借助塑性势函数(屈服函数)g(p′, q, p′H)转化为等向压力状态,以便于模拟桩周土在该应力水平的黏塑性应变:
| $ {g\left( {{p^\prime },q,p_{\rm{H}}^\prime } \right) = \frac{{{q^2}}}{{{M^2}}} - {p^\prime }\left( {p_{\rm{H}}^\prime - {p^\prime }} \right) = 0,} $ | (24) |
| $ {\left\{ \begin{array}{l} p_{i,{\rm{m}}}^\prime = \frac{{q_i^2}}{{{M^2}p_i^\prime }} + p_i^\prime ,\\ p_{{\rm{b}},{\rm{m}}}^\prime = \frac{{q_{\rm{b}}^2}}{{{M^2}p_{\rm{b}}^\prime }} + p_{\rm{b}}^\prime . \end{array} \right.} $ | (25) |
式中:p′i, m和p′b, m分别为转换后桩侧土单元和桩端土单元的等效压力;p′H为硬化参数,通过屈服曲线和p′轴的交点表示;(p′i,qi)和(p′b,qb)分别为桩侧第i个土单元和桩端土的平均有效应力和偏应力,根据上述推导由式(21)和(23)确定.
桩周土的流变自沉桩结束后已开始,在初始固结过程中亦有流变现象发生,但是考虑到流变持续数年甚至永久,远大于桩周土初始固结所需的时间,本文着重研究长期承载力,初始固结阶段流变的影响可不计.因此,假设经过沉桩、初始固结和竖向加载,平均有效应力达到p′i, m时,桩周土流变开始进行,定义此时t=0(图 4中A点).在恒定的有效应力下,微观颗粒重排引起土体的体积压缩,发生黏塑性变形,其应变率可以表示为[20]
| $ \dot{\varepsilon}_{i, i j}^{\rm{vp}}=\frac{\frac{\psi_{i}}{v_{i}(t)\left(t_{0}+t\right)}}{\left[1+\frac{\psi_{i} \ln \left(\frac{t_{0}+t}{t_{0}}\right)}{v_{i, 0}-v_{i, {\rm{c s}}}}\right]^{2}} \frac{1}{\mid\frac{\partial g}{\partial p^{\prime}} \mid} \frac{\partial g}{\partial \sigma_{i j}^{\prime}}. $ | (26) |
式中:vi, 0和vi, cs分别为压力p′i, 0时对应的初始和临界状态的比体积;ψi为土体流变系数,对于正常固结土,ψi受应力水平影响不大,可由次固结系数换算得到;t0为土体主固结所需时间,对于滨海软黏土可取1 d;vi(t)为流变至t时刻土体的比体积,与土体当前有效应力p′i, m有关,由式(26)可得
| $ v_{i}(t)=v_{i, 0}-\lambda \ln \frac{p_{i, \mathrm{~m}}^{\prime}}{p_{i, 0}^{\prime}}-\frac{\psi_{i} \ln \left(\frac{t_{0}+t}{t_{0}}\right)}{1+\frac{\psi_{i}}{v_{i, 0}-v_{i, \mathrm{cs}}} \ln \left(\frac{t_{0}+t}{t_{0}}\right)} . $ | (27) |
该模型定义土体的屈服面扩张只与黏塑性体应变有关,其硬化法则可表示为
| $ \delta p_{\mathrm{H}}^{\prime}=\frac{v(t) p_{\mathrm{H}}^{\prime}}{\lambda-\kappa} \delta \varepsilon_{\mathrm{p}}^{\mathrm{vp}}. $ | (28) |
结合式(26)和(28)则有
| $ p_{i, \mathrm{H}}^{\prime}(t)=\exp \left(\frac{v_{i, \mathrm{cs}}-v_{i}(t)-\kappa \ln p_{i, \mathrm{~m}}^{\prime}+\lambda \ln p_{i, 0}^{\prime}}{\lambda-\kappa}\right) . $ | (29) |
通过比较当前的屈服面轨迹p′H和应力水平p′m对应的塑性势面的大小,可确定屈服的临界状态.如图 4所示,当前应力状态位于屈服轨迹以外时(屈服轨迹A、B),黏塑性变形随时间发展,屈服轨迹随之扩张以适应压缩后的体积状态,直至屈服轨迹与当前应力状态重合(屈服轨迹C),流变停止发展,此时的应力-应变响应为纯弹性.

|
图 4 屈服轨迹扩张示意 Fig. 4 Schematic diagram of expansion of yield locus |
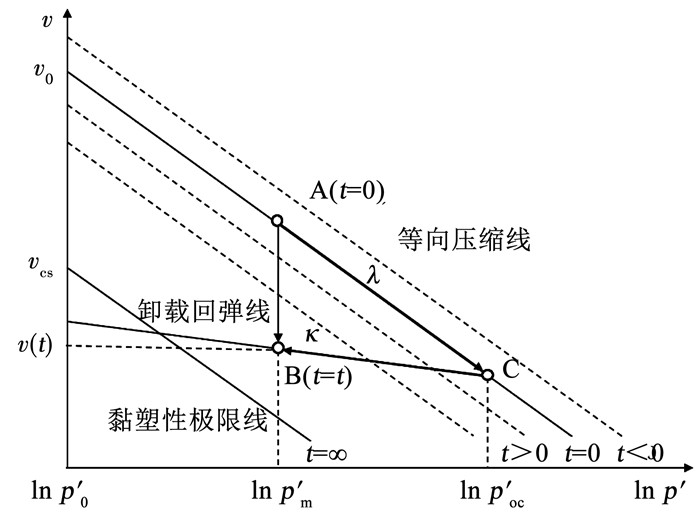
图 5绘制了承载状态下桩周土比体积随时间的变化.在有效应力恒定的条件下,黏塑性应变不断累积(图 5中直线AB),桩周土因体积压密而形成更加稳固的结构.而经过短暂加载后再卸载的超固结土体(图 5中折线ACB),由于塑性变形未随卸载而恢复,也能达到相同的比体积.因此,桩周土流变引起的强化可看作一种拟似超固结效应.
|
图 5 拟似超固结效应示意 Fig. 5 Schematic diagram of quasi-overconsolidation effect |
桩周土经加压再卸载后土体的比体积与平均有效应力的关系可以表示为
| $ v_{i}=v_{i, 0}-\lambda \frac{\ln p_{i, \mathrm{oc}}^{\prime}}{\ln p_{i, 0}^{\prime}}+\kappa \ln \left(\frac{p_{i, \mathrm{oc}}^{\prime}}{p_{i}^{\prime}}\right). $ | (30) |
式中:p′i, oc为各向等压条件下拟似先期固结压力.令式(30)中p′i=p′i, m,vi=vi(t),则初始固结完成后任一时刻拟似先期固结压力可以表示为
| $ p_{i, \mathrm{oc}}^{\prime}(t)=\exp \left(\frac{v_{i, 0}-v_{i}(t)-\kappa \ln p_{i, \mathrm{~m}}^{\prime}+\lambda \ln p_{i, 0}^{\prime}}{\lambda-\kappa}\right) . $ | (31) |
土体在流变过程中有效应力保持不变,拟似先期固结压力随流变发展而逐渐增长,则拟似超固结比可定义为
| $ R_{\mathrm{QOC}i}(t)=\frac{p_{i, \mathrm{oc}}^{\prime}(t)}{p_{i, \mathrm{~m}}^{\prime}}. $ | (32) |
将式(27)、(31)代入式(32)中,当t=0时,可得RQOCi=1,即流变尚未开始时,先期固结压力等于当前应力,认为土体处于正常固结状态,此后随流变的发展,RQOCi>1,说明土体处于拟似超固结状态,且拟似超固结比随时间增大.当时间接近无穷大时,式(26)中黏塑性应变率降至极小,屈服轨迹同塑性势轨迹几乎重合,流变基本停止.
基于上述分析,结合临界状态理论对于土体强度的定义[14],可将桩周任意计算深度处的土体在流变阶段任意时刻的三轴不排水强度表示为
| $ S_{i, \mathrm{utc}}(t)=\frac{1}{2} M p_{i, \mathrm{~m}}^{\prime}\left(\frac{R_{\mathrm{QOC}i}(t)}{2}\right)^{\varLambda}. $ | (33) |
将式(33)代入式(15)中,可得极限单位摩阻力随时间的变化,即
| $ \tau_{i, \mathrm{su}}(t)=\frac{3 \sqrt{3} \sin \varphi_{0} \cos \varphi^{\prime} p_{i, \mathrm{~m}}^{\prime}}{4 \cos \psi_{\mathrm{f}} \sqrt{2+\sin ^{2} \varphi_{0}}}\left(\frac{R_{\mathrm{QOC}i}(t)}{2}\right)^{\varLambda}. $ | (34) |
极限端阻力随时间的变化可通过总应力法计算,将式(32)代入式(19)得
| $ \tau_{\mathrm{bu}}(t)=\frac{N_{\mathrm{c}} M p_{\mathrm{b}, \mathrm{m}}^{\prime}}{2}\left(\frac{R_{\mathrm{QOCb}}(t)}{2}\right)^{\varLambda}. $ | (35) |
桩基的极限承载力由桩侧摩阻力和桩端阻力两部分构成,可以表示为
| $ Q_{\mathrm{u}}(t)=\sum\limits_{i=1}^{n} \tau_{i, \mathrm{su}}(t) U_{\mathrm{p}} L_{i}+\tau_{\mathrm{bu}}(t) A_{\mathrm{p}}. $ | (36) |
式中Up和Ap分别为桩基截面的周长和桩端面积,Li为荷载传递法中第i段桩长.
上式解答考虑了天然软黏土地层中静压沉桩、初始固结、桩基加载以及次固结流变过程中桩周土的应力状态和强度发展,可以较为合理地预测静压桩的长期承载力.
3 验证与分析 3.1 现场试验验证为验证本文理论预测方法的合理性和有效性,将饱和黏土地层中静载试验结果与预测值进行对比.试验场地位于上海市浦东新区周浦镇,该地属于滨海平原地貌,土层分布情况及土体参数见表 1.
| 表 1 场次土层特性 Tab. 1 Properties of soil strata at test site |
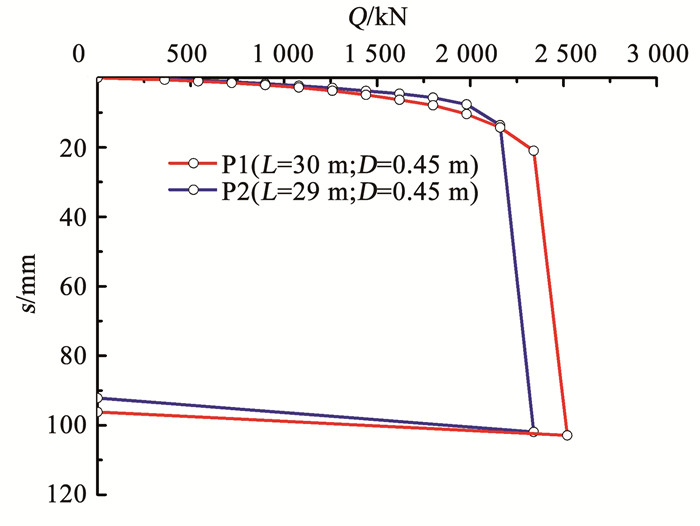
场地内原有建筑拆除后留有大量旧桩,试验分别测试了两根服役约29.4 a的静压桩,其中一根入土深度30 m,另一根入土深度29 m,两根桩桩径均为0.45 m.试验采用慢速维持荷载法测试其承载力,当桩顶在某一级荷载作用下沉降量大于前一级荷载作用下沉降量的5倍且桩顶总沉降量超过40 mm时终止加载,并取发生明显陡降的起始点对应荷载值为单桩极限承载力,试验所得荷载-沉降曲线如图 6所示.由于原建筑项目距今时间久远,该场地内旧桩短期承载力的数据缺失.考虑到本文旨在研究静压单桩的长期承载力,下文仅通过服役29.4 a后的试桩数据对上述理论方法进行对比验证.
|
图 6 试桩荷载-沉降曲线 Fig. 6 Load-settlement curves of test piles |
根据上海软土地层的固结特性,取超固结比ROC为1.1,侧压力系数K0为0.55,假定v′为0.35,根据上海场地土的实测变形指标[22],正常固结黏土λ/κ介于4.8~6.9,取平均值为5.8.Mesri等[23]指出,大部分无机软黏土次固结系数和压缩指数的比介于0.03~0.05,将其换算至v-ln p′平面,取平均值ψ=0.04λ.同时,根据桩身混凝土强度等级,取桩体弹性模量为40 GPa.为保证计算精度,将桩身划分为300个微段并按照上述理论方法编写MATLAB程序计算静压桩极限承载力随时间的变化规律,理论预测结果同现场测试结果的对比见图 7.可以看出,本文理论解析方法预测得出的极限承载力与实测值基本吻合,故本文提出的理论解析方法可以较为合理地预测软黏土中静压桩的长期承载力.从图 7还可以观察到,流变进行的前期承载力增长较快,尽管后期的趋势逐渐平缓,仍以较低的速度发展,难以达到稳定状态,这也符合软黏土流变的相关试验结论[1].

|
图 7 不同时刻长期承载力实测值与预测值对比 Fig. 7 Comparison between predicted and measured values of long-term bearing capacity at different time points |
从以上理论解析过程得知,对于静压桩,其承载力随时间的发展与λ、κ、ψ等参数密切相关,这种变化可以通过拟似超固结比的增长来模拟.假设表 2中静压桩P1位于均一的软黏土地层中,土体参数参照表 1中第④层土,其中不同深度处的土体初始比体积可通过下式计算
| $ \begin{array}{l} {v_0} = {v_{{\rm{cs}}}} + (\lambda - \kappa )\ln 2 - \lambda \ln \left[ {p_0^\prime {R_{{\rm{OC}}}}\left( {1 + \frac{{p_0^{\prime 2}}}{{{M^2}q_0^2}}} \right)} \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \kappa \ln \left[ {{R_{{\rm{OC}}}}\left( {1 + \frac{{p_0^{\prime 2}}}{{{M^2}q_0^2}}} \right)} \right]. \end{array} $ | (37) |
在此基础上,研究桩侧极限摩阻力、桩周土拟似超固结比随各深度、时间、土体参数κ和ψ的变化规律以及长期时效性的作用机理.
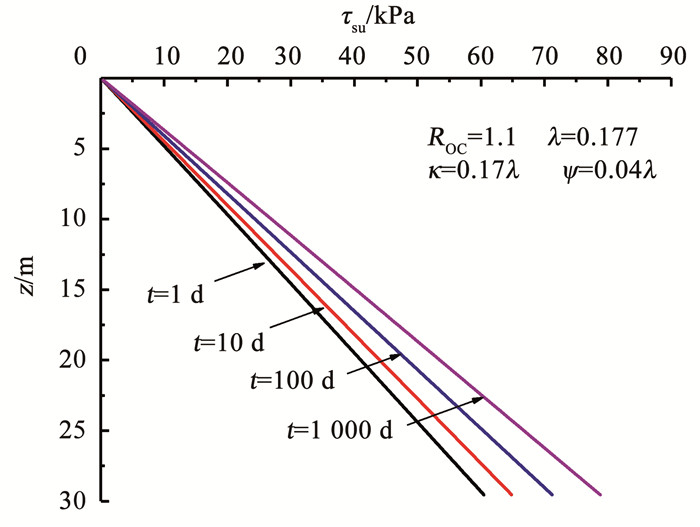
图 8给出了单桩在不同的流变时间下,桩侧极限摩阻力随深度的变化.值得注意的是,在次固结阶段的不同时刻,桩顶附近桩身发挥的摩阻力变化极小,说明流变效应引起单桩承载力的增长主要来自下部桩身摩阻力的增长.
|
图 8 不同时刻极限侧阻力随深度的变化 Fig. 8 Variation of ultimate shaft resistance with depth at different time points |
图 9为不同流变系数的土体中桩周土拟似超固结比随时间的变化.受式(26)控制,拟似超固结比在流变开始阶段增长迅速,但增长的速率逐渐降低,2 000 d后仍以较低的速度发展,但其对于单桩极限承载力的贡献可忽略不计.此外,流变系数ψ越大的土层,拟似超固结比增长越快,达到稳定所需的时间越短,且增长幅度越大.因此,ψ对软黏土中静压桩承载力的影响十分显著.

|
图 9 不同流变系数土层中拟似超固结比随时间的变化 Fig. 9 Variation of quasi-overconsolidation ratio with time under different creep indices |
图 10为不同回弹系数κ的土体中桩周土拟似超固结比随时间的变化.可以看出,经历相同时间后,随着回弹系数κ的增大,拟似超固结比增长量越大,但较比流变系数ψ,κ对于流变后桩周土强度的影响较微弱.

|
图 10 不同回弹系数土层中拟似超固结比随时间的变化 Fig. 10 Variation of quasi-overconsolidation ratio with time under different swelling indices |
1) 在沉桩效应、初始固结、竖向加载基础上,考虑软黏土流变效应,提出了便于实际应用的静压桩长期承载力的理论计算方法.该方法合理分析了旧桩服役历史中各阶段桩周土应力状态和强度特性的演化,与旧桩承载机制较为相符.
2) 随着流变的进行,桩周土孔隙比降低,强度逐渐提高,桩身下部摩阻力的增长是静压桩承载力长期时效性的主要原因.
3) 静压桩承载力在流变初期迅速增加,随后承载力随时间增长速率减缓,流变系数ψ和回弹系数κ对于承载力的发展有一定程度的影响.
| [1] |
尹振宇, 朱启银, 朱俊高. 软黏土蠕变特性试验研究: 回顾与发展[J]. 岩土力学, 2013, 34(增刊2): 1. YIN Zhenyu, ZHU Qiyin, ZHU Jungao. Experimental investigation on creep behavior of soft clays: Review and development[J]. Rock and Soil Mechanics, 2013, 34(S2): 1. DOI:10.16285/j.rsm.2013.s2.001 |
| [2] |
刘时鹏, 施建勇, 张金水, 等. 基于桩周土体固结的静压桩承载力时效性研究[J]. 中南大学学报(自然科学版), 2016, 47(10): 3454. LIU Shipeng, SHI Jianyong, ZHANG Jinshui, et al. Study on time effect of bearing capacity of jacked pile based on soil consolidation[J]. Journal of Central South University (Science and Technology), 2016, 47(10): 3454. DOI:10.11817/j.issn.1672-7207.2016.10.023 |
| [3] |
KARLSRUD K, MAHAN A. Evidence of long term ageing effects on axial capacity of piles in soft clay[C]//Proceedings of Art of Foundation Engineering Practice Congress 2010. West Palm Beach: American Society of Civil Engineers, 2010: 325. DOI: 10.1061/41093(372)13
|
| [4] |
HAQUE M N, ABU-FARSAKH M Y, CHEN Qiming, et al. Case study on instrumenting and testing full-scale test piles for evaluating setup phenomenon[J]. Transportation Research Record: Journal of the Transportation Research Board, 2014, 2462(1): 37. DOI:10.3141/2462-05 |
| [5] |
SKOV R, DENVER H. Time-dependence of bearing capacity of piles[C]//Proceedings of 3rd International Conference on the Application of Stress-Wave Theory to Piles. Ottawa: Bi-Tech Publisher, 1988: 879
|
| [6] |
DOHERTY P, GAVIN K. Pile aging in cohesive soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(9): 1620. DOI:10.1061/(ASCE)GT.1943-5606.0000884 |
| [7] |
胡琦, 蒋军, 严细水, 等. 回归法分析预应力管桩单桩极限承载力时效性[J]. 哈尔滨工业大学学报, 2006, 38(4): 602. HU Qi, JIANG Jun, YAN Xishui, et al. Regression analysis of the time effect of ultimate bearing capability of single reinforced pile[J]. Journal of Harbin Institute of Technology, 2006, 38(4): 602. DOI:10.3321/j.issn:0367-6234.2006.04.029 |
| [8] |
张继红, 顾国荣, 陈晖. 上海地区预制桩承载力时间效应的统计分析与研究[J]. 土木工程学报, 2002, 35(4): 98. ZHANG Jihong, GU Guorong, CHEN Hui. Statistical study of time effect on bearing capacity of prefabricated piles in Shanghai region[J]. China Civil Engineering Journal, 2002, 35(4): 98. DOI:10.3321/j.issn:1000-131x.2002.04.018 |
| [9] |
KARLSSON M, YANNIE J, DIJKSTRA J. Modeling aging of displacement piles in natural soft clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(10): 04019070. DOI:10.1061/(ASCE)GT.1943-5606.0002110 |
| [10] |
LI Lin, LI Jingpei, SUN Dean, et al. Semi-analytical approach for time-dependent load-settlement response of a jacked pile in clay strata[J]. Canadian Geotechnical Journal, 2017, 54(12): 1682. DOI:10.1139/cgj-2016-0561 |
| [11] |
LI Lin, LI Jingpei, SUN Dean. Anisotropically elasto-plastic solution to undrained cylindrical cavity expansion in K0-consolidated clay[J]. Computers and Geotechnics, 2016, 73: 83. DOI:10.1016/j.compgeo.2015.11.022 |
| [12] |
RANDOLPH M F. Science and empiricism in pile foundation design[J]. Géotechnique, 2003, 53(10): 847. DOI:10.1680/geot.2003.53.10.847 |
| [13] |
RANDOLPH M F, WROTH C P. Application of the failure state in undrained simple shear to the shaft capacity of driven piles[J]. Géotechnique, 1981, 31(1): 143. DOI:10.1680/geot.1981.31.1.143 |
| [14] |
WOOD D M. Soil behaviour and critical state soil mechanics[M]. Cambridge: Cambridge University Press, 1990.
|
| [15] |
ZHANG Qianqing, ZHANG Zhongmiao. Simplified calculation approach for settlement of single pile and pile groups[J]. Journal of Computing in Civil Engineering, 2012, 26(6): 750. DOI:10.1061/(ASCE)CP.1943-5487.0000167 |
| [16] |
李镜培, 陈浩华, 李林, 等. 楔形单桩与群桩非线性荷载-沉降曲线计算方法[J]. 哈尔滨工业大学学报, 2017, 49(12): 102. LI Jingpei, CHEN Haohua, LI Lin, et al. A calculation approach for nonlinear load-settlement curve of single tapered pile and tapered pile group[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 102. DOI:10.11918/j.issn.0367-6234.201702001 |
| [17] |
RANDOLPH M F, WROTH C P. An analysis of the vertical deformation of pile groups[J]. Géotechnique, 1979, 29(4): 423. DOI:10.1680/geot.1979.29.4.423 |
| [18] |
LI Lin, LI Jingpei, SUN Dean, et al. Analysis of time-dependent bearing capacity of a driven pile in clayey soils by total stress method[J]. International Journal of Geomechanics, 2017, 17(7): 04016156. DOI:10.1061/(ASCE)GM.1943-5622.0000860 |
| [19] |
SALDIVAR E E, JARDINE R J. Application of an effective stress design method to concrete piles driven in Mexico City clay[J]. Canadian Geotechnical Journal, 2005, 42(6): 1495. DOI:10.1139/t05-062 |
| [20] |
KELLN C, SHARMA J, HUGHES D, et al. An improved elastic-viscoplastic soil model[J]. Canadian Geotechnical Journal, 2008, 45(10): 1356. DOI:10.1139/t08-057 |
| [21] |
TAVENAS F, LEROUEIL S, LA ROCHELLE P, et al. Creep behaviour of an undisturbed lightly overconsolidated clay[J]. Canadian Geotechnical Journal, 1978, 15(3): 402. DOI:10.1139/t78-037 |
| [22] |
何平, 王卫东, 徐中华. 上海黏土压缩指数和回弹指数经验关系[J]. 岩土力学, 2018, 39(10): 3773. HE Ping, WANG Weidong, XU Zhonghua. Empirical correlations of compression index and swelling index for Shanghai clay[J]. Rock and Soil Mechanics, 2018, 39(10): 3773. DOI:10.16285/j.rsm.2018.0231 |
| [23] |
MESRI G, CASTRO A. Cα/Cc concept and K0 during secondary compression[J]. Journal of Geotechnical Engineering, 1987, 113(3): 230. DOI:10.1061/(ASCE)0733-9410(1987)113:3(230) |
 2021, Vol. 53
2021, Vol. 53


