锁相环(Phase locked loop, PLL)是目前射频接收机中频率综合器的主要结构形式,其基于参考时钟产生高精度、低相位噪声的输出时钟信号.参考时钟的频率及PLL的分频比决定了输出时钟信号的频率.通过提高参考时钟频率,降低PLL的分频比可以降低PLL输出信号的带内噪声和小数分频量化噪声.
在PLL系统输入时钟频率难以提高的应用场景中,文献[1-4]加入参考时钟倍频器(Reference frequency doubler, RFD)对PLL输入参考时钟进行频率倍增,有效降低了PLL的带内噪声和量化噪声.然而,这些倍频器主要采用异或门(XOR)结构,若输入信号的占空比偏离50%,输出二倍频信号的频率稳定性会降低,以该二倍频信号为参考时钟会恶化PLL的相位噪声,增大输出信号的杂散.因此需要在RFD中对输入时钟占空比进行校准.传统的占空比校准方式分为数字校准和模拟校准两种.文献[5]的比较显示:数字校准精度受延时长度限制,且对工艺角、电压和温度(Process corner, voltage and temperature, PVT)变化敏感,对杂散的抑制有限.模拟占空比校准方式虽然可以实现更高的校准精度,但其占空比校准范围通常较小.
本文提出了一种集成数模混合占空比校准的参考时钟倍频器对PLL的噪声和杂散性能进行改善.在占空比校准电路中通过对数字边沿调整技术扩大了占空比校准范围,采用模拟占空比校准环路提高占空比校准精度,并通过控制算法协调两种占空比校准电路的工作流程.最后通过仿真对占空比校准的范围与精度进行验证,并通过测试对倍频器带来的PLL相位噪声改善和由占空比校准带来的的杂散性能优化进行验证.
1 具有RFD的PLL系统特性分析 1.1 具有RFD的PLL系统具有RFD的PLL系统如图 1所示,图中PLL结构中包括鉴频鉴相器(Phase/frequency detector,PFD)、电荷泵(Charge pump,CP)、环路滤波器(Loop filter,LF)、压控振荡器(Voltage controlled oscillator,VCO)、分频器(divider)和ΔΣ调制器(Delta sigma modulator,DSM).RFD对系统输入时钟进行倍频,产生稳定的两倍频时钟,并将其作为参考时钟输入PLL.

|
图 1 具有RFD的PLL系统框图 Fig. 1 Structure of a PLL system with an RFD |
对于PLL,使用RFD对输入时钟倍频可以改善其带内噪声和小数分频量化噪声.PLL的带内噪声主要由输入参考时钟、电荷泵和分频器贡献.由于这3个模块的等效输出噪声均正比于PLL分频比的平方,参考时钟频率增大一倍可以使带内噪声降低约6 dB.ΔΣ调制器具有对噪声的高通整形特性,其量化噪声主要位于环路带宽外.对于L阶的多级噪声整形ΔΣ调制器, 其在载波附近的噪声与参考时钟频率的2L-1次幂成反比,那么使用参考时钟倍频器会使量化噪声减小到原来的1/22L-1.
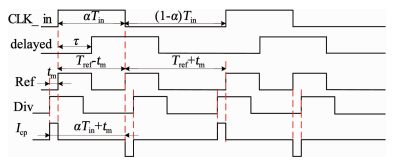
1.2 RFD非理想特性引入的杂散异或门倍频器通过将输入时钟与其延时信号异或得到二倍频信号.图 2为具有RFD的PLL系统在环路锁定时,输入时钟(CLK_in)、延时信号(delayed)、参考时钟(Ref)、PLL分频时钟(Div)与电荷泵电流(Icp)的时域波形.
|
图 2 RFD信号及其在PLL锁定时引起的周期电流脉冲 Fig. 2 Signals in RFD and generated periodic current pulse when PLL locks |
图中Tin为外部输入时钟周期,Tref是PLL的参考时钟周期,为Tin的1/2,α为输入时钟占空比,τ为异或门倍频器中的延时长度,tm为PLL锁定时参考时钟与分频时钟的固定边沿差.其中tm满足:
| $ {t_{\rm{m}}} = \frac{{1 - 2\alpha }}{4}{T_{{\rm{in}}}}. $ | (1) |
当α不为50%时,倍频器输出在时域上表现为每两个相邻周期的长度不同.与文献[6-7]中参考杂散的产生原因与表现形式相似,倍频后的参考时钟进入PFD/CP后,在环路稳定时会产生周期稳定的脉冲式电荷泵输出电流.
由输入时钟占空比误差导致的失配电流是一个周期性的信号,其周期为2Tref,所产生的控制电压会导致VCO的输出具有其谐波分量,根据文献[8]中VCO的数学模型可以得到VCO的输出电压为
| $ \begin{array}{l} {V_{{\rm{out}}}}\left( t \right) \approx {V_0}\left[ {{\rm{cos}}{\omega _0}t - \frac{{\Delta \varphi }}{2}{\rm{cos}}\left( {{\omega _0} - \frac{{{\omega _{{\rm{ref}}}}}}{2}} \right)t + } \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\Delta \varphi }}{2}{\rm{cos}}\left( {{\omega _0} + \frac{{{\omega _{{\rm{ref}}}}}}{2}} \right)t} \right]. \end{array} $ | (2) |
式中: V0为VCO摆幅; ω0为VCO谐振角频率; ωref为参考时钟角频率; Δφ为由电荷泵失配电流引起的VCO相位偏移.从式(2)中可以看到,由占空比偏离50%产生的杂散位于f0±fref/2处.类比文献[7]中对PLL参考杂散的推导,由占空比失准引起的杂散功率与边沿时间差tm的关系如下:
| $ \begin{array}{l} {P_{{\rm{spur}}}} \approx 20{\rm{log}}\left[ {\frac{{{f_{{\rm{BW}}}}}}{{{f_{{\rm{ref}}}}}} \cdot N \cdot \frac{{\left( {2{\rm{ \mathsf{ π} }}} \right)}}{{\sqrt 2 }} \cdot \frac{{{T_{{\rm{ref}}}} - {t_{\rm{m}}}}}{{2{T_{{\rm{ref}}}}}} \cdot \frac{{{t_{\rm{m}}}}}{{2{T_{{\rm{ref}}}}}}} \right] - \\ \;\;\;\;\;\;\;\;\;20{\rm{log}}\left( {\frac{{{f_{{\rm{ref}}}}}}{{{f_{{\rm{P}}1}}}}} \right). \end{array} $ | (3) |
式中:fBW为PLL的环路带宽; N为PLL的分频比; fP1为PLL环路滤波器的首个带外极点频率.进一步可以得到杂散功率与输入时钟占空比α的关系:
| $ {P_{{\rm{spur}}}} \approx 20{\rm{log}}\left[ {\frac{{{f_{{\rm{BW}}}}}}{{{f_{{\rm{ref}}}}}} \cdot N \cdot \frac{{{{\left( {2{\rm{ \mathsf{ π} }}} \right)}^2}}}{{\sqrt 2 }} \cdot \frac{{\left( {1 - 4{\alpha ^2}} \right)}}{{16}}} \right] - 20{\rm{log}}\left( {\frac{{{f_{{\rm{ref}}}}}}{{{f_{{\rm{P}}1}}}}} \right). $ | (4) |
式(4)可以发现,当输入时钟信号占空比α距50%越远时,引起的杂散功率越大.
假设倍频器输入信号频率为100 MHz,占空比为49%,N取40,fBW为800 kHz,环路滤波器的首个带外极点fP1位于2 MHz,此时tm为0.05 ns,则由占空比失准在距载波100 MHz频偏处引入的杂散约为-66.98 dBc.需要通过高精度的占空比校准消除或降低该杂散.
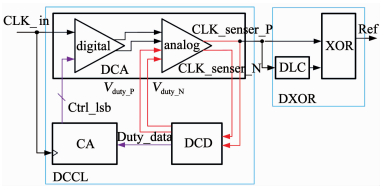
2 基于数模混合占空比校准的RFD架构设计 2.1 RFD架构设计本文提出的基于数模混合占空比校准的RFD主要包括一个延时异或单元(Delayed exclusive OR,DXOR)和一个占空比校准环路(Duty cycle calibration loop,DCCL),如图 3所示.其中DXOR对输入时钟信号进行倍频,DCCL用于对输入信号的占空比进行校准,以降低在距离PLL输出载波fref/2频偏处的杂散.
|
图 3 RFD架构框图 Fig. 3 Structure of RFD |
在DXOR中,校准后的时钟信号经延时器延时(Delay circuit, DLC)后,和原信号一同通过异或门(XOR)得到二倍频信号. DXOR采用文献[9]中的传统结构,如图 4所示.在该结构中,延时产生的相移只要处于0°和180°之间,异或门即可产生稳定的二倍频信号.

|
图 4 延时异或单元结构 Fig. 4 Structure of DXOR |
本文提出的DCCL利用数字边沿调整和模拟校准环路进行占空比校准.其主要结构包含占空比检测器(Duty cycle detector,DCD)、占空比调节器(Duty cycle adjuster, DCA)及其控制算法电路(Controlling algorithm,CA).其中DCD作为DCCL的核心,参与数字边沿调整和模拟占空比校准两个过程.DCD根据输入信号产生指示占空比与50%关系的数字信号Duty_data,并将输入信号的占空比误差转换为模拟电压.在进行数字边沿调整时,控制算法电路根据Duty_data通过DCA数字部分对输入信号的占空比进行粗调; 进行模拟占空比校准时,DCA模拟部分则通过与DCD形成的模拟校准环路进行高精度的占空比校准.
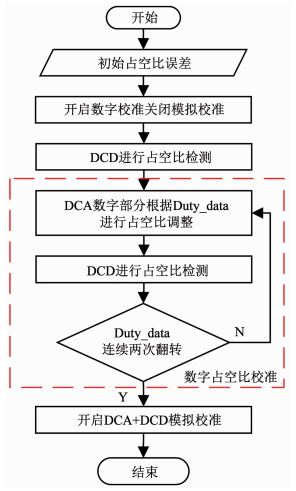
2.2 控制算法与流程控制算法电路主要用于占空比校准中数模电路的工作流程控制和数字校准锁定的判断.其控制流程如图 5所示.
|
图 5 占空比校准流程图 Fig. 5 Flowchart of duty cycle calibration |
系统启动后输入时钟进入RFD,此时首先关闭模拟校准以防止其对数字校准完成的判断造成影响.DCD对输入信号的初始占空比进行检测,得到指示信号Duty_data.然后启动数字占空比校准,控制算法根据Duty_data控制DCA数字部分调整信号边沿,然后重新比较并更新Duty_data,重复调整和比较的过程直至数字校准完成.完成后启动模拟校准,通过DCA模拟部分与DCD构成的模拟环路进行精度更高的校准.至此系统执行过程结束.其中数字校准的完成通过Duty_data的翻转情况判断.若Duty_data连续两次在0和1之间翻转则说明此时的占空比误差已小于最小调节步进,数字校准完成.
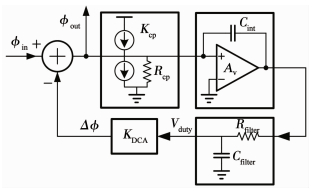
2.3 模拟占空比校准环路分析所提出的倍频器占空比校准电路在数字粗调完成后通过DCCL中的模拟环路进行细调,以同时获得较大的校准范围和较高的校准精度.文献[10-13]通过对模拟占空比校准环路进行建模可以分析和设计其环路特性及校准精度.为方便分析,本文采用单端形式进行建模,如图 6所示,其中
|
图 6 占空比模拟校准环路模型 Fig. 6 Model of analog part of DCCL |
| $ {\phi _{out}} = {\phi _{{\rm{in}}}} - {K_{{\rm{DCA}}}}\cdot{V_{{\rm{duty}}}}. $ | (5) |
式中:φin、φout分别为校准环路的输入和输出占空比误差; KDCA为DCA模拟部分输出占空比关于控制电压Vduty的斜率; Vduty为DCD的输出信号,其值为
| $ {V_{{\rm{duty}}}} = {\phi _{{\rm{out}}}}{K_{{\rm{CP}}}}{H_{{\rm{int}}}}\left( s \right){H_{{\rm{LPF}}}}\left( s \right) $ | (6) |
式中:KCP为电荷泵每周期的净输出电流关于φout的斜率; Hint(s)为积分器输入电流到输出电压的传递函数; HLPF(s)为低通滤波器的传递函数.设运算放大器的增益为Av,其中低频增益为A0,主极点角频率为ωA,则有:
| $ {H_{{\rm{int}}}}\left( s \right) = \frac{{{R_{{\rm{CP}}}}{A_{}}v}}{{1 + s{R_{{\rm{CP}}}}{C_{{\rm{int}}}}(1 + {A_{\rm{v}}})}}, $ | (7) |
| $ {A_v} = \frac{{{A_0}}}{{1 + s/{\omega _{\rm{A}}}}}, $ | (8) |
| $ {H_{{\rm{LPF}}}}\left( s \right) = \frac{1}{{1 + s/{\omega _{{\rm{LPF}}}}}} = \frac{1}{{1 + s{R_{{\rm{filter}}}}{C_{{\rm{filter}}}}}}, $ | (9) |
式中, ωLPF为一阶低通滤波器的极点角频率,由上述各式可以得到环路增益:
| $ \begin{array}{l} {H_{{\rm{loop}}}}\left( s \right) = {K_{{\rm{DCA}}}}{V_{{\rm{duty}}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{K_{{\rm{DCA}}}}{{\rm{K}}_{{\rm{CP}}}}{R_{{\rm{CP}}}}{A_0}}}{{1 + s({R_{{\rm{CP}}}}{C_{{\rm{int}}}}{A_0} + 1/{\omega _{\rm{A}}}) + {s^2}{R_{{\rm{CP}}}}{C_{{\rm{int}}}}/{\omega _{\rm{A}}}}}\cdot\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{1 + s/{\omega _{{\rm{LPF}}}}}}. \end{array} $ | (10) |
由于Hloop(s)第1项中积分器输出点的高频极点远高于系统频率,那么环路增益可以简化为
| $ {H_{{\rm{loop}}}}\left( s \right) \approx \frac{{{K_{{\rm{DCA}}}}{{\rm{K}}_{{\rm{CP}}}}{R_{{\rm{CP}}}}{A_0}}}{{\left( {1 + s{R_{{\rm{CP}}}}{C_{{\rm{int}}}}{A_0}} \right)\left( {1 + s/{\omega _{{\rm{LPF}}}}} \right)}}. $ | (11) |
来自积分器电容的密勒效应使得环路的主极点约为250 kHz,低通滤波器的极点约为50 MHz,距离主极点非常远,所以环路稳定性不受滤波器极点的影响.根据实际电路参数计算得到环路的闭环低频增益为36 dB,相位裕度约为90°,根据增益计算得到,占空比校准后输出占空比误差将降低为输入占空比误差的1.58%.
3 RFD电路设计 3.1 占空比检测器(DCD) 3.1.1 DCD电路结构作为DCCL的核心,DCD将输入信号的占空比误差转换为电压信号,进而配合DCA和控制算法一同对输入信号的占空比进行校准.
占空比检测器的电路结构如图 7所示,其中第1级电荷泵采用推挽输出的运放,将电压占空比转换为电荷泵输出电流的占空比,再利用积分器转换为电压信号.在一个时钟周期内,当CLK_senser_P> CLK_senser_N时,M2断开,M4将电流灌入C2.另外一路,为满足基尔霍夫电流定律,M1还需要从C1中抽取另外的0.5It,造成流经C1和C2的电流方向相反.当占空比偏离时,C1和C2产生不同的平均电荷积累量,从而得到与占空比相关的差分输出电压,经一阶低通滤波器滤波留下直流分量Vduty_P和Vduty_N,输出到比较器和DCA模拟部分.控制算法电路会根据比较器输出判断下一步的占空比调整方向.在这里需要在电阻R1、R2和电容C3、C4之间做噪声性能和面积的折中:当电阻较大时,可以有效减小电容的面积,但电阻会对Vduty贡献相当一部分噪声; 当电阻较小时,电容面积将扩大,但噪声性能将得到改善.

|
图 7 DCD结构框图 Fig. 7 Structure of DCD |
占空比校准环路的非理想效应主要来自两方面:电荷泵电流失配和比较器的失调电压.其中电荷泵的电流失配对占空比校准的精度有较为重要的影响.
1) 电荷泵电流失配.电荷泵电流失配是指由于版图不对称和电流镜电路中沟道长度调制等因素造成的电荷泵左右两路电流不匹配.对于输入管M1和M2,假设图 7的DCD中电荷泵的尾电流为It,输入管作为理想开关工作,由于两个输入管不会同时导通,所以每路N管在导通时总是流过全部的尾电流It,输入管的失配对校准结果的影响较小.对于P管电流源,假设M3和M4的电流分别为mIt和(1-m)It,输入信号占空比为α,当占空比校准完成后电荷泵输出电流在积分器中每周期积累的电荷量相等,即
| $ \begin{array}{l} m{I_{\rm{t}}}\cdot\alpha T - \left( {1 - m} \right){I_{\rm{t}}} \cdot \left( {1 - \alpha } \right)T = \\ \;\;\left( {1 - m} \right){I_{\rm{t}}} \cdot \left( {1 - \alpha } \right)T - m{I_{\rm{t}}} \cdot \alpha T, \end{array} $ | (12) |
化简后可得
| $ \alpha = 1 - m. $ | (13) |
所以,在只考虑电荷泵失配时,校准完成后输出信号的占空比误差等于电荷泵两路P管的电流误差.为了减小该失配带来的影响,在设计中采用了共源共栅结构和版图匹配技术来抑制由沟道长度调制和其他版图因素引起的失配.
2) 比较器失调电压.由于数字调节的锁定是由比较器的比较结果决定的,所以过大的比较器失调电压会影响数字占空比校准的精度.由于比较器和控制算法的时钟为输入时钟的256分频信号,所以比较器的失调电压只需小于DCA数字部分调节步长在一个时钟周期内累积的Vduty变化.仿真结果显示,在输入时钟为100 MHz时,比较器失调电压约为3 mV,而数字校准锁定时一个周期内Vduty的变化量超过20 mV,此时比较器的失调电压不会影响数字调节锁定的判断.
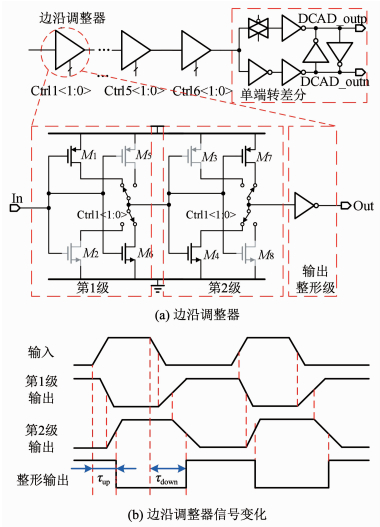
3.2 占空比调节器(DCA) 3.2.1 DCA数字部分本文采用的DCA数字部分及其边沿调整器如图 8(a)所示.
|
图 8 边沿调整器结构及其信号变化 Fig. 8 Structure of edge adjustor and its changes in signals |
文献[11-14]中采用多级反相器扩大调整范围的做法,所提出的DCA数字部分采用六级边沿调整器对信号边沿的延时差进行调整,进而调整输入方波的占空比,其调节前后波形变化如图 8(b)所示.每级边沿调整器的延时差均为前一级的两倍,便于算法使用二进制码进行调节程度的控制.
基于反相器结构,由快/慢速PMOS和快/慢速NMOS组成,其中M1~M4具有相同的宽长比W/L,速度较慢,M5~M8具有更大的宽长比W/L,速度更快.慢速PMOS可以将输入信号下降沿减慢为缓慢输出上升沿,慢速NMOS则可以将输入信号上升沿减慢为缓慢的输出下降沿.当输出信号进入后一级反相器时,不同的边沿速度在同一反相器阈值下即可转化为不同的延时.当前后两个反相器设置为相反的极性时,即可对不同的边沿产生延时差.两种边沿的延时差Δτ会造成信号的占空比缩小Δτ/T.图 8(a)中第1级设置为减缓输出上升沿,第2级为减缓输出下降沿,当输入信号进入后,两级反相器对输入信号的下降沿延时较高,而对输入信号上升沿的延时较低,增大了信号占空比.仿真结果显示,在六级边沿调整器对输入信号的延时差调整范围为±1 382 ps,调节步长约10.8 ps,对于100 MHz的输入时钟,其最大可调范围为50%±13.82%,最大调节误差为±0.11%.根据模拟占空比校准环路分析的推导,数模混合校准之后的理论占空比误差将低于0.001 8%.
3.2.2 DCA模拟部分当DCA数字部分完成校准后,占空比误差已经缩小到模拟部分校准范围内,此时固定数字校准码字,算法电路控制模拟校准环路启动进行精度更高的占空比校准.
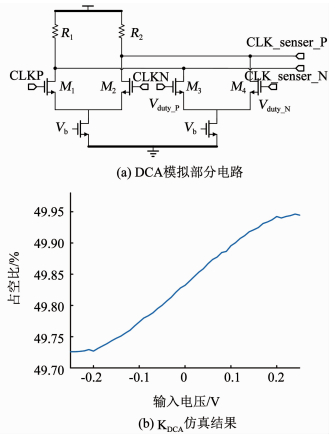
DCA模拟部分如图 9(a)所示.模拟占空比调节通过改变时钟缓冲器的差分输出直流偏置,即改变信号过零点调整占空比.对DCA模拟部分的校准斜率KDCA进行仿真,结果如图 9(b)所示,对于100 MHz输入信号,其KDCA约为0.57%/V.
|
图 9 DCA模拟部分及KDCA仿真结果 Fig. 9 Analog part of DCA and simulated KDCA |
对整个系统进行数模混合仿真,其中输入信号频率为100 MHz,占空比约为49.2%,RFD输出信号频率如图 10(a)所示,DCA输出信号占空比变化如图 10(b)所示.可以看到,DCA数字部分将占空比缩小至50.03%后,进入模拟校准过程,最终占空比均值稳定在50.002%附近,由于波动引起的最大占空比误差为0.007%.RFD的输出频率误差约为380×10-6.

|
图 10 倍频器输出频率误差及DCA输出占空比仿真结果 Fig. 10 Simulated frequency error of RFD output and duty cycle of DCA output |
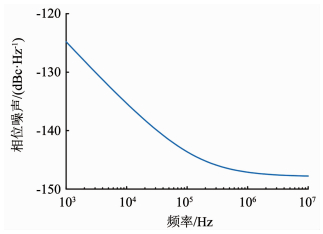
对倍频器输出的二倍频信号进行相位噪声仿真,结果如图 11所示,可以看到在参考时钟噪声贡献占比较高的带内部分,二倍频信号的相位噪声从1 kHz频偏处开始已低于125 dBc/Hz,远低于常规PLL的带内噪声,可以认为由RFD额外引入的相位噪声不会对PLL的输出相位噪声造成影响.
|
图 11 倍频器输出相位噪声仿真结果 Fig. 11 Simulated phase noise of RFD output |
在不同PVT环境下对电路进行仿真,得到DCA输出信号的最大占空比误差,结果见表 1.
| 表 1 不同PVT条件下的最大校准误差仿真结果 Tab. 1 Simulated maximum errors of calibration in different PVT conditions |
本文所述电路使用40 nm CMOS工艺进行了流片验证,芯片显微照片及版图如图 12所示,其中差分输入信号通过图中所示的管脚CLK_in_P和CLK_in_N输入RFD,经占空比校准和倍频后进入PLL.

|
图 12 倍频器显微照片及版图 Fig. 12 Microphotograph and layout of RFD |
将该倍频器的输出信号作为参考时钟输入PLL,并对该PLL的相位噪声及杂散进行测试,测试结果可以反映出倍频器对相位噪声和杂散的改善能力.测试采用的输入正弦信号频率为40 MHz.令PLL工作在小数分频模式,使ΔΣ调制器的量化噪声突显出来.当参考时钟倍频器被旁路时,PLL的分频比N设置为100,VCO振荡在4 GHz.参考时钟倍频器开启后,PLL参考时钟被倍频为80 MHz,分频比N降低为50,以保证相同的输出频率.PLL输出信号的相位噪声如图 13所示.其中使用倍频器后带内噪声最多下降约6.67 dB,ΔΣ调制器量化噪声最多下降约5.61 dB.

|
图 13 PLL相位噪声及量化噪声抑制测试结果 Fig. 13 Measured suppression of phase noise and quantization noise of PLL |
同时,在输入时钟频率为100 MHz时验证占空比校准对杂散的改善状况.PLL的输出频谱如图 14所示, 当输入时钟占空比偏离50%时,在距输出载波100 MHz处的杂散约为-66.59 dBc/Hz; 当输入时钟占空比得到校准后,距输出载波100 MHz处的杂散降低至-76.11 dBc/Hz.由校准带来的杂散抑制达到9.52 dB.

|
图 14 占空比校准前后杂散测试结果对比 Fig. 14 Measured spurs of PLL with or without DCC |
表 2为本文提出的倍频器与近年部分相关文献中相似电路的性能比较.在杂散性能上,所提出的RFD与PLL构成的系统在距PLL输出载波1/2参考频率偏移处和参考时钟频率偏移处的杂散性能均优于类似结构的论文.在占空比校准性能上,由于数模校准的结合,本文最大占空比校准误差理论值为0.001 8%,低于根据文献[4]中数字调节步长计算得到的最大误差.通过仿真验证,最大占空比误差远低于采用纯模拟和其他数模混合方式进行校准的文献.所提出的占空比校准范围为36.18%~63.82%,在高校准精度的前提下达到了符合应用需求的校准范围.
| 表 2 相似类型电路性能对比 Tab. 2 Comparison between similar circuits |
1) 本文提出了一种集成数模混合占空比校准环路的新型参考时钟倍频器,该倍频器通过数字边沿调整技术扩大了占空比校准的输入误差范围,通过模拟占空比校准环路提高了占空比校准的精度.两种校准技术通过算法控制协同工作,在扩大校准范围的同时提高了校准的精度.并通过仿真和流片测试进行了验证.
2) 仿真结果显示,数模混合占空比校准电路能够将占空比误差降低至0.007%,倍频器输出信号的频率误差能够降低至380×10-6.
3) 测试结果显示,通过所提出的参考时钟倍频器对锁相环输入时钟进行倍频,该倍频器能够使锁相环的带内噪声和小数分频量化噪声分别降低6.67 dB和5.61 dB.在该RFD与PLL组成的系统中进行输入时钟占空比校准,可以使由100 MHz输入时钟占空比误差引起的1/2参考频率偏移处的杂散降低9.52 dB.
| [1] |
SIRIBURANON T, LIU Haili, NAKATA K, et al. A 28-GHz fractional-N frequency synthesizer with reference and frequency doublers for 5G cellular[C]//Proceedings of the 41st European Solid-State Circuits Conference. Graz: IEEE, 2015: 76. DOI: 10.1109/ESSCIRC.2015.7313832
|
| [2] |
ELKHOLY A, COOMBS D, NANDWANA R K, et al. A 2.5-5.75-GHz ring-based injection-locked clock multiplier with background-calibrated reference frequency doubler[J]. IEEE Journal of Solid-State Circuits, 2019, 54(7): 2049. DOI: 10.1109/JSSC.2019.2904884
|
| [3] |
WU Wanghua, YAO C W, GODBOLE K, et al. A 28-nm 75-fsrms analog fractional-N sampling PLL with a highly linear DTC incorporating background DTC gain calibration and reference clock duty cycle correction[J]. IEEE Journal of Solid-State Circuits, 2019, 54(5): 125. DOI:10.1109/JSSC.2019.2899726 |
| [4] |
KIM H, KIM Y, KIM T, et al. A 2.4 GHz 1.5 mW digital MDLL using pulse-width comparator and double injection technique in 28 nm CMOS[C]//2016 IEEE International Solid-State Circuits Conference. San Francisco, CA: IEEE, 2016: 328. DOI: 10.1109/ISSCC.2016.7418040
|
| [5] |
RAGHAVAN L, WU Ting. Architectural comparison of analog and digital duty cycle corrector for high speed I/O link[C]//Proceedings of the 23rd International Conference on VLSI Design. Bangalore: IEEE, 2010: 270. DOI: 10.1109/VLSI.Design.2010.83
|
| [6] |
SHU Keliu, SANCHEZ-SINENCIO E. CMOS PLL synthesizers: Analysis and design[M]. 1st ed. Boston, MA: Springer, 2005: 164. DOI:10.1007/b102174
|
| [7] |
RHEE W. Multi-bit delta-sigma modulation technique for fractional-N frequency synthesizers[D]. Urbana, IL: University of Illinois at Urbana-Champaign, 2012
|
| [8] |
RAZAVI B. RF microelectronics[M]. 2nd ed. Upper Saddle River NJ: Prentice Hall, 2011: 206.
|
| [9] |
JACKSON B R, SAAVEDRA C E. An L-band CMOS frequency doubler using a time-delay technique[C]//Topical Meeting on Silicon Monolithic Integrated Circuits in RF Systems. San Diego, CA: IEEE, 2006: 131. DOI: 10.1109/SMIC.2005.1587925
|
| [10] |
CHENG K H, SU C W, CHANG K F. A high linearity, fast-locking pulsewidth control loop with digitally programmable duty cycle correction for wide range operation[J]. IEEE Journal of Solid-State Circuits, 2008, 43(2): 399. DOI:10.1109/JSSC.2007.914286 |
| [11] |
LIN Weiming, HUANG Hongyi. A low-jitter mutual-correlated pulsewidth control loop circuit[J]. IEEE Journal of Solid-State Circuits, 2004, 39(8): 1366. DOI:10.1109/JSSC.2004.831499 |
| [12] |
RAJA I, BANERJEE G, ZEIDAN M A, et al. A 0.1-3.5-GHz duty-cycle measurement and correction technique in 130-nm CMOS[J]. IEEE Transactions on Very Large Scale Integration Systems, 2016, 24(5): 1975. DOI:10.1109/TVLSI.2015.2478804 |
| [13] |
JAISWAL A, FANG Yuan, NAWAZ K, et al. A wide range programmable duty cycle corrector[C]//IEEE International System-on-chip Conference. Erlangen: IEEE, 2013: 192. DOI: 10.1109/SOCC.2013.6749686
|
| [14] |
YOON H, KIM J, PARK S, et al. A-31 dBc integrated-phase-noise 29 GHz fractional-N frequency synthesizer supporting multiple frequency bands for backward-compatible 5G using a frequency doubler and injection-locked frequency multipliers[C]//IEEE International Solid-State Circuits Conference. San Francisco, CA: IEEE, 2018: 366. DOI: 10.1109/SOCC.2013.6749686
|
| [15] |
QIU Yusong, ZENG Yun, ZHANG Feng. 1-5 GHz duty-cycle corrector circuit with wide correction range and high precision[J]. Electronics Letters, 2014, 50(11): 792. DOI:10.1049/el.2014.0170 |
| [16] |
HAN S, KIM J. Hybrid duty-cycle corrector circuit with dual feedback loop[J]. Electronics Letters, 2011, 47(24): 1311. DOI:10.1049/el.2011.2710 |
 2021, Vol. 53
2021, Vol. 53


