2. 空军工程大学 航空工程学院, 西安 710038
2. Aeronautics Engineering College, Air Force Engineering University, Xi'an 710038, China
UCAV空战机动决策是实现无人自主空战的关键技术之一[1],其目的是通过决策方法生成UCAV可执行的空战机动轨迹,实现由当前状态到空空导弹可发射状态的有效攻击占位,并最终实现导弹发射,完成整个空战回路.针对一对一空战条件下的机动决策问题,国内外学者进行了广泛的研究,取得了丰富的研究成果.常见的机动决策方法包括影响图方法、微分对策方法和矩阵对策方法[2]等,其中应用最广、工程上更易于实现的是矩阵对策方法,从决策过程来看,大部分矩阵对策方法又可以称作试探机动决策.所谓试探机动决策,是指在每一个决策节点,决策系统根据当前时刻敌我双方的相对态势,生成一系列可能作为决策结果备选项的机动动作,每一个机动备选项被称为一个试探机动[3].决策系统对执行每一个试探机动后的结果进行预测,并通过评价函数对预测后的敌我双方相对态势进行评价,其中对评价指标最有利的试探机动即为最终的决策结果.
针对试探机动决策问题,文献[4]提出并设计了7种基本操纵动作,空战双方基于决策评价函数,基于MAX-MIN方式从7种基本操纵动作库中选出最优的机动动作,作为下一时域的机动执行项; 在此基础上,文献[5]将飞行员的心理因素和人的生理限制考虑在内,构建了模糊控制逻辑,以生成更为合理的决策控制量; 文献[6]将7种基本操纵动作在空间内扩展到45种,在MAX-MIN机动决策方式的基础上基于统计学原理筛选出最佳的机动动作,以提高机动决策的鲁棒性.文献[7]设计了更为精细的试探机动策略,构建了729种机动备选项,通过机动试探的方式,选择最优的机动策略; 同时文献[7]基于贝叶斯推理,对当前态势下的空战态势进行评估,使决策因子的权重值自适应变化,这种方式可以生成更为连续变化的控制量,且通过态势评估使得空战结果朝向更有利于攻击占位的方向发展.
分析现有文献,其在模型选择时,均选用了简化的三自由度模型[4-7],难以保证所生成轨迹的合理性; 在决策过程中,往往使用简化的可发射区或攻击区模型[2],且缺乏对空空导弹攻击状态的有效评估,生成的决策机动轨迹难以保证导弹作战使用的科学性.为了提高空战决策及轨迹生成过程的真实性与可靠性,空战决策过程应紧紧围绕可靠的气动耦合模型和制导武器的作战使用性能实现,而基于制导武器作战使用性能的机动决策问题至今尚无公开文献涉及.基于这一角度,本文对试探机动决策问题进行了研究和探索,以期形成一个更为真实高效的UCAV自主空战机动决策系统.
1 试探机动决策系统的构建思路一个完整的UCAV试探机动决策系统[8]应包括机动策略库、机动决策评价函数、态势评估与决策权值判定逻辑三部分内容.首先将UCAV空战机动过程分割划分成彼此毗邻的离散的时间域; 在每个时间域内,基于所构建的机动决策评价函数和态势评估判定准则,根据当前态势下,UCAV与敌方相对状态信息,从机动动作库中优选出当前状态下UCAV应该采用的最优机动策略; 通过执行最优机动策略,完成该时域内的UCAV机动飞行.在每个时域内重复上述决策过程,直到构成空空导弹的发射条件,决策终止.所有时域内,UCAV所执行机动的叠加就是UCAV的最终飞行轨迹[9].
在试探机动策略库的构建过程中,最典型的是采用NASA学者提出的7种基本操纵动作[4],这种机动动作库构建方式采取极限操控的bang-bang控制的形式,不符合真实的空战机动实际, 且可供选择的机动空间过少,难以表征复杂的空战对抗过程; 虽然文献[6-7]通过更为精细的划分方式将该类机动动作库进行了扩充,但由于仍然采用简化的三自由度模型,不考虑UCAV推力大小及气动参数的变化,因而难以体现出UCAV真实的运动动力学特性.为此本文将构建包含有升力、阻力等气动力以及发动机实际推力的高耦合三自由度运动动力学模型,采用F-4战斗机的相关参数及气动数据进行UCAV试探决策系统的构建,以保证决策的高可靠性; 通过设计精细的试探决策控制量以保证机动策略的可执行性.其次,为充分体现空空导弹的作战使用实际,本文基于当前态势下空空导弹火控解算结果,根据空空导弹的战术使用性能和导弹可发射距离解算值构建机动决策评价函数; 基于当前态势下的空空导弹攻击状态实际进行态势评估,使决策因子的权值可以依据导弹攻击状态自适应变化,以实现UCAV最优机动占位和导弹战术使用性能的充分发挥.综上,本文构建的试探机动决策系统的逻辑构成如图 1所示.

|
图 1 试探机动决策系统的构建逻辑 Fig. 1 Construction logic of the trial maneuvering decision system |
UCAV采用包含气动耦合关系的三自由度运动动力学模型,控制量为u=[α, μ, δ]T,其中,α、μ、δ分别为攻角、航迹滚转角和油门设置; 状态量为X =[x, y, h, v, γ, ψ, m]T,其中:(x, y, h)为UCAV在惯性坐标系下的坐标,v为UCAV速度,γ、ψ、m分别为UCAV的航迹倾角、航迹偏角及UCAV质量; 后文为了使UCAV与目标机区分,分别用下标u和t进行表示,模型的参数定义如图 2所示.在忽略随机风场影响的条件下,模型可公式定义为
|
图 2 UCAV运动动力学模型参数示意图 Fig. 2 Schematic of UCAV kinematic model parameters |
| $ \left\{\begin{array}{l} \dot{x}=v \cos \gamma \cos \psi, \\ \dot{y}=v \cos \gamma \sin \psi, \\ \dot{h}=v \sin \gamma, \\ \dot{v}=\frac{T \cos \alpha-D}{m}-g \sin \gamma, \\ \dot{\gamma}=\frac{(L+T \sin \alpha) \cos \mu}{m v}-\frac{g}{v} \cos \gamma, \\ \dot{\psi}=\frac{(L+T \sin \alpha) \sin \mu}{m v \cos \gamma}, \\ \dot{m}=-c T, T=\delta T_{\max }\left(\bar{v}, h_{c}\right), \\ L=\frac{1}{2} \rho v^{2} S C_{L}, D=\frac{1}{2} \rho v^{2} S C_{D} . \end{array}\right. $ | (1) |
式中:g为重力加速度; T、D、L分别为发动机推力、空气阻力、升力; ρ为空气密度; S为UCAV参考截面积; CL, CD分别为升力系数和阻力系数; c为燃料消耗系数; Tmax为发动机最大推力.
文中UCAV平台均采用F-4战斗机的相关参数和气动数据[10-11].当α≤15°时,基于该机实际气动数据拟合得到UCAV升阻力系数计算公式为[10]
| $ \left\{\begin{array}{lll} C_{L}=(-0.043\ 4+0.136\ 9 \alpha) \sin \alpha+ \\ \ \ \ \ \ \ \ \ \ \ (0.131+3.082\ 5 \alpha) \cos \alpha, \\ C_{D}=\left(\begin{array}{lll} 0.043\ 4-0.136\ 9 \alpha) \cos \alpha+\end{array}\right. \\ \ \ \ \ \ \ \ \ \ \ (0.131+3.082\ 5 \alpha) \sin \alpha . \end{array}\right. $ | (2) |
基于F-4搭载的两台J79涡喷发动机相关数据[11],拟合出UCAV发动机最大可用推力计算公式为
| $ T_{\max }=\left[\begin{array}{c} 1 \\ \bar{v}_{u} \\ \bar{v}_{u}^{2} \\ \bar{v}_{u}^{3} \\ \bar{v}_{u}^{4} \end{array}\right]\left[\begin{array}{rrrrrr} 30.21 & -0.668 & -6.877 & 1.951 & -0.151\ 20 \\ -33.80 & 3.347 & 18.130 & -5.865 & 0.475\ 70 \\ 100.80 & -77.560 & 5.441 & 2.864 & -0.335\ 50 \\ -78.99 & 101.400 & -30.280 & 3.236 & -0.108\ 90 \\ 18.74 & -31.600 & 12.040 & -1.785 & 0.094\ 17 \end{array}\right]\left[\begin{array}{c} 1 \\ h_{c} \\ h_{c}^{2} \\ h_{c}^{3} \\ h_{c}^{4} \end{array}\right] . $ | (3) |
式中:v u为UCAV飞行马赫数; hc为UCAV的转换飞行高度,单位为10 000 ft,即3 048 m; Tmax的单位是1 000 lb,即4 436.26 N.
综上所述,该模型升力、阻力系数与攻角大小相互耦合; 最大推力与速度、高度大小相互耦合,可见该模型是一个高度耦合的模型.由于考虑了气动力、推力及UCAV质量变化,该模型相较于常用的三自由度模型[7],更加接近实际,因而具有更高的应用价值.同时,由于需要考虑大量的耦合关系,模型的控制过程也更为困难.为保证机动实施时的平台可飞行,应充分考虑UCAV飞行包线约束和状态安全性约束等实际约束,对于该问题,文献[12]有着详实的论述,本文不做进一步的展开.
2.2 UCAV试探机动控制量优化设计UCAV的机动控制过程是通过寻找当前状态下的最优控制量,使得决策评价函数的收益值最大.假设当前时域内UCAV的飞行控制量为uk=[αk, μk, δk]T,下一时域初始时刻的飞行控制量uk+1需要通过优化方法求得,控制量uk+1在该时域内保持恒定,且使得预测状态下,时域终止时刻UCAV具有最大的优势.为了减少优化过程的搜索空间,提高优化效率,以飞行控制量的变化率Δuk=[Δαk,Δμk,Δδk]T为优化对象[13],通过遍历试探的方法,在给定的梯度空间内寻找最优的控制量变化率Δ uk*=[Δαk*,Δμk*, Δδk*]T,使得终止时刻决策评价函数的收益值最大,则下一时域内的飞行控制量为uk+1=[αk+Δαk*, μk+Δμk*, δk+Δδk*]T.
为了简化搜索流程,提高机动决策的快速性,控制量变化率备选值通过等距梯度的方法提前给定; 为保证做出的机动选择对整体空战态势最优,需要构建备选项更为丰富且完备的试探机动策略库; 由于高耦合度的三自由度运动动力学模型各变量之间存在更为复杂的耦合关系,模型的控制过程更为精细,若机动的试探选择过少,则难以保证机动轨迹的平滑过渡和UCAV机体的稳定控制,同时过多的机动选择,又会耗费更长的计算时间,折中考虑所有可能的情况,本文对飞行控制量进行较为精细的划分,每个控制量在UCAV允许的范围内设置11个梯度的待选方案,共计113=1 331种试探机动方案.攻角、航迹滚转角和油门设置3个飞行控制量的梯度变化值分别设置为:
| $ \Delta \alpha_{k} \in\left\{\begin{array}{l} \Delta \alpha_{k, \min }, \Delta \alpha_{k, \min } / 2, \Delta \alpha_{k, \min } / 4, \Delta \alpha_{k, \min } / 8, \\ \Delta \alpha_{k, \min } / 10, 0, \Delta \alpha_{k, \max } / 10, \Delta \alpha_{k, \max } / 8, \\ \Delta \alpha_{k, \max } / 4, \Delta \alpha_{k, \max } / 2, \Delta \alpha_{k, \max } \end{array}\right\}, $ | (4) |
| $ \Delta \mu_{k} \in\left\{\begin{array}{l} \Delta \mu_{k, \min }, \Delta \mu_{k, \min } / 2, \Delta \mu_{k, \min } / 4, \Delta \mu_{k, \min } / 8, \\ \Delta \mu_{k, \min } / 10, 0, \Delta \mu_{k, \max } / 10, \Delta \mu_{k, \max } / 8, \\ \Delta \mu_{k, \max } / 4, \Delta \mu_{k, \max } / 2, \Delta \mu_{k, \max } \end{array}\right\}, $ | (5) |
| $ \Delta \delta_{k} \in\left\{\begin{array}{l} \Delta \delta_{k, \min }, \Delta \delta_{k, \min } / 2, \Delta \delta_{k, \min } / 4, \Delta \delta_{k, \min } / 8, \\ \Delta \delta_{k, \min } / 10, 0, \Delta \delta_{k, \max } / 10, \Delta \delta_{k, \max } / 8, \\ \Delta \delta_{k, \max } / 4, \Delta \delta_{k, \max } / 2, \Delta \delta_{k, \max } \end{array}\right\}. $ | (6) |
式中,下标min和max分别为控制量变化率允许的最小值和最大值.
3 空战机动决策评价函数构建空战机动决策评价函数的目的是通过评价函数的构建,导引UCAV稳定接敌和有效攻击占位.在保持自身态势优势的同时,充分发挥武器系统的战术使用性能,快速消灭目标.基于空空导弹的作战使用实际,本文将构建包含角度、距离和能量决策因子的决策评价函数,以期获得更大态势优势.
3.1 空战过程中的相对位置关系表述在进行相对状态计算和导弹可发射距离解算时,为了简化计算过程,本文忽略攻角对相对状态产生的影响,即认为速度方向与UCAV机身轴线的方向保持一致.某态势下,UCAV与目标机的相对位置关系,如图 3所示.图中,

|
图 3 UCAV与目标机的相对位置关系示意 Fig. 3 Relative positions between UCAV and target |
假设UCAV和目标机位置坐标分别为(xu, yu, hu)和(xt, yt, ht),存在如下对应关系:
| $ \overrightarrow{\boldsymbol{R}}=\left[x_{t}-x_{u}, y_{t}-y_{u}, h_{t}-h_{u}\right], $ | (7) |
| $ \vartheta_{u}=\arccos \frac{\overrightarrow{\boldsymbol{R}} \cdot \overrightarrow{\boldsymbol{v}}_{u}}{\|\overrightarrow{\boldsymbol{R}}\| \times\left\|\overrightarrow{\boldsymbol{v}}_{u}\right\|}, \vartheta_{u} \in\left[0^{\circ}, 180^{\circ}\right], $ | (8) |
| $ \vartheta_{t}=\arccos \frac{\overrightarrow{\boldsymbol{R}} \cdot \overrightarrow{\boldsymbol{v}}_{t}}{\|\overrightarrow{\boldsymbol{R}}\| \times\left\|\overrightarrow{\boldsymbol{v}}_{t}\right\|}, {\vartheta}_{t} \in\left[0^{\circ}, 180^{\circ}\right], $ | (9) |
| $ \overrightarrow{\boldsymbol{v}}_{u}=\left[v_{u} \cos \gamma_{u} \cos \psi_{u}, v_{u} \cos \gamma_{u} \sin \psi_{u}, v_{u} \sin \gamma_{u}\right], $ | (10) |
| $ \overrightarrow{\boldsymbol{v}}_{t}=\left[v_{t} \cos \gamma_{t} \cos \psi_{t}, v_{t} \cos \gamma_{t} \sin \psi_{t}, v_{t} \sin \gamma_{t}\right]. $ | (11) |
角度决策因子是空战机动决策中最重要的机动评价指标之一,通过优化和调和UCAV与目标机之间的相对角度关系,使UCAV满足尾后攻击的优势态势,可以保证UCAV免受目标攻击,保证自身安全; 同时,在空战对抗中,尾后攻击必然使UCAV具备较高的时间裕度,使得攻击机可以实现更为灵活的机动选择,从而有助于空空导弹作战使用性能的充分发挥.现役第3代空空导弹具有全向攻击、离轴发射的特性,在UCAV提前角满足导弹离轴发射角的条件下,空空导弹即可完成瞄准、锁定过程,因而现代空战条件下,UCAV并不一定以纯跟踪的形式使机头直接瞄准目标[14],因此,保证UCAV提前角在导弹离轴发射角允许的范围内是导弹能够稳定瞄准、锁定目标的基础性前提.综合考虑UCAV优势态势的获取和空空导弹的离轴攻击的特性需求,构建角度决策因子评价函数ηA为
| $ \eta_{A}=\left\{\begin{array}{l} 1 \cdot\left(1-\frac{\vartheta_{t}}{180^{\circ}}\right), 0 \leqslant \vartheta_{u} \leqslant k_{a} \varphi_{D_{0}}; \\ \left(1-\frac{\vartheta_{u}}{180^{\circ}}\right) \cdot\left(1-\frac{\vartheta_{t}}{180^{\circ}}\right), \vartheta_{u}>k_{a} \varphi_{D_{0}}. \end{array}\right. $ | (12) |
式中:φD0为空空导弹离轴发射所允许的最大离轴发射角,也称作最大动态视场角; ka为离轴发射角度值修正参数,且0 < ka≤1.由文献[15]可知,导弹对离轴方位角小的目标具备更强的攻击能力,且离轴方位角接近导弹最大离轴发射角处的目标,很容易通过逃逸机动的方式摆脱导弹攻击,因而ka根据需要调整角度判定值,以充分发挥空空导弹的攻击特性.
3.3 距离决策因子评价函数UCAV与目标机相对距离位于当前态势下空空导弹可发射距离区间范围内,构成空空导弹的稳定发射条件,是空战机动决策的最终目的.因此需要构建距离决策因子,以实现对导弹可发射条件的有效导引.为了提高导弹的命中概率,当前态势下的发射距离判断值,采用文献[15]构建的基于目标逃逸机动预估的空空导弹可发射距离解算值,模型定义为
| $ \left\{\begin{array}{l} R_{\max }=f\left(v_{t_{0}}, v_{m_{0}}, h_{m_{0}}, a_{\mathrm{asp}}, a_{\mathrm{off}}, \gamma_{m_{0}}, u_{t}\right), \\ R_{\min }=f\left(v_{t_{0}}, v_{m_{0}}, h_{m_{0}}, a_{\mathrm{asp}}, a_{\mathrm{off}}, \gamma_{m_{0}}, u_{t}\right). \end{array}\right. $ | (13) |
式中:Rmin和Rmax分别为当前态势下空空导弹可发射距离的最大、最小值.构建距离决策因子ηR为
| $ \eta_{R}=\left\{\begin{array}{l} \mathrm{e}^{\frac{R-R_{\min }}{R_{\min }}}, R<R_{\min }; \\ 1, R_{\min } \leqslant R \leqslant R_{\max }; \\ e^{\frac{R_{\max }-R}{R_{\max }}}, R>R_{\max }. \end{array}\right. $ | (14) |
式中,
空战能量主要包括动能和势能两个方面,分别与速度[16]和高度呈正相关.一方面,UCAV所具备的能量越大,其机动能力就越强,可发挥的潜力就越大,通过能量转化[17],有助于快速攻击和优势机动占位; 另一方面高的能量,有助于空空导弹攻击能力的充分发挥.图 4给出了某型空空导弹在高度为10 km的条件下,对进入角为0°,且以0.8 Ma速度做匀速非机动飞行的目标,所具备的三维可发射包络.当目标初始位置位于该包络内时,导弹能以一定的概率命中目标.

|
图 4 空空导弹的三维可发射包络 Fig. 4 3D launchable envelope of air-to-air missile |
由图 4可知,在目标动能一定的条件下,随目标高度降低,导弹的可攻击范围逐渐增大.当目标高度大于导弹高度,目标势能大于UCAV势能时,空空导弹的水平可发射区范围明显小于与之相反时的水平可发射区.换言之,当空空导弹的所具备的相对能量越大时,空空导弹可攻击的范围越大,因此,高的能量有助于空空导弹战术使用性能的充分发挥.综合考虑动能和势能两个因素,从UCAV角度构建能量决策因子ηE为
| $ {\eta}_{E}=\mathrm{e}^{\frac{\frac{1}{2} v_{u}^{2}+g h_{u}}{\frac{1}{2}v_{u}^{2}+g h_{u}+\frac{1}{2} v_{t}^{2}+g h_{t}}-1}. $ | (15) |
整体评价函数的目的是对空战整体态势做出评价,基于角度、距离和能量3个因素,构建机动决策整体评价函数为
| $ S=\left[\begin{array}{lll} w_{A} & w_{R} & w_{E} \end{array}\right] \cdot\left(\left[\begin{array}{lll} \eta_{A} & \eta_{R} & \eta_{E} \end{array}\right]\right)^{\mathrm{T}}, $ | (16) |
式中,wA、wR和wE分别为3个决策因子的权重系数.
3.6 基于统计学原理的机动优选策略在机动决策时,本文不对目标机动过程进行预测,且忽略决策时域内目标机的状态变化.通过试探机动的方法,从1 331种机动备选方案中,选择最优的飞行控制量uu(k+1),使得S(Xu(k+1), Xt(k))取值最大,其中Xu(k+1)为试探终止时刻的UCAV状态,Xt(k)为决策初始时刻的目标机状态.考虑到在1 331种遍历试探方案中,可能存在多种方案使整体评价函数取值最大,为此,参照文献[6]提出的机动决策方法,通过进一步比较决策函数各组成部分的统计学量值,遴选出统计学意义上最优试探机动方案; 并将该方案对应的飞行控制量uu(k+1)作为最终的决策控制量.具体表述如下.
Step1 假设第k个决策时域内,决策因子的权重系数为[wAk wRk wEk ],第i种试探方案,对应的机动因子评价函数为
Step2 计算第i种试探机动方案下的,对应集合Mk+1i的数学期望MEk+1i和方差MVk+1i, 有:
| $ M E_{k+1}^{i}=\frac{1}{3}\left(w_{A_{k}}+w_{R_{k}} \eta_{R_{k+1}}^{i}+w_{E_{k}} \eta_{E_{k+1}}^{i}\right), $ | (17) |
| $ \begin{aligned} M V_{k+1}^{i}=& \frac{1}{3}\left[\left(w_{A_{k}} \eta_{A_{k+1}}^{i}-M E_{k+1}^{i}\right)^{2}+\left(w_{R_{k}} \eta_{R_{k+1}}^{i}-\right.\right.\\ &\left.\left.M E_{k+1}^{i}\right)^{2}+\left(w_{E_{k}} \eta_{E_{k+1}}^{i}-M\right)^{2}\right]. \end{aligned} $ | (18) |
Step3 比较每种方案下对应的MEk+1i和MVk+1i,选取使期望值MEk+1i取值最大的方案i为即将执行的机动方案; 当MEk+1i取值为最大的方案个数超过1时,选取使方差MVk+1i取值最小的方案作为第k个决策时域内最终的选定方案,即当前时刻UCAV即将执行的方案.
综上所述,期望值最大的飞行控制方案即为决策整体评价函数取值最优的方案; 对机动选择的冗余选项,通过方差判别的方法,使得决策评价函数的3个组成部分尽可能的朝向一致收敛的方向靠拢,保证了整体评价函数最终收敛至优势态势; 减缓了由于目标机状态变化,给整体态势造成的影响,从而提高了机动决策的鲁棒性[6].需要说明的是,本文对1 331种可行空间采用的是遍历试探的方法,主要目的在于简化工程应用复杂度,与此同时这种方法可能会存在一定的搜索效率问题,采用启发式或智能搜索[18-19]等方法加以克服将是下一步研究的重点,在此不做赘述.
4 导弹攻击状态评估的权重因子分级模型各决策因子的权重大小,对机动决策评价函数的数值及机动方案的选择具有很大影响.文献[7]通过相对角度和距离对空战态势进行评估,基于贝叶斯推理判定双机状态处于4种优劣态势中的任一种态势,并通过专家系统方法综合确定机动决策权值.机动决策的最终目的是尽可能迅速的构成空空导弹的发射条件,因此各机动决策因子权值应结合当前态势下的导弹攻击状态,在对空空导弹发射/攻击状态评估的基础上综合设定; 而文献[7]所构建的基于位置信息的评估方法,未能体现空空导弹的状态信息,可能使空空导弹可发射状态的达成缺乏时效性.因此,本文将构建基于导弹攻击状态评估的权重因子分级自适应模型,以满足导弹的作战使用实际.在空空导弹未构成允许发射状态的前提下,主要存在以下3种不同攻击状态.
1) 当前态势下,目标离轴方位角[15] aasp过大,使提前角
| $ \vartheta_{u}>\varphi_{D_{0}}. $ | (19) |
2) 提前角
| $ \vartheta_{u} \leqslant \varphi_{D_{0}}, R \notin\left[R_{\min }, R_{\max }\right]. $ | (20) |
3) 提前角
| $ \vartheta_{u} \leqslant \varphi_{D_{0}}, \left[R_{\min }, R_{\max }\right]=(0, 0). $ | (21) |
3种攻击状态下,UCAV(导弹)与目标的相对位置关系如图 5所示,图中C1、C2、C3分别对应上述提到的3种导弹攻击状态; C4表示最理想的情况,此时空空导弹构成允许发射状态.针对导弹的3种不同攻击状态,分别设置以下3种优先级:

|
图 5 不同攻击状态下UCAV与目标的相对位置关系 Fig. 5 Relative positions between UCAV and target under different attack states |
1) 当
| $ \vartheta_{u}>\varphi_{D_{0}}, \vartheta_{t}>\varphi_{D_{t}} , $ | (22) |
| $ \vartheta_{u}>\varphi_{D_{0}}, \vartheta_{t} \leqslant \varphi_{D_{t}}, $ | (23) |
式中φDt为目标机导弹的最大动态视场角.
在式(22)表示的情况下,应主要考虑减小UCAV提前角
2) 在
3) 针对
综上所述,在对空空导弹攻击状态评估的基础上,设置权值对应规则见表 1.导弹攻击状态为标号(1)和(3)时,其可发射距离解算结果为零,此时应该给定可发射区间参考值[Rmin_ref, Rmax_ref],以实现距离决策因子的有效输出和UCAV的有效导引.
| 表 1 基于导弹攻击状态评估的决策因子权重 Tab. 1 Decision factor weights based on missile attack state assessment |
为充分验证试探机动模型的决策能力和基于导弹攻击状态评估的权重因子分级模型对空战态势变化的适应水平,仿真验证部分包括:包含决策过程的UCAV对抗不包含决策过程的目标、包含评估过程的UCAV对抗不包含评估过程的目标两部分内容.仿真中目标机和UCAV选用同一机动及武器平台,基于文献[15]所构建的模型,实时解算当前态势下导弹可发射距离区间值; 当导弹可发射区间解算结果为零时,可发射距离参考值设置为[Rmin_ref, Rmax_ref]=[500 m, 2 000 m].交战区域位于水平15 km×15 km,高1~2 km的空间范围内,超出该空域即判定空战无效.仿真终止条件为:目标位于导弹可发射区范围内,且允许发射的状态稳定持续3 s,此时UCAV完成攻击占位,导弹发射.
5.1 仿真1:包含决策过程的UCAV对抗不含决策过程的目标本仿真旨在验证所构建的试探机动策略及决策模型的整体效果.仿真初始时刻,目标与UCAV分别位于交战空域水平投影的某段对角线上,且构成直接迎头的相对态势.目标初速度为vt=250 m/s,航迹倾角为γt=0°,航迹偏角ψt=45°,水平坐标(x, y)=(0, 0)m; UCAV初速度和航迹倾角与目标机相同,航迹偏角为ψu=225°,水平坐标(x, y)=(10 000, 10 000)m; 目标与UCAV初始控制量相同,均为u =[0°, 0°, 0.5]T.
当前航电系统的信号响应周期约为40 ms,为使得控制量输入与航电系统的响应周期相匹配,仿真步长设置需满足系统响应周期的整数倍; 高动态的空战态势变化,使得空战决策需要具备很强的实时性; 同时,若控制量在短时间内剧烈变化,又将使得机体的稳定控制变得十分困难.综合考虑航电系统信号响应的周期性、空战决策的实时性和UCAV机体稳定操控的可行性,本文将空战决策的仿真步长设置为1 s.仿真中,UCAV采用本文构建的决策及评估模型,权重因子随导弹攻击状态自适应变化; 考虑到所选用运动动力学模型的高耦合性,若重新为目标机设计控制率将比较困难,因而目标在机体可飞的约束范围内,每一步均从1 331种试探方案中,随机选取一种方案作为该时域内的机动方案.在UCAV相对目标机构成高度劣势、均势和优势的3种情况下分别进行仿真验证,3种情况下的UCAV和目标的高度初值(hu0, ht0)分别设置为(8, 12)km、(8, 8)km、(12, 8)km.由于目标控制量随机产生,为体现一般性,每种情况均各进行50次蒙特卡洛空战仿真.受文章篇幅限制,仅给出UCAV处于相对高度劣势情况下的一组仿真实验加以描述,其空战机动轨迹如图 6所示.仿真中UCAV实现了对目标机的稳定追踪,在整体上保持了尾后攻击的攻击策略.仿真飞行时间为141 s时,UCAV所携带的空空导弹满足发射条件,仿真终止.

|
图 6 UCAV处于高度劣势下的空战机动轨迹 Fig. 6 Air combat maneuver trajectory when UCAV is at a height disadvantage |
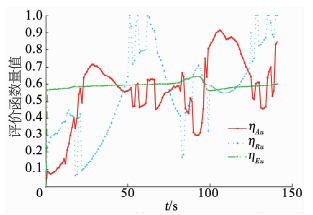
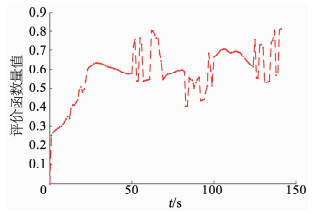
图 7、8分别给出了UCAV各决策因子评价函数及整体评价函数随时间的变化曲线,可见整体评价函数值总体上实现稳定增长,各分量决策因子依据态势关系动态变化.其中,角度决策因子在数值上增长更为显著,说明UCAV随空战态势变化占据了更大的角度优势; 距离决策因子变化更为剧烈,在仿真飞行时间分别为50 s和124 s时出现峰值,这主要是因为距离决策因子的构建与空空导弹的最大最小发射距离相关,若当前态势下不存在可发射距离时,决策函数将接通参考距离[Rmin_ref, Rmax_ref],因此距离因子评价函数的变化更为剧烈,峰值部分表明,UCAV通过决策与评估模型实现了对导弹允许发射状态的有效导引; 由于UCAV与目标机采用相同的机动平台,且初始时刻,目标机占据高度优势,因此UCAV能量决策因子函数变化并不显著,当仿真时间为93 s时,UCAV爬升至目标机上方,此时能量决策因子出现明显峰值.空战中,UCAV通过决策过程,由初始时刻的高度劣势,最终实现对自身有利态势的状态转化.
|
图 7 UCAV各决策因子评价函数的变化曲线 Fig. 7 Change curve of evaluation function of decision factors |
|
图 8 UCAV整体评价函数变化曲线 Fig. 8 Change curve of overall decision evaluation function |
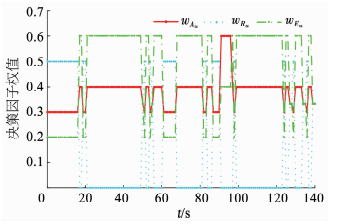
图 9给出了UCAV空空导弹可发射距离区间解算值及UCAV与目标的相对距离随时间的变化曲线.其中导弹可发射区间的边值连线与相对距离曲线的交点,代表着当前态势下导弹与目标的相对距离位于导弹的可攻击距离范围内,导弹构成允许发射状态.由图 9可知,空空导弹可发射距离区间值随空战态势不断变化; 导弹有9次时机构成允许发射状态,在第7次构成可发射状态时,导弹实现对目标的稳定跟踪,且该状态稳定持续3 s时导弹离轴发射; 发射时刻,导弹与目标的相对距离R=2 431.25 m,目标离轴方位角[15]为aasp=50.64°,水平分量aasp_y=48.47°,垂向分量aasp_z=15.17°; 目标进入角水平分量aoff_y=39.16°,垂向分量aoff_z=-13.41°; 导弹发射倾角γm0=-6.27°; 导弹可发射距离区间为[393.62, 2 915.47]m.图 10给出了UCAV各决策因子权值随时间的变化曲线,可见,各决策因子的权重值随空战态势不断变化.结合图 9、10可知,随空战态势变化,基于导弹攻击状态评估的权重因子稳定输出; 导弹数次由不利态势转为允许发射状态,可以判定所构建的权重因子分级策略是有效的.图 11给出了UCAV各飞行控制量随时间的变化曲线.可见在空战过程中,UCAV保持了持续加力状态,以最大油门持续飞行,迎角和航迹滚转角实现了较为连续的变化,没有出现大幅度波动,说明所构建的1 331种试探机动策略保证了UCAV飞行控制量的连续稳定输出.

|
图 9 导弹可发射区间及相对距离随时间的变化曲线 Fig. 9 Variation of missile transmittable interval and UCAV-target relative distance with time |
|
图 10 决策因子权值随时间的变化曲线 Fig. 10 Variation of decision factor weighting with time |

|
图 11 UCAV飞行控制量随时间的变化曲线 Fig. 11 Variation of UCAV flight control volume with time |
3种初始态势下的150次蒙特卡洛空战仿真结果见表 2,由于目标飞行控制量随机产生,因而存在大量超出可飞区的无效空战状态; 在所有的107次有效空战对抗中,UCAV有90次取得了最终空战的胜利,整体胜率保持在84.11 %,说明本文构建的决策模型对各种随机态势具有很强的适应能力.实验室环境下[20],150次空战仿真的单步决策的平均仿真时间为0.008 7 ms,说明本文构建的1 331种机动遍历选择具有较低的时间耗费,对空战整体态势的影响不大,满足工程应用的基本需求.
| 表 2 150次蒙特卡洛空战仿真实验结果统计 Tab. 2 Results of 150 Monte Carlo air combat simulation experiments |
设置对照仿真实验,仿真中目标机除权重因子的设置不同外,其余状态与UCAV完全一致.UCAV的权重因子在对导弹攻击状态评估的基础上动态变化; 目标机各决策因子的权重值始终保持恒定,并设定权重因子为wA=wR=wE=1/3, 角度修正量固定为ka=0.85.仿真中UCAV相对目标机分别构成高度劣势、均势和优势,高度初值的取值空间与仿真1保持一致,仍仅给出UCAV处于高度劣势下的仿真结果,其空战机动轨迹如图 12所示,可见UCAV与目标之间具有明显的缠斗过程,随着空战进行,UCAV逐渐获得了更大的角度优势,在机动轨迹上逐渐呈现尾后攻击的攻击预设策略.空战时间为83 s时,UCAV所携带的空空导弹首先满足了稳定发射条件,UCAV取得空战博弈的胜利.图 13给出了敌我双方各自空空导弹的可发射区间值变化曲线,可见UCAV能够通过攻击占位多次使目标接近或位于导弹的可发射区间范围内,使得导弹具有更大的几率完成稳定发射状态,说明基于导弹攻击状态评估的权重因子分级模型有助于实现对空战整体有利的态势转化.
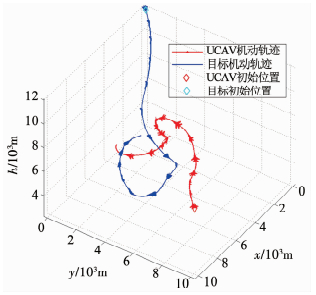
|
图 12 UCAV处于高度劣势下的空战机动轨迹 Fig. 12 Air combat maneuver trajectory when UCAV is at a height disadvantage |

|
图 13 导弹可发射区间变化曲线 Fig. 13 Variation of missile transmittable interval |
整体仿真中,在UCAV分别处于高度劣势和优势的两种情况下,包含导弹攻击状态评估过程的UCAV均取得了空战胜利,说明所构建的权重分级策略是整体有效的.此外,在UCAV与目标机处于高度均势的情况下,UCAV与目标机同时构成导弹稳定发射条件,空战以平局告终.这主要是因为在等高度正向迎头的情况下,导弹的可发射范围很大[20],UCAV和目标机均不需要做大的机动就可完成攻击过程,其相关状态变化在此不做赘述.
6 结论1) 本文设计的试探机动方案,在其空战决策过程中紧紧围绕可靠的气动耦合模型和制导武器的作战使用性能实现,基于空空导弹的可发射区解算结果进行评估与决策,使得所构建的试探机动策略具有更强的可靠性和合理性,保证了UCAV机动攻击占位的科学性和高效性.
2) 构建的UCAV决策模型对各种随机初始态势具有很强的适应能力,实验室条件下UCAV随机空战对抗仿真的获胜率接近85%.
3) 所构建的基于导弹攻击状态评估的权重因子分级优先模型,在不同空战态势下均实现了对空空导弹可发射状态的高效导引,有助于空空导弹的作战使用性能的充分发挥.
| [1] |
黄长强, 唐上钦. 从"阿法狗"到"阿法鹰"——论无人作战飞机智能自主空战技术[J]. 指挥与控制学报, 2016, 2(3): 261. HUANG Changqiang, TANG Shangqin. From Alphago to Alphaeagle: on the intelligent autonomous air combat technology for UCAV[J]. Journal of Command and Control, 2016, 2(3): 261. DOI:10.3969/j.issn.2096-0204.2016.03.0261 |
| [2] |
傅莉, 谢福怀, 孟光磊, 等. 基于滚动时域的无人机空战决策专家系统[J]. 北京航空航天大学学报, 2015, 41(11): 1994. FU Li, XIE Fuhuai, MENG Guanglei, et al. An UAV air-combat decision expert system based on receding horizon control[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(11): 1994. DOI:10.13700/j.bh.1001-5965.2014.0726 |
| [3] |
柳嘉润, 钟友武, 张磊, 等. 自主空战决策的试探机动方法及仿真研究[J]. 系统仿真学报, 2008, 20(5): 1238. LIU Jiarun, ZHONG Youwu, ZHANG Lei, et al. Study of trial maneuver scheme in autonomous air combat decision-making system and simulation[J]. Journal of System Simulation, 2008, 20(5): 1238. |
| [4] |
AUSTIN F, CARBONE G, FALCO M, et al. Automated maneuvering decisions for air-to-air combat[C]//Guidance, Navigation and Control Conference. Monterey: AIAA, 1987: 659. DOI: 10.2514/6.1987-2393
|
| [5] |
SUN T Y, TSAI S J, LEE Y N, et al. The study on intelligent advanced fighter air combat decision support system[C]// IEEE International Conference on Information Reuse & Integration. Waikoloa: IEEE, 2006: 39. DOI: 10.1109/IRI.2006.252385
|
| [6] |
国海峰, 侯满义, 张庆杰, 等. 基于统计学原理的无人作战飞机鲁棒机动决策[J]. 兵工学报, 2017, 38(1): 160. GUO Haifeng, HOU Manyi, ZHANG Qingjie, et al. UCAV robust maneuver decision based on statistics principle[J]. Acta Armamentarii, 2017, 38(1): 160. DOI:10.3969/j.issn.1000-1093.2017.01.021 |
| [7] |
HUANG Changqiang, DONG Kangsheng, HUANG Hanqiao, et al. Autonomous air combat maneuver decision using Bayesian inference and moving horizon optimization[J]. Journal of Systems Engineering and Electronics, 2018, 29(1): 86. DOI:10.21629/JSEE.2018.01.09 |
| [8] |
DONG Yiqun, AI Jianliang. Trial input method and own-aircraft state prediction in autonomous air combat[J]. Journal of Aircraft, 2012, 49(3): 947. DOI:10.2514/1.C031671 |
| [9] |
WANG Yuan, HUANG Changqiang, TANG Chuanlin. Research on unmanned combat aerial vehicle robust maneuvering decision under incomplete targetinformation[J]. Advances in Mechanical Engineering, 2016, 8(10): 1. DOI:10.1177/1687814016674384 |
| [10] |
WILLIAMS P. Three-dimensional aircraft terrain-following via real-time optimal control[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(4): 1201. DOI:10.2514/1.29145 |
| [11] |
杜海文, 崔明朗, 韩统, 等. 基于多目标优化与强化学习的空战机动决策[J]. 北京航空航天大学学报, 2018, 44(11): 2247. DU Haiwen, CUI Minglang, HAN Tong, et al. Maneuvering decision in air combat based on multi-objective optimization and reinforcement learning[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(11): 2247. DOI:10.13700/j.bh.1001-5965.2018.0132 |
| [12] |
丁达理, 王杰, 董康生, 等. 基于RBF网络的UCAV战术机动轨迹快速生成方法[J]. 系统工程与电子技术, 2019, 41(1): 96. DING Dali, WANG Jie, DONG Kangsheng, et al. Rapid generation method of UCAV tactical maneuver trajectory based on RBF network[J]. Systems Engineering and Electronics, 2019, 41(1): 96. DOI:10.3969/j.issn.1001-506X.2019.01.14 |
| [13] |
VIRTANEN K, RAIVIO T, HÄMÄLÄINEN R P. Decision theoretical approach to pilot simulation[J]. Journal of Aircraft, 1999, 36(4): 632. DOI:10.2514/2.2505 |
| [14] |
吴文海, 张楠, 周思雨, 等. 基于航炮的近距空战仿真结束判定方法[J]. 飞行力学, 2012, 30(6): 569. WU Wenhai, ZHANG Nan, ZHOU Siyu, et al. Research on method of ending judgment in the dogfight simulation using gun[J]. Flight Dynamics, 2012, 30(6): 569. DOI:10.13645/j.cnki.f.d.2012.06.021 |
| [15] |
王杰, 丁达理, 许明, 等. 基于目标逃逸机动预估的空空导弹可发射区[J]. 北京航空航天大学学报, 2019, 45(4): 722. WANG Jie, DING Dali, XU Ming, et al. Air-to-air missile launchable area based on target escape maneuver estimation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(4): 722. DOI:10.13700/j.bh.1001-5965.2018.0462 |
| [16] |
赵克新, 黄长强, 魏政磊, 等. 改进决策树的无人机空战态势估计[J]. 哈尔滨工业大学学报, 2019, 51(4): 66. ZHAO Kexin, HUANG Changqiang, WEI Zhenglei, et al. Situation assessment for unmanned aerial vehicle air combat based on anti-reasoning rules decision tree[J]. Journal of Harbin Institute of Technology, 2019, 51(4): 66. DOI:10.11918/j.issn.0367-6234.201801006 |
| [17] |
VEERASAMY N. A high-level mapping of cyberterrorism to the OODA loop[C]//Proceedings of 5th European Conference on Information Management and Evaluation.Red Hook: Curren Associates Inc, 2011: 352
|
| [18] |
李世豪, 丁勇, 高振龙. 基于直觉模糊博弈的无人机空战机动决策[J]. 系统工程与电子技术, 2019, 41(5): 1063. LI Shihao, DING Yong, GAO Zhenlong. UAV air combat maneuvering decision based on intuitionistic fuzzy game theory[J]. Systems Engineering and Electronics, 2019, 41(5): 1063. DOI:10.3969/j.issn.1001-506X.2019.05.19 |
| [19] |
左家亮, 杨任农, 张滢, 等. 基于启发式强化学习的空战机动智能决策[J]. 航空学报, 2017, 38(10): 321168. ZUO Jialiang, YANG Rennong, ZHANG Ying, et al. Intelligent decision-making in air combat maneuvering based on heuristic reinforcementlearning[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(10): 321168. DOI:10.7527/S1000-6893.2017.321168 |
| [20] |
王杰, 丁达理, 许明, 等. 基于目标机动预估的空空导弹可发射区建模与仿真分析[J]. 弹道学报, 2018, 30(4): 44. WANG Jie, DING Dali, XU Ming, et al. Modeling and simulation analysis of allowable launch envelope of air-to-air missile based on target maneuver estimation[J]. Journal of Ballistics, 2018, 30(4): 44. DOI:10.12115/j.issn.1004-499X(2018)04-008 |
 2021, Vol. 53
2021, Vol. 53


