2. 寒地城乡人居环境科学与技术工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Laboratory of Cold Region Urban and Rural Human Settlement Environment Science and Technology(Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
能源清洁化是全球城市现代化发展的一个重要标志,天然气作为最清洁的化石能源和可持续发展的重要能源,已成为应对气候变化和能源转型的必然选择[1],城市燃气日负荷的准确预测关乎于居民生活的用气保障、燃气公司的经济效益、城市智慧燃气的发展等多方面问题.
国内外学者对城镇燃气日负荷组合预测展开了相关研究,Beyzanur等[2]采用自回归移动平均法和遗传算法相结合的方法对土耳其伊斯坦布尔的燃气日负荷进行预测,结果表明该组合预测方法具有较强的鲁棒性.Ervural等[3]用于预测的递归神经网络模型的输入向量的选取来源于灰色理论模型计算得出的级比残差值序列和模糊理论得到的输出向量,预测结果表明该组合方法优于传统的递归神经网络模型.祖广磊等[4]在对原始数据进行离群点预处理的基础上,将燃气负荷分解成为趋势性和季节性两种序列,分别利用ARIMA模型和BP神经网络进行预测,最后采用信息熵理论,将两种模型产生的预测结果进行加权组合.陈庆明[5]分别建立了回归分析、支持向量机、小波神经网络等模型,并以平均相对误差为目标函数,建立了组合预测模型,实验结果表明组合预测模型的预测精度更高.在上述研究中建立的组合预测模型多基于不变权理论,参与组合预测的单项预测模型往往缺少前期的模型筛选过程,权重计算的目标函数多基于单一准则.
为此,本文建立了岭回归分析(Ridge)、差分自回归积分滑动平均模型(ARIMA)、支持向量机回归(SVR)、极端梯度提升树(XGB)共4类单项预测模型,在组合预测前,利用多个评价准则计算出的综合评价指标对模型进行筛选,最后基于蚁群算法对组合预测模型的权重系数进行计算,通过预测实例,对比了组合预测模型与各单项预测模型的预测效果.
1 单项预测模型的建立城镇燃气日负荷预测是企业调度部门日常工作的重点和难点.日负荷影响因素多,当地气候因素、各类燃气用户用气规律都不同程度的决定着日负荷的变化和趋势;另外周末、节假日和平常工作日的用气规律也有很大不同.上述各种因素对负荷的影响有些具有一定的相关性和规律性,如负荷与气温成反相关关系,同时存在以年为周期的变化,如图 1所示.但是燃气负荷系统存在更多的不确定性和随机性,因此预测对象复杂、难度大,选择多样性的燃气负荷预测模型并组合优化可以改善在一个时段上的预测效果.

|
图 1 燃气日负荷及日平均温度变化曲线 Fig. 1 Variation of daily gas load and average temperature with time |
现有的众多预测模型,在建模机理和建模采用数据方面都有差异,比如:针对燃气负荷序列的ARIMA模型,要求时间序列大样本,通过差分处理后能够满足准平稳性要求.负荷与气温的相关性表明基于回归原理的岭回归分析适于用气象和历史负荷建模.人工智能等算法近年来被推广应用于预测领域,基于统计学习理论的支持向量机(SVM)模型和极端梯度提升树模型等,通过将输入向量映射到更高维空间,可以按任意精度逼近非线性函数,类似于模式识别的算法同样适于探讨复杂多因素变量的燃气负荷预测系统.因此本文选择下面4种方法建立单项预测模型.
1.1 岭回归分析典型线性回归基于最小二乘法的代价函数假设残差服从均值为零的高斯分布[6],然而实际燃气日负荷的数据所服从的概率分布很难用一个或多个分布的混合去拟合,则需要引入正则化因子,而岭回归则是结构风险最小化的正则化因子上使用模型参数向量的二范数形式,它是一种用于共线性数据分析的有偏估计回归方法,通过放弃无偏性去获得更符合实际的回归系数[7].
本文基于Python的机器学习Sklearn库中的岭回归分析模块进行建模,模型各项参数设置见表 1,岭回归模型的具体输入向量见表 2.
| 表 1 岭回归模型参数设置表 Tab. 1 Parameters in ridge regression model |
| 表 2 岭回归模型输入向量表 Tab. 2 Vector parameters in ridge regression model |
输入向量近似按365 d为负荷周期选择,这里忽略农历的周期性是因为闰年等变化可能仅对部分季节或时段负荷的影响较大,本文作为预测方法运用的研究目的,简化为负荷以365 d为周期.
1.2 ARIMA时间序列模型ARIMA(p, d, q)模型为差分自回归积分滑动平均模型,参数p为自回归项,参数q为滑动平均项,参数d为数据差分化处理的次数[8].
本文建模时间序列为预测起始日的前180 d的负荷数据,建模流程如下:
1) 连接数据库,获取需要的日负荷时间序列数据,依次绘制时序散点图、ACF(自相关系数)图和PACF(偏自相关系数)图.
2) 如果序列ADF值大于检验水平的临界值,则表明该负荷数据序列是非平稳的,则对序列进行一阶差分处理,处理后再进行差分检验,直至满足平稳性要求.
3) 采取“网格搜索”的方式来确定ARIMA(p, d, q)时间序列模型的最优参数值.由定义的参数三元组的不同组合分别计算AIC(Akaike信息标准)值来对模型进行训练和评估.
4) 对模型进行检验,通过假设检验诊断残差序列是否具有白噪声,通过参数估计检验模型的统计意义.
5) 调用模型预测,并对产生的预测值进行差分还原处理.
1.3 支持向量机回归支持向量机(SVM)是基于统计学习理论的VC维理论和结构风险最小化理论的机器学习理论,它是一种二分类模型,通过间隔最大化的分割原理来寻找一个超平面来分类样本[9].由于其具有全局极小值点和收敛速度快的优点,且可以按任意精度逼近非线性函数,近年来被推广应用于预测领域,即基于支持向量机理论的SVR模型.SVR的建模过程是通过选取的核函数(特征转换函数)将输入向量映射(分线性映射)到更高维空间并确定超平面.
本文基于Python中的Sklearn库中的SVM类中的SVR模块建立预测模型.以均方误差为目标准则,通过K折交叉验证法,动态选取模型的核函数以及包括惩罚因子C、核系数gamma、不敏感损失系数ε.参与交叉验证试算的各参数取值范围见表 3,SVR模型的输入向量见表 4.
| 表 3 SVR模型参数设置表 Tab. 3 Parameters in SVR model |
| 表 4 SVR模型输入向量表 Tab. 4 Vector parameters in SVR model |
XGB的全称是eXtreme Gradient Boosting,它是梯度提升机器算法(GBDT)的扩展,即极端梯度提升树[10].Boosting分类器是集成学习模型的一种,其基本思路是把大量的分类精度较低的单个树模型进行组合,构成一个稳定性和精确度较高的模型.XGB相比于传统的GBDT算法,具有速度快、效果好、能处理大规模数据、支持多种语言、支持自定义损失函数等多种优点.
本文基于Python中的xgboost库建立预测模型,建立XGB模型需要设置3类参数,第1类是控制提升过程中决定booster使用类型的通用参数,第2类是选取的booster的内置参数,第3类是控制学习场景的学习目标参数.本文选取树模型作为梯度提升算法,通过k折交叉验证试算法确定其他各项参数,参与交叉验证的各参数取值范围见表 5,XGB模型的输入向量见表 6.
| 表 5 XGB模型参数设置表 Tab. 5 Parameters in XGB model |
| 表 6 XGB模型输入向量表 Tab. 6 Vector parameters in XGB model |
基于权重分配方式的组合预测实际上是单项预测模型的信息进行选择利用的过程[11],在过去多数燃气日负荷组合预测的相关文献中,参与组合预测的单项预测模型大都是通过预测研究人员逐一试算各预测模型效果后,主观地根据已有的经验选择单项预测模型直接建立组合预测模型.但是实际预测中的某些特定时间段,并非所有的预测模型都对组合预测的精准度提升有帮助,也不是其提供的信息一定具有价值.因此,有必要在组合预测前剔除这些冗余模型,否则不仅会影响组合预测模型的预测精度,而且还会增加计算时间.
评价预测模型的预测性能以及衡量模型泛化能力需要通过对预测结果进行度量分析,构建这种度量分析的损失函数需要基于不同的评价指标,不同的指标的侧重点和适应范围均不一样.本文选取以下5种常见的评价准则来度量预测值与真实值之间的误差.
1) 平均相对误差(MAPE).
| $ \mathrm{MAPE}=\frac{1}{n} \sum\limits_{t=1}^{n}\left|\frac{x^{(0)}(t)-\hat{x}^{(0)}(t)}{x^{(0)}(t)}\right|. $ | (1) |
式中: MAPE(x(0),
2) 均方根误差(RMSE).
| $ \mathrm{RMSE}=\frac{1}{n} \sqrt{\sum\limits_{t=1}^{n}\left[\frac{x^{(0)}(t)-\hat{x}^{(0)}(t)}{x^{(0)}(t)}\right]^{2}}, $ | (2) |
式中, RMSE(x(0),
3) 灰色关联度. 预测值负荷序列与真值负荷序列的关联程度可以用两条曲线几何形状的相似度来表示,即两序列间的差值可作为其关联程度的衡量标准[12].预测值数列与真值数列在各个时刻(即曲线中的各点)的关联系数ξx可由下式计算得出:
| $ \xi_{x}=\frac{\Delta(\min )+\rho \Delta(\max )}{\Delta_{x}(k)+\rho \Delta(\max )}. $ | (3) |
式中:ξx为预测负荷序列与真值负荷序列上各点的关联系数; Δx(k)为预测负荷序列与真值负荷序列上第k点的绝对值差值, m3; ρ为分辨系数,一般在0~1之间,通常取0.5.
因为关联系数是预测值负荷序列与真值负荷序列在各个时刻的关联程度值,所以为了便于进行整体性比较,需求各个时刻的关联系数的平均值,即为两序列的灰色关联度,当二序列的灰色关联度越大,则表明关联程度越高.
| $ \gamma_{i}=\frac{1}{N} \sum\limits_{k=1}^{N} \xi_{i}(k). $ | (4) |
式中: γi为预测负荷序列与真值负荷序列的灰色关联度; ξi(k)为预测负荷序列与真值负荷序列上第k点的关联系数; N为预测日长, d.
4) 相关系数.相关系数常用于度量预测的精准度,当预测值序列越接近真值序列时,两者的相关系数就越大[13].
| $ P\left(x^{(0)}, \hat{x}^{(0)}\right)=\frac{\operatorname{Cov}(X, \hat{X})}{\sqrt{\operatorname{Var}[X] \operatorname{Var}[\hat{X}]}}. $ | (5) |
式中: P(x(0),
5) Theil不等系数.Theil不等系数用于计算两个序列的一致性指标,当Theil不等系数越接近0时,二序列越一致,当越接近1时,二序列越不一致[14].
| $ \begin{array}{*{20}{l}} {T\left( {{x^{(0)}}, {{\hat x}^{(0)}}} \right) = }\\ {\frac{{\sqrt {\frac{1}{n}\sum\limits_{t = 1}^n {{{\left( {{x^{(0)}}(t) - {{\hat x}^{(0)}}(t)} \right)}^2}} } }}{{\sqrt {\frac{1}{n}\sum\limits_{t = 1}^n {{{\left( {{x^{(0)}}(t)} \right)}^2}} } + \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{{\hat x}^{(0)}}(t)} \right)}^2}} } }}} \end{array}. $ | (6) |
式中: T(x(0),
本文采取的模型预测效果综合评价值的计算方法为各单一准则结果数据标准化处理后,利用加权平均的方式计算得出,权重系数由操作预测软件的人员在用户界面端口进行修改,初始权重为等权权重.
2.2 蚁群算法计算组合预测权重蚁群算法是一种模拟蚂蚁觅食行为的仿生式迭代搜索算法[15],蚁群算法在解决组合优化问题和最优解问题时的主要优势在于它具有较强的自组织性和自适应性、易于分布式运行、搜索高效、算法优化融合特性较好等[16].
本文应用蚁群算法确定组合预测各单项模型权重系数的具体实现步骤如下:
1) 初始化数据. 权重系数的取值范围为[0, 1],将权重取值区间平均分为100份,即为[0, 0.01],[0.01, 0.02], …, [0.99, 1.00].设共有N种单项方法参与到组合预测中,则每个取值区间可以表示为[xij, xi(j+1)], i=1, 2, …, N,j=0, 1, …, 99,同时初始化各取值区间的信息素浓度均为1.
2) 初始参数设置. 算法需要确定的各项参数的定义和取值见表 7.
| 表 7 蚁群算法参数设置表 Tab. 7 Parameters in ant colony algorithm |
3) 蚁群搜索.蚁群依次搜索各单项预测方法的各权重区间.单只蚂蚁的具体搜索过程的算法实现主要分为以下4步.
① 通过Python中随机数生成器确定蚂蚁的出生位置,并设置禁忌表,保证蚂蚁搜索各单项预测方法有且仅有一次.
② 通过下式计算转移概率,即计算蚂蚁选择该单项预测方法各权重取值区间的概率:
| $ p_{j}^{k}=\left\{\begin{array}{l} \frac{\left[\tau_{j}\right]^{\alpha} \cdot\left[n_{j}\right]^{\beta}}{\sum\limits_{s \in J_{k}}\left[\tau_{s}\right]^{\alpha} \cdot\left[n_{s}\right]^{\beta}}, j \in J_{k} ; \\ 0, \text { 其他. } \end{array}\right. $ | (7) |
式中:pjk(t)为蚂蚁k转移到权重区间j的概率, i, j=0, 1…, 99;τj为权重区间j的信息素量; nj为权重区间j的信息期望启发参数; Jk为蚂蚁k下一步可选择的权重区间的集合; α为信息启发因子; β为期望启发因子.
③ 通过轮盘赌的方式确定蚂蚁选择的权重区间,本文轮盘赌算法的具体实现是先将该预测方法的各区间取值概率pj(j=0, 1, …, 99)求和得到总概率P,再在概率[0, P]之间生成一个随机概率,再依次循环遍历所有区间,做轮次相减,首先出现概率小于0的区间即为蚂蚁最终选择该方法的权重区间.
④ 蚂蚁依次遍历其他参与到组合预测的单项预测方法的权重区间的搜索.
4) 信息素更新.每次迭代需要对各权重区间的信息素浓度更新,本文选取基于全局信息更新的蚁周模型对各权重区间信息素计算并更新,即蚁群所有蚂蚁完成一次搜索后,计算各蚂蚁选择的权重区间下的组合预测模型综合评价指标,获取最优蚂蚁的路径,对其选择的权重区间利用式(8)进行信息素更新,对其他权重区间利用式(9)进行信息素更新.
| $ \tau_{i}=(1-\rho) \tau_{i-1}+L $ | (8) |
| $ \tau_{i}=(1-\rho) \tau_{i-1} $ | (9) |
式中: τi为第i次迭代权重区间信息素增量; ρ为信息挥发因子; L为最优蚂蚁选择的权重区间下的组合预测模型综合指标值.
3 预测实例分析选取2015—2016年的各日负荷数据为训练集,2017年的各日负荷数据为测试集,预测天数为7 d,以2017年1月10日为预测起始日,得到各负荷预测模型的预测结果如图 2所示,基于多准则评价指标的模型预测效果评价结果见表 8.
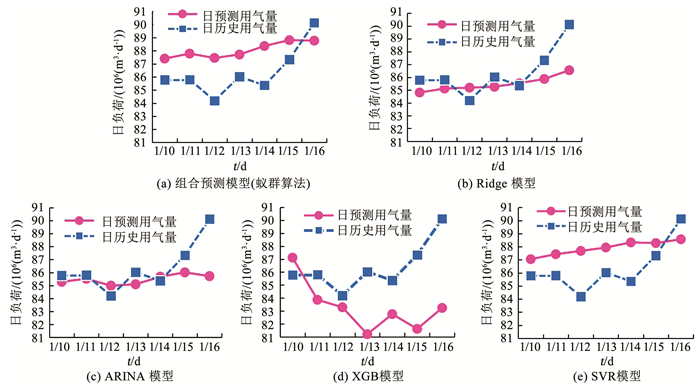
|
图 2 燃气日用气量预测值与实测值对比 Fig. 2 Comparision between predicted and measured results of daily gas load |
| 表 8 2017年1月10日各模型评价指标计算结果 Tab. 8 Calculation results of model evaluation indexes on January 10th, 2017 |
同时,以2017年1月份为例,计算得到各模型综合预测效果评价表见表 9.本文将反向指标,包括平均相对误差MAPE、均方根误差RMSE、Theil不等系数T的值,改用它们的等价值表示:1-MAPE,1-RMSE,1-T的值作为评价指标值,得到的综合评价指标值越高模型效果越好.
| 表 9 2017年1月各模型综合预测效果评价表 Tab. 9 Comprehensive prediction evaluation of each model in January, 2017 |
表 9给出的数据表明组合预测-蚁群算法的综合评价指标最高,其次是岭回归和ARIMA模型,这一结果表明具有解释性原理的岭回归和ARIMA模型具有更好的预测效果.表 8数据显示某一日的岭回归预测好于组合预测,但在一个时间段上的综合预测模型好于单一模型,基于权重分配方式的组合预测模型的泛化能力较强,能够提高预测模型容错率和稳定性.
4 结论1) 单项日负荷模型为:岭回归分析(Ridge)、差分自回归积分滑动平均模型(ARIMA)、支持向量机回归(SVR)、极端梯度提升树(XGB).各单项负荷预测模型在不同时间段上的预测效果存在较为显著的差异,其中具有可解释性原理的岭回归和ARIMA模型具有较好的预测效果.
2) 以5个单一评价准则计算的综合评价指标为目标函数的权重系数计算方法所构建的组合预测模型,对各单一评价准则的精度均有改善.组合预测前的模型筛选可以有效避免冗余模型的干扰,提升组合预测模型的精度.
3) 组合预测-蚁群算法的综合评价指标最高,权重分配式组合预测模型的泛化能力较强.虽然组合预测模型在具体某一天的预测精度要低于单一模型,但是能够提高预测模型在一个综合时间段上预测的容错率和稳定性.
4) 蚁群算法应用于求解组合预测模型权重系数问题上,具有较强的自组织性和自适应性、易于分布式运行、搜索高效、算法优化融合特性好等优点.
| [1] |
刘金源. 基于组合模型的燃气负荷预测技术研究[D]. 西安: 西安石油大学, 2018 LIU Jinyuan. Research on gas load forecasting technology based on combination model[D]. Xi'an: Xi'an Shiyou University, 2018 |
| [2] |
ERVURAL B C, BEYCA O F, ZAIM S. Model estimation of ARMA using genetic algorithms: A case study of forecasting natural gas consumption[J]. Procedia-Social and Behavioral Sciences, 2016, 235: 537. DOI:10.1016/j.sbspro.2016.11.066 |
| [3] |
TASPINAR F, CELEBI N, TUTKUN N. Forecasting of daily natural gas consumption on regional basis in turkey using various computational methods[J]. Energy and Buildings, 2013, 56(1): 23. DOI:10.1016/j.enbuild.2012.10.023 |
| [4] |
祖广磊, 陆黎明, 徐晓钟. 短期燃气预测的信息熵组合模型研究[J]. 计算机应用与软件, 2013, 30(5): 129. ZU Guanglei, LU Liming, XU Xiaozhong. Study on information entropy combination model for short-term gas load prediction[J]. Computer Applications and Software, 2013, 30(5): 129. DOI:10.3969/j.issn.1000-386x.2013.05.037 |
| [5] |
陈庆明. 基于组合方法的短期燃气负荷预测的研究[D]. 上海: 上海师范大学, 2014: 30 CHEN Qingming. Research on short-term gas-load forecasting based on combined method[D]. Shanghai: Shanghai Normal University, 2014: 30. DOI: 10.7666/d.Y2526865 |
| [6] |
张杨竣, 高文学, 王启, 等. 天然气大气式灶具的CO排放特性预测[J]. 天然气工业, 2016, 36(11): 114. ZHANG Yangjun, GAO Wenxue, WANG Qi, et al. Prediction on CO emission performance of atmospheric gas cookers[J]. Natural Gas Industry, 2016, 36(11): 114. DOI:10.3787/j.issn.1000-0976.2016.11.015 |
| [7] |
NAIK J, BISOI R, DASH P K. Prediction interval forecasting of wind speed and wind power using modes decomposition based low rank multi-kernel ridge regression[J]. Renewable Energy, 2018, 129: 378. DOI:10.1016/j.renene.2018.05.031 |
| [8] |
曾鸣, 李树雷, 王良, 等. 基于ARMA模型和BP神经网络组合优化算法的风电预测模型[J]. 华东电力, 2013, 41(2): 349. ZENG Ming, LI Shulei, WANG Liang, et al. Wind power prediction model based on the combined optimization algorithm of ARMA model and BP neural networks[J]. East China Electric Power, 2013, 41(2): 349. |
| [9] |
简献忠, 顾祎婷. 一种基于全过程优化支持向量机的短期电力负荷预测方法[J]. 电力科学与工程, 2018, 34(11): 46. JIAN Xianzhong, GU Yiting. Short-term electric load forecasting method based on global optimization support vector machine[J]. Electric Power Science and Engineering, 2018, 34(11): 46. DOI:10.3969/j.ISSN.1672-0792.2018.11.007 |
| [10] |
许裕栗, 杨晶, 李柠, 等. Xgboost算法在区域用电预测中的应用[J]. 自动化仪表, 2018, 39(7): 5. XU Yuli, YANG Jing, LI Ning, et al. Application of Xgboost algorithm in the regional electricity consumption forecast[J]. Process Automation Instrumentation, 2018, 39(7): 5. DOI:10.16086/j.cnki.issn1000-0380.2017120007 |
| [11] |
张超. 基于组合模型的我国能源消费预测研究[D]. 长沙: 湖南大学, 2017: 28 ZHANG Chao. Forecast of China's energy consumption based on combination model[D]. Changsha: Hunan University, 2017: 28 |
| [12] |
王彬. 基于灰色回归组合模型的铁路客运量预测研究[J]. 重庆理工大学学报(自然科学), 2017, 31(11): 233. WANG Bin. Forecast of railway passenger traffic based on grey linear regression combined model[J]. Journal of Chongqing University of Technology (Natural Science), 2017, 31(11): 233. DOI:10.3969/j.issn.1674-8425(z).2017.11.035 |
| [13] |
JADEVICIUS A. The use of combination forecasting approach and its application to regional market analysis[J]. Region, 2014, 1(1): Y6. |
| [14] |
孙浩, 杨桂元. 基于Theil不等系数的IGOWLA算子最优组合预测模型[J]. 西华师范大学学报(自然科学版), 2017, 38(3): 294. SUN Hao, YANG Guiyuan. The combination forecasting model based on Theil coefficient and Induced Geometric Ordered Weighted Logarithm Averaging (IGOWLA) operator[J]. Journal of China West Normal University (Natural Science), 2017, 38(3): 294. DOI:10.16246/j.issn.1673-5072.2017.03.011 |
| [15] |
李智, 谢兆鸿, 秦建华. 蚁群算法在天然气输送管道优化设计中的应用[J]. 天然气工业, 2005, 25(9): 104. LI Zhi, XIE Zhaohong, QIN Jianhua. Application of ant colony algorithms in optimized design of gas transmission pipelines[J]. Natural Gas Industry, 2005, 25(9): 104. DOI:10.3321/j.issn:1000-0976.2005.09.034 |
| [16] |
XU mingle, YOU xiaoming, LIU sheng. A novel heuristic communication heterogeneous dual population ant colony optimization algorithm[J]. IEEE Access, 2017, 5: 18510. DOI:10.1109/ACCESS.2017.2746569 |
 2021, Vol. 53
2021, Vol. 53


