2. 机械制造系统工程国家重点实验室(西安交通大学),西安 710049;
3. 智能机器人陕西省重点实验室(西安交通大学),西安 710049;
4. 河北工程大学 机械与装备工程学院,河北 邯郸 056038a
2. State Key Laboratory for Manufacturing Systems Engineering (Xi'an Jiaotong University), Xi'an 710049, China;
3. Shaanxi Key Laboratory of Intelligent Robots (Xi'an Jiaotong University), Xi'an 710049, China;
4. School of Mechanical and Equipment Engineering, Hebei University of Engineering, Handan 056038, Hebei, China
机床误差主要包括几何误差、热误差、切削力误差和控制误差等。对于精密加工,热误差可以占到总误差的40%~70%[1-2]。主轴作为机床的关键零部件,也是机床的主要热源之一。研究减小主轴热误差的方法对提高机床加工精度具有十分重要的意义。研究表明,热误差补偿是一种经济、有效的提高机床精度的方法,而建立高精度、高鲁棒性的热误差模型是热误差补偿技术中十分关键的环节,很大程度上决定了最终的补偿效果。广大学者针对主轴热误差建模进行了大量卓有成效的研究,提出了多种建模算法,包括多元线性回归[3-5]、神经网络[6-9]、支持向量机[10-12]和灰色系统[13-14]等。但是,模型的精度和鲁棒性仍需进一步提高以满足工厂的实际使用需求。Yang等[15]指出,前述建模方法鲁棒性差的主要原因为机床热变形是整体温度场的作用结果,利用少量离散的测温点建立热变形的预测模型时会丢失温度信息,产生图 1所示的“伪滞后”现象,即距离热源较近位置的温度变化超前于热变形,而距离热源较远位置的温度变化滞后于热变形。因此,当选取的温度测点位置不合适时,热变形ΔL(τ)和温度t(τ)之间的关系曲线呈现较强的非线性,且在升降温时不重合,采用ΔL(τ)=f1(t1(τ))或ΔL(τ)=f2(t2(τ))的建模方式难以同时描述升降温曲线。杨建国等[16]针对热变形伪滞后问题指出,对于主轴单端受热情况,在靠近热源大概x=0.4L处,主轴热变形ΔL(τ)和温度t(τ)呈近似的线性关系且升降温曲线基本重合。但是,该结论在实际应用时存在主轴上无法布置温度传感器,主轴箱上与主轴0.4L处等效的温度点不易寻找且受结构限制也可能无法布置温度传感器的问题。目前,多采用时间序列建模算法解决机床热变形伪滞后问题,将温度和热变形的历史数据作为模型输入,弥补以离散测温点替代整体温度场进行建模时造成的信息缺失[17-19]。此外,动态神经网络因包含延迟或反馈环节,也常被用来解决热变形伪滞后问题[20]。时间序列算法和动态神经网络的应用对热误差模型的精度和鲁棒性的提高起到了一定的效果,但是也引入了新的问题。如在应用时间序列建模时没有统一的定阶方法,并且模型系数完全由试验数据确定,不具备物理意义,而动态神经网络需要设计更符合伪滞后效应的反馈单元结构[21]。Fraser等[22]指出,热误差模型的数学形式不具备物理意义也是影响模型精度和鲁棒性的重要因素。Hou等[23]和颜宗卓等[24]针对该问题,提出了将理论建模与经验建模相结合的方法:首先,将主轴箱热传导简化为半无限大平板传热,计算得到其温度场和热变形的解析表达式;然后,通过一定的数学简化得到主轴箱热变形的模型形式;最后,利用实验获取模型系数。这种建模方法提高了模型的物理支持,但是推导过程中的数学简化在一定程度上降低了模型的精度。
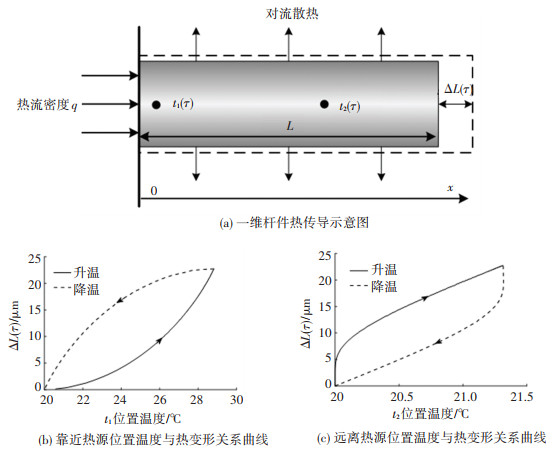
|
图 1 热变形伪滞后效应 Fig. 1 Pseudo-hysteresis effect of thermal deformation |
为了降低伪滞后效应对热误差模型精度和鲁棒性的影响,同时为了提高模型的物理意义,本文将主轴简化为一维杆件,从传热学的角度推导出一维杆在变化热源条件下热变形的一阶自回归模型。通过理论推导确定了自回归模型阶数为一阶,并根据模型系数的表达式确定了系数与主轴物理特性、自回归模型时间间隔以及热源条件的关系。整个推导过程不存在数学简化,仅仅是进行形式变换,因此模型精度更高。
1 主轴热变形计算及一阶自回归模型推导 1.1 主轴温度场和热变形理论求解将主轴简化为图 1(a)所示的一维杆结构,在左端施加热源,通过圆柱面进行对流散热,其导热微分方程和定解条件为:
| $ \left\{\begin{array}{l} \frac{\partial^{2} t}{\partial x^{2}}=\frac{2 h}{\lambda R}\left(t-t_{\mathrm{am}}\right)+\frac{\rho c}{\lambda} \frac{\partial t}{\partial \tau} \\ t(x, 0)=f(x) \quad(0 \leqslant x \leqslant L) \\ \left.\frac{\partial t}{\partial x}\right|_{x=0}=-\frac{q}{\lambda} \\ \left.\frac{\partial t}{\partial x}\right|_{x=L}=0 \end{array}\right. $ | (1) |
式中:t(x, τ)为一维杆温度分布函数(℃),x为一维杆轴向坐标(m),τ为时间(s),h为表面传热系数(W/(m2·K)),λ为导热系数(W/(m·K)),R为一维杆半径(m),tam为环境温度(℃),ρ为一维杆密度(kg/m3),c为比热容(J/(kg·℃)),t(x, 0)为初始时刻一维杆的温度场分布(℃),f(x)为任意函数,L为一维杆长度(m),q为热流密度(W/m2)。
引入过余温度θ(x, τ):
| $ \theta(x, \tau)=t(x, \tau)-t_{\mathrm{am}} $ | (2) |
并且设:
| $ a=\lambda /(\rho c), b=2 h /(\rho c R), \theta_{0}(x)=f(x)-t_{\mathrm{am}} $ | (3) |
将式(2)和式(3)代入式(1)可得:
| $ \left\{\begin{array}{l} a \frac{\partial^{2} \theta}{\partial x^{2}}=b \theta+\frac{\partial \theta}{\partial \tau} \\ \theta(x, 0)=\theta_{0}(x) \\ \left.\frac{\partial \theta}{\partial x}\right|_{x=0}=-\frac{q}{\lambda} \\ \left.\frac{\partial \theta}{\partial x}\right|_{x=L}=0 \end{array}\right. $ | (4) |
对式(4)进行求解可得温度场分布:
| $ \begin{array}{l} \theta (x,\tau ) = \sum\limits_{n = 1}^\infty {\left( {{k_1}(n,\tau ) + {k_2}(n,\tau )} \right)} \cos \frac{{n{\rm{ \mathsf{ π} }}}}{L}x - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{qa}}{{\lambda bL}}\left( {{{\rm{e}}^{ - b\tau }} - 1} \right) + \frac{1}{L}{{\rm{e}}^{ - b\tau }}\int_0^L {{\theta _0}} (x){\rm{d}}x \end{array} $ | (5) |
式中:
| $ {{k_1}(n,\tau ) = \frac{{ - 2qaL}}{{\lambda \left( {a{n^2}{{\rm{ \mathsf{ π} }}^2} + b{L^2}} \right)}}\left( {{{\rm{e}}^{ - \frac{{a{2^2}{{\rm{ \mathsf{ π} }}^2} + b{L^2}}}{{{L^2}}}\tau }} - 1} \right)} $ | (6) |
| $ {{k_2}(n,\tau ) = \frac{2}{L}{{\rm{e}}^{ - \frac{{a{n^2}{{\rm{ \mathsf{ π} }}^2} + b{L^2}}}{{{L^2}}}\tau }}\int_0^L {{\theta _0}} (x)\cos \frac{{n{\rm{ \mathsf{ π} }}}}{L}x{\rm{d}}x} $ | (7) |
从式(5)中可以看出,当初始过余温度θ0(x)=0时,一维杆位置x在τ时刻的温升与热流密度q成正比。此推论在后续将被用于估计不同转速下主轴受热的热流密度之间的关系。一维杆的热变形为
| $ \begin{aligned} \Delta L(\tau)=& \int_{0}^{L} \alpha \theta(x, \tau) \mathrm{d} x=-\frac{q \alpha a}{\lambda b}\left(\mathrm{e}^{-b \tau}-1\right)+\\ & \alpha \mathrm{e}^{-b \tau} \int_{0}^{L} \theta_{0}(x) \mathrm{d} x \end{aligned} $ | (8) |
式中:ΔL(τ)为一维杆的轴向热膨胀量(m),α为热膨胀系数(1/K)。
1.2 主轴热变形一阶自回归模型推导1) 一维杆初始温度与环境温度相同,则θ01(x)=0,式中上标1表示这是第一阶段一维杆的初始过余温度。设Δτ为时间间隔,在τ=0时刻一维杆左端施加热流密度q1,则热变形计算如下:
| $ \left\{\begin{array}{l} \Delta L_{1}(0)=0 \\ \Delta L_{1}(\Delta \tau)=-q_{1} \alpha a /(\lambda b)\left(\mathrm{e}^{-b \Delta \tau}-1\right)= \\ \ \ \ \ \ \ \ \ \ \ \ \ \Delta L_{1}(0) \mathrm{e}^{-b \Delta \tau}-q_{1} \alpha a /(\lambda b)\left(\mathrm{e}^{-b \Delta \tau}-1\right) \\ \Delta L_{1}(2 \Delta \tau)=-q_{1} \alpha a /(\lambda b)\left(\mathrm{e}^{-2 b \Delta \tau}-1\right)= \\ \ \ \ \ \ \ \ \ \ \ \ \ \Delta L_{1}(\Delta \tau) \mathrm{e}^{-b \Delta \tau}-q_{1} \alpha a /(\lambda b)\left(\mathrm{e}^{-b \Delta \tau}-1\right) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cdots \\ \Delta L_{1}(m \Delta \tau)=-q_{1} \alpha a /(\lambda b)\left(\mathrm{e}^{-m b \Delta \tau}-1\right)= \\ \ \ \ \ \ \ \ \ \ \ \ \ \Delta L_{1}((m-1) \Delta \tau) \mathrm{e}^{-b \Delta \tau}- \\ \ \ \ \ \ \ \ \ \ \ \ \ q_{1} \alpha a /(\lambda b)\left(\mathrm{e}^{-b \Delta \tau}-1\right) \end{array}\right. $ | (9) |
2) 在mΔτ时刻一维杆左端热流密度变为q2,此时视为第二阶段的初始时刻,初始温度为
| $ \begin{array}{l} \theta _0^2(x) = \sum\limits_{n = 1}^\infty {\left( {{k_1}(n,m\Delta \tau ) + {k_2}(n,m\Delta \tau )} \right)} \cos \frac{{n{\rm{ \mathsf{ π} }}}}{L}x - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {q_1}a/(\lambda bL)\left( {{{\rm{e}}^{ - mb\Delta \tau }} - 1} \right) \end{array} $ | (10) |
因此,第二阶段热变形:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {\Delta {L_2}(\Delta \tau ) = - {q_2}\alpha a/(\lambda b)\left( {{{\rm{e}}^{ - b\Delta \tau }} - 1} \right) + \alpha {{\rm{e}}^{ - b\Delta \tau }}\int_0^L {\theta _0^2} (x){\rm{d}}x = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {q_2}\alpha a/(\lambda b)\left( {{{\rm{e}}^{ - b\Delta \tau }} - 1} \right) - {q_1}\alpha a/(\lambda b){{\rm{e}}^{ - b\Delta \tau }}\left( {{{\rm{e}}^{ - mb\Delta \tau }} - } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1) = \Delta {L_1}(m\Delta \tau ){{\rm{e}}^{ - b\Delta \tau }} - {q_2}\alpha a/(\lambda b)\left( {{{\rm{e}}^{ - b\Delta \tau }} - 1} \right)} \end{array}\\ \begin{array}{*{20}{l}} {\Delta {L_2}(2\Delta \tau ) = \alpha {{\rm{e}}^{ - 2b\Delta \tau }}\int_0^L {\theta _0^2} (x){\rm{d}}x - {q_2}\alpha a/(\lambda b)\left( {{{\rm{e}}^{ - 2b\Delta \tau }} - 1} \right) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {q_1}\alpha a/(\lambda b){{\rm{e}}^{ - 2b\Delta \tau }}\left( {{{\rm{e}}^{ - mb\Delta \tau }} - 1} \right) - {q_2}\alpha a/(\lambda b)\left( {{{\rm{e}}^{ - 2b\Delta \tau }} - } \right.}\\ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1) = \Delta {L_2}(\Delta \tau ){{\rm{e}}^{ - b\Delta \tau }} - {q_2}\alpha a/(\lambda b)\left( {{{\rm{e}}^{ - b\Delta \tau }} - 1} \right),\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots \end{array} \end{array}\\ \begin{array}{*{20}{l}} {\Delta {L_2}(k\Delta \tau ) = \alpha {{\rm{e}}^{ - kb\Delta \tau }}\int_0^L {\theta _0^2} (x){\rm{d}}x - {q_2}\alpha a/(\lambda b)\left( {{{\rm{e}}^{ - kb\Delta \tau }} - } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1) = - {q_1}\alpha a/(\lambda b){{\rm{e}}^{ - kb\Delta \tau }}\left( {{{\rm{e}}^{ - mb\Delta \tau }} - 1} \right) - {q_2}\alpha a/}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\lambda b)\left( {{{\rm{e}}^{ - kb\Delta \tau }} - 1} \right) = \Delta {L_2}((k - 1)\Delta \tau ){{\rm{e}}^{ - b\Delta \tau }} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {q_2}\alpha a/(\lambda b)\left( {{{\rm{e}}^{ - b\Delta \tau }} - 1} \right)} \end{array} \end{array} \right. $ | (11) |
由上述推导可知,一维杆热变形可表述为
| $ \Delta L(n \Delta \tau)=C_{1} \Delta L((n-1) \Delta \tau)+C_{2}(q) $ | (12) |
式(12)为一阶自回归形式,即当前时刻的热变形可以由上一时刻的热变形推导得到。式中:
| $ C_{1}=\mathrm{e}^{-b \Delta \tau} $ | (13) |
| $ C_{2}(q)=-q \alpha a /(\lambda b)\left(\mathrm{e}^{-b \Delta \tau}-1\right) $ | (14) |
由式(13)和式(14)中可看出,C1与一维杆物理特性及时间间隔Δτ相关,而一维杆物理特性通常可以认为是固定不变的,因此在时间间隔选定后,C1可视为常数。C2(q)与一维杆物理特性、时间间隔及热流密度相关,在一维杆物理特性和时间间隔确定的条件下,系数C2与热流密度q成正比。
主轴在实际使用时为三维传热,而且结构比一维杆要复杂很多,散热系数等边界条件也不易精确确定。因此本节的推导只是为主轴热误差提供一种建模的数学形式,并为不同转速(热流密度)下模型系数的修正提供一定的理论依据,而模型的实际系数需要根据实验测得的数据进行确定。
2 一阶自回归模型的有限元仿真对一阶自回归模型进行有限元仿真。取有限元单元类型为brick 20node 226,一维杆R=0.1 m,长度L=0.8 m,导热系数λ=50 W/(m·K),密度ρ=7 850 kg/m3,比热容c=460 J/(kg·℃),弹性模量E=206 GPa,泊松比为0.3,热膨胀系数为12×10-6/K,表面传热系数h=55 W/(m2·K),设定环境温度、杆的初始温度以及参考温度均为20 ℃。
为一维杆施加热流密度时以工厂典型的零件加工过程为参考,即上午加工4.0 h,中午停机1.5 h,下午加工4.0 h,最后停机14.5 h完成一天的生产过程。另外,机床在加工不同的零件时,加工工艺的不同导致主轴受热的热流密度不同。因此,进行两组计算,分别取升温时的热流密度为2 000 W/m2和3 000 W/m2,降温时的热流密度为0。设自回归模型时间间隔Δτ=30 s,则计算可得C1=e-bΔτ≈0.990 9,C2(2000)≈0.198 5,C2(3 000)≈0.297 7,C2(0)=0。
利用得到的一阶自回归模型系数计算一维杆热变形,并与有限元仿真数据进行对比,结果如图 2和图 3所示。可以看出, 前述一阶自回归建模方法可有效描述一维杆在变化热源条件下的热变形规律,但是也存在误差:一方面是由于在进行有限元在计算时并不是单纯的一维传热,还存在径向的热传导与变形;另一方面是数值计算方法本身存在的误差。
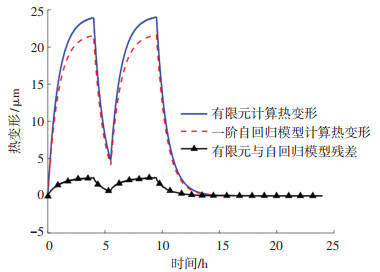
|
图 2 有限元与自回归模型计算热变形对比(q =2 000 W/m2) Fig. 2 Comparison between finite element method and autoregressive model in calculating thermal deformation (q=2 000W/m2) |
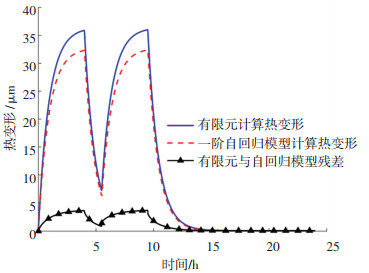
|
图 3 有限元与自回归模型计算热变形对比(q =3 000W/m2) Fig. 3 Comparison between finite element method and autoregressive model in calculating thermal deformation (q=3000W/m2) |
在实际使用时机械主轴采用双端轴承支撑结构,即为双端受热。杨建国等[16]经研究指出,一维杆在单端热源条件下的热变形规律可以推广至双端热源。因此,第1、2节的分析结果可应用至实际主轴的热变形。本研究以海德曼T65车床为对象,进行主轴热伸长一阶自回归建模方法的验证。温度测量采用PT100温度传感器,量程为-20~100 ℃,精度为A级;热变形测量采用合肥置信WD502A型电涡流传感器,量程为2 mm,非线性误差为0.5%,分辨率为0.2 μm。温度点布置见图 4(a)。实验时,将涡流传感器调整至量程中部以减少非线性误差,并采用连续启停的方式,以60 s为一个周期。在一个周期内主轴运转55 s后准停在某一固定位置5 s用于位移数据的采集。这种测量方式可以减少主轴转动时的跳动带来的误差以及检棒自身的制造误差。
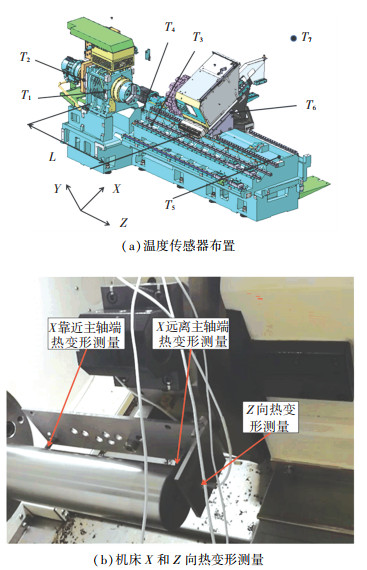
|
T1—主轴箱前部;T2—主轴箱后部;T3—床身中部;T4—床身左;T5—床身右;T6—滑鞍;T7—环境温度 图 4 T65机床热误差实验 Fig. 4 Thermal error experiment on T65 machine tool |
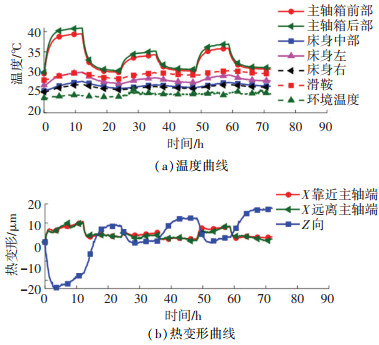
本研究进行了3组实验,以第1组实验数据进行建模,并以另外两组实验数据进行模型鲁棒性验证。3组实验中主轴均运行12 h然后停机降温12 h,转速分别为2 000、1 000和1 500 r/min,测量结果如图 5所示。
|
图 5 T65机床温度和热变形 Fig. 5 Temperature and thermal deformation of T65 machine tool |
由图 5可看出,在转速2 000 r/min的条件下,主轴轴承位置温升达到10 ℃以上,会使主轴箱在竖直方向以及主轴在轴向产生较大的热变形,从而影响机床的加工精度。床身整体温升较小,在靠近主轴箱处温升稍大,但是因为床身尺寸较大,其热变形对加工精度的影响不可忽略。由热变形曲线可知,机床在X向热变形较小,基本控制在10 μm以内,Z向热变形较大,当主轴转速为2 000 r/min时,Z向热变形达到30 μm。本文依据一维杆轴向热变形规律推导得到一阶自回归模型,而且机床X向热误差基本满足加工要求,因此本文主要针对机床Z向热变形进行模型验证及补偿。
由机床结构分析可知,机床Z向热变形主要受床身和主轴的热膨胀影响,其中床身热膨胀使传感器架和检棒之间的距离变大,而主轴热膨胀使传感器架和检棒之间的距离变小。在机床升温初始阶段,主轴温升较快,其热变形占主导地位;升温一段时间后,主轴温升变缓,床身的热变形占主导地位。这就是机床Z向热变形曲线先迅速变小,一段时间后变平缓甚至增大的原因。因此机床Z向热误差为
| $ \Delta L_{Z}=\Delta L_{\text {bed }}-\Delta L_{\text {sp }} $ | (15) |
式中:ΔLbed为床身Z向热变形,ΔLsp为主轴Z向热变形。
床身的热膨胀变形为
| $ \Delta L_{\text {bed }}=\alpha * L * \Delta T_{3} $ | (16) |
式中:L为主轴箱后部至X轴丝杠位置的床身长度,约为1.2 m,如图 4(a)中所示,α为铸铁的热膨胀系数,取10×10-6/℃,ΔT3为床身中部位置的温升,近似视为床身的平均温升。
对于主轴的热膨胀变形,采用式(12)所述的一阶自回归方法进行估计,其中时间间隔Δτ=60 s,主轴的物理特性虽为常数但是无法准确获取,这里通过最小二乘法估计主轴转速n=2 000 r/min时模型系数,得C1=0.995 5,C2n=2 000=0.22,C2n=0=0。
综上所述,基于一阶自回归方法得到的模型为
| $ \left\{\begin{array}{l} \Delta L_{\mathrm{sp}}^{n=2\ 000}(0)=0 \\ \Delta L_{\mathrm{sp}}^{n=2\ 000}(\tau)=0.995\ 5 \times \Delta L_{\mathrm{sp}}^{n=2\ 000}(\tau-\Delta \tau)+0.22 \\ \Delta L_{\mathrm{zar}}^{n=2\ 000}(\tau)=-\Delta L_{\mathrm{sp}}^{n=2\ 000}(\tau)+12 \times \Delta T_{3}(\tau) \end{array}\right. $ | (17) |
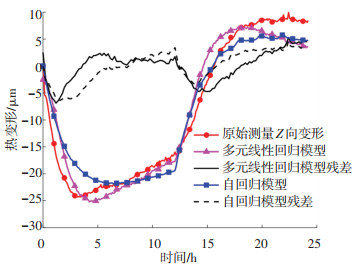
式中ΔLzarn=2000(τ)为采用自回归模型计算得到的机床Z向热变形,模型拟合结果如图 6所示。图 6中的多元线性回归模型利用主轴箱前部、主轴箱后部、床身中部和床身左部4个测点的温升进行建模,通过最小二乘法估计模型系数,模型形式如下:
|
图 6 机床Z向热误差建模(n =2 000 r/min) Fig. 6 Modeling of machine tool thermal error in Z-direction (n= 2 000 r/min) |
| $ \begin{aligned} \Delta L_{\mathrm{zmlr}}=&-2.544\ 4-1.411\ 8 \Delta T_{1}+0.354\ 3 \Delta T_{2}+\\ & 26.417\ 6 \Delta T_{3}-20.741\ 0 \Delta T_{4} \end{aligned} $ | (18) |
从图 6的曲线形式可初步判断出自回归模型的残差不满足白噪声的特性。为进一步判断,本文对自回归模型的残差进行LB检验,构造的统计量为
| $ Q=n(n+2) \sum\limits_{k=1}^{m} \frac{\hat{\rho}_{k}^{2}}{n-k} $ | (19) |
式中:n为样本数,m为滞后阶数,
| 表 1 自回归模型残差的LB检验 Tab. 1 LB test for residuals of autoregressive model |
由图 6可知,一阶自回归建模方法与多元线性回归建模方法对于建模数据具有相近的拟合精度,拟合残差基本控制在±5 μm。但是,多元线性回归模型依据残差平方和最小标准对数据进行拟合,模型系数缺乏物理意义。从式(18)中可以看出多元线性回归模型床身的系数偏大,该模型对床身温度的波动较为敏感。
3.2 一阶自回归模型鲁棒性验证为验证一阶自回归模型的鲁棒性,用前述建立的模型预测主轴转速为1 000、1 500 r/min时机床Z向热变形,并与多元线性回归模型进行对比。
由第1、2小节可知,利用一阶自回归方法建模时,对于不同的转速,需要依据热流密度估计系数C2(q),而这里需要依据前述得到的C2n=2 000估计C2n=1 000和C2n=1 500。从式(5)的温度场分布函数可知,某一固定位置x在τ时刻的温升与热流密度q成正比。因此,本文依据主轴箱后部温度在前100 min的温升数据(见表 2)估计不同转速下的热流密度关系。
| 表 2 不同转速下主轴箱后端在前100 min内的温升 Tab. 2 Temperature rise of the rear position of headstock during the first 100 min under different rotating speeds |
由表 2可得:
| $ \frac{C_{2}^{n=2\ 000}}{C_{2}^{n=1000}}=\frac{q_{n=2\ 000}}{q_{n=1\ 000}} \approx \frac{7.46}{3.02}=2.47 $ | (20) |
| $ \frac{C_{2}^{n=2\ 000}}{C_{2}^{n=1\ 500}}=\frac{q_{n=2\ 000}}{q_{n=1\ 500}} \approx \frac{7.46}{4.11}=1.82 $ | (21) |
求得C2n=1 000=0.08 9,C2n=1 500=0.121。因此,在主轴转速1 000、1 500 r/min条件下自回归模型为
| $ \left\{\begin{array}{l} \Delta L_{\mathrm{sp}}^{n=1\ 000}(0)=0 \\ \Delta L_{\mathrm{sp}}^{n=1\ 000}(\tau)=0.995\ 5 \times \Delta L_{\mathrm{sp}}^{n=1\ 000}(\tau-\Delta \tau)+0.089 \\ \Delta L_{\mathrm{zar}}^{n=1\ 000}(\tau)=-\Delta L_{\mathrm{sp}}^{n=1\ 000}(\tau)+12 \times \Delta T_{3}(\tau) \end{array}\right. $ | (22) |
| $ \left\{\begin{array}{l} \Delta L_{\mathrm{sp}}^{n=1\ 500}(0)=0 \\ \Delta L_{\mathrm{sp}}^{n=1\ 500}(\tau)=0.995\ 5 \times \Delta L_{\mathrm{sp}}^{n=1\ 500}(\tau-\Delta \tau)+0.121 \\ \Delta L_{\mathrm{zar}}^{n=1\ 500}(\tau)=-\Delta L_{\mathrm{sp}}^{n=1\ 500}(\tau)+12 \times \Delta T_{3}(\tau) \end{array}\right. $ | (23) |
利用求得的自回归模型预测机床在转速为1 000、1 500 r/min时Z向热变形,并与式(18)的多元线性回归模型的结果进行对比,如图 7所示。

|
图 7 机床Z向热误差预测 Fig. 7 Prediction of machine tool thermal error in Z-direction |
从图 7中可以看出,在主轴转速为1 000 r/min时,一阶自回归模型预测残差为4 μm,预测精度为69%;多元线性回归模型的预测残差为6 μm,预测精度为54%。在主轴转速为1 500 r/min时,一阶自回归模型预测残差为5 μm,预测精度为70%;多元线性回归模型预测残差为9 μm,预测精度为47%。因此,一阶自回归模型对于非建模工况具有更好的精度保持性。
3.3 机床Z向热误差补偿利用前述分析结果对T65机床进行热误差补偿。本实验所用T65机床采用西门子828D数控系统,具有专用的热误差补偿接口,西门子系统将热误差补偿值分为与位置无关的补偿值和与位置相关的补偿值,其补偿原理为
| $ \Delta K_{Z}=K_{0}(T)+\tan \beta(T) \times\left(P_{Z}-P_{0}\right) $ | (24) |
式中:ΔKZ为位置PZ上的温度补偿值,K0(T)为与位置无关的补偿值,PZ为轴的实际位置,P0为轴的参考位置,tan β(T)为与位置相关的温度补偿的系数。
本文只考虑机床Z向与位置无关的热误差。利用自主开发的温度补偿模块采集温度数据,并将式(17)建立的一阶自回归热误差模型写入模块内部计算热误差补偿量,通过将模块并口与西门子PP 72/48D 2/2A PN外设模块的X111口连接,将温度和补偿量数据传输至PLC,编写PLC程序将补偿量写至Z轴的SD43900参数中。为实现热误差补偿,需将参数MD32750设定为1,即与位置无关的温度补偿功能生效,通过“垂度补偿+温度补偿”参数可实时查看生效的补偿值。
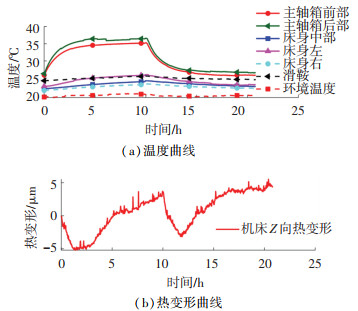
实施热误差补偿后,机床主轴转速为2 000 r/min时Z向热变形测量结果见图 8。从图 8中可以看出,机床Z向热误差控制在10 μm内,满足工厂的实际使用需求,从而验证了一阶自回归模型的有效性。
|
图 8 实施热误差补偿后机床Z向热变形(n =2 000 r/min) Fig. 8 Thermal deformation of machine tool in Z-direction after thermal error compensation (n=2 000 r/min) |
本文提出了变热源条件下主轴轴向热变形的一阶自回归建模方法,并通过有限元仿真及实验验证了模型的有效性,主要结论如下:
1) 一阶自回归建模形式符合主轴在变热源条件下的物理变形规律,建模鲁棒性比多元线性回归更高,并且不受伪滞后效应的影响。
2) 自回归模型系数C1是与主轴物理特性及时间间隔Δτ相关的常数;C2(q)是与主轴物理特性、时间间隔及热流密度相关的系数,当主轴转速不同时,C2(q)需要依据热流密度进行修正。
本文提出的主轴热变形一阶自回归建模方法适用于机床环境温度基本恒定的情况。当车间环境温度波动较大时,机床温度场分布和热变形规律会发生较大改变,从而影响热误差模型精度。如何使模型适应环境温度的变化还需进一步研究。
| [1] |
BRYAN J. International status of thermal error research[J]. CIRP Annals, 1990, 39(2): 645. DOI:10.1016/s0007-8506(07)63001-7 |
| [2] |
MAYR J, JEDRZEJEWSKI J, UHLMANN E, et al. Thermal issues in machine tools[J]. CIRP Annals-Manufacturing Technology, 2012, 61(2): 771. DOI:10.1016/j.cirp.2012.05.008 |
| [3] |
PAHK H J, LEE S W. Thermal error measurement and real time compensation system for the CNC machine tools incorporating the spindle thermal error and the feed axis thermal error[J]. The International Journal of Advanced Manufacturing Technology, 2002, 20(7): 487. DOI:10.1007/s001700200182 |
| [4] |
孙志超, 陶涛, 黄晓勇, 等. 车床主轴与进给轴耦合热误差建模及补偿研究[J]. 西安交通大学学报, 2015, 49(7): 105. SUN Zhichao, TAO Tao, HUANG Xiaoyong, et al. Modeling and compensation of coupled thermal error of spindle and feed shafts[J]. Journal of Xi'an Jiaotong University, 2015, 49(7): 105. DOI:10.7652/xjtuxb201507018 |
| [5] |
丛明, 李泳耀, 孙宗余, 等. 机床温度测点优化方法研究及试验验证[J]. 大连理工大学学报, 2015, 55(6): 582. CONG Ming, LI Yongyao, SUN Zongyu, et al. An optimization method of temperature measuring points for machine tools and experimental verification[J]. Journal of Dalian University of Technology, 2015, 55(6): 582. DOI:10.7511/dllgxb201506004 |
| [6] |
LI Bo, TIAN Xitian, ZHANG Min. Thermal error modeling of machine tool spindle based on the improved algorithm optimized BP neural network[J]. The International Journal of Advanced Manufacturing Technology, 2019, 105(9): 1497. DOI:10.1007/s00170-019-04375-w |
| [7] |
MA Chi, ZHAO Liang, MEI Xuesong, et al. Thermal error compensation of high-speed spindle system based on a modified BP neural network[J]. The International Journal of Advanced Manufacturing Technology, 2017, 89(9/10/11/12): 3071. DOI:10.1007/s00170-016-9254-4 |
| [8] |
GUO Qianjian, FAN Shuo, XU Rufeng, et al. Spindle thermal error optimization modeling of a five-axis machine tool[J]. Chinese Journal of Mechanical Engineering, 2017, 30(3): 746. DOI:10.1007/s10033-017-0098-0 |
| [9] |
张宏韬, 姜辉, 杨建国. 模糊神经网络理论在数控机床热误差补偿建模中的应用[J]. 上海交通大学学报, 2009, 43(12): 1950. ZHANG Hongtao, JIANG Hui, YANG Jianguo. Application of fuzzy neural network theory in thermal error compensation modeling of NC machine tool[J]. Journal of Shanghai Jiaotong University, 2009, 43(12): 1950. DOI:10.16183/j.cnki.jsjtu.2009.12.021 |
| [10] |
苗恩铭, 龚亚运, 成天驹, 等. 支持向量机回归在数控加工中心热误差建模中的应用[J]. 光学精密工程, 2013, 21(4): 980. MIAO Enming, GONG Yayun, CHENG Tianju, et al. Application of support vector regression machine to thermal error modelling of machine tools[J]. Optics and Precision Engineering, 2013, 21(4): 980. DOI:10.3788/OPE.20132104.0980 |
| [11] |
林伟青, 傅建中, 许亚洲, 等. 基于最小二乘支持向量机的数控机床热误差预测[J]. 浙江大学学报(工学版), 2008, 42(6): 905. LIN Weiqing, FU Jianzhong, XU Yazhou, et al. Thermal error prediction of numerical control machine tools based on least square support vector machine[J]. Journal of Zhejiang University (Engineering Science), 2008, 42(6): 905. DOI:10.3785/j.issn.1008-973X.2008.06.001 |
| [12] |
TAN Feng, YIN Ming, WANG Lin, et al. Spindle thermal error robust modeling using LASSO and LS-SVM[J]. The International Journal of Advanced Manufacturing Technology, 2018, 94(9): 2861. DOI:10.1007/s00170-017-1096-1 |
| [13] |
要小鹏, 殷国富, 李光明. 基于OE_CM算法的机床主轴热误差建模与补偿分析[J]. 中国机械工程, 2015, 26(20): 2757. YAO Xiaopeng, YIN Guofu, LI Guangming. Thermal error modeling and compensation analysis based on OE-CM algorithm for machine tool spindles[J]. China Mechanical Engineering, 2015, 26(20): 2757. DOI:10.3969/j.issn.1004-132X.2015.20.011 |
| [14] |
雷春丽, 芮执元, 刘军, 等. 两种工况下电主轴热误差的组合预测模型[J]. 西安交通大学学报, 2011, 45(7): 50. LEI Chunli, RUI Zhiyuan, LIU Jun, et al. Thermal error combined forecasting model on motorized spindle under two operating conditions[J]. Journal of Xi'an Jiaotong University, 2011, 45(7): 50. |
| [15] |
YANG Hong, NI Jun. Dynamic modeling for machine tool thermal error compensation[J]. Journal of Manufacturing Science and Engineering, 2003, 125(2): 246. DOI:10.1115/1.1557296 |
| [16] |
杨建国, 范开国. 数控机床主轴热变形伪滞后研究及主轴热漂移在机实时补偿[J]. 机械工程学报, 2013, 49(23): 131. YANG Jianguo, FAN Kaiguo. Research on the thermal deformation pseudo-lag and real-time compensation for CNC machine tool spindle[J]. Journal of Mechanical Engineering, 2013, 49(23): 131. DOI:10.3901/JME.2013.23.129 |
| [17] |
谢飞, 王玲, 谭峰, 等. 基于新陈代谢原理的机床热误差伪滞后建模[J]. 哈尔滨工业大学学报, 2019, 51(7): 154. XIE Fei, WANG Ling, TAN Feng, et al. Pseudo-hysteresis modeling for machine tool thermal error based on metabolic theory[J]. Journal of Harbin Institute of Technology, 2019, 51(7): 154. DOI:10.11918/j.issn.0367-6234.201807117 |
| [18] |
LI Yang, ZHAO Wanhua, WU Wenwu, et al. Thermal error modeling of the spindle based on multiple variables for the precision machine tool[J]. The International Journal of Advanced Manufacturing Technology, 2014, 72(9/10/11/12): 1415. DOI:10.1007/s00170-014-5744-4 |
| [19] |
杨军, 梅雪松, 冯斌, 等. 时序分析在电主轴热误差建模中的应用[J]. 计算机集成制造系统, 2015, 21(5): 1359. YANG Jun, MEI Xuesong, FENG Bin, et al. Application of time series analysis in thermal error modeling of motorized spindle[J]. Computer Integrated Manufacturing Systems, 2015, 21(5): 1359. DOI:10.13196/j.cims.2015.05.025 |
| [20] |
YANG Hong, NI Jun. Dynamic neural network modeling for nonlinear, nonstationary machine tool thermally induced error[J]. International Journal of Machine Tools and Manufacture, 2005, 45(4/5): 455. DOI:10.1016/j.ijmachtools.2004.09.004 |
| [21] |
王海同, 李铁民, 王立平, 等. 机床热误差建模研究综述[J]. 机械工程学报, 2015, 51(9): 121. WANG Haitong, LI Tiemin, WANG Liping, et al. Review on thermal error modeling of machine tools[J]. Journal of Mechanical Engineering, 2015, 51(9): 121. DOI:10.3901/jme.2015.09.119 |
| [22] |
FRASER S, ATTIA M H, OSMAN M O M. Modelling, identification and control of thermal deformation of machine tool structures, part 1: concept of generalized modelling[J]. Journal of Manufacturing Science and Engineering, 1998, 120(3): 625. DOI:10.1115/1.2830167 |
| [23] |
HOU Ruisheng, DU Hongyang, YAN Zongzhuo, et al. The modeling method on thermal expansion of CNC lathe headstock in vertical direction based on MOGA[J]. The International Journal of Advanced Manufacturing Technology, 2019, 103(2): 3629. DOI:10.1007/s00170-019-03728-9 |
| [24] |
颜宗卓, 陶涛, 侯瑞生, 等. 机床电主轴热特性卷积建模研究[J]. 西安交通大学学报, 2019, 63(6): 1. YAN Zongzhuo, TAO Tao, HOU Ruisheng, et al. Convolution modeling for thermal properties of motorized spindle in machine tools[J]. Journal of Xi'an Jiaotong University, 2019, 63(6): 1. DOI:10.7652/xjtuxb201906001 |
 2021, Vol. 53
2021, Vol. 53


