随着空间技术和机器人技术的发展,空间机器人成为实现在轨服务的关键技术途径。空间机器人在轨捕获目标是实现在轨服务的基本环节,例如利用空间机器人捕获空间碎片、待维修航天器、待装配零部件等。其主要涉及4个基本阶段,即观测、接近、抓捕和抓捕后系统的自稳定。在接近目标的过程中,空间机器人的运动控制精度决定了其能否成功捕获目标。由于微重力环境下空间机器人基座和机械臂之间存在着动力学耦合,且太空中存在各种干扰力/力矩的作用,使得空间机器人系统的控制问题变得十分复杂。
针对空间机器人系统的运动控制问题,国内外学者进行了广泛的研究。控制策略可分为两种方式,即基座最小干扰控制和主动控制。第一种方式主要是通过使空间机器人的机械臂按特定的轨迹进行运动,从而减小对基座姿态的干扰,如文献[1-3]。然而,要实现空间机器人按期望的运动轨迹运动,同时对基座无干扰,往往以机械臂的冗余自由度为前提,从而造成了机械臂结构的复杂性和高成本。因此,在空间机器人机械臂运动的同时,通过推进器或飞轮对基座实施姿态的主动控制十分必要。
基于准确的空间机器人动力学模型,PID控制和非线性控制方法被应用于空间机器人的主动运动控制[4-8],然而,实际空间机器人的动力学参数很难准确给出,且必须考虑太空环境的干扰。针对系统的不确定性问题,自适应控制方法通过实时更新控制参数来保证系统的稳定性,被广泛应用于空间机器人的运动控制[9-15]。此外,滑模控制可根据系统的动态特性设计滑模面,从而约束运动误差至滑模面并沿其收敛到原点,被应用于系统参数不确定情况下的控制问题。但由于控制输入的不连续性,传统的滑模控制会使系统产生抖振,该现象可能会造成系统共振甚至结构性破坏。为了解决该问题,二阶滑模控制器被应用于空间机器人的运动控制[16-18]。文献[19]将一种基于滑模控制思想的鲁棒控制器用于非合作目标的抓捕过程。文献[20-22]通过滑模控制实现了绳系空间机器人对空间碎片的抓捕。针对控制力矩陀螺驱动的空间机器人的轨迹追踪问题,文献[23]提出了一种自适应滑模控制方法,但该控制器不能应用于控制参数阈值不确定的情形。陈力等[24]针对漂浮基空间机器人双臂捕获航天器后系统镇定力和运动控制问题,设计了闭链混合体系统夹持操作的镇定运动力/位置模糊滑模控制方案。然而,滑模控制算法在维持良好鲁棒性的同时,往往需要较大的非确定控制力矩,且很难确保很高的控制精度。
本文针对系统不确定性和干扰存在的背景,基于滑模控制和自适应控制思想,为了克服传统滑模控制存在抖振现象和精度较低的特点,引入可变增益,根据空间机器人的不确定度和运动状态对其进行实时调整,提高了控制精度,实现了对空间机器人基座姿态和机械臂运动的协同控制。此外,应用Simscape Multibody软件模块,通过与空间机器人三维模型运动输出进行对比,完成了理论动力学模型准确性的验证,并实现了空间机器人运动的可视化。在此基础上,将提出的控制算法作用于空间机器人三维模型,通过与传统计算力矩法进行对比,证明了该算法具有很好的鲁棒性和更高的控制精度。1空间机器人系统模型
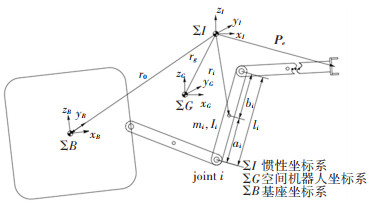
1.1 场景描述本文主要研究空间机器人接近待捕获目标的运动过程中,其基座姿态和机械臂运动的协同控制算法。如图 1所示,空间机器人主要由可移动基座和多自由度机械臂组成。场景的具体描述如下:
|
图 1 空间机器人模型 Fig. 1 Space robot model |
1) 机械臂由旋转关节连接的n个刚性连杆组成,则空间机器人可看作由n+1个单体串联而成的刚体,i=0表示空间机器人的基座,i=1至n代表连杆。因此,空间机器人有n+6个自由度,其中n个自由度表示机械臂的运动,其余6个自由度表示基座的位姿。图中空间机器人的各参数定义如表 1所示。
| 表 1 空间机器人参数及其含义 Tab. 1 Parameters of space robot and their meaning |
2) 在接近目标的过程中,空间机器人基座的位置不受控制,且目标始终保持在空间机器人的工作空间内。
3) 推进器在接近目标的过程中不点火,基座的姿态由飞轮进行调整,作用于系统的外部力/力矩可忽略不计,线动量和角动量守恒定律均成立。
1.2 空间机器人的动力学模型令ΦS=[α, β, γ]T代表基座的姿态,ΦM=[Φ1, Φ2…Φn]T代表机械臂关节的角度,Φ=[ΦST, ΦMT]T代表广义坐标,τ=[τx, τy, τz, τ1, τ2, …, τn]T代表基座姿态调整力矩和关节输入力矩,根据拉格朗日法,得到空间机器人的动力学方程如下:
| $ \mathit{\boldsymbol{H \boldsymbol{\ddot \varPhi} }} + \mathit{\boldsymbol{C \boldsymbol{\dot \varPhi} }} = \mathit{\boldsymbol{\tau }} $ | (1) |
式中:H∈R(n+3)×(n+3)代表空间机器人的惯量矩阵,正定且对称;
若空间机器人期望轨迹为Φd,则轨迹跟踪误差向量可定义为e1=Φ-Φd,e2=
| $ \left\{\begin{array}{l} \dot{\boldsymbol{e}}_{1}=\boldsymbol{e}_{2} \\ \dot{\boldsymbol{e}}_{2}=-\boldsymbol{H}^{-1} \boldsymbol{C}\left(\boldsymbol{e}_{2}+\dot{\boldsymbol{\varPhi}}_{d}\right)-\ddot{\boldsymbol{\varPhi}}_{d}+\boldsymbol{H}^{-1} \boldsymbol{\tau} \end{array}\right. $ | (2) |
将状态方程(2)写成如下形式:
| $ \begin{aligned} \dot{e}=&\left[\begin{array}{cc} \boldsymbol{e}_{2} & \\ -\boldsymbol{H}^{-1} \boldsymbol{C}\left(\boldsymbol{e}_{2}+\dot{\boldsymbol{\varPhi}}_{d}\right) & -\ddot{\boldsymbol{\varPhi}}_{d} \end{array}\right]+\left[\begin{array}{c} \boldsymbol{O} \\ \boldsymbol{H}^{-1} \end{array}\right] \boldsymbol{\tau}=\\ &\boldsymbol{f}^{\prime}(\boldsymbol{e}, t)+\boldsymbol{g}(\boldsymbol{e}) \boldsymbol{\tau} \end{aligned} $ | (3) |
式中:
考虑到系统的不确定性(当H和C矩阵中的参数不完全已知或参数不精确的情况下),令Ĥ=H+ΔH,其中Ĥ代表H的估计值,ΔH代表矩阵H的不确定度。构造一个力矩矢量τ*,τ*是将τ经对角化获得。τ*可以表示为
| $ \boldsymbol{\tau}^{*}=\hat{\boldsymbol{H}}^{-1} \boldsymbol{\tau} $ | (4) |
将τ=(Ĥτ*=H+ΔH)τ*代入到ė2的表达式中,得
| $ \begin{aligned} \dot{\boldsymbol{e}}_{2}=&-\boldsymbol{H}^{-1} \boldsymbol{C}\left(\boldsymbol{e}_{2}+\dot{\boldsymbol{\varPhi}}_{d}\right)-\ddot{\boldsymbol{\varPhi}}_{d}+\boldsymbol{H}^{-1}(\boldsymbol{H}+\Delta \boldsymbol{H}) \boldsymbol{\tau}^{*}=\\ & \boldsymbol{f}(\boldsymbol{e}, t)+\boldsymbol{\tau}^{*}+\boldsymbol{h}(\boldsymbol{e}, t) \end{aligned} $ | (5) |
式中f(e, t)=-H-1C(e2+
此部分内容旨在开发相应的控制算法以控制空间机器人以期望的轨迹运动。考虑到控制力矩法是经典的实用的控制方法,通过调节控制参数可达到较好的控制精度和误差收敛速度,目前仍被广泛应用。因此,为了给本文提出的可变增益滑模控制器提供参照,基于计算力矩法设计的控制器在下文中也进行了简要的介绍。
2.1 计算力矩法由于传统的PID算法难以直接应用于空间机器人这种强非线性系统,可采用计算力矩法来设计控制方案。其基本思路是:首先在控制回路中引入一非线性控制,使空间机器人系统模型转变为更易于控制的线性定常系统,在此基础上设计PID控制器,实现对空间机器人的运动控制。具体步骤如下:
首先引入控制律
| $ \boldsymbol{\tau}=\boldsymbol{C} \dot{\boldsymbol{\varPhi}}+\boldsymbol{H} \boldsymbol{u} $ | (6) |
式中u为引入的中间变量,将上式代入到空间机器人的动力学方程(1)中,有
| $ H \ddot{\boldsymbol{\varPhi}}+\boldsymbol{C} \dot{\boldsymbol{\varPhi}}=\boldsymbol{C} \dot{\boldsymbol{\varPhi}}+\boldsymbol{H} \boldsymbol{u} $ | (7) |
由于H可逆,故上式等价于一个解耦的线性定常系统
| $ \ddot{\boldsymbol{\varPhi}}=\boldsymbol{u} $ | (8) |
当期望轨迹Φd给定时,引入如下的PID控制律:
| $ \boldsymbol{u}=\ddot{\boldsymbol{\varPhi}}_{d}+\boldsymbol{K}_{d}\left(\dot{\boldsymbol{\varPhi}}-\dot{\boldsymbol{\varPhi}}_{d}\right)+\boldsymbol{K}_{p}\left(\boldsymbol{\varPhi}-\boldsymbol{\varPhi}_{d}\right)=\ddot{\boldsymbol{\varPhi}}_{d}+\boldsymbol{K}_{d} {\dot{\boldsymbol{e}}}_{1}+\boldsymbol{K}_{p} \boldsymbol{e}_{1} $ | (9) |
式中:Kd、Kp均为具有正实数元素的对角阵。结合式(9)和式(10),可得
| $ \ddot{\boldsymbol{e}}_{1}+\boldsymbol{K}_{d} \dot{\boldsymbol{e}}_{1}+\boldsymbol{K}_{p} \boldsymbol{e}_{1}=\bf{0} $ | (10) |
因此,
综上,根据计算力矩法,得到的控制律的完整表达式为
| $ \boldsymbol{\tau}=\boldsymbol{H}\left(\ddot{\boldsymbol{\varPhi}}_{d}+\boldsymbol{K}_{d} \dot{\boldsymbol{e}}_{1}+\boldsymbol{K}_{p} \boldsymbol{e}_{1}\right)+\boldsymbol{C} \dot{\boldsymbol{\varPhi}} $ | (11) |
一个合适的滑模面应当确保系统方程一旦到达滑模面,误差向量就能收敛到0。定义滑模面的方程为
| $ \boldsymbol{\sigma}(\boldsymbol{e})=\left(\frac{\mathrm{d}}{\mathrm{d} t}+\boldsymbol{\varLambda}\right)^{p-1} \boldsymbol{e}_{1}=\dot{\boldsymbol{e}}_{1}+\boldsymbol{\varLambda} \boldsymbol{e}_{1}=\boldsymbol{S e} $ | (12) |
式中:p=2,S∈R(n+3)×2(n+3)定义为
| $ \boldsymbol{S}=[\boldsymbol{\varLambda} \boldsymbol{I}]=\left[\begin{array}{cccccc} \lambda_{1} & & & & 1 & & & \\ & \lambda_{2} & & & & 1 & & \\ & & \ldots & & & & \ldots & \\ & & & \lambda_{n+3} & & & & 1 \end{array}\right] $ |
式中:Λ∈R(n+3)×(n+3)是对角线元素为λi的对角阵,I∈R(n+3)×(n+3)是单位阵。
根据上述表达式可知,系统到达滑模面后,能够得到一系列的常系数线性微分方程,即σi=ė1i+λie1i≡0,i=1, 2,…, n+3。每个方程均具有唯一解e1i=0,从而证明了空间机器人的轨迹跟踪误差能够收敛到零。
2.2.2 控制律的推导设控制力矩τi*满足以下条件:
| $ \begin{array}{c} \left\{\begin{array}{l} \tau_{i}{ }^{*}<\left\{-\left(f_{i}+\lambda_{i} e_{2 i}+h_{i}\right)\right\}_{\min }, \sigma_{i}>0 \\ \tau_{i}{ }^{*}>\left\{-\left(f_{i}+\lambda_{i} e_{2 i}+h_{i}\right)\right\}_{\max }, \sigma_{i}<0 \end{array}\right.\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=1,2, \cdots, n+3 \end{array} $ | (13) |
定理1 在式(13)所示控制律的作用下,系统能够到达并且保持在滑模面σ(e)=0上。
证明 令李雅普诺夫方程为
| $ V=\frac{1}{2} \boldsymbol{\sigma}^{\mathrm{T}} \boldsymbol{\sigma} $ | (14) |
则当σ≠0时满足V>0。求滑模面函数(12)相对于时间的导数,可得
| $ \begin{array}{l} \dot{\boldsymbol{\sigma}}=\frac{\partial \boldsymbol{\sigma}}{\partial \boldsymbol{e}} \dot{\boldsymbol{e}}=\frac{\partial \sigma}{\partial \boldsymbol{e}}\left[\begin{array}{c} \dot{\boldsymbol{e}}_{1} \\ \dot{\boldsymbol{e}}_{2} \end{array}\right]=\boldsymbol{S}\left[\begin{array}{c} \boldsymbol{e}_{2} \\ \boldsymbol{f}(\boldsymbol{e}, t)+\boldsymbol{\tau}^{*}+\boldsymbol{h}(\boldsymbol{e}, t) \end{array}\right]=\\ \left[\begin{array}{c} f_{1}+\lambda_{1} e_{21}+h_{1}+\tau_{1}^{*} \\ f_{2}+\lambda_{2} e_{22}+h_{2}+\tau_{2}^{*} \\ \vdots \\ f_{n+3}+\lambda_{n+3} e_{2, n+3}+h_{n+3}+\tau_{n+3}^{*} \end{array}\right] \end{array} $ | (15) |
则李雅普诺夫方程的微分形式为
| $ \dot{V}=\boldsymbol{\sigma}^{\mathrm{T}} \dot{\boldsymbol{\sigma}}=\sum\limits_{i=1}^{n+3} \sigma_{i}\left(f_{i}+\lambda_{i} e_{2 i}+h_{i}+\tau_{i}^{*}\right) $ | (16) |
从上式可以看出,当控制力矩τi*满足式(13)所示条件时,都有
接下来讨论当考虑系统的不确定性时,系统的控制力矩表达式。根据式(13),可得系统的等效控制力矩τeq*的表达式为
| $ \boldsymbol{\tau}_{\mathrm{eq}i}^{*}=-\hat{f}_{i}-\lambda_{i} e_{2 i}-\hat{h}_{i}=-\lambda_{i} e_{2 i}+\ddot{\varPhi}_{d i}-\hat{\bar{f}}_{i}-\hat{h}_{i} $ | (17) |
式中
| $ \left\{\begin{array}{l} \varDelta \boldsymbol{f}=\max (\|\bar{\boldsymbol{f}}-\hat{\bar{\boldsymbol{f}}}\|) \\ \varDelta \boldsymbol{h}=\max (\|\boldsymbol{h}-\hat{\boldsymbol{h}}\|) \end{array}\right. $ | (18) |
为了使
| $ k_{i}=\varDelta f_{i}+\varDelta h_{i}+\alpha_{r i}>0 $ | (19) |
式中:αri>0为一值很小的正实数。
综上,考虑系统不确定性的控制力矩可以表示为
| $ \begin{aligned} \tau_{i}^{*}=&-\hat{\bar{f}}_{i}-\lambda_{i} e_{2 i}+\ddot{\phi}_{d i}-\left(\varDelta f_{i}+\varDelta h_{i}+\right.\\ &\left.\alpha_{r i}\right) \operatorname{sgn}\left(\sigma_{\mathrm{i}}\right), i=1,2, \cdots, n+3 \end{aligned} $ | (20) |
定理2 在考虑系统不确定性的条件下,式(20)所示的控制律能够保证系统到达且保持在滑模面σ(e)=0上。
证明 将式(20)代入到李雅普诺夫函数的微分表达式(16),则
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \dot{V}=\sum\limits_{i=1}^{n+3} \sigma_{i}\left(f_{i}+\lambda_{i} e_{2 i}+h_{i}+\tau_{i}{}^{*}\right)= \\ \sum\limits_{i=1}^{n+3} \sigma_{i}\left[\left(f_{i}+\lambda_{i} e_{2 i}+h_{i}\right)-\hat{\bar{f}}_{i}-\lambda_{i} e_{2 i}+\ddot{\phi}_{d i}-\right. \\ \left.\left(\varDelta f_{i}+\varDelta h_{i}+\alpha_{r i}\right) \operatorname{sgn}\left(\sigma_{\mathrm{i}}\right)\right]=\sum\limits_{i=1}^{n+3}\left[\sigma_{i}\left(\bar{f}_{i}-\hat{\bar{f}}_{i}\right)+\right. \\ \left.\sigma_{i}\left(h_{i}-\hat{h}_{i}\right)-\left(\varDelta f_{i}+\varDelta h_{i}+\alpha_{r i}\right)\left|\sigma_{\mathrm{i}}\right|\right] \leqslant \sum\limits_{i=1}^{n+3}\left[\left(\mid \bar{f}_{i}-\right.\right. \\ \left.\left.\hat{\bar{f}}_{i} \mid-\varDelta f_{i}\right)\left|\sigma_{i}\right|+\left(\left|h_{i}-\hat{h}_{i}\right|-\varDelta h_{i}\right)\left|\sigma_{i}\right|-\alpha_{r i}\left|\sigma_{i}\right|\right] \end{array} $ | (21) |
由式(18)可知|fi-
实际上,为了节省发射时的燃料消耗,空间机器人应优先设计为轻量级结构,从而其结构会呈现一定的柔性。由于控制力矩中函数sgn(x)的引入,会使得驱动力矩呈现正负值的频繁转换从而引起电机的振动,进而可能导致系统部件之间的共振,甚至破坏系统结构。为了消除此种现象,将sgn(x)函数替换成sat(x)函数,其表达式为
| $ \operatorname{sat}\left(\sigma_{i}\right)=\left\{\begin{array}{cc} \operatorname{sgn}\left(\sigma_{i}\right), \ \ \text { for }\left|\sigma_{i}\right|>\varepsilon \\ \sigma_{i} / \varepsilon,\ \ \text { for }\left|\sigma_{i}\right| \leqslant \varepsilon \end{array}\right. $ | (22) |
式中:ε为一个很小的正值。则控制律的最终表达式为
| $ \begin{array}{c} \tau_{i}^{*}=-\hat{\bar{f}}_{i}-\lambda_{i} e_{2 i}+\ddot{\phi}_{d i}-\left(\varDelta f_{i}+\varDelta h_{i}+\right. \\ \left.\alpha_{r i}\right) \operatorname{sat}\left(\sigma_{\mathrm{i}}\right), i=1,2, \cdots, n+3 \end{array} $ | (23) |
本节主要基于Simulink中的物理仿真工具Simscape Multibody,其支持由CAD软件构建的三维模型的导入,并能输入特定的控制信号,从而进行对空间机器人的理论动力学模型和控制算法的验证。
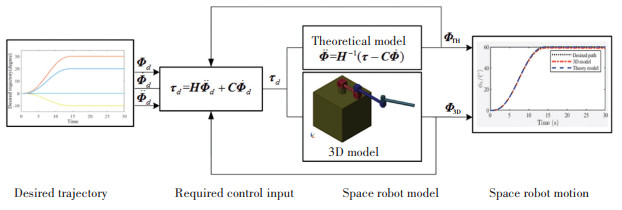
3.1 空间机器人理论动力学模型的验证空间机器人理论动力学模型验证的主要思路如图 2所示。根据规划的期望轨迹(Φd,
|
图 2 理论动力学模型验证示意图 Fig. 2 Schematic diagram of dynamics verification |
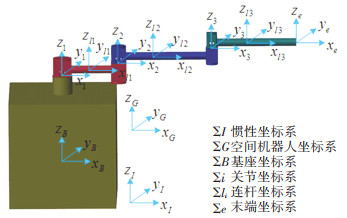
空间机器人由基座、连杆、关节电机、减速器、联轴器等组成,其三维模型和参数分别如图 3和表 2所示。空间机器人的理论动力学模型中的惯量矩阵和非线性项通过MATLAB进行推导获得。Simscape自身具有三维建模功能,但是一般适用于建立较为简单的模型。本文所涉及的空间机器人结构较复杂,在Simscape建模相对繁琐且效率低下。因此,选择在专业的三维建模软件SolidWorks中建立模型,通过Simscape Multibody与SolidWorks的接口模块,将装配体格式的空间机器人三维模型转换为xml格式,再导入到Simscape Multibody建立的模型中。
|
图 3 空间机器人的三维模型及坐标系定义 Fig. 3 3D model and coordinate system of space robot |
| 表 2 空间机器人的参数 Tab. 2 Parameters of space robot |
仿真环境配置的主要步骤如下:
1) 设置环境参数,如重力、基础坐标系、传感器测量坐标系等。
2) 定义关节。在将机器人从SolidWorks中导入Simscape后,机器人各部件之间的连接方式为固定连接。因此需要根据机器人的构型添加相应的转动关节。另外,在添加相应关节时,需要明确机器人各关节间的坐标变换关系,设置合适的变换参数。
3) 对空间机器人的关节施加相应的驱动,主要包括位置驱动和力矩驱动,由于本文中的控制输入信号为力矩,所以此处只涉及力矩驱动。
4) 设置空间机器人的传感器,主要包括关节位置、角速度、角加速度的测量。
空间机器人的期望轨迹通过五次多项式进行规划,其表达式为
| $ \begin{aligned} \boldsymbol{\varPhi}_{d}(t)=& \boldsymbol{\varPhi}(0)+\left(15 t_{n}^{4}-6 t_{n}^{5}-\right.\\ &\left.10 t_{n}^{3}\right)\left(\boldsymbol{\varPhi}(0)-\boldsymbol{\varPhi}\left(t_{f}\right)\right) \end{aligned} $ | (24) |
其中初始角度为Φ(0)=[0, 0, 0, 0, 0, 0]T,终止角度为Φ(tf)=[0, 0, 0, -10°, 20°, 30°]T,tf=15 s为从初始角度运动到终止角度的所需时间,tn=t/tf。
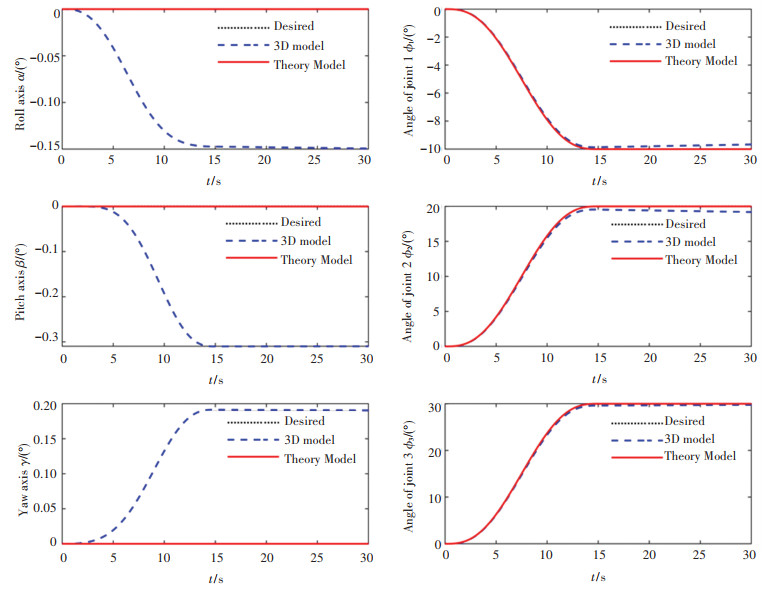
基于上述条件,进行理论动力学模型的仿真验证实验,观察空间机器人理论模型和三维模型的运动输出。如图 4所示,理论模型能够按照预期的关节轨迹值运动,三维模型的角度输出和预期轨迹的最大误差出现在基座俯仰姿态的跟踪上,误差值约为0.3°,误差较小,在可接受的范围内。误差的产生主要是由于在推导理论模型的过程中对极小项的忽略。综上,仿真结果表明了空间机器人的理论动力学模型的准确性,为接下来的控制律验证部分奠定了基础。
|
图 4 理论动力学模型验证 Fig. 4 Theoretical dynamics verification |
控制算法的验证思路如图 5所示:规划期望运动轨迹,根据空间机器人的理论模型和控制算法计算所需力矩,将其输入到三维模型中,测量空间机器人的运动输出,并将其反馈到控制器中,最后计算实际运动轨迹和期望轨迹的误差。
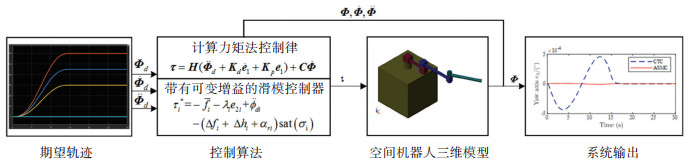
|
图 5 控制算法验证示意图 Fig. 5 Schematic diagram of control algorithm verification |
本节主要对以下两种运动场景进行仿真:
1) 多关节运动;
2) 系统参数不确定条件下控制算法的鲁棒性验证。相关控制参数如表 3所示。
| 表 3 控制参数 Tab. 3 Control parameters |
空间机器人的初始角度为Φ(0)=[0, 0, 0, 0, 0, 0]T,令终止角度Φ(tf)=[0, 0, 0, 30°, 45°, 60°]T,tf=15 s,期望轨迹表达式同式(24)。图 6和图 7分别表示在给定期望运动轨迹时,空间机器人的轨迹跟踪效果和轨迹跟踪误差。
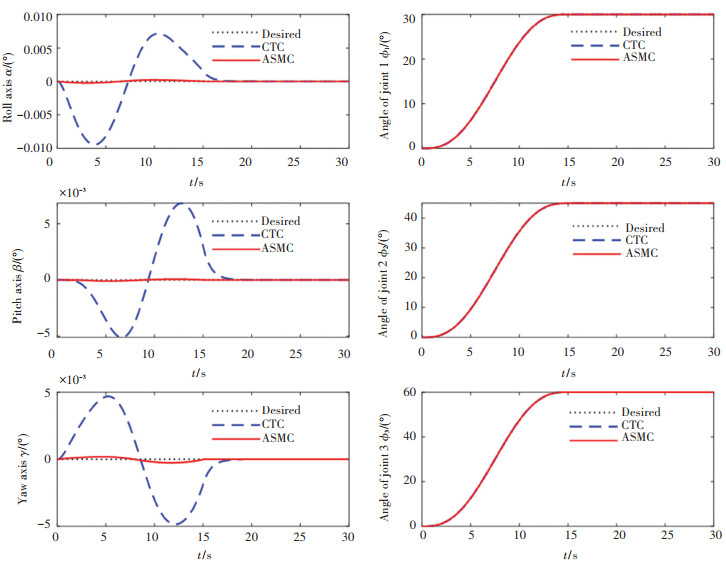
|
图 6 多关节运动时CTC和ASMC的轨迹跟踪效果 Fig. 6 Path tracking of CTC and ASMC for multiple joint motion |
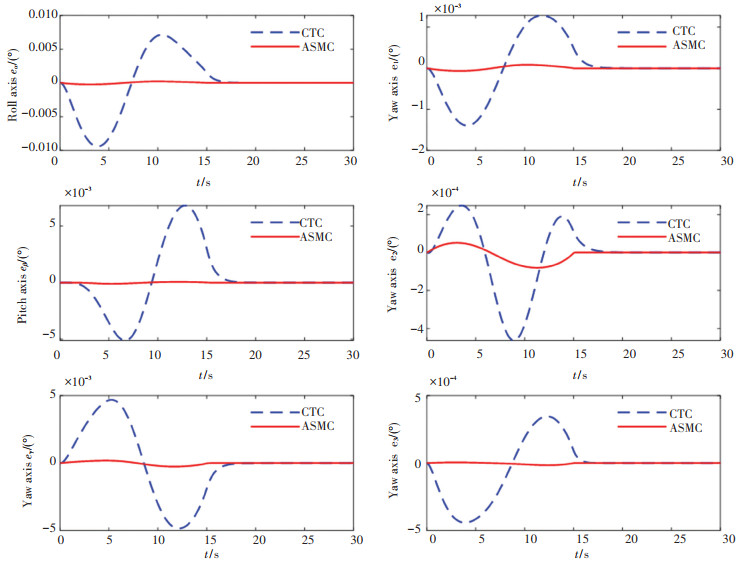
|
图 7 多关节运动时CTC和ASMC的轨迹跟踪误差 Fig. 7 Path tracking error of CTC and ASMC for multiple joint motion |
由图 6和图 7可以看出,在计算力矩法(Computed Torque Control, CTC)和可变增益滑模控制器(Adaptive Sliding Mode Control, ASMC)的作用下,空间机器人都能够实现对期望轨迹的跟踪,跟踪误差分别控制在10-3deg和10-5deg以内,计算力矩法的收敛时间约为18 s,而ASMC算法的收敛时间约为15 s。因此,本文提出的控制算法控制精度较高,且收敛速度较快。
3.2.2 鲁棒性验证为了验证算法的鲁棒性,本文利用加入高斯噪声作为干扰的方法来模拟系统参数不确定时系统的状态。令d=N(0, 0.000 12)Nm,高斯噪声D=[d, d, d, d, d, d]T,作用时间为20 s,其余相关设定同3.2.1。
图 8和图 9分别表示基于上述条件,两种控制器作用下空间机器人的驱动力矩和轨迹跟踪误差。结果表明,无论是计算力矩法还是带有可变增益的滑模控制算法都能够使空间机器人的关节角收敛到期望值,并保持基座的三个姿态角基本不变,说明两种控制器均具有很好的鲁棒性。但相比之下,带有可变增益的滑模控制器的轨迹跟踪误差比计算力矩法的轨迹跟踪误差小,且收敛速度快。
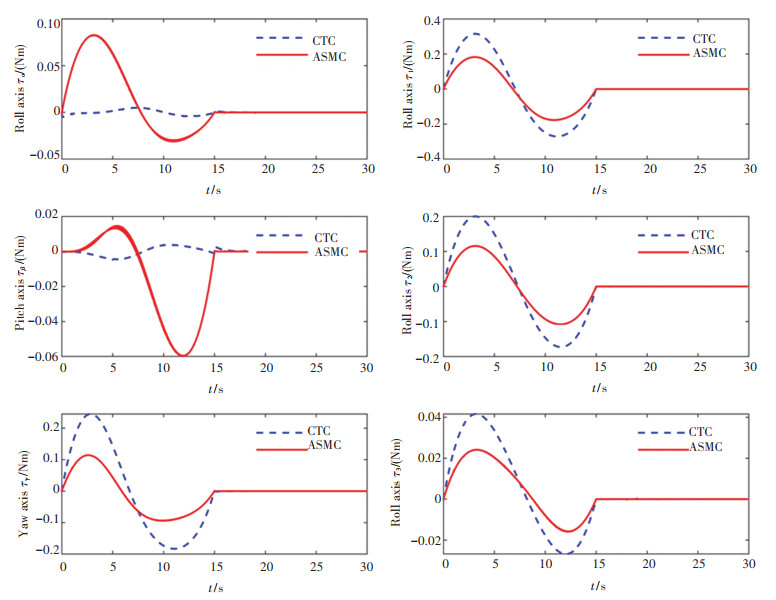
|
图 8 高斯噪声作用下的控制力矩 Fig. 8 Control torques of the system with Gaussian noise |
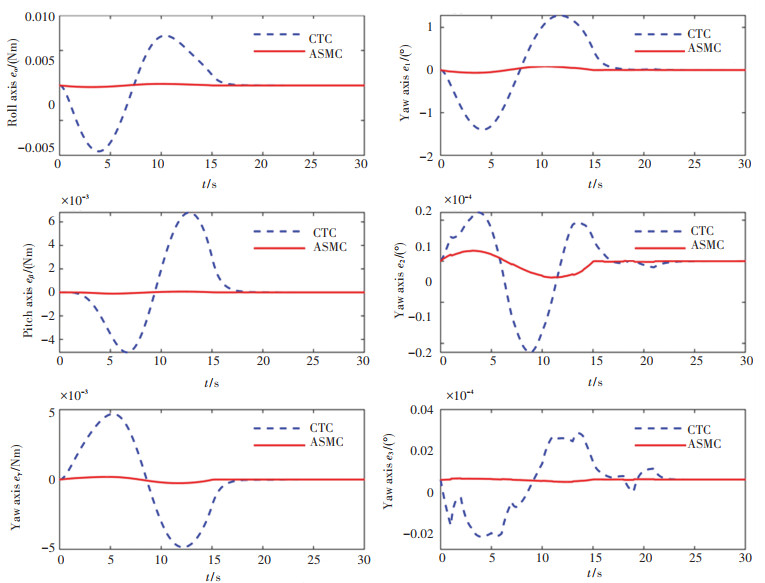
|
图 9 高斯噪声作用下的轨迹跟踪误差 Fig. 9 Path tracking error of the system with Gaussian noise |
本文针对空间机器人捕获目标过程中的鲁棒运动控制算法进行了研究。文中推导了空间机器人系统参数不确定时的动力学方程,基于该动力学模型提出了具有可变增益的滑模控制算法,并通过Simscape Multibody软件模块对空间机器人的理论模型和控制算法进行了验证。
仿真结果表明,基于经典的计算力矩法控制器和本文提出的带有可变增益的滑模控制器,均可以实现对空间机器人关节空间的轨迹跟踪,跟踪误差分别控制在10-3deg和10-5deg以内,误差收敛时间分别约为18 s和15 s,证明了带有可变增益的滑模控制器的控制精度比传统的计算力矩法精度高,且误差收敛速度快。在系统参数不确定且存在外部干扰力矩的情况下,带有可变增益的滑模控制器呈现出很好的鲁棒性,并在运动控制精度和误差收敛速度方面依旧优于经典的计算力矩控制器。
本文提出的控制器适用于对运动控制精度和速度要求较高、系统具有不确定性的场合。但需说明的是,本文的运动控制局限于关节空间,后续应拓展到任务空间。此外,本文的继承性工作还包括以近年来空间机器人的自适应滑模控制方法为参照,用以评价本文提出的控制器性能的优劣。
| [1] |
SABATINI M, GASBARRI P, PALMERINI G B. Coordinated control of a space manipulator tested by means of an air bearing free floating platform[J]. Acta Astronautica, 2017, 139: 296. DOI:10.1016/j.actaastro.2017.07.015 |
| [2] |
VIRGILI-LLOP J, DREW J V, ZAPPULLA II R, et al. Laboratory experiments of resident space object capture by a spacecraft manipulator system[J]. Aerospace Science and Technology, 2017, 71: 530. DOI:10.1016/j.ast.2017.09.043 |
| [3] |
ZONG L, LUO J, WANG M. Optimal detumbling trajectory generation and coordinated control after space manipulator capturing tumbling targets[J]. Aerospace Science and Technology, 2021, 112: 106626. DOI:10.1016/j.ast.2021.106626 |
| [4] |
OKI T, NAKANISHI H, YOSHIDA K. Time-optimal manipulator control of a free-floating space robot with constraint on reaction torque [C]//IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS. Nice: IEEE, 2008: 282. DOI: 10.1109/IROS.2008
|
| [5] |
GANGAPERSAUD R A, LIU G, DE RUITER A H. Detumbling a non-cooperative space target with model uncertainties using a space manipulator[J]. Journal of Guidance, Control, and Dynamics, 2019, 42(4): 910. DOI:10.2514/1.G003111 |
| [6] |
SPICER R L, BLACK J. Simulating the dynamics and control of a free-flying small satellite with a robotic manipulator for 3D printing [C]//AIAA Scitech 2020 Forum. Orlando: AIAA, 2020: 1432
|
| [7] |
PAPADOPOULOS E, DUBOWSKY S. Coordinated manipulator/spacecraft motion control for space robotic systems [C]//Proceedings of the 1991 IEEE International Conference on Robotics and Automation, ICRA. [s. l. ]: IEEE, 1991: 1696
|
| [8] |
SENDA K, MUROTSU Y, NAGAOKA H, et al. Attitude control for free-flying space robot with CMG(control moment gyroscopes) [C]//Guidance, Navigation, and Control Conference. Baltimore: AIAA, 1995: 3336
|
| [9] |
XU Y, SHUM H Y, LEE J J, et al. Adaptive control of space robot system with an attitude controlled base. Space robotics: Dynamics and control[M]. [s. l. ]: Springer, 1993: 229
|
| [10] |
PARLAKTUNA O, OZKAN M. Adaptive control of free-floating space manipulators using dynamically equivalent manipulator model[J]. Robotics and Autonomous Systems, 2004, 46(3): 185. DOI:10.1016/j.robot.2003.11.007 |
| [11] |
李梁, 李剑飞, 张大伟, 等. 自由漂浮空间双臂机器人动目标抓捕控制[J]. 北京理工大学学报, 2019, 39(6): 615. LI Liang, LI Jianfei, ZHANG Dawei, et al. Control of free-floating space dual-arm robot for capturing moving targets[J]. Transactions of Beijing Institute of Technology, 2019, 39(6): 615. |
| [12] |
FAN L, HUANG H, SUN L, et al. Robust attitude control for a rigid-flexible-rigid microsatellite with multiple uncertainties and input saturations[J]. Aerospace Science and Technology, 2019, 95: 105443. DOI:10.1016/j.ast.2019.105443 |
| [13] |
NEKOO S R. Model reference adaptive state-dependent riccati equation control of nonlinear uncertain systems: regulation and tracking of free floating space manipulators[J]. Aerospace Science and Technology, 2019, 84: 348. DOI:10.1016/j.ast.2018.10.005 |
| [14] |
LU Y, HUANG P, MENG Z. Adaptive prescribed performance control for the post-capture tethered combination via dynamic surface technique[J]. Aerospace Science and Technology, 2019, 94: 105366. DOI:10.1016/j.ast.2019.105366 |
| [15] |
XIE Y, YAN Y, SHI Z, et al. Adaptive optimal tracking control for multi-joint manipulator on space robot[J]. Optimal Control Applications and Methods, 2020, 41(6): 1. DOI:10.1002/oca.2613 |
| [16] |
ARISOY A, BAYRAKCEKEN M K, BASTURK S. High order sliding mode control of a space robot manipulator [C]//Proceedings of 5th International Conference on Recent Advances in Space Technologies. Istanbul: IEEE, 2011: 833
|
| [17] |
HUANG X, BIGGS J D, DUAN G. Post-capture attitude control with prescribed performance[J]. Aerospace Science and Technology, 2020, 96: 105572. DOI:10.1016/j.ast.2019.105572 |
| [18] |
WANG X, SHI L, KATUPITIYA J. A strategy to decelerate and capture a spinning object by a dual-arm space robot[J]. Aerospace Science and Technology, 2021, 113: 106682. DOI:10.1016/j.ast.2021.106682 |
| [19] |
TSUDA S, KOBAYASHI T. Space robot control for unknown target handling[C]//Intelligent Control and Innovative Computing. [S. l. ]: Springer, 2012: 11
|
| [20] |
HUANG P, ZHANG F, CAI J, et al. Dexterous tethered space robot: design, measurement, control, and experiment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1452. DOI:10.1109/TAES.2017.2671558 |
| [21] |
MA Z, HUANG P, KUANG Z. Fuzzy approximate learning-based sliding mode control for deploying tethered space robot[J]. IEEE Transactions on Fuzzy Systems, 2020. DOI:10.1109/TFUZZ.2020.3006583 |
| [22] |
ZHANG F, HUANG P. Fuzzy-based adaptive super-twisting sliding-mode control for a maneuverable tethered space net robot[J]. IEEE Transactions on Fuzzy Systems, 2020, 99(11). DOI:10.1109/tfuzz.2020.2985325 |
| [23] |
JIA Y, MISRA A K. Robust trajectory tracking control of a dual-arm space robot actuated by control moment gyroscopes[J]. Acta Astronautica, 2017, 137: 287. DOI:10.1016/j.actaastro.2017.04.031 |
| [24] |
艾海平, 陈力. 空间机器人双臂捕获航天器操作的力/位置控制[J]. 哈尔滨工程大学学报, 2020, 41(12): 1847. AI Haiping, CHEN Li. Force/position fuzzy control of space robot capturing spacecraft by dual-arm clamping[J]. Journal of Harbin Engineering University, 2020, 41(12): 1847. DOI:10.11990/jheu.201905014 |
 2021, Vol. 53
2021, Vol. 53


