2. 机械工业泵及特殊阀门工程研究中心,兰州 730050;
3. 浙江盾安阀门有限公司,浙江 诸暨 311800
2. Machinery Industry Pump and Special Valve Engineering Research Center, Lanzhou 730050, China;
3. Zhejiang Dunan Valve CO., LTD., Zhuji 311800, Zhejiang, China
动态流量平衡阀是通过改变阀芯流通面积,在一定的压差范围内,实现阀门末端流量的自动平衡,作为区域供暖、制冷等系统中的关键性流体控制元件,对系统的水力平衡及稳定性起着至关重要的作用,是节能环保的重要环节[1]。在实际使用中,小口径产品流量波动严重,不能达到±5%流量控制精度的要求,无法实现对系统末端流量的自动控制,造成很大的能源浪费。因此提高动态流量平衡阀流量控制精度有着重大的意义和应用价值[2]。
已有多名学者对动态流量平衡阀阀芯型线的理论设计和动态性能分析进行了相关研究。Liu等[3]通过模拟调节阀流量来调整性能,并得出流量与孔口之间的关系,这是优化孔口的基础;汤中彩等[4]采用同心环缝隙流量公式设计动态流量平衡阀阀芯曲线,并通过数值模拟和实验,验证了设计的阀芯曲线能够实现动态流量平衡阀高精度恒流量功能;徐娟娟等[5]通过引入线弹性不等值力修正系数优化动态流量平衡阀阀芯开口型线,该优化结构有一定的流量控制;沈新荣等[6]采用CFD(计算流体力学Computational Fluid Dynamics) 数值模拟方法对动态流量平衡阀进行了深入的研究,并结合实际试验,获得了平衡阀流量压差特性关系;Li等[7]研究了动态流量平衡阀的弹簧刚度,阀芯的壳体结构以及阀芯表面几何缺陷对流量控制精度的影响;Ramanath等[8]使用数值模拟方法计算了动态流量平衡阀的内部流速和流量,在此基础上结合RP技术快速优化设计动态流量平衡阀的结构。
本文以公称直径为DN15,压差为15~150 kPa的动态流量平衡阀为研究对象,采用CFD(计算流体力学Computational Fluid Dynamics)计算方法,对动态流量平衡阀优化前后的内部非定常流场进行数值求解,提出压差补偿因子修正阀芯开孔型线方程,并搭建动态流量平衡阀流量测试试验台进行验证。
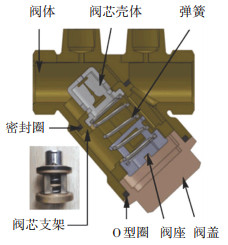
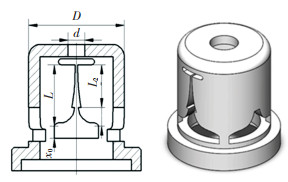
1 动态流量平衡阀结构及原理动态流量平衡阀的主要部件如图 1所示。该阀由主要由阀体、阀芯、阀芯壳体、阀芯支架、弹簧、阀盖、阀座等组成。
|
图 1 动态流量平衡阀结构 Fig. 1 Dynamic flow balance valve structure |
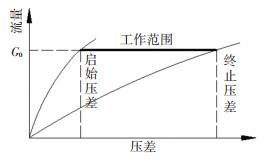
动态流量平衡阀是通过改变不同压差下阀芯流通面积,适应阀前后的压差变化, 而控制阀后的流量平衡。其控制原理如图 2所示,平衡阀处于工作压差范围时,此时的“流量-压差”特性曲线如图 2中粗线所示,在这个区间内不管压差如何变化,阀门的流量始终维持不变。阀芯组件结构的合理设计,可以使动态流量平衡阀在设计的压差范围内,当阀门入口压力变化时,保持出口流量恒定。
|
图 2 动态流量平衡阀动作原理图 Fig. 2 Action diagram of dynamic flow balance valve |
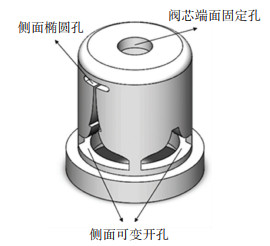
如图 3所示,阀芯的开口由端面固定孔、侧面椭圆孔和侧面可变孔组成,其中阀芯端面和侧面开对称孔结构以减缓压力脉动造成的阀芯振动[9]。
|
图 3 动态流量平衡阀芯的结构 Fig. 3 Structure of dynamic flow balance valve core |
依据孔板流量理论[10]和同心环状缝隙流方程[11],对动态流量平衡阀阀芯开孔的型线进行初步推导。动态流量平衡阀最大压差时的总流量由阀芯端面固定孔流量Q1和侧面椭圆孔流量Q2两部分组成,开孔结构如图 3所示,其流量方程为
| $ Q=Q_{1}+Q_{2}=C_{1} A_{1} \sqrt{\frac{2 \varDelta p_{\max }}{\rho}}+C_{n} A_{2} \sqrt{\frac{2 \varDelta p_{\max }}{\rho}} $ | (1) |
式中:C1、A1分别为阀芯端面通流孔流量系数和流通面积,Cn、A2分别为侧面固定孔流量系数和流通面积。
动态流量平衡阀最小压差时的总流量由端面固定孔流量Q1、侧面椭圆孔流量Q2和侧面可变开孔流量Q3三部分构成,流量方程为
| $ \begin{array}{l} Q=Q_{1}+Q_{2}+Q_{3}=C_{1} A_{1} \sqrt{\frac{2 \varDelta p_{\min }}{\rho}}+ \\ \ \ \ \ \ \ \ \ \ 2\left[C_{2}\left(A_{3}+A_{2}\right)\right] \sqrt{\frac{2 \varDelta p_{\min }}{\rho}} \end{array} $ | (2) |
式中:A3为侧面可变开孔面积,C2为侧面可变开孔流量系数。
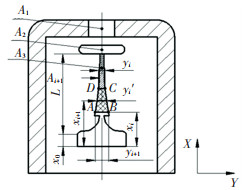
如图 4所示,将可变孔的轴向长度L分为N等分,在L区域内选取微元体SABCD进行分析,当微元体取yi, y′i, yi+1时,应沿X方向投影宽度为xi, x′i, xi+1。当阀芯行程为yi时,弹簧压缩量为Y0+yi,阀芯通流面积为Ai,此时,阀芯前后的介质力与弹簧力相等,即
|
图 4 阀芯侧面开孔型线坐标示意图 Fig. 4 Schematic diagram of spool side-opening line coordinates |
| $ P_{i}=\frac{Y_{0}+y_{i}}{Y_{0}} \times \varDelta p_{\min } $ | (3) |
式中Pi为任意位置时阀芯受到的压差,Y0为弹簧初始压缩量,由最大和最小压差确定:
| $ Y_{0}=\left(\frac{\varDelta p_{\min }}{\varDelta p_{\max }-\varDelta p_{\min }}\right) L $ | (4) |
在微元体SABCD=Ai-Ai+1内
| $ S_{A B C D}={x^{\prime}}_{i} \times\left(y_{i+1}-y_{i}\right)={x^{\prime}}_{i} \times \frac{L}{n} $ | (5) |
令
| $ x_{i}=\frac{Q_{n}}{8 C_{i} L} \sqrt{\frac{\rho Y_{0}}{\varDelta p_{\min }}}\left[\sqrt{\frac{1}{Y_{0}+y_{i-1}}}-\sqrt{\frac{1}{Y_{0}+y_{i+1}}}\right] $ | (6) |
由以上公式可推得
| $ \left\{\begin{array}{l} x_{0}=2 {x^{\prime}}_{0}-x_{1} \\ x_{n}=2 {x^{\prime}}_{n-1}-x_{n-1} \end{array}\right. $ | (7) |
依据阀芯开孔型线初步设计方法,结合DN15动态流量平衡阀整体参考尺寸(如表 1所示),用Visual Basic编写程序,求解得到各点坐标,拟合阀芯可变开孔曲线,动态流量平衡阀阀芯结构如图 5所示。
| 表 1 动态流量平衡阀整体参数 Tab. 1 Dynamic flow balance valve overall parameters |
|
图 5 初步设计阀芯结构 Fig. 5 Preliminary design of the spool structure |
为了研究动态平衡阀在其工作区域内的流量特性和流量控制精度,进行模拟实验研究。CFD(计算流体力学Computational Fluid Dynamics)用于研究内部流动特性,阀内流体流动遵循动量守恒、质量守恒和能量守恒定律,联立边界条件,计算3个控制方程可以求出流体流动的流场参数。基于流体流动控制方程的大涡模拟(LES)湍流模型,结合了直接数值模拟和雷诺时均方法,可以有效地捕捉流场中小尺度的涡流,得到更加完整的瞬态流场特性,同时对计算机要求远低于直接数值模拟方法[12]。因此,本文以LES为湍流模型,采用无滑移壁面边界条件计算壁附近的流量,使用SIMPLE[13]求解方法。
选取不同的开度,通过式(3)计算不同开度下动态流量平衡阀前后的压差,将得到不同开度的压差作为压力边界条件,将稳态计算结果作为瞬态计算的初始值,湍流黏度项采用高阶格式,对流项采用二阶迎风差分格式,扩散项采用中心差分格式,压力耦合方程的求解使用SIMPLE算法,收敛残差判据设定为1e-5。为更加准确计算瞬态特性[14],设置时间步长为1e-3模拟计算优化前后动态流量平衡阀瞬态流场,研究阀内压力脉动。
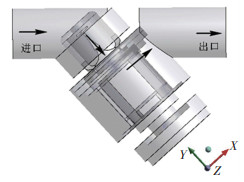
3.2 计算模型依据阀芯开口型线,建立动态流量平衡阀三维模型,通过反向建模得到流道三维模型如图 6所示。离散网格的质量直接决定数值计算的准确性及计算效率,因此,流体域网格划分应根据流场中物理量的分布及模型复杂程度进行合理的网格划分,并且以出口质量流量和y+为标准,进行网格无关性检验。不同质量网格计算结果如表 2所示。
|
图 6 动态流量平衡阀流体域模型 Fig. 6 Dynamic flow balance valve fluid domain model |
| 表 2 网格无关性检验 Tab. 2 Grid independence test |
CFD湍流模型对于近壁面的处理结合了壁面函数法,y+用于描述边界层网格,与边界和雷诺数有关,动态流量平衡阀内流体流动雷诺数较小,要求近壁面网格的y+在30~150之间[15]。综合考虑流量和y+以及计算资源,选取网格数为904266的网格进行计算,如图 7所示。

|
图 7 动态流量平衡阀流体域网格 Fig. 7 Dynamic flow balance valve fluid domain grid |
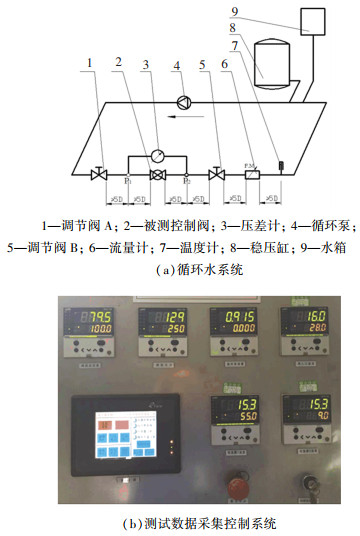
搭建动态流量平衡阀流量测试系统如图 8所示,该测试系统由循环水系统和测试数据采集控制系统组成。
|
图 8 动态流量平衡阀流量测试实验系统 Fig. 8 Dynamic flow balance valve flow test experiment system |
循环水系统提供动态流量平衡阀测试的环境以及阀门前后压差;测试数据采集控制系统通过信号传感器把不同工况下动态流量平衡阀的压差及流量转化成电信号,经过特殊处理转换为直接可读数字信号。在该试验系统中,电磁流量计仪表的精度等级为0.2%,压力传感器仪表的精度等级为1%。为了获得系统误差并保证实验的可行性,采用概率统计方法计算系统误差。实验系统的误差σ为
| $ \sigma=\pm \sqrt{\sum\limits_{i=1}^{n} \sigma_{i}^{2}} $ | (8) |
式中σi是每种仪器的误差。
根据此公式计算得整个系统误差为±1.42%。该值在工程误差的允许范围内,因此测试测量值可靠。
4 压差补偿因子优化修正 4.1 型线优化动态流量平衡阀阀芯可变开孔型线是影响流量控制精度的关键因素[16]。因此,从阀芯可变开孔型线计算公式出发,优化阀芯型线,提高动态流量平衡阀流量控制精度。研究阀芯不同行程的理论压差与实际压差值之间的波动误差,并提出采用压差补偿因子修订阀芯开孔型线方程。将阀芯行程分为0~11共12个开度进行分析研究,则阀芯在开启过程中,不同开度下阀芯前后理论压力差为
| $ p_{i}=i \times\left(p_{1}-p_{2}\right) / L+p_{2}, \quad i=1,2, \cdots, 11 $ | (9) |
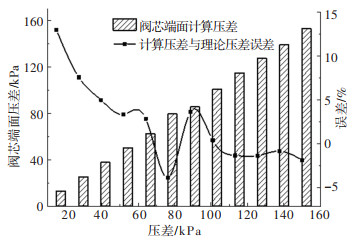
由式(13)可得阀芯在不同开度下的理论压差值,将此值作为边界条件代入CFX软件中进行三维定常流动仿真模拟,监测阀芯面的压力,可得阀芯在不同行程时的仿真压差值,并与理论压差值对比,进行误差分析,监测数据对比结果如图 9所示。
|
图 9 阀芯面压差及误差对比图 Fig. 9 Comparison of pressure difference and error of valve |
根据图 9数据结果,依据式(9)转换成阀芯行程-误差曲线,引入压差补偿系数因子ε,采用最小二乘多项式拟合法,进行曲线拟合,求解相应的函数关系,得到平衡阀压差补偿系数因子修正函数为
| $ \varepsilon_{i}=\left\{\begin{array}{ll} 0.13 i^{4}-1.18 i^{3}+4.12 i^{2}-8.75 i+13, & 0 \leqslant i<4 \\ 8.577 \mathrm{e}-39 \mathrm{e}^{3.5498 i}, & 4 \leqslant i<8 \\ -0.032 i^{4}+0.9 i^{3}-8.21 i^{2}+24.66, & 9 \leqslant i \leqslant 11 \end{array}\right. $ | (10) |
式中i为阀芯行程。
将压差补偿因子代入阀芯开孔型线方程可得
| $ {P_{I}}^{\prime}=\frac{Y_{0}+y_{i}}{Y_{0}} \times P_{\min } \times \varepsilon_{i} $ | (11) |
| $ \bar{x}_{i}=\frac{Q n}{8 C_{i} L} \sqrt{\frac{\rho Y_{0}}{\varDelta p_{\min }}}\left[\sqrt{\frac{1}{\left(Y_{0}+y_{i-1}\right) \varepsilon_{i-1}}}-\sqrt{\frac{1}{\left(Y_{0}+y_{i+1}\right) \varepsilon_{i+1}}}\right] $ | (12) |
式中:i∈L, xi为修订后X方向上高度,则修订后的阀芯可变开孔曲线形状计算公式为
| $ \left\{\begin{array}{l} \bar{x}_{0}=2 \bar{x}_{0}-\bar{x}_{1} \\ \bar{x}_{n}=2 {\bar{x}^{\prime}}_{n-1}-\bar{x}_{n-1} \end{array}\right. $ | (13) |
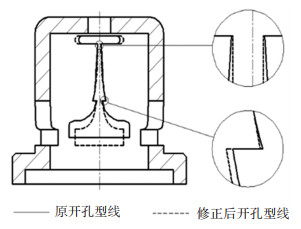
使用Visual Basic编写程序,求解得到各点坐标,拟合阀芯可变开孔曲线如图 10所示。
|
图 10 优化前后阀芯可变开孔型线对比图 Fig. 10 Comparison of spool variable-opening profiles before and after optimization |
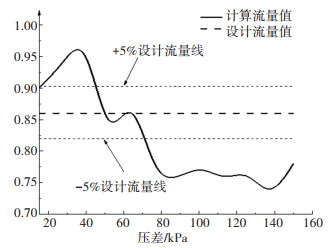
根据初步设计结构流量计算结果(如图 11所示),平衡阀流量控制精度满足±5%的压差段,在51 kPa时流量曲线出现波谷,因此选取阀前后压差为51 kPa时流场信息说明阀芯优化前后阀内流动。
|
图 11 初步设计阀芯压差流量曲线 Fig. 11 Preliminary design of spool differential pressure flow curve |
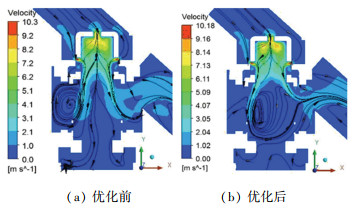
图 12是优化开孔型线前后,动态流量平衡阀流域稳态计算对称面流线图。总体来看,流体通过阀芯端面和侧面开孔流入阀腔,由于流通截面变小使得流速迅速增加,在阀芯底部速度达到最大,约为10 m/s左右。比较两种不同阀芯结构,阀芯优化前(图 12(a)所示),流体进入阀腔后,在阀腔边缘出现分布不均匀的旋涡;阀芯优化后(图 12(b)所示),流体流过阀芯后在阀腔中心形成一个主涡流后直接流出阀后出口,其他部位旋涡相对减弱。
|
图 12 Δp=51 kPa时优化前后阀内流线图 Fig. 12 Valve flow diagram before and after optimization when Δp=51 kPa |
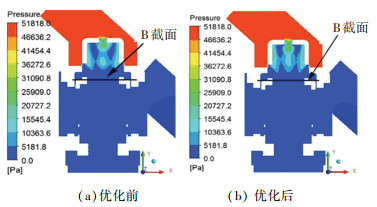
图 13是阀芯开孔型线优化前后,动态流量平衡阀流域稳态计算对称面压力分布图。整体来看,阀芯端面之前压力分布均匀,流体流经阀芯开孔时,压力随之下降,阀芯内部压力分布不均,产生局部低压。比较两种不同结构,优化前阀芯组件(图 13(a)所示)内部形成两个低压区,流体流经端面孔之后中心区域压力分布不连续;相比之下,优化后的阀芯组件(图 13(b)所示)内部中心区域压力分布连续。
|
图 13 Δp=51 kPa时优化前后阀内压力分布图 Fig. 13 Valve pressure distribution before and after optimization when Δp=51 kPa |
图 14为Δp=51 kPa时阀芯开孔型线优化前后动态流量平衡阀瞬态计算不同时刻B截面相对压力分布图。
|
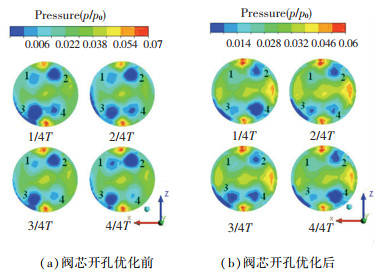
图 14 Δp=51 kPa时不同时刻B截面相对压力分布图 Fig. 14 Relative pressure distribution of B section at different times when Δp=51 kPa |
总体来看,阀芯开孔型线优化前后,B截面相对压力分布不同,优化前最大相对压力为0.07,优化后最大相对压力为0.06。图 14(a)显示,阀芯优化前B截面压力分布在一个完整的T时间内不断发生变化,1/4T时间,截面内有4个低压区,1、4区面积较小,2、3区面积较大,随着时间延续,1、3低压区面积逐渐减小,压力逐渐升高,在3/4T时间1、3低压区面积达到最小,压力开始下降。针对阀芯开孔优化后的结构(图 14 (b)所示),B截面压力分布相对均匀,在整个T时间内,低压区不断发生变化,1/4T时刻4区域压力最低,随着时间变化3区域低压面积逐渐增大,压力逐渐降低,4区域面积逐渐减小,压力开始升高,在3/4T时刻开始向相反方向发展,4/4T时刻压力分布与1/4T时刻基本相同。因此,阀芯节流后流域内压力随着时间变化呈周期性变化,并且阀芯开孔型线影响阀芯处压力脉动,优化阀芯开孔型线后,阀内压力分布相对均匀,相对压力幅值较小。
以无量纲压力脉动系数cp分析不同压差下的压力脉动特性。
| $ c_{p}=\frac{p_{0}-p}{0.5 \rho u^{2}} $ | (14) |
式中:p为不同时刻阀芯面静压,p0为阀内进口压力,u为动态流量平衡阀流域内平均流速。
将阀芯端面压力变化按式(9)进行统一无量纲化,通过快速傅里叶转换(FFT)得到优化前后阀芯面无量纲压力脉频域信息如图 15所示。
|
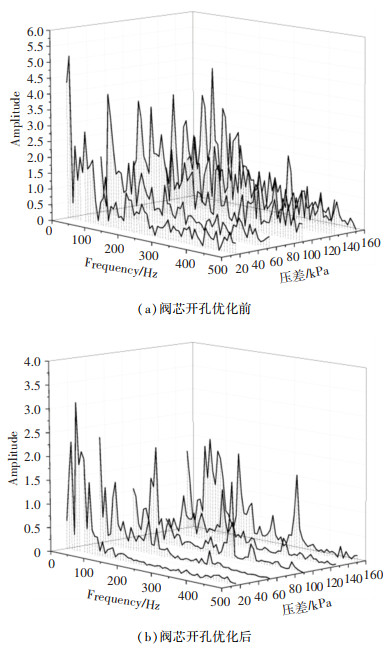
图 15 阀芯开孔型线优化前后压力脉动频谱图 Fig. 15 Pressure pulsation spectrum before and after optimization of spool opening profile |
由图 15可知,动态流量平衡阀开孔型线优化后,整个压差范围内最大振幅从优化前的5.1减小到3.2,不同压差下,阀芯开孔型线优化后的结构阀芯面压力脉动振幅明显降低。结合优化前后不同压差流量曲线(如图 16所示)可知,相比优化前,阀芯开孔优化后流量在±5%流量控制精度内波动,在整个压差范围内均未超出±5%的流量控制精度。由此可见,阀芯可变开孔型线影响阀芯面压力脉动和动态流量平衡阀末端流量,压差补偿因子修正法优化阀芯可变开孔型线方程,能有效减小阀芯端面压力脉动幅值,可保证小压差下流量在±5%的流量控制精度范围内。

|
图 16 不同间隙阀芯组件数值计算流量图 Fig. 16 Numerical calculation flow chart for valve core assemblies with different gaps |
原结构和优化后的动态流量平衡阀流量及误差对比如图 17所示。由图 17可知,原结构动态流量平衡阀在整个压差范围内流量波动严重,很大范围超出±5%流量控制精度要求,相比之下,优化后动态流量平衡阀在整个压差范围内流量在小范围内波动,最大误差为3.7%,平均误差在2.56%左右,满足±5%的流量控制要求。

|
图 17 阀芯可变开孔型优化前后实验流量及误差对比图 Fig. 17 Comparison of experimental flow and error before and after optimization of valve spool variable-opening type |
在动态流量平衡阀流量测试系统中对优化后的动态流量平衡阀实体样机进行不同压差下动态流量平衡阀的流量测试实验,记录不同压差下的流量,对比实验数据如图 18所示。

|
图 18 阀芯开孔型线优化后数值计算与实验流量对比图 Fig. 18 Comparison of numerical calculation and experimental flow after optimization of spool opening profile |
由图 18可知,在压差补偿因子修正的基础上优化阀芯开孔型线后,数值模拟流量值与实验流量值变化趋势相同,两者最大误差在3.9%左右,整个压差范围内实验流量值最大流量为0.89 m3/h,整体流量控制精度为2.56%,已达到±5%流量控制精度要求。
6 结论本文基于CFD和实验方法,对依据孔板流量和同心环状缝隙流方程初步设计的动态流量平衡阀进行优化,将阀芯优化前后阀内非定常流动数值模拟结果进行对比,定量分析阀芯开孔型线对阀内压力脉动及流量控制精度的影响规律,并通过实验进行验证,结论如下:
1) 动态流量平衡阀流量测试实验结果表明,基于CFD的数值计算方法可用于动态流量平衡阀设计计算及流场信息预测。
2) 初步设计阀芯流量控制精度无法满足实际工况要求,流量波动严重,很大范围内均超出±5%流量控制精度。通过动态流量平衡阀阀芯优化前后非定常流动对比分析,开孔型线影响阀内压力脉动和流量控制精度。
3) 将基于CFD的压差补偿因子修正方法用于阀芯可变开孔型线方程的修订,可有效减小阀内压力脉动幅值,提高动态流量平衡阀流量控制精度,使得流量最大误差为3.7%,平均误差约为2.56%,满足±5%的流量控制精度要求。
| [1] |
GUO J, LIU C. A new adjustable dynamic flow balancing valve and its application in central air-conditioning water system[C]//International Conference on Building Energy & Environment. Dalian: [s. n. ], 2008
|
| [2] |
LI B, GUO S, MAO X Y, et al. Characteristic analysis and experiment of a dynamic flow balance valve[C]// IOP Conference Series. [S. l. ]: IOP Publishing, 2017, 100(1): 012107
|
| [3] |
LIU J B, XIE H B, HU L, et al. Realization of direct flow control with load pressure compensation on a load control valve applied in overrunning load hydraulic systems[J]. Flow Measurement and Instrumentation, 2017(53): 261. |
| [4] |
汤中彩. 大口径动态流量平衡阀的数值模拟和实验研究[D]. 杭州: 浙江大学, 2012 TANG Zhongcai. The numerical simulation and experimental study on dynamic flow balance valves[D]. Hangzhou: Zhejiang University, 2012 |
| [5] |
李树勋, 徐娟娟, 范宜霖, 等. 动态流量平衡阀启闭过程中的线弹性不等值力[J]. 西南交通大学学报, 2015, 50(6): 1150. LI Shuxun, XU Juanjuan, FAN Yilin, et al. Linear elastic nonequivalence force for dynamic flow balance valve in opening and closing process[J]. Journal of Southwest Jiaotong University, 2015, 50(6): 1150. DOI:10.3969/j.issn.0258-2724.2015.06.025 |
| [6] |
沈新荣, 陆冰, 李江莉, 等. 一种自动流量平衡阀的数值分析及实验研究[J]. 液压与气动, 2006(1): 56. SHEN Xinrong, LU Bing, LI Jiangli, et al. The numerical analysis and experimental investigation of automatic flux compensation vavle[J]. Chinese Hydraulics & Pneumatics, 2006(1): 56. DOI:10.3969/j.issn.1000-4858.2006.01.025 |
| [7] |
LI S, LI C, LI Z, et al. Design optimization and experimental performance test of dynamic flow balance valve[J]. Engineering Applications of Computational Fluid Mechanics, 2020, 14(1): 700. DOI:10.1080/19942060.2020.1756914 |
| [8] |
RAMANATH H S, CHUA C K. Application of rapid prototyping and computational fluid dynamics in the development of water flow regulating valves[J]. The International Journal of Advanced Manufacturing Technology, 2006, 30(9/10): 828. DOI:10.1007/s00170-005-0119-5 |
| [9] |
李树勋, 范宜霖, 叶琛, 等. 基于改进设计的动态流量平衡阀开孔型线优化及试验[J]. 浙江大学学报(工学版), 2015, 49(5): 908. LI Shuxun, FAN Yilin, YE Chen, et al. Optimization and test for opening profile line of balance valve based on improved design[J]. Journal of Zhejiang University(Engineering Science), 2015, 49(5): 908. DOI:10.3785/j.issn.1008-973X.2015.05.014 |
| [10] |
李江莉. 一种自动流量平衡阀的数值分析与实验研究[D]. 杭州: 浙江大学, 2006 LI Jiangli. The numerical analysis and experimental investigation of the automatic balancing valve[D]. Hangzhou: Zhejiang University, 2006 |
| [11] |
侯英哲. 动态流量平衡阀优化研究及动态特性分析[D]. 兰州: 兰州理工大学, 2014 HOU Yingzhe. The optimization research of dynamic flow balance valve and the analysis of dynamic characteristics [D]. Lanzhou : Lanzhou University of Technology, 2014 |
| [12] |
杜晓庆, 林伟群, 施春林, 等. 高雷诺数下并列双圆柱绕流的大涡模拟[J]. 哈尔滨工业大学学报, 2019, 51(6): 193. DU Xiaoqing, LIN Weiqun, SHI Chunlin, et al. Large eddy simulation of flow around two side-by-side circular cylinders at a high Reynolds number[J]. Journal of Harbin Institute of Technology, 2019, 51(6): 193. DOI:10.11918/j.issn.0367-6234.201806039 |
| [13] |
林谢昭, 应济, 陈子辰. 静电无阀微泵两种仿真模型的比较研究[J]. 哈尔滨工业大学学报, 2010, 42(12): 1943. LIN Xiezhao, YING Ji, CHEN Zichen. Comparing research on two different numerical models of electrostatically actuated valveless micropump[J]. Journal of Harbin Institute of Technology, 2010, 42(12): 1943. DOI:10.11918/j.issn.0367-6234.2010.12.020 |
| [14] |
司乔瑞, 袁寿其, 袁建平, 等. 基于CFD/CA的离心泵流动诱导噪声数值预测[J]. 机械工程学报, 2013, 49(22): 177. SI Qiaorui, YUAN Shouqi, YUAN Jianping, et al. Flow-induced noise calculation of centrifugal pumps based on CFD/CA method[J]. Journal of Mechanical Engineering, 2013, 49(22): 177. |
| [15] |
HOU C W, QIAN J Y, CHEN F Q, et al. Parametric analysis on throttling components of high multi-stage pressure reducing valve[J]. Applied Thermal Engineering, 2017, 128: 1238. |
| [16] |
李忠. 动态流量平衡阀小口径流量精度修订及阀芯振动抑制研究[D]. 兰州: 兰州理工大学, 2017 LI Zhong. The research of revision of small caliber flow accuracy and suppression of valve core vibration for dynamic flow balance valve[D]. Lanzhou: Lanzhou University of Technology, 2017 |
 2021, Vol. 53
2021, Vol. 53


