2. 轨道交通安全关键技术国际合作联合实验室(中南大学),长沙 410075
2. Joint International Research Laboratory of Key Technology for Rail Traffic Safety (Central South University), Changsha 410075, China
点对点运动广泛存在于机器人、数控装备、起重机械等领域。利用目标位置与当前位置的误差进行反馈控制,是很多点对点运动控制系统普遍采用的算法,这种方法存在着初始控制量大、过程不可控以及振动和冲击较大等缺陷。为了解决这个问题,通常采用轨迹规划法。合理的点对点轨迹规划应该将最大速度、加速度、加加速度等进行合理约束,并能根据被控对象特点有效调整加、减速过程,且保证系统平稳运行。目前,大多数轨迹规划是根据点对点运动所经历的加速、匀速、减速过程构造分段函数,然后利用各种方法对各段的衔接处进行平滑处理[1-6]。文献[2]将取放路径分解为两个正交的坐标轴,基于三次B样条曲线设计了高速取放并行机器人的四阶连续平滑轨迹。文献[7]建立了基于四元数的直线与圆弧运动的位姿模型,并采用弧长增量法插补技术实现了机械手空间轨迹规划。文献[8]将三角函数与直线连接组成加速度曲线,提出一种加加速度无突变且起止端连续的S型加减速规划算法。文献[9]采用五阶S曲线加减速方法对电机启动输入信号进行规划来抑制系统扭振,并运用粒子群优化算法选取五阶S曲线参数。文献[10]以循环计算方式获得加速段的运动距离与速度、最大速度的作用时间,提出了四阶S型轨迹规划算法。文献[11]通过设计机器人末端位置和姿态的数学表达式,在过渡节点之间采用一种有限项的正弦级数进行曲线拟合,提出了一种工业机器人连续轨迹规划过渡算法。文献[12]将两个周期不同的三角函数叠加,构造了伺服电机加减速曲线,降低了伺服电机的功率要求。文献[13]将速度和位移方程转换为单一凸形函数,并根据加速度、速度约束条件进行修正,提出了一种高效的加减速时间规划算法。文献[14]针对加速度的不连续变化,研究了一种基于S型速度曲线的轨迹规划方法。文献[15]使用五次多项式修改生成的轨迹,给出了由三点确定一般平面曲线的条件,提出了一般曲线插值方法,在此基础上设计了一种新轨迹。文献[16]将取放路径分解为两个正交的坐标轴,基于三次B样条曲线设计了高速取放并行机器人的四阶连续平滑轨迹。根据标准逻辑函数构造了分段S型加速度函数,得到了一条在速度、加速度、加加速度约束下四阶可微的轨迹。文献[17]将三次多项式和贝塞尔曲线相结合,设计了起、始点都光滑的轨迹。文献[18]探讨了最大速度曲线的特点,提出了一种最大或最小加速度的简便计算方法。文献[19]为减少高速运动阶段的残余振动,设计了一条加加速度约束下的非对称运动轨迹。文献[20]提出了一种基于相平面分析的轨迹规划法,可将台车速度、加速度以及负载最大摆幅始终约束在允许范围内。文献[21]利用三角函数设计了S型速度曲线,并利用其对旋转起重机两级残留摆角进行了控制。
综上可以看出,绝大部分轨迹规划都以梯形、S型速度或加速度曲线为基础,生成的轨迹表达式都是在加速、匀速、减速段的衔接点存在断点的分段函数。采用高次多项式、在衔接点采用正弦、余弦、样条或者双曲正切等光滑函数过渡,可以提升轨迹的平滑性和可微的阶次,但是这种方法通常增加了曲线衔接点的个数,使曲线表达形式更加复杂,时间规划更加困难,而且这些曲线参数众多,难以根据被控对象要求对启停进行针对性调整,使其效率或精度受到影响。
本文利用两段双曲正切函数构造衔接点在匀速段的非对称S型速度曲线,并将S型曲线与跟踪微分器结合,生成一种高阶连续的点对点运动轨迹(HCPPMT),其具有结构简单、光滑、冲击强度可控、各阶段的快慢程度可调、适用范围广等优点。与其他两种轨迹的性能指标进行对比,说明了HCPPMT的优越性。
1 高阶连续的点对点运动轨迹规划点对点运动要求启动平稳、停车精准,而其所经历的加、减速阶段势必对其产生冲击,缓慢运行可减少冲击,但低下的效率使人难以接受。因此,需要根据被控对象特点,设计一条冲击强度可调、在匀速段能以最大速度运行、终点恰好为目标点的高效运动轨迹。S型曲线包含加、减及匀速3个阶段,符合点对点运动的特点,因此,先构造各阶段状态都可按需调整的S型曲线。为了避免S型曲线在加速、匀速、减速段的衔接点出现断点,构造一个具有加速、匀速、减速特点,且能光滑过渡的函数就很关键。
以v1表示运动点的实时位置,sd表示目标位置,当v1∈[0, sd/2],即运动点在起点和中点之间时,利用双曲正切函数设计包含加速和部分匀速段、且变化率可调的光滑连续曲线S1:
| $ f_{1}\left(v_{1}, s_{d}\right)=-k_{d} \cdot \tanh \left[\left(v_{1}+\varepsilon\right) \cdot r_{1}\right] $ | (1) |
式中:kd为额定速度;r1为加速调节因子,可调节加速阶段的快慢程度,r1∈ R+,r1越小,近似线性部分斜率越小,越平缓; ε为启动加速度调节因子,用于调节启动加速度。
当v1∈(sd/2, sd],即运动点在中点和目标点之间时,设计包含部分匀速和减速段、且变化率可调的光滑连续曲线S2:
| $ f_{2}\left(v_{1}, s_{d}\right)=k_{d} \cdot \tanh \left[\left(v_{1}-s_{d}\right) \cdot r_{2}\right] $ | (2) |
式中r2为减速调节因子,可调节减速阶段的快慢程度,r2∈ R+。
将曲线S1和S2在中点进行衔接,形成包含加速、匀速及减速段的S型曲线:
| $ f\left(v_{1}, s_{d}\right)=\left\{\begin{array}{l} -k_{\mathrm{d}} \cdot \tanh \left[\left(v_{1}+\varepsilon\right) \cdot r_{1}\right], v_{1} \leqslant s_{d} / 2 \\ k_{\mathrm{d}} \cdot \tanh \left[\left(v_{1}-s_{d}\right) \cdot r_{2}\right], v_{1}>s_{d} / 2 \end{array}\right. $ | (3) |
该曲线中点附近处于匀速段,保障了整个S型曲线的连续性,利用双曲正切函数的平滑特性实现了点对点运动中加速、匀速、减速阶段的平滑过渡,有效避免了传统点对点运动轨迹规划中分别设计加速、匀速、减速段,然后采用平滑函数连接各段的繁琐过程,有效克服了传统设计中加速、匀速、减速衔接点处高阶不可微、使系统冲击和振动大的弊端。
被控对象启动时相当于被施加了一阶跃信号,该信号高阶不可微,会对被控对象造成严重冲击,阶跃信号经过跟踪微分器后,其输出曲线变为一条平滑曲线,可有效消除初始点高阶不可微的问题,因此对0点到v1-sd点用跟踪微分器处理,得
| $ \left\{\begin{array}{l} \dot{v}_{1}=v_{2} \\ \dot{v}_{2}=-r^{2}\left(v_{1}-s_{d}\right)-2 r v_{2} \end{array}\right. $ | (4) |
式中r为速度调节因子,可调节被控对象的运行速度,r∈ R+。
对式(3)、(4)进行综合,得到速度、加速度和加加速度始终有界,可准确收敛至目标点,且高阶连续的点对点光滑运动轨迹(HCPPMT):
| $ \left\{\begin{array}{l} \dot{v}_{1}=v_{2} \\ \dot{v}_{2}=-r^{2} f\left(v_{1}, s_{d}\right)-2 r v_{2} \end{array}\right. $ | (5) |
从HCPPMT的构造过程可以看出,在中点处存在衔接点,处理不当会产生断点,致使其高阶不可微。为克服这一缺陷,应使式(3)在sd/2邻域都处于匀速段。在目标点较远时,式(3)可保证被控对象以最大速度匀速运行较长距离,不会出现断点。而目标点很近时,若加、减速阶段运行的总距离等于sd,则意味着加速到最大运行速度后就需要减速,这时就会出现拐点,使其高阶不可微。因此,需调整速度调节因子r,使速度至少在sd/2邻域的2N个计算步长内都以最大速度匀速运行,N表示可微的阶数。最大运行速度根据目标点距离sd,加速阶段和减速阶段的调节因子r1、r2,额定速度kd,速度调节因子r,用龙格库塔法通过数值计算确定。
式(5)描述的高阶连续点对点运动轨迹具有如下性质:1)收敛至目标点sd处;2)速度始终有界,且r∈[0, 2]时,0≤v2≤kd;3)加速度和加加速度始终有界。
2 高阶连续的点对点运动轨迹性质证明定理1 高阶连续的点对点运动轨迹(HCPPMT) 收敛至目标位置sd处。
考虑到启动加速度调节因子ε的数值很小,为使证明过程简洁明晰,将其忽略不计。
构造如下函数h(v1):
| $ h\left(v_{1}\right)=\left\{\begin{array}{l} \frac{k_{d} r^{2}}{r_{1}}\left(Q-\ln \left(\cosh \left(r_{1} v_{1}\right)\right)\right), v_{1} \leqslant \frac{s_{d}}{2} \\ \frac{k_{d} r^{2}}{r_{2}} \ln \left(\cosh \left(\left(v_{1}-s_{d}\right) \cdot r_{2}\right)\right), v_{1}>\frac{s_{d}}{2} \end{array}\right. $ | (6) |
式中Q=ln(cosh(r1sd/2))。当v1≤sd/2时,ln(cosh(r1v1))≤ln(cosh(r1sd/2)),又ln(cosh(r1v1))≥0,且kd、r、r1均为正数,因此式(6)≥0。
将式(6)对时间求导,可得
| $ \dot{h}\left(v_{1}\right)=\left\{\begin{array}{l} -k_{d} r^{2} \tanh \left(r_{1} v_{1}\right), v_{1} \leqslant \frac{s_{d}}{2} \\ k_{d} r^{2} \tanh \left(\left(v_{1}-s_{d}\right) \cdot r_{2}\right), v_{1}>\frac{s_{d}}{2} \end{array}\right. $ | (7) |
构造如下Lyapunov候选函数:
| $ V=h\left(v_{1}\right)+\frac{1}{2} v_{2}^{2} $ | (8) |
根据式(6)可知,V为恒大于等于0的函数,将V对时间求导,可得
| $ \dot{V}=\dot{h}\left(v_{1}\right) v_{2}-r^{2} v_{2} f\left(v_{1}, s_{d}\right)-2 r v_{2}{}^{2}=-2 r v_{2}{}^{2} $ | (9) |
由式(9)≤0可知,HCPPMT是Lyapunov意义下稳定的。
定义集合Γ为包含所有满足
综合式(3)、(5)可知,当t→∞时,f(v1, sd)=0,因此可得
| $ \lim \limits_{t \rightarrow \infty} v_{1}(t)=s_{d} $ | (10) |
定理2 HCPPMT的期望轨迹速度始终大于0且有界,且r∈[0, 2]时,0≤v2≤kd。
证明 构造新函数:
| $ g\left(v_{1}\right)=\left\{\begin{array}{l} 2 r_{1} k_{d} v_{1}, 0 \leqslant v_{1}<\frac{1}{2 r_{1}} \\ k_{d}, \frac{1}{2 r_{1}} \leqslant v_{1}<\frac{2 s_{d}-1}{2 r_{2}} \\ 2 k_{d}\left(s_{d}-r_{2} v_{1}\right), \frac{2 s_{d}-1}{2 r_{2}} \leqslant v_{1} \leqslant \frac{s_{d}}{r_{2}} \end{array}\right. $ | (11) |
令G(v1)=g(v1)+ f(v1, sd),接下来证明G(v1) ≥0。
当0≤v1 < 1/(2r1)时,
| $ G\left(v_{1}\right)=k_{d}\left(2 r_{1} v_{1}-\tanh \left(r_{1} v_{1}\right)\right) $ | (12) |
对式(12)针对v1求导,可得
| $ \dot{G}\left(v_{1}\right)=k_{d} r_{1}\left(1+\tanh ^{2}\left(r_{1} v_{1}\right)\right) \geqslant 0 $ | (13) |
因此,在[0, 0.5/r1]内,G(v1)为单调递增函数,又因为G(0)= 0,因此在[0, 0.5/r1]内,G(v1)≥0。
当1/(2r1)≤v1 < (2sd-1)/(2r2)时,很显然G(v1)≥0;当(sd -0.5)/r2≤v1 < sd/r2时,
| $ G\left(v_{1}\right)=k_{d} \tanh \left(r_{2}\left(v_{1}-s_{d}\right)\right)-2 k_{d}\left(r_{2} v_{1}-s_{d}\right) $ | (14) |
对式(14)中的v1求导,得
| $ \dot{G}\left(v_{1}\right)=k_{d} r_{2}\left(-1-\tanh ^{2}\left(v_{1}-s_{d}\right)\right)<0 $ | (15) |
因此,在[(sd-0.5)/r2,sd/r2]内,G(v1)为单调递减函数,又因为G(sd)= 0,因此,在[(sd-0.5)/ r2,sd/r2]内,G(v1)≥0。
综上证明可得,在[0, sd/r2]内,
| $ -f\left(v_{1}, s_{d}\right) \leqslant g\left(v_{1}\right) $ | (16) |
接下来构造一个新微分方程:
| $ \left\{\begin{array}{l} \dot{v}_{1}=v_{2} \\ \dot{v}_{2}=r^{2} g\left(v_{1}\right)-2 r v_{2} \end{array}\right. $ | (17) |
假定到达目标位置的时间为t,到达v1=0.5/r1的时间为t1,到达v1=(sd-0.5)/r2的时间为t2,到达v1=sd的时间为t3,对式(17)中的
| $ \begin{aligned} &\int_{0}^{t}\left[r^{2} g\left(v_{1}\right)-2 r v_{2}\right] \mathrm{d} t=\int_{0}^{t_{1}}\left(2 r^{2} r_{1} k_{d} v_{1}-2 r v_{2}\right) \mathrm{d} t+ \\ &\int_{t_{1}}^{t_{2}}\left(r^{2} k_{d}-2 r v_{2}\right) \mathrm{d} t+\int_{t_{2}}^{t_{3}}\left[2 r^{2} k_{d}\left(s_{d}-r_{2} v_{1}\right)-2 r v_{2}\right] \mathrm{d} t \end{aligned} $ | (18) |
当0≤t≤t1时,v · 2=2r2r1kdv1-2rv2,求解该方程,可得v1的表达式为
| $ v_{1}=c_{1} \mathrm{e}^{\psi_{11} t}+c_{2} \mathrm{e}^{\psi_{12} t} $ | (19) |
其中
对式
| $ \begin{aligned} &\int_{0}^{t_{1}}\left(2 r^{2} r_{1} k_{d} v_{1}-2 r v_{2}\right) \mathrm{d} t=\left(\frac{2 r^{2} r_{1} k_{d} c_{1}}{\psi_{11}}-2 r c_{1}\right) \cdot \\ &\left(\mathrm{e}^{\psi_{11} t_{1}}-1\right)+\left(\frac{2 r^{2} r_{1} k_{d} c_{2}}{\psi_{12}}-2 r c_{2}\right)\left(\mathrm{e}^{\psi_{12} t_{1}}-1\right) \end{aligned} $ | (20) |
其中:c1、c2为待定参数(根据初始状态确定),kd为额定速度,显然式(20)是有界的。
由于t=0时,v1=0,将其代入式(19),可得
| $ c_{1}=-c_{2} $ | (21) |
由v1≥0可知,c1为正数。
对式(19)求导,并结合式(21),可得
| $ v_{2}=c_{1}\left(\psi_{11} \mathrm{e}^{\psi_{11} t}-\psi_{12} \mathrm{e}^{\psi_{12} t}\right) $ | (22) |
| $ \dot{v}_{2}=c_{1}\left(\psi_{11}^{2} \mathrm{e}^{\psi_{11} t}-\psi_{12}^{2} \mathrm{e}^{\psi_{12} t}\right) $ | (23) |
由于ψ11>ψ12,因此当0≤t≤t1时,v2(t)≥0,
当t1≤t≤t2时,
| $ v_{1}=c_{3}+c_{4} \mathrm{e}^{-2 r t}+\frac{r k_{d}}{2} t $ | (24) |
对式(24)求导,得速度v2:
| $ v_{2}=\frac{r}{2} k_{d}-2 r c 4 \mathrm{e}^{-2 r t} $ | (25) |
对式(25)求导,并将t1代入,得
| $ \dot{v}_{2}\left(t_{1}\right)=4 r^{2} c_{4} \mathrm{e}^{-2 r t_{1}} $ | (26) |
由
当t2≤t≤t3时,
| $ \dot{v}_{2}=2 r^{2} k_{d}\left(s_{d}-r_{2} v_{1}\right)-2 r v_{2} $ | (27) |
将
| $ \ddot{v}_{1}+2 r \dot{v}_{1}+2 r^{2} k_{d} r_{2} v_{1}=2 r^{2} k_{d} s_{d} $ | (28) |
这是一个典型的二阶系统,当r2≤1/kd时,其阶跃响应可以无超调地跟踪设定值sd,因而其位移是有界的,当然速度也是有界的。又由于无超调的阶跃响是单调上升的,因此当t2≤t≤t3,r2 ≤1/kd时,v2>0且有界。
由于所规划轨迹的最大速度在匀速段,而匀速段所在区间为[t1, t2],该区间内的最大速度为rkd/2,因而整个区间的速度都小于rkd/2。
综合以上分析,可得期望轨迹速度始终大于0且有界,且r∈[0, 2]时,0≤v2≤kd。
定理3 HCPPMT的期望轨迹加速度和加加速度分别有界。
根据式(23)、(26)、(27),显然加速度有界。
将式(5)对时间求导,得
| $ \ddot{v}_{2}=\left\{\begin{array}{l} r^{2} k_{d}\left(1-r_{1} \tanh ^{2}\left(r_{1} v_{1}+r_{1} \varepsilon\right)\right)-2 r\dot{v}_{2}, v_{1}<s_{d} / 2 \\ -r^{2} k_{d}\left(1-r_{2} \tanh ^{2}\left(r_{2} v_{1}-r_{2} s_{d}\right)\right)-2 r\dot{v}_{2}, v_{1} \geqslant s_{d} / 2 \end{array}\right. $ | (29) |
由于加速度有界,且tanh函数为有界函数,因此式(29)有界,即加加速度有界。
3 可调参数对HCPPMT的影响分析对不同被控对象,在加速、匀速、减速阶段有不同要求。譬如:为提高效率,起重机械要求较快加速到最大运行速度后匀速运行,为保证安全,其最大运行速度也要根据环境风速进行调整,减速阶段则要求缓慢地停靠在目标点,以实现精准定位。因此,有必要研究可调参数对HCPPMT各阶段状态和冲击强度的影响规律,使其在不同的应用场合发挥最大效能。
为研究最大速度调节因子r对HCPPMT的影响,令sd =30 m、kd=2 m/s、ε=0.01、r=2、r2=0.4,当r分别取2、1.61和1.24时,位移、速度、加速度随时间的变化如图 1所示,从图中可以看出,当r等于2时,轨迹的最大匀速运行速度等于额定速度。r越小,最大匀速运行速度越小,在作业距离一定时,耗时也越长。因此,作业距离越远,应使r越大,以便尽可能提高作业效率,但r不能大于2;近距离作业时,则应使r较小,但太小会降低作业效率,因此以在sd/2邻域的2N个计算步长内都以最大速度匀速运行为前提。对在室外环境中作业的起重机械,为保证安全,应根据风速等级,选择合适的r值。
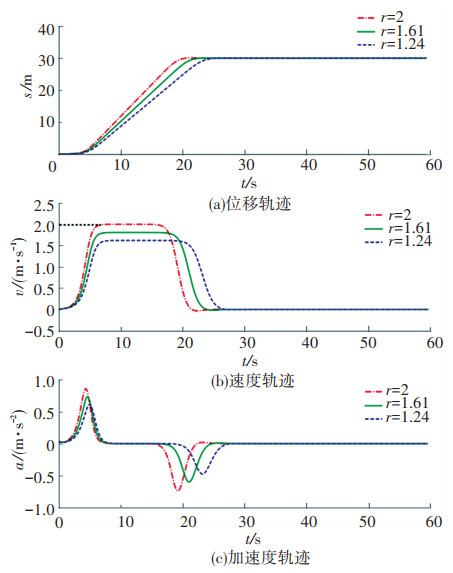
|
图 1 参数r对HCPPMT轨迹的影响 Fig. 1 Effect of parameter r on HCPPMT |
为研究加速调节因子r1对HCPPMT的影响,令sd =30 m、kd=2 m/s、ε=0.01、r=2、r2=0.4,当r1分别取0.65、1和1.8时,HCPPMT的位移、速度、加速度随时间的变化如图 2所示,从图 2中可以看出,r1越小,轨迹初始阶段越平缓,到达最大速度的时间变长,运行规定距离所耗费的时间也越多,随着r1的增加,加速度变大,冲击强度增加,到达最大速度的时间变短,匀速段和减速段提前,但最大速度大小和减速阶段状态不受影响。因此,对于需要慢启动的精密机械,应取较小的r1值,以减小冲击,而对于行程较长的起重机械,在不超过最大加速度的前提下,则宜使用较大r1值,以便提高效率。
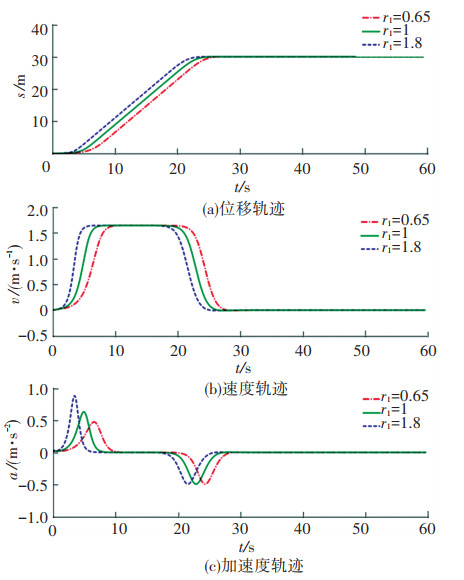
|
图 2 参数r1对轨迹的影响 Fig. 2 Effect of parameter r1 on HCPPMT |
为研究减速调节因子r2对HCPPMT的影响,令sd=30 m、kd =2 m/s、ε=0.01、r=1.24、r1=1,当r2分别取0.2、0.28和0.36时,HCPPMT的位移、速度、加速度随时间的变化如图 3所示,从图中可以看出,在进入减速段前,整个轨迹曲线保持不变,但r2越小,进入减速段的时间越早,使匀速段的时间变短,减速段的时间变长,完成整个作业过程的时间增多,但变化趋势越平缓,接近目标点时的速度也越慢,对于需要在目标点精确对位的精密装备,如岸桥起重机,宜选择较小的r2值。
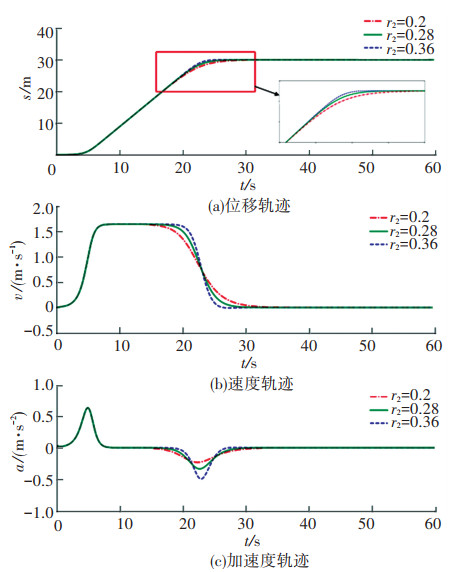
|
图 3 参数r2对轨迹的影响 Fig. 3 Effect of parameter r2 on HCPPMT |
为了检验HCPPMT的效果,取sd=20 m、kd=5 m/s、ε=0.01、r=1.28、r1=0.5、r2=0.2,计算步长取0.05进行仿真,得仿真结果T1。同时,在相同目标位置和计算步长下,将S型速度曲线的仿真结果记为T2,S型位移曲线的仿真结果记为T3。
S型速度曲线采用文献[22]中的形式,为便于对比,将角度转换成位移:
| $ \dot{y}=\left\{\begin{array}{l} \dot{y}_{c}\left(1-\cos \left({\rm{ \mathsf{ π} }} t / t_{1}\right)\right), t \in\left[0, t_{1}\right) \\ \dot{y}_{c}, t \in\left[t_{1}, t_{1}+t_{2}\right) \\ \dot{y}_{c}\left(1+\cos \left({\rm{ \mathsf{ π} }} t /\left(T-t_{1}-t_{2}\right)\right)\right), t \in\left[t_{1}+t_{2}, T\right) \end{array}\right. $ | (30) |
其中:yc为该轨迹的最大速度,t1为加速阶段时间,t2为匀速阶段时间,T为总时间,具体参数取值分别为yc=3.065 m/s,t1=2.345 s,t2=12 s、T=18.69 s。
S型位移曲线采用文献[23]中的表达式:
| $ y(t)=\frac{s_{d}}{2}+\frac{v_{e}{}^{2}}{4 a_{e}} \ln \left[\frac{\cosh \left(2 a_{e} t / v_{e}-\kappa\right)}{\cosh \left(2 a_{e} t / v_{e}-\kappa-2 s_{d} a_{e} / v_{e}{}^{2}\right)}\right] $ | (31) |
其中:ve为最大速度,ae为最大加速度,κ为初始加速度调节因子,κ=1.4,ve=3.056 m/s,ae=2.2 m/s2。
将仿真时间步长设置为0.01 s,仿真结果如图 4及表 1所示。

|
图 4 3种轨迹的运动状态随时间的变化曲线 Fig. 4 Motion state changes in three trajectories with time |
| 表 1 3种轨迹各项指标最大值对比 Tab. 1 Comparison of maximum values of three trajectories |
图 4中自上至下分别为T1、T2、T3的位移、加速度,加加速度,加加加速度随时间t的变化曲线,从图中4(a)可以看出:3种轨迹几乎同时到达指定位置,也就是在合适条件下它们的运行效率基本相同。从图 4(b)及表 1可以看出:轨迹T3的加速度在初始阶段出现了突变,说明利用轨迹T3进行跟踪控制时,在起动时需要很大驱动力,这势必要求提高执行器的功率,而且会对系统产生严重冲击,T1、T2的加速度都是连续的,但轨迹T1的最大加速度更小,说明所需的最大驱动力更小,对执行器的最大功率要求也就更低,有利于降低成本,而且T2在各段(加速、匀速、减速)衔接处出现了明显转折,而轨迹T1的加速度在整个过程中都比较平滑,因而利用T1进行轨迹跟踪控制,系统运行更平稳。从图 4(c)及表 1可以看出:T3初始阶段的加加速度也出现了突变,会对系统产生很大的柔性冲击,使其大幅振动,T2则在各段衔接处出现了最大值为2.73 m/s3的跃变,会对系统产生明显的冲击和振动,而T1加加速度的最大值为1.24 m/s3,远小于T2、T3的加加速度最小值,并且T2的加加速度平滑且连续,不会对系统产生大冲击和振动。从图 4(d)可以看出,轨迹T2、T3的加加加速度在各段衔接处都出现了突变,而轨迹T1的加加加速度光滑且连续,且最大值只有2.75 m/s4,即使进行更高阶微分,都将是平滑且连续的,因此特别适用于需要进行高阶微分的场合(图中↑表示在该时刻,纵坐标值为无穷大值)。
5 HCPPMT在三自由度机械臂轨迹规划中的应用分析三自由度机械臂运动轨迹曲线对机械臂末端运动有着重要影响,如果轨迹的加速度或者加加速度过大,会使机械臂在运行过程中出现振荡、使运动关节经受大冲击,太大的加速度还将使机械臂执行器饱和,使机械臂无法完成既定任务。三自由度机械臂的结构如图 5所示,其中,l1、l2、l3分别表示机械臂1、2、3的长度,分别为0.85、0.95、0.65 m;θ1、θ2、θ3分别表示机械臂1、2、3的转动角度,末端执行器坐标为(px、py、pz),机械臂轨迹规划是通过对机械臂末端执行器空间坐标的x轴、y轴、z轴进行点对点规划,再利用末端执行器坐标和机械臂的转动角度关系式,将设计好的x轴、y轴、z轴的轨迹转化为关节的转动,实现末端执行器的空间运动。末端执行器坐标和机械臂的转动角度关系式可用式(32)描述[16]:
| $ \left\{\begin{array}{l} \theta_{1}=\arctan \frac{p_{y}}{p_{x}} \\ \theta_{2}=\arctan \frac{p_{z}-l_{1}}{\sqrt{p_{x}^{2}+p_{y}^{2}}}- \\ \ \ \arcsin \sqrt{\frac{4 l_{2}^{2} l_{3}^{2}+\left[p_{x}^{2}+p_{y}^{2}+\left(p_{z}-l_{1}\right)^{2}-l_{2}^{2}-l_{3}^{2}\right]^{2}}{4 l_{2}^{2}\left[p_{x}^{2}+p_{y}^{2}+\left(p_{z}-l_{1}\right)^{2}\right]}} \\ \theta_{3}=\arccos \frac{p_{x}^{2}+p_{y}^{2}+\left(p_{z}-l_{1}\right)^{2}-l_{2}^{2}-l_{3}^{2}}{2 l_{2} l_{3}} \end{array}\right. $ | (32) |
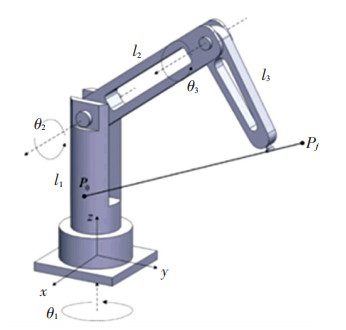
|
图 5 三自由度机械臂的结构 Fig. 5 Structure of three-degree-of-freedom manipulator |
为了验证HCPPMT的有效性,在同样条件下将HCPPMT和文献[16]设计的光滑7段式三自由度机械臂末端执行器运动轨迹(SJM)进行对比,SJM的表达式为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ j(t)=\operatorname{sign}(D) \cdot \\ \left\{\begin{array}{l} \int_{\max } \frac{1}{1+\mathrm{e}^{-a\left(1 /\left(1-\tau_{i}\right)-1 / \tau_{i}\right)}}, t_{0} \leqslant t<t_{1}, t_{12}<t \leqslant t_{13} \\ J_{\max }, t_{1} \leqslant t<t_{2}, t_{13} \leqslant t<t_{14} \\ J_{\max } \frac{1}{1+\mathrm{e}^{a\left(1 /\left(1-\tau_{i}\right)-1 / \tau_{i}\right)}}, \quad t_{2} \leqslant t<t_{3}, t_{14} \leqslant t<t_{15} \\ 0, t_{3} \leqslant t<t_{4}, t_{7} \leqslant t<t_{8}, t_{11} \leqslant t<t_{12} \\ -J_{\max } \frac{1}{1+\mathrm{e}^{-a\left(1 /\left(1-\tau_{i}\right)-1 / \tau_{i}\right)}}, t_{4} \leqslant t<t_{5}, t_{8} \leqslant t<t_{9} \\ -J_{\max }, t_{5} \leqslant t<t_{6}, t_{9} \leqslant t<t_{10} \\ -J_{\max } \frac{1}{1+\mathrm{e}^{a\left(1 /\left(1-\tau_{i}\right)-1 / \tau_{i}\right)}}, t_{6} \leqslant t<t_{7}, t_{10} \leqslant t<t_{11} \end{array}\right. \end{array} $ | (33) |
式中:D为定位距离,Jmax为最大加加速度。
与文献[16]一样,根据表 2中机械臂末端执行器起始点、目标点坐标和路径距离用HCPPMT算法进行仿真,并与SJM进行对比,得到的结果如图 6、图 7、图 8和表 2所示。从这些图中可以看出,在整个过程中,这两种方法的加速度、加加速度、加加加速度都光滑连续,但HCPPMT法在这3个指标上均比较有优势,其最大值都小于SJM法的最大值,然而,HCPPMT法到达目标点的时间稍长,这是由于加入跟踪微分器后虽然进一步保证了HCPPMT的高阶可微性,但是使启停过程变得比较平缓,因此需要探寻既能使两段双曲S型轨迹高阶可微,又不影响启停快慢的函数与其结合,这是后续将深入研究的课题。
| 表 2 末端执行器对应的坐标和距离 Tab. 2 End-effector coordinates of desired path points and displacements |

|
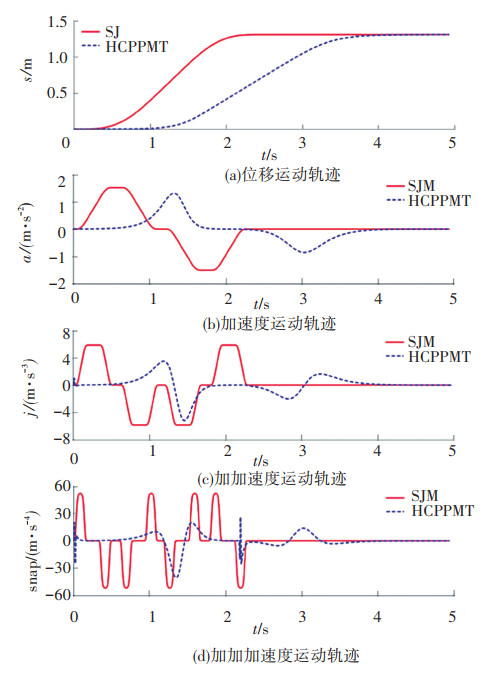
图 6 末端执行器x轴方向的运动轨迹 Fig. 6 End-effector trajectories in x-axisdirection |
|
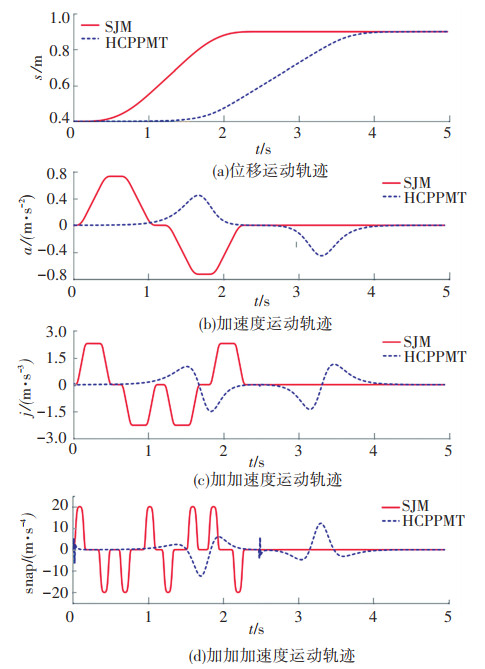
图 7 末端执行器y轴方向的运动轨迹 Fig. 7 End-effector trajectories in y-axis direction |
|
图 8 末端执行器z轴方向的运动轨迹 Fig. 8 End-effector trajectories in z-axis direction |
从表 3可以看出,为了在相同时间内到达目标点,采用SJM法,y轴方向的最大加速度比z轴方向的最大加速度大1.18 m/s2,比x轴方向的最大加速度大1.69 m/s2;y轴方向的最大加加速度比z轴方向的最大加加速度大3.63 m/s3,比x轴方向的最大加加速度大5.22 m/s3;y轴方向的最大加加加速度比z轴方向的最大加加加速度大32.07 m/s4,比x轴方向的最大加加加速度大46.12 m/s4;而采用HCPPMT法,y轴方向的最大加速度比z轴方向的最大加速度大0.70 m/s2,比x轴方向的最大加速度大1.18 m/s2;y轴方向的最大加加速度比z轴方向的最大加加速度大3.29 m/s3,比x轴方向的最大加加速度大4.56 m/s3;y轴方向的最大加加加速度比z轴方向的最大加加加速度大26.32 m/s4,比x轴方向的最大加加加速度大35.16 m/s4。因此,定位距离越大,采用HCPPMT法的加速度、加加速度、加加加速度的增量越小,对执行器功率的要求越低,出现执行器饱和而不能完成指定任务的概率就越小;对系统的冲击越小,系统振动幅度也就越低,系统的运动精度也就越高。
| 表 3 末端执行器加速度、加加速度、加加加速度最大值 Tab. 3 Maximum values of acceleration, jerk, and snap of end-effector on each coordinates |
1) 通过利用两段双曲正切函数构造衔接点在匀速段的S型速度曲线,并将其与跟踪微分器结合,生成了结构简单、高阶连续的点对点运动轨迹,实现了点对点运动加速、匀速、减速过程的平滑过渡,减少了加速、匀速、减速段切换过程中的冲击,增强了运动的平稳性。
2) 通过调整HCPPMT的相关参数,可调节加、减速阶段的快慢程度、匀速阶段的最大速度、作业时间,使HCPPMT的平滑程度、冲击强度可控,各阶段状态可调,且HCPPMT的收敛性及物理性质都通过了严格的数学证明,适用于不同应用场合。后续将利用HCPPMT对数控机床、起重机等进行轨迹跟踪控制研究。
3) 通过和其他两种轨迹对比,以及在三自由度机械臂末端执行器轨迹规划上的应用,说明了HCPPMT的优越性。
| [1] |
KORAYEM M H, ESFEDEN R A, NEKOO S R, et al. Path planning algorithm in wheeled mobile manipulators based on motion of arms[J]. Journal of Mechanical Science and Technology, 2015, 29(4): 1753. DOI:10.1007/s12206-015-0349-x |
| [2] |
LI Y, HUANG T, CHETWYND D G, et al. An approach for smooth trajectory planning of high-speed pick-and-place parallel robots using quintic B-splines[J]. Mechanism and Machine Theory, 2018, 126: 479. DOI:10.1016/j.mechmachtheory.2018.04.026 |
| [3] |
ALI S A, ANNUAR K A M, MISKON M F. Trajectory planning for exoskeleton robot by using cubic and quintic polynomial equation[J]. International Journal of Applied Engineering Research, 2016, 11: 7943. |
| [4] |
HUANG J, HU P, WU K, et al. Optimal time-jerk trajectory planning for industrial robots[J]. Mechanism and Machine Theory, 2018, 121: 530. DOI:10.1016/j.mechmachtheory.2017.11.006 |
| [5] |
BAI Y, CHEN X, SUN H, et al. Time-optimal freeform S-curve profile under positioning error and robustness constraints[J]. IEEE-ASME Transactions on Mechatronics, 2018, 23(4): 1993. DOI:10.1109/TMECH.2018.2835830 |
| [6] |
REW K, KIM K. A closed-form solution to asymmetric motion profile allowing acceleration manipulation[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2499. DOI:10.1109/TIE.2009.2036032 |
| [7] |
李振娜, 王涛, 王斌锐, 等. 基于带约束S型速度曲线的机械手笛卡尔空间轨迹规划[J]. 智能系统学报, 2019, 14(4): 655. LI Zhenna, WANG Tao, WANG Binrui, et al. Trajectory planning for manipulator in Cartesian space based on constrained S-curve velocity[J]. CAAI Transactions on Intelligent Systems, 2019, 14(4): 655. |
| [8] |
李志杰, 蔡力钢, 刘志峰. 加加速度连续的S型加减速规划算法[J]. 计算机集成制造系统, 2019, 25(5): 1192. LI Zhijie, CAI Ligang, LIU Zhifeng. S type acceleration & deceleration fast planning algorithm with continuous jerk[J]. Computer Integrated Manufacturing Systems, 2019, 25(5): 1192. |
| [9] |
刘志峰, 张森, 蔡力钢, 等. 基于粒子群优化五阶段S曲线加减速控制算法[J]. 北京工业大学学报, 2015, 41(5): 641. LIU Zhifeng, ZHANG Sen, CAI Ligang, et al. Five-phase S-curve method based on particle swarm optimization[J]. Journal of Beijing University of Technology, 2015, 41(5): 641. |
| [10] |
朱其新, 陈健亨, 刘红俐, 等. 一种新型四阶S型轨迹规划算法的研究与应用[J]. 系统科学与数学, 2017, 37(4): 1034. ZHU Qixin, CHEN Jianheng, LIU Hongli. On a novel fourth order S-shaped motion profile algorithm and its applications[J]. Journal of Systems Science and Mathematics, 2017, 37(4): 1034. |
| [11] |
许健, 梅江平, 段晓斌, 等. 一种工业机器人连续轨迹规划过渡算法[J]. 工程设计学报, 2016, 23(6): 537. XU Jian, MEI Jiangping, DUAN Xiaobin, et al. An algorithm for segment transition in continuous trajectory planning of industrial robot[J]. Chinese Journal of Engineering Design, 2016, 23(6): 537. |
| [12] |
宋清玉, 郭宝峰, 李建, 等. 伺服压力机柔性加减速控制算法[J]. 农业机械学报, 2013, 44(6): 269. SONG Qingyu, GUO Baofeng, LI Jian, et al. Flexible acceleration and deceleration control algorithm for servo press[J]. Transaction of the Chinese Society for Agriculture Machines, 2013, 44(6): 269. |
| [13] |
杨亮亮, 许守金, 史伟民, 等. 始末速度小为零的S型加减速时间规划算法研究[J]. 机械工程学报, 2016, 52(23): 199. YANG Liangliang, XU Shoujin, SHI Weimin, et al. Research on S type acceleration and deceleration time planning algorithm with beginning and end speed non-zero[J]. Journal of Mechanical Engineering, 2016, 52(23): 199. |
| [14] |
JAHANPOUR J, ALIZADEH M. A novel acc-jerk-limited NURBS interpolation enhanced with an optimized S-shaped quintic feedrate scheduling scheme[J]. The International Journal of Advanced Manufacturing Technology, 2015, 77(9): 1889. |
| [15] |
ZHANG N, SHANG W, CONG S. Dynamic trajectory planning for a spatial 3-DoF cable-suspended parallel robot[J]. Mechanism and Machine Theory, 2018, 122: 177. DOI:10.1016/j.mechmachtheory.2017.12.023 |
| [16] |
FANG Y, HU J, LIU W, et al. Smooth and time-optimal S-curve trajectory planning for automated robots and machines[J]. Mechanism and Machine Theory, 2019, 137: 127. DOI:10.1016/j.mechmachtheory.2019.03.019 |
| [17] |
DINCER U, CEVIK M. Improved trajectory planning of an industrial parallel mechanism by a composite polynomial consisting of Bézier curves and cubic polynomials[J]. Mechanism and Machine Theory, 2019, 132: 248. DOI:10.1016/j.mechmachtheory.2018.11.009 |
| [18] |
MANSOURI S, SADIGH M J, FAZELI M, et al. A computationally efficient algorithm to find time-optimal trajectory of redundantly actuated robots moving on a specified path[J]. Robotica, 2019, 37(1): 62. DOI:10.1017/S0263574718000863 |
| [19] |
LI H. A jerk-constrained asymmetric motion profile for high-speed motion stages to reduce residual vibration[J]. Journal of Computer Applications in Technology, 2016, 53(2): 149. DOI:10.1504/IJCAT.2016.074453 |
| [20] |
SUN N, FANG Y, ZHANG X, et al. Transportation task-oriented trajectory planning for underactuated overhead cranes using geometric analysis[J]. IET Control Theory and Applications, 2012, 6(10): 1410. DOI:10.1049/iet-cta.2011.0587 |
| [21] |
欧阳慧珉, 王健, 张广明, 等. 双摆旋转起重机轨迹生成[J]. 控制理论与应用, 2019, 36(8): 1265. OUYANG Huimin, WANG Jian, ZHANG Guangming, et al. Trajectory generation for double-pendulum rotary crane[J]. Control Theory & Applications, 2019, 36(8): 1265. |
 2021, Vol. 53
2021, Vol. 53


