2. 机器人技术与系统国家重点试验室(哈尔滨工业大学),哈尔滨 150001
2. State Key Laboratory of Robotics and System(Harbin Institute of Technology), Harbin 150001, China
长期以来传统机翼是一种折衷方案,虽然飞机在多种工况下飞行,但每个工况的性能都是次优的。如机翼能够在起飞和降落时采用小后掠角、大展相比和高相对厚度的高升力外形,同时在超声速巡航和机动状态采用大后掠角、小展弦比和低相对厚度的小阻力外形,使得气动性能最优,从而扩大飞行包线,适应不同的飞行环境,满足不同的任务需求,减少能耗,提高飞行效率[1-3]。
机翼变形方式最早可追溯到莱特兄弟利用绳索滑轮机构控制和调节飞机飞行。随着飞行速度与任务适应性的不断提高,设计出升降舵、副翼以及襟翼等小尺度局部变形方式来改善气流[4]。为解决军用飞机不同设计点气动布局矛盾,改善多功能性,提高作战功能,出现了伸缩、折叠、后掠等这种对机翼整体改变的大尺度变形,如F-14和B-1等战斗机采用变后掠机翼技术。然而这些改变远没有达到高效率飞行的目的,一方面刚性部件会破坏机翼表面光滑性,产生额外阻力,另一方面,刚性固定机翼从根本上难以满足人类对于飞机性能的要求。研究人员尝试将仿生结构应用到机翼变形上,如旺超等[5]研究了翼型厚度和翼型弯度对飞扑翼气动性能的影响,为变翼型的气动设计提供了理论指导和技术参考。Luca等[6]通过模拟翅膀改变机翼形状,提高了低速机动、高速抗风性能,并采用不对称变形提高了滚动控制,然而存在机构铰链脆弱,难以等比例缩小等问题。Jenett等[7]研制了基于超轻弹性体单元的离散分布、可逆装配的主动扭转变形翼机构,这种离散式多胞元结构实现了机翼的轻量化。Andersen等[8]提出了滑动蒙皮方案,能实现面积与后掠角的单独变化,创新性的为变形机翼提供了新思路;然而,其变面积与变后掠的翼肋不连续,不适用较大样机,并且翼根强度较小,机翼刚度受气动影响较大。变后掠机翼结构的分布式驱动的位置与数目优化对飞行效率具有很大影响,最具有代表性的为Joo等[9-10]研究了变形结构中驱动器的优化布置,得出驱动器在结构中的最佳位置。Johnson等[11-12]采用遗传算法和基于梯度的优化方法对不同工况下驱动器的位置进行优化。朱华等[13]提出了利用超声电机来驱动小型变体飞行器变形所要研究的关键问题,目前只适用于机翼局部变形。于晓至[14]提出了新型分布式结构变形翼,并对其进行了非线性动力学建模与控制器研究,研究基于二、三单元,尚缺少整翼的多单元以及实验验证,没有应用电机实现结构驱动。在机构变形方面,Xi等[15]提出了一种冗余驱动的单自由度系统来解决空间和负载限制的问题,Moosavian等[16]使用参数化曲线,通过单输入的多环连杆机构来改变翼型,在一定程度上减缓了机翼增重,是变构型在机翼上的一次创新应用,然而并未讨论在翼展方向如何布置机构。上述研究的变形翼多数结构复杂,质量大,承载能力弱,无法实现多维度的大变形,并且变弦长时受到刚性翼肋的限制,大多是采用翼肋自身变形这种复杂结构,同时驱动略显笨重单一,影响飞机驱动效率,难以适应大变形需求。
本文设计的变形翼要满足大变形、高刚度,兼顾高、低速飞行工况,并需要结合所给定变形结构的各项参数,对放置其内的驱动器位置做出合适优化,试图找到驱动器最优位置以及此时蒙皮初始状态,同时探索分布式驱动与机翼结构刚度之间的关系,使得驱动效率能够达到最大。
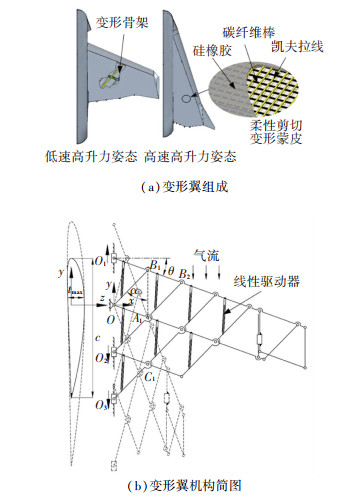
1 平行连杆变形翼设计 1.1 变形原理机翼是基于二维翼型建立的三维几何体,机翼变形最大难点是需要考虑机翼平面与翼型两个维度的协调。变形翼由主动变形的骨架与柔性剪切变形蒙皮组成,可实现低速高升力状态和高速低阻力状态,如图 1所示。
|
图 1 变形翼机构原理 Fig. 1 Principle of morphing wing mechanism |
剪切变形蒙皮[17]由镶嵌在硅橡胶中的碳纤维棒和凯夫拉线固化而成,在骨架支撑下,维持气动外形。取x轴正方向为翼展方向,y轴正方向在机翼平面内垂直于x轴方向指向飞行方向,xy平面内平行连杆构成的多单元变后掠翼以O点为转轴,通过内置在四边形的线性驱动器改变夹角或者直线驱动O3,使得翼根的O1、O2、O3上下滑动来改变后掠角、机翼面积、展长、弦长等,虚线为变形后的高速状态。yz平面内,初始翼型为低速翼型,在变形时,沿任意展向翼剖面翼型均在同一剖面上变化,如,翼肋上的B1、A1、C1一直在一条线上,变形后翼型只在弦长方向伸长。
1.2 机翼几何参数建模与分析评价机翼变形带来的气动效益,最主要看衡量机翼气动外形的几何参数如何变化。B1B2=l1, B1O=l2,定义K=l1/l2为顺气流优势,O1B2与翼展方向的夹角为后掠角,记为θ,翼肋与来流方向的夹角为α=sin-1(Kcos θ),翼根弦长为c,半翼展为l/2,机翼面积为S (单位面积,下同)。展弦比为λ= l2/S=6.45Kcos2θ/cos(α-θ),相对厚度为tmax/c。
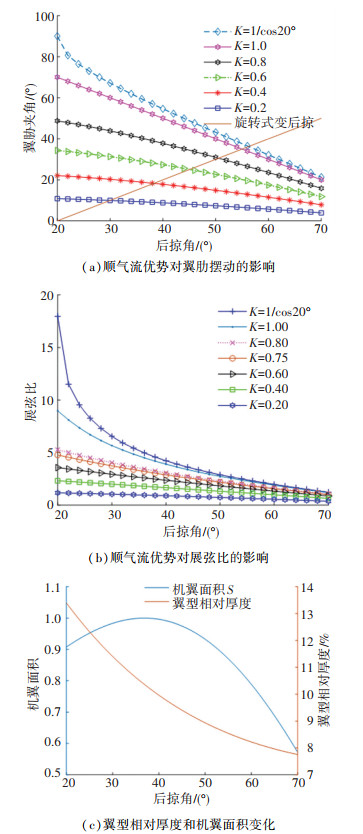
相比旋转式变后掠的翼肋与气流方向夹角增大,平行连杆结构变后掠时最大特点是翼肋做趋向于“顺气流摆动”,即:随着后掠角的增大,翼肋与气流方向的夹角变小,如图 2所示。
|
图 2 机翼几何参数变化曲线 Fig. 2 Variation curves of geometric parameters of wing |
K越小,翼肋摆动程度越小,使得翼型趋向于初始最优翼型,这对需要在高亚音速巡航的飞机来说具有一定的工程意义。然而,“顺气流摆动”的夹角不能无限变小,其一,在结构上翼肋会无限增长,其二,展弦比变化率会减小,为满足翼肋趋向于顺气流方向以及大展弦比变化的宽速域,使得机翼在低、高速时均有较好的效率,文中折中选取K=0.75。
后掠角θ在20.0°~70.0°变化时,展弦比由4.8减小到1.0,相对厚度由13.4%减小到7.76%;后掠角θ在20.0°~53.4°时,机翼面积整体均要大于θ在53.4°~70.0°时的值; 当θ≈36.7°时,机翼面积达到最大值,面积变化率达到175%;小后掠角对应大展弦比和高相对厚度,带来高升力,适合爬升;大后掠角对应小展弦比和低相对厚度,降低阻力,适合高速机动。
2 变形翼分布式驱动配置 2.1 驱动器在单元中的位置优化 2.1.1 单元参数建模放置在变形翼内部的线性驱动器的尺寸、位置会影响到机翼驱动效率,因此需要对驱动器在单元中的位置合理优化[9-10]。
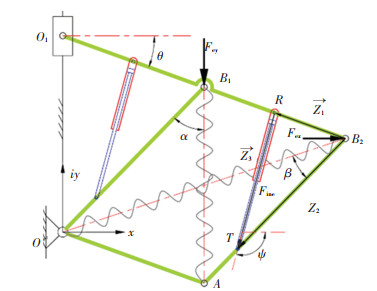
平行连杆式变形翼为单自由度结构,只对单个单元进行研究,如图 3所示。驱动器主要受外载荷和柔性剪切蒙皮的作用,蒙皮跟随骨架变形时,碳纤维棒与凯夫拉线挤压硅橡胶,与弹簧的作用相似,因此将蒙皮对骨架的作用等效为OB2、AB1两个方向的弹簧,弹性系数分别为:Kd、Ky,弹簧OB2与A1B2夹角为β。该单元结构所受的外载荷在x轴和y轴方向的投影分别为Fex、Fey;驱动器的位置在单元结构中由两个向量Z1和Z2来确定。其中驱动器的长度和角度用向量Z3表示,驱动器伸长方向与x轴的夹角为ψ。
|
图 3 单元结构在外载荷和驱动力下的模型简图 Fig. 3 Schematic diagram of a basic structure unit of morphing wing under external load and actuator force |
驱动器的长度为
| $ \left| {{Z_3}} \right| = \sqrt {{Z_1}^2 + {Z_2}^2 + 2{Z_1}{Z_2}\sin \left( {\theta - \alpha } \right)} $ | (1) |
因此驱动器伸长的方向与x轴正方向的夹角为
| $ \psi = \arcsin \left[ {\frac{{ - {Z_2}\cos \;\arcsin (K\cos \theta ) - {Z_1}\sin \theta }}{{\left| {{Z_3}} \right| = \sqrt {{Z_1}^2 + {Z_2}^2 + 2{Z_1}{Z_2}\sin (\theta - \alpha )} }}} \right] $ | (2) |
Z2的大小由驱动器初始长度Z30和参数Z1确定,
| $ \begin{array}{l} {Z_2} = \sqrt {Z_3^{02} - Z_1^2{{\cos }^2}(\theta - \alpha )} - {Z_1}\sin (\theta - \alpha ), \\ \;\;\;\;\;\;\;\left( {{Z_1} > 0} \right) \end{array} $ | (3) |
在上述所有参数中,后掠角θ、Fex、Fey和K在求解过程中已知,以Z1为变量进行优化求解。
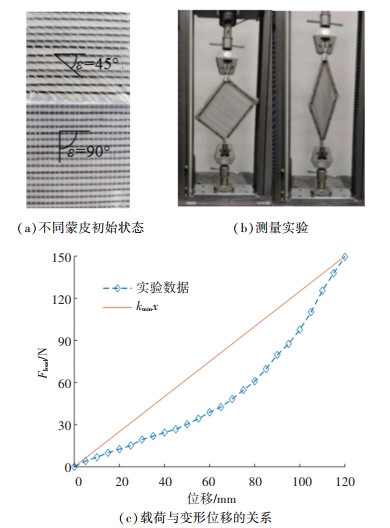
2.1.2 蒙皮等效刚度测定定义初始后掠角θ0时蒙皮处于初始状态,此时蒙皮不对骨架单元产生张拉作用。如图 4所示,当蒙皮初始状态为碳纤维棒与凯夫拉线的夹角ε=90°时,初始后掠角θ0≈36.7°,此时单元结构刚好为矩形,以此状态进行蒙皮刚度拉伸试验。在静加载试验机上通过拉伸带有蒙皮的单元框架,得到加载载荷Fload与对角线位移x之间的关系,为了简化,等效弹簧的Kd(Ky)值应该满足:kminx≥Fload,得到拟合直线的斜率即为等效弹簧的刚度值,由于是单对角线受拉,故取一半kmin值,即为柔性剪切变形蒙皮等效弹簧刚度Kd=Ky≈kmin/2=0.625 N/mm。
|
图 4 试验载荷与输出位移的关系 Fig. 4 Relationship between test load and output displacement |
机翼在变形时,柔性蒙皮除了初始状态,整个过程均对骨架产生作用力,单元在蒙皮、驱动器和外载荷的作用下,通过准静态力学分析方法得到驱动力的表达式:
| $ {F_{{\rm{ine }}}} = \frac{{{B_{1x}}{l_1}\sin \theta + {B_{1y}}{l_1}\cos \theta }}{{{Z_1}\sin (\psi + \theta )}} $ | (4) |
其中:
| $ \begin{array}{l} {B_{1y}} = \left[ {{F_{{\rm{e}}\mathit{x}}}\frac{{{l_2}\cos \alpha }}{{{l_1}\cos \theta }} + {K_{\rm{d}}}\left( {\sqrt {l_1^2 + l_2^2 + 2{l_1}{l_2}\sin (\alpha - \theta )} - } \right.} \right.\\ \;\;\;\;\;\;\left. {\sqrt {l_1^2 + l_2^2 + 2{l_1}{l_2}\sin \left( {{\alpha _0} - {\theta _0}} \right)} } \right)[\sin (\alpha + \beta )\tan \theta + \\ \;\;\;\;\;\;\;\cos (\alpha + \beta )]]/( - (1 + \tan \alpha \tan \theta )) + \\ \;\;\;\;\;\;\;{F_{{\rm{e}}\mathit{y}}} - {K_{\rm{y}}}\left( {\sqrt {l_1^2 + l_2^2 + 2{l_1}{l_2}\sin (\alpha - \theta )} - } \right.\\ \left. {\;\;\;\;\;\;\sqrt {l_1^2 + l_2^2 + 2{l_1}{l_2}\sin \left( {{\alpha _0} - {\theta _0}} \right)} } \right) \end{array} $ |
| $ \begin{array}{l} {B_{1x}} = \left[ {{F_{{\rm{e}}\mathit{x}}}\frac{{{l_2}\cos \alpha }}{{{l_1}\cos \theta }} + {K_{\rm{d}}}\left( {\sqrt {l_1^2 + l_2^2 + 2{l_1}{l_2}\sin (\alpha - \theta )} - } \right.} \right.\\ \left. {\;\;\;\;\;\;\sqrt {l_1^2 + l_2^2 + 2{l_1}{l_2}\sin \left( {{\alpha _0} - {\theta _0}} \right)} } \right)[\sin (\alpha + \beta )\tan \theta + \\ \;\;\;\;\;\;\cos (\alpha + \beta )]\tan \alpha /( - (1 + \tan \alpha \tan \theta )) \end{array} $ |
式(4)说明了驱动力的大小取决于蒙皮初始状态、蒙皮刚度、外载荷Fex、Fey的大小、驱动器的位置Z1、驱动器的方向Ψ以及可变后掠角θ。当外载荷作用与输出方向相反时,驱动器的力大于Fine时才能实现该变形结构的运动。
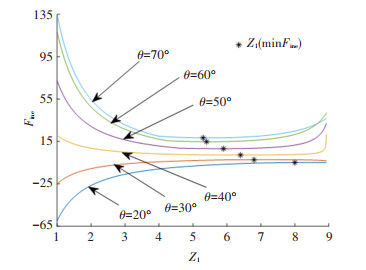
为此研究出不同后掠角时驱动力Fine与Z1的关系,以便在给驱动力赋值时满足Fin≥Fine。定义驱动器初始长度为10(单位长度,下同),Fex=Fey=10(单位力,下同)。如图 5所示,驱动力负值代表驱动力方向与伸长方向一致。
|
图 5 不同后掠角时驱动力与设计参数Z1的关系 Fig. 5 Relationship between actuator force and design parameter Z1 under different sweep angles |
驱动器的位置Z1距离单元变形结构的铰接(B1或B2)越近时,所需要的驱动力就越大,距离铰接处越远驱动力越小;随着后掠角的增大,驱动器所需最小驱动力(min Fine)的Z1值在减小,因此预估Z1的最优值在5~8范围内。
2.1.4 变形效率的描述在整个变形范围内,结构在驱动器、蒙皮和外载荷作用下,所做的变形量越大效率越高。定义变形后的角度为θf,根据虚功原理,θf满足
| $ \begin{array}{l} \;\;\;\;\;\;{F_{{\rm{ine }}}}\frac{{{Z_1}{Z_2}\cos \left( {{\theta _{\rm{f}}} - {\alpha _{\rm{f}}}} \right)\left( {1 + \frac{{K\sin {\theta _{\rm{f}}}}}{{\sqrt {1 - {{\left( {K\cos {\theta _{\rm{f}}}} \right)}^2}} }}} \right)}}{{\sqrt {{Z_1} + {Z_2} + 2{Z_1}{Z_2}\sin \left( {{\theta _{\rm{f}}} - {\alpha _{\rm{f}}}} \right)} }} - \\ {F_{{\rm{e}}\mathit{x}}}2{l_1}\sin {\theta _{\rm{f}}} + {F_{{\rm{e}}\mathit{y}}}\left( { - {l_1}\cos {\theta _{\rm{f}}} - \frac{{{K^2}\sin {\theta _{\rm{f}}}\cos {\theta _{\rm{f}}}}}{{\sqrt {1 - {{\left( {K\cos {\theta _{\rm{f}}}} \right)}^2}} }}} \right) = \\ \;\;\;\;\;\;{K_{\rm{d}}}\left[ {\sqrt {l_1^2 + l_2^2 + 2{l_1}{l_2}\sin \left( {{\alpha _0} - {\theta _0}} \right)} - } \right.\\ \left. {\;\;\;\;\;\;\sqrt {l_1^2 + l_2^2 + 2{l_1}{l_2}\sin \left( {{\alpha _{\rm{f}}} - {\theta _{\rm{f}}}} \right)} } \right] \cdot \\ \;\;\;\;\;\;\frac{{{l_1}{l_2}\cos \left( {{\alpha _{\rm{f}}} - {\theta _{\rm{f}}}} \right)\left( {\frac{{K\sin {\theta _{\rm{f}}}}}{{\sqrt {1 - {{\left( {K\cos {\theta _{\rm{f}}}} \right)}^2}} }} + 1} \right)}}{{\sqrt {l_1^2 + l_2^2 + 2{l_1}{l_2}\sin \left( {{\alpha _{\rm{f}}} - {\theta _{\rm{f}}}} \right)} }} + \\ \;\;\;\;\;\;{K_{\rm{y}}}\left[ {\sqrt {l_1^2} + l_2^2 + 2{l_1}{l_2}\sin \left( {{\theta _{\rm{f}}} - {\alpha _{\rm{f}}}} \right) - } \right.\\ \left. {\;\;\;\;\;\;\sqrt {l_1^2 + l_2^2 + 2{l_1}{l_2}\sin \left( {{\theta _0} - {\alpha _0}} \right)} } \right] \cdot \\ \;\;\;\;\;\;\frac{{{l_1}{l_2}\cos \left( {{\theta _{\rm{f}}} - {\alpha _{\rm{f}}}} \right)\left( {1 + \frac{{K\sin {\theta _{\rm{f}}}}}{{\sqrt {1 - {{\left( {K\cos {\theta _{\rm{f}}}} \right)}^2}} }}} \right)}}{{\sqrt {l_1^2 + l_2^2 + 2{l_1}{l_2}\sin \left( {{\theta _{\rm{f}}} - {\alpha _{\rm{f}}}} \right)} }} \end{array} $ | (5) |
定义单元结构输出位移为:
| $ {X_{{\rm{out}}}} = 2{l_1}\left( {\cos {\theta _0} - \cos {\theta _{\rm{f}}}} \right) $ | (6) |
| $ {Y_{{\rm{out }}}} = {l_1}\left( {\sin {\theta _{\rm{f}}} - \sin {\theta _0}} \right) + {l_2}\left( {\cos {\alpha _{\rm{f}}} - \cos {\alpha _0}} \right) $ | (7) |
变形量L=Xout+Yout,建立驱动器位置优化的目标函数与约束条件为:
| $ \left\{ \begin{array}{l} \mathop {\max }\limits_{{Z_1}} L = {X_{{\rm{out}}}} + {Y_{{\rm{out}}}}\\ {\rm{s}}.{\rm{t}}.\;{F_{{\rm{in}}}} \ge {F_{{\rm{ine}}}}\\ 5 \le {Z_1} \le 8 \end{array} \right. $ | (8) |
通过matlab优化工具箱fmincon函数可以计算出任意初始后掠角时的驱动器最优位置。
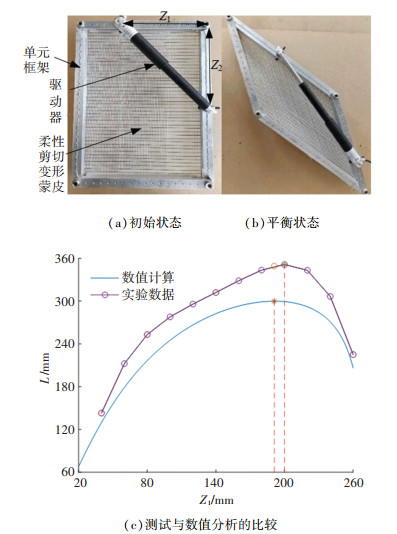
2.1.5 最优位置求解在求解最优位置之前,进行实验来验证理论模型的准确性,并将测试结果与理论分析进行比较。实验装置如图 6所示,采用线性驱动器驱动带有柔性剪切蒙皮的铰链单元框架来测定变形量L,单元框架尺寸为270 mm×360 mm,驱动器初始长度为270 mm,以后掠角36.7°为初始状态,即ε=90°。驱动力Fine=500 N,测得单元框架的变形量L,重复4次取平均值,调整驱动器的位置Z1,在多个位置进行测试,得到驱动器位置与变形量L的关系。单元理论分析和实验测试结果如图 6(c)所示,数值优化结果表明,最大变形量L对应的最优位置Z1=190.755 mm。由于选取等效弹簧刚度值遵循了Kminx≥Fload,转动副之间有摩擦,实验测得数据整体大于理论分析值,但实验数据与理论计算趋势一致,因此采用等效弹簧的单元模型与柔性蒙皮实验模型基本接近,最优位置相差5.7%。
|
图 6 测试装置与数值结果 Fig. 6 Test setup and numerical results |
将该研究方法扩展到整个后掠角范围内以确定最佳执行器位置,通过之前分析,不同后掠角时最佳驱动器位置也不同,但是在飞行时驱动器不能主动改变位置,因此需要一个在全局变后掠范围内将L最大化的位置。优化中,后掠角由20°到70°,每7.5°和特殊位置(36.7°)作为节点。
首先在整个变后掠范围内给定一个后掠角,记作@θ,代表此时为初始后掠角,蒙皮在此时为初始状态,得出对应的驱动器最佳位置Z1(单位长度,下同);其次对每个最佳位置Z1给定初始后掠角,计算变形时的L,如表 1所示。通过式(9)可以计算出每一个位置对应的全局变形量Ltotal:
| $ \left\{ {\begin{array}{*{20}{c}} {{L_{{\rm{total }}}}\mid {Z_1}\left( {@{\theta _1}} \right) = {L_{{\theta _1}}} + {L_{{\theta _2}}} + \cdots + {L_{{\theta _n}}}}\\ {{L_{{\rm{total }}}}\mid {Z_1}\left( {@{\theta _2}} \right) = {L_{{\theta _1}}} + {L_{{\theta _2}}} + \cdots + {L_{{\theta _n}}}}\\ \vdots \\ {{L_{{\rm{total }}}}\mid {Z_1}\left( {@{\theta _n}} \right) = {L_{{\theta _1}}} + {L_{{\theta _2}}} + \cdots + {L_{{\theta _n}}}} \end{array}} \right. $ | (9) |
| 表 1 不同后掠角的最优位置在全局变后掠中的变形量 Tab. 1 Deformation of the optimal position of different sweep angles in global sweep |
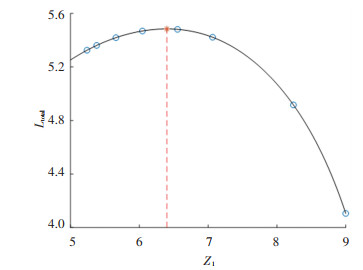
采用Lagrange插值对全局变形量Ltotal进行拟合,得到全局最优驱动器位置Z1=6.39, 如图 7所示,与之前所预测的最优区间相符合。
|
图 7 驱动器不同位置与变形量的关系 Fig. 7 Relationship between actuator position and deformation |
对全局变后掠驱动器最佳位置优化后,得到当Z1=6.39时,在变形范围内输出位移之和最大,最优位置对应的初始后掠角为45°,因此最优的柔性剪切变形蒙皮的初始状态为碳纤维棒与凯夫拉线的夹角ε=68.2°。这与变形机翼在飞行过程中保持中等后掠角条件相一致。
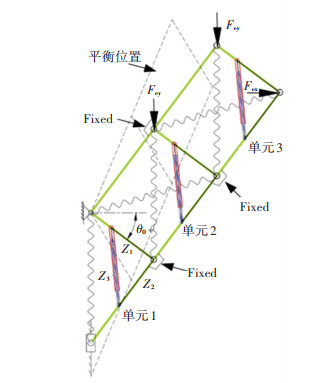
2.2 多单元驱动器布局与传统机翼相比,分布式驱动变形机翼进一步增大了机翼的质量,驱动器数量将作为主要影响因素。将单个单元的讨论扩展到多个单元机构中,多单元结构可以看作是在载荷作用下刚柔耦合可变体系,通过Ansys仿真模拟机构运动与弹性变形的耦合作用,求解出可变体系在载荷作用下最终平衡状态。忽略弹性变形对驱动器最优位置的影响,研究结构刚度与驱动器布局、杆件截面积参数d之间的关系,如图 8所示。该结构中的杆件采用铝合金,横截面积为d;单元杆件尺寸为OA1=270 mm,OC=360 mm;驱动器初始长度Z30=270 mm;驱动器的位置优化结果Z1=190.755 mm;等效弹簧刚度Kd=Ky=0.625 N/mm;外载荷Fex=Fey=10 N。
|
图 8 在外载荷和驱动器作用下三单元结构示意图 Fig. 8 Schematic diagram of three-cell model with actuators and external load |
为了找出结构刚度与分布执行器布置之间的关系,研究以下6种情况:①在单元1中驱动力1 500 N、②在单元3中驱动力1 500 N、③分布在单元1、2中驱动力各1 000 N、④分布在单元1、3中驱动力各1 000 N、⑤分布在单元2、3中驱动力各1 000 N、⑥分布在单元1、2、3中驱动力各500 N。通过式(5)可知6种状态下的理论平衡位置是一致的,其中当驱动器数量有限制时,③和⑤中的驱动器集中在结构一端,称为弱分布式驱动布局,④分散在两侧,为强分布式驱动布局。
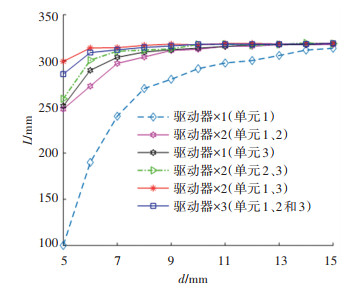
以结构杆件的截面积参数d为变量,对蒙皮初始状态在后掠角θ0=36.7°的情况进行研究,在外载荷、弹簧刚度、驱动力和设计参数Z1下达到平衡角,通过ANSYS进行瞬态动力学仿真,得到6种驱动器布置在一系列截面积参数情况的总变形,6种布置下驱动器布局与变形量的关系如图 9所示。可以看出,当结构刚度较低时,驱动器分布在1、2、3单元中所获得的变形量均比其余的大,若驱动器数量减少,位于分散单元1、3的强分布式驱动方式要比位于相对集中单元1、2或2、3的弱分布式驱动的变形量大;当机翼结构刚度逐渐增强时,分布式驱动与单个驱动的变形量均收敛在理想值。
|
图 9 驱动器布置和刚度对变形量的影响 Fig. 9 Influence of actuator arrangement and stiffness on deformation |
当驱动器靠近翼根,部分驱动器输入能量作为应变能存储在结构中,结构刚度越低,能量传递越无法传递到翼尖,因此,需要分布式驱动以最大化变形量。当截面积逐渐增加或采用分布式驱动器,会通过减小机构远端上的外力引起的挠度来最大化的传递能量。因此分布式驱动系统对于柔性结构是必不可少的。
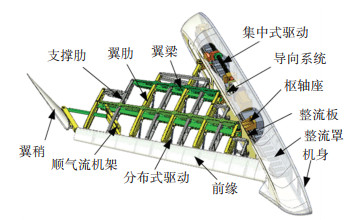
3 结构设计与样机功能演示变形翼骨架为翼梁与翼肋组成的平行连杆结构,如图 10所示。变形翼根部与导向系统连接,主翼梁与枢轴座铰接,变形时,在翼根处丝杠驱动翼肋或内置在四边形单元的分布式驱动器改变单元的夹角,使得前缘前移,可以减缓变后掠带来的气动中心后移[18]。该种翼肋布置方式在变后掠过程中会使翼肋产生沿气流方向的摆动,因此在变后掠翼稍处安装顺气流机架,使得翼尖沿气流方向,并在机架上安装变弯度翼稍,翼梢通过改变沿翼展方向分布的载荷来降低巡航时诱导阻力。得益于“摆动式”翼肋,变形翼的机翼弦长与相对厚度也发生变化,翼型的变化并不是由翼肋本身变形来实现的,解决了刚性翼肋变化难的结构问题,实现了机翼多维度的大变形。
|
图 10 变形翼骨架结构 Fig. 10 Morphing wing skeleton structure |
根据设计的变形翼进行变后掠部分的加工与蒙皮的制作、安装,为下一步实验做准备。变形翼样机如图 11所示,在翼根处的集中式驱动下,变形翼可以实现后掠角20°到70°的连续变形。后掠角20°时,机翼面积S=0.779 m2,最大半翼展1.41 m,最小弦长0.92 m;后掠角36.7°,Smax=0.890 m2;后掠角70°,Smin=0.540 m2,最小翼展为0.634 m,最大弦长1.643 m。

|
图 11 变形翼样机 Fig. 11 Prototype of morphing wing |
本文设计了一种兼顾高低速飞行的多维度变形翼骨架,确定了分布在变形翼骨架结构中执行器的最佳位置和蒙皮初始状态,对多个单元进行机构运动与弹性变形耦合分析,主要结论如下:
1) 翼肋摆动的平行连杆变形翼机构在变后掠的同时,可实现变面积、变弦长、变相对厚度,解决了机翼平面维度和翼型维度之间的结构矛盾,从结构上减缓变后掠带来的气动中心后移。
2) 确定当顺气流优势K=0.75时,后掠角θ在20°~70°范围内,展弦比由4.8减小到1.0,面积变化率为175%,相对厚度由13.4%减小到7.76%。当θ≈36.7°时,机翼面积最大,满足高升力爬升、小阻力机动状态。
3) 随着后掠角的增大,驱动器所需最小驱动力的Z1值逐渐减小;建立的单元数值模型能够在一定误差范围内模拟驱动器位置与变形量的关系,当Z1在63.9%处、初始后掠角为45°时,变形翼在整个变形范围内驱动效率最高,此时柔性剪切蒙皮的最佳初始状态ε=68.2°。
4) 当结构刚度较低时,分布式驱动布局所获得的变形量均比其余的大。若驱动器数量减少,驱动器传递的一部分能量会以应变能的形式存储在结构中,强分布式驱动方式要比弱分布式驱动的变形量大。当机翼结构刚度增强时,分布式驱动与单个驱动所做的变形量均收敛在理想值,采用多个驱动器和单个驱动器对变形能力影响不大。
| [1] |
尹维龙, 石庆华. 变体飞行器蒙皮材料与结构研究综述[J]. 航空制造技术, 2017(17): 24. YIN Weilong, SHI Qinghua. Review of material and structure for morphing aircraft skin[J]. Aeronautical Manufacturing Technology, 2017(17): 24. DOI:10.16080/j.issn1671-833x.2017.17.024 |
| [2] |
聂瑞. 变体机翼结构关键技术研究[D]. 南京: 南京航空航天大学, 2018 NIE Rui. Research on key technologies of morphing wing structures[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018 |
| [3] |
VALE J, LEITE A, LAU F, et al. Aero-structural optimization and performance evaluation of a morphing wing with variable span and camber[J]. Journal of Intelligent Material Systems and Structures, 2011, 22(10): 1057. DOI:10.1177/1045389X11416031 |
| [4] |
BARBARINO S, BILGEN O, AJAJ R M, et al. A review of morphing aircraft[J]. Journal of Intelligent Material Systems and Structures, 2011, 22(9): 823. DOI:10.1177/1045389X11414084 |
| [5] |
汪超, 周超英, 谢鹏, 等. 翼型厚度和弯度对前飞扑翼气动性能的影响[J]. 哈尔滨工业大学学报, 2018, 50(4): 28. WANG Chao, ZHOU Chaoying, XIE Peng, et al. Effects of thickness and camber on aerodynamic performance of flapping wings during forward flight[J]. Journal of Harbin Institute of Technology, 2018, 50(4): 28. DOI:10.11918/j.issn.0367-6234.201612156 |
| [6] |
DI LUCA M, MINTCHEV S, HEITZ G, et al. Bioinspired morphing wings for extended flight envelope and roll control of small drones[J]. Interface Focus, 2017, 7(1): 20160092. DOI:10.1098/rsfs.2016.0092 |
| [7] |
JENETT B, CALISCH S, CELLUCCI D, et al. Digital morphing wing: active wing shaping concept using composite lattice-based cellular structures[J]. Soft Robotics, 2017, 4(1): 33. DOI:10.1089/soro.2016.0032 |
| [8] |
ANDERSEN G R, COWAN D L, PIATAK D J. Aeroelastic modeling, analysis and testing of a morphing wing structure[C]//48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Honolulu: AIAA, 2007: 359. DOI: 10.2514/6.2007-1734
|
| [9] |
JOO J J, SANDERS B, JOHNSON T, et al. Optimal actuator location within a morphing wing scissor mechanism configuration[C]// Proceedings of SPIE 6166, Smart Structures and Materials: Modeling, Signal Processing, and Control. San Diego: SPIE, 2006: 616603. DOI: 10.1117/12.658830
|
| [10] |
JOO J J, SANDERS B. Optimal location of distributed actuators within an in-plane multi-cell morphing mechanism[J]. Journal of Intelligent Material Systems and Structures, 2009, 20(4): 481. DOI:10.1177/1045389X08096049 |
| [11] |
JOHNSON T, FRECKER M I, ABDALLA M, et al. Nonlinear analysis and optimization of diamond cell morphing wings[J]. Journal of Intelligent Material Systems and Structures, 2009, 20(7): 815. DOI:10.1177/1045389X08098098 |
| [12] |
JOHNSON T, FRECKER M. Optimal placement of active material actuators using genetic algorithm[C] // Proceedings of SPIE 5383, Smart Structures and Materials: Modeling, Signal Processing, and Control. San Diego: SPIE, 2004: 221. DOI: 10.1117/12.540050
|
| [13] |
朱华, 刘卫东, 赵淳生. 变体飞行器及其变形驱动技术[J]. 机械制造与自动化, 2010, 39(2): 8. ZHU Hua, LIU Weidong, ZHAO Chunsheng. Morphing aircraft and its morph-driving techniques[J]. Machine Building and Automation, 2010, 39(2): 8. DOI:10.3969/j.issn.1671-5276.2010.02.002 |
| [14] |
于晓至. 分布式结构变形翼的控制研究[D]. 南京: 南京航空航天大学, 2016 YU Xiaozhi. Research on the control problem of distributed structure morphing wings[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016 |
| [15] |
XI Fengfeng, MOOSAVIAN A, CAMPOS G H, et al. Analysis and control of an actuation-redundant parallel mechanism requiring synchronization[J]. Journal of Mechanisms and Robotics, 2020, 12(4): 044501. DOI:10.1115/1.4045653 |
| [16] |
MOOSAVIAN A, SUN Congzhu, XI Fengfeng, et al. Dimensional synthesis of a MultiLoop linkage with single input using parameterized curves[J]. Journal of Mechanisms and Robotics, 2017, 9(2): 021007. DOI:10.1115/1.4035799 |
| [17] |
WU Rui, SUN Jian, CHANG Zhizhong, et al. Elastic composite skin for a pure shear morphing wing structures[J]. Journal of Intelligent Material Systems and Structures, 2015, 26(3): 352. DOI:10.1177/1045389X14526796 |
| [18] |
李桦, 田正雨, 潘沙. 飞行器气动设计[M]. 2版. 北京: 科学出版社, 2017: 251. LI Hua, TIAN Zhengyu, PAN Sha. Aircraft aerodynamic design[M]. 2nd ed. Beijing: Science Press, 2017: 251. |
 2022, Vol. 54
2022, Vol. 54


