光伏发电作为一种技术成熟的可再生能源产生途径,因兼具环保性和经济性而得到广泛的发展。由于传统的地面刚性光伏支架具有一定的场地限制性,近年来一种由预应力拉索体系所组成的大跨度柔性光伏支架结构(简称:光伏结构)正得到越来越多的应用。然而,随着结构跨度和组件高度的增大,其受风荷载的影响也更为显著。而绝大多数情况下,风荷载作为光伏支架结构设计的控制荷载,其取值的大小将直接影响支架的设计成本。因此有必要对大跨柔性光伏支架的风压分布特性和风振响应进行研究,这将有助于该类光伏支架结构抗风设计的优化。
现有研究大多针对屋面或地面安装光伏支架。文献[1]通过风洞试验对平屋盖及双坡屋盖光伏系统风荷载特性进行了研究,结果表明平屋盖上光伏板的最不利净风压极值吸力大,且当附属面积较大时,已有研究的板面设计风荷载取值偏于保守;文献[2-5]研究了遮挡效应、底部阻塞率等对光伏板面风荷载分布的影响;文献[6]结合风洞试验,在对比分析中国规范和日本规范的基础上,提出了光伏阵列风压梯形分布模型;文献[7]通过风洞试验和有限元数值模拟分析了群体光伏支架风压分布规律;文献[8]通过试验研究了阵列间距对地面和屋面安装光伏风荷载分布特征的影响,分析了阵列中组件对荷载的干扰效应;文献[9]通过风洞试验研究了倾角可调的光伏模型在不同倾角、风向角下面板风荷载及各关键位置处力矩作用;文献[10-12]的研究表明光伏板布置方式对板面风荷载取值有较大影响。此外,文献[13]采用有限元法对某常见的展厅式太阳能板结构进行风载响应分析,结果表明竖向作用力会对风荷载引起的结构水平向位移有微小的影响;文献[14]通过气弹试验对某悬索式光伏支架阵列风振特性进行研究,并提出了控制结构振动的措施。以上研究大多集中于组件板面风荷载影响因素,而对结构风振系数及响应研究相对缺乏。
本文基于设计的一种可调节倾角的光伏结构刚性模型开展了风压分布特性试验研究,系统分析了0°、10°两种常见组件布置倾角和全风向角(0°~360°,间隔15°)下,大跨度光伏组件的平均风荷载和脉动风荷载分布特征;结合光伏组件板面的风压分布特性,基于风洞试验风压系数,利用有限元数值仿真技术分析了结构的风振响应并给出了相应的风振系数。本文可以为光伏结构的抗风设计提供参考。
1 刚性模型测压风洞试验基于相似关系和量纲原则设计了大跨柔性光伏支架刚性试验模型,通过开展刚性模型测压试验,研究了大跨柔性光伏支架的风压分布特性。为保证试验结果的准确性,试验模型应具有足够的强度和刚度,以避免在试验风速下发生明显的变形和振动。
模型中光伏面板采用ABS板加工而成,拉索则采用刚度较大的钢材。为便于调节光伏面板的倾角,设计和加工如图 1(a)所示的倾角可调节的光伏结构模型,模型包括立柱和光伏面板(含端部螺纹钢索)两部分,后排立柱设有对穿螺孔,通过插拔螺纹钢索实现光伏面板倾角可调(0°和10°),待将光伏面板调节到预期倾角后将螺纹钢索与立柱在两者贯通处采用螺栓固定。

|
图 1 试验模型 Fig. 1 Wind tunnel test model |
试验在浙江大学ZD-1边界层风洞中进行,原型大跨度柔性光伏支架结构的跨度和高度分别为15.3 m和3.6 m。选定模型几何缩尺比为1∶10,模型长度和宽度分别为1 530 mm和100 mm,由7块光伏组件构成,单块组件尺寸为200 mm(长)×100 mm(宽)×4 mm(高),拉索垂度控制为6 mm,模型组件编号从左往右依次为P1~P7,如图 1(b)所示,其中倾角α定义为光伏面板与来流方向的水平夹角,θ为来流风向角。光伏组件离地高度H=360 mm,光伏面板布置双面测点,考虑到模型的对称性,在组件P1~P4的上下表面各布置27个测点,其中测点7、13和23的位置见图 1(b)。
试验风速为10 m/s,参考高度为0.4 m,来流风为均匀湍流,湍流度为10%。试验中对光伏组件上下表面风压进行0°~345°风向角下的同步风压测试,测试风向角间隔为15°,试验采样频率为312.5 Hz,总采样时间为32 s。
2 试验结果与分析 2.1 数据处理与计算为对比研究不同倾角下大跨度柔性支撑光伏支架的风荷载分布特性,本次测压试验中各测点风压系数和单块光伏组件整体风压系数:
| $ C_{p i}=\frac{P_i-P_{\infty}}{0.5 \rho U_{\infty}^2} $ | (1) |
| $ C_p=\frac{\sum\limits_{i=1}^n C_{p i} A_i}{A} $ | (2) |
式中:Cpi、Cp分别是光伏板表面某测点i的风压系数和单块光伏组件整体风压系数;Pi是测点i的风压值,双面测点时为上、下表面对应测点的风压差值,各测点风压方向为测点处的法线方向;P∞是参考点风压值;ρ为空气密度;U∞是参考点的风速;Ai是某测点i的控制面积,A为单块光伏组件的面积,n为单块组件板面测点数。
由式(1)可知,模型上各测点的无量纲风压系数Cpi即为原型结构对应点的风压系数。在式(1)的基础上,通过下式计算平均风压系数和脉动风压系数:
| $ C_{p i, \mathrm{~m}}=\frac{1}{N} \sum\limits_{i=1}^N C_{p i} $ | (3) |
| $ C_{p i, \mathrm{rms}}=\sqrt{\frac{1}{N-1} \sum\limits_{i=1}^N\left(C_{p i}-C_{p i, \mathrm{~m}}\right)} $ | (4) |
式中:Cpi, m为平均风压系数,Cpi, rms为脉动风压系数,N为样本数。
极值风压系数可以根据下式计算:
| $ C_{p, \min }=C_{p, \mathrm{~m}}-g C_{p, \mathrm{rms}} $ | (5) |
| $ C_{p, \max }=C_{p, \mathrm{~m}}+g C_{p, \mathrm{rms}} $ | (6) |
式中:Cp, min、Cp, max分别为风压系数的极小值和极大值;Cp, m和Cp, rms分别为单块光伏组件的平均、脉动风压系数;g为峰值因子,取3.5。
2.2 不同风向角下光伏组件风压系数分布特性为了研究不同风向角下光伏组件板面风压分布特性,考虑到模型的对称性,图 2仅给出了倾角α=10°时,典型风向角下光伏组件P1~P4板面平均风压系数分布等值线图。

|
图 2 平均风压系数云图(α=10°) Fig. 2 Contour of mean wind pressure coefficient(α=10°) |
试验结果表明,当风向角θ=0°、180°时,板面受负风吸力(正风压力)作用,且组件板面风压分布在垂直来流方向呈现出一定的对称性,沿着来流方向平均风压系数表现出明显的梯度分布规律且绝对值迅速衰减。从组件迎风前缘到后缘,θ=0°时,光伏组件P1(P2、P3、P4)平均风压系数绝对值由1.70(1.5、1.6、1.4)递减至0.12(0.23、0.40、0.33),θ=180°时平均风压系数绝对值由1.3(1.2、1.2、1.3)递减至0.29(0.21、0.17、0.19)。这种风压系数的梯度分布会使得光伏面板承受力矩作用,在抗风设计时应适当加强组件与钢索间的连接措施。在斜风向角(θ=30°、150°)下,光伏面板的平均风压系数也呈现出沿着来流方向绝对值递减。同时,随着风向角的增加,风压系数绝对值最大值出现在组件迎风端角部附近。因此在设计时应予以考虑。
图 3所示为α=10°时,典型风向角下(θ=0°、30°、150°、180°)的光伏组件P1~P4板面脉动风压系数等值线图。分析图 3可知光伏组件脉动风压系数沿来流方向逐渐减小;随着风向角的增大,脉动风压系数的最大值向光伏组件角部移动。综合图 2、3可知,在不同风向角下组件板面风压系数分布有较大差异。

|
图 3 脉动风压系数云图(α=10°) Fig. 3 Contour of fluctuating wind pressure coefficient(α=10°) |
为进一步探讨光伏组件脉动风压的分布特性,图 4给出了α=10°时,处于光伏组件不同位置处部分测点的脉动风压功率谱图,其中测点7、13、23的分布位置见图 1(b)。分析图 4可知迎风前缘处的测点(测点7)峰值出现的频率比中、后缘测点高;在风向角θ=0°(30°)下,上游测点7的峰值出现在频率20(45) Hz附近,而中、下游测点13和23的峰值出现频率小于10 Hz;在风向角θ=90°下,结构光伏组件短边迎风,因此上游测点7峰值出现频率略大于中、下游测点13和23。对于作用在光伏组件上主导漩涡的尺度通常由分离区的大尺度漩涡向再附区的小尺度漩涡转变[15]。测点7峰值大部分出现在高频段,主要控制能量为小尺度漩涡,其处于来流风的分离再附区内,而测点23低频段的能量占主要控制地位,此时光伏组件的主导漩涡为大尺度漩涡,来流风在光伏组件后缘附近发生分离。

|
图 4 脉动风压谱 Fig. 4 Spectra of fluctuating wind pressure |
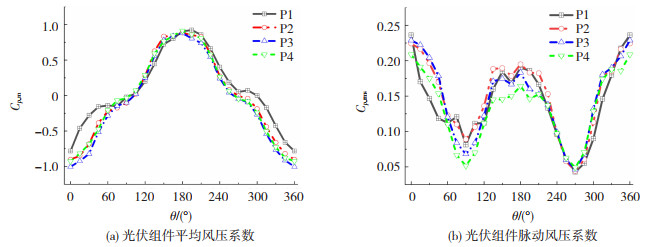
为了研究光伏结构最不利风向角的取值,图 5给出了全风向角下,倾角α=10°时各光伏组件板面整体平均风压系数和脉动风压系数。由图 5可知,平均风压系数取值随风向角的变化呈现出抛物线型对称,在θ=0°(180°)取得极小(大)值。随着风向角的增大,光伏组件P1~P4均从受负压控制变为受正压控制,同时脉动风压系数随之先减小后增大,在90°时取得最小值。在风向角θ=0°(180°)时,组件P1~P4的体型系数分别为-0.78、-0.90、-1.00、-0.93(0.90、0.88、0.88、0.91)。
|
图 5 光伏组件风压系数(α=10°) Fig. 5 Wind pressure coefficient of photovoltaic module(α=10°) |
图 6给出了光伏组件P1~P4的极值风压随风向角的变化情况,分析图 6可知,极值风压随风向角的变化近似呈抛物线型,各光伏组件极值风压在风向角0°或180°取得,其中风向角θ=180°,P1~P4板面风压取得极大值,分别为1.57、1.57、1.52、1.49,风向角θ=0°,P1~P4板面风压取得极小值,分别为-1.61、-1.69、-1.80、-1.66。因此,在结构抗风设计时,对于极值风压及其最不利风向角应予以考虑。

|
图 6 光伏组件极值风压系数(α=10°) Fig. 6 Extreme wind pressure coefficient of photovoltaic module(α=10°) |
为了探索初始组件倾角对大跨度支架结构风振响应的影响,图 7给出了两个风压系数取值较大的风向角下(即θ=0°、180°)、不同组件倾角时(α=0°、10°),P1~P4板面整体风压系数的变化情况。由图 7可知,沿着光伏结构跨度方向,平均风压系数和脉动风压系数从组件P1到P4略有下降的趋势,这与端部组件受到立柱的影响造成了气流的分离再附、涡脱等有关,使得来流风的脉动作用更为显著。随着组件倾角的增大,平均风压系数和脉动风压系数均随之增大。

|
图 7 光伏组件风压系数随倾角变化 Fig. 7 Variation of wind pressure coefficient of photovoltaic module with inclination angle |
以0°风向角为例,这是因为组件倾斜时,下表面迎风面积随之增大,下表面基本受正压控制而上表面受负压控制,二者作用相互叠加,而平放的组件上下表面均受负压控制,使得其所受的净风吸力有所减弱。
3 风振响应数值分析及风振系数为研究光伏结构的风振响应,利用ANSYS有限元仿真软件,建立了大跨柔性支撑光伏组件计算模型。有限元模型中光伏组件尺寸与刚性测压模型一致,其与原型结构物理参数间的缩尺关系见表 1。单块光伏组件质量为25 g,弹性模量为90 GPa,用SHELL181单元模拟,钢拉索截面积0.28 mm2,弹性模量为206 GPa,用LINK10单元模拟,钢索和光伏面板之间通过板的4个节点固定连接,同时为使光伏组件垂度满足要求,通过静力分析,在钢拉索施加150 N的预张力。利用测压试验计算的风压系数,对模型进行加载,以获得结构的风振响应。图 8给出了精细化有限元模型,模型光伏组件倾角α=10°,其中L1~L4表示与固结点连接处的钢索,N1~N4、N5~N8分别为光伏组件P4、P3的角点。模型结构的动力特性见表 2。
| 表 1 有限元模型物理参数缩尺比 Tab. 1 Scaling of physical parameters of finite element model |

|
图 8 有限元模型 Fig. 8 Finite element model |
| 表 2 模型结构动力特性 Tab. 2 Dynamic characteristics of model structure |
图 9、10分别给出了风向角θ=0°时不同风速下光伏组件P4的节点顺风向和竖向位移响应以及钢索L1~L4张力响应随风速的变化关系,分析图 9可知随着风速U的增加,竖向位移响应(均值和方差)近似以抛物线形式增长,同时顺风向位移响应相较竖向位移值较小。由图 10可知张力对风速的变化并不敏感,当风速从2 m/s增加到10 m/s时,张力的增大率小于5%。当风速大于6 m/s时,张力响应方差的增长较快,说明此时结构的脉动响应较为显著。

|
图 9 组件位移响应随风速变化 Fig. 9 Variation of displacement response of photovoltaic module with wind speed |

|
图 10 张力随风速变化 Fig. 10 Variation of tension with wind speed |
表 3、4分别给出了张力风振系数和光伏组件P3、P4位移风振系数随风速变化的取值。可以看出,张力风振系数对风速的变化不敏感,因此采用位移风振系数描述结构的风振响应较为合理。由表 4可知,光伏组件P3和P4的顺风向位移风振系数略大于竖向位移风振系数,同时P3组件节点的位移风振系数(竖向、顺风向)较P4组件略小,因此位移风振系数应以P4组件控制为主。表 4中,顺风向、竖向位移风振系数均在U=8 m/s时取得极值,分别为2.11和1.98。值得注意的是,本文缩尺模型加载风速U=8 m/s对应的实际风速为25.3 m/s,接近了大部分地区的结构设计风速,因此本文给出的顺风向、竖向位移风振系数取值2.11和1.98有一定的参考价值。
| 表 3 不同风速下的张力风振系数 Tab. 3 Tension wind vibration coefficient at different wind speeds |
| 表 4 不同风速下的位移风振系数 Tab. 4 Displacement wind vibration coefficient at different wind speeds |
本文对典型大跨度柔性光伏支架结构的风振特性进行了刚性测压试验研究,分析了0°和10°两种常见组件布置倾角和全风向角下结构风压分布特性,并采用有限元数值仿真方法探索了不同风速下结构的风振响应,计算得到了结构的风振系数,主要结论如下:
1) 风向角、倾角对光伏组件板面的风压分布(平均风压和脉动风压)影响显著。0°和180°风向角时,平均风压系数沿来流方向呈现出梯度分布规律且绝对值递减,这种梯度分布会使得光伏面板承受力矩作用,在抗风设计时应适当加强组件与钢索间的连接措施;30°和150°斜风向角下,光伏面板的迎风端角部区域会出现极大的局部风压系数。组件脉动风压系数分布规律与平均风压类似。风向角θ=0°或180°,P1~P4板面风压取得极值,且极值负风吸力大于正风压力。
2) 随着光伏组件倾角的增大,光伏组件整体风压系数呈增大趋势。沿着结构跨度方向,平均风压系数和脉动风压系数从组件P1到P4略有下降的趋势。
3) 竖向位移响应较顺风向位移响应对风速变化更为敏感。相比结构位移响应,钢索张力响应对风速变化不敏感,因此采用位移风振系数描述结构的风振响应较为合理。位移风振系数的取值应以P4组件控制为主,顺风向和竖向位移风振系数均在U=8 m/s时取得极大值,分别为2.11和1.98。
| [1] |
王京学, 杨庆山, 刘敏, 等. 平屋盖及双坡屋盖光伏系统风荷载特性试验研究[J]. 建筑结构学报, 2018, 39(10): 21. WANG Jingxue, YANG Qingshan, LIU Min, et al. Experimental research on characteristics of wind loads of solar arrays mounted on flat and gable roofs[J]. Journal of Building Structures, 2018, 39(10): 21. DOI:10.14006/j.jzjgxb.2018.10.003 |
| [2] |
马文勇, 马成成, 王彩玉, 等. 光伏阵列风荷载干扰效应风洞试验研究[J]. 实验流体力学, 2021, 35(4): 19. MA Wenyong, MA Chengcheng, WANG Caiyu, et al. Wind tunnel experimental study on the wind load interference effect of solar panel arrays[J]. Journal of Experiments in Fluid Mechanics, 2021, 35(4): 19. DOI:10.11729/syltlx20200127 |
| [3] |
马文勇, 柴晓兵, 刘庆宽, 等. 底部阻塞对太阳能光伏板风荷载的影响研究[J]. 建筑结构, 2019, 49(2): 129. MA Wenyong, CHAI Xiaobing, LIU Qingkuan, et al. Study on effect of bottom flow obstruction on wind load of solar photovoltaic panels[J]. Building Structure, 2019, 49(2): 129. DOI:10.19701/j.jzjg.2019.02.023 |
| [4] |
楼文娟, 单弘扬, 杨臻, 等. 超大型阵列光伏板体型系数遮挡效应研究[J]. 建筑结构学报, 2021, 42(5): 47. LOU Wenjuan, SHAN Hongyang, YANG Zhen, et al. Study of shielding effect on shape coefficient of super-large photovoltaic arrays[J]. Journal of Building Structures, 2021, 42(5): 47. DOI:10.14006/j.jzjgxb.2019.0754 |
| [5] |
许宁, 李旭辉, 高晨崇, 等. 光伏系统风荷载体型系数分析[J]. 太阳能学报, 2021, 42(10): 17. XU Ning, LI Xuhui, GAO Chenchong, et al. Analysis of shape coefficients of wind loads of photovoltaic system[J]. Acta Energiae Solaris Sinica, 2021, 42(10): 17. DOI:10.19912/j.0254-0096.tynxb.2017-1018 |
| [6] |
贺广零, 蒋华庆, 单建东, 等. 光伏方阵风荷载模型研究[J]. 电力建设, 2012, 33(10): 5. HE Guangling, JIANG Huaqing, SHAN Jiandong, et al. Research of wind load model in photovoltaic array[J]. Electric Power Construction, 2012, 33(10): 5. DOI:10.3969/j.issn.1000-7229.2012.10.002 |
| [7] |
王东, 王璐璐, 方伟定. 基于风洞试验和数值模拟的群体光伏支架体型系数研究[J]. 特种结构, 2020, 37(4): 42. WANG Dong, WANG Lulu, FANG Weiding. Study on shape coefficient of group photovoltaic support based on wind tunnel test and numerical simulation[J]. Special Structures, 2020, 37(4): 42. DOI:10.19786/j.tzjg.2020.04.008 |
| [8] |
WARSIDO W P, BITSUAMLAK G T, BARATA J. Influence of spacing parameters on the wind loading of solar array[J]. Journal of Fluids and Structures, 2014, 48: 295. DOI:10.1016/j.jfluidstructs.2014.03.005 |
| [9] |
殷梅子, 邹云峰, 李青婷, 等. 单排跟踪式光伏结构风荷载风洞试验研究[J]. 铁道科学与工程学报, 2020, 17(9): 2354. YIN Meizi, ZOU Yunfeng, LI Qingting, et al. Wind tunnel test study on wind load of single row tracking photovoltaic structure[J]. Journal of Railway Science and Engineering, 2020, 17(9): 2354. DOI:10.19713/j.cnki.43-1423/u.T20191016 |
| [10] |
KOPP G A, FARQUHAR S, MORRISON M J. Aerodynamic mechanisms for wind loads on tilted, roof-mounted, solar arrays[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 111: 40. DOI:10.1016/j.jweia.2012.08.004 |
| [11] |
BROWNE M T L, GIBBONS M P M, GAMBLE S, et al. Wind loading on tilted roof-top solar arrays: the parapet effect[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 123: 202. DOI:10.1016/j.jweia.2013.08.013 |
| [12] |
CAO Jinxin, YOSHIDA A, SAHA P K, et al. Wind loading characteristics of solar arrays mounted on flat roofs[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 123: 214. DOI:10.1016/j.jweia.2013.08.014 |
| [13] |
刘春雨, 白冰, 李腊梅. 太阳能板支架体系等效静力风荷载响应分析[J]. 山西建筑, 2017, 43(27): 45. LIU Chunyu, BAI Bing, LI Lamei. Response analysis of equivalent static wind load of solar panel support system[J]. Shanxi Architecture, 2017, 43(27): 45. DOI:10.13719/j.cnki.cn14-1279/tu.2017.27.022 |
| [14] |
HE Xuhui, DING Hao, JING Haiquan, et al. Wind-induced vibration and its suppression of photovoltaic modules supported by suspension cables[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 206: 104275. DOI:10.1016/j.jweia.2020.104275 |
| [15] |
邹琼. 槽式聚光镜组系统的抗风性能研究[D]. 长沙: 湖南大学, 2016 ZOU Qiong. Research on wind resistant performance of trough solar collector system[D]. Changsha: Hunan University, 2016 |
 2022, Vol. 54
2022, Vol. 54





