2. 山西建筑工程集团有限公司,太原 030006;
3. 山西二建集团有限公司,太原 030013
2. Shanxi Construction Engineering Group Co. Ltd., Taiyuan 030006, China;
3. Shanxi Erjian Group Co. Ltd., Taiyuan 030013, China
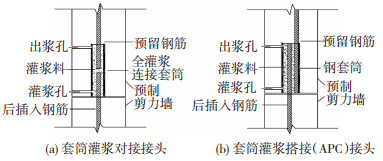
套筒灌浆对接连接是目前运用较多、发展相对成熟的预制构件节点钢筋连接技术,其在对接钢筋外部设置套筒,并在套筒内部注入无收缩灌浆料,以实现预制构件间的可靠连接,见图 1(a)。
|
图 1 2种套筒灌浆连接接头示意 Fig. 1 Schematic of two kinds of grouted sleeve connectors |
2013年Alias等[1]研究了带螺旋筋的套筒灌浆连接接头的拉伸性能;2016年郑永峰等[2]通过单拉及反复拉压试验探究了一种新型钢筋连接用灌浆套筒接头的强度和变形情况;2017年郑清林等[3]通过单拉试验探究了灌浆缺陷对钢筋套筒灌浆连接试件受力性能的影响;2018年许成顺等[4]研究了高应力反复拉压作用对钢筋套筒灌浆接头连接性能的影响;2019年吴涛等[5]通过单拉试验对钢制和球墨铸铁半灌浆套筒连接件的力学性能进行了对比研究。以上研究表明,设计参数合理的套筒灌浆连接接头具有良好的受力性能,满足实际应用要求。
传统灌浆套筒节点需在套筒内壁设置剪力键、刻痕等以提高其传力性能,对套筒材料性能和铸造工艺要求较高,制作成本较高。且该类接头套筒口径较小,对施工精度要求高,当多根钢筋同时插入套筒时,施工难度较大,施工质量难以保障。
基于以上研究,2015年余琼[6]提出了一种新型套筒灌浆搭接接头,简称APC(all vertical members precasted in concrete structures)接头,见图 1(b)。其原理为在搭接钢筋外部设置套筒,向套筒内注入灌浆料,利用钢筋与灌浆料间的黏结作用传力。该接头具有内径大、搭接长度小、施工方便、成本低等优势[7]。
2016年许志远[8]以钢筋直径与搭接长度为变量进行了APC接头的单拉试验,研究了试件的极限承载力、破坏形态和荷载-位移曲线等;2017年宫鑫[9]通过单拉试验研究了APC接头的破坏形态、强度、延性以及钢筋和套筒的应变变化规律,分析了接头的受力机理;2018年许坤[10]以套筒截面尺寸和搭接长度为变量进行了APC接头单拉试验,研究分析了试件破坏形态、极限承载力、延性及钢筋和套筒的荷载-应变曲线;2019年匡轩[11]利用ABAQUS对APC接头建立数值模型,分析了搭接长度、钢筋直径等对接头拉伸性能的影响。
这些研究表明,该接头受力合理,能有效传递钢筋应力,具有良好的延性性能。但以上试验的后插钢筋位置相对固定,后插钢筋位置对APC接头力学性能的影响尚未研究。
本文进行了45个APC接头的单拉试验,并利用ABAQUS建立了13个该类接头的精细化模型进行数值模拟和参数分析,研究了后插钢筋位置、钢筋直径和套筒偏转对APC接头力学性能的影响。以钢筋搭接长度为变量建立8个APC接头精细化模型,补充研究了搭接长度对接头力学性能的影响。研究成果可为APC接头工程应用提供理论指导。
1 试验概况 1.1 试验材料性能| 表 1 钢筋材料性能 Tab. 1 Material properties of rebar |
灌浆料采用某公司的H40型灌浆料。测得40 mm×40 mm×160 mm试件抗折、抗压强度[13]分别为7.3、74.7 MPa,150 mm×150 mm×150 mm试件劈裂抗拉强度[14]为4.12 MPa,150 mm×150 mm×300 mm试件的轴心抗压强度为73.6 MPa。
套筒采用Q235无缝钢管,制作3根狗骨试件进行单拉试验[12],测得套筒平均屈服强度为267.0 MPa,平均极限强度为417.2 MPa。
1.2 试验方案与试件设计为模拟接头在实际工程中的应用,试件预留钢筋在套筒两端进行点焊(固定钢筋位置)。本试验设计了4种可能的后插钢筋最不利位置(位置一、位置二、位置三、位置四)及1种后插钢筋较有利位置(位置五),见图 2。其中位置一、位置三、位置四后插入钢筋紧贴套筒内壁,分别为贴近预留钢筋、与预留钢筋夹角90°、与预留钢筋夹角180°,位置二后插入钢筋紧贴预留钢筋且两者圆心位于套筒同一直径,位置五后插入钢筋位于套筒圆心,套筒内均灌入无收缩灌浆料。

|
图 2 后插钢筋位置示意 Fig. 2 Schematic of positions of post-installed rebar |
试件分为15组,每组3个试件,套筒采用Q235无缝钢管,其内径D为70 mm,壁厚t为3 mm,长度L为120 mm,钢筋直径d=12、16和20 mm试件的搭接长度(套筒长度)分别为10d、7.5d和6d,试件详细尺寸见表 2。不同后插钢筋位置试件示意见图 3。
| 表 2 试验结果统计 Tab. 2 Statistics of test results |

|
图 3 不同后插钢筋位置试件示意(mm) Fig. 3 Schematic of specimens with post-installed rebar at different positions(mm) |
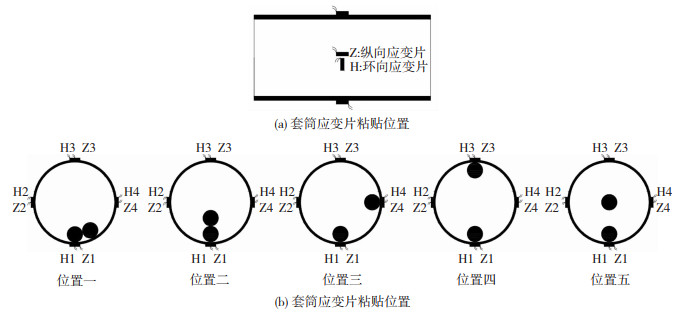
套筒应变测点位置见图 4。在套筒中部沿套筒纵向贴放4个应变片Z1~Z4,沿套筒环向贴放4个应变片H1~H4,其中编号为H的应变片测量套筒中部环向应变,编号为Z的应变片测量套筒中部纵向应变。
|
图 4 不同后插钢筋位置试件套筒应变片粘贴位置 Fig. 4 Locations of strain gauges on specimens with post-installed rebar at different positions |
加载采用同济大学万能试验机,试验装置见图 5。试验开始时以1 kN/s的应力速率加载至450 MPa(接近钢筋屈服强度),后以20 mm/min的分离速率加载,直至试件发生破坏[15]。

|
图 5 试验装置示意 Fig. 5 Setup of the test |
各试件的屈服强度fy、屈服位移δy、极限强度fu、极限荷载位移δu、极限平均黏结应力τu和破坏形态列于表 2。试件有两种破坏形式:钢筋拔出破坏和钢筋拉断破坏,后者分为钢筋拉断于钢筋母材处和钢筋拉断于焊接处。其中钢筋直径为20 mm的试件主要发生滑移破坏,其余试件主要为钢筋拉断破坏。试件破坏情况见图 6。

|
图 6 试件破坏情况 Fig. 6 Failure modes of specimens |
试件典型荷载-位移曲线见图 7。发生钢筋拉断或拔出破坏的试件,在荷载-位移曲线上升段基本相同,而下降段不同。发生钢筋拉断破坏的试件(图 7(a)~(b)),具有明显屈服台阶,钢筋发生颈缩后随即被拉断,荷载迅速下降到零,反映在曲线上为一段笔直的下降段。发生钢筋拔出破坏的试件(图 7(c)),当荷载达到试件的极限承载力后,钢筋与灌浆料间的黏结性能由于肋间灌浆料的压碎而迅速降低,承载力迅速下降,而钢筋与灌浆料间的相对滑移持续增长,钢筋与挤碎后的灌浆料粉末堆积物产生了新的滑移面,荷载-位移曲线进入残余段,承载力缓慢下降,同时滑移值不断增大,直到钢筋被完全拔出。

|
图 7 试件典型荷载-位移曲线 Fig. 7 Typical load-displacement curves of specimens |
由图 7可知,在试件达到屈服荷载前,在相同承载力下,位移按后插钢筋位置一、二、五、三、四次序逐渐增加,表明位置一试件刚度最大,位置四试件刚度最小。这主要与两根钢筋的距离有关,后插钢筋为位置一、二的试件,两根钢筋的距离为d,位置五试件两根钢筋的距离>d,位置三试件两根钢筋的距离更大,位置四试件两根钢筋的距离最大,为D-d。而试件加载过程中,由于两根钢筋受力并不共线,试件会发生偏转变形(套筒偏转方向位于两钢筋圆心连线方向),使上下两钢筋有趋于共线的趋势,图 8为加载后套筒偏转情况。两根钢筋的距离越大,试件在受力过程中偏转变形越大,则试件的刚度越低。

|
图 8 加载后试件偏转示意 Fig. 8 Schematic of deflection of specimen after loading |
为保证接头的延性,要求其位移延性系数[16-17] Rd≥4。Rd=δu/δy,δy为试件的屈服位移,δu为极限承载力对应的位移。试件位移延性系数见表 2。
2.2.1 后插钢筋位置对延性的影响以A组试件(钢筋拉断破坏)为例进行分析,位置一的试件延性系数最大,其次为位置二、五、三,位置四的试件延性系数最小,这与试件刚度变化规律一致。由于试件在加载过程中存在偏转现象,且两钢筋的距离越大,试件偏转程度越大,这使得试件在屈服前的位移较大,因而延性系数降低(B组试件具有相同特征)。发生钢筋拔出破坏的C组试件,延性系数与钢筋位置未表现出明显关系。主要是因为钢筋与灌浆料的黏结强度对延性也有影响。
2.2.2 钢筋直径对延性的影响钢筋直径由12 mm增加至20 mm,延性系数呈降低趋势。钢筋直径为12 mm,钢筋与灌浆料间的黏结力充足,钢筋从屈服到极限荷载时变形发展较为充分,延性最大;当钢筋直径增加到16 mm,由于试件承载力增大,套筒偏转使端部灌浆料压碎脱落更为严重,灌浆料对钢筋约束作用减小,钢筋屈服位移加大,而极限荷载位移与钢筋直径为12 mm时相差不大,故延性降低;发生滑移破坏的试件,钢筋从屈服到极限承载力时过程很短,钢筋的延性发挥较少,故试件延性最低。
2.3 接头黏结强度分析 2.3.1 后插钢筋位置对黏结强度的影响由表 2可知,钢筋直径为20 mm的试件(试件C-4-1除外)主要发生钢筋拔出破坏,灌浆料与钢筋的黏结强度得到了充分发挥,故后插钢筋位置会影响试件的极限承载力及黏结强度。
图 9为后插钢筋位置对黏结强度的影响。可见,后插钢筋在套筒中部时(位置五)黏结强度最大;后插钢筋紧贴预留钢筋及套筒时(位置一)黏结强度最小;两根钢筋均与套筒接触时(位置一、位置三、位置四),黏结强度随两根钢筋间距增大而增大;当仅一根钢筋与套筒接触时(位置二、位置五),黏结强度随两根钢筋间距增大而增大。

|
图 9 不同后插钢筋位置对黏结强度的影响 Fig. 9 Influence of position of post-installed rebar on bonding strength |
位置五的后插钢筋,由于其在套筒中部,四周均被灌浆料握裹,故试件受拉时,钢筋肋与灌浆料充分接触,钢筋间的灌浆料可以有效传力,承载力最高。位置一的后插钢筋紧贴预留钢筋和套筒,造成两根钢筋与套筒壁间的空隙灌浆困难,形成了一定的灌浆缺陷,导致钢筋肋与灌浆料接触并不充分,从而使试件的承载力与黏结强度最低。
后插钢筋为位置一、三、四的试件,虽然两钢筋均紧贴套筒,但预留钢筋与后插钢筋的距离不同,因而试件的承载力不同。位置四的后插钢筋与预留钢筋距离最远,虽然加载过程中试件的偏转最大,但其套筒的环向应力大于后插钢筋为位置三的试件,表明套筒对钢筋及灌浆料的约束更强,且两钢筋距离远,相互影响小,故后插钢筋为位置四的试件承载力较高。
决定接头承载力有两个因素,钢筋与套筒是否接触及钢筋间距离。钢筋与套筒贴近易在接触面产生灌浆缺陷,接头承载力降低;钢筋间距离减小,两钢筋间灌浆料受力更加不利,接头承载力降低。从位置五黏结强度大于位置四、位置二的黏结强度大于位置三可以看出,钢筋与套筒接触对黏结强度降低起控制作用。
2.3.2 后插钢筋直径对极限承载力的影响图 10为钢筋直径对极限承载力的影响。由表 2、图 10可知,随钢筋直径增加,试件的极限承载力增加,同时试件的破坏模式由钢筋拉断转化为钢筋拔出破坏。

|
图 10 钢筋直径对极限承载力的影响 Fig. 10 Influence of rebar diameter on ultimate bearing capacity |
对于钢筋直径为12、16 mm的试件,由于钢筋抗拉承载力较低,在钢筋与灌浆料的黏结强度充分发挥之前,钢筋即被拉断,试件的承载力主要取决于钢筋材性。而对于钢筋直径为20 mm的试件(试件C-4-1除外)主要发生钢筋拔出破坏,其承载力主要取决于钢筋与灌浆料的黏结作用。对于具有横向约束的试件,其黏结强度随钢筋直径的增加而增大[18-19],且锚固长度相同时,钢筋直径越大表面积越大,故C组试件虽然发生钢筋拔出破坏,但其极限承载力依然大于A、B组试件。
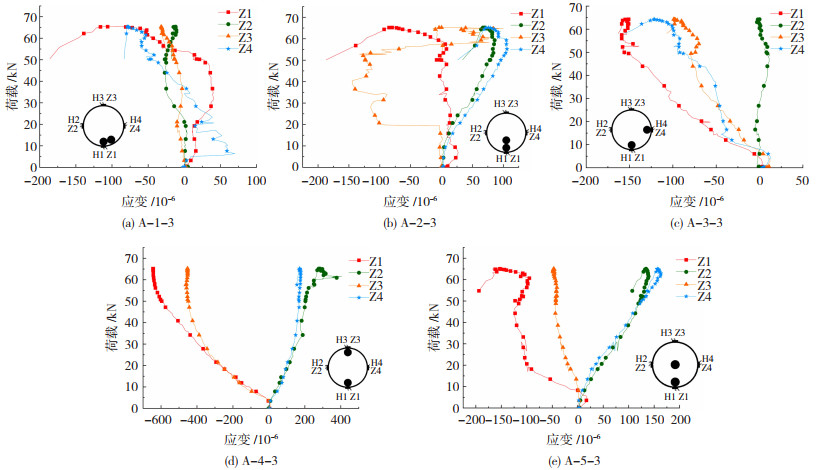
2.4 接头荷载-套筒纵向应变曲线试件中部截面典型的荷载-纵向应变曲线见图 11(压应变为负)。加载过程中,各试件套筒纵向应变始终小于2 000×10-6,即套筒的纵向应变未超过其母材的屈服应变。
|
图 11 套筒中部截面典型的荷载-纵向应变曲线 Fig. 11 Typical load-longitudinal strain curves of middle section of sleeve |
套筒的纵向应变主要受3种因素影响:一是钢筋黏结力引起套筒的剪应力形成套筒的轴向力,在加载初期,灌浆料与钢筋间黏结力引起套筒中部受拉,但拉应力较小,随着荷载增大,拉应变增加到一定程度向压应变转化[20];二是灌浆料膨胀变形,使套筒环向受拉,由于泊松比效应,引起套筒纵向受力;三是试件偏转使紧贴钢筋的套筒纵向受压。
由图 11可知,在加载初期,偏转方向的套筒应变(如位置一、三的Z1、Z4,位置二、四、五的Z1、Z3)存在受拉趋势,随荷载增加,套筒纵向受压,其压应变随试件受力增大而增大。这是由于在加载初期,套筒偏转引起的压应力小于灌浆料黏结力引起的拉应力;而在加载后期,灌浆料的黏结力亦引起压应力[20],与套筒偏转引起的压应力叠加,套筒纵向受压。
非偏转方向的套筒应变(如位置二、四、五的Z2、Z4)受套筒偏转变形的影响较小,套筒纵向应变主要由灌浆料与钢筋间黏结力及灌浆料膨胀变形引起。在加载初期为拉应变,随着荷载增大,灌浆料膨胀变形使套筒环向受拉、纵向受压,同时灌浆料黏结应力引起的拉应变增加到一定程度向压应变转化,因而其拉应变减小。
2.4.1 后插钢筋位置对套筒纵向应变的影响图 12为后插钢筋位置对极限荷载时Z3的影响。后插钢筋为位置四的试件,其测点Z3的纵向应变绝对值明显高于其他位置。钢筋因试件偏转会在套筒端部产生弯曲变形(见图 8),因而端部套筒环向受拉,纵向受压。由于套筒长度较短(为120 mm),套筒端部因受压而产生的塑性变形会影响套筒中部应变,因而与后插钢筋紧贴的套筒中部纵向受压。位置四试件的偏转变形最大,故Z3纵向压应变值最大。
|
图 12 后插钢筋位置对极限荷载时Z3影响 Fig. 12 Influence of position of post-installed rebar on Z3 under ultimate load |
位置五试件的Z3纵向压应变值大于位置二。这是由于处在试件偏转方向的套筒纵向应变受偏转影响较大,且套筒纵向应变趋势相同。位置二、五试件的测点Z3位于试件偏转方向,位置五试件的偏转变形大于位置二,且位置五的Z3测点距后插钢筋更近,极限荷载时黏结应力引起的套筒轴向压力更大,故其纵向压应变值较大。
位置一、三试件的Z3测点位于非偏转方向,其纵向应变主要受灌浆料黏结作用的影响,可能为压应变或拉应变,其绝对值始终小于5×10-4,由于位置三的Z3测点距后插钢筋更近,套筒受力更大,故其应变值较大。
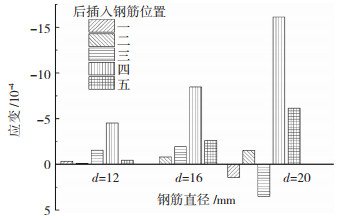
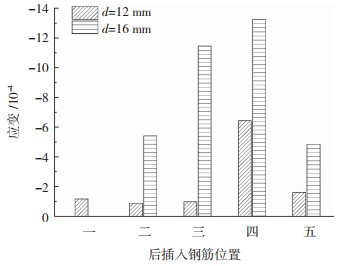
2.4.2 钢筋直径对套筒纵向应变的影响图 13为钢筋直径(d=12、16 mm)对极限荷载时Z1的影响。试件在极限承载力下,紧贴钢筋的套筒纵向受压,且钢筋直径增大,套筒纵向压应变增大。这是因为钢筋直径从12 mm到16 mm,钢筋与灌浆料的黏结强度增大,极限荷载时灌浆料黏结力引起的套筒压应变增大;且试件承载力提高,钢筋的弯曲变形也加大,套筒端部抵抗钢筋弯曲产生的塑性变形较大。钢筋直径主要通过影响套筒端部变形和灌浆料黏结应力的大小对套筒纵向应变产生作用,钢筋直径为20 mm的试件多发生钢筋拔出破坏,钢筋的强度尚未充分发挥,套筒纵向应变无明显规律。
|
图 13 钢筋直径对极限荷载时Z1影响 Fig. 13 Influence of rebar diameter on Z1 under ultimate load |
试件中部截面典型荷载-环向应变曲线见图 14。A、B组试件在加载过程中套筒环向应变始终小于2 000×10-6,即环向应变未超过套筒的屈服应变,套筒处于弹性工作阶段。C组试件在加载过程中套筒局部环向应变超过了套筒的屈服应变,处于塑性工作阶段,由于应变较大,部分H1应变片发生破坏。

|
图 14 套筒中部截面典型荷载-环向应变曲线 Fig. 14 Typical load-circumferential strain curves of middle section of sleeve |
套筒中部截面环向应变以拉应变为主,主要受3种影响因素:一是钢筋黏结力引起套筒的剪应力形成套筒的轴向力,由于泊松比效应,引起套筒环向受力;二是灌浆料膨胀变形,使套筒环向受拉;三是套筒约束钢筋的分离趋势和弯曲变形,使套筒环向受拉。
在加载初期,由于灌浆料与钢筋间黏结力引起套筒中部受拉,但拉应力较小,因而套筒环向应变存在受压趋势;随荷载增加,灌浆料发生膨胀变形,使套筒环向受拉;同时在加载后期,灌浆料的黏结应力使套筒纵向受压,套筒环向受拉;紧贴钢筋的套筒应变(如测点H1、位置三的H4、位置四的H3)受钢筋分离趋势和弯曲变形的影响较大,因而套筒环向拉应力更大。
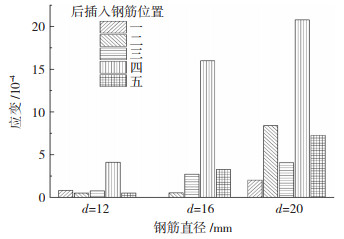
2.5.1 后插钢筋位置对套筒环向应变的影响图 15为后插钢筋位置对极限荷载时H3的影响。后插钢筋为位置四的试件,其测点H3的应变值要显著高于其他位置。这是因为位置四试件两钢筋间距最大,其偏转变形最大,测点H3侧套筒不仅要约束灌浆料膨胀变形,还要直接抵抗两钢筋的分离趋势和钢筋的弯曲变形,故套筒环向变形最大。而其他位置试件的应变测点H3远离后插钢筋,套筒以约束灌浆料膨胀变形为主,故应变较小。由图 14也可知,紧贴预留钢筋的应变测点H1显著高于远离钢筋测点H2、H3(位置四除外)、H4(位置三除外)的应变值。
|
图 15 后插钢筋位置对极限荷载时H3影响 Fig. 15 Influence of position of post-installed rebar on H3 under ultimate load |
由图 14可知,非偏转方向的套筒环向应变值较小,如位置一的H2、H3、位置二的H2、H4、位置三的H2、H3、位置四的H2、H4、位置五的H2、H4,这是因为垂直于钢筋偏转方向的套筒主要受灌浆料膨胀变形和黏结作用的影响,受试件偏转影响小,故环向应变值较小。
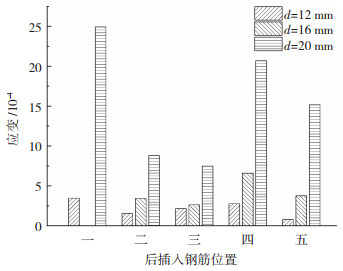
2.5.2 钢筋直径对套筒环向应变的影响图 16为钢筋直径对极限荷载时套筒中部截面平均环向应变的影响。后插钢筋位置相同时,随钢筋直径d增大,套筒1/2截面的平均环向拉应力增大,这表明套筒横向约束增强。这是因为随钢筋直径的增大,试件的极限承载力增大,灌浆料受力膨胀变形增大;同时,钢筋的偏转力也增加,套筒环向应变增大。
|
图 16 极限荷载时套筒中部截面平均环向应变 Fig. 16 Average circumferential strain of middle section of sleeve under ultimate load |
目前,套筒内灌浆料应力-应变关系尚无成熟的理论模型,文献[21-22]研究表明ABAQUS中的混凝土塑性损伤模型可以较好地模拟单调荷载作用下的构件反应。故本文采用混凝土塑性损伤模型来实现混凝土的塑性变形、刚度退化、损伤开裂等。
3.1.2 钢材本构在实际应用中,钢材的横截面积随荷载的增加逐渐减小,且本文有限元模拟的非线性分析属于几何大变形问题,采用名义应力误差较大,因此本文根据文献[23]计算得到套筒和钢筋的真实应力-应变关系。
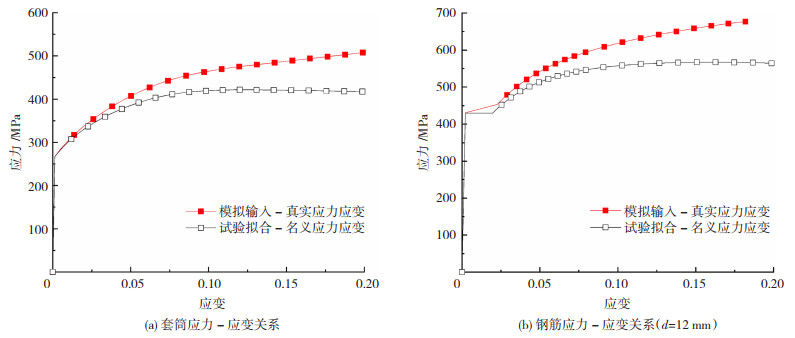
参考材性试验结果,取套筒弹性段杨氏模量为200 GPa,屈服强度为267.0 MPa,屈服应变为0.001 335,极限强度为421.7 MPa,极限应变为0.20,则由此得到的套筒真实应力-应变关系见图 17(a)。取d=12 mm钢筋的屈服强度为430 MPa,极限强度为567 MPa,拉断应变为0.20,则钢筋(d=12 mm)真实应力-应变关系见图 17(b)。同样可得到d=16 mm、d=20 mm钢筋的真实屈服强度分别为476、451 MPa,极限强度分别为671、742 MPa,真实拉断应变为0.18。
|
图 17 本构关系 Fig. 17 Constitutive relation |
以钢筋直径和后插钢筋位置为变量,建立13个APC接头精细化模型,模型详细尺寸见表 3(由于钢筋直径为20 mm时,C2和C5模型基本一致,故仅建立C2模型,后插钢筋位于套筒中部,即位置五)。接头整体模型及网格划分见图 18。
| 表 3 模拟结果统计 Tab. 3 Statistics of simulation results |

|
图 18 接头整体模型及网格划分 Fig. 18 Overall model of the connector and mesh division |
ABAQUS/Explicit中的四面体二阶单元几乎能模拟任何几何形状,且对大变形和接触问题的模拟有足够高的精度,因此本文模拟采用四面体实体单元C3D10M。
为更好模拟灌浆料与钢筋和套筒内壁之间黏结滑移,本文将法向行为设定为硬接触,切向行为选项中将接触面的摩擦公式设定为“罚”,接触中选用粘性行为并设定其牵引分离为线性。为避免ABAQUS/Standard分析复杂接触问题时出现不收敛情况,模拟采用动力显示分析,分析步类型为“动力,显式”。
计算过程中,采用以下约束模拟接头在单向拉伸作用下的受力边界条件:1)套筒偏转模型:预留钢筋端面采用固定位移约束(即U1、U2、U3、UR1、UR2、UR3均为0),后插入钢筋端面除Z方向(U3)外的位移约束(U1、U2、UR1、UR2、UR3)均为0;2)套筒不偏转模型:预留钢筋端面和后插入钢筋端面边界约束条件同套筒偏转模型,套筒外表面除Z方向(U3)外的位移约束(U1、U2、UR1、UR2、UR3)均为0;3)在固定端钢筋断面、加载端钢筋断面的截面中心分别设置参考点,并分别与固定端钢筋断面、加载端钢筋断面建立运动耦合约束;4)本次模拟采用位移加载模式,设定加载位移为75 mm,幅值曲线类型为平滑分析步;5)灌浆料刚度退化为初始刚度的0.75时失效。
3.3 试验工况下数值模拟与试验结果对比分析模拟试验结果见表 3。偏转模拟试件与先期试验试件的破坏形态一致,即有钢筋拉断破坏和钢筋拔出破坏。
3.3.1 钢筋拉断破坏时荷载-位移曲线(以A组试件为例)钢筋拉断破坏时模拟试件与试验试件的荷载-位移曲线对比见图 19。图中SY表示先期试验试件,PZ表示偏转模拟试件。

|
图 19 钢筋拉断破坏时试件荷载-位移曲线 Fig. 19 Load-displacement curves of specimens with tensile failure of rebars |
模拟曲线在弹性段和强化段与试验曲线拟合较好,而在极限荷载位移方面与试验结果有差异,模拟试件的极限荷载位移一般大于试验试件。这主要是因为模拟时所定义材料属性为各向同性且分布均匀,而实际材料性质并非理想,材料中的细微缺陷、焊接部位施工工艺不稳定等均会使钢筋伸长率小于理想状态。
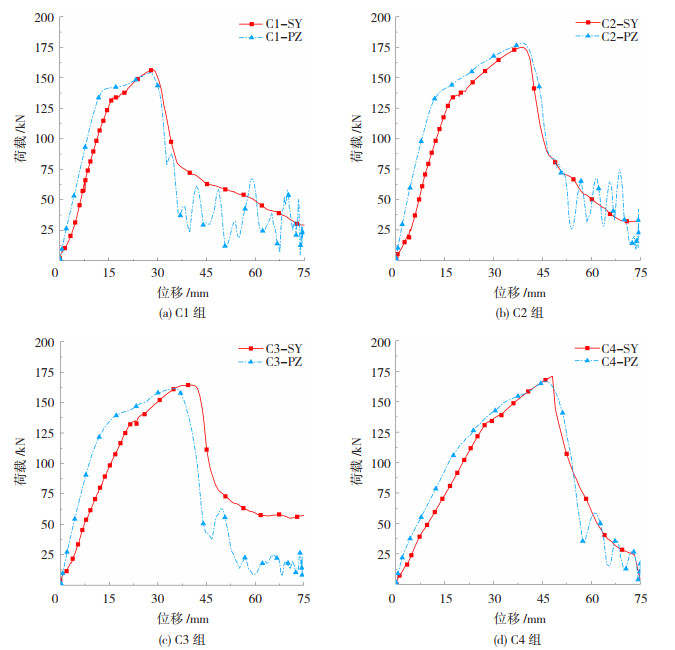
3.3.2 钢筋拔出破坏时荷载-位移曲线钢筋拔出破坏时试验与模拟试件的荷载-位移曲线对比见图 20。可以看出,弹性阶段试件刚度试验值小于模拟值,主要表现在初始加载时,由于夹具滑移,试件初始位移较大,而模拟中位移的发展比较均匀。
|
图 20 钢筋拔出破坏时试件荷载-位移曲线 Fig. 20 Load-displacement curves of specimens with pull-out failure of rebars |
模拟曲线的下降段出现了波动,与试验曲线有明显差异。由于在ABAQUS模拟中是通过变形检测将变形过大的灌浆料单元删除,在单元删除的瞬间钢筋与灌浆料间出现了间隙,因此荷载迅速下降;当钢筋滑移到与灌浆料重新接触时,荷载逐渐增大,由此表现出下降段的波动。而试验中钢筋肋间灌浆料被压碎后仍然存在,灌浆料与钢筋肋之间不会突然出现较大间隙,而钢筋滑移时与灌浆料表面有一定摩擦,因而荷载位移曲线下降段相对平滑。
试件破坏时的极限荷载对比情况见表 3。极限荷载的模拟值与试验值较为接近,A、B、C组试件的最大误差绝对值分别为2.66%、2.90%、3.78%。结果表明模型参数取值合理,模拟方法准确可行。
4 套筒偏转对接头承载能力的影响对套筒外表面施加约束,使套筒不发生偏转,此工况下模拟接头的极限承载力见表 3。发生拉断破坏的模拟试件,非偏转试件极限承载力大于偏转试件,偏转影响约为0.46%~5.52%。这是因为偏转模拟试件的钢筋在灌浆料端部发生弯折易使钢筋提前拉断,强化段发展不充分。发生拔出破坏的模拟试件,非偏转试件极限承载力大于偏转试件,偏转影响约为7.93%~15.53%。这是由于端部灌浆料在钢筋弯曲的挤压作用下发生破坏,钢筋的有效锚固长度减小。可见偏转对发生钢筋拔出破坏试件的极限承载力影响较大,对发生钢筋拉断破坏试件的影响较小。
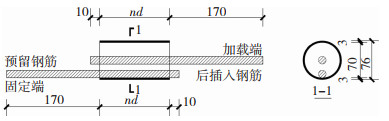
5 搭接长度对接头性能的影响以搭接长度为变量,建立8个非偏转状态(接近实际应用工况)的APC接头精细化模型,分别为16-5-(4.0d~7.5d),试件编号含义为“钢筋直径-后插钢筋位置-搭接长度”,即钢筋直径为16 mm,取位置五工况,搭接长度为4.0d~7.5d(增量为0.5d),套筒内径为70 mm,壁厚3 mm。不同搭接长度试件示意见图 21。
|
图 21 不同搭接长度试件示意(mm) Fig. 21 Schematic of specimens with different lap lengths(mm) |
图 22为非偏转模拟试件随搭接长度变化时的荷载-位移曲线。试件破坏形式有3种:钢筋未屈服拔出破坏(16-5-4.0d、16-5-4.5d)、钢筋屈服后拔出破坏(16-5-5.0d、16-5-5.5d)和钢筋拉断破坏(16-5-6.0d~16-5-7.5d)。

|
图 22 不同搭接长度试件荷载-位移曲线(d=16 mm) Fig. 22 Load-displacement curves of specimens with different lap lengths (d=16 mm) |
发生钢筋拉断破坏的模拟试件,其荷载位移曲线相近,极限承载力基本相同,承载力主要取决于钢筋材性。发生钢筋屈服后拔出破坏的模拟试件,搭接长度增加时,最大位移明显增大。这是由于搭接长度增大时,钢筋强化程度提高,故破坏后位移较大。
由图 22可知,模拟试件16-5-5.5d的荷载位移曲线与发生钢筋拉断破坏的模拟试件16-5-6.0d比较接近,因此可近似认为钢筋拉断破坏的临界搭接长度为6.0d。模拟试件16-5-4.5d的极限荷载为94.71 kN,与钢筋屈服荷载(约为95 kN)非常接近,且本文模拟采用的钢筋屈服应力高于400 MPa,因而试件发生钢筋屈服后拔出破坏的临界搭接长度约为4.5d。
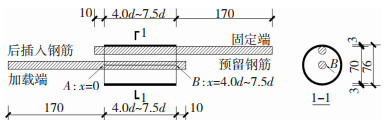
5.2 接头非偏转时搭接长度对黏结应力的影响为探究加载钢筋沿埋置长度的黏结应力分布情况,在ABAQUS中选取一具有代表性的钢筋黏结应力输出路径(钢筋表面A点到B点)进行应力输出,见图 23,得到沿图中直线A到B上的黏结应力分布曲线。如上所述对搭接长度为4.0d~7.5d的位置五试件进行应力输出,图 24为加载过程中黏结应力沿加载钢筋埋置长度的分布情况。图中注明了极限荷载时黏结应力分布曲线与平均黏结应力的交点坐标,定义极限荷载时黏结应力分布饱满程度为
| $ p=\frac{\mid \text { 交点横坐标差值 } \mid}{\text { 搭接长度 }} \times 100 \% $ |
|
图 23 位置五试件钢筋黏结应力输出路径(mm) Fig. 23 Output path of bonding stress of rebar at position 5(mm) |

|
图 24 加载过程中钢筋与灌浆料间黏结应力沿加载钢筋埋置长度的分布情况 Fig. 24 Distribution of bonding stress between rebar and grouting material along the embedded length of loaded rebar during loading |
式中p为黏结应力分布饱满程度,即表示黏结应力分布的均匀程度。
由图 24可知,随荷载增加,灌浆料与钢筋黏结作用逐渐失效,每一阶段的峰值黏结应力在加载过程中由加载端向自由端移动。搭接长度较短时(4.0d~5.5d),试件滑移破坏,极限荷载峰值黏结应力靠近自由端;搭接长度较长时(6.0d~7.5d),钢筋拉断,极限荷载峰值黏结应力逐渐靠近套筒中部截面。
极限荷载时不同搭接长度试件黏结应力曲线特征见图 25。发生拔出破坏的试件,搭接长度从4.0d增加到5.0d,由于黏结应力沿钢筋黏结长度的不均匀分布和泊松比效应[24],黏结长度越长,黏结应力分布越不均匀,黏结强度的高应力区相对短而窄,曲线分布趋于陡峭,因此随相对搭接长度增加,曲线黏结应力峰值增大,饱满程度下降。

|
图 25 极限荷载时不同搭接长度试件黏结应力曲线特征 Fig. 25 Characteristics of bonding stress curve of specimens with different lap lengths under ultimate load |
相对搭接长度从5.0d增加到7.5d,曲线黏结应力峰值减小,饱满程度增大。这是因为试件的极限荷载变化不大,但钢筋与灌浆料的接触面积不断增加,平均黏结应力减小,灌浆料整体损伤程度减小,曲线分布趋于均匀。
搭接长度为5.5d的试件虽发生钢筋拔出破坏,但其极限荷载大于114 kN(见图 24),与钢筋拉断荷载基本一致,因此黏结应力曲线分布与钢筋拉断破坏试件较为接近,曲线饱满程度高于搭接长度为5.0d的试件。这也说明,在搭接长度4.5d~5.5d之间存在一临界搭接长度(本试验中为5.0d) 使黏结应力曲线饱满程度最小,即曲线分布最不均匀,随搭接长度继续增加,黏结应力曲线分布趋于均匀。
6 极限黏结强度计算公式参考文献[20],影响接头黏结强度的因素有:灌浆料强度fts、配箍率ρsv(近似取t/D)、套筒相对厚度D/d、相对搭接长度的倒数d/l,故选取如式(1)所示函数对APC接头的极限黏结强度进行拟合。
| $ \bar{\tau}_{\mathrm{u}}=\left(\alpha+\beta \frac{d}{l}\right)\left(\gamma+m \frac{D}{d}+n \frac{t}{D}\right) f_{\mathrm{ts}} $ | (1) |
式中:α,β,γ,m,n为待定常系数;τu为极限荷载平均黏结应力;d为钢筋直径;l为钢筋搭接长度;D为套筒内径;t为套筒厚度;fts为灌浆料劈裂抗拉强度。
结合本次钢筋拔出破坏试件及课题组前期系列试验[8-10]拟合得到套筒灌浆搭接连接黏结强度计算公式:
| $ \bar{\tau}_{\mathrm{u}}=\left(0.39+4.52 \frac{d}{l}\right)\left(3.96-0.07 \frac{D}{d}+18.27 \frac{t}{D}\right) f_{\mathrm{ts}} $ | (2) |
拟合值与试验值偏差情况见图 26。数据编号1~15为本次试验黏结应力试验值与拟合值,拟合值约为试验值的0.95倍,拟合值相对偏低。这是由于前期试验(数据编号16~78)试件所取钢筋位置为位置一、二,位置一试件黏结强度最低,而位置二试件黏结强度与其他三组(位置三、四、五)试件总黏结强度平均值相近(见图 9),故由此拟合的极限黏结强度公式偏于保守。同时考虑到公式应用的简易性,故公式中不再考虑钢筋位置对黏结强度的影响因素。

|
图 26 极限黏结强度的拟合值与试验值比较 Fig. 26 Comparison between fitted value and test value of ultimate bond strength |
拟合值与本课题组前期系列试验平均黏结应力之比τu/τue在0.83~1.40范围内,平均值为1.00,标准差为0.05,变异系数为0.049,式(2)对试验结果的整体拟合程度较高。
极限黏结应力试验拟合值τu、试件偏转模拟极限黏结应力τuPZ、拟合值与偏转模拟值对比τu/τuPZ,见表 4。
| 表 4 极限荷载时黏结应力拟合值与有限元试件模拟值对比 Tab. 4 Comparison between fitted value of bonding stress and simulated value of finite element specimen under ultimate load |
对于偏转模拟试件,τu/τuPZ在0.80~1.23范围内,平均值为0.93,标准差为0.12,变异系数为0.13;偏转模拟与公式拟合值较为接近。因此,对更靠近实际工况的非偏转模拟试件而言,式(2)偏于安全,可以作为黏结强度计算公式。
7 结论进行了后插钢筋位置等变量的APC接头单拉试验及数值分析,得出的结论可为APC接头应用提供试验研究基础及理论依据。
1) 试件的初始刚度和延性与两钢筋间距离有关。随后插钢筋与预留钢筋间距离增大,试件偏转程度增大,导致钢筋屈服前位移增加,试件初始刚度及延性逐渐减小。
2) 接头承载力受两个因素影响,钢筋与套筒是否接触及钢筋间距离。钢筋与套筒贴近易在接触面产生灌浆缺陷,接头承载力降低;钢筋间距离减小,两钢筋间灌浆料受力更加不利,接头承载力降低;钢筋与套筒接触对黏结强度降低起控制作用。
3) 极限荷载时,偏转方向的套筒中部截面纵向受压,钢筋拉断破坏试件,其压应变随钢筋直径的增大而增大;非偏转方向的套筒可能受压或受拉,应变值相对较小。
4) 近钢筋侧套筒环向拉应力大,远钢筋侧套筒环向应力小(可能为压应力);随着钢筋直径增大,套筒中部截面的环向平均拉应力增大,套筒横向约束增强。
5) 偏转模拟接头的破坏形式、荷载-位移曲线、黏结强度等与前期试验结果吻合较好,A、B、C组试件的极限荷载模拟值与试验值最大误差绝对值分别为2.66%、2.90%、3.78%,验证了试验结果的准确性。
6) 模拟结果表明,偏转降低试件的极限承载力。偏转对发生钢筋拔出破坏试件的极限承载力影响较大,对发生钢筋拉断破坏试件的影响较小。
7) 搭接长度模拟分析表明,钢筋直径d=16 mm时,相对搭接长度从4.0d增加到5.0d,曲线黏结应力峰值增大,饱满程度下降;相对搭接长度从5.0d增加到7.5d,曲线黏结应力峰值减小,饱满程度增大。
8) 极限黏结强度计算公式对试验值的拟合程度较高,可作为实际工程参考。
| [1] |
ALIAS A, ZUBIR M A, SHAHID K A, et al. Structural performance of grouted sleeve connectors with and without transverse reinforcement for precast concrete structure[J]. Procedia Engineering, 2013, 53: 116. DOI:10.1016/j.proeng.2013.02.017 |
| [2] |
郑永峰, 郭正兴. 循环荷载作用下新型钢筋套筒灌浆连接结构性能[J]. 湖南大学学报(自然科学版), 2016, 43(11): 131. ZHENG Yongfeng, GUO Zhengxing. Structural performance of innovative grout sleeve splicing for rebars under cyclic loading[J]. Journal of Hunan University (Natural Sciences), 2016, 43(11): 131. DOI:10.16339/j.cnki.hdxbzkb.2016.11.018 |
| [3] |
郑清林, 王霓, 陶里, 等. 灌浆缺陷对钢筋套筒灌浆连接试件性能影响的试验研究[J]. 建筑科学, 2017, 33(5): 61. ZHENG Qinglin, WANG Ni, TAO Li, et al. Experimental study on effects of grout defects on the connection behaviors of grout sleeve splicing for reinforcing bars[J]. Building Science, 2017, 33(5): 61. DOI:10.13614/j.cnki.11-1962/tu.2017.05.010 |
| [4] |
许成顺, 刘洪涛, 杜修力. 高应力反复拉压作用下钢筋套筒灌浆连接性能试验研究[J]. 建筑结构学报, 2018, 39(12): 178. XU Chengshun, LIU Hongtao, DU Xiuli. Experimental study on connection performance of grouted sleeve splicing for rebars under high stress repeated tension-compression loading[J]. Journal of Building Structures, 2018, 39(12): 178. DOI:10.14006/j.jzjgxb.2018.12.021 |
| [5] |
吴涛, 王珅, 刘毅斌, 等. 钢筋套筒灌浆连接件的力学性能[J]. 建筑科学与工程学报, 2019, 36(2): 21. WU Tao, WANG Shen, LIU Yibin, et al. Mechanical performance of reinforcement grouted sleeve connection[J]. Journal of Architecture and Civil Engineering, 2019, 36(2): 21. |
| [6] |
余琼. 一种新型的约束搭接套筒: ZL 201420656653.0[P]. 2015-04-01 YU Qiong. A new confined lapping sleeve: ZL 201420656653.0[P]. 2015-04-01 |
| [7] |
余琼, 许志远, 袁炜航, 等. 两种因素影响下套筒约束浆锚搭接接头拉伸试验[J]. 哈尔滨工业大学学报, 2016, 48(12): 34. YU Qiong, XU Zhiyuan, YUAN Weihang, et al. Experimental study of grouted sleeve lapping connectors varied in two factors under tensile load[J]. Journal of Harbin Institute of Technology, 2016, 48(12): 34. DOI:10.11918/j.issn.0367-6234.2016.12.004 |
| [8] |
许志远. 钢筋套筒灌浆搭接接头力学性能试验研究[D]. 上海: 同济大学, 2016 XU Zhiyuan. Experimental study on mechanical properties of grouted sleeve lapping connectors[D]. Shanghai: Tongji University, 2016 |
| [9] |
宫鑫. 大直径钢筋套筒灌浆搭接接头受拉性能试验研究[D]. 上海: 同济大学, 2017 GONG Xin. Experimental study on tensile properties of grouted sleeve lapping connectors of large diameter rebars[D]. Shanghai: Tongji University, 2017 |
| [10] |
许坤. 套筒尺寸对套筒灌浆搭接接头受拉性能影响试验[D]. 上海: 同济大学, 2018 XU Kun. Influence of sleeve section size on tensile performance of grouted sleeve lapping connectors[D]. Shanghai: Tongji University, 2018 |
| [11] |
匡轩. 钢筋套筒灌浆搭接连接有限元模拟[D]. 上海: 同济大学, 2019 KUANG Xuan. Finite element simulation of reinforcement grouted sleeve lapping connectors[D]. Shanghai: Tongji University, 2019 |
| [12] |
金属材料拉伸试验第1部分: 室温试验方法: GB/T 228.1—2010[S]. 北京: 中国标准出版社, 2010 Metallic materials-Tensile testing—Part 1: method of test at room temperature: GB/T 228.1—2010[S]. Beijing: Standards Press of China, 2010 |
| [13] |
水泥胶砂强度检验方法: GB/T 17671—1999[S]. 北京: 中国标准出版社, 1999 Method of testing cements—Determination of strength: GB/T 17671—1999[S]. Beijing: Standards Press of China, 1999 |
| [14] |
普通混凝土力学性能试验方法标准: GB/T 50081—2002[S]. 北京: 中国建筑工业出版社, 2003 Standard for test method for mechanical properties on ordinary concrete: GB/T 50081—2002[S]. Beijing: China Architecture and Building Press, 2003 |
| [15] |
钢筋机械连接技术规程: JGJ 107—2016[S]. 北京: 中国建筑工业出版社, 2016 Technical specification for mechanical splicing of steel reinforcing bars: JGJ 107—2016[S]. Beijing: China Architecture and Building Press, 2016 |
| [16] |
Building code requirements for structural concrete: ACI 318-14[S]. Michigan: American Concrete Institute, 2014
|
| [17] |
Structural use of concrete—Part 1: code of practice for design and construction: BS 8110-1[S]. London: British Standards Institution, 1997
|
| [18] |
ZUO J, DARWIN D. Splice strength of conventional and high relative rib area bars in normal and high-strength concrete[J]. ACI Structural Journal, 2000, 97(4): 630. |
| [19] |
刘明, 张炳成, 肖树勇. 月牙肋钢筋相对投影肋面积的计算和保证[J]. 冶金标准化与质量, 1999(2): 23. LIU Ming, ZHANG Bingcheng, XIAO Shuyong. Calculation and assurance of the specific projected rib area for crescent ribbed bars[J]. Metallurgical Standardization and Quality, 1999(2): 23. |
| [20] |
余琼, 王子沁, 白少华, 等. 套筒灌浆搭接接头拉伸试验及受力机理分析[J]. 哈尔滨工业大学学报, 2021, 53(4): 109. YU Qiong, WANG Ziqin, BAI Shaohua, et al. Sleeve lap joint grouting tensile test and stress mechanism analysis[J]. Journal of Harbin Institute of Technology, 2021, 53(4): 109. DOI:10.11918/202006123 |
| [21] |
聂建国, 王宇航. ABAQUS中混凝土本构模型用于模拟结构静力行为的比较研究[J]. 工程力学, 2013, 30(4): 67. NIE Jianguo, WANG Yuhang. Comparison study of constitutive model of concrete in ABAQUS for static analysis of structures[J]. Engineering Mechanics, 2013, 30(4): 67. DOI:10.6052/j.issn.1000-4750.2011.07.0420 |
| [22] |
周小军. ABAQUS中弥散裂缝模型与损伤塑性模型的比较[J]. 福建建筑, 2010, 143(5): 55. ZHOU Xiaojun. The comparison of smeared crack model and concrete damaged plasticity model in ABAQUS[J]. Fujian Architecture and Construction, 2010, 143(5): 55. |
| [23] |
刘希月, 王元清, 石永久. 基于微观机理的高强度钢材及其焊缝断裂预测模型研究[J]. 建筑结构学报, 2016, 37(6): 231. LIU Xiyue, WANG Yuanqing, SHI Yongjiu. Micromechanical fracture prediction model of high strength steel and its weld[J]. Journal of Building Structures, 2016, 37(6): 231. DOI:10.14006/j.jzjgxb.2016.06.028 |
| [24] |
孙明德, 高日, 陈应陶, 等. 高强钢筋与活性粉末混凝土粘结性能试验研究[J]. 桥梁建设, 2016, 46(6): 20. SUN Mingde, GAO Ri, CHEN Yingtao, et al. Experimental study of bond performance between high-strength rebar and reactive powder concrete[J]. Bridge Construction, 2016, 46(6): 20. |
 2022, Vol. 54
2022, Vol. 54


