2. 哈尔滨供水集团有限责任公司,哈尔滨 150010;
3. 中国节能环保集团有限公司,北京 100082
2. Harbin Water Supply Group Co., Ltd., Harbin 150010, China;
3. China Energy Conservation and Environmental Protection Group, Beijing 100082, China
城镇污水厂是重要的城镇基础设施,日益严格的环保要求和不断增长的污水处理量,给污水厂造成了更大的处理压力,对于污水厂的运行管理提出了更高的要求。进水条件与操作参数相关联,及时掌握进水水质变化特征对于运行控制方案的制定,以及保障出水稳定达标具有重大的意义[1-2]。BOD5(5 d生化需氧量)作为耗氧第一要素,是污水厂重要的日常监测水质参数,进水BOD5对于曝气控制与碳源投加方式具有一定的指导作用。因此,实现BOD5快速和准确的测定有利于污水厂的科学运维和优化管理。
BOD5的传统测定方法是稀释与接种法,流程简单,但具有测量耗时和干扰性大的主要缺点[3]。为解决传统测量方法分析时间滞后的弊端,近年来BOD5检测方法的研究集中于快速测定和软测量方法。微生物传感器法是目前研究最深入和应用最广泛的一种快速测定方法,大多数方法需要平均30 min估计BOD5,最快的系统可以在70 s内提供样品的BOD5,为BOD的现场快速检测提供了依据。由于生化反应的复杂性,各种快速测定方式都具有一定局限性,如适用范围窄、维护保养复杂、花费昂贵等。与硬件测量相比,软测量方法响应迅速、投资成本低,能当作硬件仪表的软冗余和用于过程优化以及故障诊断。随着工业过程中记录数据可用性和数据处理计算能力可用性的提升,软测量技术将具有更加广阔的应用前景[4]。常用的软测量建模方法有机理分析建模、统计回归建模、人工神经网络等机器学习建模。水质监测过程中的软测量建模,最常用的有传统的线性统计模型如多元线性回归(MLR)、各种神经网络如BP神经网络、RBF神经网络以及支持向量回归机(SVR)方法[5]。此外还有模糊逻辑、深度学习模型、组合模型等,对于处理过程出水水质还有耦合机理模型(活性污泥模型ASM1、ASM2、ASM3)的参数预测[6-8]。据2008—2019年国内涉及不同软测量技术的相关论文统计,基于神经网络的软测量技术是污水处理行业最常见的软测量技术手段,其中BP网络常作为对比方法出现在论文中,其次是支持向量机方法,占比约35%[9]。
机器学习的模型训练过程常常使用优化算法实现参数的快速高效优化。刘帮等[10]采用粒子群优化算法SVR方法建立序批式活性污泥反应器出水BOD5的软测量模型,并对比BP网络和标准的SVR,结果表明,粒子群优化算法SVR模型误差小、精度高,降低了模型的复杂度,提高了其泛化能力,能达到较好的预测效果。Bagheri等[11]建立神经网络- 遗传算法模型预测污泥体积指数(SVI),采用遗传算法对神经网络的权值和阈值进行优化,训练和验证模型显示SVI的实验值和预测值几乎完全匹配。Huang等[12]将粒子群优化算法(PSO)、遗传算法(GA)和网格搜索算法(GS)改进后的支持向量机(SVM)方法应用于铁路危险货物运输系统的风险识别,发现标准SVM算法的优化时间最短,GA-SVM算法的准确率最高。优化算法的使用改善了模型学习效率低、收敛速度慢和容易陷入局部极小等缺点,因此,本研究考虑了不同优化算法对SVR模型预测性能的影响,以期实现更好的预测效果。
目前,BOD的测量多集中于预测出水水质而忽略进水水质BOD检测,本研究分别采用BP神经网络以及GS-SVR、PSO-SVR和GA-SVR 4种方法,通过建立其他进水参数与进水BOD5的数学关系模型,即软测量模型,实现对进水BOD5快速测定。并通过对比各机器学习模型的性能,建立适用进水BOD5预测的软测量模型。
1 研究方法 1.1 BP神经网络误差反向传播人工神经网络(BP-ANN)最早由Rumelhart等[13]提出,其显著特点是输入样本信息正向传播、输出误差反向传播,结构上具有输入层、隐含层和输出层,隐含层可以为一层或多层,上一层与下一层之间的神经元全互连,不存在其他的连接方式。网络学习和训练过程主要由正向计算过程和反向计算过程组成。
在正向传播阶段,输入层神经元负责接收外界数据并传递信息给隐含层神经元;隐含层各神经元进行信息的加工处理,将从输入层传递来的输入值,按对应的连接权重加权求和,通过传递函数映射以产生神经元的输出,最后传给输出层的神经元;输出层向外传递处理结果。神经网络的某个输出为
| $ y_{k}=f_{\mathrm{o}}\left[\sum\limits_{j=1}^{q} \nu_{j k} \times f_{\mathrm{h}}\left(\sum\limits_{i=1}^{n} \omega_{i j} x_{i}+b_{j}\right)+b_{k}\right] $ | (1) |
式中:n和q分别为输入层和隐含层神经元个数;ωij为第i个输入层神经元与第j个隐含层神经元的连接权值;xi为来自第i个输入层神经元的输入值,即训练样本第i维属性的观测值;bj为第j个隐含层神经元的阈值;fh为隐含层神经元的传递函数,通常视需求采用tansig函数或logsig函数等;νjk为第j个隐含层神经元与第k个输出层神经元的连接权值;bk为第k个输出层神经元的阈值;fo为输出层神经元传递函数,采用线性传递函数purelin(即Y=X)。
当实际输出与期望输出不相符,进入输出误差的反向传播阶段。误差由输出层开始,按照梯度下降的方式,通过隐含层向输入层逐层反传,误差因此分摊给各层所有神经元。各单元以获得的误差信号修正节点的连接权值和自身阈值,完成一次迭代,经过反复信息正向、误差反向传递过程,直到误差达到预设的程度才停止训练。
BP网络的关键步骤是确定隐含层数、隐含层神经元数,其直接影响网络对复杂问题的映射能力。研究证明单隐层的BP网络可以实现对任意连续函数的逼近[14],故选择使用率最高的经典三层BP网络。隐含层神经元数常用经验公式确定大致区间,并结合基准比较,选择最合适的值:
| $ q=\sqrt{n+m}+\alpha $ | (2) |
式中:n和m分别为输入层和输出层的神经元个数,α为[1, 10]的常数。
标准的BP网络依赖用误差函数的梯度下降调整权值,BP算法也存在一些固有缺陷,例如,迭代次数过多时会降低学习效率,导致收敛速度很慢;权值沿局部改善方向调整使网络对初始权重敏感,结果容易陷入局部极小。因此,为提高网络训练速度和精度,避免落入局部极小,在实际应用中,需要采用BP算法的改进算法,包括启发式学习算法如附加动量法、自适应学习率算法和基于数值最优化理论的训练算法如L-M(Levenberg-Marquardt)算法、共轭梯度算法、拟牛顿法以及动量- 自适应学习速率调整算法等优化算法的组合[15]。
1.2 SVR模型SVR是Drucker等在支持向量机分类的基础上,引入核函数和损失函数,通过将数据映射到高维空间,找到最优拟合超平面,使所有的训练样本与该面的总偏差最小,以解决非线性回归问题。
给定训练样本集D={(xi, yi)|i=1, 2, …n},SVR的目标是找到一个回归函数f(x),使其与实际输出y尽可能接近:
| $ f(\boldsymbol{x})=\boldsymbol{\omega}^{\mathrm{T}} \varphi(\boldsymbol{x})+b $ | (3) |
式中:ω和b分别为函数模型的法向量和截距;φ(·)为非线性映射函数,作用是将样本从原始输入空间映射到更高维的特征空间。
同时,考虑到由于微小噪声的影响,训练样本中可能存在特异点,需要定义一个损失函数,可以忽略真实值某个上下范围内的误差,通常采用如下的ε不敏感损失函数:
| $ L_{\varepsilon}(f(\boldsymbol{x}), y)=\left\{\begin{array}{l} |f(\boldsymbol{x})-y|-\varepsilon, |f(\boldsymbol{x})-y| \geqslant \varepsilon \\ 0, \text { 其他 } \end{array}\right. $ | (4) |
式中ε为指定的参数,是函数的拟合精度。当预测值f(x)和真实值y之间的差值绝对值大于ε时,才计算损失,否则损失为0。
因此,SVR模型寻找最优回归函数转化为两个优化目标,使间隔尽可能大同时使偏差尽量小,通常引入松弛变量ξi≥0、ξi*≥0描述损失函数,优化的目标函数可形式化为
| $ \begin{array}{c} \min _{\omega, b} \frac{1}{2}\|\boldsymbol{\omega}\|^{2}+C \sum\limits_{i=1}^{n} L_{\varepsilon}\left(f\left(\boldsymbol{x}_{i}\right), y_{i}\right) \\ \text { s. t. } f\left(\boldsymbol{x}_{i}\right)-y_{i} \leqslant \varepsilon+\xi_{i} \\ y_{i}-f\left(\boldsymbol{x}_{i}\right) \leqslant \varepsilon+\xi_{i}^{*} \\ \xi_{i} \geqslant 0, \xi_{i}^{*} \leqslant 0, i=1, 2, \cdots, n \end{array} $ | (5) |
式中常数C>0为惩罚因子,用于控制对超出误差ε的样本的惩罚程度,以综合两个目标的权重。
运用拉格朗日乘子法对式(3)进行求解,目标函数转化为对偶形式:
| $ \begin{array}{c} \max\limits_{\alpha, \alpha^{*}, \mu, \mu^{*}} \sum\limits_{i=1}^{n} y_{i}\left(\alpha_{i}^{*}-\alpha_{i}\right)-\sum\limits_{i=1}^{n} \varepsilon\left(\alpha_{i}^{*}-\alpha_{i}\right)-\\ \frac{1}{2} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n}\left(\alpha_{i}^{*}-\alpha_{i}\right)\left(\alpha_{j}^{*}-\alpha_{j}\right) \varphi\left(\boldsymbol{x}_{i}\right) \cdot \varphi\left(\boldsymbol{x}_{j}\right) \\ \text { s.t. } \sum\limits_{i=1}^{n}\left(\alpha_{i}^{*}-\alpha_{i}\right)=0 \\ 0 \leqslant \alpha_{i}, \alpha_{i}^{*} \leqslant C \end{array} $ | (6) |
式中:αi≥0,αi*≥0,μi≥0,μi*≥0为拉格朗日乘子。
因此,可以用核函数K(xi, xj)=φ(xi)·φ(xj)代替特征空间内积φ(xi)·φ(xj)实现非线性回归,于是得到的回归函数即SVR的解为
| $ f(\boldsymbol{x})=\sum\limits_{i=1}^{n}\left(\alpha_{i}^{*}-\alpha_{i}\right) K\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)+b $ | (7) |
式中K(xi, xj)应满足Mercer条件,选择的核函数不同,构造的SVR不同,但寻找支持向量的方法是不变的。常用的核函数有线性核、多项式核、高斯径向基(RBF)核和sigmoid核函数。
研究表明,一般RBF核函数泛化能力最好、稳定性高,适用于不同样本和各种维度问题的处理,本研究核函数类型设置为RBF,其表达式如下:
| $ K\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\exp \left(-\gamma\left\|\boldsymbol{x}_{i}-\boldsymbol{x}_{j}\right\|^{2}\right) $ | (8) |
式中γ为核函数参数。
1.3 改进的SVR模型根据SVR原理,SVR模型需要确定两类参数,第一类是SVR算法的固有参数,包括不敏感损失函数ε和惩罚因子C;另一类是SVR算法引入的核函数参数γ。参数对假设的高维空间规模以及搜索计算方式都有很大的影响,因此,寻找最优的参数组合对于SVR是必须考虑的关键问题。目前,对于SVR参数的优化选取,常用的方法有网格搜索算法(GS)、粒子群优化算法(PSO)和遗传算法(GA),基于这些优化算法提出了改进的支持向量回归模型。
1.3.1 GS-SVR网格搜索法是一种对待求参数值进行穷举搜索的方法,其原理是将待定的参数在一定的搜索范围内,沿着搜索方向根据一定的调节步长生成相交的网格,形成对应可能的最优参数组合的网格点,然后寻遍所有网格点确定误差最小的最优参数组合。当需要调整的参数过多时,GS算法会十分消耗计算内存和时间,因此,GS算法通常用于调整SVR模型的惩罚因子和核参数,具体操作步骤如下:
1) 确定初始参数C和γ的搜索范围和步长,并根据其建立参数网格搜索空间。
2) 计算搜索空间内每个网格点参数的适应度,不断更新适应度极值,直到获得最佳适应度对应的C和γ,实现网格搜索优化。
3) 将获取的最优C和γ代入SVR模型,建立训练集数据的数学回归模型并将测试集用于该回归模型完成预测。
1.3.2 PSO-SVRPSO是一种基于种群的算法。粒子的个体集合在一个区域内步进移动,在每一步中,算法评估每个粒子的目标函数,评估之后,算法决定每个粒子的新速度。粒子移动,然后算法重新评估。该算法的灵感来自成群的鸟或昆虫。每个粒子都在某种程度上被吸引到迄今为止它所发现的最佳位置,也吸引到群体中任何成员所发现的最佳位置。PSO是一种启发式算法,能减小计算复杂度、提高SVR的运行收敛速度,实现在更大的范围内更快速寻找最佳参数组合。PSO算法对SVR模型参数调整的具体操作步骤如下:
1) 确定参数C、ε和γ的寻优范围。
2) 设置PSO的基本参数,包括种群规模、学习因子、最大迭代次数等。初始化所有粒子的速度和位置。
3) 计算每一代进化中各个粒子的适应度函数值。若该粒子当前的适应度函数值优于历史最优值,则替换最优适应值和相应位置。
4) 直到达到最大迭代次数或最优解不再变化,则终止迭代,输出最优参数C、ε和γ。
5) 将获取的最优参数组合代入SVR模型,建立训练集数据的数学回归模型并将测试集用于该回归模型完成预测。
1.3.3 GA-SVRGA是一种解决约束和无约束优化问题的方法,其基于自然选择,自然选择是驱动生物进化的过程。遗传算法反复修改个体解的群体。在每一步中,遗传算法从当前群体中随机选择个体作为父母,并使用它们为下一代产生孩子。经过连续几代,种群“进化”到一个最优解。GA算法对SVR模型参数的优化选择步骤如下:
1) 确定参数C、ε和γ的寻优范围。
2) 初始化GA的基本参数,包括种群规模、交叉概率、变异概率等。一组(C, ε, γ)表示种群中的一个个体。
3) 计算个体适应度值并判断是否满足终止迭代条件,若满足则转到步骤4),若不满足将进行选择、交叉、变异,产生新种群,返回步骤2)。
4) 迭代结束得到的最优(C, ε, γ)组合代入SVR模型,建立训练集数据的数学回归模型并将测试集用于该回归模型完成预测。
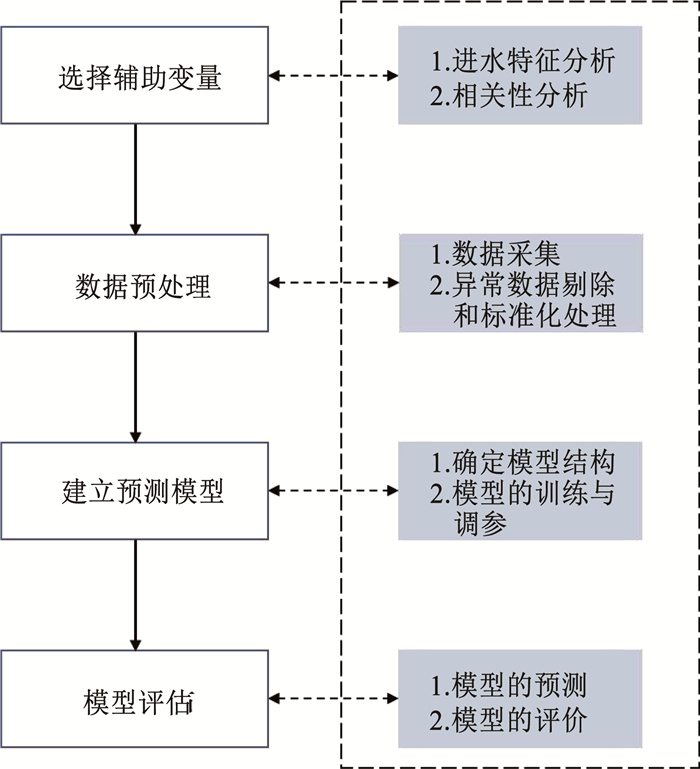
1.4 基于BP-ANN和改进SVR的进水BOD软测量模型进水BOD5的软测量建模过程如图 1所示。首先,需要通过对进水BOD5进行机理分析,选取与进水BOD5关联性强的变量作为辅助变量,其次,对选取和收集到的变量数据进行异常数据剔除和数据标准化处理,然后选择合适的软测量模型建模方法建立进水BOD5预测模型。本研究采用BP-ANN和GS-SVR、PSO-SVR、GA-SVR 3种改进SVR模型作为进水BOD5软测量建模方法,最后,将获得的软测量模型对进水BOD5训练、预测,并根据模型评价指标对模型进行合理的评估。具体步骤如下。
|
图 1 进水BOD5软测量建模流程 Fig. 1 Flow chart of modeling of influent BOD5 soft sensing |
1) 选择辅助变量。分析进水BOD5的来源、组成、特性及其测定过程的影响因素,初步选择进水COD、SS、NH4+-N、TN、TP这5个水质关键指标作为初始辅助变量,然后通过变量间的相关性分析,确认初始辅助变量与主导变量是否关联性密切,决定最终的辅助变量。
2) 数据预处理。使用“3σ方法”对采集到的数据进行异常值剔除,并在输入模型前进行数据标准化处理,以消除数据级、量纲的差别影响,数据标准化的公式如下:
| $ x_{i j}^{\text {new }}=\frac{x_{i j}-x_{j}^{\min }}{x_{j}^{\max }-x_{j}^{\min }} $ | (9) |
式中:xjmin和xjmax分别为样本在第j个观测变量中的最小值和最大值,xij和xijnew分别为原始样本值和处理后的样本值。
3) 建立预测模型。分别应用BP-ANN和改进SVR进行模型构建,样本训练集和测试集按照8∶ 2的比例进行随机划分。根据不同建模方法的情况,进行模型参数的调节和优化,得到最优模型。
4) 模型评估。采用平均绝对误差(EMS)和相关系数R对模型进行评估,计算方法如下:
| $ E_{\mathrm{MS}}=\frac{1}{n} \sum\limits_{i=1}^{n}\left(y_{i}-y_{i}^{*}\right)^{2} $ | (10) |
| $ R=\frac{\sum\limits_{i}^{n}\left(y_{i}-\bar{y}\right)\left(y_{i}^{*}-\bar{y}^{*}\right)}{\sqrt{\sum\limits_{i}^{n}\left(y_{i}-\bar{y}\right)^{2} \sum\limits_{i}^{n}\left(y_{i}^{*}-\bar{y}^{*}\right)^{2}}} $ | (11) |
式中:yi为实测值,yi*为模型预测值,n为样本总数,y和y*分别为样本实测值均值和样本预测值均值。
1.5 模型搭建平台使用MatlabR2016a为实验平台,实现BP-ANN和SVR模型,此外,为实现优化算法在建立基于SVR的进水BOD5软测量模型时,运用了李洋编写的SVM工具包[16]。
2 结果与分析 2.1 数据的收集与处理本研究数据采集自黑龙江省某污水处理厂2017年1月1日—12月31日的运行参数监测报表,包括每日水质指标COD、BOD5、SS、NH4+-N、TN、TP进水监测值,水质监测位置为污水厂进水口。排查并剔除了6组缺失值、26组异常值,预处理后的数据集包含333组数据,如图 2所示。样本数据集按8∶ 2的比例随机划分为训练集(NTrain=266)和测试集(NTest=67)并进行0-1标准化的预处理。

|
图 2 预处理后的数据集 Fig. 2 Preprocessed data set |
通过该污水厂6个水质指标的进水数据相关性分析发现(表 1),进水BOD5与5个初始辅助变量的相关性均大于0.2,呈现显著相关,故选择这5个关键水质指标作为最终的辅助变量[17]。即进水COD、SS、NH4+-N、TN、TP作为模型的输入,进水BOD5作为输出。
| 表 1 进水水质指标的相关系数 Tab. 1 Correlation coefficient of influent water quality parameters |
在确定辅助变量和主导变量后,网络的输入层与输出层的神经元个数分别确定为5和1,选择构建单隐层的BP网络。由经验公式(2),并通过基准比较,确定BP软测量模型的网络拓扑结构为[5 10 1]。选择tansig函数作为隐层神经元的传递函数,使用基于数值最优化L-M(Levenberg-Marquardt)算法的“trainlm”训练函数,学习函数为带动量项的BP梯度下降学习规则“learngdm”,其他参数为默认值。由于网络权值随机初始化,需将建立的BP-ANN软测量模型进行多次运行,以拟合度最高及均方差最小为原则,得到最优的网络模型。
训练集拟合结果和测试集的预测效果如图 3所示,可以看出,整个数据集的EMS为656.22,训练集和测试集的实测值与预测值的相关系数分别为0.81和0.80,说明该最优模型的泛化性能较好。

|
图 3 基于BP网络的BOD5实测值与预测值的线性回归 Fig. 3 Linear regression of measured and predicted BOD5 values based on BP network |
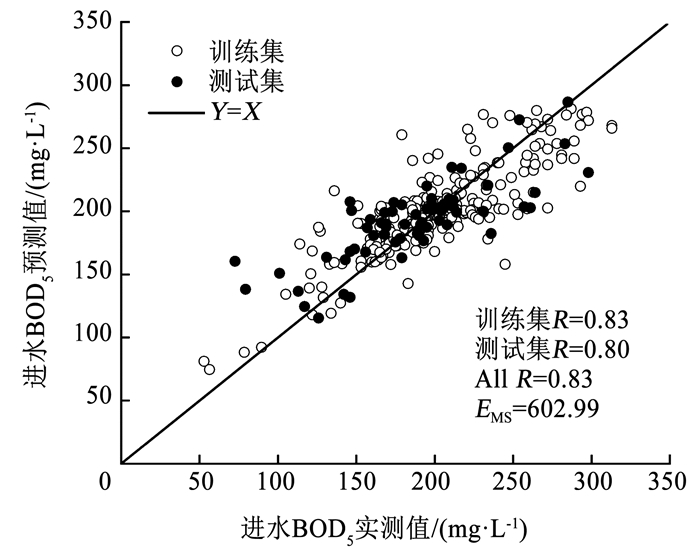
采用网格搜索法选取最优参数组合,设定惩罚参数C和RBF核参数γ的取值均为[2-5,25],步长为1(以2为底的幂指数下变化),采用5折交叉验证方法进行训练,获得每个参数组合下模型性能,结果见图 3~5。得到最优参数C和γ分别为0.5(2-1)和8(23),最小标准化训练数据的EMS为0.012 6。根据计算得到的最优参数C和γ,对测试数据进行回归预测。训练集和测试集的拟合结果如图 4所示,可以看出,训练集和预测集的R分别为0.83和0.80,数据集的EMS为602.99,表明基于GS-SVR的软测量模型也具有较好的泛化能力,同时,训练集的拟合结果优于BP-ANN软测量模型,而且不需要进行多次运行。
|
图 4 基于GS-SVR的BOD5实测值与预测值的线性回归 Fig. 4 Linear regression of measured and predicted BOD5 values based on GS-SVR |
|
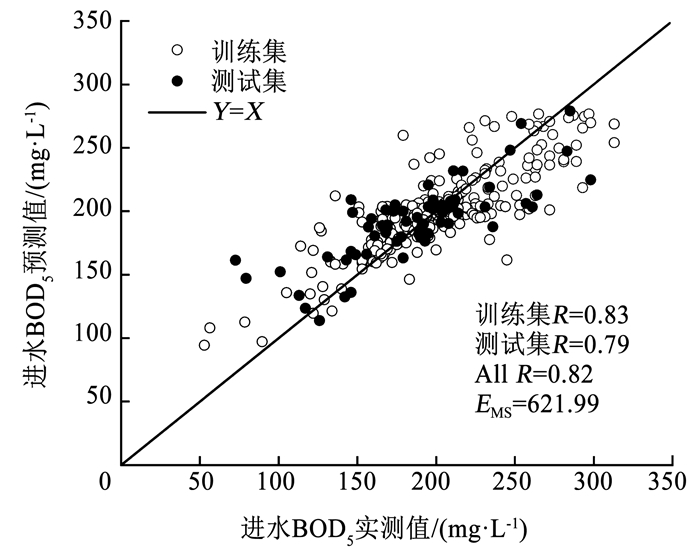
图 5 基于PSO-SVR的BOD5实测值与预测值的线性回归 Fig. 5 Linear regression of measured and predicted BOD5 values based on PSO-SVR |
使用PSO算法进行参数寻优,具体参数设定:种群个数为20,最大进化代数即最大迭代次数设置为200,取C的搜索范围为[0, 100],γ的搜索范围为[0,1 000],ε的搜索范围为[0.01,1]。自我学习因子c1和群体学习因子c2设置为1.5和1.7,分别代表PSO的局部搜索能力和全局搜索能力,初始惯性权重w=1。得到最优参数C和γ分别为0.433 2和3.098 9,参数ε为0.01,最小标准化训练数据的EMS为0.052 548。根据计算得到的最优参数组合对测试集进行回归预测,结果如图 5所示。训练集和预测集的R分别为0.83和0.79,整个训练集的EMS为621.99,介于BP-ANN模型与GS-SVR模型之间,表明PSO的参数寻优方法没有GS的参数寻优效果好,可能是由于GS的参数取值范围和步长的设置比较合理。
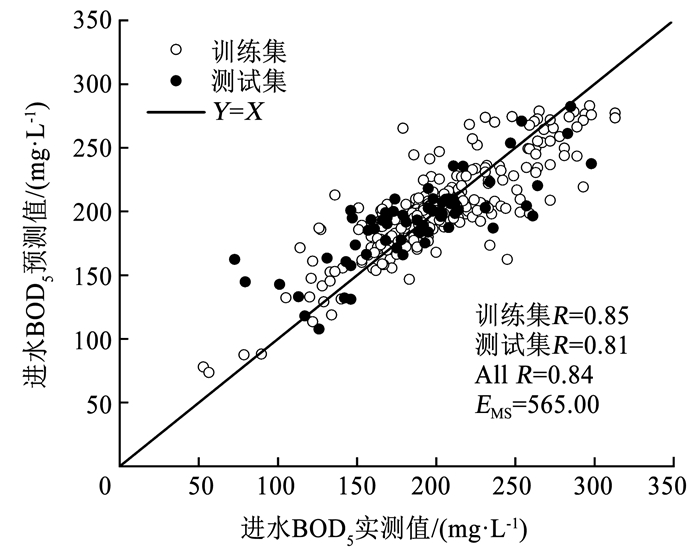
2.4.3 基于GA的参数寻优通过GA算法进行参数寻优,具体参数设定:种群个数为20,最大进化代数即迭代次数设置为200,取C的搜索范围为[0, 100],γ的搜索范围为[0,1 000],ε的搜索范围为[0.01,1]。采用间接二进制编码,每条染色体长度为54个基因,设置交叉概率为0.9,变异概率为0.01。最终得到最优参数C和γ分别为0.532 7和9.976 4,参数ε为0.033 5,最小标准化训练数据的EMS为0.012 4。根据计算得到的最优参数组合对测试集进行回归预测,实测值与预测值的比较结果见图 6。训练集和预测集的R分别为0.85和0.81,整个训练集的EMS为565.00,较GS-SVR和PSO-SVR模型分别降低了6.3%和9.2%,表明GA算法增强了SVR的参数全局最优搜索能力,能够改善其预测性能。
|
图 6 基于GA-SVR的BOD5实测值与预测值的线性回归 Fig. 6 Linear regression of measured and predicted BOD5 values based on GA-SVR |
本研究分别采用BP神经网络和改进的SVR方法建立了BOD5的软测量模型,可以看出,两类模型有各自的特点。BP-ANN受随机初始化权值阈值的影响大,需要调整确定的超级参数较多,学习记忆不稳定; SVR模型在较好的拟合效果的同时具有好的泛化性能,稳定性高。不同模型的性能比较如表 2所示,可以看出,无论是训练集还是预测集,基于GA-SVR的软测量模型的拟合度最高,误差最小,其次是GS-SVR和PSO-SVR、BP-ANN软测量模型,说明GA-SVR的预测效果更为理想,能够提升SVR建模方法的预测性能,更适用于污水厂的进水BOD5预测。
| 表 2 不同软测量模型的性能比较 Tab. 2 Performance comparison of different soft sensing models |
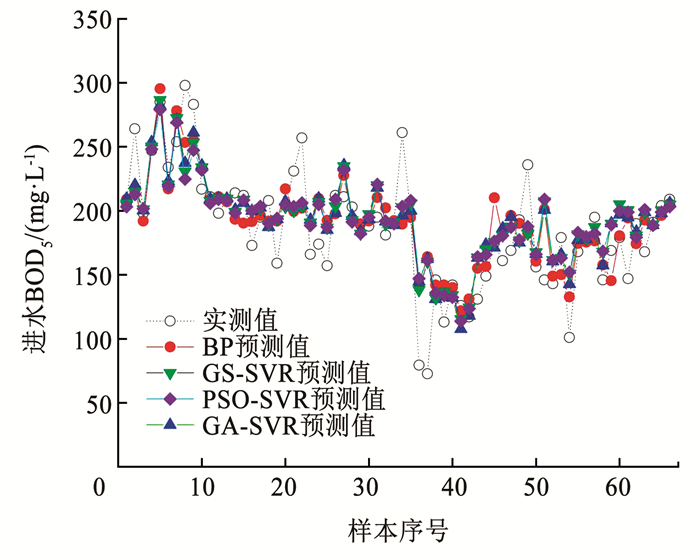
图 7为不同软测量模型预测结果,可以看出,GS-SVR、PSO-SVR和GA-SVR模型的拟合曲线很接近,都是基于同一非线性映射函数,均有不错的全局搜索能力,这可能是由于建立SVR模型时,本研究的数据集具有合适的参数区间,GS-SVR的拟合效果略优于PSO-SVR,但遗传算法相对网格搜索有更强的跳出局部最优解的能力。
|
图 7 不同软测量模型预测结果比较 Fig. 7 Comparison of prediction results of different soft sensing models |
模型的预测误差如表 3所示,对于实际BOD5质量浓度在250 mg/L以上和100 mg/L以下时,4种模型的预测偏差均较大,这可能是实际测量等原因导致数据集本身存在异常,或者在建模时还需要考虑天气、水温等其他因素,才能更进一步地提高软测量模型的精确度。
| 表 3 不同进水BOD5范围下模型的预测误差 Tab. 3 Prediction error of models in different influent BOD5 ranges |
针对现阶段水质参数BOD5难以实现在线测量的特点,以污水厂日常监测指标数据为基础,基于BP-ANN、GS-SVR、PSO-SVR和GA-SVR方法构建了相应的进水BOD5软测量模型。在污水厂进水BOD5质量浓度预测中,3种SVR模型均优于BP网络模型,误差排序为BP-ANN>PSO-SVR>GS-SVR> GA-SVR,采用GA优化的SVR模型预测效果最好,整体数据集的R和EMS分别为0.84和565.00,具有较好的精度和泛化能力,为实现污水厂进水BOD5的实时监测提供了可能性,对污水厂的管理具有一定的应用价值。
| [1] |
樊杰, 曹亮, 高乘, 等. 基于统计学分析的污水厂运行性能诊断[J]. 工业水处理, 2020, 40(7): 98. FAN Jie, CAO Liang, GAO Cheng, et al. Statistical diagnosis of performance of wastewater treatment plant[J]. Industrial Water Treatment, 2020, 40(7): 98. DOI:10.11894/iwt.2019-0595 |
| [2] |
ZHANG Xinyu, FU Ying. Analysis on biological stability and influencing factors of northern living district water distribution system[J]. Journal of Harbin Institute of Technology(New Series), 2018, 25(1): 85. DOI:10.11916/j.issn.1005-9113.17048 |
| [3] |
JOUANNEAU S, RECOULES L, DURAND M J, et al. Methods for assessing biochemical oxygen demand (BOD): a review[J]. Water Research, 2014, 49: 62. DOI:10.1016/j.watres.2013.10.066 |
| [4] |
HAIMI H, MULAS M, CORONA F, et al. Data-derived soft-sensors for biological wastewater treatment plants: an overview[J]. Environmental Modelling & Software, 2013, 47: 88. DOI:10.1016/j.envsoft.2013.05.009 |
| [5] |
NOORI R, YEH H D, ABBASI M, et al. Uncertainty analysis of support vector machine for online prediction of five-day biochemical oxygen demand[J]. Journal of Hydrology, 2015, 527: 833. DOI:10.1016/j.jhydrol.2015.05.046 |
| [6] |
MA Jun, DING Yuexiong, CHENG J C P, et al. Soft detection of 5-day BOD with sparse matrix in city harbor water using deep learning techniques[J]. Water Research, 2020, 170: 115350. DOI:10.1016/j.watres.2019.115350 |
| [7] |
ZHU Junjie, KANG Lulu, ANDERSON P R. Predicting influent biochemical oxygen demand: balancing energy demand and risk management[J]. Water Research, 2018, 128: 304. DOI:10.1016/j.watres.2017.10.053 |
| [8] |
连晓峰, 李晓婷, 潘峰. 机理模型与补偿模型相结合的污水处理工艺出水指标软测量预测模型研究[J]. 计算机与应用化学, 2013, 30(10): 1143. LIAN Xiaofeng, LI Xiaoting, PAN Feng. Research on the soft measuring prediction model based on mechanism with compensation model combined for the effluent water indicators of sewage treatment process[J]. Computers and Applied Chemistry, 2013, 30(10): 1143. DOI:10.3969/j.issn.1001-4160.2013.10.013 |
| [9] |
杨吉祥. 污水处理软测量技术研究进展[J]. 净水技术, 2020, 39(4): 12. YANG Jixiang. Advances of soft-sensor technology for wastewater treatment[J]. Water Purification Technology, 2020, 39(4): 12. DOI:10.15890/j.cnki.jsjs.2020.04.003 |
| [10] |
刘帮, 秦斌, 王欣, 等. PSO-LIBSVM在污水水质建模中的应用[J]. 湖南工业大学学报, 2015, 29(2): 89. LIU Bang, QIN Bin, WANG Xin, et al. Application of PSO-LIBSVM in modeling of sewage water quality[J]. Journal of Hunan University of Technology, 2015, 29(2): 89. DOI:10.3969/j.issn.1673-9833.2015.02.017 |
| [11] |
BAGHERI M, MIRBAGHERI S A, BAGHERI Z, et al. Modeling and optimization of activated sludge bulking for a real wastewater treatment plant using hybrid artificial neural networks-genetic algorithm approach[J]. Process Safety and Environmental Protection, 2015, 95: 12. DOI:10.1016/j.psep.2015.02.008 |
| [12] |
HUANG Wenchang, LIU Hongyi, ZHANG Yue, et al. Railway dangerous goods transportation system risk identification: comparisons among SVM, PSO-SVM, GA-SVM and GS-SVM[J]. Applied Soft Computing, 2021, 109: 107541. DOI:10.1016/j.asoc.2021.107541 |
| [13] |
RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323(6088): 533. DOI:10.1038/323533a0 |
| [14] |
STATHAKIS D. How many hidden layers and nodes[J]. International Journal of Remote Sensing, 2009, 30(8): 2133. DOI:10.1080/01431160802549278 |
| [15] |
刘天舒. BP神经网络的改进研究及应用[D]. 哈尔滨: 东北农业大学, 2011 LIU Tianshu. The research and application on BP neural network improvement[D]. Harbin: Northeast Agricultural University, 2011 |
| [16] |
LI Yang. A toolbox with implements for support vector machines based on Libsvm[EB/OL][2021-10-03]. https://github.com/faruto/Libsvm-FarutoUltimate-Version
|
| [17] |
NOURANI V, ASGHARI P, SHARGHI E. Artificial intelligence based ensemble modeling of wastewater treatment plant using jittered data[J]. Journal of Cleaner Production, 2021, 291: 125772. DOI:10.1016/j.jclepro.2020.125772 |
 2022, Vol. 54
2022, Vol. 54


