2. 黑龙江省极地环境与生态研究重点实验室(哈尔滨工业大学),哈尔滨150090
2. Heilongjiang Provincial Key Laboratory of Polar Environment and Ecosystem(Harbin Institute of Technology), Harbin 150090, China
2020年伊始,一场突如其来的新型冠状病毒肺炎疫情席卷全球,截至2021年1月27日,全球已有超过一亿人感染新型冠状病毒[1]。2020年末,新型冠状病毒疫苗陆续问世[2],让人们看到了抗疫的曙光,但当下全球范围内新冠肺炎疫情依然十分严峻, 秋冬季节更是新型冠状病毒传播高发期[3]。同时,无症状感染者以及冷链传播途径的发现,使得人们开始重新评估疫情彻底结束的时间。另一方面,世界各地陆续通报存在新型冠状病毒变异的情形[1],这使得人们开始担忧疫苗的有效性受到影响。
寄宿制学校作为人员流动密集与接触频繁的场所,一旦出现感染病例,较其他场所更容易出现疫情的大面积扩散。2020年在大连[4]以及2021年初在石家庄[5]出现的新型冠状病毒零星传播事件都波及到了寄宿制学校,对师生的正常学习生活产生了严重影响。研究寄宿制学校疫情传播速度与防控措施之间的关系,是校园疫情高效防控策略制定的需要,同时关系到校园正常学习、工作、生活秩序的保障及广大师生员工的身心健康。利用传染病模型对新型冠状病毒的传播进行预测,是研究新冠肺炎疫情传播与制定防控决策的重要手段。国内外已有多篇针对新型冠状病毒建立传播模型并进行仿真分析的报告[6],这些报告提及的新型冠状病毒模型可以预测病毒的传播行为,但没有考虑不同防控措施对传染模型的影响。本研究以某寄宿制学校宿舍为原型,通过建立校园内传染病模型,考察不同防疫措施下疫情的传播速度,对疫情彻底结束前返校复课的风险进行评估,寻找疫情控制的关键因素,为高校制定复学计划和精准高效的防疫措施提供信息支持。
1 校园疫情防控措施设定根据师生校园工作、生活、行居规律,预设了学生返校后具有可行性的校园疫情防控行居策略:
1) 一级防控。寝室之外的所有室内空间全员全程(包括上课)戴口罩、自行尽量保持时空安全间距、楼内进出路径尽量单向设置、严禁随地吐痰、室内空气消毒、卫生间洗漱前后要戴口罩。
2) 二级防控。在一级防控基础上,采取网上订餐、食堂统一打饭回寝就餐、饭盒统一送回方式[7](学生在寝室楼洗碗及产生的厨余垃圾会增加传染风险)。
3) 三级防控。在二级防控基础上,教学楼电梯、全封闭楼梯对学生关闭,教学楼外间隔排队进楼,同层教室错峰上下课,公寓电梯同寝方可同乘,电梯保持长效消毒,教室、寝室门口布设消毒脚垫。
4) 四级防控。在完成三级防控条件基础上,返校一周后,只有具备保持2 m间隔距离条件的班级上课。
5) 五级防控。在完成三级防控条件基础上,返校两周后,只有具备保持2 m间隔距离条件的班级上课。
如果出现确诊病例,则在三级防控基础上,异地隔离观察同寝室内人员,同班同学寝室所在楼层封闭,整层楼统一送餐。
防控时间范围:学生年龄段(17~30岁)病例的最长潜伏期平均为13 d。
2 校园疫情传播建模 2.1 建模原理采用基于统计与概率判断的健康者- 感染者(SI)传染模型, 模型建立原理如下[8]。
人群中存在两种人,即未感染病毒的“健康者”与感染病毒的“感染者”。在日常生活与工作中,人与人之间难免相互接触,在感染者与健康者接触的过程中,便有一定概率将携带的病毒传染给健康者,使其转化为感染者。除此途径外,健康者不会自行转化为感染者,且在较短时间内,感染者也不会自行转化为健康者。
以S代表健康者的人数,I代表感染者的人数,单位时间后,每一名感染者均与若干名健康者接触,记第i名感染者单位时间接触到的健康者人数为Ti。对于这些健康者,每个人都有一定概率被感染,记被感染的概率为β,则该感染者因接触导致传染者人数增加了βTi。对于所有感染者,在不考虑重复接触的条件下,因接触传播导致健康者转化为感染者的人数即为
因此,单位时间内健康者的人数变化
| $ \left\{\begin{array}{l} \frac{\mathrm{d} S}{\mathrm{~d} t}=-\sum\limits_{i=1}^{I} \beta T_{i} \\ \frac{\mathrm{d} I}{\mathrm{~d} t}=\sum\limits_{i=1}^{I} \beta T_{i} \end{array}\right. $ | (1) |
式中:Ti为第i名感染者在单位时间接触到的健康者人数,β为感染者与健康者接触时发生有效感染的概率。
2.2 建模过程针对不同等级的防控措施,设置相应情境下的接触人数与传染概率,利用传染病模型(SI)模拟不同防控措施与疫苗接种与否等条件下的感染情况,对防控等级与新冠疫苗阻断疫情传播的效果进行评估。如图 1所示。

|
图 1 传染病模拟环境设定和防控措施及疫苗接种评估框架示意 Fig. 1 Framework of infection simulation scenario setting and evaluation of protection and vaccination |
以某高校两栋结构不同的公寓楼作为模拟场景,假定公寓楼中出现了一名病毒携带者,依据目前已知症状可识别时间的上限[9],讨论在两周内不同防控等级下的病毒传播发展态势。
1) 公寓楼A。共7层,每层70间宿舍,每间宿舍4人,共160人。每层楼设两间公共卫生间。
2) 公寓楼B。共6层,每层50间宿舍,每间宿舍6人,共1 800人。每间宿舍带独立卫生间。
学生每天的作息分为洗漱、外出、上课、就餐、回寝5个阶段。每个阶段学生之间都会发生若干次接触,当病毒携带者与健康者接触时,有一定概率将病毒传染给健康者,使其成为病毒携带者。
2.3 模型运行步骤与参数设定传染过程按阶段进行。例如,某宿舍存在一名感染者,将病毒传播给同宿舍的其他几人;在下一次情境模拟中,这几个人将作为新的传播种子,分别与其他人进行接触传播。
模型运行的步骤如下:
1) 数据初始化。生成一个包含学生编号、学生所在宿舍楼层及编号、学生身体状况(0—健康,1—感染)和感染时间的数据表,每名学生的编号唯一,与宿舍楼层、宿舍编号、床位号绑定。初始时,所有学生均为健康状态。
2) 随机选取一名学生作为0号感染者,将其健康状态改为1。
3) 按照洗漱、外出、上课、就餐、回寝的顺序依次进行传染过程模拟。
由于传染过程中只有感染者接触到健康者并使其感染才算有效感染,在模拟过程中,先从数据表中读取所有感染者的学生编号,用随机方式生成该学生在某一情境下可能接触到的健康学生编号列表,再对每一名健康学生,通过生成一个随机数,与设定的传染概率进行比对,判断该次接触是否为有效感染。
传染过程模拟结束后,统计所有被感染学生编号,更新数据表。
4) 当5种传染情境全部模拟完成后,视为一天结束,更新学生的被感染时间和感染者名单,准备开始新一天的传染情境模拟,共模拟14 d。
根据宿舍楼结构和防疫措施等级要求,参考国内疫情初期建立的传染模型[9-10]以及国外学者针对英国[11]和印度[12]传染情况建立的SI传染模型中参数的选取,设置公寓楼A每个传染情境下的接触人数、范围和接触传染概率,如表 1所示。
| 表 1 不同防控等级和传染情境下公寓楼A设置的接触人数和传染概率 Tab. 1 Contact number and infection probability in apartment A under different prevention levels and infection scenarios |
接触传染的概率设置考察了学生在每个情境下的接触时间、接触距离以及是否佩戴口罩等因素。随着防控等级的提高,学生在不同情境下的接触时间和接触距离发生变化,因而设置的传染概率也有所变化。
1) 洗漱情境。由于公寓A每层设置两间公共卫生间,将同一层的学生分为两等分,该情境下每名学生的人员接触范围为位于同一楼层的一半学生(140人)。公共卫生间水池一排有4~5个水龙头,考虑到进出卫生间与并排洗漱人员的数量,接触人数设置为4。洗漱时学生不佩戴口罩,接触距离短,接触时间短,传染概率设置为低于回寝阶段的0.4;一级防控以上时,由于采取消毒措施,设置传染概率降低至0.2。
2) 外出情境。学生的人员接触范围为所有学生(1 960人)。结合往来宿舍与学院楼的实际情况,接触人数设置为10。外出阶段学生接触时间短,接触距离长,且佩戴口罩,因此,设置传染概率在5种情境中最低,为0.1,一级防控以后为0.001。
3) 上课情境。学生的人员接触范围为所有学生(1 960人)。大学课堂学生数量多,座位密集、紧凑,接触人数设置为20。上课情境下学生接触时间长,接触距离短,故传染概率设置为较高的0.5;一、二级防控下学生佩戴口罩,接触概率降低,传染概率设置为0.2;三级防控下错峰上课,学生密度降低,故设置接触人数降低至10,传染概率降至0.01;四级防控下,要求返校一周后,只有具备保持2 m间隔距离条件的班级上课,因此,在模拟的14 d中,前7 d在上课情境下的接触传染概率与后7 d的接触传染概率不同,降低至0,在表格中作出区分。
4) 就餐情境。学生的人员接触范围为所有学生(1 960人)。食堂涉及排队打饭、同桌就餐与送返餐具,接触人员较多,设置为20人。该情境下学生接触时间短,但接触距离短,且就餐时无法佩戴口罩,因而传染概率较大,设置为0.6;从二级防控开始,采取网上订餐、食堂统一打饭回寝就餐、饭盒统一送回措施,因此,不存在学生统一在食堂就餐的情境,之后该情境的接触传染概率设为0。
5) 回寝情境。学生的人员接触范围为同寝室其余学生(3人),寝室内人员接触密集、频繁,故接触人数与接触范围相同,为3人。寝室情境下学生的接触时间长,接触距离短,且一般不佩戴口罩,因而接触传染概率最高,设置为0.8。
与公寓楼A不同的是,公寓楼B每间宿舍带独立卫生间,因此,在情境模拟时将洗漱情境删去。
不同防控等级和传染情境下公寓楼B设置的接触人数和传染概率如表 2所示。
| 表 2 不同防控等级和传染情境下公寓楼B设置的接触人数和传染概率 Tab. 2 Contact number and infection probability in apartment B under different prevention levels and infection scenarios |
每个情境下人员接触范围、接触人数和传染概率的设置与公寓A相同。
对每一防控等级,进行10次14 d的传染模拟试验,统计经过相应天数后模拟感染人数的均值和标准差。
3 校园疫情扩散态势模拟 3.1 公寓楼A的疫情传播模拟假定公寓楼A中出现一名病毒携带者,在不同等级防控措施条件下的模拟结果如表 3所示。
| 表 3 不同防控等级下经过相应天数后公寓楼A总模拟感染人数的均值和标准差 Tab. 3 Mean and standard deviation of number of infected persons in apartment A after corresponding days under different prevention levels |
不同防控等级下公寓楼A模拟感染人数随时间变化如图 2所示。

|
图 2 不同防控等级下公寓楼A模拟感染人数随时间变化 Fig. 2 Variation of number of infected persons in apartment A with time under different prevention levels |
与公寓楼A相同,假定公寓楼B中出现一名病毒携带者,在不同等级防控措施条件下的模拟结果如表 4所示。
| 表 4 不同防控等级下经过相应天数后公寓楼B总模拟感染人数的均值和标准差 Tab. 4 Mean and standard deviation of number of infected persons in apartment B after corresponding days under different prevention levels |
不同防控等级下公寓楼B模拟感染人数随时间变化如图 3所示。

|
图 3 不同防控等级下公寓楼B模拟感染人数随时间变化 Fig. 3 Variation of number of infected persons in apartment B with time under different prevention levels |
尽快为在校生接种新型冠状病毒疫苗,实现疫苗接种背景下的群体免疫,是有效阻断新型冠状病毒在校内传播的重要手段。
假设已经为宿舍楼所有学生接种了新冠疫苗,且该疫苗的保护率为80%,即80%的学生在接种疫苗后拥有新型冠状病毒的抗体,将带有新型冠状病毒抗体的学生称为抗体携带者(健康状态记为2)。在传染情境模拟中,抗体携带者与感染者接触并传染后成为病毒携带者(健康状态记为3),病毒携带者不会发病,但在当天结束前会和感染者一样可将病毒传播给健康者或抗体携带者,使其成为感染者或病毒携带者。当天结束后,经过消毒措施,所有病毒携带者恢复为抗体携带者。
同时,由于接种疫苗后学生体内存在抗体,在各种情境下接触传染的成功概率有所降低。为讨论方便,假定接种疫苗后接触传染概率的降低分为5个等级,即分别为不设防控时的1/10、1/20、1/30、1/40、1/50,考察疫苗接种后的传染情形。
考察接种疫苗后不同传染率等级下公寓楼A和公寓楼B的模拟感染人数均值与方差,结果如表 5、6所示。
| 表 5 接种疫苗后不同传染率等级下经过相应天数后公寓楼A总模拟感染人数的均值和标准差 Tab. 5 Mean and standard deviation of number of infected persons in apartment A after corresponding days under different infection rate levels after vaccination |
| 表 6 接种疫苗后不同传染率等级下经过相应天数后公寓楼B总模拟感染人数的均值和标准差 Tab. 6 Mean and standard deviation of number of infected persons in apartment B after corresponding days under different infection rate levels after vaccination |
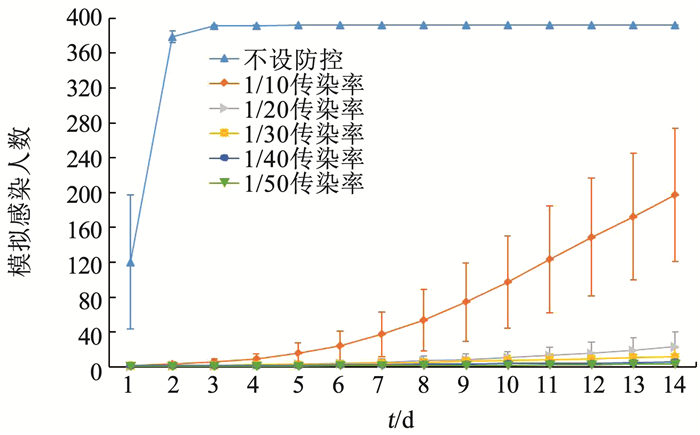
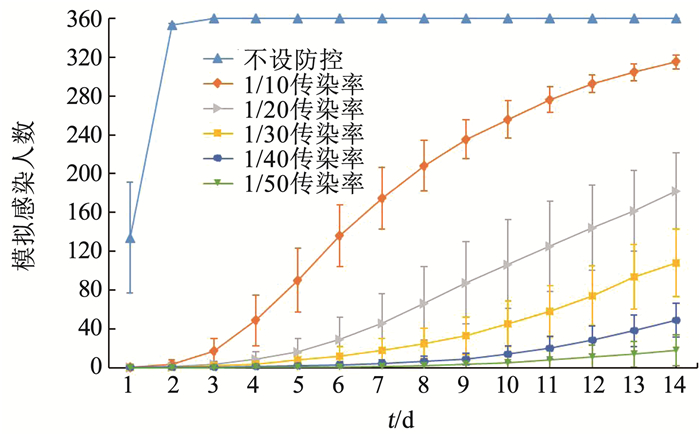
接种疫苗后不同传染率等级下公寓楼A和公寓楼B模拟感染人数随时间变化如图 4、5所示。
|
图 4 接种疫苗后不同传染率等级下公寓楼A模拟感染人数随时间变化 Fig. 4 Variation of number of infected persons in apartment A with time under different infection rate levels after vaccination |
|
图 5 接种疫苗后不同传染率等级下公寓楼B模拟感染人数随时间变化 Fig. 5 Variation of number of infected persons in apartment B with time under different infection rate levels after vaccination |
从公寓A和公寓B的疫情传播模拟结果可以看出,新型冠状病毒的传染性非常强,在不设任何防控的情境下,仅需2~3 d就使得一栋宿舍楼内接近2 000名学生全部被感染。考虑到寄宿制学校封闭环境中人员在一些场景聚集密度及交错强度都较大,需要采取严格的防疫措施防止大面积传染现象出现。
随着防控等级的不断提升,段内被感染学生数均值逐渐减小。其中,一级防控到二级防控的提升反映就餐措施的改变对疫情传播的影响,虽然减缓了传播速度,但仅仅使公寓楼A全体感染的时间推迟了2 d,公寓楼B则除了相应天数下感染人数减少,对全体感染的时间无影响。从二级防控到三级防控的提升反映上课阶段采取措施与否对疫情传播的影响,这一步发生了质变,无论是公寓楼A还是公寓楼B,感染人数的上升趋势都明显放缓,公寓楼A的同期平均模拟感染人数降低至二级防控时的1/10,全体感染的时间推迟了5 d,公寓楼B的同期平均模拟感染人数则在三级防控下降低至二级防控时的1/100,14 d平均感染人数降至531人,不到总数的1/3,直接避免了全体感染,这说明加强上课情境的防控措施对抑制病毒传播扩散发挥了很大的作用。
此外,独立卫生间的存在对阻断疫情传播的影响非常大。在三级防控前公寓楼A与公寓楼B的传染趋势基本一致,表明洗漱阶段对疫情传播的影响有限。但在三级及更强的防控等级下,没有独立卫生间的公寓楼A疫情扩散的速度明显高于拥有独立卫生间的公寓楼B。在为期两周的潜伏期内,即使采取五级防控等级,公寓楼A最终也有超过75%的学生被感染,而同样时间内,采取五级防控等级的公寓楼B,平均仅有15人被感染,疫情阻断效果非常好。
通过上述分析可以看出,在校园疫情防控过程中,就餐、洗漱和上课是非常关键的因素。教学楼与教室是学生与教师聚集并发生接触的主要场所,一旦疏忽便可能造成大范围传染。考虑到目前抗疫工作的严峻形势,全面恢复以往的授课安排风险很大,采取网络授课形式、避免直接接触是最安全的措施。
独立卫生间对学生自主隔离、阻断疫情传播起到很大作用,然而并不是所有的公寓楼都设有独立卫生间,对公寓楼A的传染模拟情况说明,公共卫生间洗漱极大地加快了病毒的传播速度。因此,对于没有独立卫生间的公寓楼,需要对公共卫生间采取一定的改造和管理措施,如增加隔板、采用负压设计、限制学生使用卫生间的时间段等,降低洗漱情境下的接触感染概率,便可大大减缓疫情的传播速度。
为验证这一想法,在公寓楼A采取五级防控的基础上,将洗漱情境下的接触感染概率降低至0.01,记为六级防控,重新计算了六级防控等级下公寓楼A模拟感染人数的均值和标准差,结果如表 7所示。可以看出,在六级防控下对公共卫生间采取改造和限制使用措施后,病毒传播速度明显降低,潜伏期14 d后感染概率从五级的56.9%降至1.8%,疫情阻断效果明显。
| 表 7 五级防控和六级防控下经过相应天数后公寓楼A总模拟感染人数的均值和标准差 Tab. 7 Mean and standard deviation of number of infected persons in apartment A after corresponding days under response level Ⅴ and response level Ⅵ |
考虑疫苗接种后的模拟结果表明, 疫苗可以有效保护绝大多数学生免于染病,杜绝了疫情在校内蔓延的危险。值得注意的是,由于疫苗接种使每个阶段的传染概率都得到降低,此时每间宿舍的学生数(相当于多少学生为一组进行隔离)成为影响病毒传播速度的最主要因素。对于4人一间宿舍的公寓楼A,当疫苗接种使得接触传染概率降低至不设防控时的1/30时,就已经取得了较好的疫情阻断效果。而对于6人一间宿舍的公寓楼B,在接触传染概率降低至不设防控时的1/30时,平均仍有108人感染,占未保护人群的1/3,需要降低至不设防控时的1/50才能达到与公寓楼A相同的结果。因此,对于多人一间宿舍的公寓楼,可以在条件允许的前提下采取安排学生异地住宿、减少宿舍人数的方式来减缓疫情的传播。
5 结论与建议1) 就餐、洗漱和上课是病毒在校园、宿舍传播速度的重要影响因素。其中,上课对疫情传播的影响最大,采取严格防控可使同期感染人数降低1/10~1/100,推迟大规模感染事件发生时间长达5 d;就餐次之,禁止堂食可以推迟大规模感染事件发生时间2 d,洗漱则在控制了上课与就餐两大因素后才体现出其影响,无独立卫生间的公寓楼14 d感染人数是有独立卫生间公寓楼的80倍。
2) 对于没有独立卫生间的公寓楼,应该对公共卫生间采取一定的改造和管理措施,以减缓疫情传播速度,可以使14 d感染率降低至最初的1/40。在公寓结构已定的事实下,可以通过调整房间学生数或其他多种因素来控制疫情传播,例如,将疑似感染的学生安排到指定宿舍隔离,安排部分学生到外面住宿以降低单个宿舍学生人数,定期在公寓内进行病毒消杀等。
3) 新型冠状病毒具有极强传播能力和较长的潜伏期,一旦校园内有人被感染,便会迅速传播扩散,形势极为严峻,防控压力巨大。因此,在中国疫情基本得到控制的条件下,采取严格的封闭式管理, 对来自疫情高风险地区的人员及物品进行严格管控,切断新型冠状病毒外部输入风险是保障寄宿制学校防疫安全的必要条件。现实证明,正是由于中国采取了严格的防疫措施,避免了疫情在寄宿制学校灾难性扩散的严重后果。
4) 接种疫苗可以有效减缓病毒传播速度,小人群隔离对疫情阻断效果更明显, 4人间感染人数是同期6人间的1/6。寄宿制学校作为疫情重点防控对象,应尽快让师生接种新冠疫苗;加强相关宣传,鼓励师生积极接种疫苗,形成免疫屏障;接种疫苗后,在疫情彻底结束前封闭空间内应尽量戴口罩。
5) 本研究仅对一个公寓楼内出现一名新型冠状病毒感染者引发的疫情传播扩散风险进行了预测与讨论,其结果已如此严重,如果同时考虑病毒经人传物再传人以及教职员工等校外人员进出的影响,其风险会急剧上升。因此,在全球新冠肺炎疫情没有彻底控制之前,校园内的人员都应在自身条件允许的情况下,尽快接种疫苗,同时尽可能保持个人防控不松懈。
| [1] |
戴凯琳. 三问"新冠病毒"[J]. 法人, 2021(2): 94. |
| [2] |
邱晓燕, 杨慧莹, 颜明明, 等. 新型冠状病毒疫苗研发进展及其潜在不良反应[J]. 中国临床药学杂志, 2021, 30(1): 64. QIU Xiaoyan, YANG Huiying, YAN Mingming, et al. Research progress of COVID-19 vaccine and its protential adverse reactions[J]. Chinese Journal of Clinical Pharmacy, 2021, 30(1): 64. DOI:10.19577/j.1007-4406.2021.01.017 |
| [3] |
张文宏. 如何在秋冬季战胜新冠病毒和其他病毒性疾病[J]. 肝博士, 2021(1): 32. |
| [4] |
吴非, 康新, 崔岩, 等. 新冠疫情下思考: 如何加强城市公共卫生治理能力——大连市2020.7.22日新冠"疫情"发生分析[J]. 中国发展, 2020, 20(6): 37. WU Fei, KANG Xin, CUI Yan, et al. Thoughts against the backdrop of the COVID-19 epidemic: how to strengthen urban public health governance capacity, an analysis of the outbreak of the COVID-19 epidemic in Dalian on Jul, 22[J]. China Development, 2020, 20(6): 37. DOI:10.15885/j.cnki.cn11-4683/z.2020.06.007 |
| [5] |
胡艺, 赵杰, 乐佳徐, 等. 2021年初石家庄市新型冠状病毒肺炎暴发流行趋势分析[J]. 上海预防医学, 2021, 33(4): 287. HU Yi, ZHAO Jie, LE Jiaxu, et al. Modeling of a coronavirus disease outbreak at the beginning of 2021 in Shijiazhuang, Hebei Province, China[J]. Shanghai Journal of Preventive Medicine, 2021, 33(4): 287. DOI:10.19428/j.cnki.sjpm.2021.20873 |
| [6] |
孙柏林. "新冠病毒"模型掠影: "新冠病毒"模型支援抗疫斗争概述[J]. 计算机仿真, 2021, 38(1): 1. SUN Bolin. A glimpse of the New Coronavirus model: overview of "New Coronavirus" model supporting the fight against epidemic[J]. Computer Simulation, 2021, 38(1): 1. |
| [7] |
陈翔, 胡志斌. 高等学校新型冠状病毒肺炎防控指南[M/OL]. 北京: 人民卫生出版社, 2020: 50[2021-03-15]. http://www.moe.gov.cn/jyb_xwfb/gzdt_gzdt/s5987/202003/W020200312377387887254.pdf CHEN Xiang, HU Zhibin. Guidelines on COVID-19 prevention and control in higher education institutes[M/OL]. Beijing: People's Medical Publishing House, 2020: 50[2021-03-15]. http://www.moe.gov.cn/jyb_xwfb/gzdt_gzdt/s5987/202003/W020200312377387887254.pdf |
| [8] |
原存德, 胡宝安. 具有阶段结构的SI传染病模型[J]. 应用数学学报, 2002, 25(2): 193. YUAN Cunde, HU Baoan. A SI epidemic model with two-stage structure[J]. Acta Mathematicae Applicatae Sinica, 2002, 25(2): 193. DOI:10.3321/j.issn:0254-3079.2002.02.001 |
| [9] |
桑茂盛, 丁一, 包铭磊, 等. 基于新冠病毒特征及防控措施的传播动力学模型[J]. 系统工程理论与实践, 2021, 41(1): 124. SANG Maosheng, DING Yi, BAO Minglei, et al. Propagation dynamics model considering the characteristics of 2019-nCoV and prevention-control measurements[J]. Systems Engineering Theory & Practice, 2021, 41(1): 124. DOI:10.12011/SETP2020-0911 |
| [10] |
周武略, 白迪, 赵继军. 武汉市发生的新冠病毒肺炎建模研究分析[J]. 复杂系统与复杂性科学, 2020, 17(4): 58. ZHOU Wulüe, BAI Di, ZHAO Jijun. Modeling and analysis of COVID-19 in Wuhan[J]. Complex Systems and Complexity Science, 2020, 17(4): 58. DOI:10.13306/j.1672-3813.2020.04.007 |
| [11] |
NADIM S S, GHOSH I, CHATTOPADHYAY J. Short-term predictions and prevention strategies for COVID-19: a model-based study[J]. Applied Mathematics and Computation, 2021, 404: 12625. DOI:10.1016/j.amc.2021.126251 |
| [12] |
SARKAR K, KHAJANCHI S, NIETO J J. Modeling and forecasting the COVID-19 pandemic in India[J]. Chaos, Solitons & Fractals, 2020, 139: 110049. DOI:10.1016/j.chaos.2020.110049 |
 2022, Vol. 54
2022, Vol. 54


