2. 中国建筑第二工程局有限公司,北京 100074
2. China Construction Second Engineering Bureau Ltd., Beijing 100074, China
中国地铁建设的过程中,人工冻结法是针对沿海地区饱和地层加固的一种有效工法。沿海地区人工冻土具有温度变化速率快、冻结范围较小、水文地质复杂的明显特征[1-3]。人工冻土的冻结过程是一个复杂的不稳定导热问题[4],温度场、渗流场和应力场相互耦合[5-7]。考虑渗透作用的人工冻土的研究有程桦等[8]基于Harlan水热耦合模型,模拟了各向同性的饱和砂土在竖井冻结时冻结壁的扩展过程。摄宇[9]模拟了渗流作用下砂土单圈管冻结温度场的冻结效果。崔灏[10]模拟了渗流作用下砂土和粉土冻结壁发育规律及对温度场的影响。Vitel等[11]建立了一个完全热力学一致的耦合热- 水- 力数值模型,并模拟了渗流条件下饱和不可变形多孔介质的人工地层冻结。Ahmed等[12]建立了一种水- 热耦合有限元模型,可在渗流情况下通过寻找最佳位置来优化砂土地层冻结管的排布。目前,针对渗流影响的冻结效应研究集中在饱和无黏性土。相比之下,细粒的黏性土在温度梯度作用下会产生可观的水分迁移,从而形成分凝冻胀,且分凝冻胀比原位冻胀大很多[9]。
考虑水分迁移的分凝冻胀理论广泛应用于天然正冻细粒土的模型计算[13-14]。与天然冻土不同,人工冻结区域范围较小,温度变化速率快,不能简单抽象成一维的缓慢冻结,现有分凝冻胀模型的适用性较低。因此,在分凝冻胀理论的基础上,通过对刚性冰模型的三维化,建立了考虑三维分凝冻胀的热- 水- 力耦合作用模型,可以模拟计算沿海各向异性饱和地层使用人工冻结法应用时的温度场、应力场、位移场。最后通过COMSOL有限元模拟上海杨树浦路人工地层冻结法缩尺模型,并与缩尺试验结果进行对比,验证了模型的有效性。
1 考虑水分迁移的多场耦合模型建立 1.1 计算模型假定软黏土是一种细粒的黏性土,其颗粒表面具有一层吸附水,土颗粒通过吸附水传递土体应力[13]。吸附水层之外的水为重力水,产生孔隙水压并驱动孔隙水流动。土体发生冻结时,首先重力水发生相变,随着温度的进一步降低,冰水相界面向吸附膜内侵入,分凝冰产生[14]。当冰相生长至完全隔绝分凝方向上土颗粒之间的联系时,暖端一侧的水分不能补给冷端一侧,从而致使冷端一侧的分凝冰停止生长[13]。由此,依据孔隙水的冻结状态可将土体分为未冻结区、相变区和已冻结区。土体孔隙水的冻结状态如图 1所示。

|
图 1 冻结土体冻结状态 Fig. 1 Frozen state of frozen soil |
人工冻结土多为饱和土,故假设: 土体中的土骨架、孔隙水、孔隙冰皆为刚性且不可压缩,土体压缩仅与孔隙率的变化有关;水分迁移仅发生在未冻结区和相变区,已冻结区不发生水分迁移。
1.2 考虑三维分凝冻胀的水- 热- 力耦合模型饱和细粒黏性土的冻胀,可以看成由原位孔隙水相变膨胀所产生的原位冻胀与由水分迁移所产生的分凝冻胀的叠加。
1.2.1 原位冻胀模型原位冻胀是由孔隙水相变时比容差所引起,即dV=Δνd[W/(1+W)],其中,V为单位质量土体的体积,W为土体的未冻结水的含水率,Δν为H2O的比容差。
1.2.2 分凝冻胀模型由于孔隙内冰、水处于相压力平衡状态,即冰、水两相应符合Clapeyron方程[13]:
| $ \frac{\mathrm{d} p_{\mathrm{w}}}{\mathrm{d} T}=\frac{L}{T \Delta \nu} $ | (1) |
式中:pw为相界面水相压强,L为相变潜热。将方程积分并展开,取液态水在273.15 K、100 kPa时会发生的相变作为积分下限。
| $ \int_{100}^{p_{\mathrm{w}}} \Delta \nu \mathrm{d} p_{\mathrm{w}}=\int_{273.15}^{T} \frac{L \mathrm{~d} T}{T} $ | (2) |
| $ p_{\mathrm{w}}=\frac{L}{\Delta \nu}(\ln T-\ln 273.15) $ | (3) |
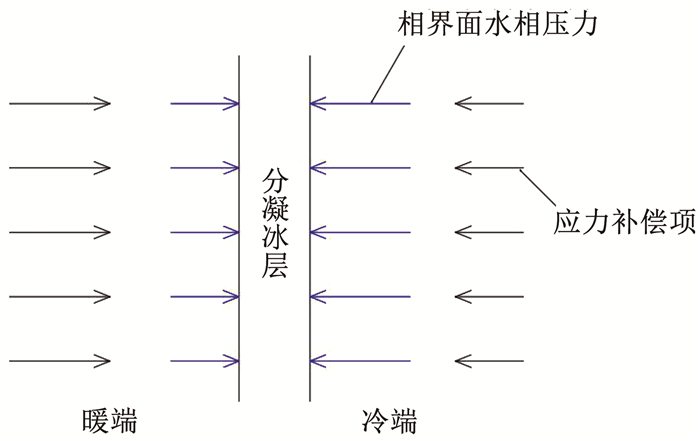
在冻结区,为保证任意一微分凝冰层颗粒处于静力平衡状态,且能完成应力传递(如图 2所示),需要在分凝冰暖端的相界面水相压力与外荷载之间引入一个平衡项uw,即
| $ u_{\mathrm{w}}+p_{\mathrm{w}}=\sigma_{\mathrm{l}} $ | (4) |
其中σl为冻结区域土体的主应力。
|
图 2 土体分凝状态 Fig. 2 Soil segregation state |
Miller等[13]认为平衡项uw即为相变区致使未冻结水迁移的驱动压力,从而有
| $ \mathrm{d} u_{\mathrm{w}}+\mathrm{d} p_{\mathrm{w}}=0 $ | (5) |
即相变区驱动孔隙水流动的水力梯度应为
| $ I_{1}=\frac{1}{\rho_{\mathrm{w}} g} \frac{\mathrm{d} u_{\mathrm{w}}}{\mathrm{d} l}=-\frac{1}{\rho_{\mathrm{w}} g} \frac{\mathrm{d} p_{\mathrm{w}}}{\mathrm{d} l} $ | (6) |
冷端需要为土体中提供足够的冷量才足以产生分凝冰。当该位置土体冷端吸热能力使得冻结锋面处水分迁移过来的孔隙水完全发生相变时,分凝冰发育迅速。土体体积应变速率应为水分迁移所引起的体积变化,即
| $ \frac{\mathrm{d} \varepsilon}{\mathrm{d} t}=-I_{1}(1-\Delta \nu) $ | (7) |
针对某一个微单元体,倘若冷端没有的冷量以支持孔隙水发生相变,该微单元体不产生分凝冰。倘若微单元体冷端传递过来的冷量不足以支持分凝所需,该微单元体就不能为冻结方向上后一个微单元体传递冷量,下一个微单元体就不产生分凝。这也表明冻结方向上的前一个微单元体有足够的冷量支持孔隙水发生相变。在这个冻结方向上,这种微单元体有且仅有一个,不能形成有效冻结带,故而可以忽略此类型的单元体。
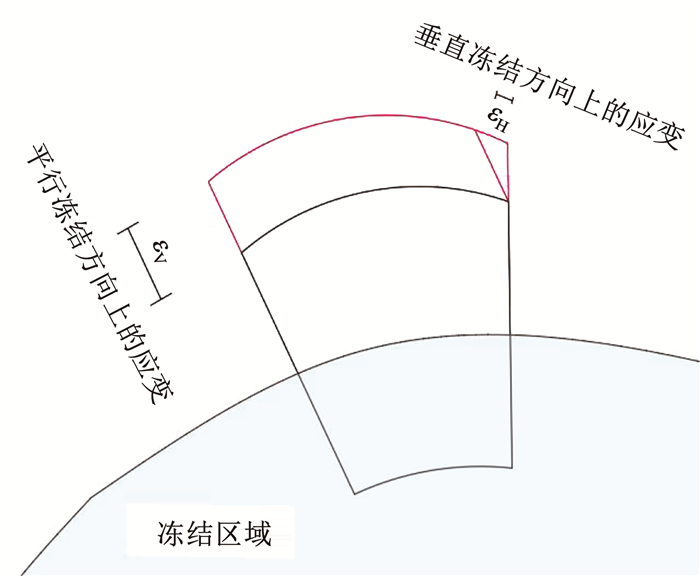
温度梯度所引起的水分迁移是土体产生冻胀的原因,水分迁移的方向是温度梯度方向,垂直于温度梯度方向可以近似地视为等温线,不具备能使水分发生迁移的动力因素。但是冻结锋面扩展前后都是一个连续的曲面。在温度梯度方向上迁移动力因素的影响下,为保证冻结锋面前后的连续性,垂直于温度梯度方向上会获得一个补偿应变量,如图 3所示。
|
图 3 土体分凝冻胀量示意 Fig. 3 Segregation frost heave of soil |
单元土体由于水分迁移所产生的总分凝冻胀量与冻结垂向和径向分凝冻胀关系应满足:
| $ \mathrm{d} \varepsilon=\mathrm{d} \varepsilon_{\mathrm{H}}+\mathrm{d} \varepsilon_{\mathrm{H}} \mathrm{d} \varepsilon_{\mathrm{V} 1}+\mathrm{d} \varepsilon_{\mathrm{H}} \mathrm{d} \varepsilon_{\mathrm{V} 2} $ | (8) |
式中dεV1、dεV2分别为冻结锋面上径向的应变量和纬向上的应变量。
对于单元土体,dεH相对较小,忽略去高阶无穷量dεHdεV1+dεHdεV2的影响,得dε=dεH。则该位置所产生冻结方向上的分凝冻胀速率为
| $ \begin{aligned} \frac{\mathrm{d} \varepsilon_{\mathrm{H}}}{\mathrm{d} t}=&-\left[\frac{\frac{K_{x}}{g \rho_{\mathrm{w}}} \partial\left(\frac{\partial u_{\mathrm{w}}}{\partial x}\right)}{\partial x}+\frac{\frac{K_{y}}{g \rho_{\mathrm{w}}} \partial\left(\frac{\partial u_{\mathrm{w}}}{\partial y}\right)}{\partial y}+\right.\\ &\left.\frac{\frac{K_{x}}{g \rho_{\mathrm{w}}} \partial\left(\frac{\partial u_{\mathrm{w}}}{\partial x}\right)}{\partial z}\right](1-\Delta \nu) \end{aligned} $ | (9) |
垂直于冻结方向上补偿应变量应与冻结方向上的应变量和冻结锋面曲率相关。该位置所产生垂直于冻结方向上的补偿应变速率为
| $ \frac{\mathrm{d} \varepsilon_{\mathrm{V} 1}}{\mathrm{~d} t}=\frac{\frac{\mathrm{d} \varepsilon_{\mathrm{H}}}{\mathrm{d} t} t}{2 F_{\mathrm{s}_{1}}}, \frac{\mathrm{d} \varepsilon_{\mathrm{V} 2}}{\mathrm{~d} t}=\frac{\frac{\mathrm{d} \varepsilon_{\mathrm{H}}}{\mathrm{d} t}}{2 F_{\mathrm{s}_{2}}} $ | (10) |
式中Fs1、Fs2为冻结锋面上的径向的曲率半径与纬向的曲率半径,可根据微分几何学公式进行计算(各向冻胀计算见图 4)。

|
图 4 各向冻胀计算示意 Fig. 4 Schematic of calculation of frost heave in all directions |
| $ F_{\mathrm{s}_{1}}=\frac{\left[1+\left(\frac{\partial a}{\partial b}\right)^{2}\right]^{3 / 2}}{\left|\frac{\partial^{2} a}{\partial b^{2}}\right|}, F_{\mathrm{s}_{2}}=\frac{\left[1+\left(\frac{\partial c}{\partial d}\right)^{2}\right]^{3 / 2}}{\left|\frac{\partial^{2} c}{\partial d^{2}}\right|} $ |
其中
| $ \frac{\partial a}{\partial b}=\frac{\frac{\partial T}{\partial z}}{\left(\frac{\partial T}{\partial x} \frac{\partial x}{\frac{\partial x}{\partial l} \partial x+\frac{\partial y}{\partial l} \partial y}+\frac{\partial T}{\partial y} \frac{\partial y}{\frac{\partial x}{\partial l} \partial x+\frac{\partial y}{\partial l} \partial y}\right) \frac{\sqrt{\left(\frac{\partial x}{\partial l}\right)^{2}+\left(\frac{\partial y}{\partial l}\right)^{2}+\left(\frac{\partial z}{\partial l}\right)^{2}}}{\sqrt{\left(\frac{\partial x}{\partial l}\right)^{2}+\left(\frac{\partial y}{\partial l}\right)^{2}}}}, $ |
| $ \frac{\partial^{2} a}{\partial b^{2}}=\frac{\partial\left(\frac{\partial a}{\partial b}\right)}{\partial z}, $ |
| $ \frac{\partial c}{\partial d}=\frac{\frac{\partial T}{\partial x} \frac{\partial x}{\frac{\partial x}{\partial l} \partial x+\frac{\partial y}{\partial l} \partial y+\frac{\partial z}{\partial l} \partial z}+\frac{\partial T}{\partial y} \frac{\partial y}{\frac{\partial x}{\partial l} \partial x+\frac{\partial y}{\partial l} \partial y+\frac{\partial z}{\partial l} \partial z}+\frac{\partial T}{\partial z} \frac{\partial z}{\frac{\partial x}{\partial l} \partial x+\frac{\partial y}{\partial l} \partial y+\frac{\partial z}{\partial l} \partial z}}{\left(\frac{\partial T}{\partial x} \frac{\partial x}{\frac{\partial x}{\partial l} \partial x+\frac{\partial y}{\partial l} \partial y}+\frac{\partial T}{\partial y} \frac{\partial y}{\frac{\partial x}{\partial l} \partial x+\frac{\partial y}{\partial l} \partial y}\right) \frac{\sqrt{\left(\frac{\partial x}{\partial l}\right)^{2}+\left(\frac{\partial y}{\partial l}\right)^{2}+\left(\frac{\partial z}{\partial l}\right)^{2}}}{\sqrt{\left(\frac{\partial x}{\partial l}\right)^{2}+\left(\frac{\partial y}{\partial l}\right)^{2}}}}, $ |
| $ \frac{\partial^2 c}{\partial d^2}=\frac{\partial\left({\frac{\partial c}{\partial d}}\right)}{\left(\frac{\partial T}{\partial x} \frac{\partial x}{\frac{\partial x}{\partial l} \partial x+\frac{\partial y}{\partial l} \partial y}+\frac{\partial T}{\partial y} \frac{\partial y}{\frac{\partial x}{\partial l} \partial x+\frac{\partial y}{\partial l} \partial y}\right) \frac{\sqrt{\left(\frac{\partial x}{\partial l}\right)^{2}+\left(\frac{\partial y}{\partial l}\right)^{2}+\left(\frac{\partial z}{\partial l}\right)^{2}}}{\sqrt{\left(\frac{\partial x}{\partial l}\right)^{2}+\left(\frac{\partial y}{\partial l}\right)^{2}}}}, $ |
| $ \frac{\partial x}{\partial l}=\frac{\frac{\partial T}{\partial x}}{\sqrt{\left(\frac{\partial T}{\partial x}\right)^{2}+\left(\frac{\partial T}{\partial y}\right)^{2}+\left(\frac{\partial T}{\partial z}\right)^{2}}}, \frac{\partial y}{\partial l}=\frac{\frac{\partial T}{\partial y}}{\sqrt{\left(\frac{\partial T}{\partial x}\right)^{2}+\left(\frac{\partial T}{\partial y}\right)^{2}+\left(\frac{\partial T}{\partial z}\right)^{2}}}, \frac{\partial z}{\partial l}=\frac{\frac{\partial T}{\partial z}}{\sqrt{\left(\frac{\partial T}{\partial x}\right)^{2}+\left(\frac{\partial T}{\partial y}\right)^{2}+\left(\frac{\partial T}{\partial z}\right)^{2}}} $ |
土体融化时相变界面水相压力差依然存在,但迁移的水分无法有效被消耗,即水分迁移路径上没有泄水出口,从而在根本上抑制了水相压力差引起的水分迁移。因此,不考虑融化时水热耦合关系引起的水分迁移。
土体融沉的过程由原位融化和融化后土体的固结沉降构成。原位融化与原位冻结相似,都是由土体孔隙冰相变所造成的体积变化引起,不同的是原位融化的水(冰)量不仅有冻结之前土体孔隙中的水分,还包括冻结过程中所迁移过来的水分量[14]。
排水固结的过程使用太沙基- 伦杜利克三维固结微分方程:
| $ C_{\mathrm{v}} \frac{\partial^{2} u}{\partial n^{2}}=\frac{\partial u}{\partial t}-\frac{\partial \sigma}{\partial t} $ | (11) |
式中:u为超孔隙水压力,n为融化锋面的法向,σ为融化时土体融化方向上的主应力,Cv为固结系数。
饱和土体融化相变时孔隙水承担所有的应力传递,融化后的孔隙水压力应与融化时土体冻胀力相同,计算时与土体一次性赋予孔隙水压力初值。随着融化的进一步进行,冻胀力消散,超孔隙水压力产生。当融化锋面在Δt时间内穿过一个长度增量时,在冻土层中排出的孔隙水体积为
| $ \Delta V=-\frac{1}{\gamma_{\rm{w}}}\left(A K \frac{\partial u}{\partial n}\right) \Delta t $ | (12) |
式中:A为土体单位的横截面面积,∂u/∂n为融化界面上的孔隙压力梯度,γw为水的重度。
水流ΔV等于厚度为Δn土层体积的变化量,则体积应变为
| $ \frac{\Delta V}{V}=\frac{\Delta V}{A \Delta V}=-\frac{K\left(\frac{\partial u}{\partial n}\right)}{\gamma_{\rm{w}}\left(\frac{\partial n}{\partial t}\right)} $ | (13) |
1) 土体含冰率:I=n0-W。
2) 土体骨架比率:S=1-I-W。
3) 未冻土孔隙率与土体应变的关系:n=n0-(εx+εy+εz)(1+n0)。其中, εx,εy,εz为土体各方向的应变;冻结区与相变区的孔隙率:n=n0-W。
4) 未冻结水含水率与温度关系拟合[15]:
5) 未冻区渗透系数与孔隙率的关系[16]:
6) 土体密度:ρ=ρwW+ρiI+ρsS,其中, ρw、ρi、ρs分别为水、冰、土颗粒的密度;土体热传导系数:λ=λwW+λiI+λsS,其中, λw、λi、λs分别为水、冰、土颗粒的热传导系数;土体比热:C=CwW+CiI+CsS,其中, Cw、Ci、Cs分别为水、冰、土颗粒的比热。
7) 当土体完全冻结后,由于分凝作用土体出现了垂直于冻结方向与平行于冻结方向的分凝冰带,层状的分凝冰带将随机出现在冻结体中,宏观可以体现一定的均匀性。将3个冻结方向上分凝冰带、原状土比拟成相互穿插的弹簧模型,从而对分凝冻结土的压缩模量进行预测(计算模型示意如图 5):
| $ E_{\mathrm{H}}=\frac{1+\varepsilon_{\mathrm{H}}}{\frac{\left(1+\varepsilon_{\mathrm{V} 1}+\varepsilon_{\mathrm{V} 2}\right)}{E_{\mathrm{c}}+E_{\mathrm{i}}\left(\varepsilon_{\mathrm{V} 1}+\varepsilon_{\mathrm{V} 2}\right)}+\frac{\varepsilon_{\mathrm{H}}}{E_{\mathrm{i}}}} $ | (14) |
| $ E_{\mathrm{V} 1}=\frac{1+\varepsilon_{\mathrm{V} 1}}{\frac{\left(1+\varepsilon_{\mathrm{H}}+\varepsilon_{\mathrm{V} 2}\right)}{E_{\mathrm{c}}+E_{\mathrm{i}}\left(\varepsilon_{\mathrm{H}}+\varepsilon_{\mathrm{V} 2}\right)}+\frac{\varepsilon_{\mathrm{V} 1}}{E_{\mathrm{i}}}} $ | (15) |
| $ E_{\mathrm{V} 2}=\frac{1+\varepsilon_{\mathrm{V} 2}}{\frac{\left(1+\varepsilon_{\mathrm{H}}+\varepsilon_{\mathrm{V} 1}\right)}{E_{\mathrm{c}}+E_{\mathrm{i}}\left(\varepsilon_{\mathrm{H}}+\varepsilon_{\mathrm{V} 1}\right)}+\frac{\varepsilon_{\mathrm{V2}}}{E_{\mathrm{i}}}} $ | (16) |
式中:Ec为土体在封闭系统内冻结完成后的压缩模量,可以由实验室测定得到;EH、EV1、EV2分别为冻结方向上的变形模量、垂直于冻结方向径向上的变形模量、垂直于冻结方向纬向上的变形模量。冻结前土体、融化后土体的弹性模量可以由试验测定得到。

|
图 5 计算模型示意 Fig. 5 Schematic of the calculation model |
使用未冻土孔隙率、相变界面的压强、相变温度、未冻结水含水率等作为模型的基本参量,对分凝冻胀理论分凝冰模型进行三维化。相较广泛应用的天然冻土分凝冻胀理论刚性冰模型,本模型更适用于冻结范围小、温度变化速率较快、土体各向异性明显、水文条件复杂的人工冻结的应用。具体为
1) 能为冻结锋面曲率半径小、冻结温度变化迅速的工况更准确地预测(温度变化、应力应变变化等);
2) 可以考虑冻结时具有强烈地下水渗流的工况,能够对具有渗透各向异性地层不规则形状的冻结进行模拟预测;
3) 能够预测各相异性冻结土的弹性模量,进而可以模拟冻结帷幕的变形特征、受力特征。
2 数值模型计算与结果分析基于上述建立的三维分凝冻胀模型,通过COMSOL有限元模拟上海12号线杨树浦路站人工地层冻结法缩尺模型,并与缩尺试验结果进行对比,对模型的有效性进行验证。
2.1 模拟工况 2.1.1 工程背景上海市地铁12号线杨树浦路地铁站是越江站(黄浦江),隧道埋深15 m,地铁联络通道建设在淤泥质软黏土中。由于临近黄浦江泄水通道,联络通道下伏着流速相对较高的微承压水粉细砂层,平均流速为0.41 m/d。地铁联络通道冻结管长为12 m,直径为89 mm,冻结帷幕一排设置7根冻结管,冻结管中冷盐水流量为3 m3/h,温度为-30 ℃。对地铁联络通道冻结工程有影响的土层为第④层淤泥质黏土、第⑤层粉细砂,其岩土、水文特性如表 1、2所示。
| 表 1 淤泥质黏土层特性 Tab. 1 Characteristics of silty clay layer |
| 表 2 粉细砂层特性 Tab. 2 Characteristics of silt fine sand layer |
缩尺模型试验以现场冻结工况为基础,采用考虑了材料、尺寸、渗流水头、土体传热、泵送盐水流量相似性的模型试验系统[17]进行试验。模型试验系统相似比为1∶30,冻结管埋深50 cm,冻结管直径8 mm,数量为7根,冻结盐水泵流量经热流密度相似计算需为30 L/min,冻结冷盐水温度为-30 ℃。试验装置如图 6所示。试验箱中填置重塑淤泥质黏土与粉细砂以模拟现场施工地层,淤泥质黏土的厚度为46 cm,下层砂土的厚度为40 cm。箱体两侧设置水槽,试验通过抽水泵为土体两侧施加水头差以模拟临江地下水的流动。设置渗流速度为0、0.25、0.50、0.75、1.2、3.0 m/d的6种试验工况。通过低温恒温箱为冻结管进行制冷以模拟现场冻结。试验首先为重塑土进行预固结,对模型土体进行制冷后实时监测土体内部各传感器的监测指标变化规律。温度传感器在相同深度沿水平渗流方向以8 cm的间距(冻结管附近间距10 cm)串联布置成一排测线,共布设了4排,分别位于冻结管、冻结帷幕上下边缘及砂层处(纵向间距6 cm)。土压力传感器在冻结管、冻结帷幕上缘及砂层各位置的中心位置各布置1个,冻结帷幕下沿处由于渗流影响较大,以10 cm的间距沿渗流方向布置了3个。位移传感器在土层上表面以8 cm的间距沿渗流方向均匀布置了5个。成排分布的土压力传感器、温度传感器使用细铁丝进行固定,以使试验过程中传感器的位置不发生较大的偏移。传感器排布位置如图 6(b)所示。温度传感器精度为0.01 ℃、土压传感器精度为0.2 kPa、位移传感器精度为0.01 mm。传感器精度较高且工作稳定性较好、尺寸效应不明显、监测频率满足试验设计要求。冻结帷幕扩展到规定厚度或当渗流速度特别大时,即使冻结足够长时间,冻结传感器监测的温度仍然达不到-10 ℃(1 h内温度下降不超过0.1 ℃),关闭制冷系统,冻结结束。当温度全部回升到17 ℃左右且地表沉降不再增加时,试验结束。

|
图 6 缩尺试验装置 Fig. 6 Reduced-scale test device |
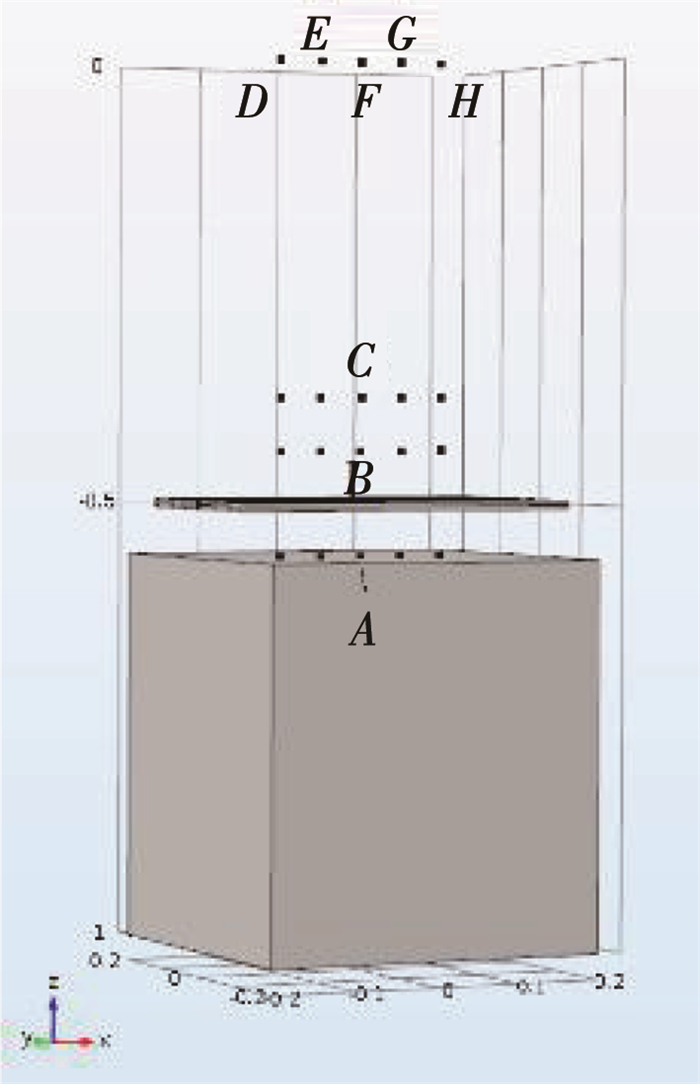
数值模拟的模型工况与缩尺模型试验工况完全相同,其等尺寸建立的模型如图 7所示。模拟冻结管温度为-30 ℃,数值监测点位置、地下水流速、冻结厚度控制、冻结温度控制等皆与缩尺模型试验相同。试验土体物理力学参数[18]如表 3所示。
|
图 7 几何模型示意 Fig. 7 Geometric model diagram |
| 表 3 模拟参数 Tab. 3 Simulation parameters |
使用COMSOL有限元的PDE模块对物理场方程进行编译。渗流在未冻结区连续性方程为
| $ -\left[\frac{\frac{K_{x}}{g} \partial\left(\frac{\partial u_{\mathrm{w}}}{\partial x}\right)}{\partial x}+\frac{\frac{K_{y}}{g} \partial\left(\frac{\partial u_{\mathrm{w}}}{\partial y}\right)}{\partial y}+\frac{\frac{K_{z}}{g} \partial\left(\frac{\partial u_{\mathrm{w}}}{\partial z}\right)}{\partial z}\right]=\frac{\partial\left(\rho_{\mathrm{w}} n\right)}{\partial t} $ | (17) |
渗流在相变区的连续性方程为
| $ \begin{gathered} -\left[\frac{\frac{K_{x}}{g} \partial\left(\frac{\partial u_{\mathrm{w}}}{\partial x}\right)}{\partial x}+\frac{\frac{K_{y}}{g} \partial\left(\frac{\partial u_{\mathrm{w}}}{\partial y}\right)}{\partial y}+\frac{\frac{K_{z}}{g} \partial\left(\frac{\partial u_{\mathrm{w}}}{\partial z}\right)}{\partial z}\right]= \\ \frac{\partial\left(\rho_{\mathrm{w}} n\right)}{\partial t}+\rho_{\mathrm{w}} \frac{\mathrm{d} \varepsilon}{\mathrm{d} t} /(1-\Delta \nu) \end{gathered} $ | (18) |
传热方程:在一个土体单元内,质量累积量的改变量、热传导量、热对流量与潜热释放量的总和为0,即
| $ \rho C \frac{\partial T}{\partial t}+\nabla(-\lambda \nabla T)+\rho_{\rm{w}} C_{\rm{w}} \nabla v \nabla T+\frac{\partial \rho C}{\partial t}=0 $ | (19) |
土体应力场采用弹塑性本构模型。
2.3 结果分析模拟结果表明,渗流对冻结效果存在临界点,即当渗流小于1.2 m/d时,冻结帷幕才能冻结完成。
2.3.1 组合地层渗流对冻结温度场的影响冻结稳定时数值模拟区域等温线分布如图 8所示。可以看出,没有渗流作用时模型土体的等温线相对水平;有渗流存在时,等温线呈一定程度的不均匀化偏移,上游等温线密集,下游等温线稀疏。渗流对冻结帷幕的厚度整体都有削弱作用,对上游削弱最为明显。

|
图 8 不同渗流速度下等温线 Fig. 8 Isotherm diagram under different seepage velocities |
土体冻结过程发生冻胀后,由于膨胀受限从而会产生向四面扩张的内应力。冻结工程中将土体冻胀受限所产生的内应力称为冻胀力。
不同渗流作用下土体冻结稳定时,冻结管中心位置土体所产生冻胀力的切片云图见图 9。可以看出,冻结管附近冻胀力集中效应明显,冻结帷幕下沿下游冻胀力明显大于上游,帷幕上沿变化不明显。冻结帷幕上沿的冻胀力整体均大于冻结帷幕下沿。

|
图 9 不同渗流速度下冻胀力云图 Fig. 9 Cloud diagram of frost heave force under different seepage velocities |
针对能够冻结完成的工况,冻结帷幕下上沿监测点A、B在不同渗流速度下冻胀力的增长如图 10、11所示。结果表明,监测点A、B冻胀力发展模式存在较大不同。监测点A冻结阶段的冻胀力开始时增长迅速,后期增长缓慢。对于监测点B,冻胀力在整个冻结阶段都在缓慢增长,冻胀力平稳不变的阶段不明显。在融沉阶段,渗流速度大的工况冻胀力消散得更快。

|
图 10 监测点A冻胀力监测图 Fig. 10 Monitoring results of frost heave force at point A |

|
图 11 监测点B冻胀力监测图 Fig. 11 Monitoring results of frost heave force at point B |
产生该现象的原因是:靠近渗流边界的地方,渗流抑制冻结方向上的温度变化,从而抑制了孔隙冰的生成速率,致使冻结帷幕下沿冻胀力增长速率缓慢。同时,渗流减少了靠近渗流边界地区冻结方向上分凝冰生成的质量,从而减小了冻胀力的最终值。
在实际工程施工中,冻胀力是监测预警的关键指标。对于冻结帷幕上沿部分,冻结前期就应重点关注冻胀力的突变增长,采取预警及措施;而冻结帷幕下沿更应该关注的是冻结后期,因为前期冻胀力增长较缓慢且数值较小。在融沉初始阶段,冻结帷幕上沿冻胀力的快速消散应是工程注意的重点。同时,渗流速度增大时,土体产生的冻胀力较小,特别是靠近渗流边界的冻结帷幕下沿。冻胀力的降低可以减小土体对隧道产生的压力,增强工程的安全性。
2.3.3 组合地层渗流对地表沉降的影响针对能够冻结完成的工况,不同渗流速度地表最终沉降量如图 12所示。可以看出,沿着渗流方向,地表最终沉降越来越大,且渗流速度越大,最终沉降越低。因此,当存在下覆较大渗流砂层情况的软黏土冻结,不均匀沉降也是需要关注的重要方面。

|
图 12 不同渗流速度地表位移 Fig. 12 Surface displacement at different seepage velocities |
产生该现象的原因是:下游区域温度较低,该区域生成了更多的孔隙冰从而最终沉降量更大。渗流可以抑制分凝冰的生成,从而使渗流大的工况分凝冰含量低,也就产生了渗流速度越大,冻胀、沉降量越低的现象。
3 模型验证选取监测点A在0.25 m/d渗流速度下的温度、冻胀力及位移分别与模型试验结果进行对比,结果如图 13所示。可以看出,温度场与应力场的数值模拟结果与实测结果接近度较大。而位移的计算结果发展规律基本一致,冻胀位移存在一定误差,融沉位移相对接近。主要原因为数值模型模拟的是完全考虑了三维水分迁移的理想开放系统,而模型试验需要对渗流进行控制,并没有做到在各个方向上给软黏土同时补水, 出现了试验测定的冻胀量要小于数值模拟估计值的现象。
4 组合地层渗流对冻结法安全影响分级以上海市地铁12号线杨树浦路地铁站为工程背景,针对不同渗流速度的冻结工况进行数值模拟,对照现行隧道安全体系,分别对隧道位移、隧道附加冻胀应力、地表隆起、地表沉降进行预测并分级。各指标的管理等级可分为:等级Ⅰ为所有渗流工况下,物理指标处于极限值的2/3~极限值,是安全隐患较高的等级阶段;等级Ⅱ为所有渗流工况下,物理指标处于极限值的1/3~2/3,是安全隐患发展的等级阶段; 等级Ⅲ为所有渗流工况下,物理指标小于极限值的1/3,是不利因素产生的初始阶段,相对安全。分级结果如表 4、5。

|
图 13 数值模拟与模型试验结果对比 Fig. 13 Comparison of numerical simulation and model test |
| 表 4 冻结阶段安全控制 Tab. 4 Safety control during freezing phase |
| 表 5 融沉阶段安全控制 Tab. 5 Safety control during thawing phase |
分级预警可以提前对工程地质不利因素的严重程度进行预先评估,从而指导工程及时应对工程地质不利因素,增强冻结施工的安全性,降低地质灾害的影响程度。
5 结论1) 在组合地层条件下,渗流会削减冻结稳定时冻结帷幕的厚度,且上游削弱最明显;当速度大于1.2 m/d时,冻结工程将不能达到设计厚度。
2) 在组合地层条件下,冻结工程靠近渗流边界的一侧冻胀力增长缓慢、最大值较低。
3) 渗流会致使地表产生不均匀沉降,下游区域的沉降量更大。对于实际工程而言,地表的不均匀沉降也是组合地层渗流冻结法需要关注的危害。
4) 通过建立的热- 水- 力三场耦合模型对组合地层渗流作用下冻结法施工及周围环境的影响进行参数分析,提出了结合组合地层渗流因素的隧道安全冻结法分级标准,可以为工程建设提供参考依据。
| [1] |
陈湘生, 汪崇鲜. 冻结法加固处理涌水冒砂地层: 上海地铁1#线思南路泵站冻结施工实施[J]. 建井技术, 1995(2): 3. CHEN Xiangsheng, WANG Chongxian. Reinforcement treatment of gushing water and sand formation by freezing method-implementation of freezing construction of Sinan Road Pumping Station of Shanghai Metro Line 1[J]. Mine Construction Technology, 1995(2): 3. DOI:10.19458/j.cnki.cn11-2456/td.1995.02.002 |
| [2] |
陈湘生, 徐兵壮. 用冻结法加固隧道连通道泵站: 上海地铁1#线宁海西路大泵站冻结工程[J]. 建井技术, 1995(2): 6. CHEN Xiangsheng, XU Bingzhuang. Reinforcing the pumping station of the tunnel connecting tunnel by freezing method: Shanghai metro 1# line Ninghai West Road large pump station freezing project[J]. Mine Construction Technology, 1995(2): 6. DOI:10.19458/j.cnki.cn11-2456/td.1995.02.003 |
| [3] |
高娟, 冯梅梅, 杨维好. 渗流作用下裂隙岩体冻结温度场分布规律研究[J]. 采矿与安全工程学报, 2013, 30(1): 68. GAO Juan, FENG Meimei, YANG Weihao. Research on distribution law of frozen temperature field of fractured rock mass with groundwater seepage[J]. Journal of Mining and Safety Engineering, 2013, 30(1): 68. |
| [4] |
张学富, 喻文兵, 刘志强. 寒区隧道渗流场和温度场两场耦合问题的三维非线性分析[J]. 岩土工程学报, 2006, 28(9): 1095. ZHANG Xuefu, YU Wenbing, LIU Zhiqiang. Three-dimensional nonlinear analysis for coupled problem of seepage field and temperature field of cold regions tunnels[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1095. DOI:10.3321/j.issn:1000-4548.2006.09.009 |
| [5] |
叶玉西, 石红伟, 杨明红. 伊犁矿区某矿副井冻结壁不交圈原因分析及处置[J]. 矿业工程, 2013, 11(6): 20. YE Yuxi, SHI Hongwei, YANG Minghong. Analysis and treatment of un-joint circle of auxiliary shaft of a Yili mining area[J]. Mining Engineering, 2013, 11(6): 20. |
| [6] |
周晓敏, 龙肖阁. 渗流地层人工冻结温度场和渗流值数值研究[J]. 煤炭学报, 2007, 32(2): 24. ZHOU Xiaomin, LONG Xiaoge. Numerical research on the temperature and seepage fields of artificial seepage ground freezing[J]. Journal of China Coal Society, 2007, 32(2): 24. |
| [7] |
唐益群, 赵文强, 周洁. 封闭系统单向冻结淤泥质黏土水分迁移特性研究[J]. 工程地质学报, 2020, 28(5): 935. TANG Yiqun, ZHAO Wenqiang, ZHOU Jie. Laboratory test study on moisture migration within mucky clay under unidirectional freezing in closed system[J]. Journal of Engineering Geology, 2020, 28(5): 935. DOI:10.13544/j.cnki.jeg.2020-268 |
| [8] |
程桦, 林键, 王彬, 等. 饱和砂层渗流冻结水热耦合模型与试验验证[J]. 科学技术与工程, 2018, 18(12): 38. CHENG Hua, LIN Jian, WANG Bin, et al. Mathematical model and test verification of seepage freezing in saturated sand layer[J]. Science Technology and Engineering, 2018, 18(12): 38. |
| [9] |
摄宇. 渗流作用下单圈管冻结温度场数值模拟[J]. 低温建筑技术, 2019, 41(3): 70. SHE Yu. Numerical simulation analysis of seepage effect on the freezing temperature field of single loop pipe[J]. Low Temperature Architecture Technology, 2019, 41(3): 70. DOI:10.13905/j.cnki.dwjz.2019.03.017 |
| [10] |
崔灏. 渗流作用下富水砂卵石层井筒冻结壁形成研究[J]. 煤炭技术, 2018, 37(12): 61. CUI Hao. Research on formation of frozen wall in water rich sand and gravel layer under seepage[J]. Coal Technology, 2018, 37(12): 61. DOI:10.13301/j.cnki.ct.2018.12.020 |
| [11] |
VITEL M, ROUABHI A, TIJANI M. Modeling heat and mass transfer during ground freezing subjected to high seepage velocities[J]. Computers and Geotechnics, 2016, 27: 1. |
| [12] |
MARWAN A, ZHOU Mengmeng, ABDELREHIM M Z, et al. Optimization of artificial ground freezing in tunneling in the presence of seepage flow[J]. Computers and Geotechnics, 2016, 32: 112. |
| [13] |
MILLER R D. Freezing and heaving of saturated and unsaturated soils[J]. Highway Research Record, 1972, 399: 1. |
| [14] |
李杨. 基于多孔介质理论的冻土水热迁移耦合模型推导[J]. 河北工程大学学报(自然科学版), 2012, 29(3): 11. LI Yang. Derivation of water and thermal migration coupled model based on theory of porous media in seasonal frozen soil[J]. Journal of Hebei University of Engineering (Natural Science Edition), 2012, 29(3): 11. |
| [15] |
裴万胜. 冻土水- 热- 力相互作用过程及数值模拟研究[D]. 北京: 中国科学院大学, 2015 PEI Wansheng. Water-heat-force interaction process and numerical simulation of frozen soil[D]. Beijing: University of Chinese Academy of Sciences, 2015 |
| [16] |
PIMENTEL E, SRES A, ANAGNOSTOU G. Large-scale laboratory tests on artificial ground freezing under seepage-flow conditions[J]. Geotechnique, 2012, 62(3): 227. |
| [17] |
周洁, 李泽垚, 肖思奇, 等. 一种组合地层渗流作用下冻结法模型设计方法及装置: ZL 2018 1 1327032.7[P]. 2019-02-15 ZHOU Jie, LI Zeyao, XIAO Siqi, et al. Design method and device of a freezing method model under combined formation seepage: ZL 2018 1 1327032.7[P]. 2019-02-15 |
| [18] |
唐益群, 李金章, 李珺. 冻融饱和粉砂动力性能试验[J]. 哈尔滨工业大学学报, 2019, 51(2): 76. TANG Yiqun, LI Jinzhang, LI Jun. Experimental study on dynamic cumulative axial strain performance of artificial frost-thawed saturated silty sand[J]. Journal of Harbin Institute of Technology, 2019, 51(2): 76. DOI:10.11918/j.issn.0367-6234.201710144 |
 2022, Vol. 54
2022, Vol. 54




