2. 中国科学院 西北生态环境资源研究院,兰州 730000
2. Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences, Lanzhou 730000, China
盐渍土作为一种特殊土,是指易溶盐质量分数大于0.3%,并具有溶陷、盐胀和腐蚀等特性的岩土,在中国广泛分布,尤其是西北干旱地区[1]。环境温度周期变化下,土体孔隙中的液态水和盐分周期性冻结融化、结晶溶解,引发冻土区冻胀融沉、盐胀开裂等一系列病害,这些病害大多和土体中水分迁移以及相变有关。冻土水分迁移、相变、盐结晶析出是一个水热盐耦合问题,主要表现在:水分迁移会导致土体热参数发生变化,冻融状态的土体热参数有较大差异,进而影响温度场;水分相变潜热、盐分结晶潜热对温度场有较大影响;盐分迁移对土体热质输运有显著影响;土体温度低于冻结温度时,土体中仍存在未冻水,且未冻水体积分数与负温保持动态平衡关系[2]。
盐分迁移研究方面,盐渍土中盐分的扩散和迁移影响土体的孔隙特性,在冻结缘附近会形成一个较大的盐晶体分布区[3]。Zhou等[4]研究了温度梯度下非饱和土的水盐迁移及变形特性,得出盐的吸附作用通过影响土体的孔隙改变土中的水盐迁移过程。吴道勇等[5]开展了盐渍土水盐迁移模型试验,探索了寒旱区土壤盐渍化机制,发现盐分迁移速率与吸力有关。Bing等[6]研究了盐渍土冻结温度的变化规律,并探讨了不同盐分类型对土体冻结温度的影响,但是没有研究盐分结晶温度的变化。之后,万旭升等[7]研究了不同降温方式下硫酸钠溶液和硫酸钠盐渍土中芒硝的析出规律。以上研究对认识冻结过程中盐分迁移具有重要作用,但是上述研究较少涉及盐分质量分数对结晶温度和冻结温度的影响。
多物理场耦合模型研究方面,Harlan[8]基于非饱和土与部分冻结土中水分运输提出了水动力学模型,但是该模型没有考虑冰透镜体的形成过程。O′Neill等[9]提出了刚冰模型,但冰透镜体的产生条件没有统一标准。Konrad等[10]基于分凝势理论建立了一个冻胀模型,但是该模型参数较难确定,上述模型促进了冻土多物理场耦合研究的发展。考虑土体水冰相变产生的冻胀应变,Li等[11]建立了土体的水热力计算模型,并构建了仿真平台,该模型在寒区工程温度场、水分场以及应力(变形)场的数值模拟中得到了广泛应用[12-13]。结合克拉伯龙方程,Lai等[14]建立了计算冻胀的水热力耦合模型,并指出负孔隙水压力是液态水从未冻区向冻结锋面迁移的主要动力。然而上述计算模型没有考虑土中盐分对水热力响应的影响,无法描述盐的迁移与结晶。之后,基于结晶动力学理论,Zhang等[15]建立了饱和冻结盐渍土的水-热-盐-力计算模型,但该模型物性参数多,使用起来并不方便。
鉴于此,基于硫酸钠盐渍土降温试验,分析了初始盐分质量分数对结晶温度的影响,建立了降温过程盐渍土水-热-盐计算模型,通过数值计算结果与试验结果的对比分析,对所提出模型的有效性进行了验证,进而对降温过程硫酸钠盐渍土温度、水分以及盐分变化进行了计算,以期为盐渍土区工程修建及数值模拟提供理论基础和科学依据。
1 试验方法试验采用青藏高原粉质黏土(塑限14.5%,液限23.8%),土体的颗粒级配如表 1所示。为了减少土中其他离子对试验结果的影响,试验前对土样进行脱盐、风干处理。所有盐渍土土样的初始水分质量分数均为20%,盐分质量分数分别为0.8%、0.9%、1.0%、1.1%、1.2%、1.8%、2.1%、2.6%、2.9%、3.2%,干密度控制在1.72~1.75 g/cm3。试验中将圆柱体样品(直径3.3 cm,高3.8 cm)装在特制的铁容器中,于土样的中间插入温度传感器(测温范围为-30~30 ℃,温度精度为0.05 ℃),并密封容器。之后将容器置于冷浴中进行降温试验,温度调节范围为25~-20 ℃,降温速率为1 ℃/min。温度降至-20 ℃后恒温,实时监测试验过程中土样的温度变化,图 1为降温过程硫酸钠盐渍土温度变化曲线。
| 表 1 土体的颗粒级配 Tab. 1 Particle gradation |

|
图 1 试验降温曲线 Fig. 1 Test cooling curves |
降温过程不同盐分质量分数盐渍土结晶温度的取值对数值模拟结果会产生重要影响,因为盐分质量分数高低决定结晶温度的高低,进而决定结晶与冻结发生的先后顺序,不同盐分质量分数盐渍土结晶温度如表 2所示。分两组拟合土体结晶温度与初始盐分质量分数的关系曲线(如图 2所示),可以看出,不同初始盐分质量分数盐渍土的结晶温度不同。当土体硫酸钠质量分数小于2%时,结晶温度小于0 ℃,并且土体硫酸钠质量分数越低,结晶温度越小(图 2(a));当土体硫酸钠质量分数大于2%时,结晶温度大于0 ℃,并且结晶温度随着盐分质量分数的增大而增大(图 2(b))。
| 表 2 不同盐分质量分数盐渍土的结晶温度 Tab. 2 Crystallization temperature of saline soil with different salt content |

|
图 2 结晶温度拟合曲线 Fig. 2 Fitting curves of crystallization temperature |
基于此,提出了盐渍土结晶温度与盐分质量分数的参数模型:
| $ T_{\mathrm{c}}=\left\{\begin{array}{l} A_{1}+\frac{B_{1}}{C_{1} c \sqrt{2 {\rm{ \mathsf{ π} }}}} \mathrm{e}^{\left(-\ln \frac{c}{D}\right) \frac{1}{C_{1}^{2}}}, 0<c<2 \% \\ A_{2} \mathrm{e}^{-\frac{c}{B_{2}}}+C_{2}, 2 \% \leqslant c \leqslant 3.2 \% \end{array}\right. $ | (1) |
式中:A1、A2、B1、B2、C1、C2、D为模型参数, A1=0.61, A2=11.05, B1=-4.29, B2=-0.03, C1=0.20, C2=-20.69, D=0.81。
2.2 导热系数及热容降温过程中,硫酸钠盐渍土存在两个物理相变过程,即盐分结晶和水-冰相变。相变会导致盐渍土各组分质量分数发生变化,进而引起导热系数及热容变化。同时,盐渍土的水-冰相变温度受过冷现象影响,盐分结晶受过饱和现象影响[16]。基于此,以初始盐分质量分数3.2%的土样为例,提出了考虑降温过程盐渍土过饱和现象和过冷现象的导热系数及热容计算方法,该盐分质量分数盐渍土的水分冻结温度和盐分结晶温度分别为273.15和285.0 K,分别引入阶跃函数H1(T)和H2(T)实现上述两个相变过程,阶跃函数H1(T)和H2(T)如图 3所示。

|
图 3 阶跃函数 Fig. 3 Step function |
根据阶跃函数特性,得到导热系数和热容的计算模型分别为
| $ \lambda=\lambda_{\mathrm{f}}+H_{1}(T)\left(\lambda_{\mathrm{u}}-\lambda_{\mathrm{f}}\right)+H_{2}(T)\left(\lambda_{\mathrm{c}}-\lambda_{\mathrm{u}}\right) $ | (2) |
| $ C=C_{\mathrm{f}}+H_{1}(T)\left(C_{\mathrm{u}}-C_{\mathrm{f}}\right)+H_{2}(T)\left(C_{\mathrm{c}}-C_{\mathrm{u}}\right) $ | (3) |
式中:C、λ分别为试样的热容和导热系数,Cc、Cu和Cf分别为土样初始阶段(水分未冻结且盐分未结晶)、水分未冻结且盐分结晶阶段以及水分冻结阶段的热容,λc、λu和λf分别为土样初始阶段(水分未冻结且盐分未结晶)、水分未冻结且盐分结晶阶段以及水分冻结阶段的导热系数。C、λ变化如图 4所示。

|
图 4 降温过程硫酸钠盐渍土导热系数、热容变化示意 Fig. 4 Variation of thermal conductivity and heat capacity of sodiumsulfate saline soil during a cooling process |
基于土体介质的热传导、冰-水相变及冻融过程中液态水的对流传热,得到考虑冰-水相变和盐分结晶潜热的非稳态温度-盐分微分方程[17]:
| $ \begin{gathered} \rho C_{\mathrm{s}} \frac{\partial T}{\partial t}=\operatorname{div}(\lambda \operatorname{grad} T)+L_{\mathrm{w}} \rho_{\mathrm{i}} \frac{\partial \theta_{\mathrm{i}}}{\partial t}+ \\ L_{\mathrm{c}} \frac{\partial m_{\mathrm{c}}}{\partial t}+C_{\mathrm{w}} \rho_{\mathrm{w}} \operatorname{grad} T \end{gathered} $ | (4) |
式中:t为时间, s; θi为含冰体积分数, m3/m3; ρ、ρi、ρw分别为土、冰和水的密度, kg/m3; T为盐渍土的温度, K; Cs、Cw分别为土体和水的比热容, J/(kg·℃); λ为导热系数, W/(m·℃); Lw、Lc分别为冰-水相变潜热和硫酸钠结晶潜热,取值分别为333.4和247.1 kJ/kg; mc为析出硫酸钠质量, kg。
含冰体积分数、硫酸钠溶解度与温度存在一定关系[2, 17]:
| $ \frac{\partial \theta_{\mathrm{i}}}{\partial t} =\frac{\partial \theta_{\mathrm{i}}}{\partial T} \frac{\partial T}{\partial t} $ | (5) |
| $ \frac{\partial m_{\mathrm{c}}}{\partial t} =\frac{\partial m_{\mathrm{c}}}{\partial T} \frac{\partial T}{\partial t} $ | (6) |
降温过程中盐渍土的未冻水体积分数可用下式计算[18]:
| $ \theta_{\mathrm{f}}=\left\{\begin{array}{l} \theta_{0}, T \geqslant T_{\mathrm{f}} \\ \left(-1.763 \ln c_{0}+1\right) \mathrm{e}^{\left(-0.645 \ln c_{0}+0.778\ 7\right)\left(T-T_{\mathrm{k} 0}\right)}+ \\ 0.026\ 5,-T_{\mathrm{k} 0}<T<T_{\mathrm{f}} \end{array}\right. $ | (7) |
式中:θ0为试样初始水分质量分数; Tf为孔隙水的冻结温度; Tk0为将摄氏温度转换为开尔文温度的常数,Tk0=273.15 K; c0为初始盐分质量分数。
由图 1可知,当盐渍土盐分质量分数大于2%时,在水分冻结温度前未冻水体积分数主要受盐分结晶影响,在0 ℃以下与温度相关。故可得到未冻水体积分数体积分数θu与温度的关系为
| $ \theta^{\prime}{}_{\mathrm{u}}=\left\{\begin{array}{l} \zeta\left[\left(-1.763 \ln c_{0}+1\right) \mathrm{e}^{\left(-0.645 \ln c_{0}+0.778\ 7\right)\left(T-T_{\mathrm{k} 0}\right)}+\right. \\ 0.026\ 5],-T_{\mathrm{k} 0}<T<T_{\mathrm{f}} \\ \theta_{0}-\zeta \frac{m_{\mathrm{w}}}{m_{\mathrm{s}}}, T \geqslant T_{\mathrm{f}} \end{array}\right. $ | (8) |
式中:ζ为水分质量分数与未冻水体积分数的转化系数,取1.8;mw、ms分别为盐分结晶消耗水的质量和土的质量。
由试验值可知,土体中盐晶体的析出造成了未冻水体积分数的损失,故引入土体影响系数对未冻水体积分数进行修正[18]:
| $ \theta_{\mathrm{u}}=\eta \theta^{\prime}{}_{\mathrm{u}} $ | (9) |
式中η为土体影响系数,表达式为
| $ \eta=\left(-0.234\ 3 c_{0}+1.048\ 5\right) \mathrm{e}^{0.015\left(T-T_{{\rm{k}} 0}\right)} $ | (10) |
硫酸钠的溶解度ξ(g/100 g)与温度的关系可表示为[2]
| $ \xi=4.494\ 3 \times 1.077\ 3^{T-T_{{\rm{k}} 0}} $ | (11) |
基于硫酸钠的溶解度公式,可以得到不同温度下盐渍土中溶解了多少硫酸钠,进而得出硫酸钠的结晶质量mc。计算中假定硫酸钠结晶后的产物为芒硝(Na2SO4·10H2O),即可通过硫酸钠结晶前后物质的量的关系,得出结晶消耗水分的质量mw。
3.2 水分迁移方程根据Richard方程,考虑孔隙冰对未冻水迁移的阻滞作用,得到非饱和冻土中未冻水迁移微分方程[13]
| $ \frac{\partial \theta_{\mathrm{u}}}{\partial t}+\frac{\rho_{\mathrm{i}}}{\rho_{\mathrm{w}}} \frac{\partial \theta_{\mathrm{i}}}{\partial t}=\operatorname{div}\left[D\left(\theta_{\mathrm{u}}\right) \operatorname{grad} \theta_{\mathrm{u}}\right]+\frac{\partial K\left(\theta_{\mathrm{u}}\right)}{\partial z} $ | (12) |
式中:D(θu)为土体的水分扩散系数, m2/s; K(θu)为重力加速度方向土体的非饱和导水率, m/s。计算公式分别为[13]
| $ D\left(\theta_{\mathrm{u}}\right)=\frac{D(\theta)}{I} $ | (13) |
| $ K\left(\theta_{\mathrm{u}}\right)=\frac{K(\theta)}{I} $ | (14) |
式中I为阻抗因子,表示孔隙冰对未冻水迁移的阻滞作用,可由下式计算[13]:
| $ I=10^{-10 \theta_{\mathrm{i}}} $ | (15) |
| $ D(\theta)=a_{1} \theta_{\mathrm{u}}^{b_{1}} $ | (16) |
| $ K(\theta)=a_{2} \theta_{\mathrm{u}}^{b_{2}} $ | (17) |
式中a1、a1、b1、b2为模型参数,取值分别为1.40×10-6 m2/s、5.88×10-5 m/s、3.98和16.40。
联立式(4)~(17),可得水热盐耦合方程为
| $ C^{*} \frac{\partial T}{\partial t}=\operatorname{div}\left(\lambda^{*} \operatorname{grad} T\right)+L_{\mathrm{w}} \rho_{\mathrm{w}} \frac{\partial K\left(\theta_{\mathrm{u}}\right)}{\partial z} $ | (18) |
其中, 土体的等效体积热容C*和等效导热系数λ*可描述为
| $ C^{*}=\rho C+L_{\mathrm{w}} \rho_{\mathrm{w}} \frac{\partial \theta_{\mathrm{u}}}{\partial T}+L_{\mathrm{c}} \frac{\partial m_{\mathrm{u}}}{\partial T} $ | (19) |
| $ \lambda^{*}=\lambda+L_{\mathrm{w}} \rho_{\mathrm{w}} D\left(\theta_{\mathrm{u}}\right) \frac{\partial \theta_{\mathrm{u}}}{\partial T} $ | (20) |
式(4)~(20)均满足协调方程
| $ \theta=\theta_{\mathrm{u}}+\frac{\rho_{\mathrm{i}}}{\rho_{\mathrm{w}}} \theta_{\mathrm{i}}+\theta_{\mathrm{c}} $ | (21) |
| $ \theta_{\mathrm{c}}=\frac{\left(c_{0}-\Delta c\right) m_{\mathrm{s}}}{\rho_{\mathrm{c}} V_{\mathrm{s}}} $ | (22) |
式中:θ为孔隙率,θc为结晶盐分的体积分数, %; Δc为由于结晶析出硫酸钠质量分数, %; ρc为硫酸钠的密度, kg/m3; Vs为土颗粒体积, m3; mu为盐渍土中未结晶的硫酸钠质量。
3.3 物理模型和计算参数基于室内试验土柱建立物理模型(如图 5所示)。计算模型的降温速率与试验外界冷浴降温速率一致,其边界条件和初始条件如表 3所示。

|
图 5 土柱降温试验物理模型(m) Fig. 5 Calculation model of soil column(m) |
| 表 3 数值计算中的初始条件与边界条件 Tab. 3 Initial condition and boundary condition in numerical calculation |
为了验证水-热-盐计算模型的准确性,用该模型对封闭条件下初始盐分质量分数为1.0%和3.2%的硫酸钠盐渍土降温试验进行反演。土样温度计算结果如图 6所示,可以看出,模型计算结果与试验结果具有很好的一致性。含盐与不含盐土体在12 ℃时第一次产生差异,主要是芒硝析出释放热量,导致含盐土体降温速率小于不含盐土体;在-2 ℃时第二次产生差异,即含盐土样降温速率大于不含盐土样,这主要是由于硫酸钠结晶产生芒硝消耗大量水分(析出1 mol芒硝消耗10 mol水)。

|
图 6 计算降温曲线 Fig. 6 Calculated cooling curves |
计算得到的未冻水体积分数与温度关系见图 7,可以看出,较高盐分质量分数土样(初始盐分质量分数为3.2%)的未冻水体积分数计算值与试验值具有很好的一致性。温度为10~15 ℃时,未冻水体积分数小幅减少,这是硫酸钠结晶形成芒硝(十水硫酸钠)所致;温度为0~-5 ℃时,未冻水体积分数大幅减少,这是土中水分冻结所致。较低盐分质量分数土样(初始盐分质量分数为1.0%)与不含盐土样的未冻水体积分数变化差异不明显。

|
图 7 未冻水体积分数变化曲线 Fig. 7 Variation of volumetric unfrozen water content |
计算得到土样的硫酸钠结晶质量(过饱和比)随温度变化曲线如图 8所示,过饱和比是试样内硫酸钠质量浓度与该温度下硫酸钠溶解度的比值,结晶压力对多孔介质材料有较大破坏作用,这与溶液的过饱和度有关。初始盐分质量分数为3.2%的土样在温度为25~20 ℃时过饱和比小于1,该温度时土样中的硫酸钠不发生结晶;土样温度为20~12 ℃时,由于“过饱和”现象,土样中的硫酸钠仍然不会结晶;温度为12 ℃时土样开始结晶,之后随着环境温度的降低,硫酸钠结晶加快(12~-2 ℃)。然而,随着温度的继续降低,土样水-冰相变加剧,形成冰晶,进而制约盐晶发育,故此时结晶极为缓慢(-2~-20 ℃)。对比初始盐分质量分数为3.2%的土样,初始盐分质量分数为1.0%土样的过饱和比在正温时比较小,不足以结晶。

|
图 8 硫酸钠结晶质量变化曲线 Fig. 8 Variation of sodium sulfate crystallization quality |
为了预测土体内部物相变化,沿用建立的盐渍土水-热-盐相互作用计算模型,取初始盐分质量分数为3.2%和1.0%的土样,绘制特定时刻(部分结晶、部分冻结以及物态稳定时刻)未冻水体积分数、盐分结晶质量分数、盐分质量浓度的横、纵剖面分布图,截取剖面如图 9所示。

|
图 9 截取剖面示意 Fig. 9 Schematic diagram of sections of soil sample |
初始盐分质量分数为3.2%土样横、纵截面的水热盐云图分别见图 10、11。从图 10(a)~10(c)同一时刻不同特征参数(如未冻水体积分数、硫酸钠结晶质量分数以及结晶质量浓度)分布可以看出,在t=1 400 s时,盐分质量分数为3.2%土样外层温度在11 ℃左右,其未冻水体积分数小幅减少(图 10(a)),硫酸钠结晶质量分数增加(图 10(b)), 硫酸钠消耗水分产生芒硝,且硫酸钠结晶质量分数较大,致使硫酸钠质量浓度减小(图 10(c))。在t=3 000 s时,土样外层温度为-3~-5 ℃,其未冻水体积分数大幅减少,而硫酸钠结晶质量分数基本稳定,此时未冻水体积分数的减少由水-冰相变引起,故硫酸钠质量浓度反而增大(图 10(a)~10(c))。在t=3 800 s时,未冻水体积分数、硫酸钠结晶质量分数以及硫酸钠质量浓度均趋于稳定(图 10(a)~10(c))。

|
图 10 初始盐分质量分数为3.2%土样横截面水热盐分布云图 Fig. 10 Contour distribution of soil sample with initial salt content of 3.2% in cross section |

|
图 11 初始盐分质量分数为3.2%土样纵截面水热盐分布云图 Fig. 11 Contour distribution of soil sample with initial salt content of 3.2% in longitudinal section |
从图 11(a)~11(c)同一时刻土样未冻水体积分数、硫酸钠结晶质量分数及结晶质量浓度分布可以看出,t=1 400 s时,土样外部产生芒硝,引起未冻水体积分数小幅减少,硫酸钠质量浓度降低(图 11(a))。t=3 000 s时,土样外部发生水-冰相变,未冻水体积分数大幅减少,硫酸钠质量浓度大幅增加(图 11(b))。t=3 800 s时,土样内部温度分布趋于均匀(图 11(c))。综合图 10、11可以看出,未冻水体积分数与结晶硫酸钠分布一致,可用硫酸钠结晶位置反映水分运移轨迹,而硫酸钠质量浓度只能反映结晶质量分数与未冻水体积分数变化的相对关系。
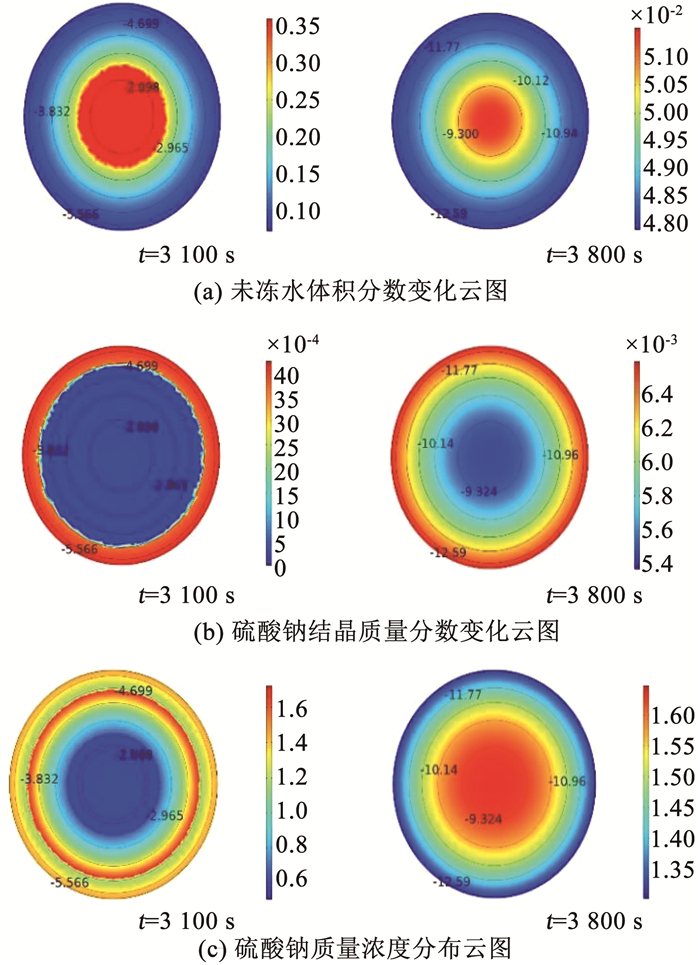
初始盐分质量分数为1.0%土样横、纵截面的水热盐云图分别如图 12、13所示。可以看出,t=3 100 s时,盐分质量分数为1.0%的土样外部未冻水体积分数和硫酸钠结晶质量分数均已发生变化,在温度-4~-5 ℃的区域未冻水体积分数发生显著变化,但其硫酸钠结晶质量分数未产生明显变化,而硫酸钠质量浓度在该温度内反而升高,这主要是由硫酸钠运移所致(图 12、13)。t=3 800 s时,未冻水体积分数稳定在5%左右,而硫酸钠结晶质量分数仍在增加,说明盐分质量分数为1.0%土样硫酸钠的结晶在水分冻结之后,且持续时间长于水-冰相变时间;而盐分质量分数为3.2%土样硫酸钠的结晶在水分冻结之前(图 10、11)。
|
图 12 初始盐分质量分数为1.0%土样横截面水热盐分布云图 Fig. 12 Contour distribution of soil sample with initial salt content of 1.0% in cross section |

|
图 13 初始盐分质量分数为1.0%土样纵截面水热盐分布云图 Fig. 13 Contour distribution of soil sample with initial salt content of 1.0% in longitudinal section |
冻土中的水分迁移、相变和盐分结晶是一个复杂的水-热-盐相互作用问题。探讨了硫酸钠盐渍土的结晶温度,提出适用的水-热-盐相互作用模型,实现了冻土温度、水分和盐分的计算。得到如下结论:
1) 硫酸钠盐渍土结晶温度模型可较好地预测降温过程盐渍土的结晶温度。不同初始盐分质量分数土样降温过程存在明显差异,高盐分质量分数土样(初始盐分质量分数为3.2%)在正温发生盐分结晶,低盐分质量分数土样(初始盐分质量分数为1.0%)在负温发生盐分结晶。
2) 降温过程中不同初始盐分质量分数土样盐分扩散运移能力存在差异,高盐分质量分数土样(初始盐分质量分数为3.2%)在正温区间盐分结晶质量分数较大,阻碍盐分运移。低盐分质量分数土样(初始盐分质量分数为1.0%)为-4~-6 ℃时盐分运移明显,局部盐分质量浓度增大。
3) 本研究虽考虑了环境温度降低时硫酸钠盐渍土出现的“过冷”、“过饱和”现象,但是在数值计算过程中体现尚不明显,这些仍是寒区冻土数值模拟中的难点,即在考虑“过冷”、“过饱和”现象中建立盐渍土水-热-盐相互作用的理论模型。
| [1] |
周幼吾, 郭东信. 我国多年冻土的主要特征[J]. 冰川冻土, 1982, 4(1): 1. ZHOU Youwu, GUO Dongxin. Principal characteristics of permafrost in China[J]. Journal of Glaciology and Geocryology, 1982, 4(1): 1. |
| [2] |
徐学祖, 王家澄, 张立新. 冻土物理学[M]. 北京: 科学出版社, 2001: 75. XU Xuezu, WANG Jiacheng, ZHANG Lixin. Permafrost physics[M]. Beijing: Science Press, 2001: 75. |
| [3] |
PANDAY S, CORAPCIOGLU M Y. Solute rejection in freezing soils[J]. Water Resources Research, 1991, 27(1): 99. DOI:10.1029/90WR01785 |
| [4] |
ZHOU Lizeng, ZHOU Fengxi, YING Sai, et al. Study on water and salt migration and deformation properties of unsaturated saline soil under a temperature gradient considering salt adsorption: numerical simulation and experimental verification[J]. Computers and Geotechnics, 2021, 134: 104094. DOI:10.1016/J.COMPGEO.2021.104094 |
| [5] |
吴道勇, 赖远明, 马勤国, 等. 季节冻土区水盐迁移及土体变形特性模型试验研究[J]. 岩土力学, 2016, 37(2): 465. WU Daoyong, LAI Yuanming, MA Qinguo. Model test study of water and salt migration and deformation characteristics in seasonally frozen soil[J]. Rock and Soil Mechanics, 2016, 37(2): 465. DOI:10.16285/j.rsm.2016.02.020 |
| [6] |
BING Hui, MA Wei. Laboratory investigation of the freezing point of saline soil[J]. Cold Regions Science and Technology, 2011, 67(1/2): 79. DOI:10.1016/j.coldregions.2011.02.008 |
| [7] |
万旭升, 赖远明. 硫酸钠溶液和硫酸钠盐渍土的冻结温度及盐晶析出试验研究[J]. 岩土工程学报, 2013, 35(11): 2090. WAN Xusheng, LAI Yuanming. Experimental study on freezing temperature and salt crystal precipitation of sodium sulphate solution and sodium sulphate saline soil[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(11): 2090. |
| [8] |
HARLANR L. Analysis of coupled heat-fluid transport in partially frozen soil[J]. Water Resources Research, 1973, 9(5): 1314. DOI:10.1029/WR009i005p01314 |
| [9] |
O′NEILL K, MILLER R D. Exploration of a rigid ice model of frost heave[J]. Water Resource Research, 1985, 21(3): 281. DOI:10.1029/WR021i003p00281 |
| [10] |
KONRAD J M, MORGENSTERN N R. The segregation potential of a freezing soil[J]. Canadian Geotechnical Journal, 1981, 18(4): 482. DOI:10.1139/t81-059 |
| [11] |
LI Shuangyang, ZHANG Mingyi, PEI Wansheng, et al. Experimental and numerical simulations on heat-water-mechanics interaction mechanism in a freezing soil[J]. Applied Thermal Engineering, 2018, 132: 209. DOI:10.1016/j.applthermaleng.2017.12.061 |
| [12] |
LI Shuangyang, ZHANG Mingyi, TIAN Yibin, et al. Experimental and numerical investigations on frost damage mechanism of a canal in cold regions[J]. Cold Regions Science and Technology, 2015, 116: 1. DOI:10.1016/j.coldregions.2015.03.013 |
| [13] |
ZHANG Mingyi, PEI Wansheng, LI Shuangyang, et al. Experimental and numerical analyses of the thermo-mechanical stability of an embankment with shady and sunny slopes in a permafrost region[J]. Applied Thermal Engineering, 2017, 127: 1478. DOI:10.1016/j.applthermaleng.2017.08.074 |
| [14] |
LAI Yuanming, PEI Wansheng, ZHANG Mingyi, et al. Study on theory model of hydro-thermal-mechanical interaction process in saturated freezing silty soil[J]. International Journal of Heat and Mass Transfer, 2014, 78: 805. DOI:10.1016/j.ijheatmasstransfer.2014.07.035 |
| [15] |
ZHANG Jing, LAI Yuanming, LI Jifeng, et al. Study on the influence of hydro-thermal-salt-mechanical interaction in saturated frozen sulfate saline soil based on crystallization kinetics[J]. International Journal of Heat and Mass Transfer, 2020, 146: 118868. DOI:10.1016/j.ijheatmasstransfer.2019.118868 |
| [16] |
WAN Xusheng, GONG Fumao, QU Mengfei, et al. Experimental study of the salt transfer in a cold sodium sulfate soil[J]. KSCE Journal of Civil Engineering, 2019, 23(4): 1573. DOI:10.1007/s12205-019-0905-5 |
| [17] |
卢宁, LIKOSW J. 非饱和土力学[M]. 北京: 高等教育出版社, 2012: 269. LU Ning, LIKOS W J. Unsaturated soil mechanics[M]. Beijing: Higher Education Press, 2012: 269. |
| [18] |
万旭升, 赖远明, 廖孟柯. 硫酸盐渍土未相变含水率与温度关系研究[J]. 岩土工程学报, 2015, 37(12): 2175. WAN Xusheng, LAI Yuanming, LIAO Mengke. Relationship between temperature and water content of sodium saline soils without phase transformation[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(12): 2175. DOI:10.11779/CJGE201512006 |
 2022, Vol. 54
2022, Vol. 54


