2. 综合交通运输大数据应用技术交通运输行业重点实验室(北京交通大学), 北京 100044
2. Key Laboratory of Transport Industry of Big Data Application Technologies for Comprehensive Transport (Beijing Jiaotong University), Beijing 100044, China
国际航权是航空公司开展国际航空运输业务不可或缺的关键资源。国际航权资源(承运人数量、通航点及数量、运力额度、第五航权等)的使用权利和总量往往需要通过国家之间的双边谈判确定,国际民航界亦形象称之为“航权交换”。不同于其他谈判场景的博弈问题,航权资源谈判除了价值对等原则以外,还需要考虑双方关系的友好互惠程度,以及谈判议题同时给双方带来的价值收益。航权资源谈判是谈判双方先后正式报价,提出议题进行谈判的过程,是典型的序贯博弈。该过程的关键问题是如何基于物质收益和友好互惠心理收益合理设置核心议题。一旦确定所有议题,就能明确谈判双方的最优博弈选择,推动谈判向更有利己方的方向发展。
在管理实践中,中国负责国际航权谈判的部门是中国民用航空局,其与外国民航主管部门开展航权谈判的总体目标是促进双方人员往来、贸易流通,争取达成互惠共赢的航权协定或者备忘录,该行为属于经济领域国际合作范畴。目前民航局主要根据国家外交战略导向和民航行业发展需要,基于行业经验数据进行议题设置,对关联产业补偿和产业空间预留价值等方面的物质收益考虑不多,亦未形成量化方法来实现物质收益与友好互惠心理收益两者之间的平衡。在学术上,目前国内外鲜有航权资源双边谈判博弈问题的研究。相关研究大多集中在互惠心理在国际安全合作[1]、国际产业合作[2]和安全预防投资[3]等谈判场景下的应用,一般采用友善度的初始信念[4]和高阶信念[5]来权衡互惠程度,用互惠敏感系数来描述互惠关系。在此基础上,文献[1-2]分别针对反恐国际合作问题和非资源型产业合作问题建立了互惠博弈模型。此外,分段赋值的思想[6]和贴现因子[7]也被用来衡量互惠关系带来的超额收益。
本文借鉴这些思路,针对航权资源双边谈判的特点,提出航权资源双边谈判博弈问题,建立基于4个价值维度的议题物质收益函数,构建了基于互惠心理收益的序贯互惠博弈模型,从而为民航局航权资源谈判的议题设置问题提供方法参考和决策支持。
1 航权资源双边谈判的博弈分析在航权资源谈判过程中,谈判双方基于战略谈判关系和价值对等原则,评估双方提案中所有议题的相对价值,并在博弈中不断调整正式报价的议题,最终达成双方都能接受的议案。如果双方处于互惠共赢的战略谈判关系,双方不再仅仅关注短期获益,还希望在未来长期谈判中的稳定获益,因此会采取使对方获益更大的谈判选择。具体来讲,双方通过议题试探阶段掌握谈判的完全信息,并在正式报价环节进行完全信息博弈,先后正式提出议题,并在议题综合价值得到双方接受的基础上达成协议。双方先后进行议题报价的博弈选择就构成了完全信息下的序贯博弈。这里的完全信息是指谈判方在谈判前和第一阶段试探中获得双方的博弈选择行为及其支付函数。
在谈判中,谈判方面对所有议题组成的资源池,可采取最低程度合作和最高程度合作两种博弈选择。对谈判方而言,资源池中所有议题,可以划分为近期和远期需求议题。当议题对应的航权资源在本国的近期资源利用计划中,则定义为该国的近期需求议题;否则,定义为该国的远期需求议题。某一谈判方的某个近期需求议题可能与对方某个近期或远期需求议题,具有相同的航权资源类型和数量,本文称之为对等议题。近期需求议题和远期需求议题的对应关系如图 1所示。从图中可以看出,两国分别针对各种航权资源设置了专门的近期或远期需求议题,并且一个国家的每个议题,对方一般均有一个对等议题。若双方提出的议题均对应双方的近期需求,双方能同时接纳对方的议题并且所涉及的航权资源数量不能更少时,则将谈判方提出上述议题的行为定义为博弈选择中的“最低程度合作”;若双方在此基础上提出更多议题,双方能同时接纳对方的议题并且所涉及的航权资源数量不能更多时,则将谈判方提出这些议题的行为定义为博弈选择中的“最高程度合作”。二者分别描述了实际谈判中设置议题“低案”和“高案”的行为。
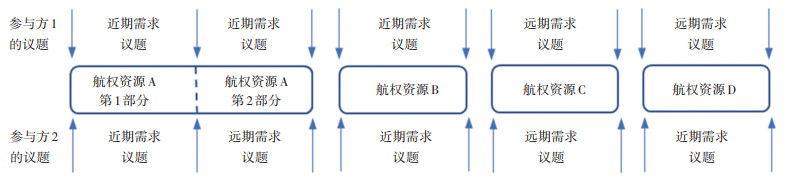
|
图 1 谈判双方需求议题之间的对应关系 Fig. 1 Corresponding relation between discussed issues of negotiators |
对谈判场景作如下假设:航权资源谈判的参与方为国家1和国家2,国家2是谈判发起方且在正式报价环节首先提出议题报价,国家1随后提出议题报价。议题资源池中只有6个议题。双方在最低程度合作的博弈选择中,分别提出了近期需求议题Ⅰ和Ⅳ,将两议题分别定义为自身的基准议题,如图 2所示。在最高程度合作的博弈选择中,在基准议题的基础上,双方又均新提出了一个近期和一个远期需求议题。将新提出的两个议题定义为扩展议题,如图 3所示。

|
图 2 最低程度合作博弈选择对应的议题 Fig. 2 Issue corresponding to the minimum cooperation strategy |
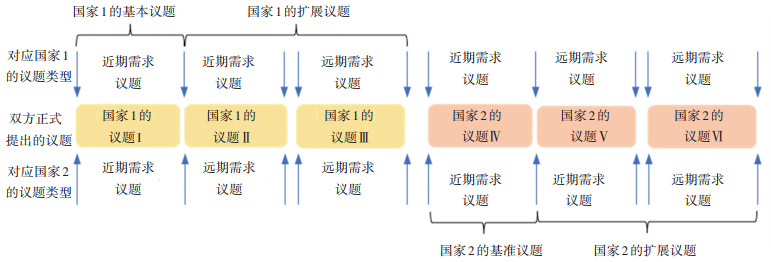
|
图 3 最高程度合作博弈选择对应的议题 Fig. 3 Issue corresponding to the maximum cooperation strategy |
对每个议题而言,各国在该议题上的综合收益U包括物质收益π和心理收益Q两部分。其中,物质收益不仅要考虑议题所对应的航权资源类型,还要考虑物质收益系数,包括议题的贴现因子θ[8-9]、关联产业补偿系数α[10]、产业空间预留价值系数β和机会成本空置耗损系数γ[11-12]。用m和n分别表示国家i的近期和远期需求议题,fim和fin表示该国能从这两个议题上直接获得的基本物质收益,则该国能从这两个议题获得的物质收益Fim和Fin分别为
| $ F_{i m}=f_{i m} \cdot\left(1+\alpha_{i}\right) \cdot \theta_{i} $ | (1) |
| $ F_{i n}=f_{i n} \cdot\left(\beta_{i n}-\gamma_{i n}\right) \cdot \theta_{i} $ | (2) |
其中,贴现因子θ是一个国家在航权谈判中议价能力的体现,θ∈(0, 1),贴现因子越大,议价能力越强。近期需求议题在近期能被利用,不仅能通过其航权资源获得直接收益,还能通过民航运输业对关联产业的带动作用获得间接收益。以关联产业补偿系数α来表征间接收益相对直接收益的大小,α越大表明对应的航权资源能拉动其他产业的能力越大。远期需求议题在近期不能被利用,不仅不会获得直接收益,还会因为谈判的机会成本造成直接额外损失,但与此同时也为行业未来预留了空间,产生了间接收益。以机会成本空置耗损系数γ和产业空间预留价值系数β来表征直接额外损失和间接收益的相对大小,β∈(0, 1),γ∈(0, 1)。γ越大,直接额外损失越大;而β越大,间接收益越大。定义β-γ为远期需求议题的机会价值收益系数,综合衡量谈判方在该议题上基于直接额外损失和间接收益的整体收益情况。上述3种物质收益系数相对大小的现实意义如图 4所示。对于国家i的某个远期需求议题而言,当产业空间预留价值系数βi大于机会成本空置耗损系数γi(对应区域1和4),此时该国家在该议题上的直接额外损失小于间接受益,整体获得正物质收益;当产业空间预留价值系数βi小于机会成本空置耗损系数γi(对应区域2和3),此时该国家在该议题上的直接额外损失大于间接受益,整体获得负物质收益。对于同一议题,当国家i的贴现因子θi大于国家j的贴现因子θj(对应区域1和2),此时在该议题上,国家i的议价能力比国家j更强;当国家i的贴现因子θi小于国家j的贴现因子θj(对应区域3和4),此时在该议题上,国家i的议价能力比国家j更弱。
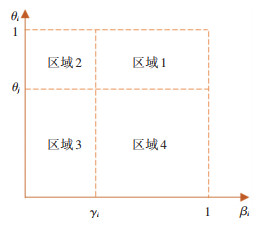
|
图 4 物质收益系数的现实意义 Fig. 4 Practical significance of material income coefficients |
结合谈判实际情况,对博弈模型进行如下假设: 1)每个国家提出的议题整体上要对己方有利,即自身获得物质收益的总和为正数;2)双方都选择最低程度合作时,在所有议题上获得的物质收益相等;3)在采取最高程度合作时,国家i提出的两个扩展议题整体上要对国家j有利,即国家j在这两个议题上获得的物质收益,与其在己方提出的基准议题和扩展议题上获得的物质收益之和为正数。
2.2 扩展议题的价值博弈场景谈判方在己方扩展议题和对方扩展议题(议题Ⅱ、Ⅲ与议题Ⅴ、Ⅵ)上的收益情况,是影响谈判场景类型的重要因素,间接影响参与方选择最低程度合作还是最高程度合作。不失一般性,谈判方在扩展议题上的物质收益存在6种情况,据此可以进一步将谈判博弈进一步细分为6个扩展议题价值博弈场景,见表 1。
| 表 1 扩展议题价值博弈场景的物质收益特征 Tab. 1 Characteristics of material income in the game scenario of extended issue value |
研究6种扩展议题价值博弈场景下双方的博弈行为。参与方的博弈策略集合S={最高程度合作,最低程度合作}。用s1和s2分别表示国家1和国家2选择的博弈策略。s1=1和s2=1表示两国均选择最低程度合作,分别只提出议题Ⅰ和议题Ⅳ;s1=2和s2=2表示两国均选择最高程度合作,国家1提出议题Ⅰ、Ⅱ和Ⅲ,国家2提出议题Ⅳ、Ⅴ和Ⅵ。用π1(s1, s2)和π2(s1, s2)分别表示国家1选择s1且国家2选择s2时,国家1和国家2的物质收益。两国在所有博弈策略组合下的物质收益分别为
| $ \pi_{1}(1, 1)=F_{11}+F_{14} $ | (3) |
| $ \pi_{2}(1, 1)=F_{21}+F_{24} $ | (4) |
| $ \pi_{1}(2, 1)=F_{11}+F_{12}+F_{13}+F_{14} $ | (5) |
| $ \pi_{2}(2, 1)=F_{21}+F_{22}+F_{23}+F_{24} $ | (6) |
| $ \pi_{1}(1, 2)=F_{11}+F_{14}+F_{15}+F_{16} $ | (7) |
| $ \pi_{2}(1, 2)=F_{21}+F_{24}+F_{25}+F_{26} $ | (8) |
| $ \pi_{1}(2, 2)=F_{11}+F_{12}+F_{13}+F_{14}+F_{15}+F_{16} $ | (9) |
| $ \pi_{2}(2, 2)=F_{21}+F_{22}+F_{23}+F_{24}+F_{25}+F_{26} $ | (10) |
若只考虑物质收益,即U1(s1, s2)=π1(s1, s2),U2(s1, s2)=π2(s1, s2),谈判双方的物质收益矩阵见表 2。
| 表 2 谈判双方的物质收益矩阵 Tab. 2 Material income matrix of two negotiators |
根据表 2可知,只要F12+F13≠0且F25+F26≠0,该博弈问题必存在子博弈完美均衡路径。具体存在以下两种情况:
1) 当F12+F13 > 0,F25+F26 > 0,有
| $ \pi_{1}(2, 2)-\pi_{1}(1, 2)>0 $ | (11) |
| $ \pi_{1}(2, 1)-\pi_{1}(1, 1)>0 $ | (12) |
| $ \pi_{2}(2, 2)-\pi_{2}(2, 1)>0 $ | (13) |
| $ \pi_{1}(1, 2)-\pi_{1}(1, 1)>0 $ | (14) |
此时,无论对方选择何种博弈策略,本方选择最高合作策略比选择最低合作策略,均能获得更大的物质收益,此序贯博弈的子博弈完美均衡路径为{最高程度合作,最高程度合作}。该情形下扩展议题的物质收益之和,符合扩展议题价值博弈场景1、2、3的特征,说明在这3个博弈场景中,谈判双方的最优博弈选择均为最高程度合作,即可以接纳提出来的所有议题并达成协议。
2) 当F12+F13 < 0,F25+F26 < 0时,无论对方选择何种博弈策略,本方选择最高合作策略比选择最低合作策略,均能获得更小的物质收益,此序贯博弈的子博弈完美均衡路径为{最低程度合作,最低程度合作}。该情形下扩展议题的物质收益之和,符合场景4、5、6的特征,说明在这3个场景中,谈判双方的最优博弈选择均为最低程度合作,只会接纳对方提出的基准议题并达成协议。
在实际谈判中,双方一般采取基于审慎的态度提出扩展议题,使得至少一方在己方扩展议题上的获益之和为正,主要对应场景4、5。此外,前续博弈只考虑了物质收益,尚未考虑心理收益。因此,本文在2.4节,把基于互惠心理效用带来的心理收益引入综合收益中,研究基于互惠关系和议题价值对等原则下场景4、5中双方的博弈行为。
2.4 考虑互惠心理收益的序贯互惠博弈模型根据假设,国家2先提出己方议题报价,国家1随后提出议题报价。在双方报价前,国家1需要分别在假设国家2提出最低程度合作和最高程度合作的基础上,选择己方的博弈策略。国家1这一策略选择过程[13-15],要平衡短期物质收益和互惠关系带来的长期心理收益,还要考虑国家2的选择,是本文要研究的序贯互惠博弈问题。
2.4.1 考虑互惠心理收益的国家1综合收益函数本文借鉴Dufwenberg的思想[5],用正数的互惠敏感系数和负数的互惠敏感系数分别描述两者在互惠关系下具有互惠动机,以及在无互惠关系下具有单方面施惠动机这两种状态。基于互惠动机和单方面施惠动机,对国家1构建考虑互惠心理收益的航权谈判综合收益函数:
| $ \begin{aligned} &U_{1}\left(s_{1}, s_{2}, c_{121}\right)= \\ &\pi_{1}\left(s_{1}, s_{2}\right)+Y_{12} \cdot K_{12}\left(s_{1}, s_{2}\right) \cdot \lambda_{121}\left(s_{2}, c_{121}\right) \end{aligned} $ | (15) |
式中:Y12·K12(s1, s2)·λ121(s2, c121)表示国家1此时的心理收益Q,Y12表示国家1对国家2的互惠敏感系数,K12(s1, s2)表示国家1对国家2的友善度,λ121(s2, c121)表示国家1认为国家2对国家1友善度的二级信念。
当Y12=0时,表示博弈双方不考虑互惠带来的收益,仍然只关注物质收益;当Y12 > 0时,表示双方已经构建稳定的互惠关系,在此次博弈中存在互惠动机,能从双方的行为组合中收获物质收益以外的互惠心理收益,Y12越大互惠动机越强。此时为了增加心理收益,国家1会倾向于采取与国家2一致的选择,具体表现为“投桃报李”的正互惠心理(双方都采取友善选择)和“以牙还牙”的负互惠心理(双方都采取不友善选择)。当Y12 < 0时,表示双方还不具备互惠动机,基于“以德报怨”或“以怨报德”的单方面施惠动机和物质收益进行选择,并从中获得声誉心理收益,引导双方关系的走向。这种基于单方面施惠动机的博弈,对应航权资源谈判中的某些情况,将在后续讨论。
K12(s1, s2)表示国家1采取s1获得的物质收益与国家1采取所有有效选项获得物质收益的平均值之差。此时,国家1有效选项的集合ES(s2),由国家2采取的s2来决定。在场景4和5中,由表 1和式(3)~(10)可知,π1(2, 2) > π1(2, 1)且π1(1, 2) > π1(1, 1)。此时,国家2选择最高程度合作就是友善行为,国家1的有效选项包括最高程度合作和最低程度合作;国家2选择最低程度合作就是不友善行为,国家1有效选项中只有代表不友善的最低程度合作。国家2的有效选项集合与国家1的有效选项集合相同。
λ121(s2, c121)表示国家1认为国家2对国家1友善度的二级信念,体现为国家2采取s2给国家1带来的期望物质收益,与国家2采取所有有效选项给国家1带来物质收益的平均值之差,即
| $ \begin{aligned} &\lambda_{121}\left(s_{2}, c_{121}\right)=\sum\nolimits_{s_{1}^{k_{1} }\in E S\left(s_{2}\right)} p\left(s_{1}^{k_{1}}\right) \cdot \pi_{1}\left(s_{1}^{k_{1}}, s_{2}\right)- \\ &\quad\frac{1}{K} \sum\nolimits_{1 \leqslant k_{2} \leqslant K} \sum\nolimits_{s_{1}^{k_{1} }\in E S\left(s_{2}{}^{k_{2}}\right)} p\left(s_{1}^{k_{1}}\right) \cdot \pi_{1}\left(s_{1}^{k_{1}}, s_{2}{}^{k_{2}}\right) \end{aligned} $ | (16) |
式中:p(s1k1)表示国家1采取策略s1k1的概率,K表示国家2所有有效选项的数量。后续令p为国家2采取最高程度合作时,国家1采取最高程度合作的概率。
2.4.2 扩展议题价值博弈场景4的序贯互惠均衡分析在场景4中,双方在对方任一选择下选择最高程度合作都比选择最低程度合作,获得的物质收益更小,但是采取最高程度合作是友善行为而采取最低程度合作是不友善行为,需要通过博弈综合权衡博弈选择,双方采取最高程度合作和最低程度合作的序贯互惠均衡分析如下:
1) 若国家2采取最高程度合作时,该选择是友善行为,国家1的有效选项可以是最高程度合作和最低程度合作。此时,国家1也要采取最高程度合作(即p=1),需满足:
| $ \left.U_{1}(2, 2)\right|_{p=1}>\left.U_{1}(1, 2)\right|_{p=1} $ | (17) |
即
| $ \begin{aligned} &Y_{12} \cdot\left(F_{22}+F_{23}\right) \cdot\left(F_{12}+F_{13}+F_{15}+F_{16}\right)> \\ &\quad-2 \cdot\left(F_{12}+F_{13}\right) \end{aligned} $ | (18) |
可得Y12的阈值y1是正数,且有
| $ Y_{12}>y_{1}=-\frac{F_{12}+F_{13}}{F_{22}+F_{23}} \cdot \frac{2}{F_{12}+F_{13}+F_{15}+F_{16}} $ | (19) |
结论1 在场景4中,国家1选择最高程度合作的序贯均衡为,当国家2选择最高程度合作时,若满足
结论1中,双方处在稳定的互惠关系中,(Y12 > 0),国家1通过国家2的友善行为获得了正向心理效用λ121(λ121 > 0),增强了互惠动机,同时通过自身的友善行为向国家2给予额外声誉收益K12(K12 > 0)。国家1最终赢得了额外的互惠心理收益,Y12·K12·λ121 > 0,加强了长期互惠共赢关系,弥补短期物质收益的损失,两者在“投桃报李”的正互惠状态。后续可以通过调整议题结构,降低互惠敏感系数的阈值,使得国家1能更容易进入该互惠博弈状态,引导互惠关系的持续发展。
2) 若国家2采取最高程度合作,国家1采取最低程度合作(即p=0),需满足:
| $ \left.U_{1}(1, 2)\right|_{p=0}>\left.U_{1}(2, 2)\right|_{p=0} $ | (20) |
可得Y12的阈值y2是正数,且有
| $ Y_{12}<y_{2}=-\frac{F_{12}+F_{13}}{F_{22}+F_{23}} \cdot \frac{2}{F_{15}+F_{16}} $ | (21) |
若国家2采取最低程度合作时,国家1的有效选项只有采取最低程度合作。
结论2 在场景4中,国家1选择最低程度合作的序贯均衡为:(a)当国家2选择最高程度合作时,若满足
结论2(a)中,当Y12 > 0时,双方具有长期互惠关系,国家1通过国家2的友善行为获得正向心理效用λ121(λ121 > 0),提高了互惠动机,但是国家1为了获得短期物质收益,选择不友善博弈行为,牺牲了互惠心理收益,Y12·K12·λ121 < 0,削弱了对方后续继续进行互惠交流的动机,损害了长期互惠关系;当Y12=0时,双方没有互惠关系,不存在互惠动机,国家1只关注物质收益;当Y12 < 0时,双方虽然没有互惠关系,但是国家1接受国家2的单方面施惠效用λ121(λ121 > 0),并对国家2采取不友善行为,从而获得额外的单方面心理收益和更高的物质收益,这是“以怨报德”的自私自利行为。结论2(b)中,互惠心理或者单方面施惠心理,都不能给双方带来心理收益,双方只关注物质收益,并基于议题的价值对等原则选择最低程度合作。
2.4.3 扩展议题价值博弈场景5的序贯互惠均衡分析在场景5中,双方面临在场景4中同样的权衡问题,双方采取最高程度合作和最低程度合作的序贯互惠均衡分析如下:
1) 若国家2采取最高程度合作时,国家1也要采取最高程度合作(即p=1),通过式(17)得知,Y12的阈值y3是负数,且有
| $ Y_{12}<y_{3}=-\frac{F_{12}+F_{13}}{F_{22}+F_{23}} \cdot \frac{2}{F_{12}+F_{13}+F_{15}+F_{16}} $ | (22) |
结论3 在扩展议题价值博弈场景5中,国家1选择最高程度合作的序贯均衡为,当国家2选择最高程度合作时,若满足
结论3中,双边没有互惠关系Y12 < 0,国家1认为对方不友善λ121(λ121 < 0),但在“以德报怨”心理下,国家1向对方单方面施惠,使对方获得额外的综合收益,同时己方也赢得了心理收益,弥补短期物质收益的损失。
2) 若国家2采取最高程度合作时,国家1采取最低程度合作(即p=0),通过式(12)得知,Y12的阈值y4=y2,该阈值是正数,且有
| $ Y_{12}<y_{4}=-\frac{F_{12}+F_{13}}{F_{22}+F_{23}} \cdot \frac{2}{F_{15}+F_{16}} $ | (23) |
结论4 在扩展议题价值博弈场景5中,国家1选择最低程度合作的序贯均衡为:(a)当国家2选择最高程度合作时,若满足
3) 根据式(22)和式(23)可知,结论3和结论4(a)对应的互惠敏感系数区间存在交集
| $ \lambda_{121}\left(2, c_{i j i}\right)=-\frac{F_{12}+F_{13}}{Y_{12} \cdot\left(F_{22}+F_{23}\right)} $ | (24) |
综合式(16)和式(24),令此时国家1在国家2采取最高程度合作时也采取最高程度合作的概率为p0,则
| $ p_{0}=-\frac{2 \cdot\left(F_{12}+F_{13}\right)+Y_{12} \cdot\left(F_{15}+F_{16}\right) \cdot\left(F_{22}+F_{23}\right)}{Y_{12} \cdot\left(F_{22}+F_{23}\right) \cdot\left(F_{12}+F_{13}\right)} $ | (25) |
结论5 在场景5中,国家1的序贯互惠混合均衡为,当国家2选择最高程度合作时,若
在国际航权双边谈判实践中,双方大多数情况下都是基于一定程度的战略谈判互惠关系,而且设置的议题往往源自国家外交战略导向和民航行业发展需要,使得议题对至少一方有利。这种情况,主要对应上述扩展议题价值博弈中场景4、5。因此,本节针对扩展议题价值博弈场景4、5,基于本文提出的航权资源谈判序贯互惠博弈模型,对两国的谈判博弈过程进行数值模拟,并通过与实际谈判结果的规律进行比较,验证模型的有效性。
3.1 场景4数值模拟结果及分析模拟场景为国家B向国家A号召发起某次航权资源谈判,双方具有互惠关系,谈判只对特定4条航线的新增航班数量进行博弈,每方提出3个议题,见表 3。两国在各议题上的物质收益系数见表 4和表 5。双方分别提出基准议题,议题一和议题四,此时双方都采用最低程度合作并实现了价值均等。在此基础上,国家B提出了两个扩展议题,议题五和议题六,而国家A只提出了一个扩展议题(议题二),希望航线1在议题一新增30个航班的基础上,再增加6个航班,并希望在航线2上提出议题三。此时,假设国家B采用了最高程度合作策略,国家A的互惠敏感系数Y > 0,显然,国家A可以采用最高程度合作和最低程度合作两种策略。基于上述情况,要研究国家A对议题三的新增航班数量、己方在议题三上对应的产业空间预留价值系数与机会成本空置耗损系数如何取值,以便能够使得己方的最优博弈选择为最大程度合作策略。
| 表 3 在场景4的模拟实验中国家A和国家B在谈判中提出的议题及其类型特征 Tab. 3 Issues raised by countries A and B and the typological characteristics of the issues in the simulation of scenario 4 |
| 表 4 在场景4的模拟实验中国家A在各议题上的物质收益系数 Tab. 4 Material income coefficients of issues corresponding to country A in the simulation of scenario 4 |
| 表 5 在场景4的模拟实验中国家B在各议题上的物质收益系数 Tab. 5 Material income coefficients of issues corresponding to country B in the simulation of scenario 4 |
基于本文提出的航权资源谈判序贯互惠博弈模型,对两国的博弈过程进行数值模拟,以展示国家A的互惠敏感系数Y、议题三的新增航班数量n13、机会成本空置耗损系数γ和产业空间预留价值系数β对国家A博弈选择的影响。为便于计算,以机会价值收益系数β-γ来代表γ和β。根据结论1和结论2(a)以及式(19)和式(21),当国家B选择最高程度合作时,若国家A的互惠敏感系数Y > y1,则国家A选择最高程度合作;若国家A的互惠敏感系数Y < y2,则国家A选择最低程度合作。在模拟实验中,议题三新增航班数量n13与机会价值收益系数β-γ取不同值时,国家A采用最高程度合作和最低程度合作的互惠敏感系数的阈值y2和y1,如图 5所示。以β-γ=-0.9,n13=17为例,此时国家A互惠敏感系数的阈值y1=4.2和y2=0.210 5,这意味着:若国家A互惠敏感系数Y > 4.2,则国家A将采取最高程度合作策略;若国家A互惠敏感系数Y < 0.210 5,则国家A将采取最低程度合作策略;若国家A互惠敏感系数0.210 5 < Y < 4.2,则国家A的策略不确定。
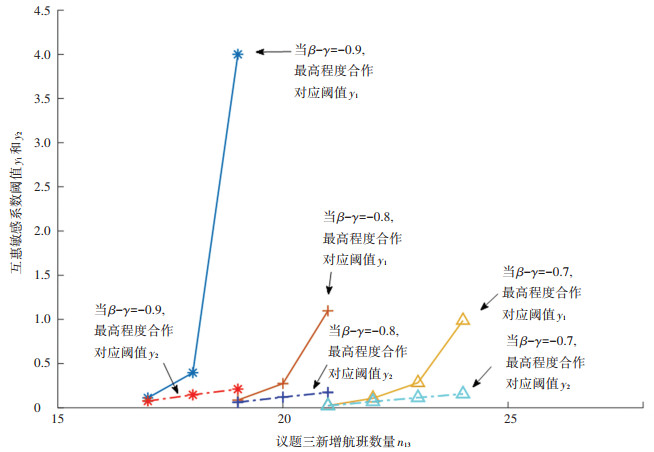
|
图 5 在场景4的模拟实验中议题三新增航班数量及机会价值收益系数对互惠敏感系数阈值的影响 Fig. 5 Influence of the number of flights addition of issue three and opportunity value revenue coefficient on the reciprocity sensitivity threshold in the simulation of scenario 4 |
令s=1表示国家A采取最低程度合作策略,s=2表示国家A将采取最高程度合作策略。在国家A的互惠敏感系数Y分别取0.02、0.11和4.2时,国家A将采取的博弈行为如图 6所示。由图 6可以看出,当双方具有较高的互惠程度(Y=4.2)时,在新增航班数量与机会价值收益系数的各组数值下,国家A在国家B选择最高程度合作的基础上都将采取最高程度合作策略。此时,双方处在“投桃报李”的正互惠状态,追求双方共赢。当双方具有很低的互惠程度(Y=0.02)时,在新增航班数量与机会价值收益系数的各组数值下,国家A在国家B选择最高程度合作的基础上都将采取最低程度合作策略。此时,国家A追求单方面获益,为了获得短期物质收益,牺牲长期互惠心理收益。当双方具有的较低互惠程度(Y=0.11)时,若议题三新增航班数量较小,国家A将采取最高程度合作策略,追求双方共赢;若议题三新增航班数量较大,国家A将采取最低程度合作策略,追求单方面获益。此外,从图中还可以看出,当双方的互惠程度都较高(Y=4.2)时,机会价值收益系数β-γ越大(从-0.9增加到-0.7),国家A提出议题三的新增航班数量可以越大(由17班增加到21班)。

|
图 6 在场景4的模拟实验中议题三新增航班数量、机会价值收益系数和互惠敏感系数对国家A博弈行为的影响 Fig. 6 Influence of the number of flights addition of issue three, opportunity value revenue coefficient, and reciprocity sensitivity on the game behavior strategy of country A in the simulation of scenario 4 |
场景5的数值模拟,与场景4的数值模拟类似。同样是假设国家B发起谈判,双方具有互惠关系,每方提出3个议题,对特定4条航线的新增航班数量进行谈判。而且,双方在基准议题(议题一和议题四)上实现了价值均等,国家B又提出了两个扩展议题(议题五和六),而国家A只提出了一个扩展议题(议题二),希望航线1在议题一新增30个航班的基础上,再增加6个航班,并希望在航线2上提出议题三。结合扩展议题价值博弈场景5中的议题物质收益特征,假设在场景5的数值模拟中,国家A提议的议题及其在所有议题上的物质收益系数,与在场景4的数值模拟中相同,见表 6和表 4;与场景4的数值模拟不同,在场景5的数值模拟中,国家B提议的议题及其在所有议题上的物质收益系数,见表 6和表 7。假设国家B采用了最高程度合作策略,国家A的互惠敏感系数Y > 0,国家A可以采用最高程度合作和最低程度合作两种策略。数值模拟该场景下的博弈行为,以展示国家A的互惠敏感系数Y、议题三的新增航班数量n13、机会成本空置耗损系数γ和产业空间预留价值系数β对国家A博弈选择的影响。
| 表 6 在场景5的模拟实验中国家A和国家B在谈判中提出的议题及其类型特征 Tab. 6 Issues raised by countries A and B and the typological characteristics of the issues in the simulation of scenario 5 |
| 表 7 在场景5的模拟实验中国家B在各议题上的物质收益系数 Tab. 7 Material income coefficients of issues corresponding to country B in the simulation of scenario 5 |
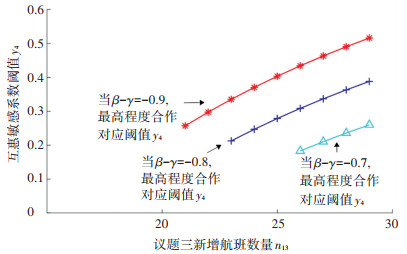
根据结论4(a)以及式(23),当国家B选择最高程度合作时,若国家A的互惠敏感系数0 < Y < y4,则国家A选择最低程度合作。在模拟实验中,议题三新增航班数量n13与机会价值收益系数β-γ取不同值时,国家A采用最低程度合作的互惠敏感系数的阈值y4,如图 7所示。以β-γ=-0.9,n13=21为例,此时国家A互惠敏感系数的阈值y4=0.257 2,这意味着,若国家A互惠敏感系数Y < 0.257 2,则国家A将采取最低程度合作策略;若国家A互惠敏感系数Y > 0.257 2,则国家A的策略不确定。
|
图 7 在场景5的模拟实验中议题三新增航班数量及机会价值收益系数对互惠敏感系数阈值的影响 Fig. 7 Influence of the number of flights addition of issue three and opportunity value revenue coefficient on the reciprocity sensitivity threshold in the simulation of scenario 5 |
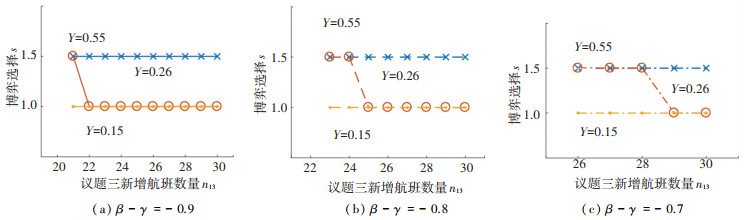
令s=1示国家A采取最低程度合作策略,s=1.5表示国家A的策略不确定。在国家A的互惠敏感系数Y分别取0.15、0.26和0.55时,国家A将采取的博弈行为如图 8所示。
|
图 8 在场景5的模拟实验中议题三新增航班数量、机会价值收益系数和互惠敏感系数对国家A博弈行为的影响 Fig. 8 Influence of the number of flights addition of issue three, opportunity value revenue coefficient, and reciprocity sensitivity on the game beahavior strategy of country A in the simulation of scenario 5 |
由图 8可以看出,当双方具有很低的互惠程度(Y=0.15)时,在新增航班数量与机会价值收益系数的各组数值下,国家A在国家B选择最高程度合作的基础上都将采取最低程度合作策略。此时,国家A能获得的短期物质收益,远大于长期互惠心理收益,在全部收益中所占比例很高,使得国家A会牺牲双方的互惠动机,追求己方单方面物质收益最大化,表现出自私自利的行为。当双方具有很高的互惠程度(Y=0.55)时,在新增航班数量与机会价值收益系数的各组数值下,若B选择最高程度合作策略,国家A不再仅限于采取最低程度合作策略,还可能选择最高程度合作策略。此时,国家A能获得的长期互惠心理收益已经具有较大规模,在全部收益中所占比例较为显著,能够在一定程度上弥补物质收益的损失,使得国家A不再表现出完全的自私自利的行为,会考虑维护双方的互惠关系,可能选择最高程度合作策略,来增强双方的互惠动机。当双方具有的较高互惠程度(Y=0.26)时,若议题三新增航班数量较小,国家A不再仅限于采取最低程度合作策略,还可能选择最高程度合作策略,追求短期物质收益和长期互惠心理收益,会考虑维护双方的互惠关系;若议题三新增航班数量较大,国家A将采取最低程度合作策略,追求己方单方面物质收益最大化。此外,从图中还可以看出,当双方的互惠程度都较高(Y=0.26)时,机会价值收益系数β-γ越大(从-0.9增加到-0.7),国家A采取最低程度合作策略对应的议题三新增航班的最小数量越大(由22班增加到29班)。
3.3 数值模拟结果总结场景4和场景5模拟实验中的博弈结论与国际航权谈判的规律基本相符。以2017年中国—法国航权谈判和2016年中国—英国航权谈判为例,双方均与中国在战略谈判关系方面建立了互惠关系,中方与英方之间的互惠关系强于中方与法方的关系。谈判结果显示,法方整体更为审慎保守,英方更积极开放,在中方提出的议题对应其远期需求时,法方只能接受范围和资源规模相对较小的议题(较高程度合作),而英方能接受议题的范围和资源规模更大(最高程度合作),中英最终在客运航权资源方面开放规模更大,并且在航空货运领域实现了航权自由化,给予双方航空公司更为灵活的市场准入。数值模拟结论与实际规律一致,验证了本文航权资源谈判序贯互惠博弈模型的有效性。
4 结论1) 创造性提出了航权资源双边谈判的序贯博弈问题,考虑议题在谈判方议价能力、关联产业补偿、产业空间预留价值和资源空置价值耗损等4个维度的价值,构建了适用不同议题的物质收益函数,提出了基于互惠心理收益的序贯互惠博弈模型,可为民航主管部门实施国际航权资源谈判提供支撑。
2) 提出了序贯博弈问题对应的6个议题价值博弈场景,根据序贯互惠博弈模型,研究得到不同议题价值博弈场景下应采取不同博弈行为的序贯互惠均衡条件,其核心影响因素是扩展议题的价值范围、先报价方的博弈行为以及互惠敏感系数。
3) 在谈判双方具有互惠关系的情况下,互惠敏感系数Y、议题航权资源规模、机会成本空置耗损系数γ和产业空间预留价值系数β,共同决定了谈判方的博弈行为策略。随着Y和β-γ的增加,双方都采取最高限度合作策略的概率越大,能够接纳的议题具备的航权资源数量越多。
| [1] |
刘德海, 周婷婷, 王维国. 反恐国际合作双重标准问题的序贯互惠博弈模型[J]. 中国管理科学, 2015, 23(增刊1): 301. LIU Dehai, ZHOU Tingting, WANG Weiguo. Sequential reciprocal game model of double standard in international anti-terrorism cooperation[J]. Chinese Journal of Management Science, 2015, 23(S1): 301. |
| [2] |
郭扬, 李金叶. 基于心理博弈的中国与中亚非资源型产业多维合作体系研究[J]. 经济问题探索, 2018(9): 131. GUO Yang, LI Jinye. Research on the multi-dimensional cooperation system of non-resource industries between China and Central Asian countries based on psychological game theory[J]. Inquiry into Economic Issues, 2018(9): 131. |
| [3] |
RENIERS G, SOUDAN K. A game-theoretical approach for reciprocal security-related prevention investment decision[J]. Reliability Engineering and System Safety, 2010, 95(1): 1. DOI:10.1016/j.ress.2009.07.001 |
| [4] |
RABIN M. Incorporating fairness into game theory and economics[J]. The American Economic Review, 1993, 83(5): 1281. |
| [5] |
DUFWENBERG M, KIRCHSTEIGER U. A theory of sequential reciprocity[J]. Games and Economic Behavior, 2004, 47(2): 2668. |
| [6] |
冯琳, 刘龙方, 李杨. 公平互惠导向下"海丝"港口合作方式的博弈选择[J]. 工业工程与管理, 2021, 26(2): 135. FENG Lin, LIU Longfang, LI Yang. Game theory selection study on port cooperation method under fair and mutual benefit concept along the maritime silk road[J]. Industrial Engineering and Management, 2021, 26(2): 135. DOI:10.19495/j.cnki.1007-5429.2021.02.017 |
| [7] |
薛小龙, 韩喜双, 王要武. 工程项目谈判行为的动态演化分析[J]. 哈尔滨工业大学学报, 2010, 42(11): 1775. XUE Xiaolong, HAN Xishuang, WANG Yaowu. Dynamic evolution of negotiation behaviors in construction projects[J]. Journal of Harbin Institute of Technology, 2010, 42(11): 1775. |
| [8] |
秦婷, 刘怀东, 王锦桥, 等. 基于讨价还价博弈理论的分布式能源合作收益分配模型[J]. 电力自动化设备, 2019, 39(1): 134. QIN Ting, LIU Huaidong, WANG Jinqiao, et al. Profit allocation model of cooperative distributed energy resources based on bargaining game theory[J]. Electric Power Automation Equipment, 2019, 39(1): 134. DOI:10.16081/j.issn.1006-6047.2019.01.020 |
| [9] |
刘佳, 王先甲. 物品价值变化下多人动态讨价还价的策略博弈均衡与参与者拖延行为[J]. 系统工程理论与实践, 2021, 41(5): 1282. LIU Jia, WANG Xianjia. Delay and the equilibria in multiplayer dynamic bargaining game under the value of negotiation resources changes[J]. Systems Engineering Theory & Practice, 2021, 41(5): 1282. |
| [10] |
杨文珂, 张广欣, 何建敏. 跨国绿色创新国际合作中机会主义行为治理机制研究[J]. 中国管理科学, 2021, 29(4): 213. YANG Wenke, ZHANG Guangxin, HE Jianmin. Research on governance mechanism of opportunistic behavior in international cooperation on green innovation[J]. Chinese Journal of Management Science, 2021, 29(4): 213. DOI:10.16381/j.cnki.issn1003-207x.2019.0862 |
| [11] |
王小胜, 胡豪, 刘欣欣, 等. 基于讨价还价模型的分享型合同节水管理利益分配[J]. 系统工程理论与实践, 2020, 40(9): 2418. WANG Xiaosheng, HU Hao, LIU Xinxin, et al. Profit allocation of benefit-sharing water saving management contract based on bargaining model[J]. Systems Engineering Theory & Practice, 2020, 40(9): 2418. |
| [12] |
SHANG T, ZHANG K, LIU P, et al. What to allocate and how to allocate? —Benefit allocation in Shared Savings Energy Performance Contracting Projects[J]. Energy, 2015, 91: 60. DOI:10.1016/j.energy.2015.08.020 |
| [13] |
BRITZ V, HERINGS J, PREDTETCHINSKI A. Non-cooperative support for the asymmetric Nash bargaining solution[J]. Journal of Economic Theory, 2010, 145(5): 1951. DOI:10.1016/j.jet.2010.04.003 |
| [14] |
CHATURVEDI R. Efficient coalitional bargaining with noncontingent offers[J]. Games and Economic Behavior, 2016, 100: 125. DOI:10.1016/j.geb.2016.08.012 |
| [15] |
MAO L. Optimal recommendation in two-player bargaining games[J]. Mathematical Social Sciences, 2020, 107: 41. DOI:10.1016/j.mathsocsci.2020.06.005 |
 2022, Vol. 54
2022, Vol. 54


