目前多站无源定位技术已广泛应用于各种军民领域[1-3],如传感器网络[4]、雷达[5]、导航[6]等。多站无源定位技术可以利用的观测量主要包括到达角(angle of arrival,AOA)、到达时间差(time difference of arrival,TDOA)、到达频率差(frequency difference of arrival,FDOA)等。而联合不同测量参数的定位体制可以融合不同参数的优势,在一定程度上提高定位精度。本文基于TDOA和FDOA的联合定位问题进行研究。
文献[7]基于TDOA/FDOA的定位问题进行了研究,并提出了经典的两步加权最小二乘法(two-stage weighted least squares,TSWLS),在噪声较低的情况下,该算法可以达到克拉美罗下限(Cramer-Rao lower bound,CRLB)。文献[8]将基于TDOA/FDOA的定位问题转换为约束加权最小二乘(constrained weighted least squares, CWLS)问题并利用拉格朗日乘子技术和牛顿法进行求解。文献[9-10]指出基于WLS的定位模型并未考虑到观测矩阵和数据向量中的噪声有着相关性和不同的方差,因此将约束总体最小二乘(constrained total least squares, CTLS)的思想应用于TDOA/FDOA定位问题中,其定位效果要优于文献[7-8]中基于WLS模型的定位方法。
但由于噪声的干扰、接收站和目标位置的分布以及接收站个数对系数矩阵的影响,以上这些基于WLS、TLS模型的方法中的系数矩阵在实际应用中可能会出现病态的问题。而且文献[11]从数值分析的角度指出,CTLS方法的求解过程实际上是一个降正则化的过程,会使得系数矩阵出现更为严重的病态。而正则化方法是解决此类病态问题的有效方法[12]。文献[13]在CTLS模型的基础上提出了一种正则化约束总体最小二乘方法(regularized constrained total least squares,RCTLS),并将该方法用于处理图像恢复中的病态问题。文献[14]对RCTLS算法进行了扰动分析,从理论上证明RCTLS算法通过合理地选取正则化参数可以降低CTLS算法的均方根误差。文献[15]将RCTLS的思想应用于基于DOA和TDOA的单站无源定位中,并且证明了RCTLS方法的定位精度和鲁棒性要优于CTLS方法,但文献[15]中提出的这种基于RCTLS思想的方法是一种迭代法,而且也无需考虑目标函数的约束条件。
针对TDOA/FDOA无源定位问题中的系数矩阵病态问题,本文基于RCTLS的思想提出了两步正则化约束最小二乘方法(two-stage regularized constrained total least squares,TRCTLS),这种方法在CTLS模型的基础上引入了正则化参数,通过合理地选取正则化参数来提高定位的均方根误差并抑制系数矩阵的病态性,而且不同于文献[9-10]中的迭代类方法,TRCTLS方法是一种闭式的解析法。仿真实验结果表明所提方法通过合理选择正则化参数可以在CTLS方法的基础上进一步降低算法的均方根误差,同时在系数矩阵出现病态时的定位性能也更加稳定。
1 定位模型假设在三维空间中利用M个接收站对移动的目标辐射源进行定位,目标辐射源的位置和速度分别为uo=[x, y, z]T、
| $ r_{i}^{\rm o}=\left\|\boldsymbol{u}^{\rm o}-\boldsymbol{s}_{i}\right\|=\sqrt{\left(\boldsymbol{u}^{\rm o}-\boldsymbol{s}_{i}\right)^{\mathrm{T}}\left(\boldsymbol{u}^{\rm o}-\boldsymbol{s}_{i}\right)} $ | (1) |
选取其中任意一个接收站为主站,编号为1,其余为辅站,则主站与各辅站之间的真实距离差为
| $ r_{i 1}^{\rm o}=r_{i}^{\rm o}-r_{1}^{\rm o} $ | (2) |
式中:ri1o由真实的TDOA数据计算得到,其向量形式可记为ro=[r21o, r31o, …, rM1o]T,联合式(1)和式(2)可得基于TDOA的定位方程:
| $ r_{i 1}^{\mathrm{o} 2}+2 r_{i 1}^{\mathrm{o}} r_{1}^{\mathrm{o}}=\boldsymbol{s}_{i}^{\mathrm{T}} \boldsymbol{s}_{i}-\boldsymbol{s}_{1}^{\mathrm{T}} \boldsymbol{s}_{1}-2\left(\boldsymbol{s}_{i}-\boldsymbol{s}_{1}\right)^{\mathrm{T}} \boldsymbol{u}^{\mathrm{o}} $ | (3) |
对式(1)进行求导可得接收站与目标辐射源之间真实距离变化率的定义式:
| $ \dot{r}_{i}^{\mathrm{o}}=\frac{\left(\dot{\boldsymbol{u}}^{\mathrm{o}}-\dot{\boldsymbol{s}}_{1}\right)^{\mathrm{T}}\left(\boldsymbol{u}^{\mathrm{o}}-\boldsymbol{s}_{i}\right)}{r_{i}^{\mathrm{o}}} $ | (4) |
对式(3)进行求时间导数可得基于FDOA的定位方程:
| $ \begin{gathered} 2\left(\dot{r}_{i 1}^{\mathrm{o}} r_{i 1}^{\mathrm{o}}+\dot{r}_{i 1}^{\mathrm{o}} r_{1}^{\mathrm{o}}+r_{i 1}^{\mathrm{o}} \dot{r}_{1}^{\mathrm{o}}\right)=2\left(\dot{\boldsymbol{s}}_{i}^{\mathrm{T}} \boldsymbol{s}_{i}-\dot{\boldsymbol{s}}_{1}^{\mathrm{T}} \boldsymbol{s}_{1}\right)- \\ \left(\dot{\boldsymbol{s}}_{i}-\dot{\boldsymbol{s}}_{1}\right)^{\mathrm{T}} \boldsymbol{u}^{\mathrm{o}}-\left(\boldsymbol{s}_{i}-\boldsymbol{s}_{1}\right)^{\mathrm{T}} \dot{\boldsymbol{u}}^{\mathrm{o}} \end{gathered} $ | (5) |
式中
| $ \begin{gathered} \boldsymbol{r}=\boldsymbol{r}^{\mathrm{o}}+\Delta \boldsymbol{r}=\boldsymbol{r}^{\mathrm{o}}+c \Delta \boldsymbol{t} \\ \dot{\boldsymbol{r}}=\dot{\boldsymbol{r}}^{\mathrm{o}}+\Delta \dot{\boldsymbol{r}}=\dot{\boldsymbol{r}}^{\mathrm{o}}+c \Delta \dot{\boldsymbol{t}} \end{gathered} $ | (6) |
式中:TDOA测量数据和FDOA测量数据中所包含的测量噪声分别为Δr=[Δr21, Δr31, …, ΔrM1]T以及
| $ E\left(\left[\Delta \boldsymbol{r}^{\mathrm{T}}, \Delta \dot{\boldsymbol{r}}^{\mathrm{T}}\right]^{\mathrm{T}}\left[\Delta \boldsymbol{r}^{\mathrm{T}}, \Delta \dot{\boldsymbol{r}}^{\mathrm{T}}\right]\right)=\boldsymbol{Q}^{2} $ | (7) |
将包含噪声的TDOA测量值r=ro+Δr和FDOA测量值
| $ \boldsymbol{\varepsilon}_{\mathrm{t}}=r_{i 1}^{2}+\boldsymbol{s}_{1}^{\mathrm{T}} \boldsymbol{s}_{1}-s_{i}^{\mathrm{T}} s_{i}+2 r_{i 1} r_{1}^{\mathrm{o}}+2\left(\boldsymbol{s}_{i}-\boldsymbol{s}_{1}\right)^{\mathrm{T}} \boldsymbol{u}^{\mathrm{o}} $ | (8) |
| $ \begin{gathered} \boldsymbol{\varepsilon}_{\mathrm{f}}=2\left(\dot{r}_{i 1} r_{i 1}+\dot{\boldsymbol{s}}_{1}^{\mathrm{T}} \boldsymbol{s}_{1}-\dot{\boldsymbol{s}}_{i}^{\mathrm{T}} \boldsymbol{s}_{i}\right)+2 \dot{r}_{i 1} r_{1}^{\mathrm{o}}+2 r_{i 1} \dot{r}_{1}^{\mathrm{o}}+ \\ 2\left(\dot{\boldsymbol{s}}_{i}-\dot{\boldsymbol{s}}_{1}\right)^{\mathrm{T}} \boldsymbol{u}^{\mathrm{o}}+2\left(\boldsymbol{s}_{i}-\boldsymbol{s}_{1}\right)^{\mathrm{T}} \dot{\boldsymbol{u}}^{\mathrm{o}} \end{gathered} $ | (9) |
式中:εt=BΔr,为TDOA方程的误差项;
构造辅助变量
| $ (\boldsymbol{A}+\Delta \boldsymbol{A}) \boldsymbol{\theta}_{1}=\boldsymbol{b}+\Delta \boldsymbol{b} $ | (10) |
其中:
| $ \begin{array}{l} \boldsymbol{A}=-2\left[\begin{array}{cccc} \left(\boldsymbol{s}_{2}-\boldsymbol{s}_{1}\right)^{\mathrm{T}} & \mathit{\pmb{0}}^{\mathrm{T}} & r_{21} & 0 \\ \vdots & \vdots & \vdots & \vdots \\ \left(\boldsymbol{s}_{M}-\boldsymbol{s}_{1}\right)^{\mathrm{T}} & \mathit{\pmb{0}}^{\mathrm{T}} & r_{M 1} & 0 \\ \left(\dot{\boldsymbol{s}}_{2}-\dot{\boldsymbol{s}}_{1}\right)^{\mathrm{T}} & \left(\boldsymbol{s}_{2}-\boldsymbol{s}_{1}\right)^{\mathrm{T}} & \dot{r}_{21} & r_{21} \\ \vdots & \vdots & \vdots & \vdots \\ \left(\dot{\boldsymbol{s}}_{M}-\dot{\boldsymbol{s}}_{1}\right)^{\mathrm{T}} & \left(\boldsymbol{s}_{M}-\boldsymbol{s}_{1}\right)^{\mathrm{T}} & \dot{r}_{M 1} & r_{M 1} \end{array}\right]\\ \boldsymbol{b}=\left[\begin{array}{c} r_{21}^{2}-\boldsymbol{s}_{2}^{\mathrm{T}} \boldsymbol{s}_{2}+\boldsymbol{s}_{1}^{\mathrm{T}} \boldsymbol{s}_{1} \\ \vdots \\ r_{M 1}^{2}-\boldsymbol{s}_{M}^{\mathrm{T}} \boldsymbol{s}_{M}+\boldsymbol{s}_{1}^{\mathrm{T}} \boldsymbol{s}_{1} \\ 2\left(\dot{r}_{21} r_{21}-\dot{\boldsymbol{s}}_{2}^{\mathrm{T}} \boldsymbol{s}_{2}+\dot{\boldsymbol{s}}_{1}^{\mathrm{T}} \boldsymbol{s}_{1}\right) \\ \vdots \\ 2\left(\dot{r}_{M 1} r_{M 1}-\dot{\boldsymbol{s}}_{M}^{\mathrm{T}} \boldsymbol{s}_{M}+\dot{\boldsymbol{s}}_{1}^{\mathrm{T}} \boldsymbol{s}_{1}\right) \end{array}\right]\\ \Delta \boldsymbol{A}=-2\left[\begin{array}{lcc} \boldsymbol{O}_{(M-1) \times 2 N} & \Delta \boldsymbol{r} & \mathit{\pmb{0}}_{M-1}^{\mathrm{T}} \\ \boldsymbol{O}_{(M-1) \times 2 N} & \Delta \dot{\boldsymbol{r}} & \Delta \boldsymbol{r} \end{array}\right]\\ \Delta \boldsymbol{b}=2\left[\begin{array}{c} \boldsymbol{r} \odot \Delta \boldsymbol{r} \\ \dot{\boldsymbol{r}} \odot \Delta \boldsymbol{r}+\boldsymbol{r} \odot \Delta \dot{\boldsymbol{r}} \end{array}\right] \end{array} $ | (11) |
式中:O(M-1)×2N为(M-1)×2N的零矩阵,0为3×1的零向量。从式中可以看出,接收站和目标位置的不合理分布、噪声的干扰均可能会导致矩阵A出现病态,比如当接收站的坐标在x轴上比较接近时,那么此时矩阵A的条件数会明显增加,矩阵将出现病态,从而导致定位结果对噪声的敏感性增加。而引入正则化参数是一种有效抑制矩阵病态问题的手段。令噪声矩阵
| $ \begin{gathered} \Delta \boldsymbol{A}=\left[\boldsymbol{F}_{1} \boldsymbol{n}, \boldsymbol{F}_{2} \boldsymbol{n}, \cdots, \boldsymbol{F}_{l} \boldsymbol{n}\right] \\ \Delta \boldsymbol{b}=\boldsymbol{F}_{l+1} \boldsymbol{n} \end{gathered} $ | (12) |
式中l为矩阵ΔA的列数, l=1, 2, …, 8;F1到F9的值可以表示为
| $ \begin{aligned} &\boldsymbol{F}_{i}=\boldsymbol{O}_{2(M-1) \times 2(M-1)}, i=1,2, \cdots, 6 \\ &\boldsymbol{F}_{7}=-2 \times \boldsymbol{I}_{2(M-1) \times 2(M-1)}\\ &\boldsymbol{F}_{8}=-2\left[\begin{array}{ll} \boldsymbol{O}_{(M-1) \times(M-1)} & \boldsymbol{O}_{(M-1) \times(M-1)} \\ \boldsymbol{I}_{(M-1) \times(M-1)} & \boldsymbol{O}_{(M-1) \times(M-1)} \end{array}\right]\\ &\boldsymbol{F}_{9}=2\left[\begin{array}{cc} \sum\nolimits_{11} & \boldsymbol{O}_{(M-1) \times(M-1)} \\ \sum\nolimits_{21} & \sum\nolimits_{22} \end{array}\right] \end{aligned} $ | (13) |
式中:
考虑到n中各项误差具有相关性且有着不同的方差,对其进行白化处理。令Q=E[nnT],对Q做Cholesky分解可得Q=PPT,则n的白化向量为σ=P-1n,同时可得到ΔA=[G1σ, G2σ, …, Glσ]、Δb=Fl+1n,其中Gi=FiP,对式(10)进行数学变换可得:
| $ \boldsymbol{A} \boldsymbol{\theta}_{1}-\boldsymbol{b}=\boldsymbol{W}_{\theta_{1}} \boldsymbol{\sigma} $ | (14) |
式中
| $ \begin{gathered} \min \left(\|\boldsymbol{\sigma}\|^{2}+\lambda_{1}\left\|\boldsymbol{\theta}_{1}\right\|^{2}\right) \\ \text { s.t. } \boldsymbol{A} \boldsymbol{\theta}_{1}-\boldsymbol{b}=\boldsymbol{W}_{\theta_{1}} \boldsymbol{\sigma} \end{gathered} $ | (15) |
经过简单的数学运算,式(15)可转换为如下函数的求极小值问题:
| $ \begin{gathered} \boldsymbol{F}\left(\boldsymbol{\theta}_{1}\right)=\left(\boldsymbol{A} \boldsymbol{\theta}_{1}-\boldsymbol{b}\right)^{\mathrm{T}}\left(\boldsymbol{W}_{\theta_{1}} \boldsymbol{W}_{\theta_{1}}^{\mathrm{T}}\right)^{-1}\left(\boldsymbol{A} \boldsymbol{\theta}_{1}-\boldsymbol{b}\right)+ \\ \lambda_{1} \boldsymbol{\theta}_{1}^{\mathrm{T}} \boldsymbol{\theta}_{1} \end{gathered} $ | (16) |
对上式进行求导可得:
| $ (\boldsymbol{A}-\boldsymbol{\varLambda})^{\mathrm{T}}\left(\boldsymbol{W}_{\theta_{1}} \boldsymbol{W}_{\theta_{1}}{ }^{\mathrm{T}}\right)^{-1}\left(\boldsymbol{A} \boldsymbol{\theta}_{1}-\boldsymbol{b}\right)+\lambda_{1} \boldsymbol{\theta}_{1}=0 $ | (17) |
式中:
| $ \boldsymbol{\varLambda}=-\left[\boldsymbol{G}_{1} \boldsymbol{W}_{\theta_{1}}^{-1}\left(\boldsymbol{A} \boldsymbol{\theta}_{1}-\boldsymbol{b}\right), \cdots, \boldsymbol{G}_{l} \boldsymbol{W}_{\theta_{1}}^{-1}\left(\boldsymbol{A} \boldsymbol{\theta}_{1}-\boldsymbol{b}\right)\right] $ | (18) |
对式(18)进行求解, 可得方程的RCTLS解:
| $ \begin{gathered} \left.\widehat{\boldsymbol{\theta}}_{1}=((\boldsymbol{A}-\boldsymbol{\varLambda})^{\mathrm{T}}\left(\boldsymbol{W}_{\theta_{1}} \boldsymbol{W}_{\theta_{1}}^{\mathrm{T}}\right)^{-1} \boldsymbol{A}+\lambda_{1} \boldsymbol{I}\right)^{-1} \\ (\boldsymbol{A}-\boldsymbol{\varLambda})^{\mathrm{T}}\left(\boldsymbol{W}_{\theta_{1}} \boldsymbol{W}_{\theta_{1}}^{\mathrm{T}}\right)^{-1} \boldsymbol{b} \end{gathered} $ | (19) |
式(19)中所得的解并未考虑约束条件,因此TRCTLS算法的第二步是利用约束条件重新构造一组方程以完成对第一步估计值的修正。假设从第一步得到的目标估计位置和速度分别为u1和
| $ \begin{gathered} r_{1}^{\mathrm{o}} \approx\left\|\boldsymbol{u}_{1}-\boldsymbol{s}_{1}\right\|^{2}-\boldsymbol{\alpha}^{\mathrm{T}} \Delta \boldsymbol{u} \\ \dot{r}_{1}^{\mathrm{o}} \approx\left(\dot{\boldsymbol{u}}_{1}-\dot{\boldsymbol{s}}_{1}\right)^{\mathrm{T}}\left(\boldsymbol{u}_{1}-\boldsymbol{s}_{1}\right) /\left\|\boldsymbol{u}_{1}-\boldsymbol{s}_{1}\right\|^{2}- \\ \boldsymbol{\alpha}^{\mathrm{T}} \Delta \dot{\boldsymbol{u}}-\boldsymbol{\beta}^{\mathrm{T}} \Delta \boldsymbol{u} \end{gathered} $ | (20) |
假设第一步得到的辅助变量估计值为r1和
| $ \begin{gathered} \boldsymbol{\alpha}=\left(\boldsymbol{u}_{1}-\boldsymbol{s}_{1}\right) / r_{1} \\ \boldsymbol{\beta}=\left[r_{1}\left(\dot{\boldsymbol{u}}_{1}-\dot{\boldsymbol{s}}_{1}\right)-\dot{r}_{1}\left(\boldsymbol{u}_{1}-\boldsymbol{s}_{1}\right)\right] / r_{1}^{2} \end{gathered} $ | (21) |
将Δu=u1-uo、
| $ (\mathit{\boldsymbol{M}} + \Delta \mathit{\boldsymbol{M}}){\mathit{\boldsymbol{\theta }}_2} = \mathit{\boldsymbol{N}} + \Delta \mathit{\boldsymbol{N}} $ | (22) |
其中:
| $ \begin{array}{l} \boldsymbol{M}=2\left[\begin{array}{cc} \left(\boldsymbol{s}_{2}-\boldsymbol{s}_{1}+r_{21} \boldsymbol{\alpha}\right)^{\mathrm{T}} & \mathit{\pmb{0}}^{\mathrm{T}} \\ \vdots & \vdots \\ \left(\boldsymbol{s}_{M}-\boldsymbol{s}_{1}+r_{M 1} \boldsymbol{\alpha}\right)^{\mathrm{T}} & \mathit{\pmb{0}}^{\mathrm{T}} \\ \left(\dot{\boldsymbol{s}}_{2}-\dot{\boldsymbol{s}}_{1}+\dot{r}_{21} \boldsymbol{\alpha}+r_{21} \boldsymbol{\beta}\right)^{\mathrm{T}} & \left(\boldsymbol{s}_{2}-\boldsymbol{s}_{1}+r_{21} \boldsymbol{\alpha}\right)^{\mathrm{T}} \\ \vdots & \vdots \\ \left(\dot{\boldsymbol{s}}_{M}-\dot{\boldsymbol{s}}_{1}+\dot{r}_{M 1} \boldsymbol{\alpha}+r_{M 1} \boldsymbol{\beta}\right)^{\mathrm{T}} & \left(\boldsymbol{s}_{M}-\boldsymbol{s}_{1}+r_{M 1} \boldsymbol{\alpha}\right)^{\mathrm{T}} \end{array}\right]\\ \boldsymbol{N}=\left[\begin{array}{c} r_{21}^{2}-\boldsymbol{s}_{2}^{\mathrm{T}} \boldsymbol{s}_{2}+\boldsymbol{s}_{1}^{\mathrm{T}} \boldsymbol{s}_{1}+2 r_{21} r_{1}+ \\ 2\left(\boldsymbol{s}_{2}-\boldsymbol{s}_{1}\right)^{\mathrm{T}} \boldsymbol{u}_{1} \\ \vdots \\ r_{M 1}^{2}-\boldsymbol{s}_{M}^{\mathrm{T}} \boldsymbol{s}_{M}+\boldsymbol{s}_{1}^{\mathrm{T}} \boldsymbol{s}_{1}+2 r_{M 1} r_{1}+ \\ 2\left(\boldsymbol{s}_{M}-\boldsymbol{s}_{1}\right)^{\mathrm{T}} \boldsymbol{u}_{1} \\ 2\left(\dot{r}_{21} r_{21}-\dot{\boldsymbol{s}}_{2}^{\mathrm{T}} \boldsymbol{s}_{2}+\dot{s}_{1}^{\mathrm{T}} \boldsymbol{s}_{1}\right)+2\left(\dot{\boldsymbol{s}}_{2}-\dot{\boldsymbol{s}}_{1}\right)^{\mathrm{T}} \boldsymbol{u}_{1}+ \\ 2\left(\boldsymbol{s}_{2}-\boldsymbol{s}_{1}\right)^{\mathrm{T}} \dot{\boldsymbol{u}}_{1}+2 \dot{r}_{21} r_{1}+2 r_{21} \dot{r}_{1} \\ \vdots \\ 2\left(\dot{r}_{M 1} r_{21}-\dot{\boldsymbol{s}}_{M}^{\mathrm{T}} \boldsymbol{s}_{M}+\dot{\boldsymbol{s}}_{1}^{\mathrm{T}} \boldsymbol{s}_{1}\right)+2\left(\dot{\boldsymbol{s}}_{M}-\dot{\boldsymbol{s}}_{1}\right)^{\mathrm{T}} \boldsymbol{u}_{1}+ \\ 2\left(\boldsymbol{s}_{M}-\boldsymbol{s}_{1}\right)^{\mathrm{T}} \dot{\boldsymbol{u}}_{1}+2 \dot{r}_{M 1} r_{1}+2 r_{M 1} \dot{r}_{1} \end{array}\right]\\ \Delta \boldsymbol{M}=2\left[\begin{array}{cc} \Delta r_{21} \boldsymbol{\alpha}^{\mathrm{T}} & \mathit{\pmb{0}}^{\mathrm{T}} \\ \vdots & \vdots \\ \Delta r_{M 1} \boldsymbol{\alpha}^{\mathrm{T}} & \mathit{\pmb{0}}^{\mathrm{T}} \\ \Delta \dot{r}_{21} \boldsymbol{\alpha}^{\mathrm{T}}+\Delta r_{21} \boldsymbol{\beta}^{\mathrm{T}} & \Delta r_{21} \boldsymbol{\alpha}^{\mathrm{T}} \\ \vdots & \vdots \\ \Delta \dot{r}_{M 1} \boldsymbol{\alpha}^{\mathrm{T}}+\Delta r_{M 1} \boldsymbol{\beta}^{\mathrm{T}} & \Delta r_{M 1} \boldsymbol{\alpha}^{\mathrm{T}} \end{array}\right]\\ \Delta \mathit{\boldsymbol{N}} = \left[ {\begin{array}{*{20}{c}} {2{r_{21}}\Delta {r_{21}} + 2\Delta {r_{21}}{r_1}}\\ \vdots \\ {2{r_{M1}}\Delta {r_{M1}} + 2\Delta {r_{M1}}{r_1}}\\ {2{{\dot r}_{21}}\Delta {r_{21}} + 2\Delta {{\dot r}_{21}}{r_{21}} + 2\Delta {{\dot r}_{21}}{r_1} + 2\Delta {r_{21}}{{\dot r}_1}}\\ \vdots \\ {2{{\dot r}_{M1}}\Delta {r_{M1}} + 2\Delta {{\dot r}_{M1}}{r_{M1}} + 2\Delta {{\dot r}_{M1}}{r_1} + 2\Delta {r_{M1}}{{\dot r}_1}} \end{array}} \right] \end{array} $ | (23) |
式中的ΔM和ΔN可分别表示为
| $ \begin{gathered} \Delta \boldsymbol{M}=\left[\boldsymbol{U}_{1} \boldsymbol{n}, \boldsymbol{U}_{2} \boldsymbol{n}, \cdots, \boldsymbol{U}_{k} \boldsymbol{n}\right] \\ \Delta \boldsymbol{N}=\boldsymbol{U}_{k+1} \boldsymbol{n} \end{gathered} $ | (24) |
式中U1, U2, …, Uk(k=6)的具体表达式略,对n进行白化处理后可得:
| $ \begin{gathered} \Delta \boldsymbol{M}=\left[\boldsymbol{V}_{1} \boldsymbol{n}, \boldsymbol{V}_{2} \boldsymbol{n}, \cdots, \boldsymbol{V}_{k} \boldsymbol{n}\right] \\ \Delta \boldsymbol{N}=\boldsymbol{V}_{k+1} \boldsymbol{n} \end{gathered} $ | (25) |
式中Vi=UiP,则式(22)可转换为以下形式:
| $ \boldsymbol{M} \boldsymbol{\theta}_{2}-\boldsymbol{N}=\boldsymbol{W}_{\theta_{2}} \boldsymbol{\sigma} $ | (26) |
式中
| $ \begin{gathered} \widehat{\boldsymbol{\theta}}_{2}=\left((\boldsymbol{M}-\boldsymbol{Z})^{\mathrm{T}}\left(\boldsymbol{W}_{\theta_{2}} \boldsymbol{W}_{\theta_{2}}{ }^{\mathrm{T}}\right)^{-1} \boldsymbol{M}+\lambda_{2} \boldsymbol{I}\right)^{-1}\\ (\boldsymbol{M}-\boldsymbol{Z})^{\mathrm{T}}\left(\boldsymbol{W}_{\theta_{2}} \boldsymbol{W}_{\theta_{2}}{ }^{\mathrm{T}}\right)^{-1} \boldsymbol{N} \end{gathered} $ | (27) |
式中
| $ \boldsymbol{Z}=-\left[\boldsymbol{V}_{1} \boldsymbol{W}_{\theta_{2}}{ }^{-1}\left(\boldsymbol{A} \boldsymbol{\theta}_{2}-\boldsymbol{b}\right), \cdots, \boldsymbol{V}_{k} \boldsymbol{W}_{\theta_{2}}{ }^{-1}\left(\boldsymbol{A} \boldsymbol{\theta}_{2}-\boldsymbol{b}\right)\right] $ | (28) |
则目标位置和速度的最终估计值分别为
正则化参数λ1和λ2的选取对TRCTLS方法的性能有着很大的影响,本节主要从最小化均方误差的原则对正则化参数进行求解。假设第一步的估计值
| $ \widehat{\boldsymbol{\theta}}_{1}=\boldsymbol{\theta}_{1}+\Delta \boldsymbol{\theta}_{1} $ | (29) |
将式(29)代入式(17)中可得:
| $ \begin{gathered} (\boldsymbol{A}-\boldsymbol{\varLambda})^{\mathrm{T}}\left(\boldsymbol{W}_{\theta_{1}} \boldsymbol{W}_{\theta_{1}}^{\mathrm{T}}\right)^{-1}\left(\boldsymbol{A} \Delta \boldsymbol{\theta}_{1}+\boldsymbol{W}_{\theta_{1}} \boldsymbol{\sigma}\right)+ \\ \lambda_{1}\left(\boldsymbol{\theta}_{1}+\Delta \boldsymbol{\theta}_{1}\right)=0 \end{gathered} $ | (30) |
令S=(A-Λ)T (Wθ1 WTθ1)-1,由式(30)可得:
| $ \Delta \boldsymbol{\theta}_{1}=-\left(\boldsymbol{S} \boldsymbol{A}+\lambda_{1} \boldsymbol{I}_{8 \times 8}\right)^{-1}\left(\boldsymbol{S} \boldsymbol{W}_{\theta_{1}} \boldsymbol{\sigma}+\lambda_{1} \boldsymbol{\theta}_{1}\right) $ | (31) |
令SWθ1σ=J,可得:
| $ \begin{gathered} \Delta \boldsymbol{\theta}_{1}^{\mathrm{T}} \Delta \boldsymbol{\theta}_{1}=\left(\boldsymbol{J}^{\mathrm{T}}+\lambda_{1} \boldsymbol{\theta}_{1}^{\mathrm{T}}\right)\left[\left(\boldsymbol{S} \boldsymbol{A}+\lambda_{1} \boldsymbol{I}_{8 \times 8}\right)^{-1}\right]^{\mathrm{T}} \\ \left(\boldsymbol{S} \boldsymbol{A}+\lambda_{1} \boldsymbol{I}_{8 \times 8}\right)^{-1}\left(\boldsymbol{J}+\lambda_{1} \boldsymbol{\theta}_{1}\right) \end{gathered} $ | (32) |
通常矩阵SA为满秩矩阵,存在一个标准正交矩阵使得SA对角化:
| $ \boldsymbol{S} \boldsymbol{A}=\boldsymbol{P}^{\mathrm{T}} \operatorname{diag}\left\{u_{1}, u_{2}, \cdots, u_{8}\right\} \boldsymbol{P} $ | (33) |
对[(SA+λ1I8×8)-1]T(SA+λ1I8×8)-1进行特征值分解可得:
| $ \left[\left(\boldsymbol{S} \boldsymbol{A}+\lambda_{1} \boldsymbol{I}_{8 \times 8}\right)^{-1}\right]^{\mathrm{T}}\left(\boldsymbol{S} \boldsymbol{A}+\lambda_{1} \boldsymbol{I}_{8 \times 8}\right)^{-1}=\boldsymbol{P}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{P} $ | (34) |
式中:P是8×8的标准正交矩阵,D=diag{(u1+λ1)-2, (u2+λ1)-2, …, (u8+λ1)-2}。考虑到E(J)=0,对式(32)取期望可得第一步估计值的均方误差为
| $ E\left[\Delta \boldsymbol{\theta}_{1}^{\mathrm{T}} \Delta \boldsymbol{\theta}_{1}\right]=E\left[\boldsymbol{J}^{\mathrm{T}} \boldsymbol{P}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{P} \boldsymbol{J}\right]+\lambda_{1}^{2} \boldsymbol{\theta}_{1}^{\mathrm{T}} \boldsymbol{P}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{P} \boldsymbol{\theta}_{1} $ | (35) |
令C1=PJ、C2=Pθ1,则C1、C2为两个列向量。设C1=[c11, c12, …, c18]T、C2=[c21, c22, …, c28]T,则E[Δθ1TΔθ1]可表示为
| $ \begin{gathered} E\left[\Delta \boldsymbol{\theta}_{1}^{\mathrm{T}} \Delta \boldsymbol{\theta}_{1}\right]=E\left[\boldsymbol{C}_{1}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{C}_{1}\right]+\lambda_{1}^{2} \boldsymbol{C}_{1}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{C}_{1}= \\ \sum\nolimits_{i=1}^{8} \frac{E\left[c_{1 i}^{2}\right]}{\left(\boldsymbol{u}_{i}+\lambda_{1}\right)^{2}}+\lambda_{1}^{2} \sum\nolimits_{i=1}^{8} \frac{c_{2 i}^{2}}{\left(u_{i}+\lambda_{1}\right)^{2}} \end{gathered} $ | (36) |
可以看出第一步中利用RCTLS算法求得的结果的均方误差是关于λ1的函数,为了求得均方误差最小值对应的λ1值,对式(36)求导可得:
| $ \frac{\partial E\left[\Delta \boldsymbol{\theta}_{1}^{\mathrm{T}} \Delta \boldsymbol{\theta}_{1}\right]}{\partial \lambda_{1}}=2 \sum\nolimits_{i=1}^{8} \frac{\lambda_{1}^{2} c_{2 i}^{2} u_{i}-E\left[c_{1 i}^{2}\right]}{\left(u_{i}+\lambda_{1}\right)^{3}} $ | (37) |
对式(37)进行分析可得,当
| $ \lambda_{1}=\frac{1}{2}\left(\min \left\{\frac{E\left[c_{1 i}^{2}\right]}{c_{2 i}^{2} u_{i}}\right\}+\max \left\{\frac{E\left[c_{1 i}^{2}\right]}{c_{2 i}^{2} u_{i}}\right\}\right) $ | (38) |
同理可得λ2的取值。注意到第一步中Λ和Wθ1均含有未知数θ1,因此在实际的计算中先假设Λ=0、(Wθ1WTθ1)-1=Q,得到初始的值后再将其代入Λ和Wθ1的表达式中,之后利用新的Λ和Wθ1重新计算θ1,如此循环3~5次即可得到最终的θ1; 同样地,在第二步对θ2进行求解时也需要进行类似的处理。
4 实验仿真及分析本节通过仿真实验对提出的TRCTLS方法进行性能分析。蒙特卡洛循环次数设置为10 000次,分别为TDOA和FDOA测量值添加均值为零的高斯白噪声,其中TDOA的噪声的方差为δd2,协方差矩阵为Rt=δd2R,R为对角线上元素为1、其余元素为0.5的矩阵。FDOA的噪声方差为TDOA噪声方差的0.1倍,其协方差矩阵为Rf=0.1δd2R。计算机仿真条件为Windows10,64位操作系统,Core i5-9300H处理器,16 GB内存,MATLAB9.0版本。利用均方根误差RMSE对定位方法进行性能分析,其表达式为
| $ R_{\mathrm{MSE}}(\widehat{\boldsymbol{\theta}})=\sqrt{\sum\nolimits_{i=1}^{L}\left\|\widehat{\boldsymbol{\theta}}_{i}-\boldsymbol{\theta}^{\mathrm{o}}\right\|^{2} / L} $ | (39) |
本文的仿真实验在3个场景下进行,其中场景1和场景2中目标辐射源的位置和速度分别为u=[285,325,275]T m和
| 表 1 场景1和场景3中的接收站位置分布 Tab. 1 Location distribution of receivers in scenario 1 and scenario 3 |
| 表 2 场景2中的接收站位置分布 Tab. 2 Location distribution of receivers in scenario 2 |
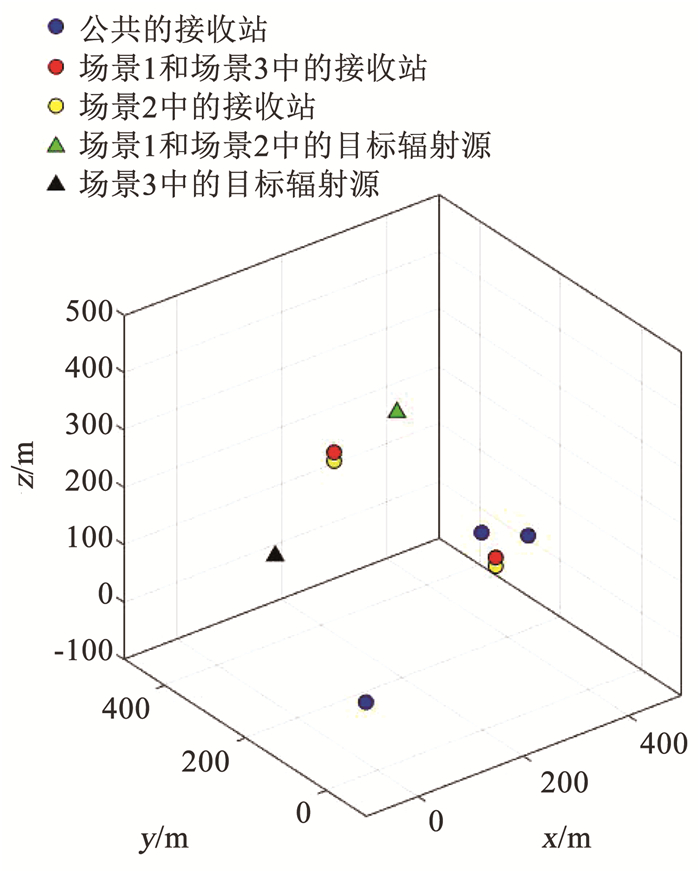
|
图 1 3个场景中接收站以及目标位置分布 Fig. 1 Distribution of receivers and target in three scenarios |
图 2是场景1中3种方法的定位情况,图 2(a)和(b)中横坐标为噪声功率,纵坐标分别为位置估计和速度估计的均方根误差。可以看出3种方法在噪声较低时均可达到CRLB,文献[16]表明了有偏估计可以通过牺牲算法的偏差来使得算法的均方根误差低于CRLB,而本文提出的基于RCTLS思想的方法是一种有偏估计,通过牺牲了无偏性来换取更低的均方根误差,因此在噪声较低的情况下本文提出的TRCTLS方法的定位均方根误差要略低于CRLB。而随着噪声的增加,3种算法均开始偏离CRLB,其中TSWLS方法受噪声影响较大,偏离CRLB的程度也最为明显,CTLS方法和本文提出的TRCTLS方法偏离CRLB程度较小,而且TRCTLS方法的偏离程度还要小于CTLS方法,这表明TRCTLS方法通过合理的选取正则化参数进一步提升了基于CTLS模型的定位算法的性能。
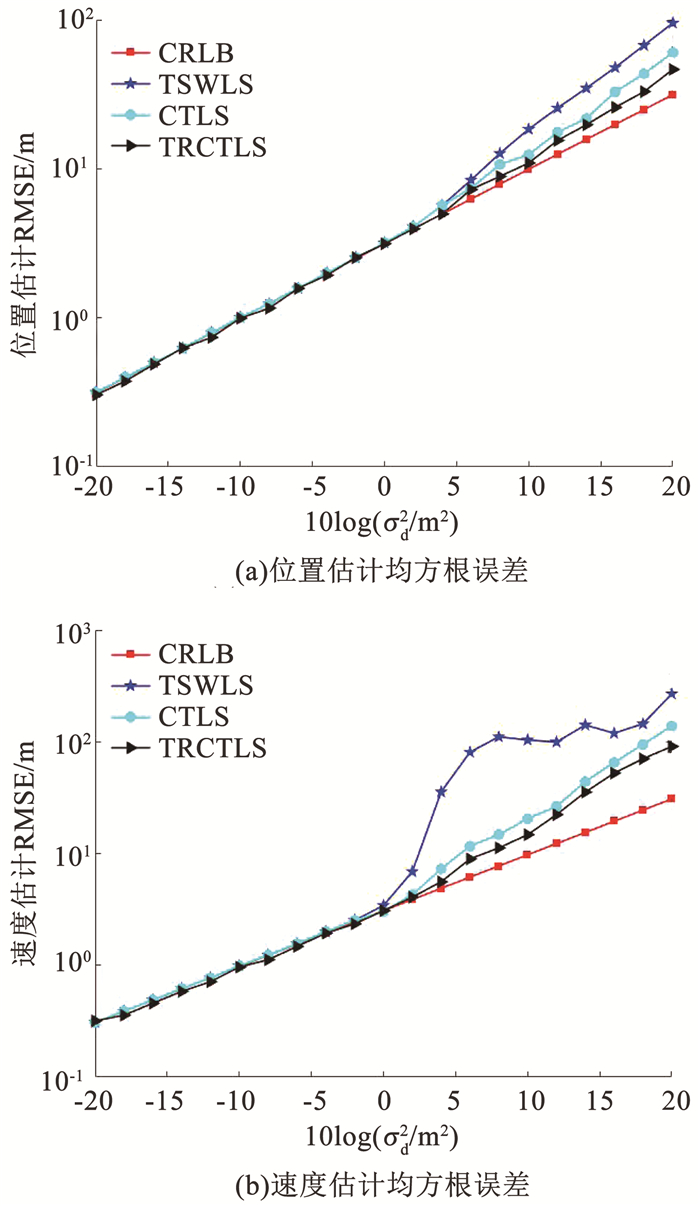
|
图 2 场景1中3种方法的定位均方根误差 Fig. 2 RMSE of three methods in scenario 1 |
图 3是场景2下3种方法的定位情况,由于场景2中5个接收站在z轴上的坐标接近,导致系数矩阵出现病态,此时估计值对噪声的敏感程度要高于场景1。因此从图 3(a)和(b)中可以看出3种方法偏离CRLB的程度均要高于在场景1中偏离CRLB的程度,但相对于TSWLS方法和CTLS方法,TRCTLS方法在场景2中的表现则更为稳定,这是因为相对于文献[7, 9]中的方法,TRCTLS方法在求解过程中引入了正则项,而引入正则项是解决病态问题的有效方法。TRCTLS方法通过合理地选取正则化参数来抑制系数矩阵的病态性,进而降低了病态矩阵对定位精度的影响,提升了定位方法在病态情况下的稳定性。可以看出,本文提出的定位方法通过合理地选取正则化参数,不仅在CTLS模型的基础上降低了均方根误差,而且在系数矩阵出现病态时的定位误差也要低于CTLS方法和TSWLS方法,提升了算法在不同定位情况下的稳定性。
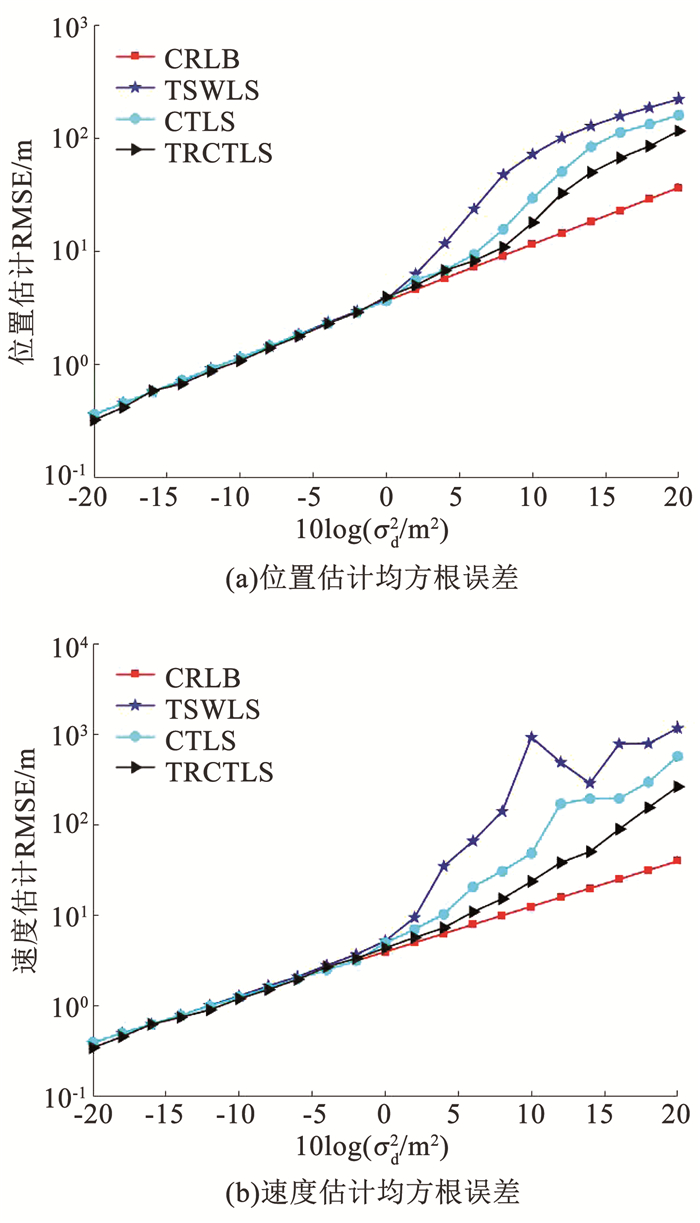
|
图 3 场景2中3种方法的定位均方根误差 Fig. 3 RMSE of three methods in scenario 2 |
图 4显示了场景3下3种方法的定位情况,可以看出,由于目标辐射源距离各个接收站的距离接近,因此系数矩阵出现了较为严重的病态问题。TSWLS方法和CTLS方法均在噪声较低的情况下便开始偏离CRLB。但与场景2中不同,TSWLS方法和CTLS方法在噪声较低时偏离CRLB的程度比在噪声较高时偏离CRLB的程度更为明显,这是因为在噪声较低时,r1, r2, …, rM的值比较接近,这会造成系数矩阵的病态,而在噪声较高时,因为受到测量误差的影响,导致r1, r2, …, rM的值出现了较大的差异,此时系数矩阵的病态性得到了较大的改善。而相较于TSWLS方法和CTLS方法,本文提出的TRCTLS方法在各种测量噪声的情况下均有着更为稳定的定位性能。
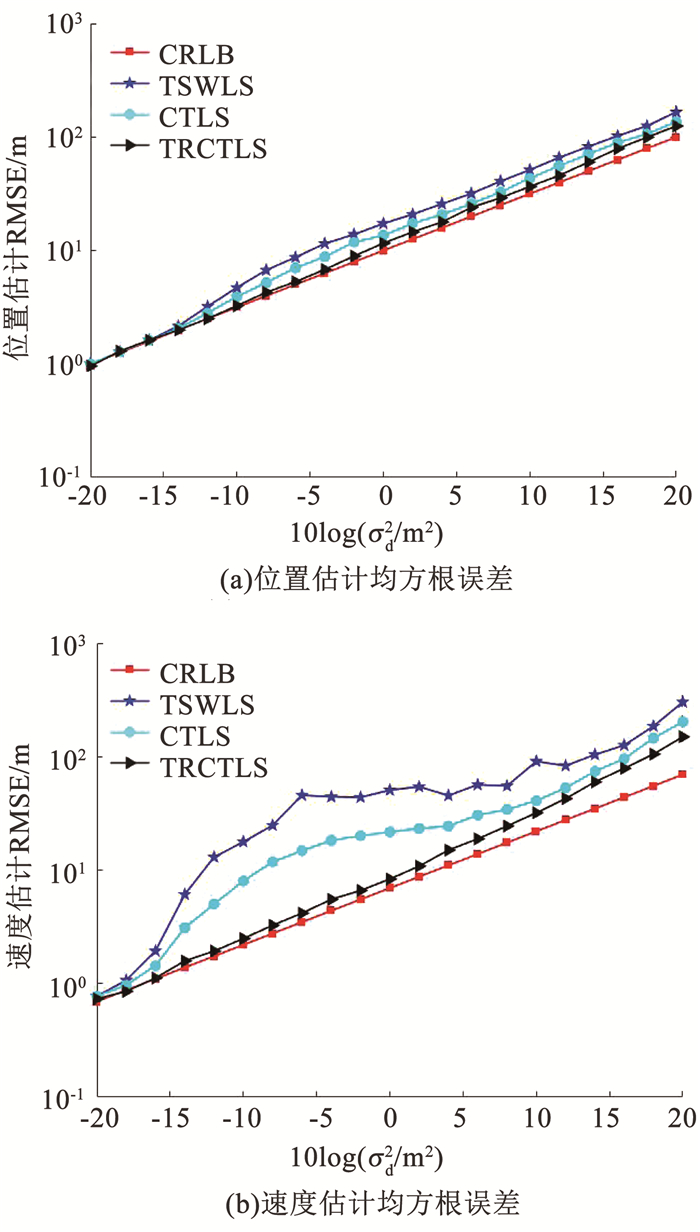
|
图 4 场景3中3种方法的定位均方根误差 Fig. 4 RMSE of three methods in scenario 3 |
最后对3种定位算法的计算复杂度和运行时间进行分析。文献[7]中提出的TSWLS方法的计算量为48M3-48M2+768M+8 010,而文献[12]中的CTLS方法为迭代法,单次迭代的计算量与TSWLS方法相近,本文提出的TRCTLS方法的计算量约为56M3+139M2+398M+1 230。在3种场景下的仿真实验中, 对3种方法的运行时间进行分析,其中CTLS方法的迭代次数设置为5次,可以得到TSWLS方法的平均运行时间为0.001 7 s,CTLS方法的平均运行时间约为0.007 4 s,而TRCTLS方法的平均运行时间为0.002 9 s,可以看出本文提出的TRCTLS方法因为具有计算正则化参数以及矩阵Λ和Z的过程,因此其运行时间要少于TSWLS方法,而CTLS方法是一种迭代法,需要利用牛顿法迭代求解拉格朗日参数,当迭代次数高于2次时,其运行速度要高于本文提出的TRCTLS方法。
5 结论针对基于TDOA/FDOA的无源定位问题,本文提出了一种基于RCTLS思想的定位方法。该方法分为两步,第一步在CTLS模型的基础上引入正则化参数后进行求解,第二步利用约束条件构造出一组关于第一步的估计误差的方程后进行求解,之后利用求解结果对第一步的估计结果进行修正以得到最终的估计值。仿真结果表明,本文方法通过牺牲了无偏性取得了低于TSWLS和CTLS方法的均方根误差,而且在系数矩阵出现病态的情况下定位性能较TSWLS方法和CTLS方法也更为稳定。同时本文的算法是一种闭式解析方法,因此在运行速度上也要优于CTLS方法。
| [1] |
HOK C, CHAN Y T. Geolocation of a known altitude object from TDOA and FDOA measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(3): 770. DOI:10.1109/7.599239 |
| [2] |
QU X, XIE L, TAN W. Iterative constrained weighted least squares source localization using TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2017, 3990. |
| [3] |
WEINSTEIN E. Optimal source localization and tracking from passive array measurements[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1982, 30(1): 69. DOI:10.1109/TASSP.1982.1163855 |
| [4] |
GUSTAFSSON T, RAO B D, TRIVEDI M. Source localization in reverberant environments: Modeling and statistical analysis[J]. IEEE Transactions on Speech & Audio Processing, 2003, 11(6): 791. |
| [5] |
王伟, 王咸鹏, 马跃华. 基于多级维纳滤波的双基地MIMO雷达多目标定位方法[J]. 航空学报, 2012, 33(7): 1281. WANG Wei, WANG Xianpeng, MA Yuehua. Multi-target localization based on multi-stage wiener filter for bistatic MIMO radar[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1281. |
| [6] |
STOICA P, LI Jian. Lecture notes-source localization from range-difference measurements[J]. IEEE Signal Processing Magazine, 2006, 23(6): 63. DOI:10.1109/SP-M.2006.248717 |
| [7] |
HO K C, XU W. An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2004, 52(9): 2453. DOI:10.1109/TSP.2004.831921 |
| [8] |
GUO Fucheng, HO K C. A quadratic constraint solution method for TDOA and FDOA localization[C]// IEEE International Conference on Acoustics, Speech and Signal Processing. Prague: IEEE, 2011: 2588
|
| [9] |
YU H, HUANG G, GAO J. Constrained total least-squares localisation algorithm using time difference of arrival and frequency difference of arrival measurements with sensor location uncertainties[J]. IET Radar Sonar & Navigation, 2012, 6(9): 891. |
| [10] |
曲付勇, 孟祥伟. 基于约束总体最小二乘方法的到达时差到达频差无源定位算法[J]. 电子与信息学报, 2014, 36(5): 1075. QU Fuyong, MENG Xiangwei. Source localization using TDOA and FDOA based on constrained total least squares algorithm[J]. Journal of Electronics and Information Technology, 2014, 36(5): 1075. |
| [11] |
GOLUB G H, VAN LOAN C F. An analysis of the total least squares problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883. DOI:10.1137/0717073 |
| [12] |
GOLUB G H, HANSEN P C, O'LEARY. Tikhonov regularization and total least squares[J]. SIAM Journal on Matrix Analysis and Application, 1999, 21(1): 185. DOI:10.1137/S0895479897326432 |
| [13] |
MESAROVIC V Z, GALATSANOS N P, KATSAGGELOS A K. Regularized constrained total least squares image restoration[J]. IEEE Transactions on Image Processing, 1995. |
| [14] |
FAN X, YOUNAN N H, TAYLOR C D. A perturbation analysis of the regularized constrained total least squares[J]. IEEE Transactions on Circuits & Systems II Analog & Digital Signal Processing, 1996, 43(2): 140. |
| [15] |
赵拥军, 赵勇胜, 赵闯. 基于正则化约束总体最小二乘的单站DOA-TDOA无源定位算法[J]. 电子与信息学报, 2016, 38(9): 2336. ZHAO Yongjun, ZHAO Yongsheng, ZHAO Chuang. Single-observer passive DOA-TDOA location based on regularized constrained total least squares[J]. Journal of Electronics & Information Technology, 2016, 38(9): 2336. |
| [16] |
SENGIJPTA S K. Fundamentals of statistical signal processing: estimation theory[J]. Technometrics, 1993, 37(4): 465. |
 2022, Vol. 54
2022, Vol. 54


