2. 长安大学 运输工程学院, 西安 710064;
3. 比亚迪汽车有限公司, 西安 710119;
4. 长安大学 基建处, 西安 710064
2. College of Transportation Engineering, Chang'an University, Xi'an 710064, China;
3. BYD Company Limited, Xi'an 710119, China;
4. Capital Construction Department, Chang'an University, Xi'an 710064, China
近年来,各种大型突发自然灾害在世界各地频频爆发,2008年发生在中国大范围地区的低温、雨雪、冰冻等自然灾害,直接经济损失达到537.9亿元。据文献[1]数据报道,同年的汶川大地震,受灾总人口达4 625.6万人,造成8 451.4亿元的重大经济损失;2013年雅安芦山地震累计造成231余万人受灾,受灾面积达12 500 km2。2021年7月,河南省中北部出现大暴雨,致使1 366.43万人受灾,直接经济损失885.34亿元。这些突发灾害通常都伴有极大的破坏性和重大的人员伤亡,带来了巨大的经济损失,因此必须及时采取有效的救援措施,做好应急救援物资配送工作,才能帮助灾区人民尽快恢复正常的秩序和生产生活。
应急车辆路径优化问题是应急物资配送的核心,是提高应急能力与提升灾后救援工作水平的重要保障,在有限的时间和资源下,实现应急车辆合理的路径规划成为了国内外学者致力于研究的问题。在应急路径优化模型目标函数构建方面,文献[2]研究了灾害应急处置中协调物流供应和疏散行动的选址分配集成问题,指出突发事件情况下的物流计划需要包括应急资源的调运方案以及伤员的疏散和转移方案。文献[3]量化了洪水影响和所需物资数量,建立了一个以库存容量、物资需求时间等为约束的多目标应急物流规划模型。文献[4]将时间满意度最大作为目标,建立了应急物流配送车辆调度模型。文献[5]提出了一种考虑应急救援车辆的调度费用成本和应急救援车辆的路径在途行程时间的双层规划的集成优化模型。可以看出,建立多目标的应急物流规划模型可以更加准确地描述应急救援过程中的实际问题。
在求解算法方面,主要求解方法有蚁群算法[6]、布谷鸟算法[7-8]、遗传算法[9]以及模拟退火算法[10]等启发式算法。文献[11]对信息素蒸发系数进行改进,提高了蚁群算法的收敛性,能够快速找到从待救援点到多个目标点的优化路径。文献[12]使用路径内搜索和路径间搜索提出了一种离散布谷鸟算法,求解带时间窗和同时取送货的车辆路径问题。文献[13]结合了两种类型的局部搜索和遗传算子,提出了一种混合萤火虫算法,提高了车辆路径问题解的质量。因此通过改进算法或进行不同算法的组合,可以明显地提高解的质量以及收敛速度。文献[14]针对重大疫情初期各地区对医用防护物资需求紧迫性的差异,总结了医用防护物资需求特征,对医用防护物资需求紧迫度相关指标进行了量化。
上述研究主要考虑救援的时效性和配送成本,较少考虑到各受灾点的受灾情况以及物资需求差异性,因此在突发灾害情况下,针对应急车辆路径优化问题进行研究,本文引入受灾点紧迫度量化及分级,尽可能优先配送受灾点需求紧迫度高的地区,寻找在约束条件内最优的路径规划方案,并设计相应的求解算法,可以为决策者提供决策依据,达到应急救援的快速响应、高效合理的目标,减少突发事件造成的损失。
1 问题描述与假设 1.1 问题描述突发灾害的发生对受灾地区资源环境和人员安全与生活造成严重危害,具有影响范围广、影响程度深的特点,由于区域内各受灾点的地理位置和需求情况存在一定的无规律性,需要制定合理高效的应急车辆路径方案,才能及时地为各受灾点运送救援物资。本文所研究的问题可以描述为:物资保障部门在对应急物资进行汇总整理后,利用不同编队数量的车队将应急物资由集中供应点配送到各物资配送中心,再运送至配送中心所辖的各受灾点。其中,各车队由物资配送中心出发,沿不同的规划路径,按照一定的运送顺序为不同区域的若干受灾点运送物资,并最终返回配送中心,形成一条完整的配送路径,在配送过程中考虑受灾点需求紧迫度、车辆随机行驶时间等条件,使得整个救援过程中的总时间最少、总费用最低、紧迫度排序指数最大,其示意图如图 1所示。

|
图 1 车辆路径问题示意图 Fig. 1 Schematic diagram of vehicle routing problem |
为方便进行后续研究工作的展开,对车辆路径问题作出以下相关假设:1)已知应急救援中应急车辆的额定装载量和平均速度,且保持不变,不考虑在救援过程中车辆的维护成本和维护时间;2)各受灾点的需求量小于应急车辆的额定装载量,且供应点的物资储备量可以满足所有受灾点的需求,且有足够的应急车辆来完成救援任务;3)应急车辆在一个闭环行程中不能多次访问同一受灾点,每个受灾点至少被应急车辆访问一次;4)从某一应急物资配送中心出发的车辆,完成运输任务后,仍需返回至起点。
2 多目标模型构建应急车辆路径优化问题受多种因素共同影响,由于应急物资来自多方途径,需要运送的受灾点较为分散,因此应急车辆路径优化模型的主要解决目标是尽可能地缩小救援过程耗费的时间和资金,并需要考虑受灾点受灾情况的差异,及时有力地保障受灾群众的物资供应。
应急救援所需总时间的长短直接影响到救援的时效性,将应急救援所需总时间按照救援过程进行划分,总时间包括应急车辆从物资供应点到配送中心的时间、从配送中心运送至各个受灾点再返回配送中心的时间以及装载物资和卸载物资花费的时间。参考文献[15]关于应急救援时间的定义,可将应急救援所需总时间表示为
| $ \begin{aligned} f_1=& \sum\limits_{i, g \in G} \sum\limits_{j, b \in B} \sum\limits_{k \in V} t_{\;\;i j}^{k^{\prime}} y_{g b}^k+\sum\limits_{k \in V} \sum\limits_{i, j \in Z_2} t_{\;\;i j}^{k^{\prime}} x_{i j}^k+\\ & \sum\limits_{k \in V} \sum\limits_{i \in Z_1} T_{1 i}^k\left(y_{g b}^k+p_{b a}^k\right)+\sum\limits_{k \in V} \sum\limits_{i \in Z_2} T_{\mathrm{u} i}^k\left(y_{g b}^k+y_{a k}\right) \end{aligned} $ | (1) |
式中:B={b|b=1, 2, …, m}为应急物资配送中心集合;G={g|g=1, 2, …, r}为供应点集合;V={k|k=1, 2, …, p}为应急车辆集合;tijk为车辆k从节点i行驶到节点j的时间;tijk′为修正时间;ygbk为0-1变量,表示应急车辆k是否从供应点g将物资运输到应急物资配送中心b;xijk为0-1变量,表示应急车辆k是否从i点行驶到j点;pbak为0-1变量,表示应急车辆k是否从配送中心b行驶到受灾点a;yak为0-1变量,表示受灾点a是否由第k辆应急车辆运送;Z1为应急救援中供应点和应急物资配送中心的集合;Z2为应急救援中受灾点和应急物资配送中心的集合;T1ik和Tuik分别为应急车辆k在i点装载和卸载应急物资所需的时间。
应急救援所需总费用影响到救援的经济成本,包括从物资供应点到配送中心的运输费用、从配送中心运送至各个受灾点再返回配送中心的运输费用、车辆固定运营成本以及装载物资和卸载物资花费的费用。应急救援所需总费用可表示为
| $ \begin{aligned} f_2=& \sum\limits_{i, g \in G} \sum\limits_{j, b \in B} \sum\limits_{k \in V} C_{i j}^k D_{g b} y_{g b}^k+\sum\limits_{i, j \in Z_2} \sum\limits_{k \in V} C_{i j}^k D_{i j} x_{i j}^k+\\ & \sum\limits_{g \in G} \sum\limits_{b \in B} \sum\limits_{a \in A}\left(\sum\limits_{k \in V} C_k y_{g b}^k+\sum\limits_{k \in V} C_k p_{b a}^k\right)+\\ & \sum\limits_{k \in V} \sum\limits_{i \in Z_1} C_{1 i}^k\left(y_{g b}^k+p_{b a}^k\right)+\sum\limits_{k \in V} \sum\limits_{i \in Z_2} C_{\mathrm{u} i}^k\left(y_{g b}^k+y_{a k}\right) \end{aligned} $ | (2) |
式中:Cijk为应急车辆k从i点将物资运输至j点的单位运输费用,Dij为节点i到节点j的距离,A={a|a=1, 2, …, n}为受灾点的集合,Ck为应急车辆k的固定运营成本,C1ik、Cuik分别为应急车辆k在i点装载和卸载应急物资的单位成本。
各受灾点的需求紧迫度综合排序指数是指受灾点的需求紧迫度与配送序列值的比值,当某受灾点需求紧迫度越大,配送序列值越小时,该受灾点越能接受优先配送。因而模型最优目标之一是各受灾点紧迫度综合排序指数之和最大,紧迫度综合排序指数为
| $ f_3=\sum\limits_{k \in V} \sum\limits_{a=n_1}^{n_i} \frac{C X_a}{\mu_i^k} $ | (3) |
式中:CXa为受灾点a的需求紧迫度,μik为第i个受灾点在第k辆车中的配送序列值。
车辆路径优化模型为多目标优化模型,考虑到目标函数包括3个优化对象f1、f2和f3,且目标函数之间存在相互制约,因此模型求解的最终方案需要满足多目标优化效果整体最优,而非每个目标个体最优,选用线性加权的方法能够很好地解决此类多目标优化问题。对各个目标函数进行无量纲操作后,为每个目标函数分别添加权重系数,最终转化为易于求解的单目标函数优化问题,进而目标函数可改写为
| $ \begin{aligned} F=& \theta_1 \frac{f_1-\min f_1}{\max f_1-\min f_1}+\theta_2 \frac{f_2-\min f_2}{\max f_2-\min f_2}+\\ & \theta_3 \frac{\max f_3-f_3}{\max f_3-\min f_3} \end{aligned} $ | (4) |
式(4)中θ1, θ2, θ3∈[0, 1], θ1+θ2+θ3=1,权重系数的取值应由应急管理决策者依据应急救援的实际情况分析确定。
约束条件为
| $ t_{i j}^{k^{\prime}}= \begin{cases}\alpha t_{i j}^k, & d_{a e} \leqslant 100 \mathrm{~km}, b>6.5 \\ \beta t_{i j}^k, & d_{a e} \leqslant 100 \mathrm{~km}, 6<b \leqslant 6.5 \\ \gamma t_{i j}^k, & d_{a e} \leqslant 100 \mathrm{~km}, 5<b \leqslant 6 \\ t_{i j}^k, & d_{a e}>100 \mathrm{~km} \text { 或 } b \leqslant 5\end{cases} $ | (5) |
| $ \sum\limits_{g \in G} \sum\limits_{k \in V} \sum\limits_{b \in B}\left(y_{g b}^k Q_k\right) \geqslant \sum\limits_{b \in B} h_b $ | (6) |
| $ \sum\limits_{a \in A} \sum\limits_{k \in V} \sum\limits_{b \in B}\left(p_{b a}^k Q_k\right) \geqslant \sum\limits_{a \in A} q_a $ | (7) |
| $ x_{i j}^k=0, \forall i, j \in B $ | (8) |
| $ \sum\limits_{i \in G} \sum\limits_{j \in B}\left(t_{i j}^{k^{\prime}} y_{g b}^k\right) \leqslant \frac{\operatorname{Max} D_k}{v}, k=1, 2, \cdots, p $ | (9) |
| $ \sum\limits_{i, j \in Z_2}\left(t_{i j}^{k^{\prime}} x_{i j}^k\right) \leqslant \frac{\operatorname{Max} D_k}{v}, k=1, 2, \cdots, p $ | (10) |
| $ \sum\limits_{i \in A} x_{i l}^k=\sum\limits_{j \in A} x_{l j}^k, k \in V, r \in A $ | (11) |
| $ \sum\limits_{a \in A} q_a=\sum\limits_{g \in G} h_g $ | (12) |
| $ \sum\limits_{a \in A} y_{a k} \leqslant 1, k=1, 2, \cdots, p $ | (13) |
| $ \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{j = 1}^n {x_{ij}^k} = 1, i \in B, j \in A, i = 1, 2, \cdots , m, \forall k \in V}\\ {\sum\limits_{j = 1}^n {x_{ji}^k} = 1, i \in B, j \in A, i = 1, 2, \cdots , m, \forall k \in V} \end{array}} \right. $ | (14) |
| $ \sum\limits_{k=1}^p y_{a k}=1, a=1, 2, \cdots, n $ | (15) |
| $ y_{a k}, y_{g b}^k, x_{a r}^k, x_{b a}^k=\{0, 1\} $ | (16) |
式(5)表示应急车辆在节点之间的实际行驶时间,dae为受灾点a到震源e的距离,b为受灾点所在位置的震级,α、β、γ为不同路况下的折损系数;式(6)表示应急车辆从供应点运往各个应急物资配送中心的需求量之和,不超过其本身的最大装载量,Qk为应急车辆k的额定装载量,hb为物资配送中心b的物资储备量;式(7)表示应急车辆从应急物资配送中心运往各个受灾点的需求之和,不超过其本身的最大装载量,qa为受灾点a的需求量;式(8)表示应急物资配送中心之间不存在物资的流动;式(9)表示应急车辆在从供应点到应急物资配送中心道路上的行驶总时间,不超过车辆本身在匀速状态下的最长运行时间,Max Dk为应急车辆k的最大行驶距离,v为应急车辆k的平均行驶速度;式(10)表示应急车辆在从应急物资配送中心到各个受灾点的行驶总时间不超过车辆本身在匀速状态下的最长运行时间;式(11)表示到达受灾点a的应急车辆仍从受灾点a出发,保证路径的连续性;式(12)表示各个受灾点物资需求量之和,等于所有应急物资配送中心总物资储备量,hg为供应点g的应急物资储备量;式(13)表示在一次交付过程中,每个受灾点不能被同一应急车辆访问两次;式(14)表示从应急物资配送中心出发的所有应急车辆最终都返回至起点;式(15)表示每个受灾点有且仅被应急车辆访问一次;式(16)规定了变量的范围。
3 算法设计 3.1 算法介绍应急车辆路径模型建立后,需要采取合适的算法求得最优方案。布谷鸟算法由于参数较少因此结构简单,全局寻优能力较强,但莱维随机飞行策略会造成全局更新的位置过于随机,在迭代过程中不能满足所有鸟巢位置都向当前最优解的方向靠拢,导致收敛速度下降,收敛精度不足。同时,针对车辆路径这类组合优化问题,蚁群算法在鲁棒性和求解速度方面具有较大优势,但存在结果为局部最优而非全局最优的问题。所以本文结合布谷鸟算法与蚁群算法的各自优势,将布谷鸟算法得到的最优解作为蚁群算法的信息素初始分布,进而获得最优路径,能够避免蚁群算法在初期进行盲目搜索,缩短了求解时间,布谷鸟-蚁群组合算法的流程如图 2所示。
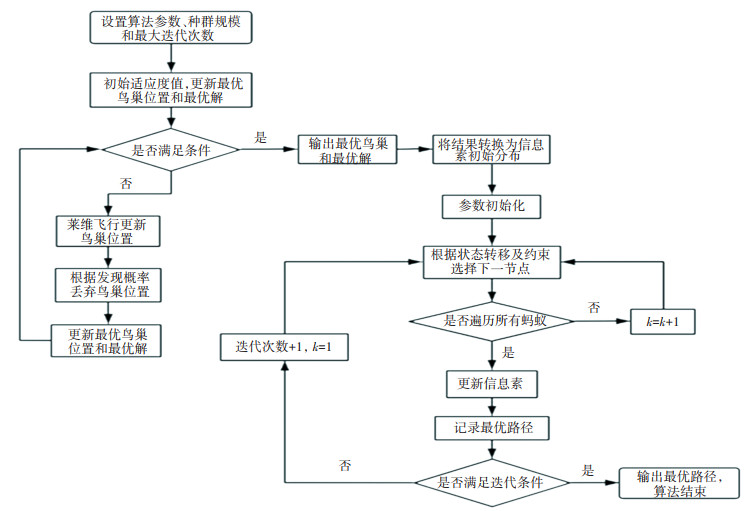
|
图 2 布谷鸟-蚁群组合算法流程图 Fig. 2 Flow chart of cuckoo-ant colonyhybrid algorithm |
本文将布谷鸟算法和蚁群算法组合求解路径优化问题,具体改进措施为:1)因为求解的应急车辆路径问题具有离散性,因此采用非负整数编码,即将实数编码个体的每一维元素映射成受灾点的编号;2)合理运用布谷鸟算法中的莱维飞行策略,利用快速排序法,将更新后鸟巢位置中的各维度数据进行排序,把每个鸟巢各维度数据的索引位置映射成每个受灾点的编号,编码形式如图 3所示, 将数据的连续性特征进行离散化处理,经过莱维策略更新后的鸟巢位置和受灾点的映射关系见表 1;3)根据文献[16]的启发,对在布谷鸟算法中对信息素启发式因子α进行自适应更新,从而改进莱维飞行位置公式;4)在传统蚁群算法中,启发函数通常取为两点间距离的倒数,但本文的优化目标不仅与距离相关,还与下一节点的紧迫度系数相关,因此将启发式函数改进为需求紧迫度与节点之间距离的比值,文献[17]表明两点间距离越短,可选择的下一节点的需求紧迫度系数越高,蚁群选择该路径的概率就越大。
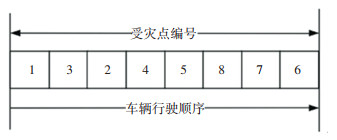
|
图 3 编码形式示意图 Fig. 3 Schematic diagram of encoding form |
| 表 1 快速排序法映射关系 Tab. 1 Quick sort mapping relationship |
本文以汶川地震为背景进行分析,参考文献[18]的民政部救助标准,从环境因素、人口因素和物资需求3个方面确定需求紧迫度影响指标,采用基于灰色关联-TOPSIS法的组合方法进行赋权,并使用SPSSAU软件进行计算,得出10个受灾较重地区的需求紧迫度,结果见表 2。其余29个受灾较轻地区数据不能完全获得,因此通过文献[19]中的地区人口、地理等客观数据进行估算,需求紧迫度系数均取0.3。
| 表 2 受灾点相关信息 Tab. 2 Information of disaster sites |
本文求解的应急车辆路径优化模型中假设前提是应急车辆数目可以用于完成供应点、物资配送中心和受灾点之间的配送任务,其中应急车辆最大行驶距离Max Dk取1 000 km,车辆额定装载量Qk取40 t,平均行驶速度v取50 km/h,单位运输成本Cijk取800元/(km·veh),固定运营成本Ck取1 000元/veh,装载和卸载物资所需时间T1ik和Tuik均取0.5 h/veh,装载和卸载物资所需费用C1ik和Cuik均取500元/veh,不同路况的折损系数α、β、γ分别取1.3、1.2、1.1,目标函数权重系数θ1、θ2、θ3分别取0.3、0.2、0.1。
4.3 结果分析本文模型求解的运行环境是在英特尔i5 2.11 GHz, 四核八线程CPU,8 GB RAM Windows 10系统的计算机操作系统的计算机进行。按照上述数据以及相关参数,采用线性加权和的方法对模型中的多个目标进行处理,并与不考虑需求紧迫度的车辆路径优化模型求解结果进行对比。
依据论文设计的改进的布谷鸟-蚁群组合算法的步骤,基于MATLAB R2018a平台,对应急车辆路径优化模型进行求解,根据以往文献和经验方法比较选取参数,得到最优参数组合,其中最大迭代次数T取500,种群数目N取30,发现概率pa取0.3,信息素启发式因子α取1,期望启发因子β取2,信息素挥发系数ρ取0.3。在参数设置相同的条件下,分别运行布谷鸟算法、蚁群算法和改进后的组合算法,得到3种算法的收敛情况如图 4所示。尽管蚁群算法最先收敛,但是后期易陷入局部最优,布谷鸟算法随着迭代次数的增加,逐步得到全局最优解,但收敛速度较为缓慢。改进后的布谷鸟-蚁群组合算法可以在保证收敛速度较快的前提下,较好地实现搜索全局最优的目标,能够弥补其他两种算法的不足,验证了模型的有效性。
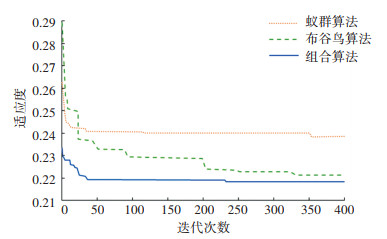
|
图 4 算法收敛性对比 Fig. 4 Comparison of algorithm convergence |
由于本文通过经纬度距离公式计算两个受灾点之间的距离,并将其作为相似性度量的公式。通过K-means算法得到的受灾点聚类结果显示,共需构建4个临时应急物资配送中心,应急物资配送中心的位置以及受灾点的划分结果见表 3。
| 表 3 应急配送中心及受灾点划分结果 Tab. 3 Division results of emergency distribution centers and disaster-stricken points |
表 4为突发事件下考虑紧迫度分级的应急车辆路径优化方案,其中,应急物资配送中心Ⅰ共需要两辆应急车辆,均按照受灾点紧迫程度进行配送;应急物资配送中心Ⅱ共需要3辆应急车辆,均优先对需求紧迫度高的受灾点进行了配送,既满足了较少的运输时间和运输费用,也使得严重灾区优先得到应急物资;应急物资配送中心Ⅲ处于受到地震灾害影响最严重的区域,物资需求量最大,应急救援任务最繁重,共需要7辆应急车辆,所有车辆全部遵守需求紧迫度大小进行配送,极大地保障了需求紧迫度高的受灾点优先获取物资的现实要求;应急物资配送中心Ⅳ被划分到的受灾点数目较多,但由于各受灾点受到地震的损害程度普遍较小,相应地对物资的需求量较小,在满足紧迫度需求的前提下,共需要两辆应急车辆进行物资的配送。考虑需求紧迫度的应急车辆路径规划图如图 5所示。
| 表 4 考虑紧迫度的应急车辆路径优化结果 Tab. 4 Emergency vehicle route optimization results considering urgency |

|
图 5 考虑紧迫度的应急车辆路径规划图 Fig. 5 Emergency vehicle route planning diagram considering urgency |
通过与不考虑需求紧迫度的应急车辆路径方案相比,在加入需求紧迫度因子优化后的应急车辆路径模型在整个配送过程中,共需要运输总时间为111.6 h,实际救援时间为42.7 h,花费4 028 559元,考虑需求紧迫度前后的各指标变化比例结果见表 5。相较于不考虑需求紧迫度的方案,优化方案的运输总时间与成本分别增加1.92%和3.43%,同时紧迫度排序指数增加11.2%,表明考虑需求紧迫度的优化方案能够更加合理地按照受灾点的紧迫程度运输应急物资,验证了模型的合理性,有助于满足应急救援物资保障的现实要求,实现了物资配送过程中应急车辆路径方案的合理优化。
| 表 5 考虑需求紧迫度与不考虑紧迫度的方案结果对比 Tab. 5 Comparison of scheme results with or without considering demand urgency |
1) 采用了K-means聚类算法确定了应急物资配送中心的选择及受灾点的划分,引入需求紧迫度构建了多目标车辆路径优化模型,设计了布谷鸟-蚁群组合算法对模型进行优化求解,能够满足突发灾害下应急物资配送的时效性、经济性与公平性。
2) 算例结果表明所提出的优化模型在物资运送的总时间和物资运送成本变化比例较小的同时,考虑了各受灾点物资需求程度的差异性,极大提高了受灾点需求紧迫度排序指数,实现了优先配送需求紧迫度较高的受灾点的目标需求。
3) 由于受灾点需求紧迫度受多种因素影响,因此需要进一步提取需求点特征,采用更为精确的量化方法计算受灾点需求紧迫度,进而提升路径优化模型的实际应用效果将是今后的研究任务。
| [1] |
高啸峰. 多配送中心应急物资配送车辆调度模型与算法研究[D]. 北京: 首都师范大学, 2011 GAO Xiaofeng. Research on vehicle routing model and algorithm of multi-depot emergency material distribution[D]. Beijing: Capital Normal University, 2011 |
| [2] |
WEI Yi, ÖZDAMAR L. A dynamic logistics coordination model for evacuation and support in disaster response activities[J]. European Journal of Operational Research, 2007, 179(3): 1177. DOI:10.1016/j.ejor.2005.03.077 |
| [3] |
GARRIDO R A, LAMAS P, PINO F J. A stochastic programming approach for floods emergency logistics[J]. Transportation Research Part E, 2015, 75: 18. DOI:10.1016/j.tre.2014.12.002 |
| [4] |
CHANG Qing. Vehicle scheduling model of emergency logistics distribution based on internet of things[J]. International Journal of Applied Decision Sciences, 2018, 11(1): 36. DOI:10.1504/IJADS.2018.088635 |
| [5] |
姚佼, 邵楚薇, 鲍雨婕, 等. 基于双层规划模型的应急救援调度与路径选择集成优化[J]. 公路交通科技, 2021, 38(6): 149. YAO Jiao, SHAO Chuwei, BAO Yujie, et al. Bi-level programming model based on integrated optimization of emergency rescue scheduling and route selection[J]. Journal of Highway and Transportation Research, 2021, 38(6): 149. DOI:10.3969/j.issn.1002-0268.2021.06.019 |
| [6] |
MARCO D, MANIEZZO V, COLORNI A. Ant system: optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 1996, 26(1): 29. DOI:10.1109/3477.484436 |
| [7] |
YANG Xinshe, DEB S. Cuckoo search via Lévy flights[C]// World Congress on Nature & Biologically Inspired Computing. Coimbatore: IEEE, 2009: 210
|
| [8] |
张海南, 游晓明, 刘升, 等. 交互式学习的布谷鸟搜索算法[J]. 计算机工程与应用, 2020, 56(7): 147. ZHANG Hainan, YOU Xiaoming, LIU Sheng, et al. Interactive learning cuckoo search algorithm[J]. Computer Engineering and Applications, 2020, 56(7): 147. |
| [9] |
郑斌, 马祖军, 周愉峰. 震后应急物流动态选址-联运问题的双层规划模型[J]. 系统管理学报, 2017, 26(2): 326. ZHENG Bin, MA Zujun, ZHOU Yufeng. Bi-level model for dynamic location-transportation problem for post-earthquake relief distribution[J]. Journal of System & Management, 2017, 26(2): 326. |
| [10] |
楼振凯. 应急物流系统LRP的双层规划模型及算法[J]. 中国管理科学, 2017, 25(11): 151. LOU Zhenkai. Bi-level programming model and algorithm of location-routing problem in emergency logistics[J]. Chinese Journal of Management Science, 2017, 25(11): 151. |
| [11] |
昝良, 许继恒, 吴天羿. 基于改进蚁群算法的应急救援路径规划[J]. 国防交通工程与技术, 2014, 12(2): 21. ZAN Liang, XU Jiheng, WU Tianyi. On the improved-ant-colony-algorithm-based planning of emergency rescue paths[J]. Traffic Engineering and Technology for National Defence, 2014, 12(2): 21. |
| [12] |
王超, 刘超, 穆东, 等. 基于离散布谷鸟算法求解带时间窗和同时取送货的车辆路径问题[J]. 计算机集成制造系统, 2018, 24(3): 570. WANG Chao, LIU Chao, MU Dong, et al. VRPSPDTW problem solving by discrete cuckoo search[J]. Computer Integrated Manufacturing Systems, 2018, 24(3): 570. |
| [13] |
ALTABEEB A M, MOHSEN A M, GHALLAB A. An improved hybrid firefly algorithm for capacitated vehicle routing problem[J]. Applied Soft Computing, 2019, 84: 105728. DOI:10.1016/j.asoc.2019.105728 |
| [14] |
陈雨珊, 吕伟, 刘毅, 等. 重大疫情下医用防护物资需求紧迫度模型研究[J]. 武汉理工大学学报(信息与管理工程版), 2021, 43(2): 112. CHEN Yushan, LV Wei, LIU Yi, et al. Research on demand urgency degrees model of medical protective materials in a major epidemic[J]. Journal of Wuhan University of Technology (Information & Management Engineering), 2021, 43(2): 112. |
| [15] |
刘长石. 震后应急物流系统中的定位-路径问题(LRP)模型与优化算法研究[D]. 成都: 电子科技大学, 2016 LIU Changshi. Research on model and algorithm of location-routing problem (LRP) for emergency logistics system in post-earthquake[D]. Chengdu: University of Electronic Science and Technology of China, 2016 |
| [16] |
METIAF A, ELKAZZAZ F, HONG W Q, et al. Multi-objective optimization of supply chain problem based NSGA-Ⅱ-Cuckoo Search Algorithm[C]//IOP Conference Series: Materials Science and Engineering. Shanghai: IOP Publishing, 2018, 435(1): 012030
|
| [17] |
熊超文. 蚁群算法的改进及其在路径规划中的应用研究[D]. 重庆: 重庆邮电大学, 2020 XIONG Chaowen. Improved ant colony algorithm and its application in path planning[D]. Chongqing: University of Posts and Telecommunications, 2020 |
| [18] |
郭晓光. 面向自然灾害的应急物流网络规划与运作研究[D]. 北京: 北京交通大学, 2013 GUO Xiaoguang. Research on the theory and methodology of the network planning for natural disaster emergency logistics[D]. Beijing: Beijing Jiaotong University, 2013 |
| [19] |
国家减灾委员会抗震救灾专家组, 科学技术部抗震救灾专家组. 汶川地震灾害综合分析与评估[M]. 北京: 科学出版社, 2008: 174. Earthquake Relief Expert Group of National Disaster Reduction Committee, Earthquake Relief Expert Group of Ministry of Science and Technology of the People's Republic of China. Comprehensive analysis and evaluation of Wenchuan earthquake disaster[M]. Beijing: Science Press, 2008: 174. |
 2022, Vol. 54
2022, Vol. 54


