2. 上海市城市建设设计研究总院(集团)有限公司, 上海 200125
2. Shanghai Urban Construction Design & Research Institute(Group) Co., Ltd., Shanghai 200125, China
山地占中国总面积的2/3,受到地形的限制,山区公路弯道多、坡度大、半径小、视距不足,客货车混行,相比于平原道路,山区道路交通环境更为复杂,这也使得山区弯道路段事故频发。山区双车道公路的事故占全国公路的15%以上,其中超过35%发生在弯道路段,而追尾事故发生占比最高[1-2]。山区道路的交通安全问题受到广泛关注,如何对山区弯坡组合路段追尾事故风险进行评估,分析追尾事故产生的影响因素,并实现事故的主动安全防控,已成为学者亟待解决得问题。
基于事故数量统计[3-5]的直接评估方法,具有简单、逻辑合理的优点[6],但考虑到事故发生的偶然与随机性,以及轻微事故未记录在案所带来的数据不完善性[7]问题,分析结果存在偏误。因此,有学者于1960—1970年提出了基于交通冲突技术的间接评估方法[8],即“交通冲突”,定义分为两类:避险措施的有无[9],与行驶车辆在空间或时间上的接近程度[10]。前者在自身应用方面存在主观判断缺陷,后者较为广泛,这也为山区弯坡组合路段的事故分析提供了理论基础。
文献[11]建立了“冲突发生”与“冲突严重程度”的两阶段交通冲突判别模型,用于预测及判别任意交通实体间的冲突;文献[12]将碰撞时间(time to collision,TTC)与避免冲突减速度[13](deceleration rate to avoid crash,DRAC或DR)两个交通冲突指标相结合,对车辆追尾风险进行评估;文献[14]基于指标冲突时间差(TDTC),对高速公路施工区车辆交通冲突进行评估;文献[15]将TTC修正得到指标MTTC(modified TTC),并结合TTC、后侵入时间(post-encroachment time,PET)和避免碰撞减速率DRAC,对事故概率进行评估;文献[16]选取碰撞时间TTC和后侵入时间PET的两个指标,运用VISSIM仿真技术对单向双车道车辆群行车风险进行评估。基于交通冲突的事故风险评估方法,虽然对现场数据采集精度的要求较高,但克服了统计分析方法事后分析的弊端。
不同交通冲突指标的侧重点存在差异,因此适用范围也有所不同。TTC适用于行驶轨迹相似的情况,文献[17]与文献[18]分别对高速公路与长隧道内车辆跟驰过程中的追尾风险进行评估;PET适用于交叉口、交织区的合流冲突,文献[19]基于PET算法对匝道合流区冲突进行识别;文献[20]将“减速”作为避险的表征对路侧停车区域非机动车冲突进行分析。国内外学者针对弯坡组合路段的研究相对欠缺,文献[1, 21-22]就线形对事故的影响展开分析,但研究对车辆在弯道路段实际的运行特点考虑欠佳。
针对交通冲突影响因素的研究较为广泛,如运用贝叶斯网络技术[14],零膨胀负二项(ZINB)[23],随机参数贝叶斯层级回归模型[15],机器学习[20]等方法,对车速、车型构成等因素进行冲突风险影响分析。但针对弯坡组合路段追尾冲突影响因素的研究相对欠缺,鉴于山区弯道路段禁止超车,在不考虑车辆横向偏移的情况下,车辆跟驰过程中的行驶轨迹近似一致,因此针对弯坡组合路段车辆运行特点,本文对车辆跟驰过程中TTC进行修正,评估车辆的追尾冲突风险并对其影响因素进行识别。通过运用CHAID(chi-squared automatic interaction detection)决策树、有序Logistic模型,分析交通流特性指标在弯坡组合路段不同区间段,对车辆行驶过程中追尾冲突的产生,以及追尾冲突严重程度的影响。研究能够帮助追尾事故的主动安全防控和实时预测,改善弯道路段的行车安全。
1 弯坡组合路段数据采集 1.1 数据采集地点和时间为获取弯坡组合路段的交通流状态数据以提取交通冲突指标,选取西安市水安路(二级公路)某路段,图 1为调查地点三视图,图中已标出路段的控制点ZH(直缓)、HY(缓圆)、QZ(曲中)、YH(圆缓)、HZ(缓直),以及沿直线路段距离ZH点50 m处(ZZ),本文将直线段(50 m)车辆跟驰过程也纳入研究范围。该弯坡组合路段为双向两车道,车道宽3.50 m,圆曲线转角值为96°,圆曲线半径为45 m。圆曲线两侧缓和曲线转角分别为39°与36°,直缓点半径为49 m。调查点坡度为2°,无中央分隔带,路面为沥青混凝土路面,最高限速为40 km/h。

|
图 1 调查地点几何线型三视图 Fig. 1 Three views of the geometric line shape of the survey site |
数据采集时间为2021年6月5日到6日,天气晴朗,采集时段包含早高峰8:30—9:30及晚高峰16:30—17:30,数据时长共4 h,数据采集方式为大疆无人机高空录像并配合现场调查人员获取。为保证数据采集的有效性,避免树木对行驶车辆的遮挡并确保拍摄清晰度,无人机静止悬停于路段中央上方250~300 m处俯视角度拍摄整个弯道,镜头分辨率调至1 080 P以上,每秒25帧数据采集设置。为克服无人机抖动、偏转、倾斜等问题带来的测量误差,在上述5个控制点处,上游与下游朝向分别放置两个雷达测速仪,对车辆速度、加速度等数据进行采集,作为无人机航拍数据的校核,另外现场调查人员记录车型、车牌及货车是否满载情况。
1.2 轨迹数据获取及处理 1.2.1 轨迹数据获取本文利用Tracker软件从无人机航拍录像中提取车辆运行轨迹,提取车辆随时间t的坐标位置(xt、yt)、瞬时速度vt与加速度at、X与Y轴的分速度vtx、vty、分加速度atx、aty及角速度ωt、角加速度βt等,并保存用于后续追尾风险评估。软件操作界面及现场调查示意如图 2所示。交通流中不同车辆类型对交通冲突的发生有显著影响,除车辆行驶轨迹之外,需划分车型。因此现场调查人员对通过车辆进行车型编号,编号规则:1代表微、小型载客汽车;2代表中型载客汽车;3代表大型载客汽车;4代表微、小型货车;5代表中型货车;6代表大型货车。

|
图 2 车辆轨迹数据提取及调查现场 Fig. 2 Extraction of vehicle track data and investigation site |
由于无人机位置固定、数据处理软件系统存在自身测量误差等问题,获取的数据与雷达测速仪数据存在差异,且有白噪音、缺失值或离群值的干扰。为进一步的研究需要,现对数据进一步处理。第1步,本文设置每秒等间隔提取10次车辆实时轨迹数据,对于缺失的数据,以数据缺失点为中心,前后区间长度总时长1 s内数据点均值进行填补。第2步,校核无人机与雷达测速仪数据,当两处雷达测速仪与无人机采集数据误差均在0~10%之间时,视为有效数据,数据取3者均值;当某处数据与其他两处属于误差大于10%时,剔除后取其余两处数据均值作为有效数据;当三处数据两两误差均大于10%时[24],视为无效数据,并剔除(本研究尚未出现无效数据)。第3步,对数据进行平稳性检验,对未通过检验的数据序列进行差值处理,直至平稳。第4步,对平稳数据进行离群值检验,当数据|xout-x|>3sd时,视为异常离群值并剔除,采用区间均值进行原始数据的填补,其中sd为标准偏差。第5步,最后对数据进行卡尔曼滤波平滑处理。综上所述,本文逻辑关系如图 3所示。
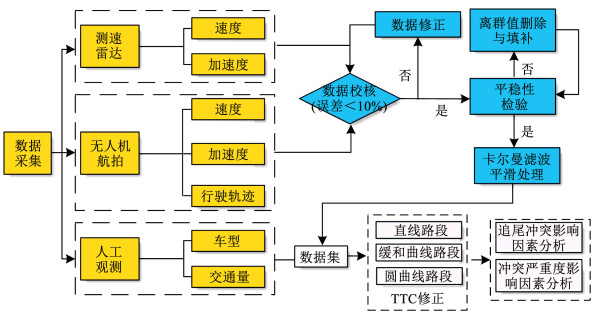
|
图 3 数据采集与处理流程图 Fig. 3 Flow chart of data acquisition and processing |
交通冲突的定义分为两类:车辆避险行为的有无[3];车辆在空间或时间上的接近程度[4]。交通冲突与事故存在换算关系,交通冲突的严重性越高,事故概率随之增加。TTC即为碰撞时间,TTC值越小,驾驶员获得的避险时间越短,事故的发生概率越高。TTC适用于前后车辆行驶轨迹相同的情况,为适应弯坡组合路段线形的特殊性,驾驶员会采取加/减速与转动方向盘的方式行驶。因此以往研究中以“引导车与跟随车保持原有速度与方向不变”为前提,即前后车车头间距与两车速度差的比值得到TTC的计算方法便不适用。本文给出弯坡组合路段的直线路段、圆曲线路段与缓和曲线路段的车辆追尾TTC的计算方法。
2.1.1 直线路段车辆TTC计算根据上/下坡直线路段车辆行驶特性对TTC的定义修正如下:前后车辆在原有速度下沿车道中心线行驶,将当前驾驶人加/减速度操作考虑其中,不采取进一步的避险措施所发生碰撞的时间,具体示意如图 4所示。追尾时车辆行驶距离计算如式(1)所示,前后两车实时TTC的求解可转化为如式(2)所示的方程求解问题。
| $ \begin{gathered} -\frac{1}{2} a_1 \mathrm{TTC}^2+v_1 \mathrm{TTC}^{+}\left(x_1^{\mathrm{c}}-x_{\mathrm{f}}^{\mathrm{c}}-l_1\right)= \\ -\frac{1}{2} a_{\mathrm{f}} \mathrm{TTC}^2+v_{\mathrm{f}} \mathrm{TTC} \end{gathered} $ | (1) |
| $ \frac{1}{2}\left(a_{\mathrm{f}}-a_1\right) \mathrm{TTC}^2+\left(v_1-v_{\mathrm{f}}\right) \mathrm{TTC}+\left(x_1^{\mathrm{c}}-x_{\mathrm{f}}^{\mathrm{c}}-l_1\right)=0 $ | (2) |

|
图 4 直线路段车辆跟驰过程中追尾示意图 Fig. 4 Schematic of rear-end collision during following the vehicle in the straight line section |
式中:xlc、xfc分别为追尾时引导车与跟随车车头的位置,m;ll为引导车辆车身长度,m;vl、vf分别为引导车与跟随车的起始车速,m/s;al、af分别为引导车与跟随车的起始加速度, m/s2。
车辆匀速行驶时,当跟随车辆初始速度大于引导车辆时,驾驶员在不采取任何制动措施的条件下,一定会发生碰撞。考虑到跟随与引导车辆加速度时,碰撞有无判断变得相对复杂。本文分为如表 1所示的情况讨论。
| 表 1 直线路段车辆追尾情况 Tab. 1 Vehicle rear-end situations straight line section |
表 1中情况a表示存在追尾碰撞的可能,两车在某一时刻teqvv会出现速度相同的情况,若teqvv前不发生追尾碰撞则无风险,teqvv计算如式(3)所示,碰撞判定条件见式(4)。
| $ t_{\mathrm{eqv}}=\frac{v_1-v_{\mathrm{f}}}{a_1-a_{\mathrm{f}}} $ | (3) |
| $ \left\{\begin{aligned} c_i= & 1, v_{\mathrm{f}} \cdot t_{\mathrm{eqv}}^{\mathrm{v}}-\frac{1}{2} a_{\mathrm{f}} t_{\mathrm{eqv}}^{\mathrm{v}}{ }^2-v_{\mathrm{f}} \cdot t_{\mathrm{eqv}}^{\mathrm{v}}+ \\ & \frac{1}{2} a_1 t_{\text {eqv }}^{\mathrm{v}}{ }^2>x_1-x_{\mathrm{f}}-l_1 \\ c_i= & 0, v_{\mathrm{f}} \cdot t_{\text {eqv }}-\frac{1}{2} a_{\mathrm{f}} t_{\text {eqv }}^2-v_{\mathrm{f}} \cdot t_{\text {eqv }}+ \\ & \frac{1}{2} a_1 t_{\text {eqv }}^2<x_1-x_{\mathrm{f}}-l_1 \end{aligned}\right. $ | (4) |
表 1中情况b表示存在追尾碰撞的可能,当两车减速至0的相对位移差大于车头间距时,两车将发生追尾(ci=1),否则无追尾风险(ci=0),判定条件见式(5)。
| $ \left\{\begin{array}{l} c_i=1, \frac{v_{\mathrm{f}}^2}{2 a_{\mathrm{f}}}-\frac{v_1^2}{2 a_1}>x_1-x_{\mathrm{f}}-l_1 \\ c_i=0, \frac{v_{\mathrm{f}}^2}{2 a_{\mathrm{f}}}-\frac{v_1^2}{2 a_1}<x_1-x_{\mathrm{f}}-l_1 \end{array}\right. $ | (5) |
表 1中情况c表示一定会出现追尾碰撞。表 1中情况d表示一定不会出现追尾碰撞。情况a与b在发生追尾碰撞时的TTC求解如(6)所示。
| $ \mathrm{TTC}=\frac{v_{\mathrm{f}}-v_1-\sqrt{\left(v_{\mathrm{f}}-v_1\right)^2-2\left(a_1-a_{\mathrm{f}}\right)\left(x_1-x_{\mathrm{f}}-l_1\right)}}{a_{\mathrm{f}}-a_1} $ | (6) |
跟随车辆随引导车辆在圆曲线段行驶的过程,可抽象为如图 5(a)所示的物体沿着固定半径在极坐标下的运动过程,αl、αf分别为引导车辆与跟随出现冲突时,两车车头与0°方向的夹角; wl、wf分别引导车与跟随车的起始角速度;βl、βf分别引导车与跟随车的起始角加速度; R为圆曲线半径。根据前文直线路段TTC的定义,圆曲线路段的TTC定义如下:前后车辆在当前角速度下沿圆曲线路段车道中心线行驶,保持原有角加/减速度不变的条件下,不采取进一步避险措施所发生碰撞的时间,具体示意如图 5所示。追尾时车辆行驶旋转角度计算如式(7)所示,TTC求解可转化为如式(8)所示的方程求解问题。
| $ \begin{gathered} -\frac{1}{2} \beta_1 \mathrm{TTC}^2+w_1 \mathrm{TTC}^{+}\left(\alpha_1-\alpha_{\mathrm{f}}-\frac{l_1}{R}\right)= \\ -\frac{1}{2} \beta_{\mathrm{f}} \mathrm{TTC}^2+w_{\mathrm{f}} \mathrm{TTC} \end{gathered} $ | (7) |
| $ \begin{gathered} \frac{1}{2}\left(\beta_{\mathrm{f}}-\beta_1\right) \mathrm{TTC}^2+\left(w_1-w_{\mathrm{f}}\right) \mathrm{TTC}+ \\ \left(\alpha_1-\alpha_{\mathrm{f}}-\frac{l_1}{R}\right)=0 \end{gathered} $ | (8) |
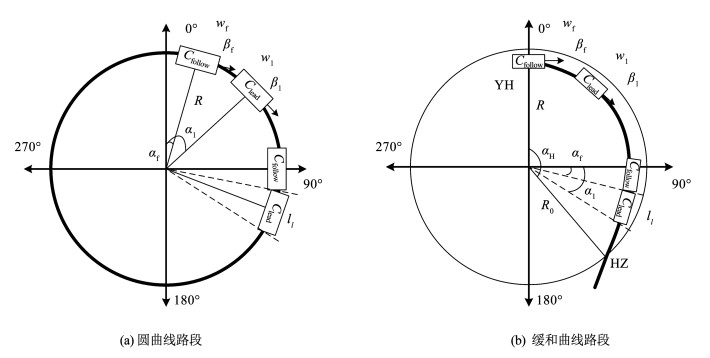
|
图 5 曲线路段车辆跟驰过程中追尾示意图 Fig. 5 Schematic of rear-end collision during following the vehicle in the curved section |
参考前文提到的直线段追尾判断准则,可推导出圆曲线路段车辆追尾事故的有无,以及TTC的计算公式。相类似,圆曲线段车辆追尾判断可分为如表 2所示的情况。
| 表 2 曲线路段车辆追尾情况 Tab. 2 Vehicle rear-end situation on curved section |
表 2中情况a表示存在追尾碰撞的可能,两车在某一时刻teqvw会出现角速度相同的情况,若teqvw前不发生追尾碰撞则无风险,碰撞判定条件见式(10)。
| $ t_{\mathrm{eqv}}^{\mathrm{w}}=\frac{w_1-w_{\mathrm{f}}}{\beta_{\mathrm{l}}-\beta_{\mathrm{f}}} $ | (9) |
| $ \left\{\begin{array}{l} c_i=1, w_{\mathrm{f}} \cdot t_{\mathrm{eqv}}^{\mathrm{w}}-\frac{1}{2} \beta_{\mathrm{f}} t_{\mathrm{eqv}}^{\mathrm{w}}{ }^2-w_{\mathrm{f}} \cdot t_{\mathrm{eqv}}^{\mathrm{w}}+\frac{1}{2} \beta_1 t_{\mathrm{eqv}}^{\mathrm{w}}{ }^2>\alpha_1-\alpha_{\mathrm{f}}-\frac{l_1}{R} \\ c_i=0, w_{\mathrm{f}} \cdot t_{\mathrm{eqv}}^{\mathrm{w}}-\frac{1}{2} \beta_{\mathrm{f}} t_{\mathrm{eqv}}^{\mathrm{w}^2}-w_{\mathrm{f}} \cdot t_{\mathrm{eqv}}^{\mathrm{w}}+\frac{1}{2} \beta_1 t_{\mathrm{eqv}}^{\mathrm{w}}{ }^2<\alpha_1-\alpha_{\mathrm{f}}-\frac{l_1}{R} \end{array}\right. $ | (10) |
表 2中情况b表示存在追尾碰撞的可能,当两车角速度减至0的相对位移角度大于引导车辆与半径的比值(ll/R)时,两车将发生追尾(ci=1),否则无追尾风险(ci=0),判定条件见式(11)。
| $ \left\{\begin{array}{l} c_i=1, \frac{w_{\mathrm{f}}^2}{2 \beta_{\mathrm{f}}}-\frac{w_1^2}{2 \beta_1}>\alpha_1-\alpha_{\mathrm{f}}-\frac{l_1}{R} \\ c_i=0, \frac{w_{\mathrm{f}}^2}{2 \beta_{\mathrm{f}}}-\frac{w_1^2}{2 \beta_1}<\alpha_1-\alpha_{\mathrm{f}}-\frac{l_1}{R} \end{array}\right. $ | (11) |
表 2中情况c表示一定会出现追尾碰撞。表 2中情况d表示一定不会出现追尾碰撞。情况a与b在发生追尾碰撞时的TTC求解如式(12)所示。
| $ \mathrm{TTC}=\frac{w_{\mathrm{f}}-w_1-\sqrt{\left(w_{\mathrm{f}}-w_1\right)^2-2\left(\beta_1-\beta_{\mathrm{f}}\right)\left(\alpha_1-\alpha_{\mathrm{f}}-\frac{l_1}{R}\right)}}{\beta_{\mathrm{f}}-\beta_1} $ | (12) |
跟随车辆随引导车辆在缓和曲线段行驶的过程,可抽象为如图 5(b)所示运动过程,R为圆曲线半径,即YH点曲率,R0为HZ点曲率;缓和曲线角为aH,曲率均匀变化,其他参数同前文。假设车辆沿车道中心线行驶,不考虑车道偏移,则车辆i的位置夹角为αi,角速度与角加速度分别为wi、βi,此时距离圆心的距离为Ri=ai·(R0-R)/αH,车辆沿缓和曲线切线速度viq与加速度aiq、驶离圆心的速度vil与加速度ail的计算如式(13)所示。
| $ \left\{\begin{array}{l} v_i^{\mathrm{q}}=w_i \cdot R_i \\ a_i^{\mathrm{q}}=\beta_i \cdot R_i \\ v_i^1=\frac{\left(R_0-R\right)}{\alpha_{\mathrm{H}}} \cdot w_i \\ a_i^1=\frac{\left(R_0-R\right)}{\alpha_{\mathrm{H}}} \cdot \beta_i \end{array}\right. $ | (13) |
参照圆曲线路段的TTC的定义,缓和曲线TTC定义如下:前后车辆在当前角速度下沿缓和曲线路段车道中心线行驶,保持原有角加/减速度不变的条件下,不采取进一步避险措施与引导车辆所发生碰撞的时间。由式(11)可知,跟随车辆随引导车辆沿缓和曲线段行驶,车辆沿车道中心线的切线速度与驶离圆心的速度为角速度的函数。因此车辆在曲率均匀变化的缓和曲线路段行驶轨迹由绕圆心的角速度与角加速度决定。这便与圆曲线路段车辆追尾的情况类似,车辆追尾与否仅与车辆角度变化有关。忽略引导车辆车头与车尾处缓和曲线半径差异,TTC求解亦转化为对式(9)的求解。缓和曲线路段车辆追尾判断亦可参考前文圆曲线路段的论述。TTC的计算公式亦可参考式(10)。
2.2 追尾冲突严重性判定TTC阈值通常被用来区分相对安全的情况和存在交通冲突的危险场景。不同环境下TTC的阈值存在差异,推荐阈值在1.5~4 s之间[17]。文献[18]指出,驾驶员在TTC约为4 s时,会采取避险措施,因此本文选取4 s为潜在交通冲突的判别阈值。跟随车与引导车辆之间的TTC随时间变化,当TTC小于4 s时,被视为出现潜在冲突。参照相关研究中冲突严重性的判断依据,本文取冲突时段内TTC最小值min(TTC),绘制其累积分布曲线,当min(TTC)小于15%、50%、85%时,分别视为严重、一般、轻微冲突[10],本研究数据统计结果严重、一般与轻微冲突的阈值分别为1.23、2.59、3.50 s。
3 追尾事故风险影响因素分析 3.1 影响因素指标选取本文按车辆上/下坡(内/外侧弯道)与进/出弯道(驶向/驶离圆曲线路段QZ点)方向,进行路段单元划分,因此弯坡组合路段被划分为12个单元(路段属性×上下坡×进出弯=3×2×2),并以1 min为数据统计单元。在借鉴相关学者对追尾事故微观分析的基础上[1, 21],追尾冲突与速度、加速度、交通量以及车头间距有关。因此选取如下8个预测指标:路段进口端断面交通量Q,pcu/h;路段平均车头间距H,m;进口端断面平均车速V,km/h;进口端断面平均绝对加速度A,km/h2;出口与进口端断面车速差DV,km/h;车行方向D,其中1表示内弯,0表示外弯;进弯方向W,其中1表示进弯,0表示出弯;是否有大型车混入B,其中1表示有,0表示无。前文提到调查人员对车型的划分为6类,为简化模型,将除2(微、小型载客汽车)与4(微、小型货车)之外的车型归为“大车”。出口与进口端断面车速差为路段单元出口端车辆平均车速减去入口端车辆平均车速。在剔除存在缺失值数据的时间段后,圆曲线段、缓和曲线、直线单位路段共分别有400、399条以及264条有效数据。
3.2 CHAID决策树原理决策树(decision trees)模型,是一种使用属性值进行离散预测的分类器方法。决策树通常是一种非参数技术,不依赖于任何函数形式,也没有先验概率知识要求。CHAID是决策树模型的一种。CHAID树具有多项分叉的优点,会划分尽可能多的子组;其次CHAID树能够处理多种类型的变量,对本文追尾冲突影响因素的识别有较好的适用性。本文将单位时间内弯坡组合路段车流中,将追尾冲突有无作为预测变量,因此使用χ2统计量或最大似然估计值L2的大小作为最优分割的判别依据。上述两者的函数表达式如下所示。本文将数据划分为训练集(80%)与测试集(20%),运用交叉验证法,使用穷举CHAID算法构建树模型。为防止过拟合现象的出现,将分组水平设置为4。此外,为了减小数据内在的不平衡性,本文选择5%的拆分节点与合并类别显著性水平,以保证CHAID树对追尾冲突更准确的分类和识别。
| $ \chi^2=\sum\limits_i \sum\limits_j \frac{\left(f_{i j}-F_{i j}\right)^2}{F_{i j}} $ | (14) |
| $ L^2=2 \cdot \sum\limits_i \sum\limits_j f_{i j} \ln \frac{f_{i j}}{F_{i j}} $ | (15) |
式中:fij为实际分布频率,Fij为与fij对应的理论分布频数的估计。
3.3 有序Logistic模型原理有序Logistic模型,适用于响应变量(因变量)为离散变量,自变量为连续变量或离散变量的问题。本文中追尾冲突等级的划分与影响因素的取值有密切关系,可根据影响因素取值对追尾冲突等级进行评估。假设追尾冲突等级划分为k个级别,则有序logistic回归分析模型有k-1个公式,累积logistic表达式为
| $ \begin{gathered} L_i=\ln \left[\sum\limits_{j=1}^J P(Y=j \mid X) / \sum\limits_{j=i+1}^k P(Y=j \mid X)\right]= \\ a_i+B X, i=1, 2, \cdots, k-1 \end{gathered} $ | (16) |
式中:Li为第i个累积Logistic模型;j为追尾冲突等级;X为预测变量指标向量;ai为第i个模型的截距参数;B为斜率向量;P(Y=j|X)为追尾冲突等级为j的概率。
由各追尾冲突等级下累积Logistic模型Li后,各追尾冲突等级的概率为
| $ \begin{gathered} P\left(Y=j \mid X_1, X_2, \cdots, X_3\right)= \\ \frac{\exp \left(a_i+b_1 X_1+b_2 X_2+\cdots+b_m X_m\right)}{1+\exp \left(a_i+b_1 X_1+b_2 X_2+\cdots+b_m X_m\right)} \end{gathered} $ | (17) |
式中:X1, X2, …, Xm为m个预测变量指标向量;b1, b2, …, bm为回归系数,本文采用极大似然估计。当
通过CHAID决策树对训练与测试集数据进行分类识别,模型对圆曲线、缓和曲线以及直线路段的总体分类准确率分别为94.0%、92.5%、92.4%。各节点的P值<0.05(显著性水平),表明本文的数结构未出现过度拟合现象。图 6~8分别为圆曲线、缓和曲线以及直线路段的追尾冲突因素识别的树结构。3个路段时空分析单元的潜在追尾冲突占比分别为22.5%、25.1%、28.8%。

|
图 6 识别圆曲线路段追尾冲突影响因素的树结构 Fig. 6 Decision tree for identifying factors influencing rear-end conflicts on circular curve sections |

|
图 7 识别缓和曲线路段追尾冲突影响因素的树结构 Fig. 7 Decision tree for identifying factors influencing rear-end conflicts on gentle curve sections |

|
图 8 识别直线路段追尾冲突影响因素的树结构 Fig. 8 Decision tree for identifying factors influencing rear-end conflicts on straight sections |
CHAID决策树最终将圆曲线路段的“出口/进口端速度差”、“路段车头间距”、“交通量”、“进口端平均车速”以及“车型构成”5个变量纳入树结构中。表明这些变量是影响圆曲线路段追尾冲突发生的显著因素。由图 6可知,当出口端车辆平均车速超过进口端3.85 km/h以上时,无追尾冲突产生;而当出口端车辆平均车速低于进口端时,车辆驶入圆曲线路段驾驶员需进行制动操作,进而导致后续跟随车辆与其出现冲突的概率增加,图 6中“出口/进口车速差≤-2.59 km/h”树分支的冲突概率远高于其他树分支的结果也进一步证明了上述观点。
当路段车头间距>69.57 m时,车辆追尾冲突的概率显著降低。这是由于当跟随车辆保持一定的跟车距离时,前车的突然制动操作,会预留给后车驾驶员充分的缓冲时间进行避险操作化解冲突。与此同时车辆驶入圆曲线路段后,存在视觉盲区,车速过快(超过40.93 km/h)导致TTC缩短,会导致追尾冲突的发生概率显著提高。大型车辆制动、加速困难,交通流大型车辆的混入,也增加了追尾冲突发生的可能性。此外,单位时间断面交通量增加时,车辆从自由流向强制流趋势演化,车辆之间的运行相互制约性增加,进而导致追尾冲突的增加。此外车辆上坡/下坡(内弯/外弯道)行驶方向、进弯/出弯行驶方向之间没有显著的追尾冲突差异。车辆驶入路段的平均绝对加速度也未纳入圆曲线路段追尾树结构中。
3.4.2 缓和曲线线路段追尾冲突风险因素分析CHAID决策树最终将缓和曲线路段的“交通量”、“车型构成”、“进弯/出弯方向”、“路段车头间距”、“进口端平均车速”以及“车辆上坡/下坡(内弯/外弯道)行驶方向”6个变量纳入树结构中(图 7)。表明这些变量是影响缓和曲线路段追尾冲突发生的显著因素。“交通量”、“车型构成”、“路段车头间距”、“进口端平均车速”对缓和曲线路段追尾冲突的作用解释与圆曲线路段类似。缓和曲线树结构中,变量“路段车头间距“的分裂值为67.35 m,略低于圆曲线路段变量分裂点;“进口端平均车速”在缓和曲线路段的树分裂值为43.89 km/h,略高于圆曲线路段的69.57 m。这表明车辆驶入圆曲线路段时,跟车间距的控制需高于缓和曲线路段,且车速需低于缓和曲线路段。
与圆曲线路段不同的是,“车辆上坡/下坡(内弯/外弯道)行驶方向”、“进弯/出弯方向”被纳入树结构中,与外弯道相比,内侧弯道车辆行驶半径小、视距短于外侧弯道。车辆沿内弯道行驶时,引导车辆制动操作后,跟随车辆驾驶员需行驶长于外侧弯道的距离发现前方制动车辆,TTC小于外侧弯道,追尾冲突提高。车流多减速驶入弯道,加速驶出弯道,进弯车辆由自由流向强制流趋势发展,而出弯车辆则相反。强制交通流内部车辆之间运行的相互制约性高于自由流车辆,进而进弯车辆追尾冲突概率高于出弯车辆。
3.4.3 直线路段追尾冲突风险因素分析CHAID决策树最终将直线路段的“进口端车辆平均绝对加速度”、“进弯/出弯方向”、“交通量”、“车型构成”、“路段车头间距”5个变量纳入树结构中,如图 8所示。“交通量”、“车型构成”、“进弯/出弯方向”对直线路段追尾冲突的作用解释与圆曲线路段类似。差异在于缓和曲线与圆曲线变量“路段车头间距“的分裂值分别为67.35 m与69.57 m, 显著高于直线路段的51.35 m分裂值。这表明缓和曲线与圆曲线路段的安全跟车间距远高于直线路段。“进口端车辆绝对加速度”被纳入树结构中,车辆在直线路段的平均绝对加速度A>36.8 km/h2时,追尾冲突概率显著提高。直线路段车辆车头间距低于缓和曲线与圆曲线路段,当驾驶员采取较大制动或加速操作时,会缩短跟随车辆与引导车辆之间的TTC,进而导致追尾冲突的发生。
针对上述3种路段的追尾冲突影响因素识别树结构,计算各路段追尾冲突影响因素的指标重要度[21],结果如图 9所示。结果表明:树结构指标的分裂层级越高,指标重要度越高。被纳入到圆曲线路段树结构的5个变量累积指标重要度为0.96;而被纳入到缓和曲线的6个变量累积指标重要度分别为0.89,略低于0.90,出口与进口端的车辆平均速度差值对路段冲突的产生有0.1的贡献度,作用原理与圆曲线路段类似,但其冲突影响效果明显略逊于圆曲线路段;直线路段的5个变量的累积指标贡献度为0.85,将变量“上坡/下坡(内外侧弯道)”纳入后,可达到0.96。表明直线路段车辆追尾冲突在上坡与下坡方向存在差异性。

|
图 9 各路段追尾冲突影响因素指标重要度 Fig. 9 Importance of indicators of factors influencing rear-end conflicts in each road section |
圆曲线路段严重、轻微、一般以及潜在冲突的占比分别为8.0%、2.5%、7.5%、4.5%;缓和曲线的分别为9.0%、3.3%、9.5%、3.3%;直线路段的分别为8.6%、7.1%、6.6%、6.5%。为克服各因素单位差异造成回归结果系数量级的差异,对因素变量进行标准化处理。回归结果见表 3,有序Logistic回归模型对圆曲线、缓和曲线以及直线路段拟合程度极佳,R2分别为0.72、0.61、0.67。
| 表 3 各路段追尾冲突严重性影响因素分析 Tab. 3 Analysis of factors influencing the severity of rear-end conflicts in each road section |
由于视距不足的问题,车辆在圆曲线路段内侧与外侧弯道(上坡/下坡)行驶时,无显著的追尾冲突严重性差异。相对于圆曲线路段,视距不足问题在缓和曲线路段的整体有所改善,且内侧弯道视距不足问题较外侧弯道更严重,这导致处于上坡方向的内侧弯道车辆追尾冲突显著高于外侧弯道(D=-2.19, Sig=0);直线路段上坡与下坡方向车辆行驶无视距差异,5%的坡度使得下坡行驶方向车辆追尾严重度高于上坡行驶车辆(D=-3.59, Sig=0)。其他指标对冲突严重性的影响,与前文追尾冲突影响因素的阐述相类似。路段进口端断面交通量的提高、大型车辆的混入、车头间距的缩短会显著提高冲突严重性。进口端断面平均车速会显著提高缓和曲线与圆曲线路段的冲突严重性,而进口端断面平均绝对加速度会提高直线路段的追尾冲突严重性。出口与进口端断面车速差降低了圆曲线与缓和曲线路段车辆追尾的严重性。缓和曲线与直线路段的车辆在驶入弯道时的冲突严重度要高于驶出弯道时。
4 结论1) 本文根据弯坡组合路段各组成部分(圆曲线、缓和曲线与直曲线路段)的道路线形与车辆运行特征,给出车辆追尾碰撞的判断准则,并对碰撞时间的计算进行修正。根据冲突时间累积分布曲线得出严重、一般、轻微与潜在追尾冲突的划分阈值。通过CHAID树模型与有序Logistic模型,对追尾冲突的产生,与冲突严重程度的影响因素进行识别。
2) 交通量、车型构成、车辆行驶速度与加速度等交通流特征指标,对弯坡组合路段的圆曲线、缓和曲线与直曲线部分的车辆追尾冲突影响存在差异性。圆曲线路段,车辆进弯与出弯,以及内侧/外侧弯道之间冲突的发生与严重性无显著差异;缓和曲线与直线路段驶入弯道的车辆追尾冲突频次与严重性要显著高于驶出弯道的车辆;缓和曲线路段内侧弯道行驶的车辆追尾冲突频次与严重度要高于外侧弯道,直线路段上坡行驶的车辆追尾冲突频次与严重性要低于下坡方向。
3) 研究结论可为弯坡组合路段追尾冲突的评估与事故防控提供帮助。但研究存在自身局限性,基础分析数据获取较为繁琐,且冲突指标是在经典TTC基础上进行修正。在未来的研究中,将对多个弯坡组合路段车辆行驶的轨迹数据进行采集,分析圆曲线路段半径、缓和曲线路段曲率、坡度、坡长等路段线性因素对车辆追尾冲突的影响;并针对道路特征提出新的交通冲突指标,将研究结果进一步完善。
| [1] |
房锐, 张琪, 胡澄宇, 等. 基于风险矩阵的干线公路弯道路段交通冲突风险评估模型[J]. 交通运输系统工程与信息, 2021, 21(2): 166. FANG Rui, ZHANG Qi, HU Chengyu, et al. Risk assessment model based on risk matrix for traffic conflict on arterial highway bend section[J]. Journal of Transportation Systems Engineering and Information Technology, 2021, 21(2): 166. |
| [2] |
陆欢, 戢晓峰, 杨文臣, 等. 高原山区公路环境下交通事故形态致因分析[J]. 中国安全科学学报, 2019, 29(5): 44. LU Huan, JI Xiaofeng, YANG Wenchen, et al. Cause analysis of different patterns of traffic accidents on plateau mountain roads[J]. China Safety Science Journal, 2019, 29(5): 44. |
| [3] |
WANG Yonggang, PRATO C G. Determinants of injury severity for truck crashes on mountain expressways in China: a case-study with a partial proportional odds model[J]. Safety Science, 2019, 117: 100. DOI:10.1016/j.ssci.2019.04.011 |
| [4] |
马聪, 张生瑞, 马壮林, 等. 高速公路交通事故非线性负二项预测模型[J]. 中国公路学报, 2018, 31(11): 176. MA Cong, ZHENG Shengrui, MA Zhuanglin, et al. Nonlinear negative binomial regression model of expressway traffic accident frequency prediction[J]. China Journal of Highway and Transport, 2018, 31(11): 176. DOI:10.3969/j.issn.1001-7372.2018.11.019 |
| [5] |
AHMED M M, MOHAMED A A. The viability of using automatic vehicle identification data for real-time crash prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(2): 459. DOI:10.1109/TITS.2011.2171052 |
| [6] |
CHAMPAHOM T, SAJJAKAJ J, AMPOL K, et al. Spatial zero-inflated negative binomial regression models: application for estimating frequencies of rear-end crashes on Thai highways[J]. Journal of Transportation Safety & Security, 2022, 14(3): 523. |
| [7] |
HAUER E, HAKKERT A. The extent and implications of incomplete accident reporting[J]. Transportation Research Record, 1988(186): 1. |
| [8] |
GLAUZ W D, MIGLETZ D J. Application of traffic conflict analysis at intersections[R]. Washington DC: Transportation Research Board, 1980
|
| [9] |
CHIN H C, QUEK S T. Measurement of traffic conflicts[J]. Safety Science, 1997, 26(3): 169. DOI:10.1016/S0925-7535(97)00041-6 |
| [10] |
朱顺应, 蒋若曦, 王红, 等. 机动车交通冲突技术研究综述[J]. 中国公路学报, 2020, 33(2): 15. ZHU Shunying, JIANG Ruoxi, WANG Hong, et al. Review of research on traffic conflict techniques[J]. China Journal of Highway and Transport, 2020, 33(2): 15. |
| [11] |
郭伟伟, 曲昭伟, 王殿海. 交通冲突判别模型[J]. 吉林大学学报(工学版), 2011, 41(1): 35. GUO Weiwei, QU Zhaowei, WANG Dianhai. Traffic conflict discrimination model[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(1): 35. |
| [12] |
QU Xiaobo, KUANG Yan, OH E, et al. Safety evaluation for expressways: a comparative study for macroscopic and microscopic indicators[J]. Traffic Injury Prevention, 2014, 15(1): 89. DOI:10.1080/15389588.2013.782400 |
| [13] |
CUNTO F, SACCOMANNO F. Calibration and validation of simulated vehicle safety performance at signalized[J]. Accident Analysis & Prevention, 2008, 40: 1171. |
| [14] |
朱顺应, 邹禾, 蒋若曦, 等. 高速公路施工区合流路段交通冲突模型[J]. 哈尔滨工业大学学报, 2020, 52(9): 70. ZHU Shunying, ZOU He, JIANG Ruoxi, et al. Traffic conflict model for confluence section in highway construction area[J]. Journal of Harbin Institute of Technology, 2020, 52(9): 70. |
| [15] |
FU Chuanyun, SAYED T. Random parameters bayesian hierarchical modeling of traffic conflict extremes for crash estimation[J]. Accident Analysis & Prevention, 2021, 157: 106159. |
| [16] |
容颖, 温惠英, 赵胜. 高速公路单向双车道车辆群行车风险度量研究[J]. 重庆交通大学学报(自然科学版), 2019, 38(9): 95. RONG Ying, WEN Huiying, ZHAO Sheng. Study on driving risk measurement for two-lane freeway vehicle group[J]. Journal of Chongqing Jiaotong University(Natural Science), 2019, 38(9): 95. |
| [17] |
YAN Kuang, QU Xiaobo, WANG Shuaian. A tree-structured crash surrogate measure for freeways[J]. Accident Analysis & Prevention, 2015, 77: 137. |
| [18] |
MENG Qiang, QU Xiaobo. Estimation of rear-end vehicle crash frequencies in urban road tunnels[J]. Accident Analysis & Prevention, 2012, 48: 254. |
| [19] |
马艳丽, 祁首铭, 吴昊天, 等. 基于PET算法的匝道合流区交通冲突识别模型[J]. 交通运输系统工程与信息, 2018, 18(2): 142. MA Yanli, QI Shouming, WU Haotian, et al. Traffic conflict identification model based on post encroachment time algorithm in ramp merging area[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(2): 142. |
| [20] |
慈玉生, 吴丽娜, 李潇逸, 等. 路侧停车区域非机动车冲突概率分布[J]. 哈尔滨工业大学学报, 2015, 47(2): 46. CI Yusheng, WU Lina, LI Xiaoyi, et al. Traffic conflict probability distribution for non-motor vehicles at curb parking area[J]. Journal of Harbin Institute of Technology, 2015, 47(2): 46. |
| [21] |
戢晓峰, 谢世坤, 覃文文, 等. 基于轨迹数据的山区危险性弯道路段交通事故风险动态预测[J]. 中国公路学报, 2022, 35(4): 277. JI Xiaofeng, XIE Shikun, TAN Wenwen, et al. Dynamic prediction of traffic accident risk in risky curve sections based on vehicle trajectory data[J]. China Journal of Highway and Transport, 2022, 35(4): 277. |
| [22] |
LIU Ziyang, HE Jie, ZHANG Chen, et al. The impact of road alignment characteristics on different types of traffic accidents[J]. Journal of Transportation Safety & Security, 2020, 12(5): 697. |
| [23] |
潘恒彦, 王永岗, 李德林, 等. 基于交通冲突的长纵坡路段追尾风险评估及预测[J]. 吉林大学学报(工学版), 2023, 53(5): 1355. PAN Hengyan, WANG Yonggang, LI Delin, et al. Evaluating and forecasting rear-end collision risk of long longitudinal gradient roadway via traffic conflict[J]. Journal of Jilin University (Engineering and Technology Edition), 2023, 53(5): 1355. |
 2023, Vol. 55
2023, Vol. 55


