滑翔增程制导炮弹是在常规炮弹的基础上增加助推火箭和制导控制系统发展而来。其借助常规火炮发射平台发射[1],以打击精度高、使用维护成本低的优点受到世界各军事大国普遍重视[2-3]。
制导炮弹的弹道优化设计在其整个生命周期中占据着举足轻重的地位。弹道优化问题本质上可视为轨迹优化问题,针对这一类问题,国内、外学者做了大量研究。史金光等[4]针对制导炮弹,利用庞特里亚金极小值原理设计纵向平面内最大射程滑翔弹道。孙瑞胜等[5]利用极小值原理,设计了一种乘波体高超声速飞行器的最大航程滑翔轨迹。上述轨迹优化问题的求解方法都基于极小值原理,这类方法求解精度高,但是推导过程繁琐,难以胜任复杂问题的求解。针对这一缺点,Benson[6]和Betts[7]提出一种最优控制问题数值解法,该方法主要分为:1)将最优控制问题(optimal control problem,OCP)转化为非线性规划问题(nonlinear programming,NLP);2)采用合适的NLP求解算法对问题进行求解。基于数值求解理论,大量多约束复杂轨迹优化问题得以求解。黄育秋等[8]采用等距梯形离散方法和序列二次规划算法设计了升力式再入飞行器的突防飞行轨迹。高长生等[9]针对高超声速滑翔飞行器,采用自适应伪谱法规划了其机动突防飞行轨迹。宣颖等[10]基于Legendre伪谱法规划三级固体火箭最大有效载荷飞行轨迹。刘超越等[11]针对二级助推火箭,采用高斯伪谱法设计了规避雷达禁飞区的最优飞行轨迹。由上述文献可以看出,数值解法可以很好地解决复杂的多阶段多约束轨迹优化问题,鉴于此,本文将采用属于数值解法的Radau伪谱法规划制导炮弹方案弹道。
相比于导弹,制导炮弹弹体空间有限,控制舵面较小,致使其机动能力有限。在这种不利条件下,为了更好地发挥制导炮弹精确打击能力,在设计方案弹道时,有必要充分考虑制导炮弹的初始弹道倾角、发射方位角、助推火箭点火时间、滑翔启控时间、导引头开启时间等弹道参数对方案弹道设计的影响。针对制导炮弹,史金光等[12]根据滑翔增程弹的飞行原理,建立弹道模型,通过数值仿真分析了滑翔增程弹的弹道特性。在此基础上,史金光等[4, 13]将制导炮弹全弹道分解为普通段、滚控段和滑翔段,分别对每一段的弹道特性进行了定性分析,并利用庞特里亚金极小值原理设计制导炮弹在纵向平面内的最优滑翔方案弹道。李勇[14]采用Gauss伪谱法规划滑翔制导炮弹最远射程方案弹道。陈琦等[15]基于Gauss伪谱法规划制导炮弹的最短飞行时间滑翔方案弹道。基于此研究,陈琦等[16]针对制导炮弹,提出一种不确定飞行环境下的弹道规划方法,该方法在纵向和侧向都显示出对随机干扰良好的抑制效果。Xu等[17]设计综合考虑滑翔效率和机动效率的复合效率因子,规划出滑翔制导炮弹滑翔和机动综合性能最优的方案弹道。陈琦[18]根据飞行过程中飞行状态差异,将滑翔增程制导炮弹全弹道分为起飞段、助推段、上升段和滑翔段4段,并采用直接配点法将4阶段弹道规划模型转换为非线性规划问题,最后采用内点法求解。在此4阶段弹道规划模型的基础上,徐秋坪[19]采用hp自适应伪谱法规划了滑翔增程制导炮弹的全弹道方案弹道。
虽然学者们对制导炮弹弹道规划问题进行了大量研究,但截至目前,考虑导引头约束的制导炮弹方案弹道规划的文章鲜有发表。基于此,本文以滑翔增程制导炮弹为研究对象,设计一种考虑导引头多约束的方案弹道规划方法(TPM-CS)。为方便区分,本文称文献[18-19]所提包含4阶段的滑翔增程制导炮弹全弹道方案弹道规划方法为传统滑翔制导炮弹弹道规划方法(TPM)。TPM没有考虑导引头的约束,因此,制导炮弹按照TPM规划的方案弹道飞行,到达末制导起始点时,目标可能不在导引头视场内,导致导引头难以捕获目标,甚至直到炮弹飞行至弹道终点也无法捕获目标。鉴于此,本文设计的TPM-CS方法将制导炮弹全弹道分为起飞段、助推段、上升段、滑翔段和末制导段5个阶段。在末制导段根据导引头最大探测距离建立末制导起始点约束,根据导引头视场角建立攻击路径约束,为了减小目标偏离导引头视场中心的距离,在目标函数中考虑对弹目视线相对导引头轴线偏离角度进行惩罚。采用多阶段Radau伪谱法将最优控制问题转换为非线性规划问题,最后调用非线性规划问题求解器SNOPT求解。为验证TPM-CS方法的有效性,本文针对导引头不同约束选取了多组算例,以控制能量最优为目标函数,规划制导炮弹大着角攻击方案弹道。最后与TPM方法进行对比仿真,以验证TPM-CS方法的优越性。
1 滑翔增程制导炮弹弹道规划模型滑翔增程制导炮弹的工作原理为:前线侦察单元发现目标后,向后方炮弹发射终端发送目标位置信息。炮弹发射终端根据目标信息和当前战场环境条件形成方案弹道加载至炮弹制导系统并发射炮弹。炮弹经过如图 1滑翔增程制导炮弹弹道示意图所示起飞段、助推段、上升段和滑翔段到达导引头开启点,导引头开机搜索捕获目标,最后进入末制导修正偏差完成对目标的精确打击。本文根据滑翔制导炮弹的工作原理建立考虑导引头多约束的弹道规划模型。
1.1 滑翔增程制导炮弹三维简化弹道模型参考文献[20]中导弹三维空间运动方程组,在小角度假设条件下,建立滑翔增程制导炮弹三维简化弹道模型:
| $ \left\{\begin{array}{l} \dot{v}=\frac{F_{\mathrm{p}}-F_x-m g \sin \theta}{m} \\ \dot{\theta}=\frac{F_y-m g \cos \theta}{m v} \\ \dot{\psi}_{\mathrm{v}}=-\frac{F_z}{m v \cos \theta} \\ \dot{x}=v \cos \theta \cos \psi_{\mathrm{v}} \\ \dot{y}=v \sin \theta \\ \dot{z}=-v \cos \theta \sin \psi_{\mathrm{v}} \\ \dot{m}=-m_{\mathrm{c}} \end{array}\right. $ | (1) |
式中: v为速度, θ为弹道倾角, ψv为弹道偏角, m为弹体质量, mc为助推火箭质量流量, Fp为助推火箭推力, Fx为气动阻力, Fy为气动升力, Fz为气动侧向力, (x, y, z)为炮弹在地面坐标系中的坐标。该模型的状态向量可以表示为
3个方向的空气动力为
| $ \left\{\begin{array}{l} F_x=\frac{1}{2} \rho v^2 S C_{x 0}\left(1+k_{\mathrm{c}}\left(\alpha^2+\beta^2\right)\right) \\ F_y=\frac{1}{2} \rho v^2 S C_{y \alpha} \alpha \\ F_z=\frac{1}{2} \rho v^2 S C_{z \beta} \beta \end{array}\right. $ | (2) |
式中:ρ为空气密度, S为参考面积, α为攻角, β为侧滑角, Cx0为零升阻力系数, kc为与诱导阻力相关的系数, Cyα为升力系数导数, Czβ为侧向力系数导数。该模型控制向量可以表示为u=[α β]T。
1.2 5段式弹道模型如图 1所示,滑翔增程制导炮弹的飞行轨迹分为5段,分别为起飞段、助推段、爬升段、滑翔段和末制导段。
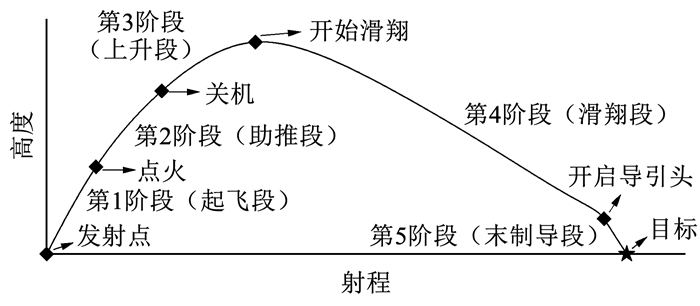
|
图 1 滑翔增程制导炮弹弹道示意 Fig. 1 Trajectory diagram of gliding extended range guided projectile |
为方便标注每一段的时间变量,定义第p阶段飞行时间区间为[t0(p), tf(p)],第p阶段持续时长为
| $ t_{\mathrm{d}}^{(p)}=t_{\mathrm{f}}^{(p)}-t_0^{(p)} $ | (3) |
式中:(·)0(p)为第p阶段初值,(·)f(p)为第p阶段末值,(·)d(p)为第p阶段持续长度。
弹道中各阶段定义如下:
1) 起飞段。始于发射位置,结束于助推火箭点火位置。助推火箭必须在炮弹出炮口一定距离后才能点火,所以规划方案弹道时,变量td(1)的下界应设置一个合理的正数。
2) 助推段。始于助推火箭点火位置,结束于助推火箭关闭点。td(2)等于助推火箭工作持续时长。
3) 爬升段。始于助推火箭关闭点,结束于滑翔起始点。现实中,助推火箭由工作状态切换到关闭状态这一扰动在一定程度上会影响弹体平衡,所以助推结束后需要经过一段时间等弹体恢复平衡再开启舵面进入滑翔段,所以变量td(3)的下界应设置为一个合理的正数。
4) 滑翔段。始于滑翔起始位置,结束于末制导起始点。
5) 末制导段。始于末制导起始点,结束于目标点。
1.3 约束条件 1.3.1 边界约束制导炮弹初速为v0,初始坐标为(x0, y0, z0),初始质量为m0。于是建立制导炮弹的初始状态约束为
| $ \left\{\begin{array}{l} v\left(t_0^{(1)}\right)=v_0 \\ x\left(t_0^{(1)}\right)=x_0 \\ y\left(t_0^{(1)}\right)=y_0 \\ z\left(t_0^{(1)}\right)=z_0 \\ m\left(t_0^{(1)}\right)=m_0 \end{array}\right. $ | (4) |
静止目标的坐标为(xt, yt, zt),为实现较好的打击效能,设末速度约束下界为vfL,落角约束上界为θfU。于是建立末状态约束为
| $ \left\{\begin{array}{l} x\left(t_{\mathrm{f}}^{(5)}\right)=x_{\mathrm{t}} \\ y\left(t_{\mathrm{f}}^{(5)}\right)=y_{\mathrm{t}} \\ z\left(t_{\mathrm{f}}^{(5)}\right)=z_{\mathrm{t}} \\ \theta\left(t_{\mathrm{f}}^{(5)}\right) \leqslant \theta_{\mathrm{fU}} \\ v\left(t_{\mathrm{f}}^{(5)}\right) \geqslant v_{\mathrm{fL}} \end{array}\right. $ | (5) |
制导炮弹在不同飞行阶段具有不同的飞行特征,受到不同的约束。助推火箭只在助推段工作,控制量在前3个飞行阶段都为零。
1) 上升段和爬升段约束:
| $ \left\{\begin{array}{l} F_{\mathrm{p}}=0 \\ m_{\mathrm{c}}=0 \\ \alpha=0 \\ \beta=0 \end{array}\right. $ | (6) |
2) 助推段约束:
| $ \left\{\begin{array}{l} F_{\mathrm{p}}=F_{\mathrm{p}}^* \\ \alpha=0 \\ \beta=0 \end{array}\right. $ | (7) |
式中,Fp*为助推火箭的平均推力。
3) 滑翔段和末制导段约束:
| $ \left\{\begin{array}{l} F_{\mathrm{p}}=0 \\ m_{\mathrm{c}}=0 \\ \alpha_{\min } \leqslant \alpha \leqslant \alpha_{\text {max }} \\ \beta_{\text {min }} \leqslant \beta \leqslant \beta_{\text {max }} \end{array}\right. $ | (8) |
式中:(·)min为该变量的下边界值,(·)max为该变量的上边界值。
1.3.3 连续性约束多阶段弹道规划,需要保证时间连续性和状态变量连续性,即
| $ \left\{\begin{array}{l} t_{\mathrm{f}}^{(p)}=t_0^{(p+1)} \\ \boldsymbol{x}_{\mathrm{f}}^{(p)}=\boldsymbol{x}_0^{(p+1)} \end{array}\right. $ | (9) |
式中:(·)(p)为第p阶段的信息(p=1, …, P-1), 其中P为全弹道分段总数。
1.3.4 末制导路径约束制导炮弹末制导过程的几何关系图如图 2所示,图中:M为制导炮弹,T为目标,θL为视线倾角,φL为视线偏角。
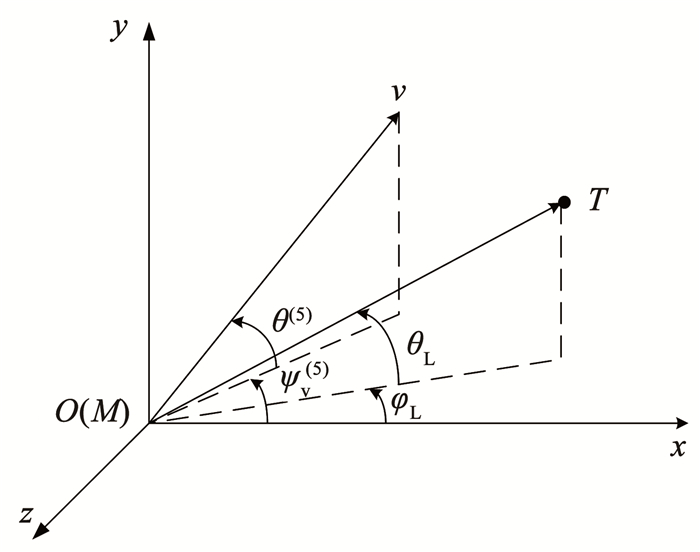
|
图 2 三维制导几何关系 Fig. 2 3D engagement geometry |
近似认为导引头基准轴和速度轴重合,则炮弹目标视线在高低和方位两个方向相对导引头基准轴线偏离角度分别为
| $ \left\{\begin{array}{l} e_\theta=\left|\theta^{(5)}-\theta_{\mathrm{L}}\right| \\ e_{\varphi}=\left|\psi_{\mathrm{v}}^{(5)}-\varphi_{\mathrm{L}}\right| \end{array}\right. $ | (10) |
其中视线角计算公式为
| $ \left\{\begin{array}{l} \theta_{\mathrm{L}}=\tan ^{-1}\left(\frac{y_{\mathrm{t}}-y}{\sqrt{\left(x_{\mathrm{t}}-x\right)^2+\left(z_{\mathrm{t}}-z\right)^2}}\right) \\ \varphi_{\mathrm{L}}=-\tan ^{-1}\left(\frac{z_{\mathrm{t}}-z}{x_{\mathrm{t}}-x}\right) \end{array}\right. $ |
末制导过程中,必须保证目标在导引头视场内。设导引头的视场角为ε,于是根据视场角可建立末制导路径约束为
| $ \left\{\begin{array}{l} e_\theta \leqslant \varepsilon \\ e_{\varphi} \leqslant \varepsilon \end{array}\right. $ | (11) |
导引头探测距离有限,过早开启导引头会浪费弹载电能,过晚开启导引头会减少制导系统修正弹目位置偏差的空间和时间。
设导引头最大探测距离为Rs,制导炮弹末制导起始点和目标的距离为
| $ R_{\mathrm{MT}}=\sqrt{\left(x_0^{(5)}-x_{\mathrm{t}}\right)^2+\left(y_0^{(5)}-y_{\mathrm{t}}\right)^2+\left(z_0^{(5)}-z_{\mathrm{t}}\right)^2} $ | (12) |
式中, (x0(5), y0(5), z0(5))为末制导起始点。
假设目标一进入导引头探测范围制导炮弹就进入末制导。于是本文设计末制导起始点约束为
| $ R_{\mathrm{MT}}-R_{\mathrm{s}}=0 $ | (13) |
为方便解释目标函数,首先定义攻角控制裕量和侧滑角控制裕量为
| $ \left\{\begin{array}{l} \zeta_\alpha=\alpha_{\text {max }}-|\alpha| \\ \zeta_\beta=\beta_{\text {max }}-|\beta| \end{array}\right. $ | (14) |
再定义视线角约束裕量为
| $ \left\{\begin{array}{l} \zeta_\theta=\varepsilon-e_\theta \\ \zeta_{\varphi}=\varepsilon-e_{\varphi} \end{array}\right. $ | (15) |
制导炮弹机动能力有限,为增强其抗干扰能力,在设计方案弹道时需要为制导控制系统预留一定量的控制裕量和视场角约束裕量。于是本文建立目标函数为
| $ J=J_1+J_2 $ | (16) |
其中:
| $ \begin{aligned} & J_1=\sum\limits_{p=4}^5 \int\limits_{t _{0}^{(p)}}^{t_{\rm f}^{(p)}} w_{1, 1}\left(\frac{\alpha}{\alpha_{\max }}\right)^2+w_{1, 2}\left(\frac{\beta}{\beta_{\max }}\right)^2 \mathrm{~d} t \\ & J_2=\int\limits_{t_0^{(5)}}^{t_{\rm f}^{(5)}} w_{2, 1}\left(\frac{e_\theta}{\varepsilon}\right)^2+w_{2, 2}\left(\frac{e_{\varphi}}{\varepsilon}\right)^2 \mathrm{~d} t \end{aligned} $ |
式中, w1, 1、w1, 2、w2, 1、w2, 2为惩罚权值。目标函数第1部分J1的作用是最小化制导控制系统对控制变量α和β的需求,以提高其控制裕量。目标函数第2部分J2的作用是最小化弹目视线相对导引头轴线的偏离角即前置角,以提高视场角约束裕量。
2 多阶段Radau伪谱法 2.1 多阶段最优控制问题模型P阶段最优控制问题性能函数可以写为
| $ \begin{aligned} & J= \sum\limits_{p=1}^P\left[{\varPhi}^{(p)}\left(\boldsymbol{x}_0^{(p)}, t_0^{(p)}, \boldsymbol{x}_{\mathrm{f}}^{(p)}, t_{\mathrm{f}}^{(p)}, \boldsymbol{s}\right)+\right. \\ &\int\limits_{t_0^{(p)}}^{t_{\mathrm{f}}^{(p)}} \left.\varGamma\left(\boldsymbol{x}^{(p)}(t), \boldsymbol{u}^{(p)}(t), t, \boldsymbol{s}\right) \mathrm{d} t\right] \end{aligned} $ | (17) |
式中:Φ(·)为端点值性能函数,Γ(·)为积分型性能指标待积分函数。
动态函数约束为
| $ \dot{\boldsymbol{x}}^{(p)}=\boldsymbol{f}\left(\boldsymbol{x}^{(p)}, \boldsymbol{u}^{(p)}, \boldsymbol{t}, \boldsymbol{s}\right), (p=1, \cdots, P) $ | (18) |
不等式路径约束为
| $ \boldsymbol{C}_{\min }^{(p)} \leqslant \boldsymbol{C}^{(p)}\left(\boldsymbol{x}^{(p)}, \boldsymbol{u}^{(p)}, t^{(p)}, \boldsymbol{s}\right) \leqslant \boldsymbol{C}_{\max }^{(p)}, (p=1, \cdots, P) $ | (19) |
以及连续性约束为
| $ \begin{gathered} \boldsymbol{L}_{\mathrm{c}}\left(\boldsymbol{x}^{(p)}\left(t_{\mathrm{f}}^{(p)}\right), t_{\mathrm{f}}^{(p)}, \boldsymbol{x}^{(p)}\left(t_0^{(p+1)}\right), t_0^{(p+1)}\right)=\mathit{\pmb{0}}, \\ (p=1, \cdots, P-1) \end{gathered} $ | (20) |
于是式(17)~(20)构成多阶段最优控制问题POCP。POCP的标准形式为
| $ \begin{cases}\min & J_{\mathrm{OCP}} \\ \text { s. t. } & \boldsymbol{h}_{\mathrm{OCP}}(\boldsymbol{x}, \boldsymbol{u}, t, \boldsymbol{s})=\mathit{\pmb{0}} \\ & \boldsymbol{g}_{\mathrm{OCP}}(\boldsymbol{x}, \boldsymbol{u}, t, \boldsymbol{s}) \leqslant \mathit{\pmb{0}}\end{cases} $ | (21) |
式中:hOCP为最优控制问题等式约束函数, gOCP为最优控制问题不等式约束函数。
2.2 多阶段最优控制问题伪谱离散Radau伪谱法(Radau pseudospectral method, RPM)将最优控制问题(OCP)的状态变量和控制变量离散到一系列Radau勒让德(Legendre-Gauss-Radau, LGR)节点上,并以经过这些节点的拉格朗日插值多项式近似状态变量和控制变量,从而将连续的无限维OCP转化为有限维NLP。LGR节点是非对称、非等间距的,采用它的根作为插值节点可以避免等距高阶多项式插值经常出现的龙格现象[21]。相比Gauss伪谱法,RPM没有附加的积分约束,更为简洁[22]。
Radau多项式是N阶勒让德多项式
| $ R_N(\tau)=\tilde{L}_N(\tau)-\tilde{L}_{N-1}(\tau), \tau \in[-1, 1] $ | (22) |
Radau伪谱法的配置点为Radau多项式的N个根τa, a=1, …, N。
RPM的伪谱时间τ∈[-1, 1]与物理时间t(p)∈[t0(p), tf(p)]的物理时间映射关系为
| $ t^{(p)}=\frac{t_{\mathrm{f}}^{(p)}-t_0^{(p)}}{2} \tau+\frac{t_{\mathrm{f}}^{(p)}+t_0^{(p)}}{2}, (p=1, \cdots, P) $ | (23) |
状态变量和控制变量由拉格朗日多项式近似为:
| $ \boldsymbol{x}^{(p)}({\tau}) \approx \boldsymbol{X}^{(p)}({\tau})=\sum\limits_{i=1}^{N^{(p)}+1} \boldsymbol{X}_i^{(p)} L_i({\tau}) $ | (24) |
| $ \boldsymbol{u}^{(p)}({\tau}) \approx \boldsymbol{U}^{(p)}({\tau})=\sum\limits_{i=1}^{N^{(p)}} \boldsymbol{U}_i^{(p)} L_i({\tau}) $ | (25) |
式中Li为第i个节点对应的拉格朗日多项式函数的基函数,写作:
| $ L_i(\tau)=\prod\limits_{\substack{h=1 \\ h \neq i}}^{N^{(p)}+1} \frac{\tau-\tau_h}{\tau_i-\tau_h}, \left(i=1, \cdots, N^{(p)}+1\right) $ | (26) |
式中:N(p)为第p个阶段配置点数目, Xi(p)、Ui(p)分别为第p个阶段第i个节点的状态变量和控制变量。
对状态插值多项式(24)两端微分可得
| $ \frac{\mathrm{d} \boldsymbol{X}^{(p)}}{\mathrm{d} \tau}=\sum\limits_{i=1}^{N(p)+1} \boldsymbol{X}_i^{(p)} \frac{\mathrm{d} L_i({\tau})}{\mathrm{d} \tau} $ | (27) |
进一步可以得到:
| $ \boldsymbol{X}^{(p)} \boldsymbol{D}=\frac{t_{\mathrm{f}}^{(p)}-t_0^{(p)}}{2} \boldsymbol{f}^{(p)}\left(\boldsymbol{X}^{(p)}, \boldsymbol{U}^{(p)}, t_0^{(p)}, t_{\mathrm{f}}^{(p)}\right) $ | (28) |
式中:
| $ \boldsymbol{D}_{a, i}=\frac{\mathrm{d} L_i\left(\tau_a\right)}{\mathrm{d} \tau}, (a=1, \cdots, N ; i=1, \cdots, N+1) $ | (29) |
RPM路径约束的离散形式为
| $ \begin{gathered} \boldsymbol{C}_{\min }^{(p)} \leqslant \boldsymbol{C}^{(p)}\left(\boldsymbol{X}_i^{(p)}, \boldsymbol{U}_i^{(p)}, {\tau}_i, t_0^{(p)}, t_{\mathrm{f}}^{(p)}\right) \leqslant \boldsymbol{C}_{\max }^{(p)}, \\ \left(p=1, \cdots, P ; i=1, \cdots, N^{(p)}\right) \end{gathered} $ | (30) |
相似地,离散化的连续性约束为
| $ \boldsymbol{L}_c\left(X_{N(p)}^{(p)}, t_{\mathrm{f}}^{(p)}, X_0^{(p+1)}, t_0^{(p+1)}\right)=0, (p=1, \cdots, P-1) $ | (31) |
由数值分析理论[23]可知,目标函数离散形式为
| $ \begin{aligned} J= & \sum\limits_{p=1}^P \varPhi^{(p)}\left(\boldsymbol{x}_0^{(p)}, t_0^{(p)}, \boldsymbol{x}_{\mathrm{f}}^{(p)}, t_{\mathrm{f}}^{((p)}, \boldsymbol{s}\right)+ \\ & \sum\limits_{p=1}^P \frac{t_{\mathrm{f}}^{(p)}-t_0^{(p)}}{2} \sum\limits_{a=1}^{N^{(p)}} \omega_a^{(p)} \phi_a^{(p)} \end{aligned} $ | (32) |
式中:ϕa(p)为第p阶段被积函数在第a个配置点的值, ωa(p)为对应配置点的积分权系数。积分系数公式为
| $ \omega_a= \begin{cases}\frac{2}{N^2}, & a=1 \\ \frac{1-\tau_a}{N^2 \tilde{L}_N\left(\tau_a\right)^2}, & a=2, \cdots, N\end{cases} $ | (33) |
于是无限维的多阶段最优控制问题POCP被转化为有限维非线性规划问题PNLP,其标准形式为
| $ \begin{cases}\min & J_{\mathrm{NLP}}(\boldsymbol{z}) \\ \text { s. t. } & \boldsymbol{h}_{\mathrm{NLP}}(\boldsymbol{z})=\mathit{\pmb{0}} \\ & g_{\mathrm{NLP}}(\boldsymbol{z}) \leqslant \mathit{\pmb{0}}\end{cases} $ | (34) |
式中:z为包含所有决策变量的决策变量向量, hNLP(z)为非线性规划问题等式约束函数列向量, gNLP(z)为非线性规划问题不等式约束函数列向量。标准化后的非线性规划问题PNLP采用序列二次规划求解器SNOPT求解。
3 仿真和分析本文针对某型号的滑翔增程制导炮弹进行仿真分析,采用多阶段Radau伪谱法对滑翔增程制导炮弹弹道规划问题进行求解。首先为验证本文TPM-CS方法的有效性,对安装不同性能(最大探测距离和视场角)导引头制导炮弹大着角方案弹道进行规划,然后与传统TPM方法进行仿真对比,以验证其优越性。
3.1 仿真参数设置滑翔制导炮弹出炮口初速为800 m/s;气动参数由风洞吹风试验获得;大气模型采用美国1976标准大气模型;为了满足大着角攻击要求,令θfU=-80°,助推火箭工作时长为14.068 s。其他参数见表 1~4。
| 表 1 制导炮弹参数 Tab. 1 Parameters of guided projectile |
| 表 2 弹道变量的上、下边界 Tab. 2 Upper and lower bounds of ballistic variables |
| 表 3 各阶段持续时长的上、下边界 Tab. 3 Upper and lower bounds of the duration of each phase |
| 表 4 目标函数权值系数 Tab. 4 Weight coefficient of the objective function |
由于本文方案弹道设计任务要求中没有禁飞区或必须经过航路点等需要较大侧向运动的需求,目标函数中对侧滑角的惩罚部分会使方案弹道近乎在弹道面内,即侧向平面内弹目视线偏离导引头轴线的角度近乎为零(仿真结果会证明这一点),于是惩罚系数w2, 2可以设置为零。
3.2 不同导引头约束仿真本文通过设置导引头最大探测距离和视场角,模拟对安装不同性能导引头的制导炮弹进行仿真分析,以验证本文TPM-CS方法的有效性。本文的数值仿真中,目标坐标为(50,0,-5)km。
3.2.1 导引头最大探测距离对方案弹道的影响本文选取3种不同性能的导引头进行仿真分析。3种导引头的视场角相同,最大探测距离不同,具体参数见表 5。
| 表 5 不同最大探测距离算例 Tab. 5 Examples of different maximum detection distances |
仿真结果如图 3和表 6、7所示。由图 3(c)、3(d)和表 5可知,炮弹目标视线相对导引头基准轴在高低和方位两个方向的偏离角都小于视场角,满足本文建立的视场角约束。由表 5、6可知,末制导起始点与目标距离RMT和导引头最大探测距离Rs相等,证明了本文建立末制导起始点约束的有效性。
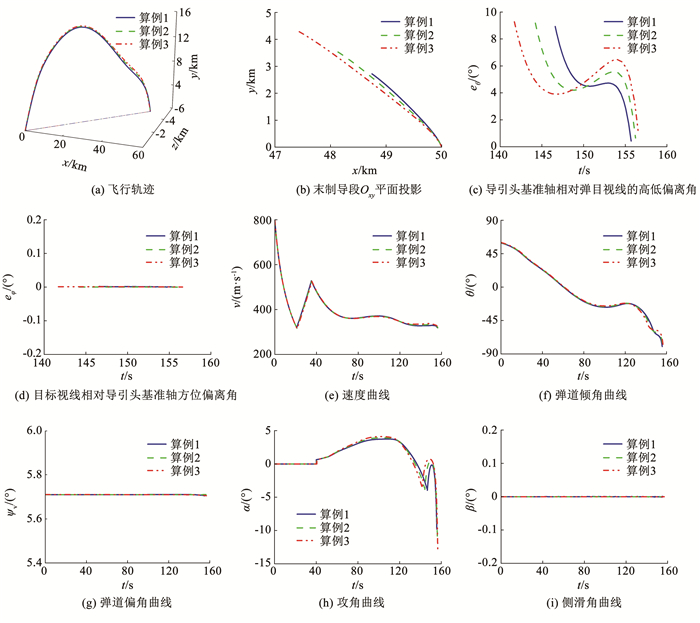
|
图 3 不同最大探测距离优化结果 Fig. 3 Optimization results of different maximum detection distances |
| 表 6 最优化末制导起始点 Tab. 6 Optimal starting point of terminal guidance phase |
| 表 7 时间节点最优解 Tab. 7 Optimal solution of time nodes |
由图 3(a)~3(i)可知,导引头最大探测距离变化主要影响纵向平面内弹道诸元,对侧向平面内弹道诸元没有影响。由图 3(f)可知,导引头最大探测距离越大,方案弹道初始弹道倾角越大,弹道高程越高。由图 3(h)可知,导引头最大探测距离越大,所需攻角控制量越大。由表 7可知,导引头最大探测距离对全弹道飞行时长影响不大。
3.2.2 导引头视场角约束对方案弹道的影响本文选取最大探测距离相同视场角不同的3种导引头,具体参数见表 8。
| 表 8 不同视场角约束算例 Tab. 8 Examples of different field of view angle constraints |
仿真结果如图 4所示(结果与导引头最大探测距离对方案弹道影响的仿真结果类似,仅展示部分对视场角约束敏感的曲线,后续仿真结果类推,不再重复说明)。
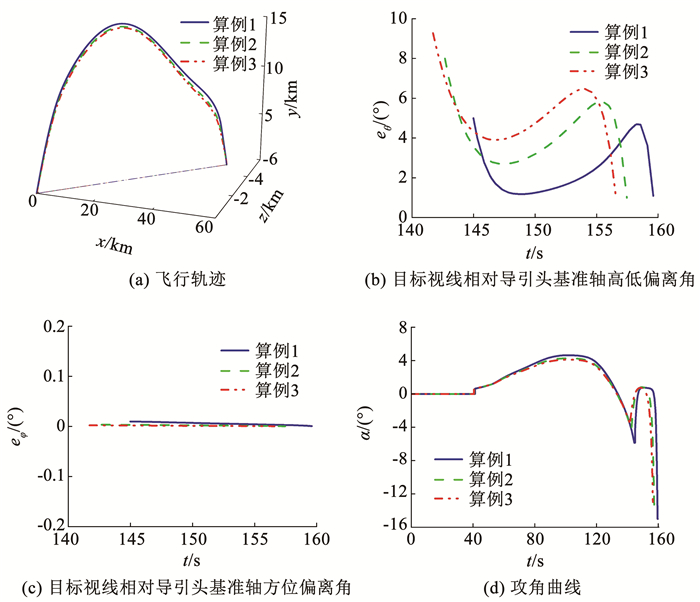
|
图 4 不同视场角约束优化结果 Fig. 4 Optimization results with different field of view angle constraints |
由图 4(d)和表 8可知,导引头视场角越小,攻角幅值越大。由图 4(b)、4(c)和表 8可知,炮弹目标视线相对导引头基准轴在高低和方位两个方向的偏离角都小于视场角,满足视场角约束。证明本文所提TPM-CS方法对安装了不同视场角大小导引头的制导炮弹都有效。
3.3 与传统TPM对比本文针对某型号的滑翔增程制导炮弹进行仿真分析,分别采用本文TPM-CS方法和文献[24]所提TPM方法规划方案弹道,以验证TPM-CS方法的优越性。
本文仿真中,导引头最大探测距离Rs=5 000 m,视场角为ε=5°,目标坐标为(50,0,0) km。
仿真结果如图 5和表 9~11所示。(注:TPM方法未单独规划末制导段,为便于对比分析,采用线性插值的方式取弹目间距RMT=Rs处为其期望末制导起始点。其真实末制导起始点为目标视线相对导引头基准轴偏离角等于导引头视场角的点,如图 5(c)中A点。)

|
图 5 TPM-CS方法和TPM方法对比仿真结果 Fig. 5 Comparison of simulation results between TPM-CS method and TPM method |
| 表 9 末制导起始点弹道倾角、视线高低角及偏差 Tab. 9 Path angle, line of sight angle and deviation at the starting point of terminal guidance phase |
| 表 10 最优化末制导起始点 Tab. 10 Optimization results of the starting point of terminal guidance |
| 表 11 时间节点最优解 Tab. 11 Optimal solution of time nodes |
由图 5(b)和表 9可知,TPM方法规划的方案弹道,在末制导起始点,导引头基准轴与弹目视线偏离17.6°,大于导引头视场角ε,导引头无法捕获目标。然而,TPM-CS方法规划的方案弹道,在末制导起始点,导引头基准轴与弹目视线仅偏离5°,偏差角缩小71.590%,目标恰好位于导引头视场边缘,且之后的飞行过程中,目标一直位于视场内部,即,导引头在开启瞬间就能捕获目标并在整个末制导段保持照射目标的状态。
由图 5(c)、5(d)可知,TPM方法规划的方案弹道,如果导引头一直保持开启状态搜索目标,给予足够时间,导引头最终亦能捕获目标,但会减少制导系统修正弹目位置偏差的时间和空间,如图 5(c)和表 11中所示,TPM方法规划的方案弹道留给制导系统修正偏差的时间仅2.069 s,而TPM-CS方法规划的方案弹道长达14.731 s,有效末制导时长增长6.120倍。如果目标的预警系统在导引头搜索过程中发现导引头搜索信号,在未被捕获前采取规避逃离动作,制导炮弹按照TPM方法规划方案弹道飞行,导引头可能无法搜索到目标,即导引头捕获目标失败。而制导炮弹按照TPM-CS方法规划的方案弹道飞行,可以在导引头最大探测距离处,在导引头开启瞬间捕获目标,不会给予目标逃离的机会。
综上所述,TPM-CS方法相较于传统TPM方法有较大优势,对于工程实践有一定现实意义。
4 结论1) 采用本文所提TPM-CS方法规划的方案弹道,均满足导引头最大探测距离约束和导引头视场角约束,验证了TPM-CS方法的有效性。
2) 采用本文所提TPM-CS方法规划的方案弹道,最大探测距离越大,对纵向控制量要求越高;导引头视场角越小,对纵向控制量要求也越高。
3) 相较于TPM方法,本文提出的TPM-CS方法实现了在导引头最大探测距离处,导引头基准轴与弹目视线的偏差角缩小71.590%,并且在末制导段导引头对目标保持照射的时间增长6.120倍,这为末制导预留了更充裕的时间修正偏差以实现最终的精确打击。
| [1] |
祁载康, 曹翟, 张天桥. 制导弹药技术[M]. 北京: 北京理工大学出版社, 2002. QI Zaikang, CAO Zhai, ZHANG Tianqiao. Guided ammunition technology[M]. Beijing: Beijing Institute of Technology Press, 2002. |
| [2] |
姜殿元. 激光制导炮弹―铜斑蛇[J]. 飞航导弹, 1989(2): 1. JIANG Dianyuan. Laser-guided cannonball-copperhead snake[J]. Aerodynamic Missile Journal, 1989(2): 1. DOI:10.16338/j.issn.1009-1319.1989.02.001 |
| [3] |
刘箴, 刘东洋. 国外典型激光制导武器发展综述[J]. 飞航导弹, 2021(4): 20. LIU Zhen, LIU Dongyang. A summary of the development of typical laser-guided weapons abroad[J]. Aerodynamic Missile Journal, 2021(4): 20. DOI:10.16338/j.issn.1009-1319.20200252 |
| [4] |
史金光, 王中原, 孙洪辉, 等. 制导炮弹滑翔弹道优化设计方法研究[J]. 南京理工大学学报, 2011, 35(5): 610. SHI Jinguang, WANG Zhongyuan, SUN Honghui, et al. Optimization design method for glide trajectory of guided projectiles[J]. Journal of Nanjing University of Science and Technology, 2011, 35(5): 610. DOI:10.14177/j.cnki.32-1397n.2011.05.022 |
| [5] |
孙瑞胜, 薛晓中, 沈坚平. 一种乘波外形导弹增程段弹道的最优控制解法[J]. 弹道学报, 2008, 20(4): 57. SUN Ruisheng, XUE Xiaozhong, SHEN Jianping. Trajectory optimization for a hypersonic waverider missile in extended range period by means of optimal control[J]. Journal of Ballistics, 2008, 20(4): 57. |
| [6] |
BENSON D. A gauss pseudospectral transcription for optimal control[D]. Boston: Massachusetts Institute of Technology, 2005
|
| [7] |
BETTS J T. Practical methods for optimal control and estimation using nonlinear programming[M]. 2nd ed. Philadelphia: SIAM, 2010. DOI:10.1137/1.9780898718577
|
| [8] |
黄育秋, 何麟书. 升力式再入飞行器多约束多阶段弹道优化设计[J]. 哈尔滨工业大学学报, 2011, 43(7): 144. HUANG Yuqiu, HE Linshu. Multi-constraints and multi-phases trajectory optimization of lift reentry vehicle[J]. Journal of Harbin Institute of Technology, 2011, 43(7): 144. DOI:10.11918/j.issn.0367-6234.2011.07.030 |
| [9] |
高长生, 陈尔康, 荆武兴. 高超声速飞行器机动规避轨迹优化[J]. 哈尔滨工业大学学报, 2017, 49(4): 16. GAO Changsheng, CHEN Erkang, JING Wuxing. Maneuver evasion trajectory optimization for hypersonic vehicles[J]. Journal of Harbin Institute of Technology, 2017, 49(4): 16. DOI:10.11918/j.issn.0367-6234.201605015 |
| [10] |
宣颖, 张为华, 张育林. 基于Legendre伪谱法的固体运载火箭轨迹优化研究[J]. 固体火箭技术, 2008, 31(5): 425. XUAN Ying, ZHANG Weihua, ZHANG Yulin. Trajectory optimization of solid launch vehicle based on Legendre pseudospectral method[J]. Journal of Solid Rocket Technology, 2008, 31(5): 425. DOI:10.3969/j.issn.1006-2793.2008.05.001 |
| [11] |
刘超越, 张成. 基于高斯伪谱法的二级助推战术火箭多阶段轨迹优化[J]. 兵工学报, 2019, 40(2): 292. LIU Chaoyue, ZHANG Cheng. Multi-stage trajectory optimization of tactical two-stage booster rocket based on Gauss pseudospectral method[J]. Acta Armamentarii, 2019, 40(2): 292. DOI:10.3969/j.issn.1000-1093.2019.02.009 |
| [12] |
史金光, 王中原, 易文俊. 滑翔增程弹方案弹道特性的研究[J]. 弹道学报, 2003, 15(1): 51. SHI Jinguang, WANG Zhongyuan, YI Wenjun. A study on the project trajectory characte-ristics of gliding extended range projectile[J]. Journal of Ballistics, 2003, 15(1): 51. DOI:10.3969/j.issn.1004-499X.2003.01.011 |
| [13] |
史金光, 王中原, 易文俊, 等. 滑翔增程弹弹道特性分析[J]. 兵工学报, 2006, 27(2): 210. SHI Jinguang, WANG Zhongyuan, YI Wenjun, et al. Analysis on the ballistic characteristics of gliding extended range projectile[J]. Acta Armamentarii, 2006, 27(2): 210. DOI:10.3321/j.issn:1000-1093.2006.02.005 |
| [14] |
李勇. 制导炮弹弹道规划与制导方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2018 LI Yong. Research on ballistic planning and guidance methods for guided projectiles[D]. Harbin: Harbin Institute of Technology, 2018 |
| [15] |
陈琦, 王中原, 常思江. 基于gauss伪谱法的滑翔弹道快速优化[J]. 弹道学报, 2014, 26(2): 17. CHEN Qi, WANG Zhongyuan, CHANG Sijiang. Rapid optimization of gliding trajectory based on Gauss pseudospectral method[J]. Journal of Ballistics, 2014, 26(2): 17. DOI:10.3969/j.issn.1004-499X.2014.02.004 |
| [16] |
陈琦, 王中原, 常思江, 等. 不确定飞行环境下的滑翔制导炮弹方案弹道优化[J]. 航空学报, 2014, 35(9): 2593. CHEN Qi, WANG Zhongyuan, CHANG Sijiang, et al. Optimal trajectory design under uncertainty for a gliding guided projectile[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(9): 2593. DOI:10.7527/s1000-6893.2014.0094 |
| [17] |
XU Qiuping, CHANG Sijiang, WANG Zhongyuan. Composite-efficiency-factor-based trajectory optimization forgliding guided projectiles[J]. Journal of Spacecraft and Rockets, 2018, 55(1): 66. DOI:10.2514/1.A33720 |
| [18] |
陈琦. 滑翔增程制导炮弹弹道优化及制导控制方法研究[D]. 南京: 南京理工大学, 2017 CHEN Qi. Investigation on trajectory optimization and guidance & control scheme for a type of gliding guided projectiles[D]. Nanjing: Nanjing University of Science and Technology, 2017 |
| [19] |
徐秋坪. 滑翔制导炮弹弹道规划及其自抗扰控制系统研究[D]. 南京: 南京理工大学, 2018 XU Qiuping. Trajectory optimization and active-disturbance-rejection control system for gliding guided projectiles[D]. Nanjing: Nanjing University of Science and Technology, 2018 |
| [20] |
钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M]. 3版. 北京: 北京理工大学出版社, 2006. QIAN Xingfang, LIN Ruixiong, ZHAO Yanan. Missile flight mechanics[M]. 3rd ed. Beijing: Beijing Institute of Technology Press, 2006. |
| [21] |
李庆扬, 王能超, 易大义. 数值分析[M]. 5版. 北京: 清华大学出版社, 2008. LI Qingyang, WANG Nengchao, YI Dayi. Numerical analysis[M]. 5th ed. Beijing: Tsinghua University Press, 2008. |
| [22] |
GARG D, PATTERSON M A, FRANCOLIN C, et al. Direct trajectory optimization and costate estimation of finite-horizon and infinite-horizon optimal control problems using a Radau pseudospectral method[J]. Computational Optimization and Applications, 2011, 49(2): 335. DOI:10.1007/s10589-009-9291-0 |
| [23] |
PATTERSON M A, RAO A V. GPOPS-Ⅱ: A MATLAB software for solving multiple-phase optimal control problems using hp-adaptive Gaussian quadrature collocation methods and sparse nonlinear programming[J]. ACM Transactions on Mathematical Software, 2014, 41(1): 1. DOI:10.1145/2558904 |
| [24] |
CHEN Qi, WANG Zhongyuan. Optimal trajectory for time-on-target of a guided projectile using direct collocation method[C]//Proceedings 2013 International Conference on Mechatronic Sciences, Electric Engineering and Computer (MEC). Shenyang, China: IEEE, 2014: 2803. DOI: 10.1109/MEC.2013.6885506
|
 2023, Vol. 55
2023, Vol. 55


