2. 机器人技术与系统国家重点实验室(哈尔滨工业大学), 哈尔滨 150000;
3. 芜湖哈特机器人产业技术研究院有限公司博士后工作站, 安徽 芜湖 241007;
4. 长三角哈特机器人产业技术研究院, 安徽 芜湖 241007;
5. 安徽工程大学 计算机与信息学院, 安徽 芜湖 241000
2. State Key Laboratory of Robotics and System (Harbin Institute of Technology), Harbin 150000, China;
3. Post-Doctoral Research Center, Wuhu HIT Robot Technology Research Institute Co., LTD, Wuhu 241007, Anhui, China;
4. Yangtze River Delta HIT Robot Technology Research Institute, Wuhu 241007, Anhui, China;
5. School of Computer and Information, Anhui Polytechnic University, Wuhu 241000, Anhui, China
工业机器人技术的研发与应用是衡量国家科技创新和高端装备制造业高质量发展的重要标志。基于工业机器人打磨已成为高端制造业中打磨和抛光等连续接触式作业的有力抓手,是解决人工作业工作效率低和工作环境危害大以及提升产品质量的重要工具之一。高性能打磨工业机器人作为新兴产业和技术的重要载体和现代产业的关键装备,强力支撑持续促进生产水平提高,有力推动智能制造高质量发展。
机器人打磨作业适应复杂曲面多变的接触环境需要具备一定的柔顺性能,从而提高工件表面加工质量。由于被动柔顺控制不能实时调整控制力大小,且通用性差,只适用于控制精度要求不高的工况,于是具有力反馈的主动柔顺控制是机器人柔顺恒力控制的主要研究方向。为了以可控方式进行机器人柔顺恒力打磨[1],国内、外学者对机器人主动柔顺控制方法开展了诸多研究。张新艳等[2]提出一种基于深度强化学习与有限元仿真集成的压边力控制模型,结合深度神经网络的感知能力与强化学习的决策能力,进行力控制策略的学习优化。Zhang等[3]设计一种基于径向基函数神经网络的控制器,用于机器人跟踪控制,减小机器人的振动与提高系统的稳定性。Xu等[4]提出一种将力/位置混合控制与PI/PD控制相结合的机器人打磨力控制方法,提高机器人打磨过程中力控制的稳定性和可靠性。Mohsin等[5]提出一种基于刀具路径规划、力控制和抛光参数优化的复杂曲面机器人抛光控制方法。Gracia等[6]提出一种基于滑模控制和任务优先级的机器人混合力/位置控制方法,用于打磨、抛光、去毛刺等工件表面处理作业。Kakinuma等[7]构建一种基于宏微机构的机器人抛光控制系统,实现动态抛光力控制。Lakshminarayanan等[8]提出一种基于阻抗控制的迭代学习控制器,用于机器人抛光作业中跟踪工件轮廓与调整位置和力。Kana等[9]提出一种基于阻抗控制的协作曲线跟踪控制方法,实现人机协作的边缘倒角和抛光任务。Zhu等[10]提出一种具有接触点变化补偿的机器人姿态/力混合控制结构,实现不确定环境下的力跟踪控制。Zhang等[11]提出一种基于阻抗控制的力协调控制方法,用于减小机器人作业工具和工件之间的临界接触造成的冲击。Ochoa等[12]提出一种阻抗控制方法,用于模具抛光任务的机器人末端执行器姿态优化。由于机器人打磨作业接触环境复杂多变且难以预测,上述控制方法[5, 7, 9]的控制性能对模型精度要求较高,控制方法[6, 10]与控制器[8]计算量较大,存在难以确定控制边界条件稳定等不足和局限。
机器人连续接触式打磨作业需要机器人和工件之间具有较好的交互性[13-14],为提高工件打磨质量,机器人打磨主动适应复杂曲面多变的接触环境、精确控制施加到工件接触面法线方向的打磨力,对于实现柔顺打磨作业尤为重要。现有力控制模型分为通过调整机器人所有关节和姿态来跟踪力的机器人控制模式[15-18]和带有可调节功能末端执行器的宏微型机器人控制模式[19-21]。前者由于存在惯性大、调节周期长等不足,容易出现控制响应慢和鲁棒性差等问题,后者可实时调整打磨力,但仍存在部分宏微型机器人控制模式的控制精度不够高或动态响应偏慢等局限,不易实现复杂曲面机器人打磨柔顺作业。另外,机器人末端执行器与工件的打磨接触作业过程具有时变且高度非线性耦合特征,加之不确定性扰动的影响,通常采用PID控制无法较好满足时变非线性系统控制的精度高和动态响应快等要求[22]。
本文为了解决机器人打磨过程中存在复杂时变非线性耦合与不确定性扰动导致机器人柔顺恒力打磨自适应调节能力不足的问题,开展机器人打磨自适应变阻抗主动柔顺恒力控制研究。首先,给出一种可以实现伸缩平移及旋转运动解耦的力控末端执行器,解决刚性末端执行器动态响应慢或运动不准确导致打磨工具或工件变形损坏甚至工件过切问题。其次,设计一种自抗扰控制器,解决机器人打磨过程中不确定性扰动的控制稳定性问题;同时,设计一种粒子群优化神经网络变阻抗控制器,用于在线自适应优化阻抗参数,动态调节打磨力修正量;在此基础上,提出一种机器人自适应变阻抗主动柔顺恒力控制方法,用于机器人力控末端执行器,解决复杂多变工况环境机器人打磨控制系统的主动适应性差与打磨作业柔顺性差的问题。最后,通过机器人打磨系统虚拟样机联合仿真实验和机器人平台实物实验,验证所提出机器人自适应变阻抗主动柔顺恒力控制方法的有效性。在此说明,本文中恒力控制的打磨力均指法向打磨力。
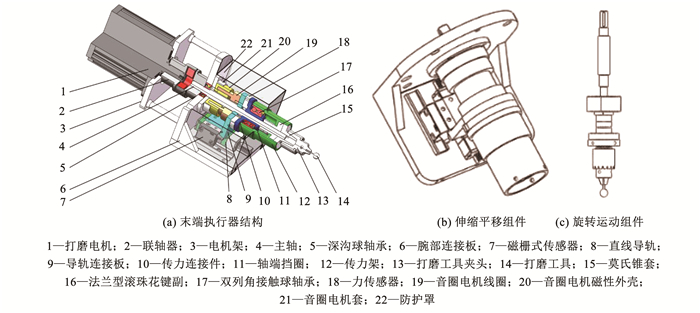
1 机器人力控末端执行器给出一种机器人力控末端执行器结构,如图 1所示。所设计结构的关键部分包括伸缩平移组件(如图 1(b)所示)和旋转运动组件(如图 1(c)所示),前者主要由音圈电机、双列角接触球轴承、传力连接件、导轨连接板组成,后者主要由打磨电机、主轴、深沟球轴承、传力架、法兰型滚珠花键副和打磨工具组成。
|
图 1 机器人力控末端执行器 Fig. 1 Robotic force-controlled end-effector |
所给出的机器人末端执行器可实现沿轴向伸缩平移运动和绕轴向旋转运动,其分别由伸缩平移组件和旋转运动组件驱动与控制,且可实现伸缩平移与旋转运动的解耦。所给出的机器人末端执行器的中空型音圈电机磁性外壳20固定安装于腕部连接板6,音圈电机线圈19连接到导轨连接板9,实现沿轴向伸缩平移运动。作业过程中传递到导轨连接板9的伸缩平移运动通过传力连接件10和中空型力传感器18传输到双列角接触球轴承17的内侧,双列角接触球轴承17的外侧与传力架12过盈配合,同时允许传力架12和传力连接件10之间的相对旋转运动。主轴4的上部连接至打磨电机1,中间部分采用深沟球轴承5支撑以承载径向负载,下部为具有滚道槽的花键轴段,与法兰型滚珠花键副16连接,传力架12连接至法兰型滚珠花键副16将旋转运动传递给打磨工具14,实现平移和旋转运动的可靠解耦。通过调节音圈电机伸缩量控制机器人法向打磨力,可以有效避免使用刚性末端执行器时因动态响应慢或运动不准确而导致打磨工具或工件变形损坏甚至工件过切问题,为实现机器人打磨系统主动柔顺恒力控制提供优良结构基础。所给出机器人末端执行器通用性强,通过腕部连接板6与机器人末端法兰装配连接,可与不同串联与并联型式机器人适配,适应多场景的打磨作业。
所给出的机器人末端执行器结构中,采用轴肩方式分别对联轴器和轴承进行轴向定位,主轴为台阶轴形式,3段轴段直径分别为10、12、16 mm;打磨电机选用松下伺服电机MSMF082L1及MCDLT35SF驱动器,额定功率为750 W,额定转速为3 000 r/min,额定扭矩为2.39 N·m;音圈电机选用MOTICONT公司HVCM-051-025-019-01及810系列驱动器,最大持续输出力为67.4 N,最大行程12.7 mm;联轴器选用LM50型梅花形弹性联轴器,公称扭矩为28.0 N·m;法兰型滚珠花键副选用SLF10,额定扭矩为15.88 N·m;力传感器选用ATI公司F/T Delta IP65六维力传感器,力采集精度为1/8 N,采样频率为3 000 Hz;磁栅式传感器选用RLS公司HILIN系列直线式增量磁栅式传感器,最高分辨率达0.1 μm;打磨工具采用球形红刚玉磨头。
2 机器人主动柔顺恒力控制机器人末端执行器与工件的打磨作业接触动力学行为具有时变且高度非线性耦合特征,加之复杂零部件打磨需频繁变换末端执行器打磨姿态,在连续非周期性外部激励和不确定性扰动作用下极易引发机器人打磨作业系统的自激特性,致使发生打磨颤振。因此,开展机器人打磨自适应变阻抗主动柔顺恒力控制研究,解决机器人打磨过程中存在的复杂时变非线性耦合与不确定性扰动致使机器人柔顺恒力打磨自适应调节能力不足,以及在复杂多变的接触环境下机器人恒力打磨作业柔顺性与稳定性差的问题,对于提高机器人打磨系统对复杂零部件打磨颤振影响的鲁棒性、提升打磨作业柔顺性具有重要理论研究意义与实际应用价值。本文设计一种自抗扰控制器和一种粒子群优化神经网络变阻抗控制器(简称为PSO-BP变阻抗控制器),在此基础上,提出一种机器人自适应变阻抗主动柔顺恒力控制方法。在所提出方法中,内环控制采用所设计的自抗扰控制器,用于在打磨初始阶段及打磨过程中对期望力的大小和误差扰动进行估计和补偿,外环控制采用所设计的PSO-BP变阻抗控制器,用于在线自适应优化阻抗参数,动态调节打磨力修正量;内、外环控制共同作用构成闭环控制回路,实现机器人打磨作业自适应主动柔顺恒力打磨控制。
2.1 自抗扰控制器设计所研究机器人打磨控制系统可表示为二阶非线性控制系统模型:
| $ \ddot{y}(t)=f(\dot{y}(t), y(t), \omega(t))+b u $ | (1) |
式中:f(
| $ \left\{\begin{array}{l} \dot{x}_{1}=x_{2} \\ \dot{x}_{2}=x_{3}+b u \\ \dot{x}_{3}=f(\dot{y}(t), y(t), \omega(t)) \\ y=x_{1} \end{array}\right. $ | (2) |
将式(2)写成下式所示的矩阵形式:
| $ \begin{aligned} \dot{\boldsymbol{x}}= & \boldsymbol{A} \boldsymbol{x}+\boldsymbol{B}_{1} u+\boldsymbol{B}_{2} f(\dot{y}(t), y(t), \omega(t))= \\ & \boldsymbol{A x}+\boldsymbol{B}_{1} u+\boldsymbol{B}_{2} f(\boldsymbol{x}, \omega) \end{aligned} $ | (3) |
式中:
假设输入信号xd的跟踪信号为r,非线性误差反馈控制量为
| $ \left\{\begin{aligned} \dot{e}_{1}= & \dot{r}_{1}-\dot{x}_{1}=r_{2}-x_{2}=e_{2} \\ \dot{e}_{2}= & \dot{r}_{2}-\dot{x}_{2}=r_{3}-\left(x_{3}+b u\right)= \\ & -k_{1}\left(e_{1}+\tilde{x}_{1}\right)-k_{2}\left(e_{2}+\tilde{x}_{2}\right)-\tilde{x}_{3} \end{aligned}\right. $ | (4) |
式中k1、k2为控制参数。
设e=[e1 e2]T,
| $ \dot{\boldsymbol{e}}(t)=\boldsymbol{A}_{1} \boldsymbol{e}(t)+\boldsymbol{A}_{2} \tilde{\boldsymbol{x}}(t) $ | (5) |
式中:
由于机器人打磨作业属于减材加工方式,通常不允许产生过切等现象。为了实现闭环系统的信号过渡,引入最速综合函数[23]fhan(),并基于非线性系统模型设计以下离散自抗扰控制器(active disturbance rejection control, ADRC),在保证快速跟踪的前提下使输入信号不产生超调,提高系统鲁棒性,从而保证机器人打磨作业不发生过切。
1) 跟踪微分器:
| $ \left\{\begin{array}{l} f_{h}=h \text { fhan }\left(r_{1}(k)-x_{\mathrm{d}}, r_{2}(k), r_{0}, h_{0}\right) \\ r_{1}(k+1)=r_{1}(k)+h r_{2}(k) \\ r_{2}(k+1)=r_{2}(k)+h f_{h} \end{array}\right. $ | (6) |
式中:h为采样周期,fhan()为最速综合函数,r0为速度因子,h0为滤波因子。
2) 非线性状态误差反馈控制律:
| $ \left\{\begin{array}{l} e_{r_{1}}(k)=r_{1}(k)-\hat{x}_{1}(k) \\ e_{r_{2}}(k)=r_{2}(k)-\hat{x}_{2}(k) \\ u_{0}(k)=k_{1} e_{r_{1}}(k)+k_{2} e_{r_{2}}(k) \\ u(k)=\left[u_{0}(k)-\hat{x}_{3}(k)\right] / b \end{array}\right. $ | (7) |
3) 扩张状态观测器:
| $ \left\{\begin{array}{l} \varepsilon_{w}=\hat{x}_{1}(k)-y(k) \\ \hat{x}_{1}(k+1)=\hat{x}_{1}(k)+h\left[\hat{x}_{2}(k)-\beta_{01} \varepsilon_{w}\right] \\ \hat{x}_{2}(k+1)=\hat{x}_{2}(k)+h\left[\hat{x}_{3}(k)-\beta_{02} \varepsilon_{w}+b u(k)\right] \\ \hat{x}_{3}(k+1)=\hat{x}_{3}(k)-h \beta_{03} \varepsilon_{w} \end{array}\right. $ | (8) |
式中:er1为位置误差,er2为位置误差的微分,εw为扩张状态观测器的观测误差,β01、β02、β03为扩张状态观测器的增益参数。
由式(6)~(8)设计自抗扰控制器(控制框图如图 2所示),实现对位置误差估计与补偿。其对模型依赖性低,具有更高的控制精度、稳定性和较强的鲁棒性。具体流程为:1)采用跟踪微分器(tracking-differentiator, TD)对输入信号xd进行平滑过渡处理,得到r1及其微分r2;2)非线性状态误差反馈控制律(nonlinear law state error feedback, NLSEF)将位置误差er1及其微分er2进行非线性组合,获得控制量u0;3)扩张状态观测器(extended state observer, ESO)对打磨过程中系统内外扰动总和进行状态观测,得到输入信号补偿

|
图 2 自抗扰控制(ADRC)框图 Fig. 2 Block diagram of active disturbance rejection controller (ADRC) |
采用Lyapunov理论分析证明自抗扰控制器系统的闭环稳定性,即证明在求解打磨非线性系统问题时所设计的自抗扰控制器的跟踪误差收敛为零。
假定扩张状态观测器的估计误差
| $ e(t)=\mathrm{e}^{\boldsymbol{A}_{1} t} e(0)+\int_{0}^{t} \mathrm{e}^{\boldsymbol{A}_{1}(t-\mu)} \boldsymbol{A}_{2} \tilde{\boldsymbol{x}} \mathrm{d} \mu $ | (9) |
令
| $ \begin{gathered} |E(t)|=\left|\int_{0}^{t_{0}} \mathrm{e}^{\boldsymbol{A}_{1}(t-\mu)} \boldsymbol{A}_{2} \tilde{\boldsymbol{x}} \mathrm{d} \mu\right|+\left|\int_{t_{0}}^{t} \mathrm{e}^{\boldsymbol{A}_{1}(t-\mu)} \boldsymbol{A}_{2} \tilde{x} \mathrm{~d} \mu\right| \leqslant \\ \eta\left(\left|\boldsymbol{A}_{1}^{-1} \boldsymbol{A}_{2}\right|+\left|\boldsymbol{A}_{1}^{-1} \boldsymbol{A}_{2} \mathrm{e}^{\boldsymbol{A}_{1} t}\right|\right) \end{gathered} $ | (10) |
于是,式(9)可写为
| $ e(t) \leqslant \mathrm{e}^{\boldsymbol{A}_{1} t} e(0)+\eta\left(\left|\boldsymbol{A}_{1}^{-1} \boldsymbol{A}_{2}\right|+\left|\boldsymbol{A}_{1}^{-1} \boldsymbol{A}_{2} \mathrm{e}^{\boldsymbol{A}_{1} t}\right|\right) $ | (11) |
由|λI-A1|=k1+k2λ+λ2=0,存在k1和k2,使得特征方程有负特征值λ1和λ2,其中λ1>λ2,则存在可逆矩阵T,使
| $ \left\|\mathrm{e}^{\boldsymbol{A}_{1} t}\right\|_{2} \leqslant\|\boldsymbol{T}\|_{2} \mathrm{e}^{\lambda_{1} t}\left\|\boldsymbol{T}^{-1}\right\|_{2} $ | (12) |
因此,当控制参数k1和k2选定后,可得
| $ \lim\limits _{t \rightarrow \infty}\left\|\mathrm{e}^{\boldsymbol{A}_{1} t}\right\|_{2}=0 $ | (13) |
当t→∞时,eA1t→0,且由于η的任意性,结合式(11)~(13),进一步可得
为了实现机器人打磨作业恒力跟踪,将机器人末端执行器打磨作业力与位置的动态变化通过阻抗来表征,采用变阻抗控制调节末端执行器与工件接触的实际打磨力,使实际打磨力F相对于期望打磨力Fn的力误差Fe逐渐趋近于零,实现机器人打磨作业的期望打磨力跟踪。采用的阻抗控制模型为
| $ \left\{\begin{array}{l} F_{\mathrm{e}}=F_{\mathrm{n}}-F \\ M\left(\ddot{x}_{n}-\ddot{x}\right)+B\left(\dot{x}_{n}-\dot{x}\right)+K\left(x_{n}-x\right)=F_{\mathrm{e}} \end{array}\right. $ | (14) |
式中:M、B、K为阻抗控制模型的阻抗参数,分别表示惯性系数、阻尼系数和刚度系数;
对于接触环境复杂多变的机器人打磨作业工况,可以采用不受控制对象模型影响、适应性和鲁棒性较强的神经网络[24]对阻抗参数进行实时优化,解决定参数阻抗控制在打磨某些曲率变化较大曲面时发生失效等问题。而传统BP神经网络收敛速度较慢,迭代次数较高,泛化能力较差,稳定性不高,容易陷入局部最优[25]。本文采用全局搜索能力较强的粒子群优化算法作为神经网络的前馈控制,结合变参数阻抗控制、BP神经网络和粒子群优化算法,设计一种PSO-BP变阻抗控制器(控制框图如图 3所示)。该控制器具有根据控制系统的信息反馈和设定性能指标进行自学习和自稳定的优点,能够输出设定性能指标下的优化阻抗参数,解决通常定参数阻抗控制无法满足复杂多变接触环境下机器人打磨作业控制要求和稳定性的问题,提高变参数阻抗控制中自学习优化阻抗参数的鲁棒性。所设计的PSO-BP变阻抗控制器的控制流程图如图 4所示,主要步骤如下。

|
图 3 PSO-BP变阻抗控制器控制框图 Fig. 3 Control block diagram of PSO-BP variable impedance controller |

|
图 4 PSO-BP变阻抗控制器控制流程 Fig. 4 Control flow chart of PSO-BP variable impedance controller |
Step1 初始化权值矩阵。由打磨力误差、位置误差和速度误差构成神经网络的输入信号,并随机初始化输入权值系数win和输出权值系数wout。
Step2 权值矩阵寻优。采用粒子群优化算法对神经网络的输入、输出权值矩阵进行寻优,粒子群维度由输入和输出权值矩阵中元素个数决定,定义粒子适应度函数为
| $ f=f_{F}\left|F_{\mathrm{n}}-F_{x}\right|^{2}+f_{x}\left|x_{n}-x\right|^{2}+f_{v}\left|\dot{x}_{n}-\dot{x}\right|^{2} $ | (15) |
式中:Fx为当前打磨力,fF、fx、fv分别为打磨力、位置和速度的权数。
Step3 权值矩阵更新。更新下一代粒子群的速度和位置,使得粒子个体极值与全局极值更新。定义第i个粒子的位置向量xi=(xi1 xi2 … xiD),速度向量vi=(vi1 vi2 … viD),优化位置pi=(pi1 pi2 … piD);整个种群的优化位置pg=(pg1 pg2 … pgD)。在迭代过程中,第i个粒子由第i代进化到第i+1代对应速度和位置的更新规则为:
| $ \boldsymbol{v}_{i d}^{(i+1)}=\boldsymbol{\xi} \boldsymbol{v}_{i d}^{(i)}+c_1 r_{d 1}\left(\boldsymbol{p}_{i d}^{(i)}-\boldsymbol{x}_{i d}^{(i)}\right)+c_2 r_{d 2}\left(\boldsymbol{p}_{g d}^{(i)}-\boldsymbol{x}_{i d}^{(i)}\right) $ | (16) |
| $ \boldsymbol{x}_{i d}^{(i+1)}=\boldsymbol{x}_{i d}^{(i)}+\boldsymbol{v}_{i d}^{(i+1)} $ | (17) |
式中:i=1, 2, …, N;d=1, 2, …, D;N为粒子群规模,取为100;D为空间维度,取为6;ξ为惯性因子,取为0.9;c1、c2为学习因子,均取为2;rd1、rd2取[0, 1]之间的随机数;最大迭代次数取为2 500。
Step4 全局极值判断。①若全局极值大于或等于设定目标值,返回Step2;②若全局极值小于设定目标值或达到迭代次数上限,寻优结束,获得神经网络输入和输出权值矩阵的优化解,执行Step5。
Step5 变阻抗参数优化。①由输入权值矩阵优化解计算隐层第m个神经元的输入αm,通过激活函数tanh()将输入信号αm进行函数变换,输出信号bm为
| $ \left\{\begin{array}{l} \alpha_{m}=\boldsymbol{x}_{i} \boldsymbol{v}_{i m} \\ b_{m}=\frac{\exp \left(\alpha_{m}\right)-\exp \left(-\alpha_{m}\right)}{\exp \left(\alpha_{m}\right)+\exp \left(-\alpha_{m}\right)} \end{array}\right. $ | (18) |
② 由输出权值矩阵的优化解计算输出层第j个神经元的输入βj,通过激活函数sigmoid()将输入信号βj进行函数变换,输出优化的阻抗参数zj(如下式所示),优化结束。执行Step6。
| $ \left\{\begin{array}{l} \beta_{j}=b_{m} w_{\text {out }} \\ z_{j}=\frac{\exp \left(\beta_{j}\right)}{\exp \left(\beta_{j}\right)+\exp \left(-\beta_{j}\right)} \end{array}(j=1, 2, 3)\right. $ | (19) |
式中:zj(j=1, 2, 3)分别为阻抗控制模型的惯性系数M、阻尼系数B和刚度系数K。
Step6 根据打磨环境下控制系统信息反馈重复Step2~Step5,继续在线优化阻抗参数,实现机器人自适应变参数阻抗控制。
2.4 机器人自适应主动柔顺恒力控制为解决机器人打磨作业在复杂多变接触环境的恒力打磨作业柔顺性和稳定性差的问题并提升对复杂非线性耦合和不确定性扰动的鲁棒性,结合设计的自抗扰控制器和PSO-BP变阻抗控制器,提出一种机器人自适应变阻抗主动柔顺恒力控制方法(控制框图如图 5所示)。该方法的内环控制采用所设计的自抗扰控制器,用于对打磨期望力的大小和误差扰动进行估计和补偿,外环控制采用所设计的PSO-BP变阻抗控制器,用于在线自适应优化阻抗参数,动态调节打磨力修正量;内、外环控制共同作用构成闭环控制回路,通过自适应调节阻抗特性使机器人打磨接触刚度与作业柔顺性主动适应多变环境打磨工况,实现机器人打磨作业的自适应主动柔顺恒力控制。所提出方法的主要构成如下。

|
图 5 机器人自适应变阻抗主动柔顺恒力控制方法 Fig. 5 Robotic active compliance constant force control method with adaptive variable impedance |
1) 将粒子群优化算法作为神经网络的前馈控制,用于优化神经网络权值矩阵,改善神经网络寻优性能;所设计外环PSO-BP变阻抗控制器根据末端执行器末端反馈信息在线自适应优化阻抗参数,实现动态调节打磨力修正量解决定参数阻抗在打磨某些曲率变化较大曲面时发生打磨过度或不足、力控制精度低等问题。
2) 建立末端执行器沿轴向伸缩位移与环境刚度打磨力补偿模型,该补偿模型根据实际打磨力F(由力传感器实时获取)以及末端执行器沿轴向伸缩平移的实际位置x(由磁栅式传感器实时获取),计算获得环境刚度打磨力补偿量Fb,并结合期望力Fn作为变阻抗控制器的输入;输出为经阻抗模型表征的位置修正量xe;环境刚度打磨力补偿模型表达式为
| $ F_{b}=\left\{\begin{array}{cc} F-k_{x}\left(x-x_{\mathrm{d}}\right), & x>x_{\mathrm{d}} \\ 0, & x \leqslant x_{\mathrm{d}} \end{array}\right. $ | (20) |
式中kx为环境刚度值,其与工件材料属性有关。
3) 将位置修正量xe与期望位置xn及实际位置x相结合,作为内环ADRC控制器的输入xd(其表示打磨过程中控制系统存在的位置扰动,包含了对位置误差、位置误差变化率、打磨力补偿与期望力以及变参数阻抗模型表征的综合作业结果),并利用ADRC控制器中跟踪微分器(TD)的平滑性以及扩张状态观测器(ESO)的力扰动估计能力,对在初始打磨条件下以及打磨过程中期望力的大小和误差扰动进行估计和补偿,解决打磨过程中控制系统存在扰动问题。
4) 将ADRC控制器输出的力补偿量Fa与末端执行器随位置变化的重力补偿值Fg相结合,作为末端执行器期望力Fn的补偿量,解决打磨过程中产生打磨过度或不足问题。
在所提出方法中,环境刚度打磨力补偿与末端执行器轴向运动的耦合关系通过式(20)所示的环境刚度打磨力补偿量Fb,以及经过阻抗模型的传递表征的运动位置修正关系两者共同表征,并通过图 5所示的内环和外环控制共同作用,实现机器人打磨作业的自适应主动柔顺恒力控制。
3 仿真与实验将提出的机器人自适应变阻抗主动柔顺恒力控制方法设计为一种机器人自适应主动柔顺控制器,并将其作用到机器人力控末端执行器。分别通过机器人打磨系统虚拟样机联合仿真实验和机器人平台实物实验,与开环控制、PID控制、PID模糊变阻抗控制和自抗扰模糊变阻抗控制进行对比,验证所提出方法的有效性。
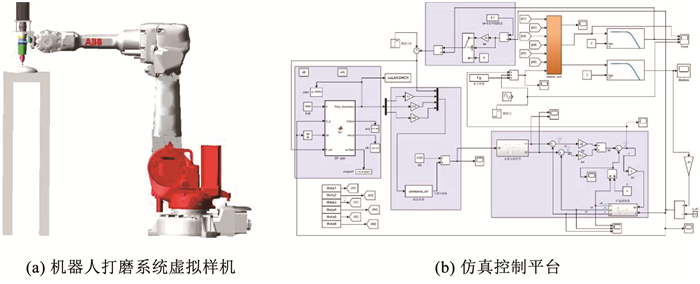
3.1 虚拟样机联合仿真实验所建立的Adams机器人打磨系统虚拟样机如图 6(a)所示(由六自由度串联工业机器人、所给出力控末端执行器及非球面曲面工件组成),Matlab/Simulink仿真控制平台如图 6(b)所示。
|
图 6 机器人打磨系统虚拟样机及仿真控制平台 Fig. 6 Virtual prototype of robotic grinding system and simulation control platform |
将机器人自适应主动柔顺控制器与开环控制、PID控制器对比,开展静态期望力打磨仿真实验,在仿真实验中,设定期望打磨运动为0.3 m/s匀速运动,打磨路径为一种光栅形路径。针对曲面工件打磨,结合环境刚度打磨力补偿与末端执行器轴向运动的耦合关系的表征形式和所提出方法的内、外环控制共同作用,并开展打磨路径规划和末端执行器位姿规划,实现曲面打磨作业。工件表面为一种二次非球面曲面,其曲面方程[26]为
| $ z=\frac{r_{e}^{2}}{R_{e}+\sqrt{R_{e}-\left(1+K_{e}\right) r_{e}^{2}}} $ | (21) |
式中:Re为顶点曲率半径,Ke为曲线常数,re2=x2+y2(x、y分别为横坐标和纵坐标),z为非球面的垂度。
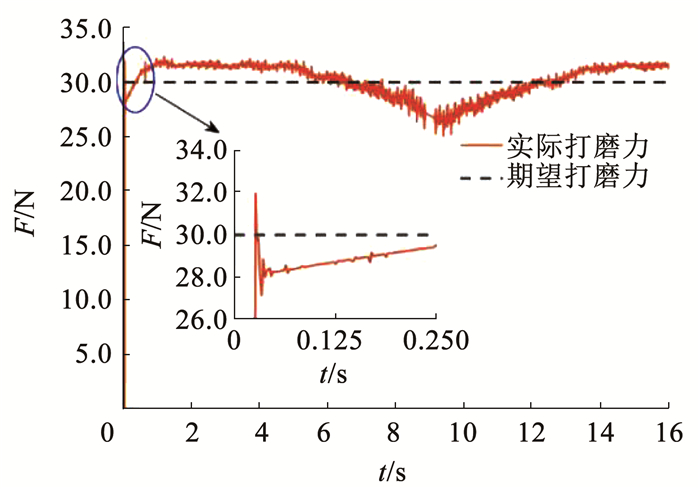
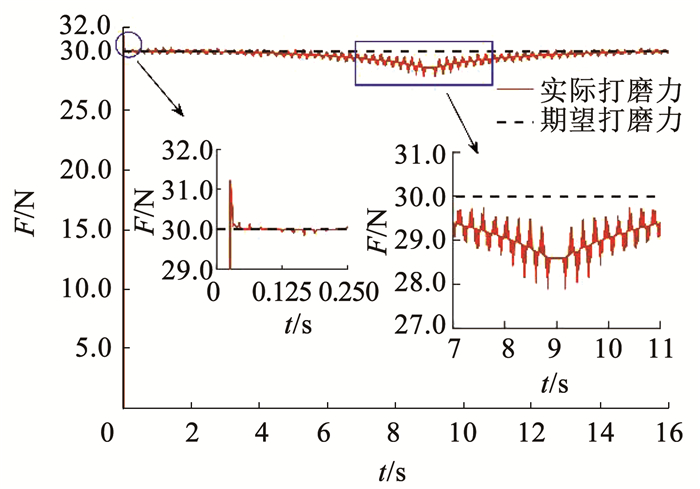
打磨电机转速均为3 000 r/min,期望打磨力设置为30.0 N。开环控制仿真结果如图 7所示,实际的最大打磨力为32.6 N,最小打磨力为25.2 N,无法满足跟踪期望打磨力要求,力稳定性较差,且在打磨工具接触工件瞬间产生超出期望打磨力的冲击力约为2.0 N,不能实现恒力控制。采用PID控制器和机器人自适应主动柔顺控制器的静态期望力仿真结果分别如图 8、9所示。其中PID控制器参数是根据经验先进行粗调整,再作微调整,多次优化调整后取KP=10,KI=0.02,KD=0.2。自抗扰控制器控制参数调整结果见表 1。
|
图 7 开环控制打磨(期望力30.0 N) Fig. 7 Open-loop control for robotic grinding(desired force 30.0 N) |
|
图 8 PID控制器打磨(期望力30.0 N) Fig. 8 PID controller for robotic grinding (desired force 30.0 N) |
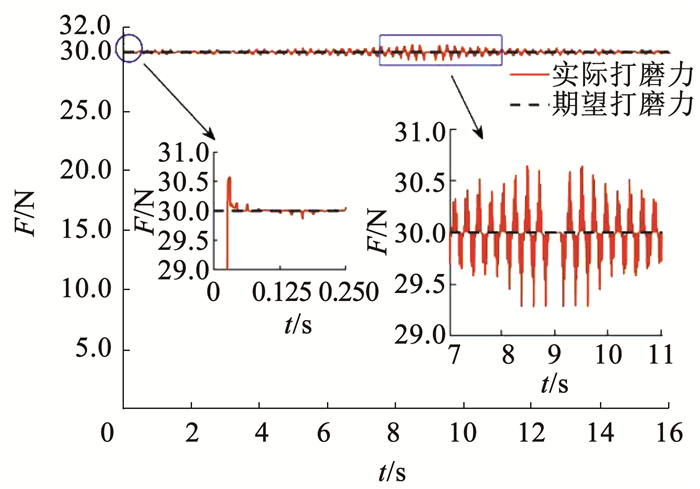
|
图 9 机器人自适应主动柔顺控制器打磨(期望力30.0 N) Fig. 9 Proposed adaptive active compliance controller for robotic grinding (desired force 30.0 N) |
| 表 1 自抗扰控制器控制参数 Tab. 1 Control parameters of active disturbance rejection controller |
通过对比可知,PID控制器能够跟踪期望打磨力趋势,但力变化稳定性略差,力最大偏差为2.2 N,打磨工具接触工件瞬间产生超出期望打磨力的冲击力约为1.2 N;与之对比,机器人自适应主动柔顺控制器在保持恒定打磨力的同时,能够显著地减小力变化量,力最大偏差为0.7 N,打磨工具接触工件瞬间产生超出期望打磨力的冲击力约为0.5 N。上述仿真分析结果表明,所提出的机器人自适应变阻抗主动柔顺恒力控制方法能够较好实现恒力控制,可以有效减小打磨力波动以及打磨工具在打磨接触初期所受的冲击力。
为进一步验证机器人自适应主动柔顺控制器在不同打磨工况环境下力跟踪的适用性和鲁棒性,设置期望打磨力为50.0 N,打磨电机转速仍为3 000 r/min,非球面曲面工件材料分别设置为铝合金和碳钢,与PID控制器进行静态期望力打磨仿真对比实验,仿真结果分别如图 10、11所示。机器人自适应主动柔顺控制器的在线自适应优化过程的变阻抗参数优化结果见表 2。

|
图 10 打磨铝合金材料工件的期望力跟踪仿真(期望力50.0 N) Fig. 10 Desired force tracking simulation for robotic grinding on aluminum alloy workpiece surface (desired force 50.0 N) |

|
图 11 打磨碳钢材料工件的期望力跟踪仿真(期望力50.0 N) Fig. 11 Desired force tracking simulation for robotic grinding on carbon steel workpiece surface (desired force 50.0 N) |
| 表 2 在线优化阻抗参数 Tab. 2 Examples of online optimization for impedance parameters |
由图 10可知,在打磨铝合金材料工件时,PID控制器和机器人自适应主动柔顺控制器对应的打磨工具接触工件瞬间产生超出期望打磨力的冲击力分别为3.0 N和1.2 N,后者比前者减小1.8 N;对应的最大超调量分别为2.2 N和0.7 N,后者比前者减小1.5 N。由图 11可知,在打磨碳钢材料工件时,两者对应的打磨工具接触工件瞬间产生超出期望打磨力的冲击力分别为3.1 N和1.0 N,后者比前者减小2.1 N;对应的最大超调量分别为2.1 N和1.3 N,后者比前者减小0.8 N。仿真结果表明,机器人自适应主动柔顺控制器对不同打磨工况环境具有较强的适应性与鲁棒性,其力控制特性曲线符合良好线性和最小滞后性,有效解决了控制系统的稳定性和收敛性问题,验证了所提出的机器人自适应变阻抗主动柔顺恒力控制方法的有效性。
为进一步验证机器人自适应主动柔顺控制器对动态期望力的跟踪性与适应性,将其与PID控制器进行一种正弦力信号动态期望打磨力跟踪仿真对比实验,仿真结果如图 12所示。由仿真结果可知,PID控制器虽然能跟踪期望打磨力变化趋势,但是具有较大的力超调量(最大值为6.3 N),且总是存在力跟踪误差,力跟踪不收敛;而机器人自适应主动柔顺控制器具有较快的动态响应和较好的动态力跟踪能力,最大力波动量在±0.7 N,不存在力超调量。

|
图 12 正弦信号动态期望力跟踪仿真 Fig. 12 Dynamic desired force tracking simulation of sinusoidal signal for robotic grinding |
通过上述仿真对比实验,验证了提出的机器人自适应变阻抗主动柔顺恒力控制方法的有效性和适用性。该方法能够有效提高机器人打磨控制系统打磨力的稳定性和鲁棒性,可以较好地满足机器人打磨作业通常不允许过切的柔顺恒力控制需求。
3.2 机器人平台实验机器人实验平台选用ABB IRB-4600机器人及IRC5机器人控制器作为机器人平台,工件为一种侧曲面圆台铸铁工件,机器人实验平台如图 13所示。采用倍福CX-260354嵌入式控制器作为实验平台控制设备,上位机控制器采用基于PC的控制软件TwinCAT3。上位机控制器与机器人IRC5控制器和传感器之间分别采用套接字通讯和EtherCAT通讯。

|
图 13 机器人实验平台 Fig. 13 Robotic experiment platform |
在实验中,通过轨迹插补获得一系列打磨作业点的位置和姿态信息,通过机器人控制器与上位机控制器通讯,将各打磨作业点的位置和姿态信息传递给上位机控制器,同时上位机控制器采集力传感器信息实时监测打磨力,并将实时打磨力信息转换为数字信号输入到倍福控制器。将采集的打磨力信息经机器人自适应主动柔顺控制器控制处理,对机器人当前位置的打磨力误差进行动态修正,从而实现机器人自适应变阻抗主动柔顺恒力控制。
在如图 13所示的机器人实验平台,分别开展机器人打磨力的开环控制实验、PID控制实验和提出的机器人自适应变阻抗主动柔顺恒力控制方法的控制实验。其中,期望打磨力均设置为10.0 N;PID参数和ADRC参数均根据经验先进行粗调整,再作微调整,取多次优化调整后的参数值。
开环控制实验的实际打磨力控制结果如图 14所示,所得到的实际打磨力为不规则曲线,这是由于工件侧曲面存在不规则加工误差,且没有对实际打磨力的变化进行调节所致。PID控制实验的实际打磨力如图 15所示,实验结果见表 3。实验结果表明,实际打磨力的波动变化较为剧烈,虽然实际打磨力在期望打磨力上、下一定范围内波动,但存在较大的偏差。提出的机器人自适应变阻抗主动柔顺恒力控制方法对应实验的实际打磨力如图 16所示,实验结果见表 3。

|
图 14 机器人打磨力开环控制实验 Fig. 14 Experimental date of robotic grinding force using open-loop control |

|
图 15 机器人打磨力PID控制实验 Fig. 15 Experimental date of robotic grinding force using PID control |
| 表 3 机器人打磨力实验结果 Tab. 3 Experimental date of robotic grinding force |

|
图 16 机器人打磨力所提出控制方法的控制实验 Fig. 16 Experimental date of robotic grinding force using proposed control method |
通过对比可知,打磨力最大值越小、打磨力最小值越大、打磨力平均误差越小对应的系统抗扰动稳定性越好。稳定打磨阶段打磨力波动值越小,恒力跟踪性能越好,动态响应能力越强。
与相同实验条件下PID模糊变阻抗控制和自抗扰模糊变阻抗控制这类机器人主动柔顺恒力打磨控制研究[27]实验对比,对应两者控制实验的实际打磨力分别如图 17、18所示,实验结果见表 3。

|
图 17 机器人打磨力PID模糊变阻抗控制方法的控制实验 Fig. 17 Experimental date of robotic grinding force using PID fuzzy variable impedance control method |

|
图 18 机器人打磨力自抗扰模糊变阻抗控制方法的控制实验 Fig. 18 Experimental date of robotic grinding force using fuzzy variable impedance control method with active disturbance rejection |
对比上述实验结果可知,开环控制不能实现恒力控制,PID控制下的实际打磨力波动较大,难以实现恒力控制;与PID控制和PID模糊变阻抗控制相比,提出的机器人自适应变阻抗主动柔顺恒力控制方法控制打磨力能够显著地减小稳定打磨阶段打磨力波动,分别减小了60.47%和50.00%,打磨力平均误差也相对大幅度显著减小,分别减小了67.39%和58.33%,并较好地减小了初始阶段力的超调量,力控制性能更加稳定,有效提高了机器人稳定恒力打磨的控制效果;与自抗扰模糊变阻抗控制相比,提出的主动柔顺恒力控制方法控制打磨力亦有较好的力控制性能,稳定打磨阶段打磨力波动减小了5.56%,打磨力平均误差减小了37.50%。通过机器人平台对比实验,验证了提出的机器人自适应变阻抗主动柔顺恒力控制方法的有效性。
4 结论1) 所提出控制方法的内环控制为设计的一种自抗扰控制器,外环控制为设计的一种粒子群神经网络变阻抗控制器,内、外环控制共同作用构成闭环控制回路,用于对期望打磨力估计和补偿、在线自适应优化阻抗参数和动态调节打磨力修正量;通过自适应调节阻抗特性使机器人打磨接触刚度与作业柔顺性主动适应多变环境打磨工况,实现机器人打磨作业的自适应主动柔顺恒力控制。
2) 采用Lyapunov理论分析证明了所提出的机器人自适应变阻抗主动柔顺恒力控制方法对力跟踪误差的闭环稳定性,并通过机器人打磨系统虚拟样机联合仿真开展了静态与动态期望打磨力跟踪实验和不同打磨工况环境下力跟踪实验,有效解决了机器人打磨过程中存在的打磨力波动、力超调和打磨初期打磨工具处存在冲击力等问题,验证了所提出方法的有效性和适用性。
3) 通过机器人平台实物实验对比,所提出的主动柔顺恒力控制方法与PID控制、PID模糊变阻抗控制和自抗扰模糊变阻抗控制相比,打磨力平均误差分别减小了67.39%,58.33%和37.50%,稳定打磨阶段打磨力波动分别减小了60.47%,50.00%和5.56%,验证了所提出方法的有效性。
| [1] |
ZHU Wule, BEAUCAMP A. Compliant grinding and polishing: A review[J]. International Journal of Machine Tools and Manufacture, 2020, 158: 103634. DOI:10.1016/j.ijmachtools.2020.103634 |
| [2] |
张新艳, 郭鹏, 余建波. 应用深度强化学习的压边力优化控制[J]. 哈尔滨工业大学学报, 2020, 52(7): 20. ZHANG Xinyan, GUO Peng, YU Jianbo. Optimal control of blank holder force using deep reinforcement learning[J]. Journal of Harbin Institute of Technology, 2020, 52(7): 20. DOI:10.11918/201908012 |
| [3] |
ZHANG Shuang, LEI Minjie, DONG Yiting, et al. Adaptive neural network control of coordinated robotic manipulators with output constraint[J]. IET Control Theory & Applications, 2016, 10(17): 2271. DOI:10.1049/iet-cta.2016.0009 |
| [4] |
XU Xiaohu, ZHU Dahu, ZHANG Haiyang, et al. Application of novel force control strategies to enhance robotic abrasive belt grinding quality of aero-engine blades[J]. Chinese Journal of Aeronautics, 2019, 32(10): 2368. DOI:10.1016/j.cja.2019.01.023 |
| [5] |
MOHSIN I, HE Kai, LI Zheng, et al. Path planning under force control in robotic polishing of the complex curved surfaces[J]. Applied Sciences, 2019, 9(24): 5489. DOI:10.3390/app9245489 |
| [6] |
GRACIA L, SOLANES J E, MUÑOZ-BENAVENT P, et al. Adaptive sliding mode control for robotic surface treatment using force feedback[J]. Mechatronics, 2018, 52: 102. DOI:10.1016/j.mechatronics.2018.04.008 |
| [7] |
KAKINUMA Y, OGAWA S, KOTO K. Robot polishing control with an active end effector based on macro-micro mechanism and the extended Preston's law[J]. CIRP Annals, 2022, 71(1): 341. DOI:10.1016/j.cirp.2022.04.074 |
| [8] |
LAKSHMINARAYANAN S, KANA S, MOHAN D M, et al. An adaptive framework for robotic polishing based on impedance control[J]. The International Journal of Advanced Manufacturing Technology, 2021, 112(1/2): 401. DOI:10.1007/s00170-020-06270-1 |
| [9] |
KANA S, LAKSHMINARAYANAN S, MOHAN D M, et al. Impedance controlled human-robot collaborative tooling for edge chamfering and polishing applications[J]. Robotics and Computer-Integrated Manufacturing, 2021, 72: 102199. DOI:10.1016/j.rcim.2021.102199 |
| [10] |
ZHU Renfeng, YANG Guilin, FANG Zaojun, et al. Hybrid orientation/force control for robotic polishing with a 2R1T force-controlled end-effector[J]. The International Journal of Aavanced Manufacturing Technology, 2022, 121(3/4): 2279. DOI:10.1007/s00170-022-09407-6 |
| [11] |
ZHANG Guolong, YANG Guilin, DENG Yimin, et al. Modeling and force control of a pneumoelectric end-effector for robotic continuous contact operations[J]. The International Journal of Advanced Manufacturing Technology, 2022, 121(1/2): 1219. DOI:10.1007/s00170-022-09413-8 |
| [12] |
OCHOA H, CORTESÃO R. Impedance control architecture for robotic-assisted mold polishing based on human demonstration[J]. IEEE Transactions on Industrial Electronics, 2022, 69(4): 3822. DOI:10.1109/TIE.2021.3073310 |
| [13] |
XU Peng, CHEUNG C F, LI Bing, et al. Kinematics analysis of a hybrid manipulator for computer controlled ultra-precision freeform polishing[J]. Robotics and Computer-Integrated Manufacturing, 2017, 44: 44. DOI:10.1016/j.rcim.2016.08.003 |
| [14] |
ZHU Dahu, FENG Xiaozhi, XU Xiaohu, et al. Robotic grinding of complex components: A step towards efficient and intelligent machining-challenges, solutions, and applications[J]. Robotics and Computer-Integrated Manufacturing, 2020, 65: 101908. DOI:10.1016/j.rcim.2019.101908 |
| [15] |
CAO Hongli, HE Ye, CHEN Xiaoan, et al. Smooth adaptive hybrid impedance control for robotic contact force tracking in dynamic environments[J]. Ind Robot, 2020, 47: 231. DOI:10.1108/IR-09-2019-0191 |
| [16] |
JIN Mingsheng, JI Shiming, PAN Ye, et al. Effect of downward depth and inflation pressure on contact force of gasbag polishing[J]. Precision Engineering, 2017, 47: 81. DOI:10.1016/j.precisioneng.2016.07.007 |
| [17] |
ZHAI Anbang, ZHANG Haiyun, WANG Jin, et al. Adaptive neural synchronized impedance control for cooperative manipulators processing under uncertain environments[J]. Robotics and Computer-Integrated Manufacturing, 2022, 75: 102291. DOI:10.1016/j.rcim.2021.102291 |
| [18] |
LIN Guanghui, FANG Lijin, HAN Bing, et al. Frequency-division based hybrid force/position control of robotic arms manipulating in uncertain environments[J]. Ind Robot, 2020, 47: 445. DOI:10.1108/IR-11-2019-0228 |
| [19] |
MA Zheng, POO A N, ANG M H, et al. Design and control of an end-effector for industrial finishing applications[J]. Robotics and Computer-Integrated Manufacturing, 2018, 53: 240. DOI:10.1016/j.rcim.2018.04.010 |
| [20] |
DING Bingxiao, ZHAO Jiyu, LI Yangmin. Design of a spatial constant-force end-effector for polishing/deburring operations[J]. The International Journal of Advanced Manufacturing Technology, 2021, 116(11/12): 3507. DOI:10.1007/s00170-021-07579-1 |
| [21] |
EL KHALICK MOHAMMAD A, HONG Jie, WANG Danwei, et al. Synergistic integrated design of an electrochemical mechanical polishing end-effector for robotic polishing applications[J]. Robotics and Computer-Integrated Manufacturing, 2019, 55: 65. DOI:10.1016/j.rcim.2018.07.005 |
| [22] |
张铁, 吴圣和, 蔡超. 基于浮动平台的机器人恒力控制研磨方法[J]. 上海交通大学学报, 2020, 54(5): 515. ZHANG Tie, WU Shenghe, CAI Chao. Constant force control method for robotic disk grinding based on floatingplatform[J]. Journal of Shanghai Jiao Tong University, 2020, 54(5): 515. DOI:10.16183/j.cnki.jsjtu.2020.05.009 |
| [23] |
韩京清. 自抗扰控制技术: 估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008. HAN Jingqing. Active disturbance rejection control technique: The technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press, 2008. |
| [24] |
吴云华, 张泽中, 华冰, 等. 应用卷积神经网络的遥感图像云层自主检测[J]. 哈尔滨工业大学学报, 2020, 52(12): 27. WU Yunhua, ZHANG Zezhong, HUA Bing, et al. Autonomous cloud detection for remote sensing images usingconvolutional neural network[J]. Journal of Harbin Institute of Technology, 2020, 52(12): 27. DOI:10.11918/201903102 |
| [25] |
蔡国强, 邢宗义, 潘丽莎, 等. 采用遗传神经网络的轮轨力建模方法[J]. 哈尔滨工业大学学报, 2012, 44(7): 114. CAI Guoqiang, XING Zongyi, PAN Lisha, et al. Modelling of wheel-rail force based on genetic neural networks[J]. Journalof Harbin Institute of Technology, 2012, 44(7): 114. DOI:10.11918/j.issn.0367-6234.2012.07.022 |
| [26] |
HAO Qun, TAO Xin, HU Yao, et al. Interferometric measurement of high-order aspheric surface parameter errors based on a virtual-real combination iterative algorithm[J]. Optics Express, 2021, 29(17): 27014. DOI:10.1364/OE.435252 |
| [27] |
郭万金, 于苏扬, 赵伍端, 等. 机器人主动柔顺恒力打磨控制方法[J]. 东北大学学报(自然科学版), 2023, 44(1): 89. GUO Wanjin, YU Suyang, ZHAO Wuduan, et al. Grinding control method of robotic active compliance constant-force[J]. Journal of Northeastern University (Natural Science), 2023, 44(1): 89. DOI:10.12068/j.issn.1005-3026.2023.01.013 |
 2023, Vol. 55
2023, Vol. 55


