2. 压缩机技术国家重点实验室(合肥通用机械研究院有限公司), 合肥 230031
2. State Key Laboratory of Compressor Technology (Hefei General Machinery Research Institute Company Limited), Hefei 230031, China
质子交换膜燃料电池(proton exchange membrane fuel cell, PEMFC)可以将化学能直接转化电能,具有清洁、能量密度高和体积小等优点,是解决化石燃料短缺及其燃烧所带来的环境污染问题的有效途径之一[1-2]。PEMFC系统主要由电池堆、空气供应系统和氢气循环系统等组成[3]。为提高氢气的利用效率,需要通过氢气循环泵将未反应完的氢气输送至电堆阳极入口[4]。因此,氢气循环泵是燃料电池氢气循环系统中的关键设备,其性能对PEMFC系统性能影响极大。现有的氢气循环泵的类型主要包括涡旋式[5]、罗茨式[6]和爪式[7]等。爪式氢气循环泵仅仅依靠两个相互啮合的爪式转子实现气体的内压缩,具有干式无油、结构紧凑和可靠性高等显著优点,相比之下,是用于燃料电池系统中最具潜力的理想泵型。
爪式氢气循环泵的关键部件是一对相互啮合的爪式转子,转子型线的优化设计是提高泵效率的关键因素之一。Hsieh等[8]基于共轭求解法,构建了一对相互啮合的螺杆-爪式转子,讨论了几何参数对该转子面积利用率和余隙容积的影响,结果表明螺杆-爪式转子的密封性能好,且余隙容积小。在此基础上,构建了曲爪爪式转子,得到了其截面型线的参数方程,同时研究了当两个转子不发生干涉时,其几何参数的取值范围[9]。Wang等[10]构建了全光滑的爪式转子,所提出的全光滑爪式真空泵具有余隙容积小的特点,且转子的力学性能也得到了显著改善。同时,Wang等[11]又构建了两种新型直爪转子,分析了爪式转子的独立几何参数与泵性能之间的关系;并采用有限元分析法,对比分析了两种直爪爪式转子的力学性能。Pan等[12]构建了一种新型三爪转子,推导了其截面型线的参数方程,并设计了新的排气口,结果表明新型三爪转子型线组成简单,所设计的排气口有效解决了余隙容积内气体的二次压缩问题。
在工作过程中,爪式氢气循环泵工作腔内气体流动复杂。因此,研究工作腔内部流场的分布特征,并揭示其增压过程具有重要意义。Gu等[13]分析了燃料电池用爪式氢气循环泵工作腔内的压力分布,讨论了轴向和径向间隙对工作腔内的流场和泵性能的影响;结果表明由于轴向和径向间隙的泄漏,导致在等容输送过程中工作腔内的压力显著升高。Dong等[14]研究了工作过程中泵腔内的压力随主轴转角的变化规律,得到了双爪爪式氢气循环泵在不同进口压力下的泵容积效率。并进一步研究了在不同转子材料和工作温度下,径向间隙和轴向间隙的变化规律;结果表明相比于结构钢和钛合金,铝合金转子的变形量最大,导致径向间隙减小,转子间干扰的可能性变大[15]。Zhao等[16]研究了含有不同水蒸气和氮气的氢混合物对氢气循环泵的容积效率、功耗和比功率的影响。
然而,爪式氢气循环泵在具有显著优点的同时,由于其工作腔是由啮合间隙实现封闭的,相比于其他位置处的间隙,由节圆形成的爪式转子间的啮合间隙采用点与点的啮合方式;而且,由于氢气具有密度小、黏度低等特性,导致爪式转子间的气体泄漏大,严重阻碍了氢气循环泵性能的提高。因此,如何减小转子间的气体泄漏、提高氢气循环泵的容积效率是需要攻克的关键问题。为解决上述问题,本文结合齿轮和爪式转子截面型线特点,提出一种新型曲折型啮合间隙结构,进而构建一种新型高密封型齿轮爪式转子。通过数值模拟研究齿轮爪式氢气循环泵转子间的气体泄漏,并与传统爪式氢气循环泵进行对比。研究内容对完善爪式氢气循环泵的设计理论,研制新型高效爪式氢循环泵,提高质子交换膜燃料电池系统的性能具有重要意义和价值。
1 传统爪式转子结构及其工作性能分析爪式氢气循环泵的间隙分布如图 1所示。氢气循环泵由爪式转子Ⅰ、爪式转子Ⅱ和泵腔等组成。在工作过程中,两个转子和泵腔内壁面形成了间隙Ⅰ、间隙Ⅱ,相互啮合的转子间形成了啮合间隙Ⅲ。相比于间隙Ⅰ和间隙Ⅱ,采用点与点啮合的双圆弧型间隙Ⅲ的间隙长度短、密封性能差,且其泄漏方向与爪式转子的旋转方向一致,导致转子间的气体泄漏严重。啮合的爪式转子将泵腔分割成排气腔和吸气腔,两个工作腔内的压力不同,导致间隙Ⅲ两侧的压力相差较大,氢气从排气腔泄漏至吸气腔,对爪式氢气循环泵的工作过程及效率影响极大。因此,爪式转子间的气体泄漏对泵的稳定运行和效率提升是一个很大的挑战。

|
图 1 传统爪式转子结构和间隙分布 Fig. 1 Structure of conventional claw rotors and distribution of leakage clearances |
针对在工作过程中相互啮合的爪式转子间气体泄漏严重的问题,本文构建了一种高密封型齿轮爪式转子,所构建的齿轮爪式转子采用圆弧、高次曲线及其共轭曲线代替传统爪式转子的节圆型线,形成了一种爪式转子间的新型曲折型啮合结构,进而减小转子间的气体泄漏。
齿轮爪式转子截面型线如图 2所示。齿轮爪式转子I的截面型线由摆线AB、爪顶圆弧BC、摆线CD、齿底圆弧EF、高次曲线FG、齿顶圆弧GH、高次曲线HI、齿底圆弧IJ、摆线KL、爪底圆弧LA、点B、点C和点K组成。齿轮爪式转子Ⅱ的截面型线由摆线ab、爪顶圆弧bc、摆线cd、齿顶圆弧ef、高次曲线的共轭曲线fg、齿底圆弧gh、高次曲线的共轭曲线hi、齿顶圆弧ij、摆线kl、爪底圆弧la、点b、点c和点k组成。
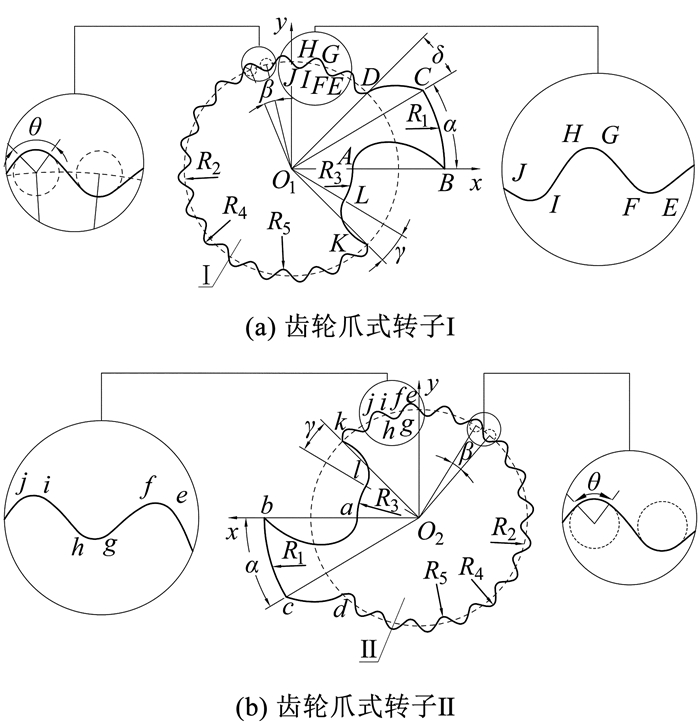
|
图 2 齿轮爪式转子截面型线 Fig. 2 Rotor profiles of gear-claw rotors |
建立如图 2所示的坐标系xO1y,再根据齿轮爪式转子Ⅰ的回转中心O1和两个转子的中心距确定齿轮爪式转子Ⅱ的回转中心O2,并建立从动坐标系xO2y。各段曲线的参数方程如下。
摆线AB的参数方程为
| $ \begin{aligned} \boldsymbol{r}_{A B}=\left[\begin{array}{l} x_{A B}(t) \\ y_{A B}(t) \end{array}\right] & =\left[\begin{array}{l} \left(R_{1}+R_{3}\right) \cos (t)-R_{1} \cos (2 t) \\ \left(R_{1}+R_{3}\right) \sin (t)-R_{1} \sin (2 t) \end{array}\right], \\ t & \in\left[-\arccos \left(\frac{R_{2}}{R_{1}}\right), 0\right] \end{aligned} $ | (1) |
式中: t为角度参数, R1为爪顶圆弧半径, R2为节圆半径, R3为爪底圆弧半径。
爪顶圆弧BC的参数方程为
| $ \boldsymbol{r}_{B C}=\left[\begin{array}{l} x_{B C}(t) \\ y_{B C}(t) \end{array}\right]=\left[\begin{array}{l} R_{1} \cos (t) \\ R_{1} \sin (t) \end{array}\right], t \in[0, \alpha] $ | (2) |
摆线CD的参数方程为
| $ \begin{aligned} \boldsymbol{r}_{C D}= & \boldsymbol{M}_{1}(\alpha+\gamma) \cdot \boldsymbol{r}_{1}=\left[\begin{array}{l} x_{C D}(t) \\ y_{C D}(t) \end{array}\right]= \\ & {\left[-\frac{\left(R_{1}+R_{3}\right)}{2} \cdot \cos (2 t+\alpha+\gamma)+\left(R_{1}+R_{3}\right) \cdot\right.} \\ & \cos (t+\alpha+\gamma)-\frac{\left(R_{1}+R_{3}\right)}{2} \cdot \sin (2 t+\alpha+\gamma)+ \\ & \left.\left(R_{1}+R_{3}\right) \cdot \sin (t+\alpha+\gamma)\right], t \in[0, \delta] \end{aligned} $ | (3) |
式中: M1为旋转矩阵, r1为摆线, α为爪顶圆弧角, γ为爪旋转角,可通过点K的坐标进行求解, δ为第1角度,可通过点D和点C的坐标进行求解。旋转矩阵M1的表达式为
| $ \boldsymbol{M}_{1}(\alpha+\gamma)=\left[\begin{array}{lr} \cos (\alpha+\gamma) & -\sin (\alpha+\gamma) \\ \sin (\alpha+\gamma) & \cos (\alpha+\gamma) \end{array}\right] $ | (4) |
摆线r1的参数方程为
| $ \begin{aligned} \boldsymbol{r}_{1}= & {\left[\begin{array}{l} x_{1}(t) \\ y_{1}(t) \end{array}\right]=\left[-\frac{\left(R_{1}+R_{3}\right)}{2} \cos (2 t)+\right.} \\ & \left(R_{1}+R_{3}\right) \cos (t)-\frac{\left(R_{1}+R_{3}\right)}{2} \sin (2 t)+ \\ & \left.\left(R_{1}+R_{3}\right) \sin (t)\right] \end{aligned} $ | (5) |
齿底圆弧EF的参数方程为
| $ \begin{aligned} \boldsymbol{r}_{E F}= & {\left[\begin{array}{l} x_{E F}(t) \\ y_{E F}(t) \end{array}\right]=\left[\left(R_{4}-R_{5}\right) \cdot \cos (t) \cdot \cos \left(\left(n+\frac{1}{2}\right) \beta\right)+\right.} \\ & \sin \left(\left(n+\frac{1}{2}\right) \beta\right) \cdot\left(\left(R_{4}-R_{5}\right) \cdot \sin (t)+\frac{\left(R_{1}+R_{3}\right)}{2}\right) \cdot \\ & \left(R_{4}-R_{5}\right) \cdot \cos (t) \cdot \sin \left(\left(n+\frac{1}{2}\right) \beta\right)+\cos \left(\left(n+\frac{1}{2}\right) \beta\right) \cdot \\ & \left.\left(\left(R_{4}-R_{5}\right) \cdot \sin (t)+\frac{\left(R_{1}+R_{3}\right)}{2}\right)\right], \\ & \left(t \in\left[-\frac{\pi}{2}-\frac{\theta}{2}, -\frac{\pi}{2}+\frac{\theta}{2}\right], n \in[0, 1, 2, 3, \cdots]\right) \end{aligned} $ | (6) |
式中: β为齿轮旋转角,
高次曲线FG的参数方程为
| $ \begin{gathered} \boldsymbol{r}_{F G}=\left[\begin{array}{c} x_{F G}(t) \\ y_{F G}(t) \end{array}\right]=\left[\begin{array}{c} t \\ a_{0}+a_{1} \cdot t+a_{2} \cdot t^{2}+a_{3} \cdot t^{3} \end{array}\right], \\ t \in\left[\frac{\pi}{2}-\frac{\theta}{2}, -\frac{\pi}{2}-\frac{\theta}{2}\right] \end{gathered} $ | (7) |
式中: a0,a1,a2, a3为高次曲线FG的系数,可通过下式进行求解:
| $ \left\{\begin{array}{l} y_{E F}\left(x_{E F}\right)=y_{F G}\left(x_{F G}\right) \\ \frac{\mathrm{d} y_{E F}\left(x_{E F}\right)}{\mathrm{d}\left(x_{E F}\right)}=\frac{\mathrm{d} y_{F G}\left(x_{F G}\right)}{\mathrm{d}\left(x_{F G}\right)} \\ y_{F G}\left(x_{F G}\right)=y_{G H}\left(x_{G H}\right) \\ \frac{\mathrm{d} y_{F G}\left(x_{F G}\right)}{\mathrm{d}\left(x_{F G}\right)}=\frac{\mathrm{d} y_{G H}\left(x_{G H}\right)}{\mathrm{d}\left(x_{G H}\right)} \end{array}\right. $ | (8) |
采用相同的方法可以得到高次曲线HI的参数方程。
齿顶圆弧GH的参数方程为
| $ \begin{aligned} \boldsymbol{r}_{G H}= & {\left[\begin{array}{l} x_{G H}(t) \\ y_{G H}(t) \end{array}\right]=\left[\left(R_{4}-R_{5}\right) \cdot \cos (t) \cdot \cos \left(\left(n+\frac{1}{2}\right) \beta\right)+\right.} \\ & \sin \left(\left(n+\frac{1}{2}\right) \beta\right) \cdot\left(\left(R_{4}-R_{5}\right) \cdot \sin (t)+\frac{\left(R_{1}+R_{3}\right)}{2}\right)- \\ & \left(R_{4}-R_{5}\right) \cdot \cos (t) \cdot \sin \left(\left(n+\frac{1}{2}\right) \beta\right)+ \\ & \left.\cos \left(\left(n+\frac{1}{2}\right) \beta\right) \cdot\left(\left(R_{4}-R_{5}\right) \cdot \sin (t)+\frac{\left(R_{1}+R_{3}\right)}{2}\right)\right], \\ & \left(t \in\left[\frac{\pi}{2}+\frac{\theta}{2}, \frac{\pi}{2}-\frac{\theta}{2}\right], n \in[0, 1, 2, 3, \cdots]\right) \end{aligned} $ | (9) |
摆线KL的参数方程为
| $ \begin{aligned} \boldsymbol{r}_{K L}= & {\left[\begin{array}{l} x_{K L}(t) \\ y_{K L}(t) \end{array}\right]=\left[\left(R_{1}+R_{3}\right) \cdot \cos (-t+\alpha)-\right.} \\ & R_{1} \cdot \cos (-2 t+\alpha)-\left(R_{1}+R_{3}\right) \cdot \sin (-t+\alpha)+ \\ & \left.R_{1} \cdot \sin (-2 t+\alpha)\right], t \in[0, \gamma] \end{aligned} $ | (10) |
爪底圆弧LA的参数方程为
| $ \boldsymbol{r}_{L A}=\left[\begin{array}{c} x_{L A}(t) \\ y_{L A}(t) \end{array}\right]=\left[\begin{array}{l} R_{3} \cos (t) \\ R_{3} \sin (t) \end{array}\right], t \in[-\alpha, 0] $ | (11) |
齿轮爪式转子Ⅱ中高次曲线HI和FG的共轭曲线fg和hi的求解过程如下。其余曲线的型线方程求解过程与齿轮爪式转子I的型线方程求解过程一致。
高次曲线HI的共轭曲线fg的参数方程为
| $ \begin{aligned} \boldsymbol{r}_{f g}= & \boldsymbol{M}_{21} \cdot \boldsymbol{r}_{H I}=\left[-2 t \cdot \cos (\varphi)^{2}+\right. \\ & \left(\left(-2 b_{3} t^{3}-2 b_{2} t^{2}-2 b_{1} t-2 b_{0}\right) \cdot\right. \\ & \left.\sin (\varphi)+2 R_{2}\right) \cdot \cos (\varphi)+t b_{3} \cdot \\ & \cos (2 \varphi) t^{3}+b_{2} \cdot \cos (2 \varphi) t^{2}+b_{1} \cdot \\ & \cos (2 \varphi) t+b_{0} \cdot \cos (2 \varphi)-\sin (2 \varphi) t+ \\ & \left.2 R_{2} \cdot \sin (\varphi)\right], t \in\left[-\frac{\pi}{2}+\frac{\theta}{2}, \frac{\pi}{2}+\frac{\theta}{2}\right] \end{aligned} $ | (12) |
式中: M21为坐标变换矩阵, φ为位置参数。
采用包络法对φ和t的关系进行求解,得到高次曲线HI的共轭曲线fg的参数方程。同理可得共轭曲线hi的参数方程。
2.1.2 齿轮爪式转子啮合关系的验证齿轮爪式转子Ⅰ和转子Ⅱ的啮合关系和啮合过程如图 3所示。在工作过程中,两个齿轮爪式转子进行同步异向双回转运动,摆线AB与点b开始啮合;随着转子的转动,点B与摆线ab、爪顶圆弧BC与爪底圆弧la、点C与摆线kl、摆线CD与点k依次啮合。随后,齿底圆弧EF、高次曲线FG、齿顶圆弧GH、高次曲线HI、齿底圆弧IJ分别与齿顶圆弧ij、高次曲线的共轭曲线hi、齿底圆弧gh、高次曲线的共轭曲线fg、齿顶圆弧ef啮合。当齿轮脱离啮合时,爪开始啮合,即点K与摆线cd、摆线KL与点c、爪底圆弧LA与爪顶圆弧bc依次啮合。

|
图 3 齿轮爪式转子啮合关系 Fig. 3 Meshing relationship of two claw rotors |
齿轮爪式转子的啮合轨迹如图 4所示。假设齿轮爪式转子Ⅰ固定,齿轮爪式转子Ⅱ绕转子Ⅰ的中心以角速度ω逆时针做公转的同时以相同的角速度自转,得到齿轮爪式转子I的包络图。同理可得齿轮爪式转子Ⅱ的包络图。从图中的啮合轨迹可以看出,齿轮爪式转子Ⅰ和转子Ⅱ的各段截面型线均能保证完全正确啮合。

|
图 4 齿轮爪式转子的啮合轨迹 Fig. 4 Meshing track of two gear-claw rotors |
啮合间隙长度Lc是指两个相互啮合的爪式转子间所形成的啮合间隙的轴向投影长度。传统和齿轮爪式转子间的啮合间隙长度Lc如图 5所示。齿轮爪式转子的Lc是由圆弧、高次曲线及其共轭曲线所构成的,传统爪式转子的Lc是由两个相互啮合的圆弧曲线形成的。Lc的增加,有利于减小转子间的泄漏。

|
图 5 啮合间隙长度 Fig. 5 Length of clearance |
为了确保转子的爪臂厚度、中心距相同,取如下几何参数不变:爪顶圆弧半径R1=50 mm、爪底圆弧半径R3=20 mm、爪顶圆弧角α=30°,改变实际齿数Z1、齿高h,明晰不同几何参数与Lc的关系,如图 6所示。齿轮爪式转子间的Lc始终大于传统爪式转子间的Lc;当实际齿数为25时,齿轮爪式转子间的Lc最小,为5.10 mm,其仍比传统爪式转子间的Lc大3.29 mm。Z1和Lc的关系如图 6(a)所示。随着Z1的增加,Lc迅速下降后趋于稳定。当Z1从3增加至15时,Lc从31.49 mm下降至7.88 mm,在该范围内Z1对Lc有显著影响。h和Lc的关系如图 6(b)所示。随着h的增加,Lc呈近似线性关系增长,当h从3.20 mm增加至4.80 mm时,Lc从9.95 mm增加至12.83 mm。综上所述,Z1的减小和h的增大均有利于啮合间隙长度的增加。

|
图 6 不同几何参数与啮合间隙长度的关系 Fig. 6 Relationship between different geometric parameters and meshing clearance length |
容积利用率是表征氢气循环泵有效空间利用程度的性能指标。容积利用率λ可表示为
| $ \lambda=\frac{V_{\mathrm{A}}-V_{\mathrm{R}}-V_{\mathrm{Cmax}}}{V_{\mathrm{A}}} \times 100 \% $ | (13) |
式中: VCmax为余隙容积, VA为泵腔容积, VR为两个齿轮爪式转子的体积。
当R1=50 mm、R3=20 mm、R2=35 mm、齿轮圆弧角θ=40°、齿轮旋转角β=15°,改变Z1和α,研究不同几何参数与λ的关系,如图 7所示。随着Z1从3增加至24,λ从43.43%增加至44.55%。当α从7.52°增加至75.81°,λ从45.06%减小至42.53%。综上所述,Z1和α对λ有较大的影响,Z1的增加和α的减小均有利于容积利用率的增加。

|
图 7 不同几何参数与容积利用率的关系 Fig. 7 Relationship between different geometric parameters and volumetric efficiency |
考虑爪式转子间的气体泄漏、转子的力学性能和泵的性能,齿轮爪式转子的几何参数选取为爪顶圆弧半径R1=50 mm、爪顶圆弧角α=30°、爪底圆弧半径R3=20 mm、节圆半径R2=35 mm、齿高h=4.8 mm、实际齿数Z1=9、齿轮旋转角β=15°、齿轮圆心角θ=40°。
保证传统爪式转子和齿轮爪式转子的几何参数一致,即传统爪式转子的R1=50 mm,α=30°,R3=20 mm,R2=35 mm时,对比传统和新型齿轮爪式转子的几何参数和性能,如图 8所示。在结构方面,所提出的齿轮爪式转子采用的型线类型是传统爪式转子的2倍,齿轮爪式转子通过采用多种型线类型,使得转子间形成了曲折型啮合结构,同时型线类型的增加并没有使不光滑连接点有所增加,相同的爪臂厚度保留了传统爪式转子较好的力学性能。在性能方面,齿轮爪式转子的容积利用率要优于传统爪式转子,但两者相差不大。齿轮爪式转子间的啮合间隙长度明显高于传统爪式转子,间隙内的气体流动阻力增大,大大减小了转子间的气体泄漏。综上所述,采用圆弧、高次曲线及其共轭曲线代替传统爪式转子的节圆型线,既可以保证容积利用率和转子较好的力学性能,又在较大程度上减小了转子间的气体泄漏,提高爪式氢气循环泵的效率。

|
图 8 传统爪式转子和齿轮爪式转子的结构和性能的对比 Fig. 8 Comparison of structure and performance between conventional and novel claw rotor |
爪式氢气循环泵的一个工作周期为720°,包括混合过程Ⅰ、吸气过程、混合过程Ⅱ、压缩过程和排气过程,传统氢气循环泵的工作过程与齿轮爪式氢气循环泵的工作过程一致。选取齿轮爪式氢气循环泵的工作腔V1为控制体,泵的工作过程如图 9所示。转子的初始位置如图 9(a)所示。
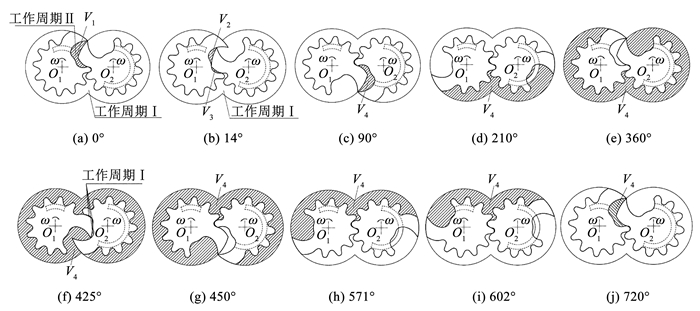
|
图 9 工作过程 Fig. 9 Working process |
混合过程Ⅰ如图 9(a)~9(c)所示。随着转子旋转,工作腔V1的容积逐渐减小,随后,V1被转子分割成工作腔V2和V3,V2和V3的容积减小,腔内气体压力升高,同时腔内气体通过间隙泄漏至前一个工作过程的吸气腔中,导致前一个工作过程的吸气腔内压力升高。之后,两个转子间形成了新的工作腔V4,V4的容积不断增大,其腔内气体压力逐渐减小。吸气过程如图 9(c)~9(e)所示,V4容积增大,腔内的气体压力为吸气压力。当吸气口关闭,V4进入混合过程Ⅱ,如图 9(e)~9(g)所示,上个工作过程中余隙容积内具有较高压力的气体与V4内的气体混合,导致V4内的气体压力增加。当混合过程Ⅱ结束,压缩过程开始,如图 9(g)~9(i)所示。在压缩过程中,V4容积不断减小,腔内压力逐渐增大。当压缩过程结束时,排气过程开始,V4容积减小,腔内压力为排气压力,如图 9(i)~9(j)所示。当排气结束时,未排出的气体残留在余隙容积中,如图 9(j)所示。
4 爪式氢气循环泵的数值模拟 4.1 三维几何模型和网格划分传统和新型齿轮爪式氢气循环泵的流体域由吸气口、工作腔、排气口和端面组成,其设计参数见表 1。
| 表 1 两个泵的设计参数 Tab. 1 Design parameters of two claw pumps |
两个泵的流体域网格如图 10所示。两个泵的流体域划分为网格重构子域和网格非重构子域。网格重构子域为旋转工作腔流体域;网格非重构子域为吸气口、端面Ⅰ、端面Ⅱ和排气口。工作腔流体域采用四面体网格,工作腔流体域的最大网格尺度为0.6 mm。非重构子域采用六面体网格,其最大网格尺寸为0.6 mm。最终确定传统爪式氢气循环泵的工作腔流体域网格数为1 366 854,齿轮爪式氢气循环泵的工作腔流体域网格数为1 353 298。传统和新型齿轮爪式泵的总网格数分别为1 531 978和1 518 422。

|
图 10 传统和齿轮氢气循环泵的网格划分 Fig. 10 Grids of conventional and gear-claw hydrogen circulating pump |
RNG k-ε湍流模型在标准k-ε模型的基础上修正了湍流黏性系数,使模型对瞬态流动和流体流动曲率做出了更好预测,提高了湍流模型的精度。因此,本文采用具有标准壁面函数的RNG k-ε湍流模型。选择氢气作为工作介质,其密度为0.089 9 kg/m3。由于爪式氢气循环泵是容积泵,边界条件设置为压力入口和压力出口,其中入口边界条件为:入口压力为0.101 325 MPa,入口温度为293.15 K;出口边界条件为:出口压力为0.21 MPa,出口温度为362.18 K。转子的转速为3 000 r/min,时间步长为1×10-6,时间步数设置为40 000。
4.3 实验验证爪式氢气循环泵的性能测试实验平台如图 11所示。实验台主要由进口罐、爪式氢气循环泵、变频电机、出口罐等部件组成。在泵的进口和出口处的管路上安装压力传感器、涡街流量计和温度传感器。通过传感器和数据采集系统监测吸气口和排气口处气体的温度、压力和流量。

|
图 11 氢气循环泵性能实验平台 Fig. 11 Hydrogen circulating pump performance test bench |
对传统爪式氢气循环泵排气口处的平均质量流量进行实验和数值模拟研究见表 2。由于氢气易燃的物理性质,本次实验选择空气作为工质,入口压力和入口温度分别为0.101 MPa和293.15 K。模拟和实验的工质和边界条件保持一致。当转速分别为2 400、3 000、3 600 r/min时,实验和数值模拟排气口处的平均质量流量偏差分别为4.51%、4.96%和5.43%。因此,数值模拟方法是准确的。
| 表 2 实验和数值模拟排气口处的平均质量流量 Tab. 2 Average mass flow at the discharge port of the experiment and simulation |
传统泵和新型泵的工作腔内的压力分布如图 12所示。在吸气、混合和排气过程中,两个泵的工作腔内的压力变化基本一致,选取工作腔V1为控制体。在吸气过程中,两个泵的V1内的气体压力均为101.33 kPa;在混合过程中,上个工作过程中余隙容积内具有较高压力的气体与V1内的气体混合,导致传统爪式氢气循环泵和新型齿轮爪式氢气循环泵V1内的气体压力分别增加至131.09、130.78 kPa;在排气过程中,两个泵的V1内的气体压力为排气压力。

|
图 12 两个泵工作腔内的压力分布 Fig. 12 Pressure distributions of two pumps in the working process |
在压缩过程中,两个泵V1内的气体压力逐渐增加,相比于传统爪式氢气循环泵,采用曲折型啮合结构的新型齿轮爪式转子间密封性好、气体泄漏小,增压效果显著。此外,从图 12中可以看出,混合过程导致两个泵在压缩过程的初始时刻V1内的气体压力均大于吸气压力101.33 kPa,因此,当压缩过程结束时,腔内压力大于排气压力,发生过压缩现象。
4.5 速度场传统和新型齿轮爪式氢气循环泵的速度分布如图 13所示。如图 13(a)所示,在压缩和排气过程中,工作腔Ⅰ、Ⅱ压力相差较大,故选压缩和排气过程中泵腔内的速度分布作为研究对象。从图 13中可以看出,在压缩和排气过程中,由于两个泵转子间的啮合间隙长度比其他间隙长度短,且其泄漏方向与爪式转子的运动方向一致,所以相比与间隙Ⅰ、Ⅱ位置处,间隙Ⅲ处的气体泄漏速度大。因此,重点分析间隙Ⅲ处的气体泄漏。在齿轮爪式氢气循环泵中,相互啮合的齿轮爪式转子间形成了狭长的曲折型啮合间隙Ⅲ,当气体流经此间隙时,间隙Ⅲ处的气体泄漏速度减小。在压缩和排气过程中,与传统氢气循环泵相比,齿轮爪式氢气循环泵间隙Ⅲ处的气体泄漏速度分别减小了31.42%和33.09%,转子间的气体泄漏显著改善。此外,通过计算,得到传统爪式氢气循环泵的容积效率为67.30%,新型齿轮爪式氢气循环泵的容积效率为78.22%,容积效率提高了10.92%。

|
图 13 爪式氢气循环泵速度分布 Fig. 13 Distribution of speed in two claw hydrogen circulating pumps |
1) 针对爪式氢气循环泵转子间气体泄漏严重的问题,采用圆弧、高次曲线及其共轭曲线代替传统节圆型线,提出了一种新型高密封型齿轮爪式转子,转子间形成了一种狭长的曲折型啮合结构,有效减小了气体泄漏。推导了新型齿轮爪式转子的型线方程,构建了新型齿轮爪式转子的啮合模型,验证了新型齿轮爪式转子的啮合性。
2) 研究了齿轮爪式转子的几何参数对齿轮爪式氢气循环泵性能的影响。齿数的减少和齿高的增加均有利于增大齿轮爪式转子间的啮合间隙长度,减小转子间的泄漏;齿数的增加和爪顶圆弧角的减小均有利于增加泵的容积利用率。
3) 保证传统爪式转子和齿轮爪式转子的几何参数一致,对比了传统和新型齿轮爪式氢气循环泵的结构和性能。发现在性能方面,齿轮爪式转子的容积利用率要优于传统爪式转子,且齿轮爪式转子间的啮合间隙长度是传统爪式转子的7倍,大大减小了转子间的气体泄漏。在结构方面,新型齿轮爪式转子型线类型多于传统爪式转子,但型线类型的增加并没有使不光滑连接点有所增加,相同的爪臂厚度使得新型齿轮爪式转子保留了传统爪式转子较好的力学性能。
4) 通过数值模拟研究了传统和新型两种氢气循环泵的工作腔压力和速度分布。发现在压缩过程中,相比于传统爪式氢气循环泵,新型齿轮爪式转子间的密封性好,增压效果显著。当气体流经狭长的曲折型啮合间隙时,转子间的气体泄漏减小。在压缩和排气过程中,相比于传统转子间的气体泄漏,新型齿轮爪式转子间的气体泄漏速度分别减小了31.42%和33.09%,容积效率增加了10.92%。
| [1] |
林林, 王晓东, 张欣欣. 直通与交叉流场质子交换膜燃料电池瞬态特性[J]. 哈尔滨工业大学学报, 2010, 42(3): 472. LIN Lin, WANG Xiaodong, ZHANG Xinxin. Numerical study on transient characteristics of PEM fuel cells with parallel and interdigitated flow fields[J]. Journal of Harbin Institute of Technology, 2010, 42(3): 472. DOI:10.11918/j.issn.0367-6234.2010.03.030 |
| [2] |
FAN Lixin, TU Zhengkai, CHAN S H. Recent development of hydrogen and fuel cell technologies: A review[J]. Energy Reports, 2021, 7: 8421. DOI:10.1016/j.egyr.2021.08.003 |
| [3] |
张立新, 李建, 李瑞懿, 等. 车用燃料电池氢气供应系统研究综述[J]. 工程热物理学报, 2022, 43(6): 1444. ZHANG Lixin, LI Jian, LI Ruiyi, et al. Research on the hydrogen supply system of fuel cell for vehicle[J]. Journal of Engineering Thermophysics, 2022, 43(6): 1444. |
| [4] |
董凯瑞, 刘广彬, 高志成. 燃料电池系统爪式氢气循环泵内部流动特性模拟[J]. 机械科学与技术, 2023, 42(8): 1236. DONG Kairui, LIU Guangbin, GAO Zhicheng. Simulating internal flow characteristics of claw-type hydrogen circulation pump in fuel cell system[J]. Mechanical Science and Technology for Aerospace Engineering, 2023, 42(8): 1236. DOI:10.13433/j.cnki.1003-8728.20220032 |
| [5] |
ZHANG Qingqing, FENG Jianmei, WEN Jie, et al. 3D transient CFD modelling of a scroll-type hydrogen pump used in FCVs[J]. International Journal of Hydrogen Energy, 2018, 43(41): 19231. DOI:10.1016/j.ijhydene.2018.08.158 |
| [6] |
ZHOU Shuangmei, JIA Xiaohan, YAN Huimin, et al. A novel profile with high efficiency for hydrogen-circulating Roots pumps used in FCVs[J]. International Journal of Hydrogen Energy, 2021, 46(42): 22122. DOI:10.1016/j.ijhydene.2021.04.038 |
| [7] |
GU Pengtai, XING Linfen, WANG Yuefei, et al. A multi-objective parametric study of the claw hydrogen pump for fuel cell vehicles using taguchi method and ANN[J]. International Journal of Hydrogen Energy, 2021, 46(9): 6680. DOI:10.1016/j.ijhydene.2020.11.186 |
| [8] |
HSIEH C F, HWANG Y W, FONG Z H. Study on the tooth profile for the screw claw-type pump[J]. Mechanism and Machine Theory, 2008, 43(7): 812. DOI:10.1016/j.mechmachtheory.2007.06.011 |
| [9] |
HSIEH C F. A study of the geometric design and gas port of the claw-type rotor[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2009, 223(9): 2063. DOI:10.1243/09544062jmes1452 |
| [10] |
WANG Jun, CUI Dong, PANG Xiaofeng, et al. Geometric design and performance analysis of a novel smooth rotor profile of claw vacuum pumps[J]. Vacuum, 2017, 143: 174. DOI:10.1016/j.vacuum.2017.06.006 |
| [11] |
WANG Jun, FENG Haozhi, ZHAO Feng, et al. Geometric design of novel straight claw rotors for claw vacuum pumps[J]. Mechanism and Machine Theory, 2019, 136: 244. DOI:10.1016/j.mechmachtheory.2019.03.009 |
| [12] |
PAN Shiyang, WANG Jun, TAN Qingpeng, et al. Analysis and numerical simulation of claw vacuum pumps with novel three-claw rotors[J]. Vacuum, 2021, 192: 110442. DOI:10.1016/j.vacuum.2021.110442 |
| [13] |
GU Pengtai, XING Linfen, WANG Yuefei, et al. Transient flow field and performance analysis of a claw pump for FCVs[J]. International Journal of Hydrogen Energy, 2021, 46(1): 984. DOI:10.1016/j.ijhydene.2020.09.154 |
| [14] |
DONG Kairui, LIU Guangbin, YANG Qichao, et al. Flow field analysis and performance study of claw hydrogen circulating pump in fuel cell system[J]. International Journal of Hydrogen Energy, 2021, 46(69): 34438. DOI:10.1016/j.ijhydene.2021.08.014 |
| [15] |
DONG Kairui, LIU Guangbin, YANG Qichao, et al. Effect of thermal deformation on leakage clearance of claw hydrogen circulating pump for fuel cell system[J]. International Journal of Hydrogen Energy, 2022, 47(66): 28655. DOI:10.1016/j.ijhydene.2022.06.196 |
| [16] |
ZHAO Bin, WEI Huan, ZHANG Zhaojun, et al. Effects of clearances size and fluid medium components on the thermodynamic performance of a claw pump for fuel cell vehicle[J]. International Journal of Energy Research, 2022, 46(11): 15054. DOI:10.1002/er.8205 |
 2023, Vol. 55
2023, Vol. 55


