富勒(R.B.Fuller)最早提出“张拉整体”的概念,因该类结构具有轻质、灵活、抗冲击和可折展等优点[1-4],被广泛应用于建筑[5]、机器人[6]、可展天线[7]等领域,是研究的热点问题。法国的Motro给出了较为完善的张拉整体结构的定义:张拉整体结构是由一组离散受压构件包含于连续的受拉构件中组成的稳定自平衡体系[8-9]。
棱柱式张拉整体结构是最常见的一类,Amendola等[10]对双材料棱柱式张拉整体结构新的组装方式和压缩响应特性进行了研究;Zhang等[11]提出利用棱柱式基本单元构造一类由杆-杆连接组成的大尺度张拉整体结构的方法;Wang等[12]提出了一种利用4棱柱张拉整体结构变形来实现机器人可操纵滚动运动的设计方法;Zhang等[13]提出了一个由4棱柱张拉整体结构和两个端板组成的变形模块并实现其对称/非对称部署;张沛等[14]用动力松弛法与反分析思想相结合的方式研究了含冗余拉索的棱柱式张拉整体结构成形过程。结构中存在拉索失效时会造成一般张拉整体结构的整体失效,若结构含冗余拉索则会在一定程度上避免此种情况,因此,含冗余拉索的棱柱式张拉整体结构比一般张拉整体结构抗破坏能力强,含冗余拉索的棱柱式张拉整体结构在桥梁建筑、机械臂等领域具有广泛的应用前景。
驱动结构变形的方式主要分为3种:杆驱动、索驱动和杆-索混合驱动,由于索驱动可保持杆长不变,保证绳索始终受拉力作用,索驱动具有可控性强的优点,是最常用的驱动方式[15]。Fraddosio等[16]研究了由主动索和被动索控制的V形膨胀器的轴向伸缩变化;Chen等[17]提出了节能索驱动策略,通过区分主、被动索的方式以V形膨胀器为例全面分析了结构的受拉、受压、弯曲、扭转和剪切变形。
本文选用索驱动的方式对含冗余拉索的棱柱式张拉整体结构的变形能力进行研究,选出能量耗散最少的驱动方式。因为改变结构形状是打破原有平衡建立新的平衡,过程涉及结构的力学性能分析,现做出如下假设:1)构件受力方向仅沿轴向,不发生转动,无转动惯量;2)材料为线弹性材料,变形范围内截面积保持不变;3)不考虑节点连接处的摩擦。
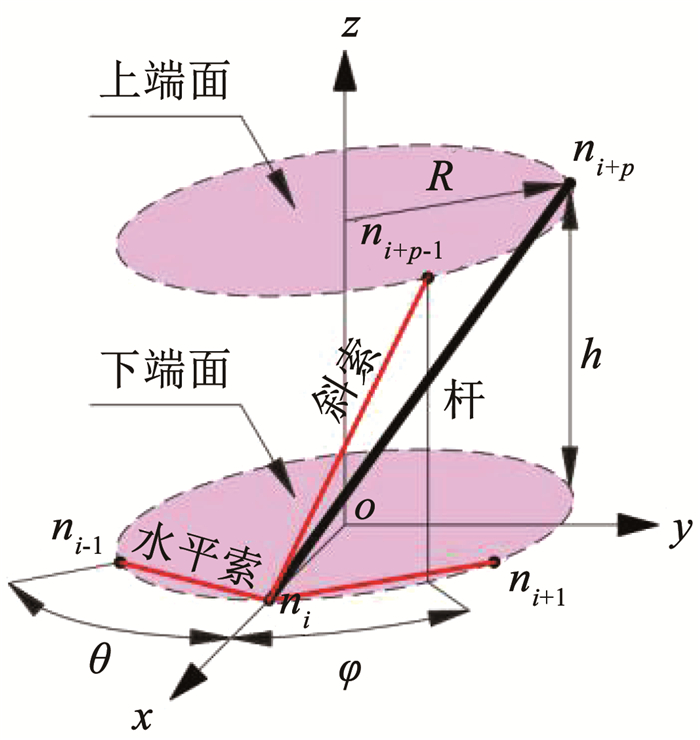
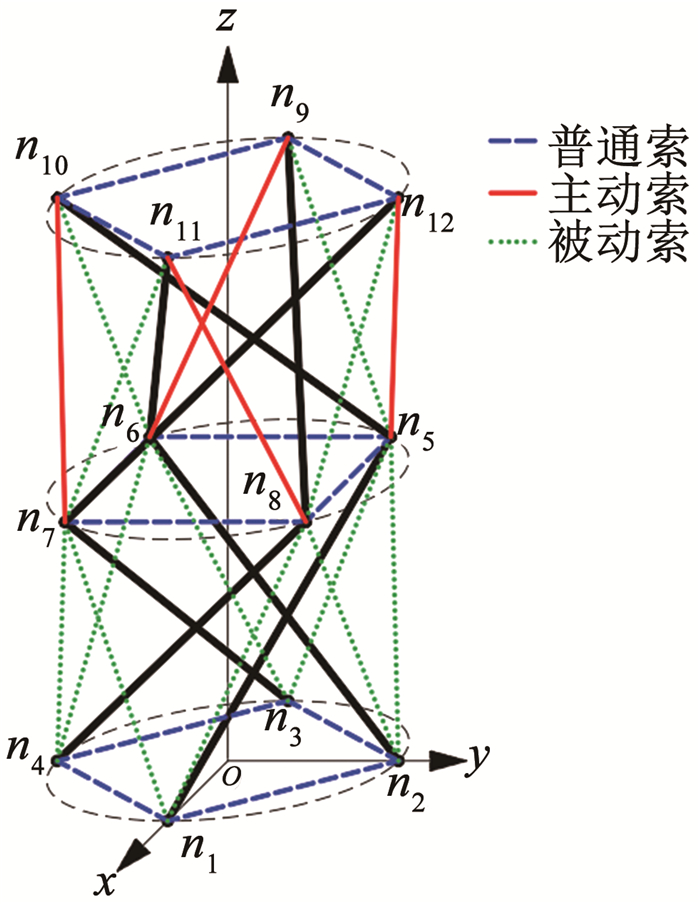
1 张拉整体结构的力学性能分析张拉整体基本单元的拓扑示意图如图 1所示,各构件与节点相连,所有节点均匀分布在上、下端面外接圆上,规则基本单元的上、下端面外接圆的半径相等,用R表示,基本单元高度为h,端面上相邻节点绕圆心的夹角称为单元内转角,用θ表示,当基本单元杆构件数为p时,单元内转角θ=2π/p,斜索上端面节点在下端面的投影与斜索下端面节点绕圆心的夹角为扭转角,用φ表示。
|
图 1 张拉整体基本单元的拓扑示意 Fig. 1 Topological diagram of prismatic tensegrity unit |
对于图 1结构,有3个索构件和1个杆构件连接于同一节点,在此基础上,每个节点额外连接一条斜索,则形成了含冗余拉索的张拉整体结构,其拓扑关系如图 2所示。

|
图 2 含冗余拉索的棱柱式张拉整体结构拓扑示意 Fig. 2 Topological diagram of prismatic tensegrity structure with redundant cables |
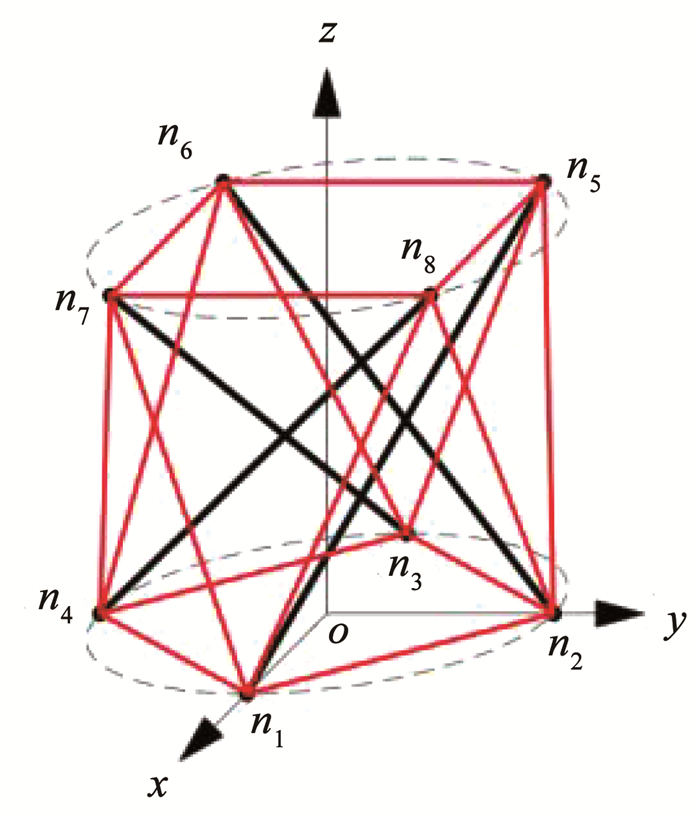
通过定义的分形参数p和几何参数R、h,可以得出节点坐标ni=[xi yi zi]T(i=1, 2, …, 2p),结合图 2所示的拓扑关系,可得到诸多含冗余拉索的张拉整体基本单元,当p=4时,基本单元如图 3所示。
|
图 3 含冗余拉索的棱柱式张拉整体基本单元 Fig. 3 A prismatic tensegrity basic unit with redundant cables |
通过节点坐标和构件与节点之间的连接关系,可得结构的平衡方程如下:
| $ \boldsymbol{A}_{1} \boldsymbol{t}=\boldsymbol{W} $ | (1) |
式中:A1∈R6p×ne为式(1)的平衡算子,ne为构件总数,t∈Rne×1为各构件内力,W∈R6p×1为作用于节点上的外载荷。
单个构件的内力计算公式为[18]
| $ t_{i}=E A \frac{l_{i}-l_{i 0}}{l_{i 0}}=k_{i} \Delta l_{i} $ | (2) |
式中:E为构件的弹性模量,A为构件的截面积,li为第i个构件长度,li0为第i个构件原长,ki为第i个构件的刚度,Δli为第i个构件长度变化量。
张拉整体结构在初始外力w0作用下达到平衡状态,表达式如下:
| $ \boldsymbol{K}_{n_{0}} \boldsymbol{n}_{0}=\boldsymbol{w}_{0} $ | (3) |
式中:n0为初始坐标节点矢量矩阵,Kn0为初始刚度矩阵。
当改变外载使之变化为dw或改变索长Δl,则会打破原有平衡状态产生一个新的平衡,新平衡时满足如下表达式:
| $ \boldsymbol{K}_{\mathrm{T}_{n_{0}}}\left(\boldsymbol{n}_{\mathrm{f}}-\boldsymbol{n}_{0}\right)=d \boldsymbol{w} $ | (4) |
式中:KTn0为切线刚度矩阵,nf为结构变形后的节点坐标矢量矩阵。
节点坐标的变化量Δn由式(4)可得
| $ \Delta \boldsymbol{n}=\boldsymbol{K}_{\mathrm{T}_{n_{0}}}^{-1} d \boldsymbol{w} $ | (5) |
新的节点坐标公式可表示为
| $ \boldsymbol{n}_{\mathrm{f}}=\boldsymbol{n}_{0}+\Delta \boldsymbol{n} $ | (6) |
研究含冗余拉索的棱柱式拼接结构的变形能力,基本单元与拼接结构的主要结构参数见表 1。
| 表 1 结构参数 Tab. 1 Parameters of tensegrity structure |
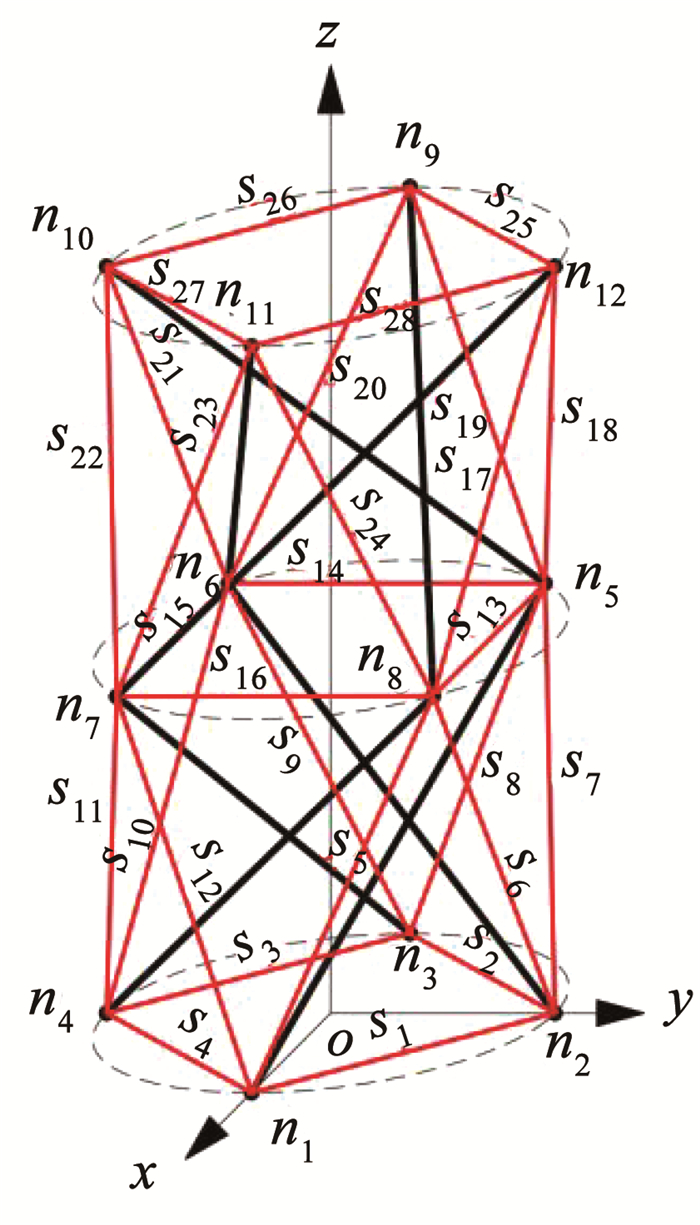
根据表 1所示参数,研究由2个含冗余拉索的4棱柱基本单元轴向拼接形成张拉整体结构的变形能力,拼接结构的上、下单元杆构件均为逆时针旋向,且上单元下端面节点与下单元上端面节点重合,将初始节点n1与x轴重合,各节点编号和索构件编号如图 4所示。
|
图 4 含冗余拉索的4棱柱轴向拼接结构 Fig. 4 Axial splice structure with redundant cables |
| 表 2 索构件连接关系 Tab. 2 Connection relationship of cables |
依据位置属性对索构件进行分类,见表 3。改变主动索索长,被动索会随之发生变化,最终实现结构变形,根据主、被动索的不同对索组赋值不同的材料属性,各构件材料属性参照文献[17],见表 4。
| 表 3 索构件分类 Tab. 3 Classification of cables |
| 表 4 构件材料属性 Tab. 4 Material properties of elements |
对棱柱式张拉整体轴向拼接结构进行变形分析,通过收缩被动索索长对结构施加初始预紧力,可以以此计算除主动索外结构初始耗散的弹性势能U0为
| $ U_{0}=\sum\limits_{i=1}^{n_{\mathrm{e}}} \frac{1}{2} \frac{E_{i} A_{i}}{l_{i}^{o}}\left(l_{i}^{\mathrm{ap}}-l_{i}^{\mathrm{p}}\right)^{2}-\sum\limits_{k=1}^{n_{\mathrm{a}}} \frac{1}{2} \frac{E_{k} A_{k}}{l_{k}^{o}}\left(l_{\mathrm{a} k}^{\mathrm{ap}}-l_{\mathrm{a}k}^{\mathrm{p}}\right)^{2} $ | (7) |
式中:lip为被动索收缩第i个构件的长度,liap为被动索收缩结构重新平衡后第i个构件的长度,lakap为被动索收缩结构重新平衡后第k个主动索的长度,lakp为被动索收缩第k个主动索的长度,na为主动索数目。
结构预紧后收缩主动索使结构发生变形,获得主动索额外做功Wa为
| $ W_{\mathrm{a}}=\sum\limits_{j=2}^{\text {steps }} \sum\limits_{i=1}^{n_{\mathrm{a}}} t_{\mathrm{a} i}^{j} \Delta l_{\mathrm{a} i}^{j} $ | (8) |
式中:taij为第j次迭代第i个主动索的额外产生的内力,Δlaij为第j次迭代第i个主动索收缩后结构重新平衡的索长与j-1次索长差值,steps为设置的迭代步数。
taij的计算公式如下:
| $ t_{\mathrm{a} i}^{j}=\frac{E_{i} A_{i}\left(l_{\mathrm{a} i}^{\mathrm{a} j}-l_{\mathrm{a} i}^{j}\right)}{l_{\mathrm{a} i}^{j}} $ | (9) |
式中:laiaj为第j次迭代第i个主动索收缩后结构重新平衡的索长,laij为第j次迭代第i个主动索收缩后索长。
通过缩短主动索索长使结构发生变形,Δlaij为负值,则Wa为负值。通过式(7)、(8),可以计算U0和Wa,Wa/U0与能量耗散有关:Wa/U0越大,能量耗散越大,因此,两者比值越小驱动效率越高。
收缩索长,会打破结构原有平衡形成新的稳定构型,不同的驱动方式结构变形不同,限制下端面节点z轴方向的自由度,保证上端面4个节点共面的基础上,研究结构轴向变形与扭转角变形能力,现定义轴向变形性能参数ε和扭转变形性能参数ω,参数ε为整体结构高度变化,参数ω为结构上端面与下端面绕z轴的转角相对于整体结构高度的变化,ε、ω的计算公式分别为:
| $ \varepsilon=\Delta h / H $ | (10) |
| $ \omega=\gamma / H $ | (11) |
式中:Δh为结构变形前、后上端面与下端面形心的高度差,H为拼接结构总高度,γ为上端面与下端面绕z轴的转角变化。
结合弹性势能U0、主动索做功Wa、轴向变形性能参数ε和扭转变形性能参数ω,定义μS和μT的计算公式分别为:
| $ \mu_{\mathrm{S}}=\frac{W_{\mathrm{a}}}{U_{0} \varepsilon} $ | (12) |
| $ \mu_{\mathrm{T}}=\frac{W_{\mathrm{a}}}{U_{0} \omega} $ | (13) |
μS、μT的表达式在包含能量的基础上又考虑到结构变形,当μS(或μT)越小时,结构变形过程中能量耗散越小,结构更易发生变形,以此选出索驱动结构变形的最优驱动方式。
3 驱动方式对结构变形的影响分析选出主、被动索,其余索构件均为普通索,赋值表 4所示的材料属性,收缩被动索索长对结构施加预紧力,后收缩主动索驱动结构发生变形,获得最终的稳定构型,通过计算被动索能量耗散值U0、主动索能量耗散做功Wa以及变形性能参数ε、ω,得出能实现结构变形的最优驱动方式。
3.1 单一轴向变形现有4种满足结构单一轴向变形要求的驱动方式,收缩20%被动索索长对结构预紧,后收缩15%主动索索长实现结构变形,根据表 1设置的基本单元高度(h=0.75 m)可以得出2个基本单元拼接结构的高度H=1.50 m,4种驱动方式下的变形结果见表 5。
| 表 5 单一轴向变形驱动方式与结果 Tab. 5 Driving methods and results of single axial deformation |
由表 5可得,4种驱动方式全部满足Δh<0,也就是结构是沿轴向被压缩的,并且,当斜索CD为主动索、CSH作为被动索时,结构的高度变化最大Δh=-0.393 3 m,轴向变形性能参数ε=-0.262 2,在相同变化高度下耗能最少μS=18.140 0,此种驱动方式对单一变形(收缩)效果最好。
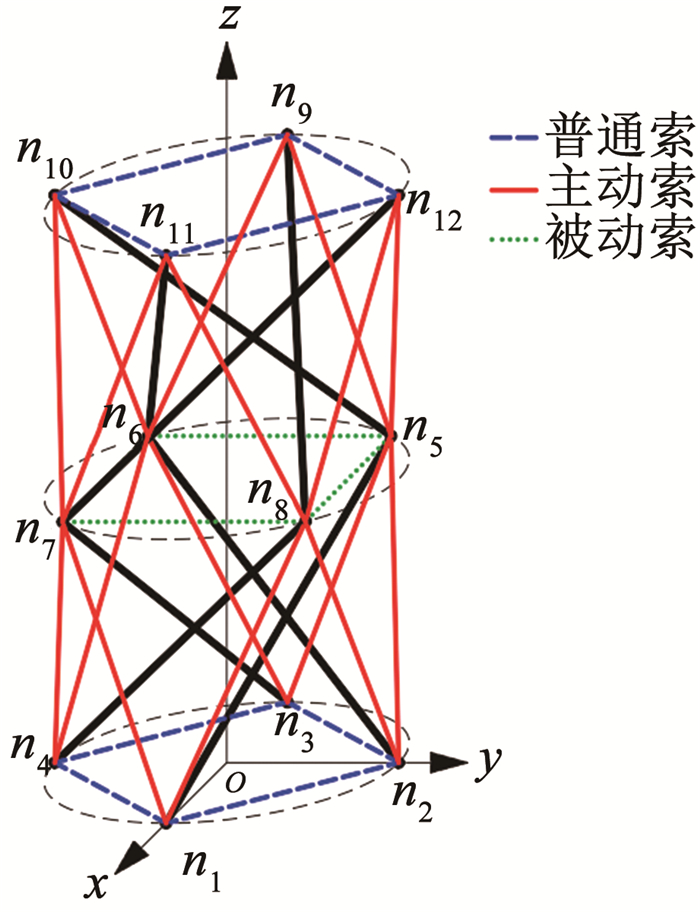
为清楚表述结构的最低能耗驱动方式,将驱动方式3的索组构件可视化,如图 5所示。获得的变形前、后的结构如图 6所示,图中虚线为变形前结构,实线为变形后结构。
|
图 5 轴向收缩的最优驱动方式 Fig. 5 Optimal driving mode of axial shrinkage |

|
图 6 变形前、后结构图 Fig. 6 Structure before and after deformation |
由图 6可以看出,结构变“矮胖”,结构的高度发生了明显减小。进一步,可以得到结构预紧后,主动索作用过程中节点坐标变化趋势和各类构件内力变化趋势,分别如图 7、8所示。

|
图 7 预紧后节点(n9)坐标 Fig. 7 Nodal coordinate (n9) after prestress |
|
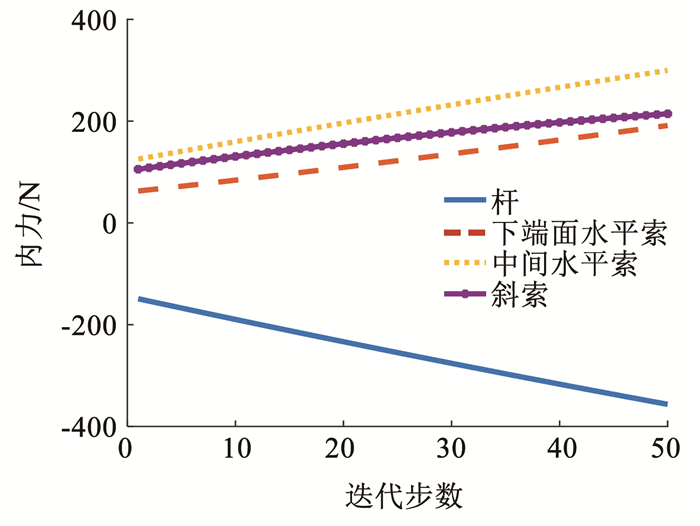
图 8 预紧后结构内力变化曲线 Fig. 8 Curve of structural internal force after prestress |
由图 7可以看出,节点n9的x轴坐标和y轴坐标基本保持不变,z轴坐标随着迭代步数的增加而逐渐减小。由图 8可得,结构预紧后构件已具备内力,随着主动索索长减小,结构的单个构件内力大小逐渐增加,杆构件提供支持力,其内力大小始终为负值,索构件提供拉力,其内力大小始终为正值,并且,对于3组索构件而言,中间水平索的内力始终最大。
3.2 轴向与扭转的复合变形棱柱式张拉整体结构最常见的复合变形是轴向变形与扭转变形的组合,与单一轴向变形的操作方式相同,先收缩20%被动索索长对结构进行预紧,后收缩5%主动索索长实现结构变形,表 6为轴向与扭转复合变形的驱动方式和结果。
| 表 6 轴向与扭转复合变形的驱动方式与结果 Tab. 6 Driving methods and results of composite axial and torsional deformation |
通过对表 6分析可得:
1) 驱动方式1的主动索为中间水平索CSH,驱动方式2的主动索为上、下端面水平索CBH,两种驱动方式的被动索皆为斜索CD,虽然两种驱动方式的主动索不同,但实现的变形效果基本相同,其高度变化为Δh=-0.060 6 m,相较于表中所列其他驱动方式,驱动方式2能够实现结构的最大扭转变形,最大扭转角γ=35.219 0°。
2) 驱动方式3、4的主动索分别为与杆构件旋向相同的下、上基本单元斜索,被动索为剩余斜索构件,两种驱动方式实现的驱动效果一致,其中μS=112.827 2、μT=-0.685 0,从数值上看μS远大于μT,说明主动索为旋向与杆构件旋向相同的斜索时结构更易发生扭转变形。
3) 驱动方式5将驱动方式3、4进行叠加,将主动索设置为旋向与杆构件旋向相同的斜索,被动索为结构中剩余斜索构件,但并未实现高度变化Δh和扭转角变化γ加倍的情况,Δh和γ较驱动方式3、4减小,μS和μT较驱动方式3、4增大,能量耗散大,不利于结构变形。
4) 复合变形的最优驱动方式为驱动方式6、7,主动索分别为与杆构件旋向相反的下、上基本单元斜索,被动索为剩余斜索,2种驱动方式实现的结构变形效果相同:高度变化为Δh=-0.081 7 m,扭转角变化γ=21.727 9°。驱动方式8是驱动方式6、7的叠加,其高度差Δh和扭转角变化γ数值上较驱动方式6、7减小近乎1/2,在能量耗散方面也较驱动方式6、7差。
最优复合变形驱动方式7如图 9所示,结构变形如图 10所示,虚线与实线分别表示变形前、后结构。
|
图 9 复合变形的最优驱动方式 Fig. 9 Optimal driving mode of composite deformation |

|
图 10 复合变形前、后结构图 Fig. 10 Structure before and after deformation |
相应地,收缩被动索对张拉整体结构预紧后,主动索作用过程中各类构件内力变化趋势和节点坐标变化趋势,分别如图 11、12所示。

|
图 11 复合变形最优驱动方式构件内力 Fig. 11 The internal force of the optimal driving mode |
|
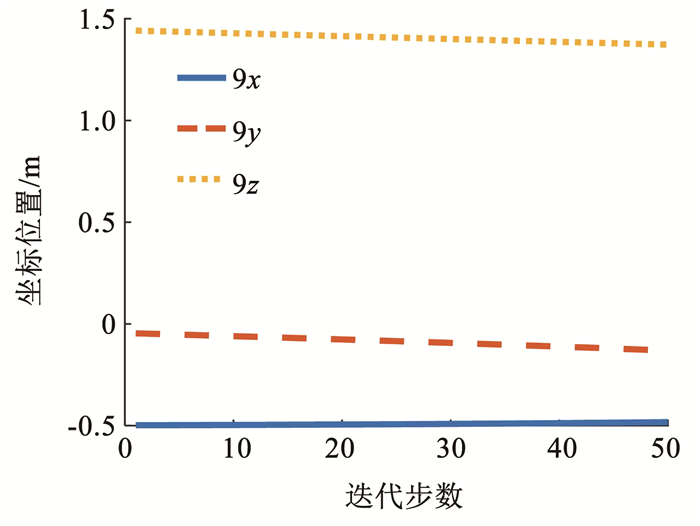
图 12 复合变形最优驱动方式节点(n9)坐标 Fig. 12 Nodal coordinate of the optimal driving mode |
由图 11可以看出,各类构件内力大小始终增加,索构件内力始终大于0,杆构件内力小于0,满足杆受压力索受拉力的条件。由图 12可得,节点n9的坐标发生微小变化,z轴和y轴坐标有下降趋势,x轴坐标变化不明显。
4 结论1) 对于双层拼接结构的单一轴向变形,当斜索为主动索、中间水平索为被动索时,结构的高度变化最大,能量耗散最少,轴向变形的驱动效率最高。
2) 对于双层拼接结构既产生高度变化又产生扭转变化的复合变形,当上单元或下单元的主动索为与杆构件旋向相反的斜索、被动索为剩余斜索时,能量耗散最少,复合变形的驱动效率最高。
| [1] |
JUAN S H, MIRATS TUR J M. Tensegrity frameworks: Static analysis review[J]. Mechanism and Machine Theory, 2008, 43(7): 859. DOI:10.1016/j.mechmachtheory.2007.06.010 |
| [2] |
罗阿妮, 刘贺平, SKELTONR E, 等. 张拉整体基本形体稳定构型理论[J]. 机械工程学报, 2017, 53(23): 62. LUO Ani, LIU Heping, SKELTON R E, et al. The theory of basic tensegrity unit stable forming[J]. Journal of Mechanical Engineering, 2017, 53(23): 62. DOI:10.3901/JME.2017.23.062 |
| [3] |
冯晓东, 胡晋荣, 撒剑波, 等. 新型环形张拉整体式穹顶结构形态设计与分析[J]. 建筑钢结构进展, 2022, 24(3): 80. FENG Xiaodong, HU Jinrong, SA Jianbo, et al. Morphology design and analysis of novel annular tensegrity-dome structures[J]. Progress in Steel Building Structures, 2022, 24(3): 80. DOI:10.13969/j.cnki.cn31-1893.2022.03.009 |
| [4] |
陈占魁, 罗凯, 田强. 张拉整体结构的动力学等效建模与实验验证[J]. 力学学报, 2021, 53(6): 1698. CHEN Zhankui, LUO Kai, TIAN Qiang. Dynamic equivalent modeling of tensegrity structures and experimental verification[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(6): 1698. DOI:10.6052/0459-1879-21-056 |
| [5] |
GILEWSKI W, KŁOSOWSKA J, OBARA P. Applications of tensegrity structures in civil engineering[J]. Procedia Engineering, 2015, 111: 242. DOI:10.1016/j.proeng.2015.07.084 |
| [6] |
SHAH D S, BOOTH J W, BAINES R L, et al. Tensegrity robotics[J]. Soft Robotics, 2022, 9(4): 639. DOI:10.1089/soro.2020.0170 |
| [7] |
TIBERT A G, PELLEGRINO S. Deployable tensegrity reflectors for small satellites[J]. Journal of Spacecraft and Rockets, 2002, 39(5): 701. DOI:10.2514/2.3867 |
| [8] |
阚子云. 张拉整体结构动力响应分析的模型和算法研究[D]. 大连: 大连理工大学, 2019 KAN Ziyun. Research on modeling and numerical method for dynamic response analysis of tensegrity structure[D]. Dalian: Dalian University of Technology, 2019. DOI: 10.26991/d.cnki.gdllu.2019.004369 |
| [9] |
MOTRO R. Tensegrity: Structural systems for the future[M]. London: Kogan Page Science, 2003.
|
| [10] |
AMENDOLA A, CARPENTIERI G, DE OLIVEIRA M, et al. Experimental investigation of the softening-stiffening response of tensegrity prisms under compressive loading[J]. Composite Structures, 2014, 117: 234. DOI:10.1016/j.compstruct.2014.06.022 |
| [11] |
ZHANG Liyuan, ZHAO Hongping, FENG Xiqiao. Constructing large-scale tensegrity structures with bar-bar connection using prismatic elementary cells[J]. Archive of Applied Mechanics, 2015, 85(3): 383. DOI:10.1007/s00419-014-0958-3 |
| [12] |
WANG Xinrui, LING Zhenchao, QIU Chen, et al. A four-prism tensegrity robot using a rolling gait for locomotion[J]. Mechanism and Machine Theory, 2022, 172: 104828. DOI:10.1016/j.mechmachtheory.2022.104828 |
| [13] |
ZHANG Liyuan, ZHENG Yang, YIN Xu, et al. A tensegrity-based morphing module for assembling various deployable structures[J]. Mechanism and Machine Theory, 2022, 173: 104870. DOI:10.1016/j.mechmachtheory.2022.104870 |
| [14] |
张沛, 冯健, 周继凯. 含冗余拉索的棱柱型张拉整体结构成形过程分析[J]. 东南大学学报(自然科学版), 2022, 52(5): 848. ZHANG Pei, FENG Jian, ZHOU Jikai. Analysis on forming process of prismatic tensegrity structures with redundant cables[J]. Journal of Southeast University (Natural Science Edition), 2022, 52(5): 848. DOI:10.3969/j.issn.1001-0505.2022.05.004 |
| [15] |
董晓. 六杆张拉整体机器人的设计与分析[D]. 哈尔滨: 哈尔滨工业大学, 2019 DONG Xiao. Design and analysis of tensegrity robot with six rods[D]. Harbin: Harbin Institute of Technology, 2019. DOI: 10.27061/d.cnki.ghgdu.2019.004778 |
| [16] |
FRADDOSIO A, MICHELETTI A, PAVONE G, et al. Analysis of novel adaptable tensegrity towers[C]//Proceedings of IASS Annual Symposia. Guildford, UK: International Association for Shell and Spatial Structures (IASS), 2020: 1
|
| [17] |
CHEN Muhao, FRADDOSIO A, MICHELETTI A, et al. Energy-efficient cable-actuation strategies of the V-Expander tensegrity structure subjected to five shape changes[J]. Mechanics Research Communications, 2023, 127: 104026. DOI:10.1016/j.mechrescom.2022.104026 |
| [18] |
MA Shuo, CHEN Muhao, SKELTON R E. Tensegrity system dynamics based on finite element method[J]. Composite Structures, 2022, 280: 114838. DOI:10.1016/j.compstruct.2021.114838 |
 2023, Vol. 55
2023, Vol. 55


