2. 清华大学 土木水利学院,北京 100084
2. School of Civil Engineering, Tsinghua University, Beijing 100084, China
为了应对环境问题和能源危机的双重挑战,中国提出了“碳中和”和“碳达峰”的双重目标。风力发电作为绿色新能源的重要组成部分,是确保实现该目标的重要手段之一[1]。与陆上风电相比,海上风电具有风速高、有效发电时间长和不占用陆地资源等优势[2]。中国海岸线较长,具有丰富的海上风电资源,大量的海上风电场已经建成或正在建设中[3-4]。
目前,大多数海上风电场主要位于近海域,基础形式以大直径单桩基础为主[5]。但是,随着海上风电场逐渐向深远海发展,大直径单桩基础已经无法满足海上风电场建造的需求,因此,需要探索和研究新型基础形式在海上风电中的应用[6]。针对海上风电的新型基础,国内外学者进行了大量研究。现有研究成果中的新型基础主要通过对大直径钢管桩附加结构来构造复合基础,从而提高基础的承载性能,常采用的措施是在泥面处增加平台结构或在单桩基础周围增加吸力筒结构[7-9]。刘润等[10]对砂土场地中单桩复合筒型基础进行了桩筒共同承载机制研究,结果表明,复合基础中桩承担了竖向荷载和大部分弯矩,而筒结构分担了由于桩身传递的水平向荷载和部分弯矩。Li等[11]在单桩周围增加下部为筒、上部可以放置石头的结构来构造新型复合基础,通过离心机模型试验对4种砂土场地中新型复合基础的承载性能进行了研究,发现新型基础的极限承载力是单桩基础的4倍。Li和Yang等[12-13]提出了一种适用于海上风电的伞形复合基础,即在上筒结构上部增加了伞形构件,针对砂土场地,通过模型试验和数值模型对这种基础进行了基础承载力性能、冲刷特性等系列研究。Chen等[14]研究桩-筒复合基础的承载性能,结果表明,桩-筒复合基础的抗弯承载力比单桩和单个筒基础两者的抗弯承载力之和大。综上,桩-筒复合基础相对单桩基础在承载性能方面有较好的优越性,但大部分研究基于均匀质场地中。中国长江三角洲、珠江三角洲等海岸带分布有大量的淤泥质海床,上部软弱的淤泥质层厚度多达10 m甚至更深[15]。中国海上风电场主要位于这些区域,这种海床特性对海上风电场建设十分不利。因此,中国海上风电场的建设必须考虑上覆软弱土层对风力发电机支撑结构承载性能的影响。
桩-筒复合基础相对单桩基础有较好的承载性能,在中国海上风场已经得到应用[16],然而对桩-筒复合基础在上覆软黏土场地中承载性能的研究较少。为了研究上覆软黏土层对海上风电桩-筒复合基础承载性能的影响,基于有限元软件ABAQUS平台,建立了上覆软黏土层的砂土场地中桩-筒复合基础有限元模型,基于建立的数值模型分析了单向荷载作用(V、H、M)下以及复合荷载作用(H-M)下上覆软土层厚度对桩-筒复合基础承载特性的影响。
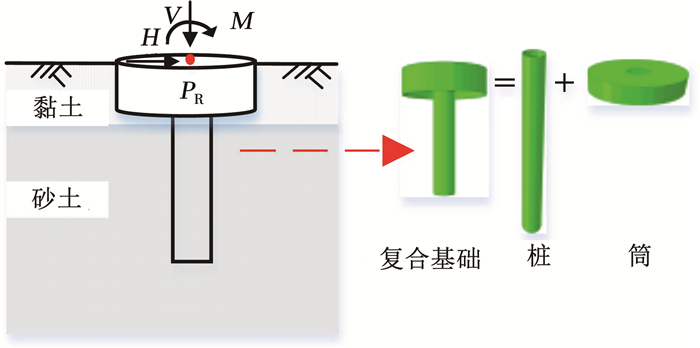
1 有限元模型桩-筒复合基础由钢管桩与筒相结合的方式构成,能够同时发挥钢管桩和筒结构的优势,如图 1所示。参照工程实际情况以及现有的研究经验[7, 10],确定了桩-筒复合基础尺寸。桩入土深度为30 m,桩外径为5 m,壁厚为0.05 m;筒结构入土深度为6 m,筒外直径为20 m,壁厚为0.05 m,筒顶盖厚度为0.06 m。桩-筒复合基础结构材质为钢材,密度为7 800 kg/m3,弹性模量为2.1×105 MPa,泊松比为0.3。
|
图 1 桩-筒复合基础模型 Fig. 1 Pile-bucket composite foundation model |
有限元模型中地基土体采用圆柱体。图 2为上覆软黏土层厚度为10 m时有限元模型的网格划分方法。为避免模型边界效应以及网格大小对有限元计算结果的影响,通过多次试算得到合理的土体边界取值范围以及有限元网格大小,最终确定土体高度为60 m,直径为100 m。计算模型中桩-筒结构在Z方向网格大小为1 m;土体在桩-筒结构埋深内网格大小为1 m,埋深以下网格大小为3 m。为保证计算结果的有效性,细化与基础结构接触的土体的网格。桩结构与筒结构之间采用绑定连接。桩-筒结构与地基土体之间的接触关系在法向采用“硬”接触,侧向采用摩擦模型,摩擦因数为tan(3φ/4),φ为土体的内摩擦角。土体底部采用固定约束,侧向边界固定横向位移(X和Y方向位移为0)。

|
图 2 有限元模型 Fig. 2 Finite element model |
有限元模型中地基土体采用Mohr-Colomb弹塑性本构模型,软黏土和砂土的模型参数如表 1所示[17]。在研究工况中,上覆软黏土厚度b分别为0、2、4、6、8、10 m。
| 表 1 土体参数 Tab. 1 Parameters of soil |
在泥面处复合基础的中心点建立参考点PR,作为荷载加载点,如图 1所示。竖向荷载V、水平荷载H以及弯矩荷载M通过位移控制法进行施加。在对复合基础施加荷载前,对模型进行地应力平衡计算,地应力平衡后模型整体竖向位移小于10-5 m,因此,可以忽略地层初始位移对计算结果的影响。
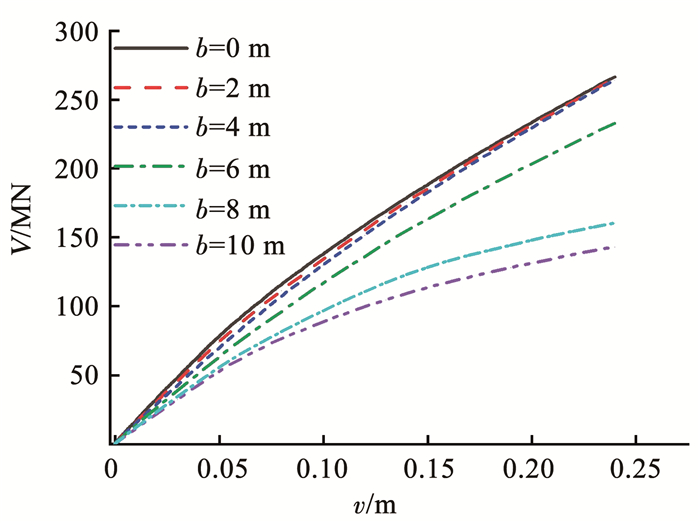
2 单向荷载作用下桩-筒复合基础承载性能 2.1 桩-筒复合基础竖向承载性能图 3为上覆软黏土层场地中桩-筒复合基础在竖向荷载作用下荷载V-位移v曲线。可以看出,随着上覆软黏土厚度的增加,桩-筒复合基础竖向承载力逐渐减小,当上覆软土层厚度超过筒结构入土深度时(b≥6 m)减小趋势有明显改变。这是由于地基下部砂土的弹性模量相对上覆软黏土的弹性模量大很多,当桩-筒复合基础中筒结构完全在软黏土中时,筒底部地基抵抗力大幅减小。Vesic等[18]认为软土地基中基础竖向位移达到基础宽度的3%~7%时,基础破坏。本文取桩-筒复合基础沉降量为0.04d(d为桩直径)时复合基础的竖向抗力V作为其竖向极限荷载。由图 3可知,当上覆软黏土层厚度b分别为0、2、4、6、8、10 m时,桩-筒复合基础竖向极限承载力分别为233.06、231.12、229.17、203.09、147.89、131.11 MN。
|
图 3 竖向荷载-位移曲线 Fig. 3 Vertical load-displacement curve |
通过上覆软黏土层厚度b分别为2、4、6、8、10 m与b为0时桩-筒复合基础竖向极限承载力计算得到竖向承载力降低率a,即
| $ a=\frac{V_{\mathrm{b} 0}-V_{\mathrm{b} i}}{V_{\mathrm{b} 0}} \times 100 \% $ | (1) |
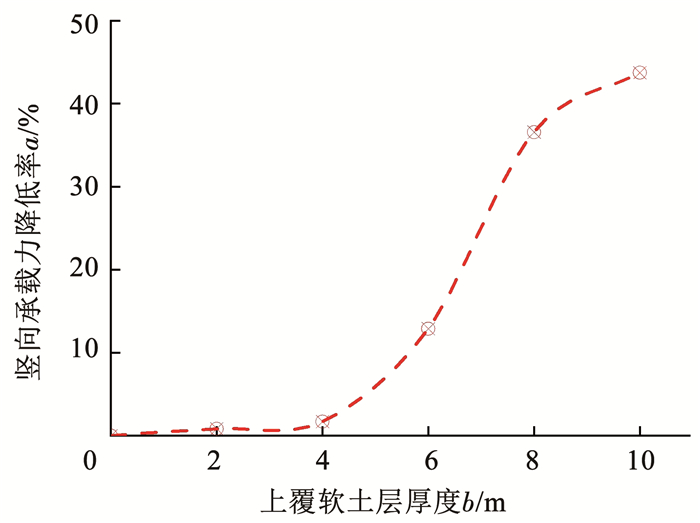
式中:Vb0为b=0时桩-筒复合基础竖向极限承载力,Vbi为b=i m(i=2、4、6、8、10)时桩-筒复合基础竖向极限承载力。计算结果如图 4所示,上覆软黏土层厚度b分别为2、4、6、8、10 m时,桩-筒复合基础的竖向承载力降低率a分别为0.84%、1.67%、12.86%、36.54%、43.74%。由图 4可以看出,当上覆软黏土层厚度小于筒结构入土深度(b≤6 m)时,复合基础中筒结构底部在弹性模量较高的砂土中,上覆黏土层对桩-筒复合基础的竖向承载力影响较小;当上覆软黏土层厚度大于筒结构入土深度(b>6 m)时,复合基础中筒结构完全在弹性模量较小的软黏土中,上覆黏土层对桩-筒复合基础的竖向承载力影响较大,但是随着黏土层厚度的继续增加,竖向承载力降低率的增加趋势渐缓。
|
图 4 上覆软黏土层对竖向承载力的影响 Fig. 4 Effect of soft clay layer on vertical bearing capacity |
为了进一步研究上覆软黏土层对桩-筒复合基础竖向承载性能的影响,分析不同软黏土层厚度时复合基础中筒结构和桩对竖向荷载的分担情况,采用筒结构竖向荷载分担比p表示为
| $ p=\frac{V_{\mathrm{B}}}{V_{\mathrm{B}}+V_{\mathrm{P}}} \times 100 \% $ | (2) |
式中:VB为复合基础承载力达到极限承载力时,筒结构所承担的竖向合力;VP为复合基础承载力达到极限承载力时,桩所承担的竖向合力。桩-筒复合基础中筒结构和桩结构各自所承担的竖向合力分别通过提取各个结构在泥面处截面Z方向的轴力得到。
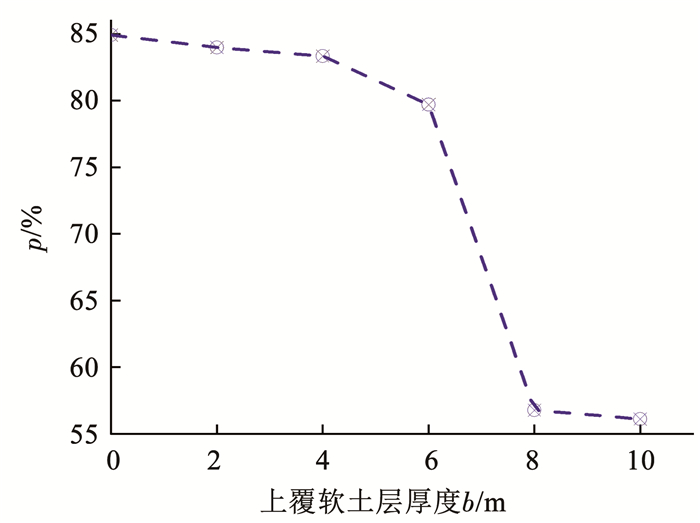
图 5为不同厚度上覆软黏土层时桩-筒复合基础中筒结构竖向荷载分担比p,上覆软黏土层厚度b分别为0、2、4、6、8、10 m时,筒结构竖向荷载分担比p分别为84.93%、84%、83.36%、79.69%、56.77%、56.10%。可以看出,当上覆软黏土层厚度小于筒结构入土深度(b≤6 m)时,桩-筒复合基础竖向承载力主要由筒结构提供,但随着上覆软土层厚度的增加,筒结构竖向荷载分担比p逐渐减小。当上覆软黏土层厚度小于筒结构入土深度(b>6 m)时,筒结构完全在软黏土层中,筒结构竖向荷载分担比p快速减小,但当上覆软土层厚度达到8 m时,随着上覆软黏土厚度的增加,筒结构竖向荷载分担比p变化较小,桩和筒结构的荷载分担比趋于稳定。
|
图 5 上覆软黏土层对竖向荷载分担比的影响 Fig. 5 Effect of soft clay layer on vertical load sharing ratio |
由图 4和5可知,上覆软黏土层的砂土地基中,桩-筒复合基础竖向承载特性受软黏土层厚度的影响,同时,以筒入土深度为分界线,复合基础中桩和筒结构的荷载分担机制发生很大的改变。这是由于桩-筒复合基础竖向承载力由侧向摩擦力和底部地基竖向抵抗力提供,且以筒结构底部端承型受荷为主。当筒结构底部在弹性模量较大的砂土中时,桩-筒复合基础的承载性能受上覆软土层厚度的影响较小,筒结构底部分担了大部分的竖向荷载;当上覆软黏土层厚度超过筒结构入土深度时,筒结构底部无法分担很大的竖向荷载,桩和筒结构的荷载分担机制发生改变,桩承受较大的竖向荷载。
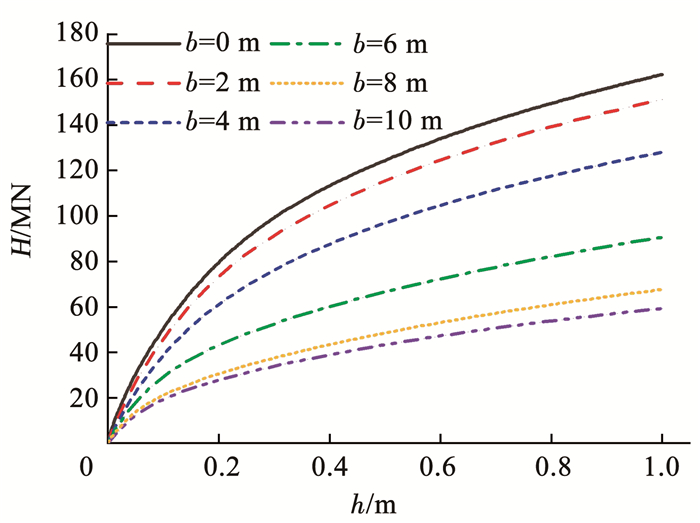
2.2 桩-筒复合基础水平承载性能图 6为有上覆软黏土层的砂土场地中桩-筒复合基础在水平荷载作用下荷载-位移曲线。可以看出,随着上覆软黏土厚度的增加,桩-筒复合基础水平承载力逐渐减小。现有海上风电相关设计规范规定,为保证海上风力发电机的正常运行,应限制支撑结构的转角[19-20]。武科[21]对软土地基中筒基础的承载特性进行了研究,结果表明,基础转角达到0.05 rad(2.8°)时,筒基础失稳破坏。取桩-筒复合基础顶部中心处转角为2.5°时作为基础失稳破坏的极限状态。本文取桩-筒复合基础达到转动的极限状态时,桩-筒复合基础水平抗力H作为其水平极限承载力。桩-筒复合基础在水平荷载作用下泥面处转角通过式(3)计算得到:
| $ \theta=\frac{\left|u_{\text {3左 }}-u_{\text {3右 }}\right|}{D} \times \frac{180}{\pi} $ | (3) |
|
图 6 水平荷载-位移曲线 Fig. 6 Horizontal load-displacement curve |
式中: u3左为基础左端的竖向位移;u3右为基础右端的竖向位移;D为筒结构直径,D=20 m。
当基础达到极限状态时,上覆软黏土层厚度b分别为0、2、4、6、8、10 m所对应的桩-筒复合基础水平极限承载力分别为124.39、115.34、96.74、66.48、48.40、43.21 MN。
计算上覆软黏土层厚度b分别为2、4、6、8、10 m时与b为0时桩-筒复合基础水平极限承载力降低率c,即
| $ c=\frac{H_{\mathrm{b} 0}-H_{\mathrm{b} i}}{H_{\mathrm{b} 0}} \times 100 \% $ | (4) |
式中:Hb0为b=0时桩-筒复合基础水平极限承载力,Hbi为b=i m(i=2、4、6、8、10)桩-筒复合基础水平极限承载力。
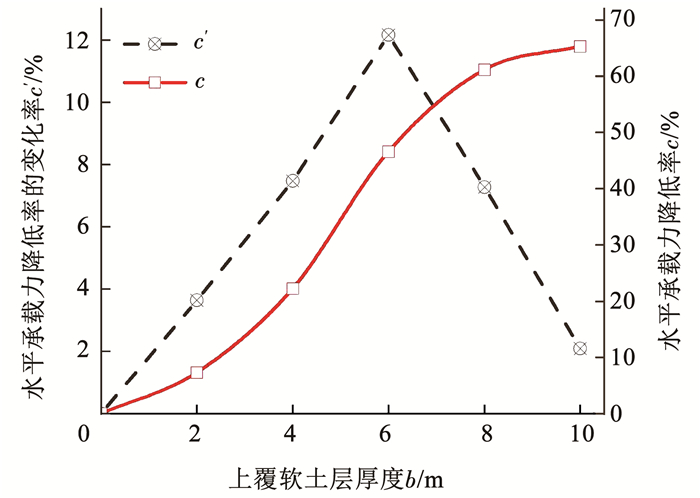
计算结果如图 7所示,上覆软黏土层厚度b分别为2、4、6、8、10 m时,桩-筒复合基础的水平承载力降低率c分别为7.27%、22.22%、46.55%、61.09%、65.26%。
|
图 7 上覆软黏土层对水平承载力的影响 Fig. 7 Effect of soft clay layer on horizontal bearing capacity |
并通过计算水平承载力降低率随上覆软土层厚度的变化率c′来描述上覆软黏土层厚度与水平承载力的变化规律,即
| $ c^{\prime}=\frac{c_i-c_{i-2}}{b_i-b_{i-2}} $ | (5) |
式中:ci为上覆软黏土层厚度b=i m时桩-筒复合基础水平极限承载力降低率,上覆软黏土层厚度bi=i m(i=2、4、6、8、10)。
桩-筒复合基础的水平承载力降低率c和水平承载力降低率随上覆软土层厚度的变化率c′计算结果如图 7所示。可以看出,随着上覆软黏土层厚度的增加,桩-筒复合基础水平承载力逐渐减小。当上覆软黏土层厚度小于筒结构入土深度(b≤6 m)时,复合基础水平承载力降低率的变化随着上覆软黏土层厚度增加呈线性增加;当上覆软黏土层厚度大于筒结构入土深度(b>6 m)时,复合基础水平承载力降低率增加趋势变缓,且降低率的变化率随着上覆软黏土层厚度增加呈线性减小。
同理,计算不同上覆软黏土层厚度下复合基础中筒结构水平荷载分担比
| $ q=\frac{H_{\mathrm{B}}}{H_{\mathrm{B}}+H_{\mathrm{P}}} \times 100 \% $ | (6) |
式中:HB为复合基础承载力达到水平极限承载力时筒结构所承担的水平合力,HP为复合基础承载力达到水平极限承载力时桩所承担的水平合力。桩-筒复合基础中筒结构和桩结构各自所承担的水平合力分别通过提取各个结构在泥面处截面的X方向剪力得到。
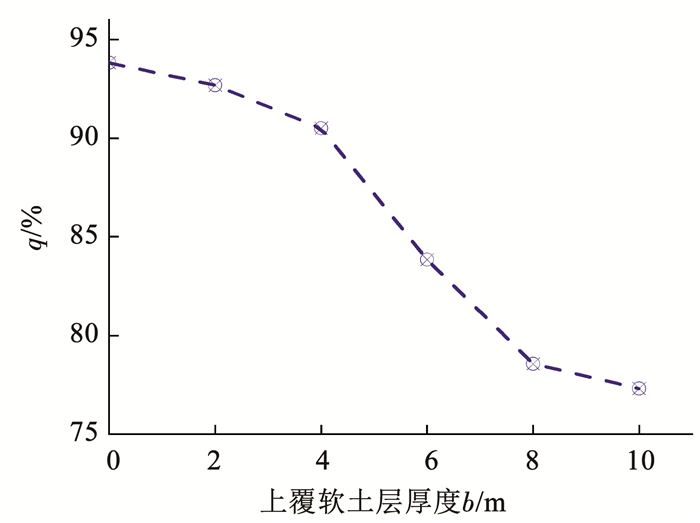
计算结果如图 8所示,上覆软黏土层厚度b分别为0、2、4、6、8、10 m时,筒结构水平荷载分担比q分别为93.83%、92.68%、90.50%、83.83%、78.55%、77.30%。可以看出,筒结构水平荷载分担比q随着上覆软黏土层厚度增加而逐渐减小,桩-筒复合基础中水平承载主要以筒结构为主。
|
图 8 上覆软黏土层对水平荷载分担比的影响 Fig. 8 Effect of soft clay layer on horizontal load sharing ratio |
图 9为不同上覆软黏土层厚度时,桩-筒复合基础达到极限状态时,复合基础的弯矩随入土深度的变化。可以看出,当上覆软黏土层厚度小于筒结构入土深度(b≤6 m)时,复合基础的弯矩以筒底部处为分界线,呈现双峰型分布;同时,上覆软黏土层厚度较小(b=2、4 m)时,上覆软黏土层厚度对复合基础的弯矩影响较小,分布形态基本相同。当上覆软黏土层厚度大于筒结构入土深度(b>6 m)时,复合基础的弯矩呈单峰型分布,复合基础中上部筒结构承受的弯矩减小,下部桩承受的弯矩增大。水平荷载作用下,由于桩-筒复合基础与土体之间的相互作用,桩-筒复合基础将荷载传递给地基土地。由于上覆软黏土层相对下部砂土层的承载性能较差,随着上覆软黏土厚度增加,上部土体承受的荷载减小并将荷载传递给下部土体,导致桩-筒复合基础上部结构承担弯矩荷载减小,下部结构承担弯矩增大。

|
图 9 弯矩随基础埋深的变化 Fig. 9 Relationship between moment and depth of foundation |
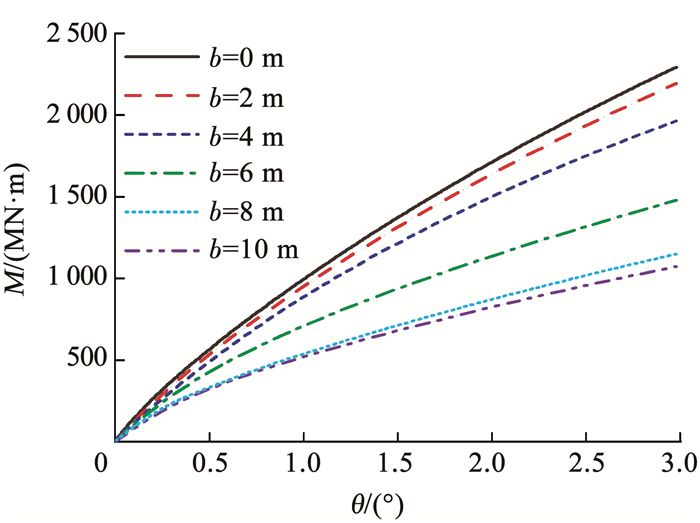
在桩-筒复合基础泥面处施加转角位移,得到泥面处参考点弯矩,结果如图 10所示。同理,取桩-筒复合基础泥面处转角为2.5°时参考点处的弯矩荷载作为基础的抗弯极限承载力。上覆软黏土层厚度b分别为0、2、4、6、8、10 m时,桩-筒复合基础水平极限承载力分别为2 022.51、1 935.76、1 750.68、1 317.39、1 017.99、956.12 MN · m。从计算结果可以看出,随着上覆黏土层厚度的增加,桩-筒复合基础的抗弯极限承载力逐渐减小。
|
图 10 弯矩与转角的关系 Fig. 10 Moment and rotation angle curve |
为进一步研究上覆软黏土层对桩-筒复合基础抗弯极限承载力的影响,计算抗弯承载力降低率d和抗弯承载力降低率随上覆软土层厚度的变化率d′,分别通过式(7)和(8)计算得到:
| $ d=\frac{M_{\mathrm{b} 0}-M_{\mathrm{b} i}}{M_{\mathrm{b} 0}} \times 100 \% $ | (7) |
| $ d^{\prime}=\frac{d_i-d_{i-2}}{b_i-b_{i-2}} $ | (8) |
式中:Mb0为b=0时桩-筒复合基础抗弯极限承载力,Mbi为b=i m(i=2、4、6、8、10)时桩-筒复合基础抗弯极限承载力,di为上覆软黏土层厚度b=i m时桩-筒复合基础抗弯极限承载力降低率,上覆软黏土层厚度bi=i m(i=2、4、6、8、10)。
计算结果如图 11所示,上覆软黏土层厚度b分别为2、4、6、8、10 m时,桩-筒复合基础的水平承载力降低率c分别为4.29%、13.44%、34.86%、49.67%、52.73%。可以看出,随着上覆软黏土层厚度的增加,桩-筒复合基础抗弯极限承载力降低率逐渐增加,抗弯极限承载力逐渐减小。当上覆软黏土层厚度小于筒结构入土深度(b≤6 m)时,桩-筒复合基础抗弯极限承载力降低率逐渐增加,上覆黏土层厚度对基础抗弯极限承载力的影响较大;当上覆软黏土层厚度大于筒结构入土深度(b>6 m)时,筒结构完全在软黏土层中,复合基础抗弯极限承载力的降低率随着上覆软黏土层厚度的增加而增大的趋势变缓。因此,当桩-筒复合基础中筒结构完全在上覆软黏土层中时,上覆软黏土层厚度的变化对基础的抗弯承载性能影响较小。

|
图 11 上覆软黏土层对抗弯承载力的影响 Fig. 11 Effect of soft clay layer on moment bearing capacity |
为了更好地解释上覆黏土层厚度对桩-筒复合基础抗弯承载性能的影响,计算不同上覆软黏土厚度时复合基础转动刚度与转角的关系,转动刚度G通过转角θ与弯矩M的关系曲线斜率得到,计算结果如图 12所示。可以看出:

|
图 12 转动刚度与转角的关系 Fig. 12 Rotation stiffness and rotation angle curve |
1) 桩-筒复合基础转角较小时(θ≤0.5°),基础的转动刚度随着转角的增大而快速减小,这是因为基础转角较小时,基础中抗弯承载力主要由上部软黏土层提供。当桩-筒复合基础转角较大时(θ>0.5°),基础转动刚度的减小趋势逐渐变缓,基础中抗弯承载力逐渐由下部砂土提供。
2) 随着上覆软黏土层厚度的增加,基础的转动刚度逐渐减小。以b=6 m为分界线,桩-筒复合基础的转动刚度变化有很明显的区别。
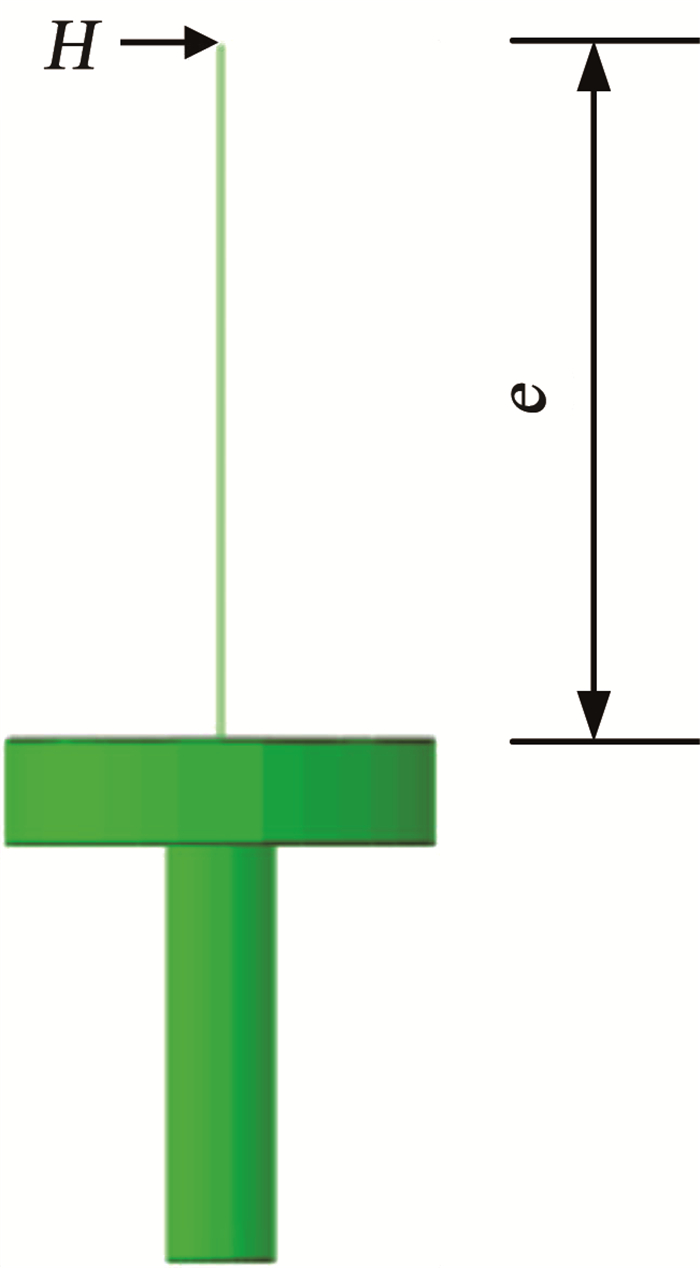
3 复合荷载(H-M)作用下桩-筒复合基础承载性能海上风电支撑结构主要承受由上部风荷载和波浪荷载产生的水平力和弯矩,海上风电基础设计时应考虑水平荷载和弯矩荷载共同作用下的承载性能。数值模型计算中,通过在桩-筒复合基础的上部附加一段长度为e的刚性梁,水平荷载在刚性梁顶端施加,通过改变刚性梁的长度得到不同的H-M荷载组合,如图 13所示。研究中e分别为0、2.5、5、10、20、40、100 m,根据力学关系可知,复合基础在泥面处受到的水平荷载为H,弯矩荷载为M=H×e。
|
图 13 H-M复合加载 Fig. 13 Combined loading H-M |
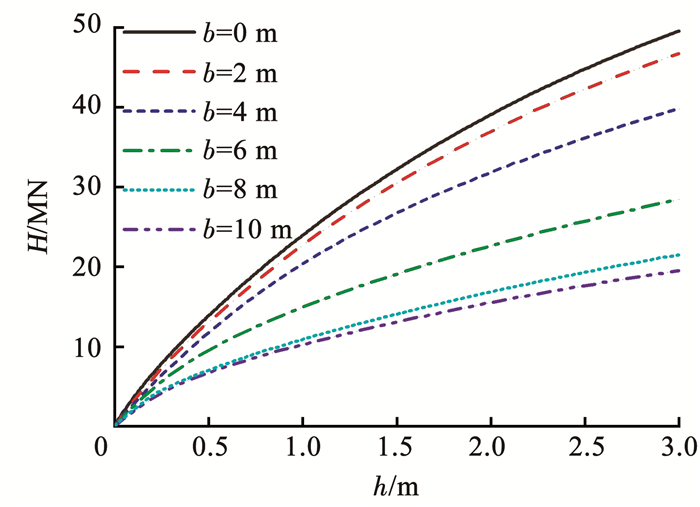
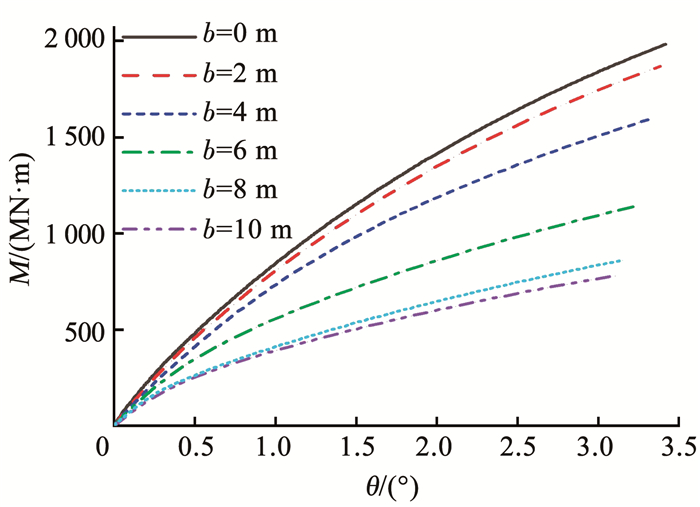
分别对不同的e情况下,不同厚度的上覆软黏土层桩-筒复合基础承载性能进行研究。图 14为e=40 m时,H-M复合作用下刚性梁顶端水平荷载和位移的关系。图 15为e=40 m时,H-M复合作用下桩-筒复合基础在泥面位置处受到的弯矩和转角的关系。从图 14和15可以看出,随着上覆软黏土层厚度的增加,相同刚性梁顶端水平位移对应的泥面位置处弯矩减小。
|
图 14 水平荷载-位移曲线 Fig. 14 Horizontal load-displacement curve |
|
图 15 弯矩与转角的关系 Fig. 15 Moment and rotation angle curve |
同样,当桩-筒复合上部转角为2.5°时,基础达到服务极限状态,刚性梁顶端受到的水平荷载为水平极限荷载Hu,泥面处基础的极限弯矩为Mu=Hu×e。图 16为e=40 m时,达到服务极限状态时,水平荷载和弯矩复合作用下基础结构受到的弯矩在长度方向的变化。可以看出,随着上覆软黏土层厚度增加,基础结构受到的弯矩荷载减小,基础抗弯性能降低。当上覆软黏土层厚度较小时,桩-筒复合基础受到的弯矩荷载在长度方向的分布形态相似,筒结构承受较大的弯矩荷载;当上覆软黏土层厚度大于筒结构入土深度时,水平荷载和弯矩荷载复合作用下复合基础中的筒结构无法承受大部分弯矩荷载,而筒结构下部的桩分担较大的弯矩荷载。结果表明,上覆黏土层厚度改变了桩-筒复合承受荷载的状态,在设计中应充分考虑上覆软黏土层对基础结构受荷状态的影响。

|
图 16 弯矩分布规律 Fig. 16 Moment distribution |
图 17为不同上覆软黏土层厚度下,不同e时基础的水平极限荷载和弯矩极限荷载。可以看出,水平极限荷载和弯矩极限荷载之间为线性关系,且随着上覆软黏土层厚度的增加而减小。

|
图 17 水平极限荷载和弯矩极限荷载 Fig. 17 Horizontal ultimate load Hu and moment ultimate load Mu |
进一步研究上覆软黏土层对桩-筒复合基础承载性能的影响,定义考虑水平荷载和弯矩荷载的复合作用下桩-筒复合基础的初始刚度kinit,通过式(9)计算得到,物理意义为当转角为0°时桩-筒复合基础水平荷载H和转角θ关系曲线的切线斜率[22]。
| $ k_{\text {init }}=\left.\frac{\Delta H}{\Delta \theta}\right|_{\theta=0} $ | (9) |
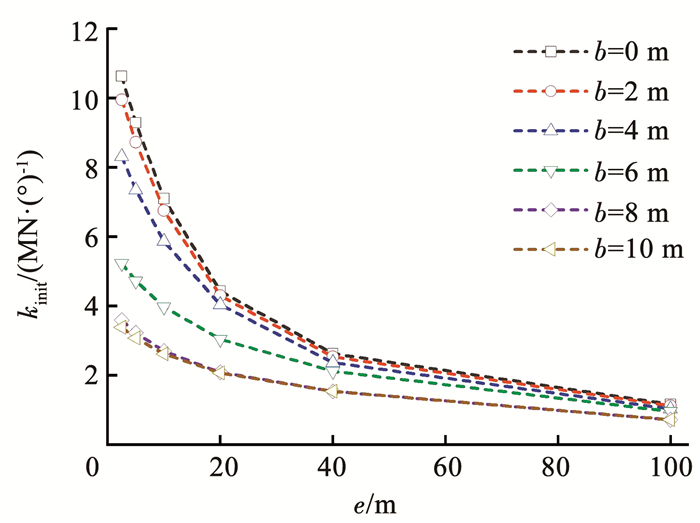
图 18和19分别为桩-筒复合基础初始刚度kinit与e(水平荷载离心率)和上覆软黏土层厚度b之间关系。从图 18可以看出,初始刚度kinit随着e的增加而减小;当e增加到一定值时,初始刚度kinit变化趋势变缓。结合图 18和19的分析可知,e较小时所对应的kinit相对e较大时所对应的kinit要大很多,导致图 19中e=40、100 m时kinit随b的变化关系显示为直线。图 20为e=40、100 m时桩-筒复合基础初始刚度kinit与上覆软黏土层厚度b的关系。
|
图 18 kinit与e的关系 Fig. 18 Relationship of kinit and e |
|
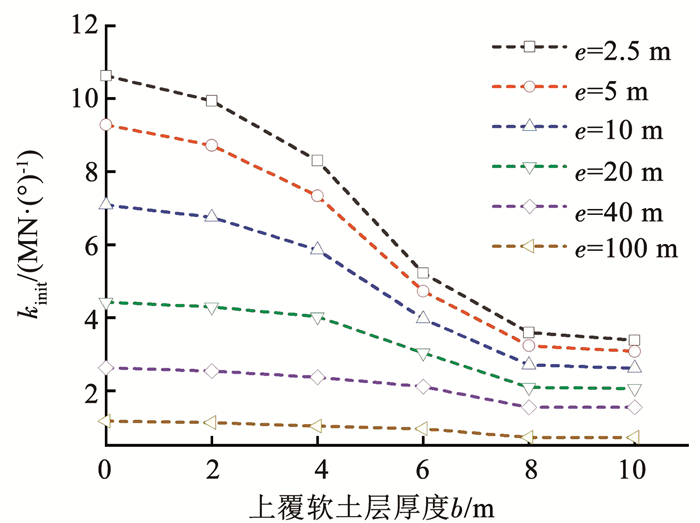
图 19 kinit与b的关系 Fig. 19 Relationship between kinit and b |
|
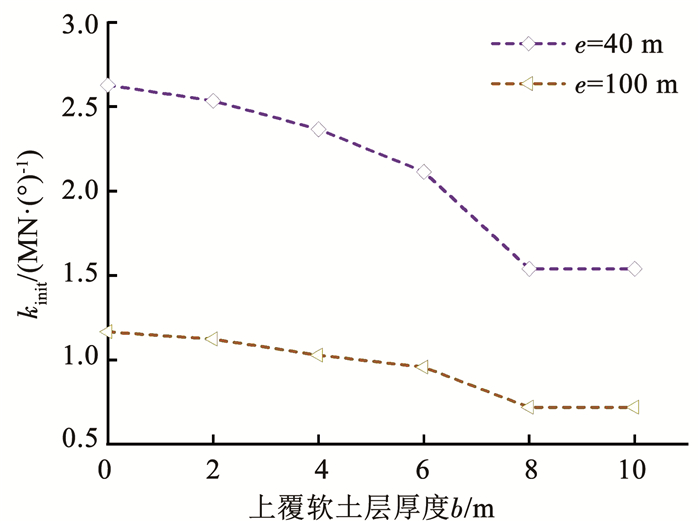
图 20 e=40和100 m时kinit与b的关系 Fig. 20 Relationship between kinit and b when e=40 and 100 m |
从图 19和20可以看出,当e较大时初始刚度kinit与上覆软黏土层厚度b的关系与e较小时的变化规律相同,均表现为初始刚度kinit随着上覆软黏土层厚度b的增加而减小。当b≤8 m时,kinit与b为曲线递减关系;当b>8 m时,kinit趋于稳定,不再随着b的增加而减小。
4 结论1) 桩-筒复合基础竖向极限承载力、水平极限承载力以及弯矩极限承载力随上覆软黏土厚度的增加而减小。当筒结构入土深度大于上覆软黏土层厚度时,各单向极限承载力随上覆软黏土层厚度的增加而快速减小。当筒结构入土深度小于上覆软黏土层厚度时,各单向极限承载力的降低率变化逐渐变缓。
2) 上覆软黏土层的存在影响了桩-筒复合基础中筒结构和桩的荷载分担机制,筒结构的竖向荷载和水平荷载分担比随上覆软黏土层厚度增加而逐渐减小。
3) 水平荷载和弯矩荷载复合作用下,桩-筒复合基础的水平极限承载力和抗弯极限承载力随上覆黏土层厚度的增加而线性减小。桩-筒复合基础的初始刚度kinit随上覆软黏土层厚度b的增加而曲线型递减,当上覆软黏土层厚度b>8 m时,kinit趋于稳定,不再随着b的增加而减小。
| [1] |
ZOU C, XIONG B, XUE H, et al. The role of new energy in carbon neutral[J]. Petroleum Exploration and Development, 2021, 48(2): 480. DOI:10.1016/S1876-3804(21)60039-3 |
| [2] |
ESTEBAN M D, DIEZ J J, LÓPEZ J S, et al. Why offshore wind energy?[J]. Renewable Energy, 2011, 36(2): 444. DOI:10.1016/j.renene.2010.07.009 |
| [3] |
周济福, 林毅峰. 海上风电工程结构与地基的关键力学问题[J]. 中国科学: 物理学力学天文学, 2013, 43(12): 1589. ZHOU Jifu, LIN Yifeng. Essential mechanics issues of offshore wind power systems[J]. SCIENTIA SINICA Physica, Mechanica & Astronomica, 2013, 43(12): 1589. DOI:10.1360/132013-335 |
| [4] |
中华人民共和国国家发展和改革委员会. 可再生能源发展"十三五"规划[R]. 2016 National Development and Reform Commission of People's Republic of China. "The 13th Five-Year" plan for renewable energy development[R]. 2016 |
| [5] |
孙毅龙, 许成顺, 杜修力, 等. 海上风电大直径单桩的修正p-y曲线模型[J]. 工程力学, 2021, 38(4): 44. SUN Yilong, XU Chengshun, DU Xiuli, et al. A modified p-y curve model of large-monopiles of offshore wind power plants[J]. Engineer Mechanics, 2021, 38(4): 44. DOI:10.6052/j.issn.1000-4750.2020.01.0051 |
| [6] |
WANG X, ZENG X, LI J, et al. A review on recent advancements of substructures for offshore wind turbines[J]. Energy Conversion And Management, 2018, 158: 103. DOI:10.1016/j.enconman.2017.12.061 |
| [7] |
朱东剑. 筒型基础与单桩相结合的新型复合风电基础研究[D]. 天津: 天津大学, 2012 ZHU Dongjian. Research of a new type of foundation for offshore wind turbines with the combining of monoplie foundation and bucket foundation[D]. Tianjin: Tianjin University, 2012 |
| [8] |
WANG X, ZENG X, YANG X, et al. Feasibility study of offshore wind turbines with hybrid monopile foundation based on centrifuge modeling[J]. Applied Energy, 2018, 209: 127. DOI:10.1016/j.apenergy.2017.10.107 |
| [9] |
WANG X, ZENG X, LI J, et al. Lateral bearing capacity of hybrid monopile-friction wheel foundation for offshore wind turbines by centrifuge modelling[J]. Ocean Engineering, 2018, 148: 182. DOI:10.1016/j.oceaneng.2017.11.036 |
| [10] |
刘润, 李宝仁, 练继建, 等. 海上风电单桩复合筒型基础桩筒共同承载机制研究[J]. 天津大学学报(自然科学与工程技术版), 2015, 48(5): 429. LIU Run, LI Baoren, LIAN Jijian, et al. Bearing characteristics of pile-bucket composite foundation for offshore wind turbine[J]. Journal of Tianjin University (Science and Technology), 2015, 48(5): 429. DOI:10.11784/tdxbz201309112 |
| [11] |
LI X, ZENG X, WANG X. Feasibility study of monopile-friction wheel-bucket hybrid foundation for offshore wind turbine[J]. Ocean Engineering, 2020, 204: 107276. DOI:10.1016/j.oceaneng.2020.107276 |
| [12] |
YANG Q, YU P, LIU Y F, et al. Scour characteristics of an offshore umbrella suction anchor foundation under the combined actions of waves and currents[J]. Ocean Engineering, 2020, 202: 106701. DOI:10.1016/j.oceaneng.2019.106701 |
| [13] |
LI H J, LIU H J, LIU S Y. Dynamic analysis of umbrella suction anchor foundation embedded in seabed for offshore wind turbines[J]. Geomechanics for Energy and the Environment, 2017, 10: S1458477515. DOI:10.1016/j.gete.2017.05.002 |
| [14] |
CHEN D, GAO P, HUANG S S, et al. Static and dynamic loading behavior of a hybrid foundation for offshore wind turbines[J]. Marine Structures, 2020, 71: 102727. DOI:10.1016/j.marstruc.2020.102727 |
| [15] |
王盛源. 工程实用软土力学[M]. 北京: 人民交通出版社, 2012.
|
| [16] |
FU Z N, WANG G S, YU Y M, et al. Model test study on bearing capacity and deformation characteristics of symmetric pile-bucket foundation subjected to cyclic horizontal load[J]. Symmetry, 2021, 13(9): 1647. DOI:10.3390/sym13091647 |
| [17] |
丁红岩, 张超, 张浦阳, 等. 上覆软土层对海上风电四筒基础承载特性影响[J]. 哈尔滨工程大学学报, 2020, 41(1): 67. DING Hongyan, ZHANG Chao, ZHANG Puyang, et al. Effect of soft soil layer on bearing capacity of four bucket foundation for offshore wind turbines[J]. Journal of Harbin Engineering University, 2020, 41(1): 67. DOI:10.11990/jheu.201808055 |
| [18] |
VESIC A S. Analysis of ultimate loads of shallow foundations[J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts, 1974, 11(11): A230. DOI:10.1016/0148-9062(74)90598-1 |
| [19] |
DNV G L. DNVGL-ST-0126: Support structures for wind turbines[S]. DNV GL, 2016
|
| [20] |
International Electrotechnical Commission. Wind turbines-Part 3 Design requirements for offshore wind turbines: IEC 61400-3[S]. Geneva: IEC, 2009
|
| [21] |
武科. 滩海吸力式桶形基础承载力特性研究[D]. 大连: 大连理工大学, 2007 WU Ke. A study on bearing capacity behavior of suction bucket foundations in beach-shallow sea[D]. Dalian: Dalian University of Technology, 2007 |
| [22] |
ACHMUS M, AKDAG C T, THIEKEN K. Load-bearing behavior of suction bucket foundations in sand[J]. Applied Ocean Research, 2013, 43: 157. DOI:10.1016/j.apor.2013.09.001 |
 2023, Vol. 55
2023, Vol. 55


