为缓解城市交通拥堵，国内部分城市设置了借道左转、移位左转等非常规交叉口^[1-3]，实地应用效果良好，是解决交叉口过饱和的有效手段。其中，连续流交叉口^[4]已在深圳进行试点应用，与平行流交叉口^[5]皆属于移位左转(displaced left-turn)设计。平行流交叉口与连续流交叉口放行规则不同，同相位放行一条道路直行车流和另一条道路左转车流，理论上能提升一倍左右的容量^[2]。平行流交叉口在2007年由Parsons首次提出^[6]，文献[7-8]研究表明，平行流交叉口的通行能力与连续流交叉口相近，操作性能相似，但平行流交叉口左转因多次停车导致通行能力低于连续流交叉口。

为解决平行流交叉口左转多次停车问题，文献[9]对其优化改进，提出了左转右置的平行流交叉口设计方案，以减少一次左转停车，同时通过主预信号协调配时，使所有流向车辆最多停车一次。在此基础上，提出了人车搭接相位的过街模式，以解决行人安全过街问题^[10]。文献[11]将两种移位左转进行组合优化设计。文献[12]探讨了流量输入对称性对平行流交叉口的影响。

以往研究仅探讨了平行流交叉口机动车控制和行人过街问题，还没有学者针对平行流交叉口非机动车过街策略进行研究。在大力推动绿色低碳出行模式下，非机动车是一种重要的出行方式，为促进平行流交叉口在中国的应用，解决非机动车过街是必不可少的环节。

钩形转弯(hook turn)^[13]也属于非常规交叉口设计，左转车流驶入最外侧进口车道，在直行绿灯启亮后，驶入交叉口相交道路进口直行车道停车线前等待，在相交道路绿灯启亮后，再驶离交叉口，实现间接左转，从而不用设置左转专用相位。已有学者探讨钩形转弯应用在机动车^[14-15]和公交车^[16]，但由于车辆转弯半径、路口可容纳车辆数的限制，仅适用于左转交通需求小的情形。考虑非机动车几何尺寸较小的优势，文献[17-18]探讨了非机动车钩形转弯控制策略。

为此，本文引入钩形转弯的概念来扩展平行流交叉口设计理念，给出左转非机动车过街控制策略，通过构建信号配时优化模型，解决平行流交叉口左转非机动车和同相位放行的直行机动车相冲突的问题，实现平行流交叉口机动车、非机动车和行人有序放行。

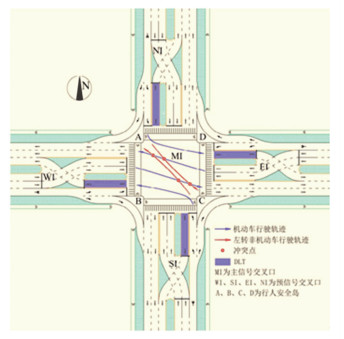
1 交通控制分析 1.1 几何设计及潜在冲突分析

平行流交叉口几何设计如图 1所示，将左转车道右置，在直行车道和左转车道之间设置移位左转车道(DLT)。左转车辆在主信号交叉口驶入DLT，以避免主信号一条道路左转车流和另一条道路直行车流冲突。

平行流交叉口主信号交叉口机动车为两相位信号控制，左转非机动车与同相位放行相交道路双向行驶的直行机动车皆存在冲突，需穿越多条直行机动车道才能实现左转，存在左转非机动车行车安全隐患，同时因直行机动车流量较大，左转非机动车很难寻找到所有直行机动车道同时存在可穿越安全间隙的过街机会。

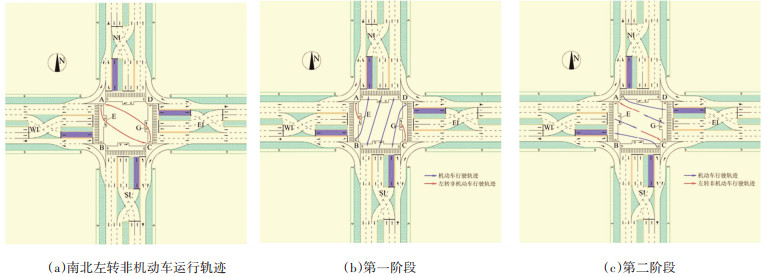
1.2 优化控制策略

信号相位方案如图 2所示，优化控制策略如下：1)机动车控制策略：各流向车辆行驶到达所遇第二个信号灯处时，相应放行相位绿灯启亮，避免二次停车。2)行人与同相位放行的左转机动车冲突区域仅为左转车道停车线前的人行横道，可通过时间分离避免两者冲突。直行非机动车的行驶路径与逆时针过街行人相同，可采用与逆时针过街行人相同的过街策略。3)由于左转非机动车与直行机动车冲突较为复杂，引入钩形转弯的概念，在直行车道前的非机动车横道的左侧设置左转非机动车待行区，如图 3所示。举例说明，当南北直行和东西左转组合通行相位绿灯启亮时，第一阶段，南向左转非机动车从安全岛(图 3中C)出发，经非机动车横道，到达左转非机动车待行区(图 3中G)等待；当东西直行和南北左转组合通行相位绿灯启亮后，第二阶段，南向左转非机动车从左转非机动车待行区(图 3中G)行驶至安全岛(图 3中A)，实现间接左转，东向直行机动车跟随在南向左转非机动车后面，避免了两者的相互冲突。考虑到左转非机动车和直行机动车行驶速度差异，需令直行机动车相位迟起，以保证直行机动车在自身的行驶速度下，始终跟随在左转非机动车后面，不会对被跟随的左转非机动车造成威胁。

2 信号配时优化模型构建

令i为交通流到来方向，i∈{W, S, E, N}分别为西、南、东和北。令k为进口路段上设置的预信号，k∈{WI, SI, EI, NI}。令φ等同$\left(i, i^{\prime}, i^{\prime \prime}, i^{\prime \prime \prime}, k\right) $，φ∈{1, 2, 3, 4}等同集合$\left(i, i^{\prime}, i^{\prime \prime}, i^{\prime \prime \prime}, k\right) $∈{(W, S, E, N, WI), (S, E, N, W, SI), (E, N, W, S, EI), (N, W, S, E, NI)}。若φ=2，有$i=S, i^{\prime}=E, i^{\prime \prime}=N, i^{\prime \prime \prime}=W, k=SI $。

2.1 目标函数

交叉口延误降低与容量增加是一个相互促进的过程^[2]，为保证延误在可接受的范围内，以交叉口机动车储备通行能力最大为优化目标^[19-20]为

$ \max \sum\limits_{\varphi=1}^4 \sum\limits_{j=1}^2 \mu q_{i j} $

(1)

式中：j为转向，j∈{1, 2, 3}分别为左转、直行和右转；q_ij为i进口j转向机动车交通需求，pcu/h；μ为流量系数，μ < 1表示未饱和，μ>1表示过饱和。

2.2 约束条件 2.2.1 主信号控制

考虑到左转非机动车和直行机动车行驶速度差异，为保证左转非机动车第二阶段行驶安全，需令直行机动车相位迟起，以保证直行机动车在自身行驶速度下，始终跟随在左转非机动车后面。根据图 2可知，各直行相位之间关系为

$ \tau_{i j}=\tilde{g}_{i j}, \varphi=1, 3 ; j=2 $

(2)

$ \tau_{i^{\prime} j}=\tau_{i j}+g_{i j}+I \zeta+\tilde{g}_{i^{\prime} j}, \varphi=1, 3 ; j=2 $

(3)

$ \tau_{i j}+g_{i j}+I \zeta=1, \varphi=2, 4 ; j=2 $

(4)

$ g_{i j}+\tilde{g}_{i j}=g_{i^{\prime \prime} j}+\tilde{g}_{i^{\prime \prime} j}, \varphi=1, 2 ; j=2 $

(5)

式中：τ_ij为主信号i进口j转向绿灯开始时刻，τ_ij∈[0, 1]；g_ij为主信号i进口j转向绿灯持续时长，g_ij∈[0, 1]；$\tilde{g}_{i j} $为主信号i进口j转向相位迟起持续时长，$\tilde{g}_{i j} \in[0, 1] $；I为绿灯间隔时间，s；ζ为周期时长倒数，s^-1。

同时，需令左转机动车相位迟起，保证行人和直行非机动车过街需求，具体为

$ \tau_{i^{\prime}(j-1)}=\tau_{i j}-\tilde{g}_{i j}+\tilde{g}_{i^{\prime}(j-1)}, \forall \varphi ; j=2 $

(6)

$ \tilde{g}_{i j}+g_{i j}=\tilde{g}_{i^{\prime}(j-1)}+g_{i^{\prime}(j-1)}, \forall \varphi ; j=2 $

(7)

2.2.2 主预信号协调控制

根据1.3节可知，各预信号相位绿灯启亮时刻计算公式为

$ \lambda_{i j}=\frac{L_{i j}^k+\vec{L}_{\mathrm{DLT}}^k}{v_{i j}}, \forall \varphi ; j=2 $

(8)

$ \lambda_{i^{\prime} j}=\frac{L_{i^{\prime} j}+L_{\mathrm{DLT}}^k}{{v}_{i^{\prime} j}}, \forall \varphi ; j=1 $

(9)

$ \tau_{i j}^k=\tau_{i j}-\lambda_{i j} \zeta+1, \varphi=1, 3 ; j=2 $

(10)

$ \tau_{i j}^k=\tau_{i j}-\lambda_{i j} \zeta, \varphi=2, 4 ; j=2 $

(11)

$ \tau_{i^{\prime} j}^k=\tau_{i^{\prime} j}+\lambda_{i^{\prime} j} \zeta, \forall \varphi ; j=1 $

(12)

式中：λ_ij为i进口j转向机动车从第1条停车线到达第2条停车线所需时间，s；L_DLT^k为预信号k控制DLT长度，m；$\vec{L}_{\mathrm{DLT}}^k $为与预信号k控制DLT平行的直行车道长度，m；L_ij^k为i进口j转向机动车在预信号k行驶轨迹长度，m；L_ij为i进口j转向机动车在主信号行驶轨迹长度，m；υ_ij为i进口j转向机动车行驶速度，m/s；τ_ij^k为i进口j转向机动车在预信号k绿灯开始时刻，τ_ij^k∈[0, 1]。

为确保车辆不会滞留在第2条停车线处，存在约束如下：

$ n_{i j}^k s_{i j}^k g_{i j}^k \leqslant n_{i j} s_{i j} g_{i j}, \forall \varphi ; j=2 $

(13)

$ n_{i^{\prime} j} s_{i^{\prime} j} g_{i^{\prime} j} \leqslant n_{i^{\prime} j}^k s_{i^{\prime} j}^k g_{i^{\prime} j}^k, \forall \varphi ; j=1 $

(14)

式中：g_ij^k为i进口j转向机动车在预信号k绿灯持续时长，g_ij^k∈[0, 1]；s_ij和s_ij^k分别为i进口j转向机动车在主信号和预信号k饱和流率，pcu/h；n_ij和n_ij^k分别为i进口j转向机动车在主信号和预信号k车道数。

2.2.3 预信号控制

预信号控制相位包括直行机动车通行相位和移位左转车道机动车通行相位计算公式为

$ \tau_{i^{\prime}(j-1)}^k=\tau_{i j}^k+g_{i j}^k+I \zeta-1, \varphi=1, 3 ; j=2 $

(15)

$ \tau_{i^{\prime}(j-1)}^k=\tau_{i j}^k+g_{i j}^k+I \zeta, \varphi=2, 4 ; j=2 $

(16)

$ g_{i j}^k+g_{i^{\prime}(j-1)}^k+2 I \zeta \leqslant 1, \forall \varphi ; j=2 $

(17)

各流向在所遇两个信号灯之间的行驶时间与预信号直行相位时长存在关系为

$ g_{i j}^k+I \zeta=\lambda_{i j} \zeta+\tilde{g}_{i^{\prime}(j-1)}-\tilde{g}_{i j}+\lambda_{i^{\prime}(j-1)} \zeta, \forall \varphi ; j=2 $

(18)

2.2.4 绿灯时长

绿灯时长存在最小、最大值约束为

$ G_{\min } \zeta \leqslant g_{i j} \leqslant G_{\max } \zeta, \forall \varphi ; j=1, 2 $

(19)

$ G_{\min }^k \zeta \leqslant g_{i j}^k \leqslant G_{\max }^k \zeta, \forall \varphi ; j=1, 2 $

(20)

式中：$G_{\min } 、G_{\max }, G_{\min }^k, G_{\max }^k $分别为上下限约束值，s。

根据非机动车过街策略，直行相位时长应不小于同相位放行非机动车通行时间和从出口侧安全岛至移位左转车道的非机动车横道清空时间，左转迟起相位时长应不小于同相位放行非机动车通行时间和从移位左转车道至进口侧安全岛的非机动车横道清空时间计算公式为

$ \begin{gathered} g_{i j}+I \zeta \geqslant \max \left\{\frac{q_{b i j}+q_{b i(j-1)}}{s_{b i^{\prime}}}, G_{b \min } \zeta\right\}+ \\ I_{b i^{\prime}}^{\prime} \zeta, \forall \varphi ; j=2 \end{gathered} $

(21)

$ \tilde{g}_{i^{\prime \prime}(j-1)} \geqslant \max \left\{\frac{q_{b i j}}{s_{b i^{\prime}}}, G_{b \min } \zeta\right\}+I^{\prime \prime}_{b i^{\prime}} \zeta, \forall \varphi ; j=2 $

(22)

式中：q_bij为i进口j转向非机动车交通需求，辆/h；s_bi为i进口前非机动车横道饱和流率，辆/h；I_bi^′和I_bi^″分别为i进口前从出口侧安全岛至移位左转车道和从移位左转车道至进口侧安全岛的非机动车横道清空时间，s；G_bmin为非机动车相位最小绿灯持续时长，s。

根据行人过街策略，左转相位时长应不小于同相位放行行人顺时针和逆时针过街通行时间和从出口侧安全岛至移位左转车道之间人行横道清空时间，左转迟起相位时长应不小于同相位放行行人顺时针和逆时针过街通行时间和从移位左转车道至进口侧安全岛之间人行横道清空时间为

$ \begin{gathered} g_{i^{\prime} j}+I \zeta \geqslant \max \left\{\frac{\max \left\{\vec{q}_{p i^{\prime}}, \overleftarrow{q}_{p i^{\prime}}\right\}}{s_{p i^{\prime}}}, G_{p \min } \zeta\right\}+ \\ I_{p i^{\prime}}^{\prime} \zeta, \forall \varphi ; j=1 \end{gathered} $

(23)

$ \tilde{g}_{i^{\prime \prime} j} \geqslant \max \left\{\frac{\vec{q}_{p i^{\prime}}}{s_{p i^{\prime}}}, G_{p \min } \zeta\right\}+I^{\prime \prime}_{p i^{\prime}} \zeta, \forall \varphi ; j=1 $

(24)

$ \tilde{g}_{i^{\prime} j} \geqslant \max \left\{\frac{\overleftarrow{q}_{p i^{\prime}}}{s_{p i^{\prime}}}, G_{p \min } \zeta\right\}+I^{\prime \prime}_{p i^{\prime}} \zeta, \forall \varphi ; j=1 $

(25)

式中：$\overleftarrow{q}_{p i} \text { 和 } \vec{q}_{p i} $分别为在i进口顺时针和逆时针行人流量，ped/h；s_pi为i进口人行横道行人过街饱和流率，ped/h；I_pi^′和I_pi^″分别为i进口前从出口侧安全岛至移位左转车道之间人行横道和从移位左转车道至进口侧安全岛之间人行横道清空时间，s；G_pmin为行人过街最小绿灯持续时长，s。

2.2.5 周期时长

主预信号周期时长相等，且存在最小、最大值约束。为构建线性约束条件，采用周期时长的倒数^[19]，计算公式为

$ \frac{1}{C_{\min }} \geqslant \zeta \geqslant \frac{1}{C_{\max }} $

(26)

式中$C_{\text {min }} \text { 和 } C_{\text {max }} $分别为最小和最大周期时长，s。

2.2.6 非机动车清空时长

非机动车清空时间可根据非机动车横道清空长度和行驶速度计算公式为

$ I_{b i}^{\prime}=\frac{L_{b i}^{\prime}}{{v}_{b i}}, \forall {\varphi} $

(27)

$ I_{b i}^{\prime \prime}=\frac{L_{b i}^{\prime \prime}}{{v}_{b i}}, \forall \varphi $

(28)

式中：L_bi^′和L_bi^″分别为i进口前从出口侧安全岛至移位左转车道和从移位左转车道至进口侧安全岛的非机动车横道长度，m；υ_bi为在i进口前非机动车横道上非机动车行驶速度，m/s。

行人清空时间可根据人行横道清空长度和行走速度计算，计算公式为

$ I_{p i}^{\prime}=\frac{L_{p i}^{\prime}}{{v}_{p i}}, \forall \varphi $

(29)

$ I_{p i}^{\prime \prime}=\frac{L_{p i}^{\prime \prime}}{v_{p i}}, \forall \varphi $

(30)

式中：L_pi^′和L_pi^″分别为i进口前从出口侧安全岛至移位左转车道之间人行横道和从移位左转车道至进口侧安全岛之间人行横道长度，m；υ_pi为在i进口前人行横道上行人行走速度，m/s。

因左转非机动车和直行机动车行驶速度差异，直行机动车相位应迟起，计算公式为

$ \tilde{g}_{i^{\prime} 2}=\zeta\left(\frac{L_{b i 1}}{{v}_{b i 1}}-\frac{L_{i^{\prime} 2}}{{v}_{i^{\prime} 2}}\right), \forall \varphi $

(31)

式中：L_bi1为i进口左转非机动车第二阶段在主信号交叉口行驶轨迹长度，m；L_i2为i进口直行机动车在主信号交叉口行驶轨迹长度，m；υ_bi1为i进口左转非机动车行驶速度，m/s。

2.2.7 待行区容量约束

平行流交叉口左转非机动车待行区所需容纳的非机动车数量约束为

$ 3600 K_b \zeta A_{b i^{\prime} 1} \geqslant q_{b i^{\prime} j}, \forall \varphi ; j=1 $

(32)

式中：A_bi1为i进口左转非机动车的待行区面积，m²；K_b为非机动车停车密度，辆/m²。本式表示一个周期到来的非机动车数量不超过其容量。

2.2.8 车道平衡

各流向机动车在主预信号行驶车道数应相等，即

$ n_{i j}=n_{i j}^k, \forall \varphi ; j=1, 2 $

(33)

2.2.9 饱和度约束

机动车各流向饱和度有最大值限制，即

$ \mu q_{i j} \leqslant n_{i j} s_{i j} g_{i j} Y_{\max }, \forall \varphi ; j=1, 2 $

(34)

$ \mu q_{i j} \leqslant n_{i j}^k s_{i j}^k g_{i j}^k Y_{\max }, \forall \varphi ; j=1, 2 $

(35)

式中Y_max为饱和度上限值。

3 案例分析 3.1 参数输入

为验证优化设计运行效益，选取常规设计、两步过街对比分析。为使对比结果更加客观，3种设计方案的机动车、行人和直行非机动车控制策略皆相同，仅左转非机动车控制策略存在区别。采用高低两种流量场景测试3种设计方案的运行性能，结果见表 1。

参考交叉口设计及控制等相关标准和文献[9-10]参数取值：I=4 s，L_i2^k=30 m，L_i2=50 m，L_i1=45 m，L_DLT^k=100 m，$\vec{L}_{\mathrm{DLT}}^k $=100 m，n_i1=1，n_i2=2，s_ij=1 500 pcu/h，s_ij^k=1 500 pcu/h，s_bi=0.75辆/s，s_pi=3 ped/s，C_min=80 s，C_max=120 s，G_bmin=5 s，G_pmin=5 s，G_min=20 s, G_max=60 s, G_min^k=20 s, G_max^k=60 s, υ_bij=3.5 m/s, υ_pi=1.0 m/s, K_b=1.5辆/m²，Y_max=0.85，L_bi^′=14 m，L_pi^′=20 m, L_bi^″=11 m，L_pi^″=5 m，υ_ij=30 km/h，L_bi1=35 m，L_i2=40 m，A_bi1=12 m²。

3.2 结果分析

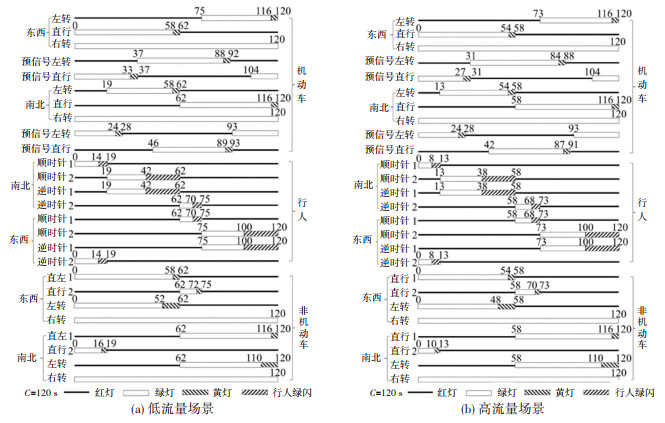
采用MATLAB求解，信号配时结果如图 4~6所示。文献[20]利用VISSIM检验其提出的一种新型连续流交叉口左转非机动车过街的运行效率，文献[21]等同样利用VISSIM分析借用出口车道左转，因国内目前还没有实际落地的平行流交叉口，为此采用VISSIM仿真验证^[22-23]，仿真结果见表 2。

机动车最大通过量分析。在低流量下，3种方案通过机动车数与输入流量相同，3种方案皆处于非饱和状态。在高流量下，常规设计通过机动车数5 243 pcu/h，二次过街、优化设计通过机动车数分别为5 463、5 478 pcu/h，说明二次过街和优化设计可降低左转非机动车对平行流交叉口直行机动车的影响。

机动车延误分析。常规设计直行机动车延误普遍比其他方案高，原因是左转非机动车对直行机动车造成干扰。从整个交叉口来看，在低流量下，二次过街、优化设计分别较常规设计降低了35.02%、42.71%的机动车延误；在高流量下，分别降低了55.52%、65.60%的机动车延误，说明二次过街和优化设计对改善平行流交叉口运行性能效果显著。因常规设计左转非机动车和直行机动车冲突，导致直行机动车延误也会受左转非机动车流量的影响，使在两条道路直行机动车流量相差不大的情况下，其延误反而存在较大差别，而二次过街和优化设计中直行机动车延误则差别不大。

非机动车延误分析。平行流交叉口采用二次过街绕行会造成左转非机动车延误大幅增加。常规设计左转非机动车延误最小，原因是左转非机动车在路口直接左转。从整个交叉口来看，在低、高流量下，二次过街较常规设计分别增加了49.08%、63.16%的非机动车延误，而优化设计非机动车延误和常规设计相差不大，优化设计优势更加明显。

4 敏感性分析

如图 7所示，随直行机动车流量增加，平行流交叉口机动车最大通过量先增加后减少，且优化设计和两步过街的机动车通行能力优于常规设计，说明两种设计方案是平行流交叉口非机动车过街设置的有效替代设计。

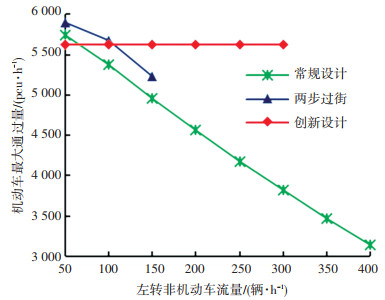
如图 8所示，随着左转非机动车流量增加，平行流交叉口常规设计机动车最大通过量迅速降低。由于直行非机动车利用左转机动车相位迟起时间穿过冲突区域，而二次过街左转非机动车会两次占用直行非机动车通行资源，当左转非机动车流量超过一定值时，在最小左转机动车绿灯持续时长的限制下，非机动车通行过饱和，导致信号配时方案不存在。左转非机动车流量对优化设计机动车最大通过量没有影响，但当一个周期到来的左转非机动车数量超过左转非机动车待行区所能容纳的非机动车时, 信号配时方案不存在。

5 结论

1) 通过引入钩形转弯的概念扩展了平行流交叉口设计理念，进而构建了优化模型，解决了左转非机动车和直行机动车冲突问题。在保证非机动车行车安全的前提下，提升了平行流交叉口机动车通行能力。

2) 针对3种方案仿真对比发现，二次过街和优化设计皆能提升机动车通行能力，降低机动车延误，且在常规设计处于过饱和状态下，效益提升更加明显；二次过街会导致左转非机动车延误大幅增加。综合考虑，推荐优化设计作为平行流交叉口非机动车左转最佳解决方案。

3) 通过敏感性分析发现，3种方案机动车最大通过量随直行机动车流量的增加先增后减，且常规设计受其影响最为显著；常规设计和二次过街受左转非机动车流量的影响较为严重，优化设计不受左转非机动车流量的影响，但一个周期到来的左转非机动车数量超过左转非机动车待行区所能容纳的车辆数时，其信号配时不存在。

4) 尽管优化设计在解决平行流交叉口左转非机动车过街方面是有效的，但考虑到文章采用VISSIM仿真验证，缺乏实测数据验证，在推广应用前须考虑几个关键问题：左转非机动车是否会对车道饱和流率造成影响，对此如何改善；交通需求和行驶速度的随机波动导致车辆滞留的概率有多大，及车辆滞留后对平行流交叉口通行能力的影响；平行流交叉口行驶规则与驾驶员行为认知不符，是否存在安全风险。后续研究将关注影响平行流交叉口实际应用的各种因素，同时考虑公交优先策略对信号控制的特殊要求，以使平行流交叉口更符合实际交通运行需要。