2. 道路与交通工程教育部重点实验室(同济大学),上海 201804;
3. 中国铁路上海局集团有限公司合肥工务段,合肥 230031
2. Key Laboratory of Road and Traffic Engineering of Ministry of Education (Tongji University), Shanghai 201804, China;
3. Hefei Track Maintenance Division, China Railway Shanghai Bureau Group Co., Ltd., Hefei 230031, China
中国高速铁路开通以来,陆续发现弹条断裂现象,并有大量弹条出现明显裂纹。弹条的断裂意味着扣件系统的失效,这将影响列车的行车安全,严重的还会引发列车脱轨等安全事故。中国高速铁路工务部门曾试图采用更换缓冲垫板和采用SKL B15小阻力扣件的方法来防治扣件弹条断裂,但效果甚微。图 1展示了现场扣件弹条断裂的情况,可发现弹条断裂部位全部出现在弹条跟端圆弧处,裂纹同样发生在相同的位置。

|
图 1 现场弹条断裂情况 Fig. 1 Fracture of fastener clips on site |
早在2005年,文献[1]就针对SKL 1型弹条在使用过程中出现的断裂现象,利用疲劳试验对比了SKL 1型弹条和SKL 12型弹条的性能。文献[2]研究了SKL 1型弹条的性能与断裂条件。文献[3]分析了扣件弹条在高速列车动荷载作用下的振动特性,并发现考虑钢轨波磨时弹条振动加速度增大近十倍。文献[4]发现扣压力会影响弹条的疲劳寿命。文献[5]利用车辆-轨道耦合动力学模型计算发现弹条危险区域的最大等效应力与应变随着实测波磨的放大而成比例的增加。文献[6]通过搭建扣件弹条实体模型获得SKL型弹条峰值频率为542 Hz和619 Hz。文献[7]利用ABAQUS分别计算了弹条在自由状态和组装状态下的模态,并通过现场频响测试测得弹条峰值频率为620 Hz,与仿真结果632 Hz基本一致。文献[8]利用有限元软件分析了不同条件下的扣件弹条力学特征,发现安装状态下的弹条已存在很大的应力值,而车轮多边形磨耗阶数的提高会进一步增大弹条应力值。文献[9]分析了WJ-7型弹条的静力特性,发现在螺栓压力荷载下弹条最大应力产生在跟端大圆弧处,且当螺栓预紧力达到27.5 kN时,弹条的最大应力已经超过材料的屈服强度。文献[10]提出了一种空心W1型弹条,能够提高原W1型弹条的固有频率。文献[11]利用数字图像相关(DIC)技术,证明了数值模拟计算结果的可信度,并通过频响分析,发现当载荷频率与弹条敏感频率接近时,弹条跟端局部应力会显著增大。文献[12]利用拉伸-扭转实验和数值模拟的方法,发现WJ-7型扣件60Si2MnA弹条断裂的原因为跟端内弯处应力集中。文献[13]利用拉伸试验和疲劳试验,发现W1型弹条内侧圆弧应力值最大且25 kN是弹条的最佳安装预压力。文献[14]通过实验发现弹条疲劳寿命随安装扭矩和疲劳载荷幅值的增加而降低,与危险点应力比呈线性关系。文献[15]发现“蝶形”弹条的500 Hz和600 Hz模态与周期性波浪磨耗产生的高频激励频率相接近从而导致了弹条疲劳断裂,并提出一种降低弹臂高度的弹条,提高了其模态频率。文献[16]基于静力试验和疲劳性能试验,提出了W1型弹条疲劳寿命预测的回归方程。文献[17]发现弹条在低频受力折断和高频共振折断时的断口分别呈现45°和90°角,激励频率和激励能量是影响弹条共振伤损的两个主要因素。
本文基于国内某正在运营的高速铁路正线出现的弹条断裂情况,利用现场测试与仿真计算相结合的方法,揭示了弹条断裂的主要原因,并针对性地为该线路提出了相关整治措施,为实际运营中遇到的类似问题,提供了解决的思路及方法。
1 高速铁路扣件弹条振动和钢轨波磨现场测试分析相关研究表明了钢轨波磨是引起扣件弹条失效的重要原因之一[18]。通过对现场的调查也发现弹条的断裂与裂纹集中出现在钢轨波磨十分严重的区段,因此现场测试主要包括SKL 15型弹条振动特性的测试与钢轨波磨的测试。
1.1 高速铁路SKL 15型弹条振动测试分析为了确定高速铁路SKL 15型弹条的振动特性,选取弹条断裂比较频繁的线路区段进行锤击法模态试验。加速度传感器的布置位置如图 2所示,传感器1、2分别布设于钢轨顶部与轨头侧面,用于测量钢轨的垂向与横向振动加速度;弹条布置4个加速度传感器,分别为传感器3、4、5、6,以测量弹条弹臂与中弯前端的振动加速度。

|
图 2 传感器布置位置示意图 Fig. 2 Schematic diagram of sensor layout |
取两个相邻扣件的中间位置为钢轨的激励截面,利用装有力传感器的力锤分别敲击钢轨轨顶、钢轨轨头侧面以及同一钢轨截面处的两个弹条的趾端,获得图 2所示各测点处的振动加速度响应。对测得的数据进行频谱处理,进而得到弹条的振动特性。现场测试情况如图 3所示。提取不同激励下的弹条拱部最高点处的加速度响应,可得弹条的振动特性如图 4所示。

|
图 3 现场测试 Fig. 3 Field test |

|
图 4 不同激励条件下扣件弹条加速度频响曲线 Fig. 4 Acceleration frequency response curves of fastener clips under different excitation conditions |
由图 4(a)~4(d)可知,左、右股钢轨弹条拱部最高点处的全局峰值频率略有不同,但大致都处于同一频率范围,即550~650 Hz。在垂向激励钢轨轨头时,左股钢轨扣件弹条出现频率为609.38 Hz的峰值,而右股钢轨扣件弹条出现频率为632.81 Hz的峰值;在垂向激励弹条趾端时,左股钢轨扣件弹条出现557.81 Hz和614.06 Hz两个频率峰值,而右股钢轨扣件弹条出现575.00 Hz和631.25 Hz两个频率峰值。当力锤作用于钢轨轨顶时,往往仅能激发出弹条的一个全局峰值频率,对应激励弹条趾端条件下的第二阶固有频率。而在力锤作用于弹条趾端时,第二阶固有频率的峰值大于第一阶固有频率。因此,SKL 15型弹条在列车荷载作用下容易激发出第二阶固有频率的振动模态。
1.2 钢轨波磨观测与分析本文利用RMF 1100波磨测量小车,对弹条断裂集中的区段进行钢轨波磨的测量。测量结果经过后续滤波处理后,得到每米最大谷深值和显著波长情况。
统计100 mm以下显著波长的分布情况如图 5所示,可见该区间的波磨显著波长主要集中在50~60 mm之间。为进一步探究波磨发展的规律,本文在一次钢轨打磨作业后,开展了为期3个月的连续性检测,检测间隔为1个月。图 6展示了3次检测中,该区段最大谷深的发展情况。

|
图 5 波磨测试显著波长分布直方图 Fig. 5 Histogram of significant wavelength distribution for rail corrugation test |
|
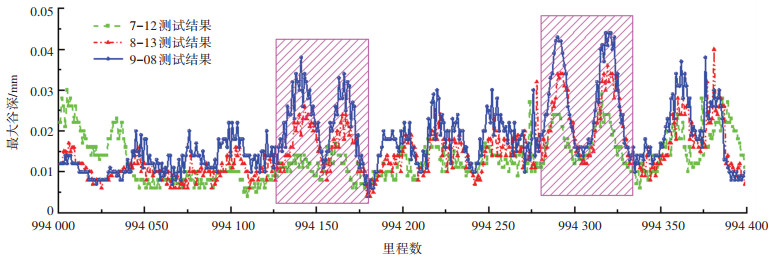
图 6 钢轨波磨最大谷深发展情况 Fig. 6 Development of maximum valley depth of rail corrugation |
由图 6可知,跟踪测试的两个月内波磨发展迅速,特别是第2个月(8-13至9-08)内,波磨的发展速度要明显大于第1个月。图中阴影部分是波磨十分严重的区段(对应里程为K994+125~K994+175及K994+275~K994+330),可见其发展的速度也非常快,单月最大波磨发展率达到了200%,两个月的最大波磨发展率达到了350%,这将导致“波磨严重-波磨发展迅速-波磨进一步加剧”的恶性循环。
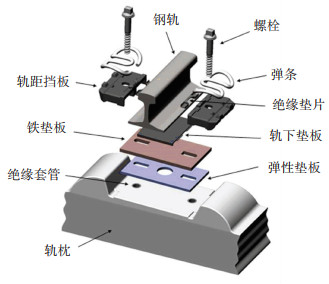
2 SKL 15型扣件弹条仿真分析 2.1 扣件系统三维有限元模型建立 2.1.1 有限元模型构成选取高速铁路比较常见的福斯罗W300-1扣件进行分析,扣件系统零部件包括SKL 15型弹条、螺栓、绝缘垫片、轨距挡板、轨下垫板、铁垫板等,如图 7所示。按照扣件系统各部件的实际尺寸和图纸,利用SolidWorks建立三维几何模型,装配后导入ANSYS有限元分析软件进行网格划分。扣件系统有限元模型的网格划分如图 8所示。
|
图 7 福斯罗W300-1扣件系统 Fig. 7 Vossloh W300-1 fastening system |

|
图 8 扣件系统网格 Fig. 8 Mesh of fastening system |
本文所建立的有限元模型中,在不影响力学的情况下,为了计算方便,对轨距挡板、绝缘垫片及螺栓进行了去除圆角等适当的形状简化,整个模型共计约22.9万个节点,12.1万个单元。
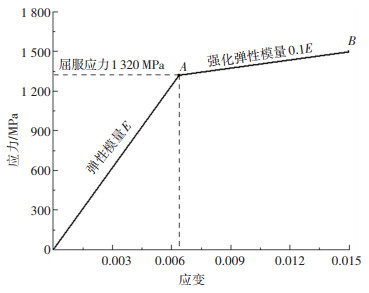
2.1.2 材料属性设置根据各部件材料的实际特性取值,各材料属性见表 1。其中SKL 15型弹条的材料为38Si7弹簧钢,需要考虑其材料的弹塑性特性。弹条材料的应力-应变关系采用理想线性强化弹塑性材料本构模型,强化模量可设置为E′=0.1E [19]。屈服强度取为1 320 MPa,强化模量取为20.7 GPa,材料的本构模型如图 9所示。
| 表 1 模型各部件材料属性 Tab. 1 Material properties of the parts of the model |
|
图 9 弹条材料本构模型 Fig. 9 Constitutive model of rail clip material |
为了真实模拟弹条的服役状态,在弹条与螺栓、弹条与轨距挡板、弹条与绝缘垫片之间建立面-面接触,接触类型设为摩擦接触。考虑到实际的安装状态与本文研究内容,为提高计算效率,在钢轨与轨下垫板、钢轨与绝缘垫片、轨下垫板与铁垫板、铁垫板与弹性垫板、轨距挡板与铁垫板以及轨距挡板与弹性垫板之间建立面-面接触,接触类型为绑定接触。各接触对设置情况见表 2。
| 表 2 模型接触设置 Tab. 2 Model contact settings |
考虑到现场扣件系统的安装状态,对模型底面及X方向侧面施加全约束。同时,为了模拟绝缘套管对螺栓的约束作用,对螺栓的水平方向和纵向施加位移约束。为了忽略边界的影响,在钢轨两端截面设置对称约束。在模拟扣件安装状态时,通过对螺栓顶部施加垂向位移,使得弹条中弯前端的垂向位移达到15 mm,即认为弹条达到安装状态。
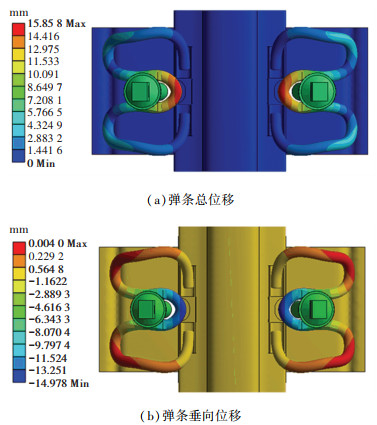
2.2 弹条静力特性分析在正常安装状态下,弹条的位移如图 10所示。图 10(a)展示了弹条的总位移情况,可见弹条的最大位移出现在弹条的中弯前端,跟端和趾端的位移较小。图 10(b)展示了弹条垂向位移的情况,垂向最大位移达到14.9 mm,可认为扣件系统达到了正常安装状态。安装时弹条中弯向下运动,弹条弹臂向上翘起,两者运动方向相反。
|
图 10 安装状态下的弹条位移 Fig. 10 Displacement of rail clip under installation |
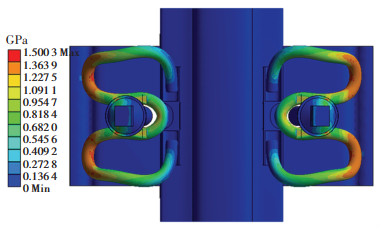
安装状态下的弹条von-Mises应力分布如图 11所示。由图 11可见,弹条的最大von-Mises应力出现在跟端后弯支点大圆弧内侧表面处,与弹条发生断裂的部位一致。该处的von-Mises应力达到了1 480 MPa左右,大于弹条材料的屈服强度1 320 MPa。后弯支点处是弹条的危险位置,此处的弹条主要受到了扭转和弯曲的作用。弹条的von-Mises应力从后弯支点沿着弹臂到前端支点逐步减小,趾端支点处等效应力最小。
|
图 11 安装状态下弹条von-Mises应力 Fig. 11 Von-Mises stress of rail clip under installation |
在不对弹条施加任何外力和接触的条件下,对其进行自由模态分析。考虑弹条在0~1 000 Hz之间的自由模态,可以得到其前6阶模态振型及固有频率如图 12所示,图中透明部分和彩色部分分别为未变形空间位置和变形后的空间位置。

|
图 12 弹条自由模态 Fig. 12 Free mode of rail clip |
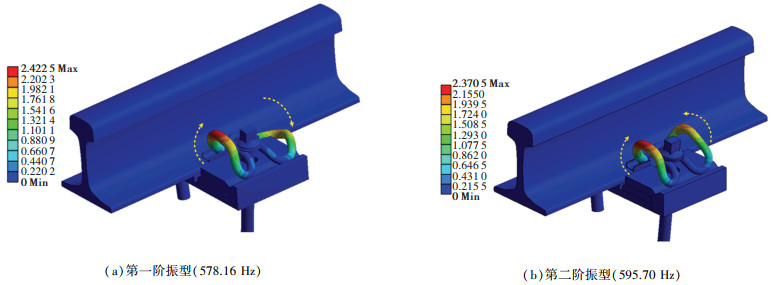
进一步分析计算弹条在标准安装状态下的模态振型及频率特点,计算结果如图 13所示。在0~1 000 Hz之间,弹条存在两阶模态,分别为578.16、595.70 Hz。
|
图 13 安装状态下弹条模态振型 Fig. 13 Modal shape of rail clip under installation |
由图 13可知,两阶模态振型的特点分别为:1)第一阶振型主要表现为弹条趾端、前拱沿纵向(Z轴)同相位往复运动,同时左右两拱沿垂向(Y轴)反相往复运动,即左右弹臂围绕弹条前后振型节点连成的轴线作扭转振动,左右弹臂一个向上一个向下;2)第二阶振型表现为弹条趾端、前后拱沿Z轴反相位往复运动,同时左右两拱沿Y轴同相位往复运动,即左右弹臂围绕弹条前后振型节点连成的轴线作扭转振动,左右弹臂同时向上或向下。
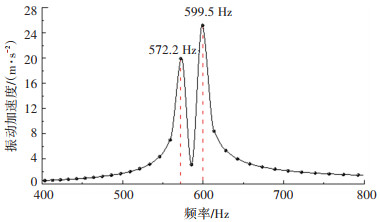
2.4 弹条谐响应分析为了反映弹条频率响应的情况,在钢轨顶面施加一个单位力,扫频频率为100~1 000 Hz,采用预应力下模态叠加的谐响应分析法。提取弹条弹臂最高点的垂向(Y向)加速度频响曲线,结果如图 14所示。在弹条趾端施加一个单位力,采用相同的计算方法,提取弹条弹臂最高点的垂向(Y向)加速度频响曲线,结果如图 15所示。

|
图 14 钢轨激励下加速度频响曲线 Fig. 14 Acceleration frequency response curve under rail excitation |
|
图 15 弹条趾端激励下加速度频响曲线 Fig. 15 Acceleration frequency response curve under excitation at toe end of clip |
由图 14、15可知,当以单位力激励钢轨时,弹条弹臂最高点处的垂向加速度响应在599.48 Hz处取得峰值,与安装状态下弹条的二阶模态(595.7 Hz)相近。当以单位力激励弹条趾端时,弹条弹臂最高点处的垂向加速度响应在572.24 Hz和599.48 Hz处存在两个全局峰值,与安装状态下的弹条前两阶模态(578.16 Hz、595.7 Hz)接近。
为进一步探究共振作用对弹条的影响,本文选取了频响分析过程中不同频率的载荷激励下的弹条应力响应情况。图 16中展示了不同频率载荷激励下的弹条von-Mises应力。本文共选取4个频率,包括两个非共振频率(100 Hz、1 000 Hz)和两个共振频率(572.24 Hz、599.48 Hz)。

|
图 16 不同频率激励下的弹条von-Mises应力 Fig. 16 Von-Mises stress of rail clip under different frequency excitations |
由图 16可知,共振频率下弹条的最大应力要远大于非共振频率下弹条的最大应力。其中,第一阶共振频率激励下弹条的最大应力是非共振频率激励下的50倍左右,第二阶共振频率激励下弹条的最大应力达到了非共振频率激励下的100倍。因此,当扣件系统所受载荷的频率与弹条组装模态固有频率接近时,弹条跟端的应力会显著放大,且第二阶频率为主要频率,会产生更强的共振作用。
3 弹条共振分析 3.1 弹条仿真结果与实测结果的对比上文中通过对扣件系统进行预应力模态分析和谐响应分析,得到了SKL 15型弹条的振动特征频率。考虑到仿真建模过程中的结构简化以及计算过程中的合理假设,因此仿真测试结果与现场测试结果有一定的误差。对比现场测试结果与仿真测试结果,在允许误差的范围内,仿真结果与现场测试结果具有较高的一致性。由图 17可见,弹条的两阶振动特征频率大致相同,均处在550~650 Hz之间,两阶模态匹配良好。

|
图 17 现场测试与仿真测试弹条固有频率 Fig. 17 Natural frequency of rail clip in field test and simulation |
除此之外,在进行谐响应分析时发现,激励钢轨仅能激发弹条的第二阶模态,激励弹条趾端时方可激发弹条的两阶模态,这一仿真测试结果与现场测试的结果高度一致,可见仿真结果具有较高的可靠性。
3.2 扣件弹条共振分析列车以不同的速度通过该区段时,会激发出不同的振动频率,而这一频率与钢轨表面的波磨波长和列车通过速度有着密切的关系。根据钢轨波磨观测结果及弹条模态测试结果,结合现场列车的运行情况,对其进行共振分析。
线路波磨区段内列车的运营速度为110~120 km/h,钢轨表面波磨的显著波长为50~60 mm。由于该区段在设计阶段的设计时速为160 km/h,考虑到高铁线路正线运营速度不宜过低,因此取速度区间为90~160 km/h进行分析,考虑列车在该速度区间内通过此区段所激发的荷载频率情况。列车通过时所激发的频率为
| $ f=\frac{v}{\lambda} $ | (1) |
式中:f为列车通过时激发的频率,Hz;v为列车运行速度,m/s;λ为钢轨波磨波长,m。
通过计算可得速度在90~160 km/h之间列车通过时所激发的频率为416.67~888.89 Hz,如图 18所示。将该区段现行速度的频带与弹条固有频率的大致范围进行对比,如图 19所示。图中黄色阴影部分代表上述列车速度在50~60 mm波磨激励下的频率范围(下文简称激振频带);红色斜线部分为弹条固有频率所在的频段(550~650 Hz)与激振频带重合的部分;绿色斜线部分为该区段现行列车通过时所激发的频带。

|
图 18 列车通过频率与车速、波磨波长关系图 Fig. 18 Relation diagram between train passing frequency, speed, and rail corrugation wavelength |

|
图 19 列车激振频带与弹条固有频率关系图 Fig. 19 Relation diagram between train passing frequency band and natural frequency of rail clip |
由图 19可知,在现有波磨条件下,以当前运行车速(110~120 km/h)通过该区段时激发的频率与弹条本身的固有频率高度重合,会引发强烈的共振作用。由前文所述,在共振作用下,弹条跟端圆弧处的应力会显著增大,从而更容易引起弹条局部的疲劳损伤。
4 整治措施本文经过现场测试与仿真分析,发现扣件系统在外界列车通过波磨区段时所激发的振动是引起弹条共振及疲劳损伤的主要原因。针对这一问题,提出如下解决措施:
1) 钢轨打磨。虽然利用钢轨打磨不能改变波磨的波长,但可以有效减小波磨波深的幅值,甚至完全消除波磨。因此打磨后能在很大程度上减小轮轨间的激励,从而使扣件承受更少的振动能量,减小扣件跟端圆弧处的应力,延长扣件的使用寿命。
2) 列车调速。造成扣件弹条断裂的原因是列车通过时所激发的振动频率与弹条的固有频率一致所引发的共振作用。而通过改变列车通过时的速度,在相同的钢轨表面状态的情况下,车致振动的频率就会发生改变。当列车激发的振动频率与弹条固有频率不一致或相差较大时,就不会产生共振现象,同样可以延长其使用寿命。根据该区段的设计时速160 km/h,建议该路段可以通过提速至150 km/h或降速至90 km/h的方法解决弹条断裂的问题。
3) 弹条结构优化。扣件弹条的固有频率主要受材料属性(刚度、强度、硬度等)、形状、质量等影响,可以考虑通过改变上述特性而改变弹条的固有频率(如黄浩志等[10]提出了一种空心弹条;王安斌等[15]降低了弹条臂高度,改变了弹条形状),以达到弹条固有频率与列车通过时的激振频率错开的目的。
5 结论结合实际高铁运营线路中遇到的弹条断裂问题,采用现场测试与仿真分析相结合的方法,分析了SKL 15型弹条的振动特性和断裂原因,得到了如下结论:
1) 所建立的扣件系统有限元模型计算结果与现场实测结果具有较好的一致性,可以确定安装状态下的SKL 15型弹条在1 000 Hz以内具有两阶固有频率,且大致处于550~650 Hz之间。
2) 当列车通过波磨区段时所激发的载荷频率与弹条安装模态频率接近或一致时,会引发弹条强烈的共振作用,导致弹条跟端应力的显著增大,从而容易引发弹条的疲劳伤损。
3) 可以通过钢轨打磨、改变列车运营速度以及改变弹条固有频率的方法,避免列车载荷频率与弹条安装模态频率一致所引发的共振作用,提高弹条的使用寿命。
| [1] |
LAKUŠIĆ S, BARTOŠ D, BAJIĆ A G. Experimental and numerical analysis of the rail fastening spring clips types SKL-1 and SKL-12[C]//22nd DANUBIA-ADRIA Symposium on Experimental Methods in Solid Mechanics. Parma: University of Parma, 2005
|
| [2] |
FERREÑO D, CASADO J A, CARRASCAL I A, et al. Experimental and finite element fatigue assessment of the spring clip of the SKL-1 railway fastening system[J]. Engineering Structures, 2019, 188: 553. DOI:10.1016/j.engstruct.2019.03.053 |
| [3] |
朱胜阳, 蔡成标, 尹镪, 等. 高速铁路扣件弹条动力学分析[J]. 工程力学, 2013, 30: 254. ZHU Shengyang, CAI Chengbiao, YIN Qiang, et al. Dynamic analysis of rail fastening clip in high-speed railway[J]. Engineering Mechanics, 2013, 30: 254. DOI:10.6052/j.issn.1000-4750.2012.05.0314 |
| [4] |
余自若, 袁媛, 张远庆, 等. 高速铁路扣件系统弹条疲劳性能研究[J]. 铁道学报, 2014, 36: 90. YU Ziruo, YUAN Yuan, ZHANG Yuanqing, et al. Fatigue properties of elastic bars of fastening systems installed with high-speed railways[J]. Journal of the China Railway Society, 2014, 36: 90. |
| [5] |
尚红霞. 钢轨波磨对扣件弹条受力分析[J]. 机械, 2014, 41: 11. SHANG Hongxia. Analysis of rail corrugations on rail fastening clip force[J]. Machinery, 2014, 41: 11. |
| [6] |
高晓刚, 王安斌, 肖俊恒, 等. 高速铁路扣件弹条伤损研究及结构优化分析[J]. 噪声与振动控制, 2018, 38: 190. GAO Xiaogang, WANG Anbin, XIAO Junheng, et al. Study on damage mechanism and structure optimization analysis of fastening clips of high-speed railways[J]. Noise and Vibration Control, 2018, 38: 190. |
| [7] |
施何瑛, 王安斌, 高晓刚. 高速铁路扣件弹条性能分析及频响特性研究[J]. 噪声与振动控制, 2019, 39: 156. SHI Heying, WANG Anbin, GAO Xiaogang. Analysis of performance and frequency response characteristics of fasteners for high-speed railway[J]. Noise and Vibration Control, 2019, 39: 156. |
| [8] |
向俊, 袁铖, 余翠英, 等. 高速铁路无砟轨道扣件弹条断裂原因分析[J]. 铁道科学与工程学报, 2019, 16: 1605. XIANG Jun, YUAN Cheng, YU Cuiying, et al. Analysis of elastic bar fracture causes of fasteners in ballastless track of high-speed railway[J]. Journal of Railway Science and Engineering, 2019, 16: 1605. |
| [9] |
黄新杰, 伍曾, 杨成标, 等. 高速铁路弹条扣件静力特性实验与模拟分析[J]. 中国水运(下半月), 2019, 19: 115. HUANG Xinjie, WU Zeng, YANG Chengbiao, et al. Experiment and simulation analysis of static characteristics of fastener elastic bar in high-speed railway[J]. China Water Transport, 2019, 19: 115. |
| [10] |
黄浩志, 王安斌, 高晓刚. 高速铁路用ω型弹条性能研究及结构改进[J]. 铁道标准设计, 2021, 65: 36. HUANG Haozhi, WANG Anbin, GAO Xiaogang. Study on performance and structural improvement of the ω type fastening clip for high-speed railway[J]. Railway Standard Design, 2021, 65: 36. |
| [11] |
姜秀杰, 刘艳, 李秋彤, 等. 高速铁路ω型扣件弹条的共振响应特征分析[J]. 铁道标准设计, 2021, 65: 20. JIANG Xiujie, LIU Yan, LI Qiutong, et al. Analysis of resonance response characteristics of the ω-clip in fastener systems of high-speed railways[J]. Railway Standard Design, 2021, 65: 20. |
| [12] |
肖洪秀, 伍曾, 黄新杰. 高铁扣件弹条疲劳断裂原因分析[J]. 工业安全与环保, 2021, 47: 50. XIAO Hongxiu, WU Zeng, HUANG Xinjie. Analysis of fatigue fracture causes of high-speed rail fasteners[J]. Industrial Safety and Environmental Protection, 2021, 47: 50. |
| [13] |
余剑, 伍曾, 张景坤, 等. W1型弹条扣压力与疲劳性能的试验研究[J]. 科学技术与工程, 2021, 21: 9088. YU Jian, WU Zeng, ZHANG Jingkun, et al. Experimental research on buckle pressure and fatigue performance of W1 type spring bar[J]. Science Technology and Engineering, 2021, 21: 9088. |
| [14] |
刘艳, 姜秀杰, 李秋彤, 等. W300-1型扣件弹条疲劳寿命的预测和评估[J]. 同济大学学报(自然科学版), 2021, 49: 1152. LIU Yan, JIANG Xiujie, LI Qiutong, et al. Fatigue life prediction and evaluation of the W300-1 fastening clip[J]. Journal of Tongji University (Natural Science), 2021, 49: 1152. |
| [15] |
王安斌, 高晓刚, 肖俊恒, 等. 轨道弹条高频疲劳断裂机理研究及优化[J]. 铁道学报, 2021, 43: 93. WANG Anbin, GAO Xiaogang, XIAO Junheng, et al. Study and optimization of mechanism of high frequency fatigue fracture of rail clip[J]. Journal of the China Railway Society, 2021, 43: 93. |
| [16] |
马薇, 伍曾, 张景坤, 等. 高速铁路W1型弹条疲劳性能试验及寿命预测[J]. 工业安全与环保, 2021, 47: 80. MA Wei, WU Zeng, ZHANG Jingkun, et al. Fatigue performance test and fatigue life prediction of W1 type spring bar for high-speed railway[J]. Industrial Safety and Environmental Protection, 2021, 47: 80. |
| [17] |
闫子权, 肖俊恒, 方杭玮, 等. 高速铁路扣件弹条共振断裂损伤机理研究[J]. 中国铁路, 2021(11): 31. YAN Ziquan, XIAO Junheng, FANG Hangwei, et al. Research on resonant fracture damage mechanism of high speed railway fastening bar-spring clips[J]. China Railway, 2021(11): 31. |
| [18] |
卢俊. 高速铁路扣件弹条振动疲劳性能与优化、试验研究[D]. 成都: 西南交通大学, 2021 LU Jun. Research on vibration fatigue performance and optimization and test methods of fastener clips for high-speed railway[D]. Chengdu: Southwest Jiaotong University, 2021 |
| [19] |
XIAO H, GUO X, WANG H Y, et al. Fatigue damage analysis and life prediction of e-clip in railway fasteners based on ABAQUS and FE-SAFE[J]. Advances in Mechanical Engineering, 2018, 10: 1. |
 2023, Vol. 55
2023, Vol. 55


