短时交通流预测为道路交通安全管理和交通诱导提供实时、动态、高效的数据支撑, 同时能够指导出行者进行科学的路线规划。国内外学者主要利用参数模型与非参数模型进行短时交通流预测:参数模型主要通过构建马尔可夫链预测模型、卡尔曼滤波预测模型[1]、自回归综合移动平均(ARIMA)模型[2]、指数平滑算法[3]等数学模型来进行预测,但上述模型在处理复杂的交通环境时存在局限性;非参数模型主要通过分析历史数据间的潜在规律与联系预测未来的交通状况,常用支持向量机[4]、K-最近邻算法[5]、人工神经网络[6]、贝叶斯网络[7]等方法。随着智能算法的提出与推广,很多学者运用其改进神经网络来提高交通流预测模型性能。文献[8]采用混合粒子群算法训练神经网络(neural network, NN)的结构和参数, 增加预测速度;文献[9]利用改进遗传算法为神经网络设置合适的参数,建立自调节神经网络,提高预测精度;蔡延光等[10]利用改进布谷鸟搜索算法优化RBF神经网络参数,用于交通流预测。
交通流数据易受环境因素影响,具有随机性、非线性的特点。神经网络能够对数据间关系进行识别[11],并从中获取信息进行泛化。其中前馈分层神经网络可以通过激活函数的特殊性更加逼近非线性函数。BP神经网络和径向基函数[12]是两种典型的前馈神经网络。BP网络是全局逼近网络,网络中的一个或多个可调参数(权值和阈值)对任意一个输出值都有很大影响,而径向基神经网络为结构精简的局部最优逼近网络,对网络输入空间的某个局部区域只有少数几个连接权值影响网络的输出。因此,径向基神经网络比BP神经网络学习更能满足具有实时性要求的交通流预测研究[13]。然而,传统的RBF神经网络隐含层中径向基函数中心的确定对预测结果有很大影响,初始中心的选择不当会导致陷入局部最优。为此,文献[14]利用正交最小二乘法确定网络中心;文献[15]利用改进人工蜂群算法确定RBF网络隐含层中心数量和中心值;文献[16]采用K-means聚类算法对RBF神经网络的径向基函数进行初始化,但用于K-means算法对噪声数据比较敏感,不能自动识别基函数中心。
为解决该问题,本文引入DBSCAN聚类改进传统RBF神经网络,该聚类可以发现任意形态、高质量的簇,进而快速有效地自动识别基函数中心数量和中心值,减少干扰数据影响。而聚类的半径和密度最小值是中心数量确定的关键,为更好寻优并降低迭代时间,将通过改进后的自适应BAS算法进行自动寻优确定。最后将训练好的短时交通流预测模型与BP神经网络、RBF神经网络、广义RBF神经网络进行对比。
1 天牛须搜索算法介绍及改进天牛须搜索算法(BAS)[17]是2017年提出的一种元启发式搜索算法,该算法模拟天牛觅食时的动态寻找过程,能够在多维空间中寻找全局最优,在优化问题上功能强大且步骤简单清晰。
原BAS通过固定的收敛步长进行位置更新,文献[18]研究发现适当的步长更新是提高收敛速度和算法稳定性的关键。文献[19]利用Adam算法改进BAS,提高原算法跳出局部最优的能力,仿真表明改进步长后算法的寻优能力明显增强。为此,本文引入NAdam算法对BAS进行改进,利用NAdam带有Nesterov动量,对步长更新有较强约束性与可靠性的特点,在确保步长方向质量同时,根据梯度信息进行步长更新。
算法中
BAS算法模拟天牛的觅食轨迹,即在自然环境中,依靠触角感知并寻找食物。函数的目标极值对应所要寻找食物位置,将气味强度分布看作二维空间,天牛的触角随机定向,以气味强度气味最浓方向作为行进方向行进一段距离后以随机方向停止,寻找下一步行进方向。天牛一直重复该循环直到找到食物位置(目标极值),这种循环过程如图 1所示。

|
图 1 天牛须搜索算法寻优过程 Fig. 1 Optimization process of BAS algorithm |
算法的目标是寻找目标函数f(x)的最优值(一般为最大值或最小值),该值与食物位置相对应。文献[20]指出天牛触角上分布着多根毛状感受器,感受器感知气味浓烈程度并发送信号到中枢神经用以判断前进方向。触角将产生的感知集合构建成相对于天牛位置的单位方向向量组,且该向量组呈标准化正态随机分布:
| $ \vec{b}=\frac{\operatorname{randn}(k, u)}{\|\operatorname{randn}(k, u)\|} $ | (1) |
根据感受器个数u产生天牛触角的方向向量B = [b1, b2, b3, …, bu]来表示每个触角感受器感应方向,感受器的位置可表示为
| $ \left\{\begin{array}{c} x_{b_1}=x_t+d_t \vec{b}_1 \\ x_{b_2}=x_t+d_t \vec{b}_2 \\ \vdots \\ x_{b_u}=x_t+d_t \vec{b}_u \end{array}\right. $ | (2) |
形成了天牛触角感受器位置集合X=[xb1, xb2, xb3, …, xbu],从而计算每个感受器对应目标函数形成目标函数集合F:
| $ \boldsymbol{F}=\left[f\left(x_{b_1}\right), f\left(x_{b_2}\right), f\left(x_{b_3}\right), \cdots, f\left(x_{b_u}\right), x \in \boldsymbol{X}\right] $ | (3) |
创建一个包含目标最小值的子集Fmin={f: f⊂F且f∈minF}和一个包含目标最大值的子集Fmax={f: f⊂F且f∈min F}来估计梯度,Fmin(x)与Fmax(x)中对应感受器位置集合xmin和xmax:
| $ \boldsymbol{x}_{\min }=\left\{x: x \subset \boldsymbol{X} \text { 且 } f \in \boldsymbol{F}_{\text {min }}(x)\right\} $ | (4) |
| $ \boldsymbol{x}_{\text {max }}=\left\{x: x \subset \boldsymbol{X} \text { 且 } f \in \boldsymbol{F}_{\text {max }}(x)\right\} $ | (5) |
感受器最小值和最大值集合对应感受器质心x∂及xe分别表示为
| $ x_{\partial}=\sum\limits_{x \in x_{\min }} \frac{x}{k} $ | (6) |
| $ x_{\mathrm{e}}=\sum\limits_{x \in x_{\max }} \frac{x}{k} $ | (7) |
上述x∂及xe对应目标函数最大值和最小值所对应感受器位置的矢量和,梯度方向gt即为最大值到最小值变化的方向:
| $ g_t=x_{\mathrm{e}}-x_{\partial} $ | (8) |
引入NAdam进行天牛位置更新,利用估计梯度方向,设定位置更新规则:
| $ x_{\text {new }}=x_t+\delta_t\left(g_t\right) $ | (9) |
步长是关于估计梯度的函数, 在这里引入NAdam更新规则得到适应性梯度,δt(gt)代表xt到xt+1的位置更新规则。本文根据NAdam定义步长更新规则:
| $ \delta_t\left(g_t\right)=\delta_0 \frac{\hat{m}_t}{\sqrt{\hat{p}_t}+\lambda} $ | (10) |
其中mt和pt表示在迭代t次时一阶动量和二阶动量,计算公式分别为
| $ m_t=\varepsilon_t m_{t-1}+\left(1-\varepsilon_t\right) \operatorname{sign}\left(f\left(x_e\right)-f\left(x_{\partial}\right)\right) g_t $ | (11) |
| $ p_t=\beta p_{t-1}+(1-\beta) g_t^2 $ | (12) |
式(11)中sign f(xe)-f(x∂) 使梯度方向始终指向最优值方向。ε的合理取值有利于函数更加精细收敛,可取值为
| $ \varepsilon_t=\min \left(1-2^{-1-\log _2\left(\frac{t}{250}+1\right)}, \varepsilon_{\max }\right) $ | (13) |
通过式(14)、(15)对一阶动量和二阶动量估计值偏差校正:
| $ \hat{m}_t=\frac{\varepsilon_{t+1} m_t}{1-\prod_i^{t+1} \varepsilon_i}+\frac{\left(1-\varepsilon_t\right) g_t}{1-\prod_i^t \varepsilon_i} $ | (14) |
| $ \hat{p}_t=\frac{p_t}{1-\beta^t} $ | (15) |
为得到最优值,当目标值f(xt) < fbest时对位置进行更新,否则重新寻找目标值,更新规则:
| $ x_{t+1}= \begin{cases}x_{\text {new }}, & f\left(x_t\right)<f_{\text {best }} \\ x_t, & f\left(x_t\right)<f_{\text {best }}\end{cases} $ | (16) |
自适应BAS算法计算过程如图 2所示。

|
图 2 自适应BAS流程图 Fig. 2 Adaptive BAS flow chart |
为验证自适应BAS算法有效性,本文采用Michalewicz函数对原算法和改进后算法进行测试:
| $ f(x)=\sum\limits_{i=1}^d \sin x_i\left[\sin \frac{i x_i^2}{\pi}\right]^{2 m} $ | (17) |
该函数为高度非线性、多峰、非凸函数。文献[17]研究发现:当m=10时该函数全局最小值为fbest≈-1.801 3,x最小值的位置在(2.20, 1.57)附近,该函数在三维空间的图像如图 3所示。

|
图 3 Michalewicz函数图像 Fig. 3 Michalewicz functional image |
运用与原算法相同初始参数进行仿真分析,仿真结果见表 1,二维搜索轨迹及收敛过程如图 4所示,结果表明自适应BAS可以更快、迭代次数更少的寻找到函数最优值及位置,在解决复杂、非线性、没有先验信息的并行问题时表现出优越性能。
| 表 1 BAS及自适应BAS仿真结果分析 Tab. 1 Analysis of simulation results of BAS and adaptive BAS |

|
图 4 算法性能测试 Fig. 4 Algorithm performance test |
步骤1 初始化个体位置,随机产生各感应器感应方向
步骤2 运用步骤1中感受器的位置对DBSCAN邻域半径Eps及密度阈值MinPts进行赋值。根据不同Eps值对输入样本进行DBSCAN进行聚类,进而得到神经网络中心数量和中心值。进行网络训练得到u个RBF神经网络结构,达到预设训练次数后得到训练输出值。
步骤3 将目标函数定义为均方根误差,式(18)中xI和
| $ F(x)=E_{\mathrm{RMSE}}=\sqrt{\frac{1}{N} \sum\limits_{I=1}^N\left(\bar{x}_I-\hat{x}_I\right)^2} \times 100 \% $ | (18) |
步骤4 设每个感受器对应目标函数值为F(xbi),将最小值对应位置与历史最优值Fbest进行对比,若F(xbi)>Fbest,则将个体前进方向设定为该感受器方向;若F(xbi) < Fbest,则返回步骤1。
步骤5 计算目标函数之间的梯度,运用NAdam梯度学习法进行步长更新,根据规则进行位置更新;
步骤6 达到预测精度后,停止寻优并返回当前最优值及训练好的RBF神经网络参数。
步骤7 输入预测数据到训练好的预测模型中,得到预测值。
2.2 交通流仿真预测及验证本文选取明尼苏达大学2018年7月份公布的城市道路交通量数据进行系统训练和预测,数据为7月2日到12日的全天数据,将数据处理为时间间隔3 min的车流量数据,将7月2日至7月11日数据作为训练数据,选取7月12日数据作为期望输出数据,利用MATLAB2018b进行预测模型编程分析,首先对数据进行预处理,去除缺失数据和漂移数据,然后对预处理后的数据进行归一化:
| $ y=\frac{y-y_{\min }}{y_{\max }-y_{\min }} $ | (19) |
式中ymax和ymin分别为数据的最大值及最小值。
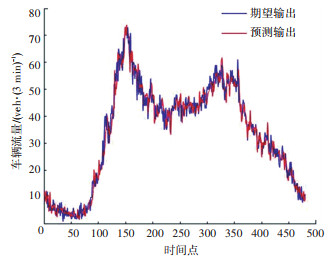
建立改进RBF神经网络预测模型,其中RBF神经网络的训练次数为100,初始学习速率0.1,训练精确度为0.000 1,自适应BAS感受器数量为20,迭代次数为100,维度为2,DBSCAN聚类邻域半径为2.5,密度阈值为5,采用梯度下降学习法进行权重和偏差更新,输出结果如图 5所示。
|
图 5 改进RBF交通流预测结果图 Fig. 5 Improved RBF traffic flow prediction results |
分别用BP神经网络、传统RBF神经网络、广义RBF神经网络及本文构建的改进RBF神经网络对处理后的数据进行短时交通流预测,将预测结果与真实数据进行对比,验证各模型的预测输出。为去除预测模型的偶发性,对各模型分别训练100次,取得其预测结果的平均值为最终预测结果,如图 6所示。

|
图 6 多种模型预测结果 Fig. 6 Prediction results of different models |
图 6(a)中基于BP短时交通流预测结果,对交通流峰值预测能力差且预测值上下波动较大,导致其预测结果误差较大,不能表示实际中的交通流;图 6(b)为基于RBF短时交通流预测结果图,该模型在预测峰值时数值向上偏移,导致误差加大,其他预测值普遍高于实际值;图 6(c)为基于广义RBF短时交通流预测结果,相较RBF短时交通流预测能较好地接近交通流峰值;图 6(d)为基于改进RBF短时交通流预测结果,该模型能较好预测交通流的峰值,与真实值拟合更好。
3.2 误差对比分析为验证预测结果的可靠性,本文采用式(20)~(23)中平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方根误差(RMSE)及拟合度(EC)4个指标对预测结果进行验证:
| $ \mathrm{MAE}=\frac{1}{N} \sum\limits_{I=1}^N\left|\bar{x}_I-\hat{x}_I\right| $ | (20) |
| $ \operatorname{MAPE}=\frac{1}{N} \sum\limits_{I=1}^N\left|\frac{\bar{x}_I-\hat{x}_I}{\bar{x}_I}\right| $ | (21) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{I=1}^N\left(\bar{x}_I-\hat{x}_I\right)^2} $ | (22) |
| $ \mathrm{EC}=1-\frac{\sqrt{\sum\limits_{I=1}^N\left(\bar{x}_I-\hat{x}_I\right)^2}}{\sqrt{\sum\limits_{I=1}^N\left(\bar{x}_I\right)^2}+\sqrt{\sum\limits_{I=1}^N\left(\hat{x}_I\right)^2}} $ | (23) |
式中xI和
通过对表 2的结果分析,改进RBF神经网络比BP神经网络的MAE和MAPE、RMSE分别降低1.87%、15.96%、3.24%;相较RBF神经网络的MAE和MAPE、RMSE分别降低1.45%、5.17%、2.4%;对比广义RBF神经网络的MAE和MAPE、RMSE分别降低1.36%、5.01%、2.19%。可以看出,BP神经网络交通流预测性能相对最差,RBF神经网络预测精度有所提高,广义RBF神经网络具有较高的预测精度,而改进RBF神经网络精度均优于上述对比模型。EC值越靠近1说明该模型的数据拟合度越好,改进RBF神经网络相较广义RBF神经网络提高了2.5%,说明改进后模型拟合度更高。综上所述,改进RBF短时交通流预测模型预测效果更好、精度更高。
| 表 2 预测结果多指标分析 Tab. 2 Multiple index analysis of prediction results |
本文对RBF神经网络交通流预测模型进行改进,提出了适应天牛须搜索算法来优化RBF神经网络短时交通流预测模型,并对结果进行了对比验证,主要结论如下:
1) 本文利用自适应步长改进BAS算法,并进行仿真验证证明自适应BAS与原算法比较,收敛速度和寻优能力都得到提高。
2) 利用自适应BAS算法及DBSCAN对传统RBF神经网络进行优化,构建了对易受环境干扰、存在随机性的非线性交通流数据识别能力更强的改进RBF神经网络短时交通流预测模型。
3) 预测模型径向基函数中心不再限制在样本数据点上,可以克服干扰数据产生的病态预测结果,防止因数据的精确度及偏差而造成的权值剧烈变化,增强了模型泛化能力,优化了预测模型的参数。
4) 预测结果表明:改进后的预测模型相较BP神经网络、传统RBF神经网络、广义RBF神经网络预测精度更高,对交通数据波峰和波谷拟合度更高。
| [1] |
杨兆升, 朱中. 基于卡尔曼滤波理论的交通流量实时预测模型[J]. 中国公路学报, 1999, 12(3): 5. YANG Zhaosheng, ZHU Zhong. A real time traffic volume prediction model based on the Kalman filtering theory[J]. China Journal of Highway and Transport, 1999, 12(3): 5. |
| [2] |
KUMAR S V, VANAJAKSHI L. Short-term traffic flow prediction using seasonal ARIMA model with limited input data[J]. European Transport Research Review, 2015, 7(3): 21. DOI:10.1007/s12544-015-0170-8 |
| [3] |
WILLIAMS B M, DURVASULA P K, BROWN D E. Urban freeway traffic flow prediction: application of seasonal autoregressive integrated moving average and exponential smoothing models[J]. Transportation Research Record: Journal of the Transportation Research Board, 1998, 1644(1): 132. DOI:10.3141/1644-14 |
| [4] |
陈磊, 张土乔. 基于最小二乘支持向量机的时用水量预测模型[J]. 哈尔滨工业大学学报, 2006, 38(9): 1528. CHEN Lei, ZHANG Tuqiao. Hourly water demand forecast model based on least squares support vector machine[J]. Journal of Harbin Institute of Technology, 2006, 38(9): 1528. |
| [5] |
BÉREAU M, DUBUISSON B. A fuzzy extended k-nearest neighbors rule[J]. Fuzzy Sets and Systems, 1991, 44(1): 17. DOI:10.1016/0165-0114(91)90029-P |
| [6] |
高大文, 王鹏, 蔡臻超. 人工神经网络中隐含层节点与训练次数的优化[J]. 哈尔滨工业大学学报, 2003, 35(2): 207. GAO Dawen, WANG Peng, CAI Zhenchao. Optimization of hidden nodes and training times in artificial neural network[J]. Journal of Harbin Institute of Technology, 2003, 35(2): 207. |
| [7] |
王永恒, 高慧, 陈炫伶. 采用变结构动态贝叶斯网络的交通流量预测[J]. 计算机科学与探索, 2017, 11(4): 528. WANG Yongheng, GAO Hui, CHEN Xuanling. Traffic prediction method using structure varying dynamic Bayesian networks[J]. Journal of Frontiers of Computer Science and Technology, 2017, 11(4): 528. |
| [8] |
LIU Siyan, LI Dewei, XI Yugeng, et al. A short-term traffic flow forecasting method and its applications[J]. Journal of Shanghai Jiaotong University (Science), 2015, 20(2): 156. DOI:10.1007/s12204-015-1604-0 |
| [9] |
RAHIMIPOUR S, MOEINFAR R, HASHEMI M. Traffic prediction using a self-adjusted evolutionary neural network[J]. Journal of Modern Transportation, 2019, 27(4): 306. DOI:10.1007/s40534-018-0179-5 |
| [10] |
蔡延光, 乐冰, 蔡颢, 等. 暴雨天气下高速公路短时交通流预测[J]. 计算机工程, 2020, 46(6): 34. CAI Yanguang, LE Bing, CAI Hao, et al. Short-term traffic flow forecast of expressway under heavy rain[J]. Computer Engineering, 2020, 46(6): 34. |
| [11] |
魏海坤, 徐嗣鑫, 宋文忠. 神经网络的泛化理论和泛化方法[J]. 自动化学报, 2001, 27(6): 806. WEI Haikun, XU Sixin, SONG Wenzhong. Generalization theory and generalization methods for neural networks[J]. Acta Automatica Sinica, 2001, 27(6): 806. |
| [12] |
FUNAHASHI K I. On the approximate realization of continuous mappings by neural networks[J]. Neural Networks, 1989, 2(3): 183. |
| [13] |
马君, 刘小冬, 孟颖. 基于神经网络的城市交通流预测研究[J]. 电子学报, 2009, 37(5): 1092. MA Jun, LI Xiaodong, MENG Ying. Research of urban traffic flow forecasting based on neural network[J]. Acta Electronica Sinica, 2009, 37(5): 1092. |
| [14] |
CHEN S, COWAN C F N, GRANT P M. Orthogonal least squares learning algorithm for radial basis function networks[J]. IEEE Transactions on Neural Networks, 1991, 2(2): 302. |
| [15] |
黄文明, 徐双双, 邓珍荣, 等. 改进人工蜂群算法优化RBF神经网络的短时交通流预测[J]. 计算机工程与科学, 2016, 38(4): 713. HUANG Wenming, XU Shuangshuang, DENG Zhenrong, et al. Short-term traffic flow prediction of optimized RBF neural networks based on the modified ABC algorithm[J]. Computer Engineering & Science, 2016, 38(4): 713. |
| [16] |
黄子炎, 王庆宾, 冯进凯, 等. 确定区域大地水准面的K-means-RBF神经网络方法[J]. 测绘科学技术学报, 2021, 38(3): 246. HUANG Ziyan, WANG Qingbin, FENG Jinkai, et al. The K-means-RBF neural network method for determining regional geoid[J]. Journal of Geomatics Science and Technology, 2021, 38(3): 246. |
| [17] |
JIANG Xiangyuan, LI Shuai. BAS: beetle antennae search algorithm for optimization problems[J]. International Journal of Robotics and Control, 2018, 1(1): 1. |
| [18] |
XIE S, CHU X, ZHENG M, et al. Ship predictive collision avoidance method based on an improved beetle antennae search algorithm[J]. Ocean Engineering, 2019, 192: 106542. |
| [19] |
KHAN A H, CAO Xinwei, LI Shuai, et al. BAS-ADAM: an ADAM based approach to improve the performance of beetle antennae search optimizer[J]. IEEE/CAA Journal of Automatica Sinica, 2020, 7(2): 461. |
| [20] |
ZHANG Jian, GUAN Lin, REN Bingzhong. Fine structure and distribution of antennal sensilla of longicorn beetles Leptura arcuata and Leptura aethiops (Coleoptera: Cerambycidae)[J]. Annals of the Entomological Society of America, 2011, 104(4): 778. |
 2023, Vol. 55
2023, Vol. 55


