2. 96851部队, 辽宁 盘锦,124202;
3. 哈尔滨工业大学 航天学院,哈尔滨 150001
2. No.96851 Troops, Panjin 124202, Liaoning, China;
3. School of Astronautics, Harbin Institute of Technology, Harbin, 150001
高超声速滑翔飞行器(Hypersonic glide vehicle, HGV)具有飞行速度快、机动范围广、全球投送能力强等明显优势,引起了各军事国的密切关注[1-2]。在HGV遂行飞行任务时,如何快速规划出一条安全且可靠的再入轨迹,成为机动飞行首要解决的问题[3]。因高超声速滑翔飞行器再入过程具有强耦合、非线性等特点,近年来,高超声速滑翔飞行器的再入轨迹优化问题已成为领域内研究的热点[4-5]。
HGV再入机动过程中除了满足终端约束和控制量约束外,还需要满足路径约束,通常的路径约束包括热流率、动压和过载[6-7]。常见的解决HGV再入轨迹优化(Reentry trajectory optimization,RTO)问题的方法主要包括间接法和直接法[8-10]。间接法依据极大值原理,推导出一阶必要条件,将HGVRTO问题转化为哈密顿两点边值问题进行进一步求解。此类方法能够求得全局最优解,求解速度快、精度高,但是推导过程复杂,对初值较为敏感[11]。直接法是指将连续控制问题通过一定的离散方法转化为非线性规划问题(Nonlinear programming problem, NLP), 进而利用NLP方法进行求解[12]。直接法对初始值要求不严格,但是无法保证得到解是问题的最优解,若通过增加离散节点数目来提高求解精度,对算法求解效率带来严重影响[13-14]。
近年来,智能优化算法因其较好的全局优化性和鲁棒性,被越来越多的学者应用到飞行器的轨迹优化领域。李宪强等[15]将蚁群算法同人工势场法相结合并应用到无人机的路径规划中,使无人机能够顺利安全的避开障碍物到达目标点。徐慧等[16]利用精英策略对鲸鱼算法(Whale optimization algorithm,WOA)进行改善,保证算法快速收敛的同时,进一步改进了WOA的全局搜索性能。余跃等[17]提出一种动态自适应樽海鞘群算法,将其作为高斯伪谱法优化的初值生成器,解决制导问题时求解速度有了一定的提高。在HGVRTO问题研究领域,采用较多的是粒子群优化算法[18](Particle swarm optimization,PSO)。Zhou等[19]提出一种改进的PSO算法在每个制导周期中优化比例导引的权重,大大提高了计算效率。周宏宇等[20]提出一种双层在线制导方法,并将PSO和改进共轭梯度法相结合优化飞行剖面,以满足过程约束和指标要求。另外,周宏宇等[21]设计了一种自动满足终端约束的全新飞行剖面,并借助强化学习方法优化PSO惯性权重,极大的提高了在线规划效率。Li等[22]采用一种随机梯度PSO算法,对攻角-速度剖面和倾侧角转换点进行优化,能够保证再入飞行器准确到达目标区域内。Sana等[23]提出一种将分数阶粒子群算法同重力搜索算法相结合的方法并利用准平衡滑翔条件,优化攻角剖面参数,能够自动满足热流率约束。但对于高超再入轨迹优化的复杂非线性强耦合问题,PSO算法同其他智能优化算法类似,存在求解效率不高、易陷于局部最优解等问题[19]。
近年来,随着对生物群体的研究加深,各种新型的智能优化算法也被提出,Xue等[24]提出的一种麻雀优化算法(Sparrow search algorithm, SSA),相较于其他优化算法在全局性和收敛性有着明显的优势,调整参数少,全局寻优能力较强,收敛快,计算简单,已经被较好的应用到无人机路径规划[25]。由于高超声速再入飞行是一个强耦合、非线性的复杂过程,如何能够在短时间内快速得到一个全局最优轨迹,是研究者关注的焦点。而SSA算法,在求解效率和计算全局最优解方面具有一定优势,能够为快速轨迹优化问题,在求解时间和求解精度上带来一定改善。SSA算法将种群分为发现者、跟随者和侦察者,3类个体对应着不同的更新策略,以获得最优位置。但面临复杂问题时,SSA作为一种智能优化算法,依然存在易陷入局部最优的问题。
针对上述问题,本文提出了一种改进的麻雀优化算法(Improved sparrow search algorithm, ISSA),并将其用于优化设计高超声速再入轨迹优化问题。首先,通过Tent混沌映射和精英反向种方法初始化种群,利用黄金正弦策略进行种群的位置更新,并通过余弦策略减少侦察者数量,采用贪婪策略对种群的最优解进行选择和更新,增强算法全局搜索能力的同时,不影响收敛速度。进而,采用ISSA算法优化攻角和倾侧角剖面,利用阻力加速度飞行走廊保证路径约束得到满足,采用罚函数法将归一化处理终端约束。多种智能优化算法的高超再入轨迹优化对比仿真实验说明本文算法的有效性,蒙特卡洛仿真实验说明本文提出算法具有较好的抗干扰性。
1 高超声速飞行器再入轨迹优化问题模型 1.1 再入运动方程高超声速滑翔飞行器再入运动方程如下:
| $ \left\{\begin{array}{l} \dot{r}=\sin \gamma \\ \dot{\theta}=V \frac{v \cos \gamma \sin \psi}{r \cos \varphi} \\ \dot{\varphi}=\frac{V \cos \gamma \cos \psi}{r} \\ \dot{V}=-\frac{D}{m}-g \sin \gamma \\ \dot{\gamma}=\frac{L \cos \sigma}{m V}-\left(\frac{g}{V}-\frac{V}{r}\right) \cos \gamma \\ \dot{\psi}=\frac{L \sin \sigma}{m V \cos \gamma}+\frac{V}{r} \cos \gamma \sin \psi \tan \varphi \end{array}\right. $ | (1) |
式中:r为飞行器质心到地心距离,θ、φ分别为飞行器当前时刻所在经度、纬度,V为飞行器当前时刻速度,γ、ψ分别为飞行航迹角和航向角,L、D为当前受到的阻力和升力,σ为倾侧角,与攻角α一起组成控制量,m为飞行器质量,g为地球引力加速度。
阻力和升力计算方式如下:
| $ \left\{\begin{array}{l} L=0.5 \rho V^2 C_{\mathrm{L}} S_{\mathrm{r}} \\ D=0.5 \rho V^2 C_{\mathrm{D}} S_{\mathrm{r}} \end{array}\right. $ | (2) |
式中: ρ为大气密度,h=r-Re,Re为地球平均半径,hs=7 100 m;Sr为飞行器参考面积;CL、CD分别为飞行器升力系数和阻力系数,是与攻角和马赫数有关的函数[26]。
1.2 再入飞行约束条件HGV再入机动飞行必须满足多种约束,尤其是过程约束能够保证飞行过程中飞行器的结构性安全,典型过程约束可记为
| $ \boldsymbol{\varPsi}_{\text {path }}=\max \left\{\frac{N_l}{N_{\max }}, \frac{q}{q_{\max }}, \frac{\dot{Q}}{\dot{Q}_{\text {max }}}\right\} \leqslant 1 $ | (3) |
式中:
| $ \left\{\begin{array}{l} N_l=\sqrt{L^2+D^2} / m \\ q=0.5 \rho V^2 \\ \dot{Q}=K_Q \rho^{0.5} V^{3.15} \end{array}\right. $ | (4) |
式中,KQ=7.968 6×10-5 Js2/(m3.5kg0.5)为热流率常数。
可将控制量可记为u=[α, σ]T,控制量约束记为
| $ \left\{\begin{array}{l} |\alpha|-\alpha_{\max } \leqslant 0 \\ |\sigma|-\sigma_{\max } \leqslant 0 \end{array}\right. $ | (5) |
HGVRTO问题目的是导引飞行器安全到达指定区域,因此本文将终端约束记为
| $ \left\{\begin{array}{l} \left|r\left(t_f\right)-r_f\right| \leqslant \Delta r \\ \left|S\left(t_f\right)-S_f\right| \leqslant \Delta S \\ V\left(t_f\right)=V_f \end{array}\right. $ | (6) |
式中: tf为终端时刻,下标“f”为终端时刻期望的状态值,Δr、ΔS分别为终端时刻高度和航程的可接受误差。
在滑翔段飞行时,HGV常常需要满足准平衡滑翔条件[27-28] (Quasi-equilibrium glide condition, QEGC),即
| $ \frac{L}{m} \cos \sigma+\left(\frac{V^2}{r}-g\right)=0 $ | (7) |
根据高超声速再入任务要求设计适当的目标函数。本文研究以再入终端速度误差最小为目标,具体形式如下:
| $ \min J(\boldsymbol{u})=\left|V\left(t_f\right)-V_{\mathrm{c}}\right| $ | (8) |
综上所述,HGVRTO问题是寻找合适的控制量变化剖面,使得式(8)为目标函数最优,同时满足式(1)、(3)、(5)~(7)的约束。
2 改进麻雀优化算法麻雀算法于2020年被提出[24],SSA算法与其他常见优化算法相比,在全局最优性和收敛速度方面有一定的优势[25]。但类似地,对于复杂问题优化求解,SSA算法也会出现搜索效率不高和易早熟的问题。对此,本文提出一种改进的麻雀优化算法,以增强面对复杂问题时的全局搜索能力。
2.1 麻雀搜索算法SSA算法通过模拟麻雀觅食的过程,将种群分为发现者和跟随者,发现者是距离食物较近,占种群数量的20%,其余为跟随者。并随机选取20%的个体作为预警麻雀,一旦超过安全阈值,则放弃食物,转移到其他安全区域进行觅食。发现者、跟随者和侦察者分别按照各自的规则进行更新[25]。
发现者更新规则如下:
| $ M_k^{t+1}= \begin{cases}M_k^t \cdot \exp \left(\frac{-k}{a \cdot T}\right), & b<s_t \\ M_k^t+d \cdot \boldsymbol{W}, & b \geqslant s_t\end{cases} $ | (9) |
式中:Mkt为第k个麻雀个体第t次迭代时的位置, T为最大迭代次数,a、b为随机数且a∈(0, 1],b∈[0, 1],d为服从正态分布的随机数,W为元素为1的向量,st为安全阈值,是一个常值。
跟随者的更新规则如下:
| $ M_k^{t+1}= \begin{cases}d \cdot \exp \left(\frac{M_{\text {worst }}^t-M_k^t}{k^2}\right), & k>N / 2 \\ M_{\text {best }}^t+\left|M_k^t-M_{\text {best }}^t\right| \cdot \boldsymbol{A}^{+} \cdot \boldsymbol{W}, & k \leqslant N / 2\end{cases} $ | (10) |
式中:Mbestt、Mworstt分别为第t次迭代时的最优位置和最差位置, N为种群大小, A为一个各元素随机设为1或者-1的矩阵,且A+=AT(AAT)-1。
侦察者的更新规则如下:
| $ M_k^{t+1}= \begin{cases}M_{\text {best }}^t+\beta \cdot\left(M_k^t-M_{\text {best }}^t\right), & f_k \neq f_{\text {best }} \\ M_{\text {best }}^t+c \cdot\left(\frac{\left|M_k^t-M_{\text {worst }}^t\right|}{\left(f_k-f_{\text {worst }}\right)+\boldsymbol{\epsilon}}\right), & f_k=f_{\text {best }}\end{cases} $ | (11) |
式中:fk为当前麻雀个体的适应度值,fbest、fworst分别为当前迭代次数下的全局最优适应度和最差适应度的值, β为服从(0, 1)的正态分布,c∈[-1, 1]为一个随机数,ϵ为一个提前设定的小量常值。
2.2 改进的麻雀优化算法针对SSA算法存在的易陷入局部最优的问题,本文提出一种将混沌映射和黄金正弦策略相结合的ISSA算法,以增强SSA算法的全局搜索能力。
首先,利用Tent混沌序列和反向学习策略生成初始种群。Tent混沌序列计算方式如下:
| $ p_{k+1, m}= \begin{cases}2 p_{k m}, & p_{k m}<0.5 \\ 2\left(1-p_{k m}\right), & p_{k m} \geqslant 0.5\end{cases} $ | (12) |
式中“m”指的是变量的第m维。将混沌序列映射到解空间得到混沌种群,计算如下:
| $ M_{k m}^p=B_{1 m}+p_{k m} \cdot\left(B_{\mathrm{u}m}-B_{\mathrm{l} m}\right) $ | (13) |
式中:上标“p”为由混沌序列p映射得到的值, Mkmp为第k个麻雀第m维位置上的取值, Bum、Blm分别为m维解空间的上、下限。将式(13)得到的麻雀种群记为Hp,则利用反向学习策略生成种群Ho,Ho中个体位置为
| $ M_{k m}^o=B_{1 m}+B_{\mathrm{u}m}-M_{k m}^p $ | (14) |
式中Mkmo为反向种群第k个个体m维的值。设初始化种群大小为N,合并种群Hp和Ho,取出适应度最好的N个麻雀个体组成初始化种群,记为H0。
发现者占种群中的20%,当b < st,觅食环境安全,个体位置更新时易陷入搜索范围过小问题,或者搜索距离过大造成计算效率的浪费。在安全环境下,本文采用黄金正弦的方法进行位置更新,在保证搜索范围有效的情况下尽可能探索解空间。发现者更新方式由式(9)改进为
| $ M_k^{t+1}= \begin{cases}M_k^t \cdot\left|\sin \left(R_1\right)\right|+R_2 \cdot & \sin \left(R_1\right) \cdot \\ \left|\xi_1 \cdot M_{\text {best }}^t-\xi_2 \cdot M_k^t\right|, & b<s_r \\ M_k^t+d \cdot \boldsymbol{W}, & b \geqslant s_r\end{cases} $ | (15) |
式中:R1、R2都是随机取值且R1∈[0, 2π],R2∈[0, π];ξ1、ξ2为控制更新步长和方向的两个参数,计算方式如下:
| $ \left\{\begin{array}{l} \xi_1=-{\rm{ \mathsf{π} }}+2 {\rm{ \mathsf{π} }}(1-\zeta) \\ \xi_2=-{\rm{ \mathsf{π} }}+2 {\rm{ \mathsf{π} }} \zeta \end{array}\right. $ | (16) |
式中ζ为黄金分割数, 即
| $ M_k^{t+1}= \begin{cases}M_k^t \cdot\left|\sin \left(R_1\right)\right|+R_2 \cdot \sin \left(R_1\right) \cdot\left|M_{\text {worst }}^t-M_k^t\right|, & k>\frac{N}{2} \\ M_{\text {best }}^t+\left|M_k^t-M_{\text {best }}^t\right| \cdot \boldsymbol{A}^{+} \cdot \boldsymbol{W}, & k \leqslant \frac{N}{2}\end{cases} $ | (17) |
侦察麻雀的数量随机选择占种群数量的20%,更新方式如式(11),但是随着迭代次数的增加,麻雀的位置都逐渐向最优位置靠近,如果依然保持较多的侦察者数量进行位置突变, 会导致算法优化效率下降,因此本文选择一种余弦策略,使得侦察者数量随着迭代次数增多而下降,计算方式如下:
| $ \text { number }^t=\left\lceil 0.2 \cdot N \cos \left(\frac{{\rm{ \mathsf{π} }}}{2} \cdot \frac{t}{T}\right)\right\rceil $ | (18) |
式中:numbert为第t次迭代时侦察者的数量,
| $ M_k^{t+1}= \begin{cases}M_{k \text { new }}^{t+1}, & f_{\mathrm{new}} \leqslant f_k, \xi_3 \leqslant 0.9 \\ M_k^t, & \text { 其他 }\end{cases} $ | (19) |
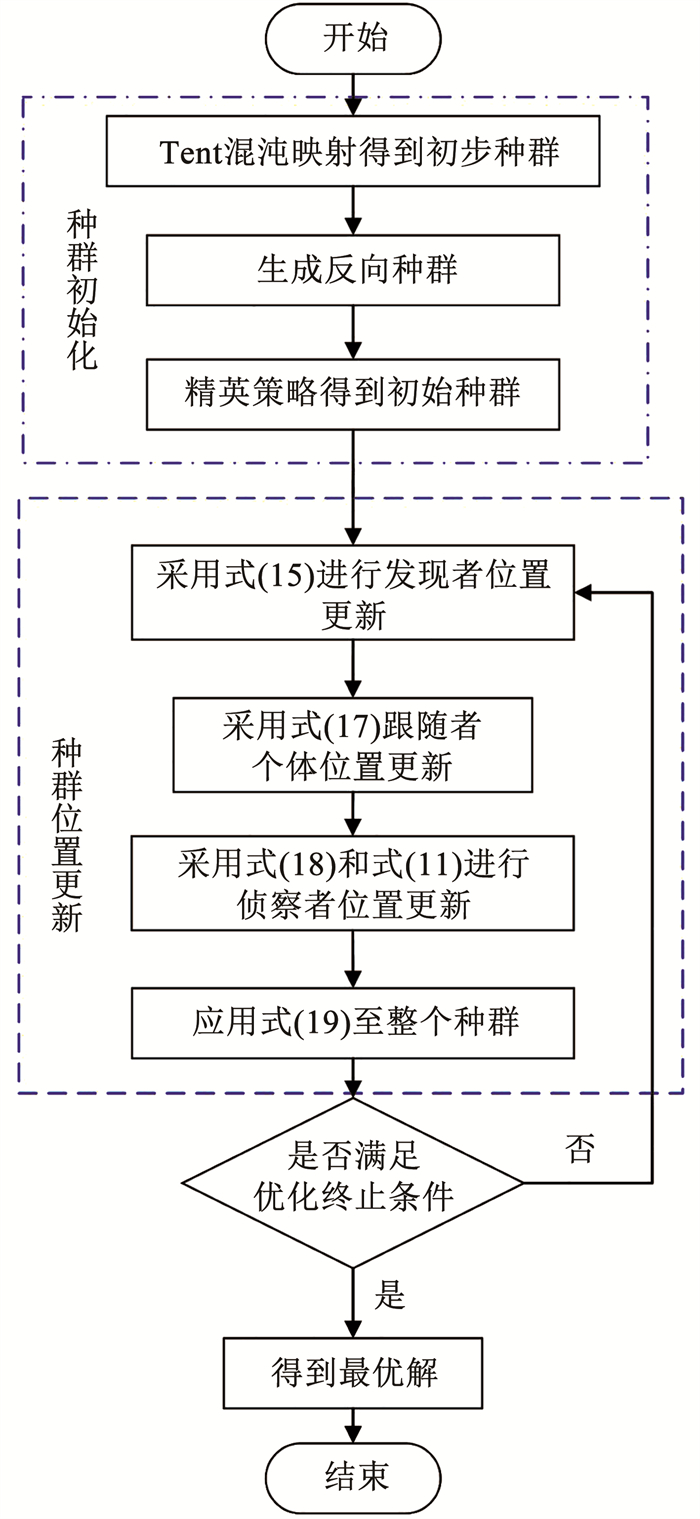
式中:fk、fnew分别为位置更新前和更新后的适应度,Mknewt+1为经过更新后的位置,ξ3是一个随机数值,且ξ3∈(0, 1]。综上所述,本文提出的ISSA能够在保证计算效率的基础上,对全局搜索能力进一步拓展,图 1展现了ISSA算法的流程。
|
图 1 ISSA算法流程图 Fig. 1 ISSA algorithm flow chart |
高超声速再入轨迹优化实际上可以看作根据再入任务寻找攻角和倾侧角的变化规律,并在完成再入任务的同时,使得目标函数最优。为了能够较好的应用智能优化算法,可对高超声速再入轨迹优化问题进行一定的简化,将其转化成一个参数优化问题。
3.1 攻角剖面设计在进行高超声速再入轨迹优化时,可将攻角剖面设计成一个与速度相关的分段线性函数,计算形式如下:
| $ \alpha= \begin{cases}\alpha_{\max }, & V_1<V \leqslant V_e \\ \frac{\left(\alpha_{\text {ratio }}-\alpha_{\max }\right)}{\left(V_2-V_1\right)} \cdot\left(V-V_1\right)+\alpha_{\max }, & V_2<V \leqslant V_1 \\ \alpha_{\text {ratio }}, & V_c<V \leqslant V_2\end{cases} $ | (20) |
式中:Ve为再入初始速度,αmax为最大攻角,αratio为最大升阻比对应的攻角,V1、V2为算法优化设计攻角剖面相关的参数。
3.2 倾侧角剖面设计考虑高超声速飞行器再入时飞行过程的特点,再入段制导问题可以分成纵向、横向轨迹设计,纵向运动可以通过设计|σ|随速度的变化,保证飞行轨迹在再入走廊内运动并满足约束条件内各种约束;横向轨迹设计利用航向角偏差走廊,改变倾侧角符号,确保飞行精度。
在进行纵向轨迹设计时,可将再入过程分为初始再入段和准平衡滑翔段考虑。初始再入段是为了再入飞行器的状态顺利进入阻力加速度剖面-速度再入走廊,并满足准平衡滑翔条件式(7),为进入滑翔段进行准备。同常见的速度-高度再入走廊一样,阻力加速度-速度再入走廊可由热流率、动压、过载的路径约束和准平衡滑翔条件得到,阻力加速度记为aD,具体约束条件如下:
| $ \left\{\begin{array}{l} a_{\mathrm{D}} \leqslant \frac{\dot{Q}_{\max } S_r}{2 K_Q m} \cdot \frac{C_{\mathrm{D}} \rho^{0.5}}{V^{1.15}} \\ a_{\mathrm{D}} \leqslant \frac{q_{\max } S_r}{m} \cdot C_{\mathrm{D}} \\ a_{\mathrm{D}} \leqslant \frac{N_{\max } g_0}{\sqrt{(L / D)^2+1}} \\ a_{\mathrm{D}} \geqslant \frac{D}{L} \cdot\left(g-\frac{V^2}{r}\right) \end{array}\right. $ | (21) |
初始再入段大气稀薄,气动作用力有限,因此常将此段过程中倾侧角大小设为一个常值σ0。初始时刻的倾侧角符号为:
| $ \operatorname{sign}\left(\sigma_0\right)=-\operatorname{sign}\left(\Delta \psi_0\right) $ | (22) |
式中:Δψ0为当前时刻航向角与目标视线角的偏差,Δψ0=ψ0-ψlos,ψ0为再入时刻航向角,ψlos为目标点视线方位角。利用攻角剖面以及初始时刻倾侧角和状态量值,不断积分即可得到初始再入段过程中的状态量和控制量,直到飞行器满足准平衡滑翔条件进入再入走廊,即到达准平衡滑翔段转换点,转换条件为
| $ \left|\frac{\mathrm{d} r}{\mathrm{~d} V}-\left(\frac{\mathrm{d} r}{\mathrm{~d} V}\right)_{\mathrm{QEGC}}\right|<\delta_1 $ | (23) |
式中:δ1为小量常值。由式(1)和式(7)可得
| $ \left\{\begin{array}{l} \frac{\mathrm{d} r}{\mathrm{~d} V}=\frac{V \sin \gamma}{-D / m-g \sin \gamma} \\ \left(\frac{\mathrm{d} r}{\mathrm{~d} V}\right)_{\text {QEGC }} \doteq \frac{C_{\mathrm{L}} S_r \cos \sigma_0 \rho V+2 m V / r}{m V^2 / r^2+\rho V^2 C_{\mathrm{L}} S_r \cos \sigma_c / 2 h_s} \end{array}\right. $ | (24) |
为保证初始再入段到准平衡滑翔段转换时控制量连续,除满足式(23)外,倾侧角还应满足:
| $ \left|\sigma_0-\sigma_{\mathrm{QEGC}}\right|<\delta_2 $ | (25) |
式中:σQEGC为准平衡滑翔条件得到的倾侧角大小,δ2为小量常值。通过不断地迭代和判断,即可求得转换点的状态量和控制量。
综上所述,在初始再入段,设计了倾侧角固定值σ0,不断的积分求得整个阶段中的状态量和控制量直至到达飞行转换点。
3.2.2 准平衡滑翔段倾侧角剖面参数化设计经过再入过程转换点之后,高超声速再入滑翔飞行器进入准平衡滑翔段,飞行过程不仅需要时刻满足D-V再入走廊,还需要满足准平衡滑翔条件。
首先可以利用D-V再入走廊近似求出倾侧角大小。由于攻角可由攻角-速度剖面得到,则可利用速度二次函数近似描述阻力加速度,形式如下:
| $ D=c_2 V^2+c_1 V+c_0 $ | (26) |
式中c0, c1, c2为3个未知系数,需要3个等式求得3个系数值。准平衡滑翔段的起始点为再入过程转换点,记为(VT, rT);滑翔段的终点即为任务终端约束(Vf, rf),结合式(2)可以得到对应的阻力加速度分别记为DT、Df。设计变量Dp,表示速度为到达(VT+Vf)/2时的阻力加速度,Dp有待于利用本文提出的优化算法进行优化。利用式(26)构造出3个等式,可求得c0, c1, c2如下:
| $ \begin{aligned} & c_0=\frac{D_T V_T V_f+D_T V_f^2-4 D_p V_T V_f+D_f V_T^2+D_f V_T V_f}{\left(V_T-V_f\right)^2} \\ & c_1=-\frac{D_T V_T+3 D_T V_f-4 D_p V_T-4 D_p V_f+3 D_f V_T+D_f V_f}{\left(V_T-V_f\right)^2} \\ & c_2=\frac{2\left(D_T-2 D_c+D_f\right)}{\left(V_T-V_f\right)^2} \end{aligned} $ | (27) |
结合式(26)即可得到设计的阻力加速度剖面。文献[22]指出可利用设计的参考阻力加速度剖面计算升阻比,记为ηref,计算如下:
| $ \eta_{\text {ref }}=\frac{1}{D}\left(g-\frac{V^2}{r}\right)-\frac{4 h_s c_0}{V^2}-\frac{h_s c_1}{V} $ | (28) |
另外,随着飞行器状态确定,也可有速度、高度和攻角计算出飞行器能够提供的升阻比η,则可得准平衡滑翔段的倾侧角大小为
| $ \left|\sigma^*\right|=\left|\arccos \frac{\eta_{\mathrm{ref}}}{\eta}\right| $ | (29) |
飞行器飞行的航迹可由倾侧角决定,但航迹与终端约束的误差可由倾侧角的符号来控制。本文采用航向角误差走廊确认倾侧角符号,航向角误差走廊分段函数表示如下:
| $ \left|\Delta \psi_{\mathrm{th}}\right|= \begin{cases}10, & 6000<V \leqslant V_0 \\ \frac{15, }{7}(V-3000)+15, & 1800<V \leqslant 3000<V \leqslant 600 \\ \frac{1200}{8, } & V \leqslant V_f\end{cases} $ | (30) |
式中:|Δψth|为航向角误差走廊的边界约束,(°);V0、Vf分别为再入时刻和终端时刻速度。本文采用倾侧角翻转策略,确保再入飞行器飞向目标终点的精度,即航向角与视线角误差Δψ一旦超过航向角误差走廊边界,则倾侧角进行反向,反向转换策略如下:
| $ \operatorname{sign}\left(\sigma^i\right)= \begin{cases}-1, & \Delta \psi \geqslant\left|\Delta \psi_{\mathrm{th}}(V)\right| \\ \operatorname{sign}\left(\sigma^{i-1}\right), & \Delta \psi \in\left(-\left|\Delta \psi_{\mathrm{th}}(V)\right|, \left|\Delta \psi_{\mathrm{th}}(V)\right|\right) \\ 1, & \Delta \psi \leqslant-\left|\Delta \psi_{\mathrm{th}}(V)\right|\end{cases} $ | (31) |
式中
| $ \tan \psi_{\mathrm{los}}=\frac{\sin \left(\theta_f-\theta\right)}{\cos \varphi \tan \varphi_f-\sin \varphi \cos \left(\theta_f-\theta\right)} $ | (32) |
式中θf、φf分别为目标点的经度、纬度。综上所述,可以得到倾侧角的大小和符号,即解算出倾侧角剖面。
3.3 终端约束处理式(6)给出了本文研究的高超声速再入轨迹优化问题的终端约束条件。智能优化算法中处理带约束问题一般采用罚函数方法。本文根据终端约束允许误差进行罚函数的设置,则目标函数式(8)可转换为
| $ \min \tilde{J}(\boldsymbol{u})=\left|V\left(t_f\right)-V_c\right|+w_1 b_r+w_2 b_S $ | (33) |
式中: w1、w2为相关约束的惩罚因子,br、bS由式(6)转化可得:
| $ \begin{aligned} & b_r= \begin{cases}0, & \left|r\left(t_f\right)-r_c\right| \leqslant \Delta r \\ \frac{\left|r\left(t_f\right)-r_c\right|}{1000}, & \left|r\left(t_f\right)-r_c\right|>\Delta r\end{cases} \\ & b_S= \begin{cases}0, & \left|S\left(t_f\right)-S_c\right| \leqslant \Delta S \\ \frac{\left|S\left(t_f\right)-S_c\right|}{1000}, & \left|S\left(t_f\right)-S_c\right|>\Delta S\end{cases} \end{aligned} $ | (34) |
本文研究中对终端约束进行一定的松弛,当高度和航程误差小于可接受误差时,认为满足终端约束;当高度和航程终端约束大于可接受误差时,则将终端误差变成一个惩罚项加入目标函数,随着算法迭代不断优化,最终趋向于最优结果。
4 仿真算例及结果分析采用提出的ISSA对求解HGVRTO问题过程中设计的V1、V2、σ0和Dp进行优化,得到满足任务目标最优的控制量剖面。本文设置4个仿真算例如下:1)使用测试函数对ISSA算法进行性能测试,并与3种群智能优化算法进行对比; 2)使用ISSA算法完成3种RTO试验任务,验证本文算法解决RTO问题有效性; 3)使用ISSA算法进行再入轨迹优化任务,并与3种群智能优化算法进行对比分析; 4)进行蒙特卡洛仿真实验,验证本文提出算法的鲁棒性。
本文仿真实验环境CPU为Intel i7 9700处理器,主频3 GHz,软件采用Matlab2019a版本。
4.1 测试函数对比分析本文仿真对比测试函数来自于文献[24], 测试函数自变量维数为30,初始化范围及最小值见表 1。对于每个测试函数,使用每种优化算法测试30次,每次测试最大迭代次数为1 000,种群个体总数为100。ISSA与SSA参数设置相同,发现者占种群20%,侦察麻雀占种群30%。
| 表 1 测试函数 Tab. 1 Test functions |
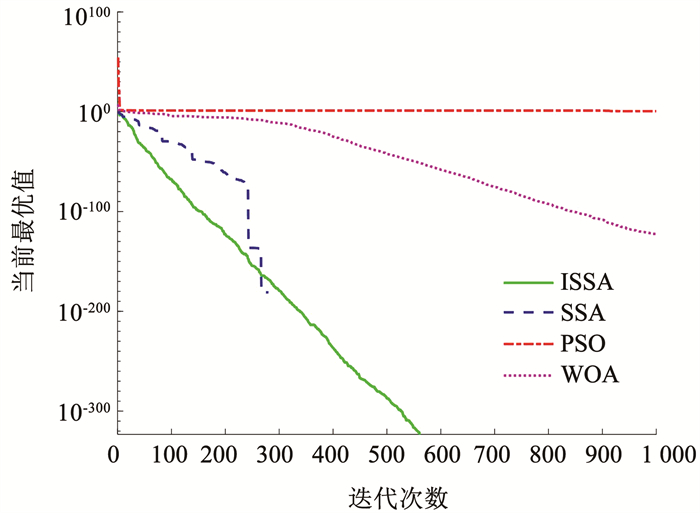
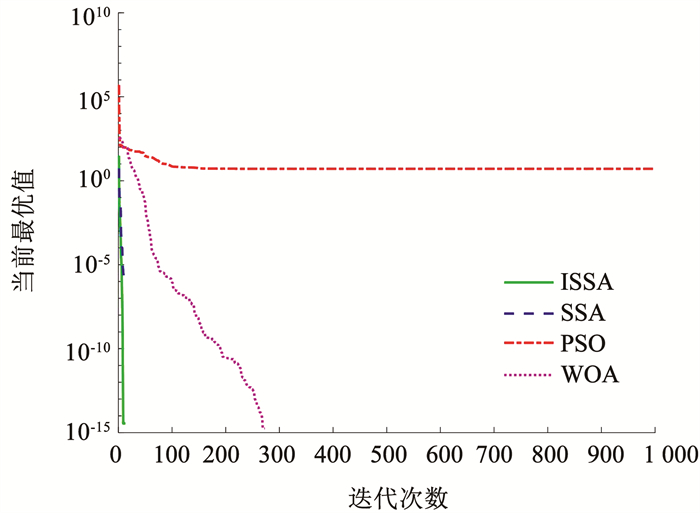
图 2~4展现了3种测试函数下4种优化算法的最优值变化情况,可知本文提出的ISSA优化算法在3个测试函数的实验中,收敛迭代次数最小,目标函数值最优,即表明在寻优性能和收敛速度方面,ISSA相较于对比算法均具有较大优势。

|
图 2 f1收敛曲线 Fig. 2 Convergence curves of f1 |
|
图 3 f2收敛曲线 Fig. 3 Convergence curves of f2 |
|
图 4 f3收敛曲线 Fig. 4 Convergence curves of f3 |
本文采用CAV-H高超声速飞行器模型进行再入轨迹优化实验,气动模型来自文献[29],质量907.2 kg,参考横截面积为0.484 m2,路径约束中热流率上限设为1 200 kW/m2,动压上限设为400 kPa,过载上限设为4。再入轨迹优化实验任务参数见表 2。
| 表 2 仿真场景参数设计 Tab. 2 Setting of the simulation |
为验证本文提出的ISSA算法对高超声速再入轨迹优化问题的有效性,本文各设计参数界限见表 3,Δr和ΔS的值分别设为1 000 m和50 km。将本文算法得到制导结果同SSA、WOA、PSO算法进行对比。
| 表 3 4个设计参数的上、下限 Tab. 3 Limitation of four parameters |
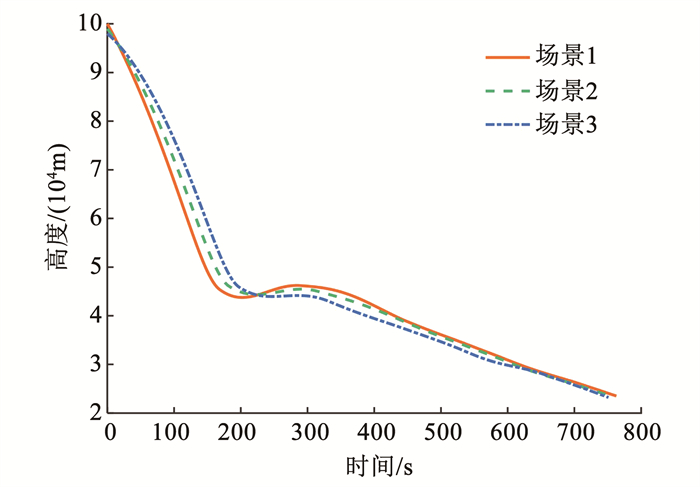
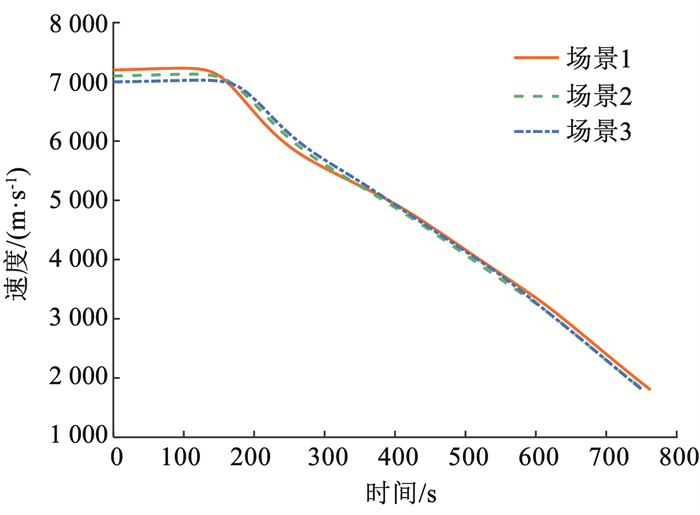
图 5~10分别展示了本文算法在3个实验场景下的结果。图 5所示,3种场景下终端高度误差在设置的阈值之内,满足终端约束要求。图 7展示了重点关注的终端速度误差分别为0.001 28、0.021 00、0.024 00 m/s,说明本文提出的算法具有较好的精度。
|
图 5 高度随时间变化 Fig. 5 Time history of the height |
|
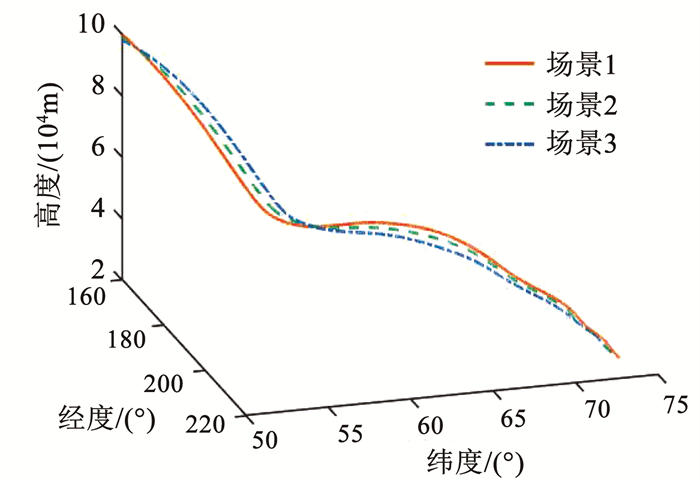
图 6 三维再入轨迹 Fig. 6 3D reentry trajectory |
|
图 7 速度随时间变化 Fig. 7 Time history of the height |

|
图 8 阻力加速度再入走廊 Fig. 8 Resistance acceleration reentry corridor |
|
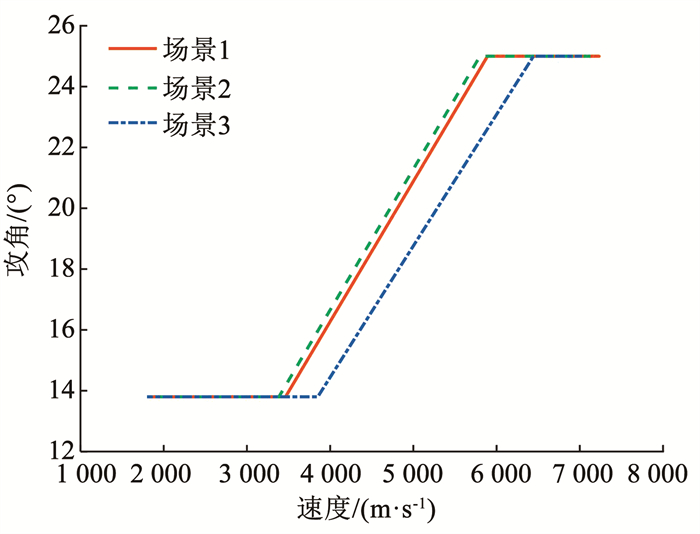
图 9 攻角随时间变化 Fig. 9 Time history of the AOA |
|
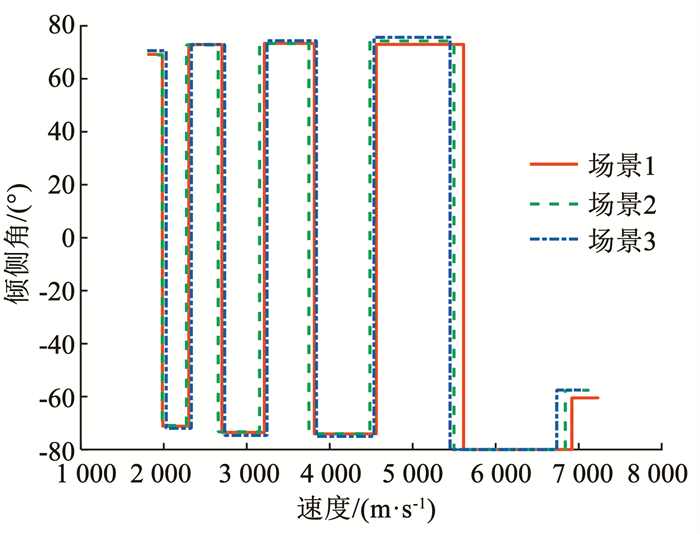
图 10 倾侧角随速度变化 Fig. 10 Velocity history of the bank angle |
图 8展现了3种实验场景下,本文算法得到的最优轨迹均能够进入再入走廊,意味着按照得到轨迹进行飞行,过程中的动压、过载、热流率密度均为超过限值。图 9、10分别展现了3种场景下的攻角和倾侧角的变化,攻角速度剖面的变化符合预期设计,切换速度满足表 3设置的上、下限范围;倾侧角翻转次数较少,且只有一次翻转到达极值,其余时间均小于约束极值,对控制系统及执行机构具有一定的意义。
综上所述,本文提出的基于ISSA的高超声速飞行器RTO方法可以得到一条精确且安全的飞行轨迹。
4.3 多种算法对比实验为更多的展现本文方法特点,以场景1为例,分别进行基于ISSA、SSA、WOA、PSO优化算法,采用本文提出的路程约束和终端约束处理方法进行再入任务轨迹优化实验,得到结果进行对比。
表 4展现了再入任务仿真过程中,基于4种优化算法得到的设计参数值、终端约束误差和目标函数值。可知4种算法得到设计参数值均满足上、下限约束;终端约束误差方面,ISSA算法得到的终端速度、高度误差最小,本文提出的ISSA算法得到的目标函数值为最优,说明了本文算法的寻优能力更强。
| 表 4 4种算法优化结果比较 Tab. 4 Results comparation of the four algorithms |
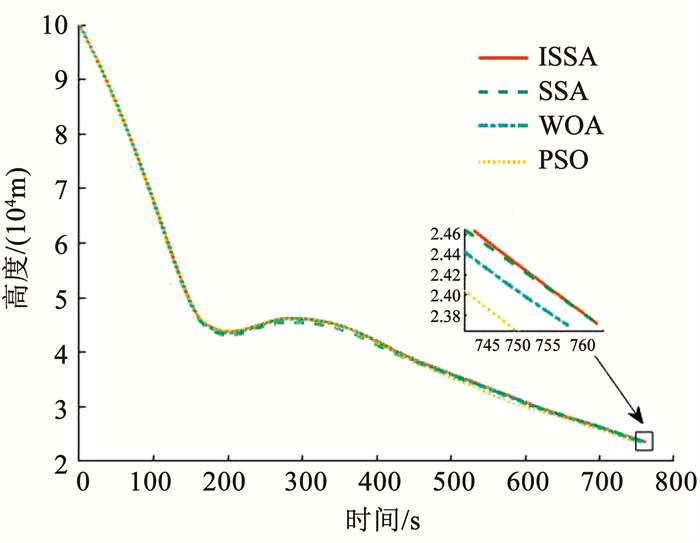
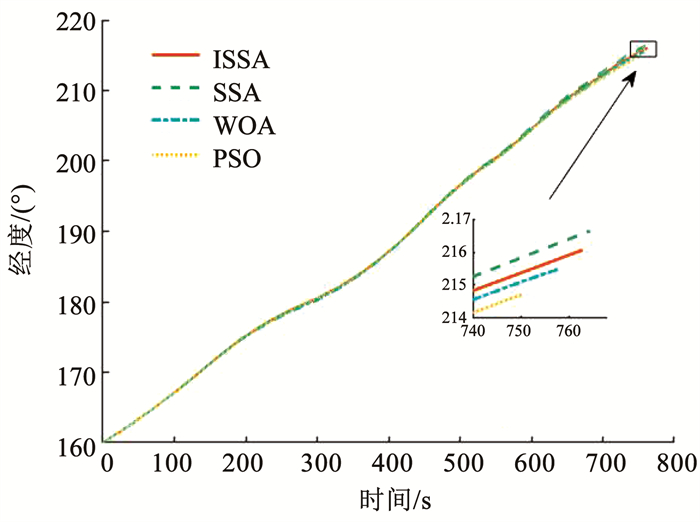
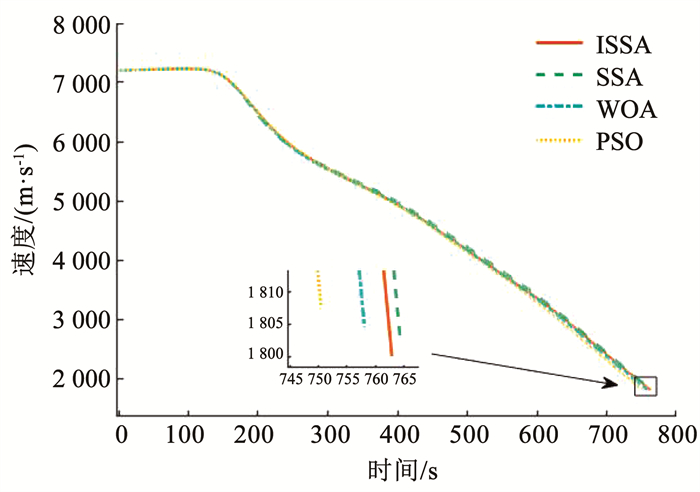
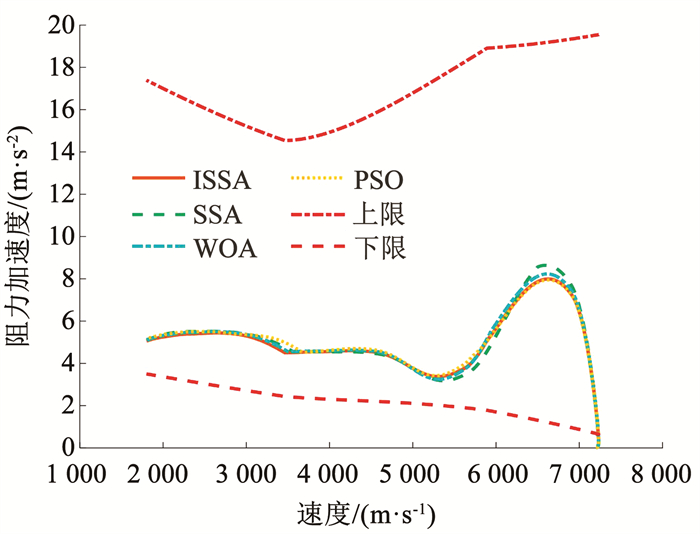
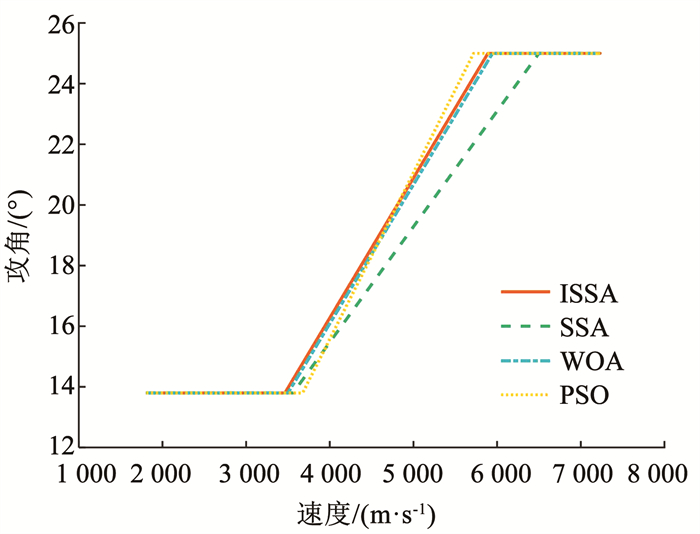
图 11~14分别展示了对比算法得到高度、经度、纬度和速度的变化,各优化算法得到的状态量及再入轨迹的变化趋势基本一致。图 11可知,ISSA算法的满足高度终端约束误差最小;由图 14可知,ISSA算法得到的轨迹终端速度误差最小,实际上,这也是仿真实验设置的目标函数,即本文提出的算法所得目标函数值最小。由图 15可知,4种方法所得动压、热流率和过载在整个飞行过程中,都能够小于本文仿真实验设置的路径约束上限,满足路径约束,本文提出的基于ISSA再入轨迹优化方法得到的过载,在整个飞行过程相较较小。与之对应的图 16,展示了4种算法得到轨迹满足阻力加速度-速度再入走廊情况,进入再入走廊,即满足路径约束和准平衡滑翔条件,是本文轨迹优化求解的一个必要条件,图 16可以看出,所提方法得到的轨迹都能顺利进入再入走廊,即能很好的满足路径约束,因此本文采用的再入走廊方法解决路径约束问题是十分有效的。图 17~18分别展现了4种算法得到的攻角和倾侧角随速度的变化对比。由图 17可知,每种算法优化得到的V1和V2值是不同的。由图 18可得,本文提出的基于ISSA的高超声速再入轨迹优化算法得到的倾侧角翻转次数较SSA和WOA方法少,对实际飞行控制量变化中具有一定的参考价值。
|
图 11 高度随时间变化 Fig. 11 Time histories of the altitude |
|
图 12 经度随时间变化 Fig. 12 Time histories of the longitude |

|
图 13 纬度随时间变化 Fig. 13 Time histories of the latitude |
|
图 14 速度随时间变化 Fig. 14 Time histories of the velocity |

|
图 15 路径约束变化 Fig. 15 Time histories of the path constraints |
|
图 16 阻力加速度再入走廊 Fig. 16 Resistance acceleration reentry corridor |
|
图 17 攻角随速度变化 Fig. 17 Velocity histories of the AOA |

|
图 18 倾侧角随速度变化 Fig. 18 Velocity histories of the bank angle |
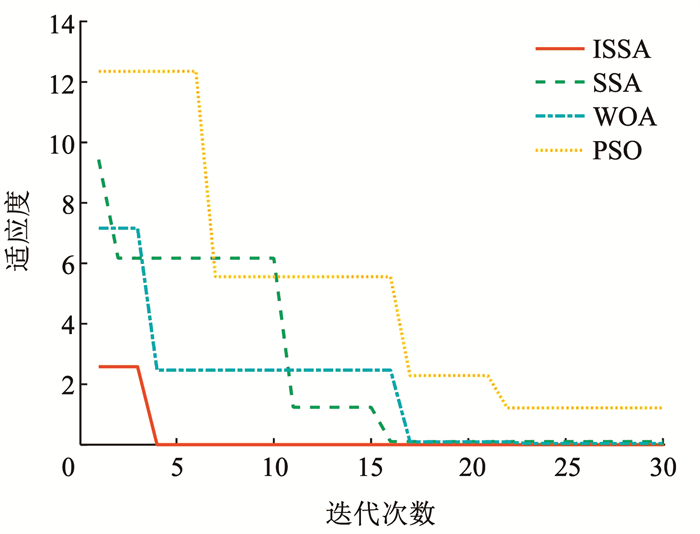
图 19展现了4种算法在求解高超再入轨迹优化问题是的收敛效率比较。本文提出的基于ISSA算法在迭代4次后即可达到收敛,平均每代计算时间约为1.542 s,收敛效率相较其他对比算法具有明显优势。
|
图 19 算法收敛效率比较 Fig. 19 Comparison of algorithms curves |
为考察本文提出的基于ISSA高超声速滑翔飞行器再入轨迹优化方法的鲁棒性能,在初始状态存在扰动情况下进行蒙特卡洛仿真实验。设置服从正态分布的扰动因素见表 5,终端条件及其他参数设置同多种算法对比实验,并进行200次的蒙特卡洛仿真。
| 表 5 蒙特卡洛仿真扰动因素设置 Tab. 5 Disturbances in the Monte Carlo |
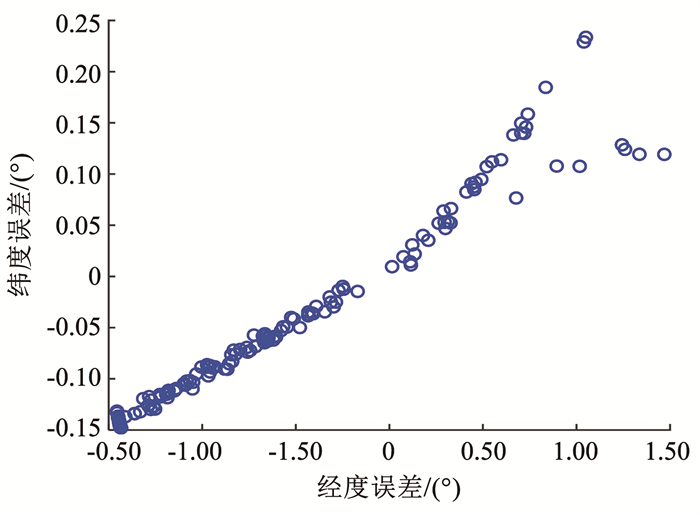
图 20展现了200次的蒙特卡洛仿真实验得到的速度随时间变化的规律,可以看出在6个状态量的初始值都进行不同程度的扰动下,本文提出的改进算法得到的终端速度皆在1 800 m/s左右,200次打靶实验终端速度误差平均值为0.443 9 m/s。图 21可知200次蒙特卡洛实验倾侧角的变化规律能够基本保持一致。图 22展现本文算法得到的终端位置,经度误差不超过±1.50°,纬度误差不超过±0.25°,落点较为集中。

|
图 20 速度随时间变化 Fig. 20 Time histories of the speed |

|
图 21 倾侧角随速度变化 Fig. 21 Velocity histories of the bank angle |
|
图 22 蒙特卡洛实验落点分布 Fig. 22 Monte Carlo drop point distribution |
综上所述,本文提出的基于ISSA的高超声速飞行器再入轨迹优化算法具有一定的鲁棒性。采用本文方法进行初始条件扰动情况下的仿真实验结果,能够为后续再入任务的设置提供一定的借鉴意义。
5 结论1) 本文将高超声速滑翔再入飞行器轨迹优化问题转化为控制量剖面参数化设计问题,采用ISSA算法对控制量剖面进行优化,仿真结果表明本文方法得到优化轨迹精度较高,相比于SSA、WOA和PSO算法,目标函数优化质量有了较大提高。
2) 再入轨迹优化任务仿真实验表明,本文算法得到的倾侧角剖面,反转次数与SSA和WOA方法相比较少,对HGV的工业设计具有一定参考意义。
3) 蒙特卡洛仿真实验结果表明,本文提出的基于ISSA的RTO算法具有较好的鲁棒性。
4) 本文算法能够在高超声速滑翔飞行器执行任务时提供一个安全且可靠的飞行轨迹,进一步地,可研究将ISSA算法应用到考虑禁飞区约束的高超声速滑翔飞行器制导问题。
| [1] |
穆凌霞, 王新民, 谢蓉, 等. 高超音速飞行器及其制导控制技术综述[J]. 哈尔滨工业大学学报, 2019, 51(3): 1. MU Linxia, WANG Xinmin, XIE Rong, et al. A survey of the hypersonic flight vehicle and its guidance and control technology[J]. Journal of Harbin Institute of Technology, 2019, 51(3): 1. DOI:10.11918/j.issn.0367-6234.201810036 |
| [2] |
张远龙, 谢愈. 滑翔飞行器弹道规划与制导方法综述[J]. 航空学报, 2020, 41(1): 023377. ZHANG Yuanlong, XIE Yu. Review of trajectory planning and guidance methods for gliding vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(1): 023377. DOI:10.7527/S10006-893.2019.23377 |
| [3] |
田栢苓, 李智禹, 吴思元, 等. 可重复使用运载器再入轨迹与制导控制方法综述[J]. 航空学报, 2020, 41(11): 624072. TIAN Bailing, LI Zhiyu, WU Siyuan, et al. Reentry trajectory optimization, guidance and control methods for reusable launch vehicles: Review[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(11): 624072. DOI:10.7527/S10006893.2020.24072 |
| [4] |
黄长强, 国海峰, 丁达理. 高超声速滑翔飞行器轨迹优化与制导综述[J]. 宇航学报, 2014, 35(4): 369. HUANG Changqiang, GUO Haifeng, DING Dali. A survey of trajectory optimization and guidance for hypersonic gliding vehicle[J]. Journal of Astronautics, 2014, 35(4): 369. DOI:10.3873/j.issn.1000-1328.2014.04.001 |
| [5] |
刘思源, 梁子璇, 任章, 等. 高超声速滑翔飞行器再入段制导方法综述[J]. 中国空间科学技术, 2016, 36(6): 1. LIU Siyuan, LIANG Zixuan, REN Zhang, et al. Review of reentry guidance methods for hyper sonic gliding vehicles[J]. Chinese Space Science and Technology, 2016, 36(6): 1. DOI:10.16708/j.cnki.1000-758X.2016.0066 |
| [6] |
李俊, 江振宇. 一种高超声速滑翔再入在线轨迹规划算法[J]. 北京航空航天大学学报, 2020, 46(3): 579. LI Jun, JIANG Zhenyu. Online trajectory planning algorithm for hypersonic glide re-entry problem[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(3): 579. DOI:10.13700/j.bh.1001-5965.2019.0262 |
| [7] |
宗群, 李智禹, 叶林奇, 等. 变信赖域序列凸规划RLV再入轨迹在线重构[J]. 哈尔滨工业大学学报, 2020, 52(3): 147. ZONG Qun, LI Zhiyu, YE Linqi, et al. Variable trust region sequential convex programming for RLV online reentry trajectory reconstruction[J]. Journal Harbin Institute of Technology, 2020, 52(3): 147. DOI:10.11918/201904253 |
| [8] |
高长生, 陈尔康, 荆武兴. 高超声速飞行器机动规避轨迹优化[J]. 哈尔滨工业大学学报, 2017, 49(4): 16. GAO Changsheng, CHEN Erkang, JING Wuxing. Maneuver evasion trajectory optimization for hypersonic vehicles[J]. Journal od Harbin Institute of Technology, 2017, 49(4): 16. DOI:10.11918/j.issn.0367-6234.201605015 |
| [9] |
宫梓丰, 刘刚, 宋睿, 等. 考虑禁飞区的高超声速飞行器再入跟踪控制[J]. 国防科技大学学报, 2020, 42(1): 66. GONG Zifeng, LIU Gang, SONG Rui, et al. Reentry tracking control of hypersonic vehicle with fly zone constraints[J]. Journal of National University of Defense Technology, 2020, 42(1): 66. DOI:10.11887/j.cn.202001010 |
| [10] |
高杨, 蔡光斌, 张胜修, 等. 多禁飞区高超声速滑翔飞行器再入机动制导[J]. 兵器装备工程学报, 2019, 40(8): 32. GAO Yang, CAI Guangbin, ZHANG Shengxiu, et al. Reentry maneuver guidance for hypersonic glide vehicles under multiple no-fly zones[J]. Journal of Ordnance Equipment Engineering, 2019, 40(8): 32. DOI:10.11809/bqzbgcxb2019.08.008 |
| [11] |
杨希祥, 杨慧欣, 王鹏. 伪谱法及其在飞行器制导设计领域的应用综述[J]. 国防科技大学学报, 2015, 37(4): 1. YANG Xixiang, YANG Huixin, WANG Peng. Overview of pseudo-spectral method and its application in trajectory optimum design for flight vehicles[J]. Journal of National University of Defense Technology, 2015, 37(4): 1. DOI:10.11887/j.cn.201504001 |
| [12] |
ZHAO Jiang, ZHOU Rui. Reentry trajectory optimization for hypersonic vehicle satisfying complex constraints[J]. Chinese Journal of Aeronautics, 2013, 26(6): 1544. DOI:10.1016/j.cja.2013.10.009 |
| [13] |
任鹏飞, 王洪波, 周国峰. 基于自适应伪谱法的高超声速飞行器再入轨迹优化[J]. 北京航空航天大学学报, 2019, 45(11): 2257. REN Pengfei, WANG Hongbo, ZHOU Guofeng. Reentry trajectory optimization for hypersonic vehicle based on adaptive pseudospectral method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(11): 2257. DOI:10.13700/j.bh.1001-5965.2019.0165 |
| [14] |
梅映雪, 冯玥, 王容顺, 等. 高超声速飞行器多约束再入轨迹快速优化[J]. 宇航学报, 2019, 40(7): 758. MEI Yingxue, FENG Yue, WANG Rongshun, et al. Fast optimization of reentry trajectory for hypersonic vehicles with multiple constraints[J]. Journal of Astronautics, 2019, 40(7): 758. DOI:10.3873/j.issn.1000-1328.2019.07.004 |
| [15] |
李宪强, 马戎, 张伸, 等. 蚁群算法的改进设计及在航迹规划中的应用[J]. 航空学报, 2020, 41(增刊2): 724381. LI Xianqiang, MA Rong, ZHANG Shen, et al. Improved design of ant colony algorithm and its application in path planning[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(Sup.2): 724381. DOI:10.7527/S10006893.2020.24381 |
| [16] |
徐慧, 蔡光斌, 穆朝絮, 等. 高超声速滑翔飞行器全程总红外辐射最小的轨迹优化[J]. 红外与激光工程, 2022, 51(4): 20220194-1. XU Hui, CAI Guangbin, MU Chaoxu, et al. Trajectory optimization of hypersonic glide vehicle with minimum total infrared radiation[J]. Infrared and Laser Engineering, 2022, 51(4): 20220194-1. DOI:10.37881/IRLA.20220194 |
| [17] |
余跃, 王宏伦. 一种高超声速飞行器再入轨迹优化方法[J]. 宇航学报, 2020, 41(7): 926. YU Yue, WANG Honglun. A reentry trajectory optimization method for hypersonic vehicles[J]. Journal of Astronautics, 2020, 41(7): 926. DOI:10.3873/j.issn.1000-1328.2020.07.011 |
| [18] |
ZHAO Jiang, ZHOU Rui. Particle swarm optimization applied to hypersonic reentry trajectories[J]. Chinese Journal of Aeronautics, 2015, 28(3): 822. DOI:10.1016/j.cja.2015.04.007 |
| [19] |
ZHOU Hongyu, WANG Xiaogang, BAI Bing, et al. Reentry guidance with constrained impact for hypersonic weapon by novel particle swarm optimization[J]. Aerospace Science and Technology, 2018, 78: 205. DOI:10.1016/j.ast.2018.04.024 |
| [20] |
周宏宇, 王小刚, 赵亚丽, 等. 空天飞行器返回滑翔段在线制导方法[J]. 宇航学报, 2021, 42(2): 175. ZHOU Hongyu, WANG Xiaogang, ZHAO Yali, et al. Online guidance for aerospace vehicle in return-gliding phase[J]. Journal of Astronautics, 2021, 42(2): 175. DOI:10.3873/j.issn.1000-1328.2021.02.005 |
| [21] |
周宏宇, 王小刚, 单永志, 等. 基于改进粒子群算法的飞行器协同轨迹规划[J]. 自动化学报, 2022, 48(11): 2670. ZHONG Hongyu, WANG Xiaogang, SHAN Yonghzi, et al. Synergistic path planning for multiple vehicles based on an improved particle swarm optimization method[J]. Acta Automatica Sinica, 2022, 48(11): 2670. DOI:10.16383/j.aas.c190865 |
| [22] |
LI Zhenhua, HU Chen, DING Chibiao, et al. Stochastic gradient particle swarm optimization based entry trajectory rapid planning for hypersonic glide vehicles[J]. Aerospace Science and Technology, 2018, 76: 176. DOI:10.1016/j.ast.2018.01.033 |
| [23] |
SANA K S, HU Weiduo. Hypersonic reentry trajectory planning by using hybrid fractional-order particle swarm optimization and gravitational search algorithm[J]. Chinese Journal of Aeronautics, 2021, 34(1): 50. DOI:10.1016/j.cja.2020.09.039 |
| [24] |
XUE Jiankai, SHEN Bo. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22. DOI:10.1080/21642583.2019.1708830 |
| [25] |
汤安迪, 韩统, 徐登武, 等. 基于混沌麻雀搜索算法的无人机航迹规划方法[J]. 计算机应用, 2021, 41(7): 2128. TANG Andi, HAN Tong, XU Dengwu, et al. Path planning method of unmanned aerial vehicle based on chaos sparrow search algorithm[J]. Journal of Computer Applications, 2021, 41(7): 2128. DOI:10.11772/j.issn.1001-9081.2020091513 |
| [26] |
高杨, 蔡光斌, 徐慧, 等. 虚拟多触角探测的高超声速滑翔飞行器再入机动制导[J]. 航空学报, 2021, 41(11): 623703. GAO Yang, CAI Guangbin, XU Hui, et al. Reentry maneuver guidance of hypersonic glide vehicle under virtual multi-tentacle detection[J]. Acta Aeronautica et Astronautica Sinica, 2021, 41(11): 623703. DOI:10.7527/S1000-6893.2019.23703 |
| [27] |
王肖, 郭杰, 唐胜景, 等. 基于准平衡滑翔的解析再入制导方法[J]. 兵工学报, 2019, 40(1): 61. WANG Xiao, GUO Jie, TANG Shengjing, et al. Analytical reentry guidance method based on quasi-equilibrium glide[J]. Acta armamentaria, 2019, 40(1): 61. DOI:10.3969/j.issn.1000-1093.2019.01.008 |
| [28] |
章吉力, 刘凯, 樊雅卓, 等. 考虑禁飞区规避的空天飞行器分段预测校正再入制导方法[J]. 宇航学报, 2021, 42(1): 122. ZHANG Jili, LIU Kai, FAN Yazhuo, et al. A piecewise predictor-corrector reentry guidance algorithm with no-fly zone avoidance[J]. Journal of Astronautics, 2021, 42(1): 122. DOI:10.3873/j.issn.1000-1328.2021.01.013 |
| [29] |
徐慧, 蔡光斌, 张胜修. 高超声速滑翔飞行器再入气动系数改进拟合模型[J]. 宇航学报, 2021, 42(9): 1139. XU Hui, CAI Guangbin, ZHANG Shengxiu. Modified aerodynamic coefficient fitting models of hypersonic gliding vehicle in reentry phase[J]. Journal of Astronautics, 2021, 42(9): 1139. DOI:10.3873/j.issn.1000-1328.2021.09.009 |
 2023, Vol. 55
2023, Vol. 55


